Иррациональность в знаменателе дроби
Если дробь содержит корень в знаменателе, то мы говорим об иррациональности в знаменателе дроби. Часто бывает необходимо освободиться от иррациональности в знаменателе дроби. То есть заменить исходную дробь, содержащую иррациональность в знаменателе на тождественно равную ей дробь, которая иррациональность не содержит. Как это сделать?
Общее правило такое: нужно числитель и знаменатель дроби умножить на выражение, сопряженное знаменателю дроби.
Выражение А называется сопряженным иррациональному выражению В, если произведение АВ не содержит знака корня, то есть произведение АВ является рациональным числом.
Рассмотрим примеры сопряженных выражений.
1. Иррациональное выражение В содержит квадратный корень.
Возможны два случая:
a) . В этом случае :
Например, чтобы исключить иррациональность из знаменателя в дроби , нужно числитель и знаменатель дроби умножить на , получим
Внимание! Обязательно умножаем на выражение, сопряженное знаменателю и числитель, и знаменатель дроби — только в этом случае мы получим дробь, тождественно равную исходной.
б) ,
В этом случае сопряженным выражением будет дополняющее до разности квадратов:
Для выражения сопряженным будет :
Соответственно, для выражения сопряженным будет :
Например, исключим иррациональность из знаменателя дроби
Для этого умножим числитель и знаменатель дроби на выражение, сопряженное знаменателю, то есть на
Получим:
2. Иррациональное выражение В содержит корень n-й степени:
В этом случае сопряженное выражение :
Пример: исключим иррациональность из знаменателя дроби
Умножим числитель и знаменатель дроби на выражение . Получим:
3. Иррациональное выражение В является одним из множителей в разложении на множители разности или суммы кубов. В этом случае сопряженным ему выражением будет второй множитель:
Исключим иррациональность из знаменателя дроби:
Рассмотрим пример упрощения выражения, содержащего иррациональность в знаменателе дроби.
Найти значение выражения:
Внимание! Если нужно упростить выражение, содержащее иррациональность в знаменателе, то первым делом исключаем иррациональность из знаменателя, даже если кажется, что без этого можно обойтись.
Итак, исключим иррациональность из знаменателя первой и второй дроби:
Подставим полученные выражения в исходное:
Итак,
И.В. Фельдман, репетитор по математике.
ege-ok.ru
Как освободиться от иррациональности в знаменателе: способы, примеры, решения
При изучении преобразований иррационального выражения очень важным является вопрос о том, как освободиться от иррациональности в знаменателе дроби. Целью этой статьи является объяснение этого действия на конкретных примерах задач. В первом пункте мы рассмотрим основные правила данного преобразования, а во втором – характерные примеры с подробными пояснениями.
Понятие освобождения от иррациональности в знаменателе
Начнем с пояснения, в чем вообще заключается смысл такого преобразования. Для этого вспомним следующие положения.
Об иррациональности в знаменателе дроби можно говорить в том случае, если там присутствует радикал, он же знак корня. Числа, которые записаны при помощи такого знака, часто относятся к числу иррациональных. Примерами могут быть 12, -2x+3, x+yx-2·x·y+1, 117-5 . К дробям с иррациональными знаменателями также относятся те, что имеют там знаки корней различной степени (квадратный, кубический и т.д.), например, 343, 1x+x·y4+y. Избавляться от иррациональности следует для упрощения выражения и облегчения дальнейших вычислений. Сформулируем основное определение:
Определение 1Освободиться от иррациональности в знаменателе дроби – значит преобразовать ее, заменив на тождественно равную дробь, в знаменателе которой не содержится корней и степеней.
Такое действие может называться освобождением или избавлением от иррациональности, смысл при этом остается тем же. Так, переход от 12 к 22 , т.е. к дроби с равным значением без знака корня в знаменателе и будет нужным нам действием. Приведем еще один пример: у нас есть дробь xx-y . Проведем необходимые преобразования и получим тождественно равную ей дробь x·x+yx-y, освободившись от иррациональности в знаменателе.
После формулировки определения мы можем переходить непосредственно к изучению последовательности действий, которые нужно выполнить для такого преобразования.
Основные действия для избавления от иррациональности в знаменателе дроби
Для освобождения от корней нужно провести два последовательных преобразования дроби: умножить обе части дроби на число, отл
zaochnik.com
Иррациональность в знаменателе дроби | Ластики.ру
Суть метода состоит в умножении и делении дроби на такое выражение, которое позволит исключить иррациональность (квадратные и кубические корни) из знаменателя и сделает его проще. После этого дроби проще привести к общему знаменателю и окончательно упростить исходное выражение.
Дробь можно освободить от иррациональности (от иррационального выражения) в в знаменателе, например, так:
Чтобы освободить дробь от иррациональности в числителе или в знаменателе, можно применять формулы сокращенного умножения, которые применительно к корням имеют вид:
Выражения
и
называются взаимно сопряженными выражениями. Их произведение равно разности подкоренных выражений:
Пример.
Освободить дроби от иррациональности в знаменателе:Решение.
Ответ:
Г) Избавьтесь от иррациональности в знаменателе (ЕГЭ)
Решение основано на основном свойстве дроби, позволяющим умножать числитель и знаменатель дроби на одно и то же, не равное нулю число. Чтобы избавиться от знаков радикала в знаменателе дроби, обычно используют ФСУ (формулы сокращенного умножения). Ведь если разность двух радикалов умножить на их сумму, то получится разность квадратов корней, т.е. получится выражение без знаков радикалов.
Д) Освободиться от иррациональности в знаменателе дроби:
Решение:
Помните: в математике главное – тренировка. Чем больше примеров Вы решаете, тем лучше Вы это делаете.
Ластики.ру желают Вам отличной учебы!
lastici.ru
Как в дроби избавиться от иррациональности в знаменателе
Автор КакПросто!
Существует несколько типов иррациональности дроби в знаменателе. Она связана с присутствием в нем алгебраического корня одной или различных степеней. Чтобы избавиться от иррациональности, нужно выполнить определенные математические действия в зависимости от ситуации.
Статьи по теме:
Инструкция
Прежде чем избавиться от иррациональности дроби в знаменателе, следует определить ее тип, и в зависимости от этого продолжать решение. И хотя любая иррациональность следует из простого присутствия корней, различные их комбинации и степени предполагают разные алгоритмы. Квадратный корень в знаменателе, выражение вида a/√bВведите дополнительный множитель, равный √b. Чтобы дробь не изменилась, умножать нужно и числитель, и знаменатель:a/√b → (a•√b)/b.Пример 1: 10/√3 → (10•√3)/3.Наличие под чертой дроби корня дробной степени вида m/n, причем n>mЭто выражение выглядит следующим образом:a/√(b^m/n).
Избавьтесь от подобной иррациональности также путем ввода множителя, на этот раз более сложного: b^(n-m)/n, т.е. из показателя степени самого корня нужно вычесть степень выражения под его знаком. Тогда в знаменателе останется только первая степень:a/(b^m/n) → a•√(b^(n-m)/n)/b.Пример 2: 5/(4^3/5) → 5•√(4^2/5)/4 = 5•√(16^1/5)/4.
Сумма квадратных корнейУмножьте обе составляющих дроби на аналогичную разность. Тогда из иррационального сложения корней знаменатель преобразуется в разность выражений/чисел под знаком корня:a/(√b + √c) → a•(√b — √c)/(b — c).Пример 3: 9/(√13 + √23) → 9•(√13 — √23)/(13 — 23) = 9•(√23 — √13)/10.Сумма/разность кубических корнейВыберите в качестве дополнительного множителя неполный квадрат разности, если в знаменателе стоит сумма, и соответственно неполный квадрат суммы для разности корней:a/(∛b ± ∛c) → a•(∛b² ∓ ∛(b•c) + ∛c²)/ ((∛b ± ∛c)• ∛b² ∓ ∛(b•c) + ∛c²) →a•(∛b² ∓ ∛(b•c) + ∛c²)/(b ± c).Пример 4: 7/(∛5 + ∛4) → 7•(∛25- ∛20 + ∛16)/9.
Если в задаче присутствует и квадратный и кубический корень, тогда разделите решение на два этапа: последовательно выведите из знаменателя квадратный корень, а затем кубический. Делается это по уже известным вам методам: в первом действии нужно выбрать множитель разности/суммы корней, во втором – неполный квадрат суммы/разности.
Видео по теме
Источники:
- как избавиться от иррациональности в дроби
Совет полезен?
Статьи по теме:
Не получили ответ на свой вопрос?
Спросите нашего эксперта:
www.kakprosto.ru
3. Разложение действительного иррационального числа в правильную бес
В предыдущей главе мы рассмотрели, как в процессе последовательного выделения целой части и перевертывания дробной рациональная дробь разлагается в конечную непрерывную дробь.
=() (1)
И, наоборот, свертывание такой непрерывной дроби приводит к рациональной дроби.
Процесс выделения целой части и перевертывания дробной можно применить к любому действительному числу.
Для иррационального числа указанный процесс должен быть бесконечным, так как конечная цепная дробь равна рациональному числу.
Выражение (где , ) (2)
Возникающее в таком процессе или заданное формально, мы будем называть правильной бесконечной цепной, или непрерывной дробью, или дробью бесконечной длины и обозначать кратко через (), а числа – ее элементами или неполными частными.
Отметим, что разложение возможно только в единственном виде, так как процесс выделения целой части – процесс однозначный.
Рассмотрим пример разложения иррационального числа .
Пусть . Выделим из его целую часть. =3, а дробную часть –3, которая меньше 1, представим в виде , где .
Повторяя операцию выделения целой части и перевертывания дробной, мы получаем:
;
;
.
Если остановиться на этом шаге, то можно записать:
С другой стороны, из формулы для видно, что =3+. Поэтому , вследствие чего, начиная с этого момента, неполные частные станут повторяться.
Бесконечная непрерывная дробь, в которой определенная последовательность неполных частных, начиная с некоторого места, периодически повторяется, называется периодической непрерывной дробью.
Если, в частности, периодическое повторение начинается с первого звена, то цепная дробь называется чисто периодической, в противном случае – смешанной периодической.
Чисто периодическая дробь записывается в виде , а смешанная периодическая в виде .
Итак, разлагается в смешанную периодическую дробь (3, 3, 6, 3, 6, …) или (3, (3, 6)).
В общем случае разложения действительного иррационального числа поступаем так же, как в примере. Останавливаясь при этом в процессе выделения целой части после k–го шага, будем иметь:
Так что
.
Числа называются остаточными числами порядка k разложения . В формуле (4) имеем кусок разложения до остаточного числа .
Для бесконечной цепной дроби (2) можно построить бесконечную последовательность конечных непрерывных дробей.
Эти дроби называют подходящими дробями. Закон образования соответствующих им простых дробей будет такой же, как и для подходящих дробей в случае конечных непрерывных дробей, так как этот закон зависит только от неполных частных и совершенно не зависит от того, является ли последним элементом или за ним следует еще элемент . Поэтому для них сохранятся также остальные свойства, которые выводятся из закона образования числителей и знаменателей подходящих дробей.
В частности, мы имеем:
1) , причем ;
2) , откуда следует несократимость подходящих дробей ;
3) .
Сравним теперь подходящую дробь и кусок разложения до остаточного числа . Имеем
,
Откуда видно, что вычисление по формально производится таким же образом, как вычисление по с тем лишь отличием, что в первом случае заменяется на , а во втором заменяется на . Поэтому на основании формулы можно сделать вывод о справедливости следующего важного соотношения
. (5)
По этой причине мы пишем также , хотя не является здесь целым положительным числом.
При помощи формулы (5) можно вывести следующую теорему и расположении подходящих дробей разложения .
Теорема. Действительное число всегда находится между двумя соседними подходящими дробями своего разложения, причем оно ближе к последующей, чем к предыдущей подходящей дроби.
Д о к а з а т е л ь с т в о: Из формулы (5) следует
Но , , так что
1) () и () имеют одинаковый знак, а это значит, что находится между и ;
2) , то есть ближе к , чем к .
Так как , то , и так далее; отсюда приходим к следующему заключению о взаимном расположении подходящих дробей:
1) больше всех подходящих дробей нечетного порядка и меньше всех подходящих дробей четного порядка;
2) подходящие дроби нечетного порядка образуют возрастающую последовательность, а четного порядка – убывающую (в случае иррационального
указанные последовательности являются бесконечными), то есть
(в случае рационального ).
———————————————————
Учитывая то, что при , вследствие чего , переходим к дальнейшему выводу, что в случае иррационального сегменты , , … образуют стягивающуюся последовательность, которая, как известно, должна иметь единственную общую точку, являющуюся общим пределом последовательностей , , … и , , … . Но так как принадлежит всем сегментам последовательности, то и совпадает с указанной точкой, так что .
Итак, мы имеем следующий важный результат:
Бесконечная последовательность подходящих дробей , которая возникает при разложении иррационального , сходится к , колеблясь около него. Или: иррациональное действительное равно пределу последовательности подходящих дробей своего разложения в бесконечную непрерывную дробь (процессом выделения целой части).
| < Предыдущая | Следующая > |
|---|
matica.org.ua
Как в дроби избавиться от иррациональности в знаменателе
Существует несколько типов иррациональности дроби в знаменателе. Она связана с присутствием в нем алгебраического корня одной либо разных степеней. Дабы избавиться от иррациональности , необходимо исполнить определенные математические действия в зависимости от обстановки.
Инструкция
1. Раньше чем избавиться от иррациональности дроби в знаменателе, следует определить ее тип, и в зависимости от этого продолжать решение. И правда любая иррациональность следует из простого присутствия корней, разные их комбинации и степени полагают различные алгорифмы.
2. Квадратный корень в знаменателе, выражение вида a/?bВведите добавочный множитель, равный ?b. Дабы дробь не изменилась, умножать необходимо и числитель, и знаменатель:a/?b ? (a•?b)/b.Пример 1: 10/?3 ? (10•?3)/3.
3. Присутствие под чертой дроби корня дробной степени вида m/n, причем n>mЭто выражение выглядит дальнейшим образом:a/?(b^m/n).
4. Избавьтесь от сходственной иррациональности также путем ввода множителя, на данный раз больше трудного: b^(n-m)/n, т.е. из показателя степени самого корня необходимо вычесть степень выражения под его знаком. Тогда в знаменателе останется только первая степень:a/(b^m/n) ? a•?(b^(n-m)/n)/b.Пример 2: 5/(4^3/5) ? 5•?(4^2/5)/4 = 5•?(16^1/5)/4.
5. Сумма квадратных корнейУмножьте обе составляющих дроби на аналогичную разность. Тогда из иррационального сложения корней знаменатель преобразуется в разность выражений/чисел под знаком корня:a/(?b + ?c) ? a•(?b – ?c)/(b – c).Пример 3: 9/(?13 + ?23) ? 9•(?13 – ?23)/(13 – 23) = 9•(?23 – ?13)/10.
6. Сумма/разность кубических корнейВыберите в качестве добавочного множителя неполный квадрат разности, если в знаменателе стоит сумма, и соответственно неполный квадрат суммы для разности корней:a/(?b ± ?c) ? a•(?b? ? ?(b•c) + ?c?)/ ((?b ± ?c)• ?b? ? ?(b•c) + ?c?) ?a•(?b? ? ?(b•c) + ?c?)/(b ± c).Пример 4: 7/(?5 + ?4) ? 7•(?25- ?20 + ?16)/9.
7. Если в задаче присутствует и квадратный и кубический корень, тогда поделите решение на два этапа: ступенчато выведите из знаменателя квадратный корень, а после этого кубический. Делается это по теснее знаменитым вам способам: в первом действии необходимо предпочесть множитель разности/суммы корней, во втором – неполный квадрат суммы/разности.
Правильная запись дробного числа не содержит иррациональности в знаменателе . Такая запись и легче понимается на вид, следственно при возникновении иррациональности в знаменателе умно от нее избавиться. В этом случае иррациональность может перейти в числитель.

Инструкция
1. Для начала дозволено разглядеть примитивный пример – 1/sqrt(2). Квадратный корень из 2-х – иррациональное число в знаменателе .В этом случае нужно домножить числитель и знаменатель дроби на ее знаменатель. Это обеспечит разумное число в знаменателе . Подлинно, sqrt(2)*sqrt(2) = sqrt(4) = 2. Умножение 2-х идентичных квадратных корней друг на друга даст в результате то, что находится под всем из корней: в данном случае – двойку.В результате: 1/sqrt(2) = (1*sqrt(2))/(sqrt(2)*sqrt(2)) = sqrt(2)/2. Данный алгорифм подходит также к дробям, в знаменателе которых корень умножается на разумное число. Числитель и знаменатель в этом случае надобно умножить на корень, находящийся в знаменателе .Пример: 1/(2*sqrt(3)) = (1*sqrt(3))/(2*sqrt(3)*sqrt(3)) = sqrt(3)/(2*3) = sqrt(3)/6.
2. Безусловно подобно надобно делать, если в знаменателе находится не квадратный корень, а, скажем кубический либо всякий иной степени. Корень в знаменателе необходимо умножать на верно такой же корень, на данный же корень умножать и числитель. Тогда корень перейдет в числитель.
3. В больше трудном случае в знаменателе присутствует сумма либо разность иррационального и разумного числа либо 2-х иррациональных чисел.В случае суммы (разности) 2-х квадратных корней либо квадратного корня и разумного числа дозволено воспользоваться классно знаменитой формулой (x+y)(x-y) = (x^2)-(y^2). Она поможет избавиться от иррациональности в знаменателе . Если в знаменателе разность, то домножать числитель и знаменатель надобно на сумму таких же чисел, если сумма – то на разность. Эта домножаемая сумма либо разность будет именоваться сопряженной к выражению, стоящему в знаменателе .Результат этой схеме отменно виден на примере: 1/(sqrt(2)+1) = (sqrt(2)-1)/(sqrt(2)+1)(sqrt(2)-1) = (sqrt(2)-1)/((sqrt(2)^2)-(1^2)) = (sqrt(2)-1)/(2-1) = sqrt(2)-1.
4. Если в знаменателе присутствует сумма (разность), в которой присутствует корень большей степени, то обстановка становится нетривиальной и освобождение от иррациональности в знаменателе не неизменно допустимо
Дробь состоит из числителя, расположенного сверху линии, и знаменателя, на тот, что он делится, расположенного внизу. Иррациональным именуется число, которое не может быть представлено в виде дроби с целым числом в числителе и естественным в знаменателе . Такими числами являются, скажем, квадратный корень из 2-х либо пи. Традиционно, когда говорят об иррациональности в знаменателе , подразумевается корень.
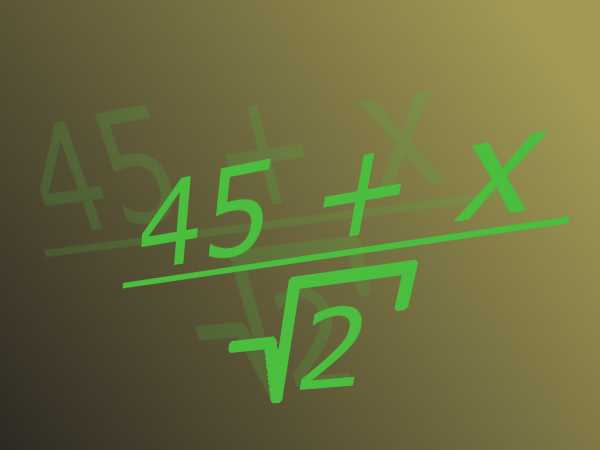
Инструкция
1. Избавьтесь от иррациональности умножением на знаменатель. Таким образом иррациональность будет перенесена в числитель. При умножении числителя и знаменателя на одно и то же число, значение дроби не меняется. Воспользуйтесь этим вариантом, если каждый знаменатель представляет собой корень.
2. Умножьте числитель и знаменатель на знаменатель надобное число раз, в зависимости от корня. Если корень квадратный, то один раз.
3. Разглядите пример с квадратным корнем. Возьмите дробь (56-y)/√(x+2). В ней есть числитель (56-y) и иррациональный знаменатель √(x+2), представляющий собой квадратный корень.
4. Умножьте числитель и знаменатель дроби на знаменатель, то есть на √(x+2). Первоначальный пример (56-y)/√(x+2) превратится в ((56-y)*√(x+2))/(√(x+2)*√(x+2)). В результате получится ((56-y)*√(x+2))/(x+2). Сейчас корень находится в числителе, а в знаменателе нет иррациональности.
5. Не неизменно знаменатель дроби каждый находится под корнем. Избавьтесь от иррациональности, воспользовавшись формулой (x+y)*(x-y)=x²-y².
6. Разглядите пример с дробью (56-y)/(√(x+2)-√y). Ее иррациональный знаменатель содержит разницу 2-х квадратных корней. Дополните знаменатель до формулы (x+y)*(x-y).
7. Умножьте знаменатель на сумму корней. Умножьте на то же самое числитель, дабы значение дроби не изменилось. Дробь примет вид ((56-y)*(√(x+2)+√y))/((√(x+2)-√y)*(√(x+2)+√y)).
8. Воспользуйтесь вышеупомянутым свойством (x+y)*(x-y)=x²-y² и освободите знаменатель от иррациональности. В итоге получится ((56-y)*(√(x+2)+√y))/(x+2-y). Сейчас корень находится в числителе, а знаменатель избавился от иррациональности.
9. В трудных случаях повторяйте оба этих варианта, применяя по необходимости. Учтите, что не неизменно допустимо избавиться от иррациональности в знаменателе .
Алгебраическая дробь — это выражение вида А/В, где буквы А и В обозначают всякие числовые либо буквенные выражения. Нередко числитель и знаменатель в алгебраических дробях имеют массивный вид, но действия с такими дробями следует делать по тем же правилам, что и действия с обычными, где числитель и знаменатель — целые позитивные числа.

Инструкция
1. Если даны смешанные дроби , переведите их в неправильные (дробь, в которой числитель огромнее знаменателя): умножьте знаменатель на целую часть и прибавьте числитель. Так число 2 1/3 превратится в 7/3. Для этого 3 умножают на 2 и прибавляют единицу.
2. Если нужно перевести десятичную дробь в неправильную, то представьте ее как деление числа без запятой на единицу со столькими нулями, сколько чисел стоит позже запятой. Скажем, число 2,5 представьте как 25/10 (если сократить, то получится 5/2), а число 3,61 – как 361/100. Оперировать с неправильными дробями нередко легче, чем со смешанными либо десятичными.
3. Если дроби имеют идентичные знаменатели, а вам нужно их сложить, то примитивно сложите числители; знаменатели остаются без изменений.
4. При необходимости произвести вычитание дробей с идентичными знаменателями из числителя первой дроби вычтите числитель 2-й дроби. Знаменатели при этом также не меняются.
5. Если нужно сложить дроби либо вычесть одну дробь из иной, а они имеют различные знаменатели, приведите дроби к всеобщему знаменателю. Для этого обнаружьте число, которое будет наименьшим всеобщим кратным (НОК) обоим знаменателям либо нескольким, если дробей огромнее 2-х. НОК — это число, которое разделится на знаменатели всех данных дробей. К примеру, для 2 и 5 это число 10.
6. Позже знака «равно» проведите горизонтальную черту и запишите в знаменатель это число (НОК). Проставьте к всему слагаемому добавочные множители — то число, на которое нужно домножить и числитель, и знаменатель, дабы получить НОК. Ступенчато умножайте числители на добавочные множители, сберегая знак сложения либо вычитания.
7. Посчитайте итог, сократите его при необходимости либо выделите целую часть. Для примера – нужно сложить ? и ?. НОК для обеих дробей — 12. Тогда добавочный множитель к первой дроби — 4, ко 2-й — 3. Итого: ?+?=(1·4+1·3)/12=7/12.
8. Если дан пример на умножение, перемножьте между собой числители (это будет числитель итога) и знаменатели (получится знаменатель итога). В этом случае к всеобщему знаменателю их приводить не нужно.
9. Дабы поделить дробь на дробь, нужно опрокинуть вторую дробь «вверх ногами» и перемножить дроби. То есть а/b : с/d = a/b · d/c.
10. Раскладывайте числитель и знаменатель на множители, если это требуется. Скажем, переносите всеобщий множитель за скобку либо раскладывайте по формулам сокращённого умножения, дабы после этого дозволено было при необходимости сократить числитель и знаменатель на НОД – минимальный всеобщий делитель.
Обратите внимание!
Числа складывайте с числами, буквы одного рода с буквами того же рода. Скажем, невозможно сложить 3a и 4b, значит в числителе так и останется их сумма либо разность — 3a±4b.
В быту почаще каждого встречаются не настоящие числа: 1, 2, 3, 4 и т.д. (5 кг. картофеля), а дробные, нецелые числа (5,4 кг лука). Множество из них представлены в виде десятичных дробей. Но десятичную дробь представить в виде дроби довольно легко.
Инструкция
1. Скажем, дано число “0,12”. Если не уменьшать эту десятичную дробь и представить ее так, как есть, то выглядеть она будет так: 12/100 (“двенадцать сотых”). Дабы избавиться от сотни в знаменателе, надобно и числитель, и знаменатель поделить на такое число, которое делит их на целые числа. Это число 4. Тогда, поделив числитель и знаменатель, получается число: 3/25.
2. Если рассматривать больше бытовую обстановку, то зачастую на ценнике у продуктов видно, что вес его составляет, к примеру, 0,478 кг либо пр. Такое число тоже легко представить в виде дроби :478/1000 = 239/500. Дробь эта довольно уродливая, и если бы была вероятность, то эту десятичную дробь дозволено было бы уменьшать и дальше. И все тем же способом: подбора числа, которое делит как числитель, так и знаменатель. Это число именуется наибольшим всеобщим множителем. “Наибольшим” множитель назван потому, что значительно комфортнее и числитель, и знаменатель сразу поделить на 4 (как в первом примере), чем разделять двукратно на 2.
Видео по теме
Десятичная дробь – разновидность дроби , у которой в знаменателе есть “круглое” число: 10, 100, 1000 и т.д., Скажем, дробь 5/10 имеет десятичную запись 0,5. Исходя из этого тезиса, дробь дозволено представить в виде десятичной дроби .

Инструкция
1. Возможен, нужно представить в виде десятичной дробь 18/25.Вначале надобно сделать так, дабы в знаменателе возникло одно из “круглых” чисел: 100, 1000 и т.д. Для этого надобно знаменатель умножить на 4. Но на 4 понадобится умножить и числитель, и знаменатель.
2. Умножив числитель и знаменатель дроби 18/25 на 4, получается 72/100. Записывается эта дробь в десятичном виде так: 0,72.
При делении 2-х десятичных дробей, когда под рукой не оказывается калькулятора, многие испытывают некоторые затруднения. На самом деле здесь нет ничего трудного. Десятичные дроби именуются таковыми, если в их знаменателе число, кратное 10. Как водится, такие числа записываются в одну строчку и имеют запятую, отделяющую дробную часть от целой. Видимо по причине наличия дробной части, которая к тому же отличается числом знаков позже запятой, многим не ясно, как изготавливать без калькулятора математические действия с такими числами.

Вам понадобится
- лист бумаги, карандаш
Инструкция
1. Выходит, для того, дабы поделить одну десятичную дробь на иную, надобно посмотреть на оба числа и определить, у какого из них огромнее знаков позже запятой. Умножаем оба числа на число, кратное 10, т.е. 10, 1000 либо 100000, число нулей в котором равно большему числу знаков позже запятой одного из 2-х наших начальных чисел. Сейчас обе десятичные дроби превратились в обычные целые числа. Берем лист бумаги с карандашом и разделяем два получившихся числа “уголком”. Получаем итог.
2. Скажем, нам надобно поделить число 7,456 на 0,43. Первое число имеет огромнее знаков позже запятой (3 знака), следственно умножаем оба числа не 1000 и получаем два примитивных целых числа: 7456 и 430. Сейчас разделяем “уголком” 7456 на 430 и получаем, что, если 7,456 поделить 0,43 выйдет приблизительно 17,3.
3. Существует еще один метод деления. Записываем десятичные дроби в виде примитивных дробей с числителем и знаменателем, для нашего случая это 7456/1000 и 43/100. Позже этого записываем выражение для деления 2-х примитивных дробей:7456*100/1000*43,после этого уменьшаем десятки, получаем:7456/10*43 = 7456/430В финальном выводе вновь получаем деление 2-х примитивных чисел 7456 и 430, которое дозволено произвести “уголком”.
Видео по теме
Полезный совет
Таким образом, способ деления десятичных дробей заключается к приведению их к целым числам с поддержкой умножения всякого из них на одно и то же число. Выполнение операций с целыми числами, как водится, не вызывает ни у кого сложностей.
Видео по теме
jprosto.ru
