Исследовать функцию и построить график. Решение задач по высшей математике
Схема исследования функции с последующим построением графика такова:
- Исследование области определения функции.
- Исследование функции на четность и нечетность.
- Нахождение точек пересечения графика с осями координат
- Исследование функции на точки разрыва. Нахождение вертикальных асимптот. Нахождение горизонтальных и наклонных асимптот.
- Исследование функции на экстремум и интервалы монотонности функции.
- Исследование функции на интервалы выпуклости и вогнутости графика функции. Нахождение точек перегиба графика функции.
- Построение графика функции.
Условие задачи
Исследовать функцию и построить ее график:
Задали объемную контрольную? Скоро важный зачет/экзамен? Нет времени на выполнение работы или подготовку к зачету/экзамену, но есть деньги? На сайте 100task.ru можно заказать решение или онлайн-помощь на зачете/экзамене
Решение задачи
Исследование области определения функции. Исследование на четность и нечетность и нахождение точек пересечения графика с осями координат
1) Область определения функции:
2)
Функция является четной
3) График функции пересекает ось в точках и . Ось график функции не пересекает.
Исследование функции на точки разрыва и нахождение асимптот
4)
В точке функция не определена
В точке существует разрыв 2-го рода.
Прямая –вертикальная асимптота.
Для нахождения наклонной асимптоты вычисляем пределы:
–горизонтальная асимптота
Исследование функции на экстремум и точки перегиба
5) Исследуем функцию на экстремум. Найдем производную функции.
Первая производная на области определения в нуль не обращается
-функция возрастает
-функция убывает
6) Исследуем функцию на интервалы выпуклости и вогнутости.
Вторая производная функции не равна нулю на всей области определения
–график функции вогнутый
– график функции вогнутый
Построение графика функции
7) График функции имеет вид:
К оглавлению решебника по высшей математике 〉
100task.ru
Исследовать функцию и построить график y=(1/2)x^3+3x^2-7
Задание
.
Решение:
I. область определения функции: множество действительных чисел R.
область значения функции — множество действительных чисел R.
Найдем точки пересечения с осями координат:
А) х=0 =>
(0;-7) -точка пересечения с осью Оy
Б) у=0 => ,
Решим кубическое уравнение вида x3+аx2+bx+c=0
Домножим, наше уравнение на 2, получим
Коэффициенты:
a = 6;
b = 0;
c = -14;
Q | = | ( a 2 — 3b ) | = | ( (6) 2 — 3 × (0)) | = 4 |
| 9 | 9 |
R | = | ( 2a 3 — 9ab + 27c ) | = | ( 2 × (6) 3 — 9 × (6) × (0) + 27 × (-14) ) | = 1 |
54 | 54 |
т. к. R 2 < Q 3 => по методу Виета-Кардано, уравнение имеет три действительных корня
x 1 = -5.545
x 2 = 1.378
x 3 = -1.833
имеем три точки пересечения с осью Ох:
(-5,545; 0), (1,378; 0), (-1,833; 0)
Функция не обладает ни свойством четности, ни свойством нечетности.
Функция не является периодической.
II. найдем интервалы монотонности функции.
Производная
Интервалы монотонности разделяются точками, в которых или не существует. Найдем эти точки:
,
=> x=0 и х=-4
Рассмотрим интервалы и проверим как на них ведет себя функция
| (-∞; -4) | -4 | (-4;0) | 0 | (0; +∞) |
Y’ | + | 0 | — | 0 | + |
| Y | 9 | -7 |
На интервале (-∞; -4) и на (0; +∞) функция возрастает
На интервале (-4;0) функция убывает
III. найдем интервалы выпуклости и вогнутости кривой.
=0, если х=-2
y« (x) < 0 при х (-∞; -2), значит функция выпукла на интервале (-∞; -2)
y« (x) > 0 при х(-2;+∞), значит функция вогнута на интервале (-2;+∞)
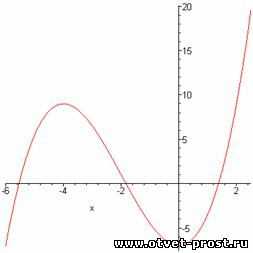
построим график функции:
==========================================
Исследовать функцию и построить график y=(1/2)x^3+3x^2-7
==========================================
2,549 просмотров всего, 4 просмотров сегодня
otvet-prost.ru
Построить график | Исследовать функцию
1) Найти область определения.
Функция определена при всех , кроме x=2.2) Проверить, является ли функция четной, нечетной, периодической.
Функция является ни четной, ни нечетной,непериодической.
3) Найти точки пересечения графика с осями координат, промежутки, где значения функции положительны, отрицательны.
График ее пересекает оси координат в одной точке (0;0). Функция положительна при и отрицательна при х<0.4) Найти точки разрыва функции.
Функция разрывна в точке х=2. Имеет разрыв второго рода: правый и левый пределы в точке х=2 стремятся к бесконечности.
5) Найти асимптоты графика.
Поскольку
прямая х=2 — вертикальная асимптота графика.
Из того, что
6) Вычислить первую производную, найти экстремумы и промежутки ее возрастания и убывания.
Вычисляем первую производную
решаем уравнение
и находим единственную точку экстремума х=6, которая является точкой минимума, y(6)=27/8.
На интервалах функция возрастает, на интервале убывает.7) Вычислить вторую производную функции,найти точки перегиба графика, промежутки выпуклости вверх или вниз.
Вычисляем вторую производную
Отсюда следует, что имеется только одна точка перегиба функции х=0. При x<0 функция выпукла вверх,при 0<x<2 и при х>2 функция выпукла вниз.
8) На основе проведенного исследования строим график функции.
allworks.su
