Карты карно калькулятор онлайн – Построение таблицы истинности онлайн | СКНФ | СДНФ | Полином Жегалкина | Таблица истинности булевой функции онлайн

Карты Карно

Аналитический метод минимизации.

В основе всех методов минимизации лежат три операции:

1. операция склеивания;
2. операция поголощения;
3. операция неполного склеивания.

1. Операция склеивания

   Для осуществления операции склеивания нужно отыскать соседние пары.

  Две конъюнкции (дизъюнкции) являются соседними,если они имеют одинаковую длину  и отличаются знаком инверсии только одной переменной.

  Например:     — одинаковая длина (по три переменные) и отличаются знаком одной переменной.Т.е. 

2. Операция поглощения

  Для осуществления операции поглощения отыскиваются одинаковые переменные, которые включает в себя данные конъюнкции, отличающиеся длиной. Конъюнкция наименьшей длины и включающая в себя одинакове переменные поглощает конъюнкцию большей длины.  

  Например:   — конъюнкция наименьшей длины поглощает конъюнкцию наибольшей длины.  НО! Если , то поглощение не происходит.

 Данные правила поглощеия применимы также и к дизъюнкции.

3. Операция неполного склеивания

  Для осуществления операции неполного склеивания также отыскиваются соседние пары конъюнкций или дизъюнкций. Но в случае неполного склеивания одна конъюнкция (дизъюнкция) может быть соседней несколько раз, т.е. она используется для склеивания с другими конъ

www.sites.google.com

Карты Карно

Карта Карно — графический способ минимизации переключательных (булевых) функций, обеспечивающий относительную простоту работы с большими выражениями. Представляет собой операции попарного неполного склеивания и элементарного поглощения. Карты Карно были изобретены в 1952 Эдвардом В. Вейчем и усовершенствованы в 1953 Морисом Карно, физиком из «Bell Labs», и были призваны помочь упростить цифровые электронные схемы. В карту Карно булевы переменные передаются из таблицы истинности и упорядочиваются с помощью кода Грея, в котором каждое следующее число отличается от предыдущего только одним разрядом.   Карта Карно может быть составлена для любого количества переменных, однако удобно работать при количестве переменных не более пяти. По сути Карта Карно — это таблица истинности составленная в 2-х мерном виде. Благодаря использованию кода Грея в ней верхняя строка является соседней с нижней, а правый столбец соседний с левым, т.о. вся Карта Карно сворачивается в фигуру тор (бублик). На пересечении строки и столбца проставляется соответствующее значение из таблицы истинности. После того как Карта заполнена, можно приступать к минимизации. Если необходимо получить минимальную ДНФ, то в Карте рассматриваем только те клетки которые содержат единицы, если нужна КНФ, то рассматриваем те клетки, которые содержат нули. Алгоритм минимизации по методу карт Карно: 1.Метод Карно основан на представлении исходной функции, заданной в форме СДНФ, в виде карты следующего вида: 2. Объединяем смежные клетки, содержащие единицы, в область так, чтобы одна область содержала  2n ( т.е. 2, 4, 8, и т.д. ) клеток (помним про то, что крайние строки и столбцы являются соседними между собой), в области не должно находиться клеток, содержащих нули, области могут пересекаться, возможно несколько вариантов покрытия. 3. Далее берём первую область и смотрим, какие переменные не меняются в пределах этой области, выписываем конъюнкцию этих переменных; если неменяющаяся переменная нулевая, проставляем над ней инверсию. Берём следующую область, выполняем то же самое, что и для первой, и т. д. для всех областей. 4. Конъюнкции областей объединяем дизъюнкцией. Пример. Методом Карно минимизировать функцию: $$y=f\left ( A,B,C \right )=\bar{A}\bar{B}\bar{C}\vee \bar{A}B\bar{C}\vee A\bar{B}\bar{C}\vee A\bar{B}C$$ Решение. 1.Заданную функцию представим с помощью карты Карно: 2. Затем производится объединение 2-х, 4-х или 8-ми единиц. В данном случае объединение двух единиц по горизонтали соответствует операции склеивания над конституентами $\bar{A}\bar{B}\bar{C}$ и $\bar{A} B \bar{C}$ , в результате которой исключается переменная B и получена импликанта $\bar{A} \bar{C}$ . Объединение двух единиц по вертикали соответствует операции склеивания над конституентами $A\bar{B}\bar{C}$ и $A\bar{B}C$ , в результате которой исключена переменная $С$ и будет получена импликанта $A\bar{B} $ . 3. Следовательно, минимальная форма заданной функции примет следующий вид: $$y= \bar{A} \bar{C} \vee A \bar{B}$$.

www.reshim.su

Минимизировать с помощью карт Карно двоичную функцию от 4-х переменных — Бесплатное решение — Банк готовых работ

Минимизировать с помощью карт Карно двоичную функцию от 4-х переменных, заданную своими значениями на наборах

а	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
F(a)	1	1	1	0	0	1	0	1	1	0	1	1	1	0	0	0

Решение.

Составим таблицу истинности:

№	X1	X2	X3	X4	F(a)
0	0	0	0	0	1
1	0	0	0	1	1
2	0	0	1	0	1
3	0	0	1	1	0
4	0	1	0	0	0
5	0	1	0	1	1
6	0	1	1	0	0
7	0	1	1	1	1
8	1	0	0	0	1
9	1	0	0	1	0
10	1	0	1	0	1
11	1	0	1	1	1
12	1	1	0	0	1
13	1	1	0	1	0
14	1	1	1	0	0
15	1	1	1	1	0

 

Перерисуем таблицу истинности в 2-х мерный вид, переставим в ней строки и столбцы в соответствии с кодом Грея и заполним её значениями из таблицы истинности:

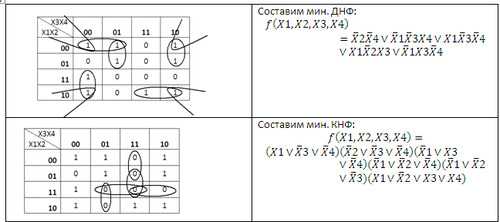
www.reshim.su

Минимизация переключательных функций

Карты Карно — это графическое представление операций попарного неполного склеивания и элементарного поглощения.

Карты Карно рассматриваются как перестроенная соответствующим образом таблица истинности функции.

Карты Карно — определенная плоская развертка n-мерного булева куба.

Строится таблица истинности функции определенным образом. Каждая клетка таблицы соответствует вполне определенной вершине булева куба. Нулевые значения не записываются.

Карта Карно для функции 4-х переменных:

Карта Карно рассматривается как поверхность фигуры под названием тор («бублик»).

p-клетки — клетки карты Карно, соответствующие единичному значению функции.

Соседние наборы — наборы, которые различаются только одним аргументом (одной орбитой).

Любой паре соседних наборов в Карте Карно соответствуют соседние клетки.

Две соседние p-клетки на карте Карно дают импликанту первого ранга. Например, клетки 1100 и 1101 отличаются только значением переменной x₃, следовательно, они дают импликанту 124.

Две соседние импликанты первого ранга образуют импликанту второго ранга.

На этой карте соседние клетки образуют импликанты a,b,c,d,e. При этом импликанты a и b являются соседними, поэтому они образуют импликанту второго ранга.

Если функция имеет 5 переменных, то рисуются 2 Карты Карно: для x₅=0 и для x₅=1. Если 6 переменных — 4 Карты, так чтобы в соседних картах соседние клетки имели одинаковые координаты:

Соседние p-клетки, соответствующие импликанте образуют компактную группу.

Количество p-клеток в компактной группе является степенью двойки.

Задача минимизации переключательной функции с помощью карт Карно заключается в нахождении импликант высшего ранга (соответствующих компактным группам наибольшей размерности), покрывающих p-клетки функции наилучшим образом.

Если на картах Карно выделить все компактные группы наибольшей размерности, то дизъюнкция соответствующих конъюнкций даст СкДНФ.

Основаны на применении соответствующих алгебр(или соответствующих алгебраический преобразований).

Вопрос 1. Интервальная форма задания функции. Постановка задачи минимизации.

Геометрический представление: (отображение функции на n-мерный булев куб) Любому набору значений аргументов соответствует элементарная конъюнкция, содержащая все эти переменные — конституента единицы.

Те вершины n-мерного булева куба, в которых функция принимает единичное значение называются 0-кубами.

Два 0-куба образуют 1-куб, если соответствующие булевы вектора(их координаты) отличаются между собой значением только одной координаты(или одной компоненты). Эти координаты носят название свободной координаты. Обозначение x, остальные координаты 0-куба называются связанными и имеют либо 1, либо 0 значение. 0-кубы, образующие 1-куб называются его гранями. Два 1-куба образуют 2-куб, если свободная координата у них одинакова и они различаются значением только одной связанной компоненты.( 1-кубы — грани соответствующего 2-куба).

…

И так далее до n-куба( в случае тавтологии).

В общем случае, r-куб-это такой куб в булевом пространстве, у которого r свободных компонент и n-r связанных компонент.

Пример:
(1x1xx1) — 3-куб
(1x1x01),(1x1x11)- два 2-куба. Они являются гранями этого 3-куба(образуют его).

Если для какой-то функции взять все возможные кубы одинаковой размерности, то получаем множество кубов(или комплекс кубов).
K^r(f) — комплекс r-кубов функции f/

Для некоторой функции всегда есть комплекс

(Если Kⁿ(f) содержит куб, то f — константа 1

оператор граней:
C^r=(a₁a₂…a_n-1a_n)-куб,
где a∈{0,1,x}, тогда для этого куба можно вычислить грани этого куба. Грани куба:

∂ip(a1a2…an-1an)=		a1a2…ai-1 p ai+1…an-1an, ai=x, p∈{0;1}
		∅, ai ≠ x

где C-получаемый куб.
При a_i=x есть две грани (вместо i-ой либо 0, либо 1).

Оператор сограней
позволяет вычислить куб большей размерности, гранью которого может быть этот куб.

δi(a1a2…an-1an)=		a1a2…ai-1 x ai+1…an-1an, ai≠x, Cr+1⊆K(f)
		∅, ai=x, Cr+1⊄K(f)

Подмножество вершин булева куба, соответствующие кубу размерности r называется интервалом булева пространства ранга r. (интервал 1 ранга — 1×1, интервал 2 ранга — x1x)
Для нашего примера:
K⁰(f)={101,110,111,010,011}
K¹(f)={01x,11x,1×1,x11,x10}
K²(f)={x1x}

В общем случае комплекс кубов определенного ранга не является покрытием исходной функции(за исключением K⁰).

В нашем примере K² не является покрытием, хотя K¹ — покрытие. K(f)=K⁰∪K¹∪K² — для нашей функции

Куб большей размерности покрывает кубы меньшей размерности, если они могут быть получены из него последовательным применением оператора граней.
(x1x) имеет грани (01x) и (11x), которые имеют грани : (010),(011) и (110),(111)

Если взять интервал булева пространства, то аналитически его можно описать в виде соответствующих элементарных конъюнкций.

Некоторый комплекс кубов — L, таких, что каждая вершина из комплекса K⁰(f) включена по крайней мер в один из кубов комплекса L, называется покрытием комплекса K функции f.

Каждое покрытие комплекса K(f) определяет некоторую ДНФ переключательной функции.

Покрытие можно рассматривать (с точки зрения реализации), как двухуровневую схему.

Уровни схемы:

Аргументы (0-ой уровень)

конъюнктивные члены(элементарные конъюнкции) (1-ый уровень)

дизъюнкция (2-ой уровень)

Не учитывается инверсия аргументов на нулевом уровне.

Минимизация
Цена r-куба: c=n-r — число связанных переменных, количество символов в элементарной конъюнкции(совпадает с ценой в смысле Квайне)
—цена покрытия, где q_r-количество кубов размерности r в покрытии L.
-вторая функция цены покрытия(учитывает число кубов)

Задача минимизации: Найти такое покрытие L комплекса K(f), цена которого будет минимальна — минимизация в смысле Квайне.

Задача решается алгебраически, вводится свой математический аппарат. Это аппарат исчисления кубических комплексов (задает операции над кубами).

Каждая операция проходит в два этапа:
I Этап. Предварительное вычисление путем покоординатной обработки кубов по правилам, задаваемым с помощью таблиц покоординатной обработки.
II Этап. Окончательный.

Зададим операции над кубами: a = (a₁ a₂ … a_n)
b = (b₁ b₂ … b_n)

1. Операция *: c=a*b

   По содержанию * — это нахождение куба некоторой размерности r, грани которого содержаться в кубах a и b.

   ci=ai*bi
   	0	1	x
   0	0	y	0
   1	y	1	1
   x	0	1	x

   a*b =		∅, если ∑αici>1
   		c, если ∑αici≤1

   
   

   где αici =		0, ci≠y
   		1, ci=y

   
   c = ([a₁*b₁] … [a_n*b_n]).

   При чем, если результат операции — y, то y заменяется на x.

   (101)*(111) после предварительной обработки: =(1y1) Окончательный вариант: =(1×1)

   
   (x11)*(101)=(1×1)
   

   (x10)
   (101)
   (1yy)
   ∅	— нет общих граней

   
   
2. Операция пересечения кубов.
   c = a ∩ b
   покоординатно!
   

   ci=ai∩bi
   	0	1	x
   0	0	∅	0
   1	∅	1	1
   x	0	1	x

   
   

   a ∩ b =		∅, если ∃i (ai∩bi = ∅
   		c в противном случае

   Пересечение — нахождение общей части булева пространства, покрываемой этими кубами (т.е. куба или грани какого-то уровня)
   (1×1)∩(x1x)=(111)

3. Операция вычитания кубов (#).
   

   ci=ai#bi
   	0	1	x
   0	z	y	z
   1	y	z	z
   x	1	0	z

   
   

   c =		a, если ∃i (ai#bi=y)
   		∅, если ∀i (ai#bi=z)
   		(a1a2…ai-1αai+1…an), αi∈{0,1}

   
   * и ∪ обладают свойством коммутативности, но a#b ≠ b#a !

   Операция вычитания кубов удаляет из куба a общую часть кубов уменьшаемого и вычитаемого (т.е. пересечение кубов a и b).

   В результате вычитания можем иметь несколько кубов.
   Если куб a входит в куб b, то результат — ∅
   Пример:
   
   a#b = (1×1)#(x11) = (z0z) = (101)
   c#b = (1xx)#(x11) = (z00) = {(10x),(1×0)}

K(f)=K⁰∪K¹∪…∪Kⁱ∪…∪K^n-1 — комплекс K функции f

z⊆K является простой импликантой этого комплекса, если δ_i(z)=∅ (δ_i — оператор сограней), то есть не существует какого-либо другого куба, который бы включал в себя исходный куб z.

Z(f)={z} — множество импликант для функции f

Необходимо получить весь комплекс K функции f, используя операторы граней и сограней.

Берем куб z из K и проверяем, есть ли какой-то куб, гранью которого является рассматриваемый.

Операция *(«звездочка») позволяет получить множество Z — кубов, соответствующих простым импликантам функции.

Алгоритм (*) — нахождение множества кубов, соответствующих простым импликантам функции.

Предположим есть некоторый комплекс Ĉ₀, являющийся покрытием комплекса K(f), т.е.

1. Ĉ₀(f) — неупорядоченное покрытие
   причем одна и та же единица функции может покрываться несколькими кубами
2. C₀ = Ĉ₀ — {c₁ | c₁ ∈ Ĉ₀ ∧ c₂ ∈ Ĉ₀ ∧ c₁ ⊆ c₂}
   (тоже, что и поглощение в методе Квайне)
3. C₀*C₀попарно
4. в результате 3) находится множество 0-кубов:

   Z₀ = { c⁰ | c⁰ * C₀ не содержит никаких 1-кубов }
   — это такие кубы, которые в результате операции * не дают никаких 1-кубов

5. вычисляется Ĉ₁:
   Ĉ₁ = C₀ ∪ (C₀*C₀)
6. C₁ = Ĉ₁ — { c | c ⊆ d, c,d∈Ĉ₁ } — {0-кубы, получившиеся в результате операции *, и Z₀}
   ( (1×1)*(x11)= (111) )
7. C₁ * C₁
8. Z₁
9. Ĉ₂
10. C₂ (удаляем 0-кубы и 1-кубы)

и так далее (итерационный процесс)

Ĉ₀(f) — исходное покрытие K(f)

C₁(f) и т.д. в общем случае покрытием функции не являются

C₁(f) ∪ Z₀ ⊆ K — является покрытием K(f)

Алгоритм заканчивается, когда на каком-то шаге получаем множество C, содержащее один куб.

Результат — множество Z — множество простых импликант.
Z = ∪Z_i

ИЗ множества простых импликант извлечь те (выбрать такое подмножество кубов) простые импликанты, которые:

1. Является покрытием исходного множества кубов функции;
2. С минимальной ценой покрытия, если покрытий несколько.

Для решения этой задачи исходные данные фактически — исходный комплекс функции, то есть некоторый исходный комплекс K⁰(f) и Z(f).

Определение: возьмем некоторую вершину d∈K₀. Говорят, что эта вершина является обособленной вершиной комплекса на множестве простых импликант Z, если существует такой куб z∈Z, что вершина d накрывается только этой импликантой z.

Такая импликанта будет простая. Вершина d называется различающей. А импликанта получила название экстремаль.

Любое минимальное покрытие содержит экстремали нулевого ранга.

Пример:

Различающие вершины: (0;0;1) и (0;1;0)
E₀={ a, d}, осталось покрыть одну вершину — (1;1;1)

Задача минимизации: необходимо найти все обособленные вершины и выделить импликанты, накрывающие эти обособленные вершины.

Такие импликанты образуют множество экстремалей.

Задача решается, если известно K⁰(f), то есть все вершины.

В общем случае задачи минимизации функция задана некоторым комплексом K(f), который состоит не только из 0-кубов. Тогда можно найти все 0-кубы и решить задачу, а можно и не находить.

1. Некоторая простая импликанта e∈Z является экстремалью, если e∩K ≠ e∩U'(e,Z)∩K, а e∩K ≠ ∅,
   U'(e,Z) = U(e,Z) — e,
   U(e,Z) = { z | z∈Z, Z∩e ≠ ∅}.
   Z — множество простых импликант,
   U(e,Z) — окрестность куба e, т.е. все простые импликанты из Z, которые имеют общие части с импликантой e.
   U'(e,Z) — окрестность без самой импликанты.

   Функция может быть не полностью определена:

   L — комплекс, где функция определена и равна 1,

   D — комплекс, где значение функции не определено,

   тогда K=L∪D.

   но чаще экстремали вычисляют по одному соотношению:

2. [e#(Z-e)]∩K≠∅
   e#(Z-e) — те вершины булева куба, которые накрываются только e и не накрываются всех оставшейся частью Z.
   + эти вершины присутствуют в комплексе K (или L для неполностью определенной функции)

   Если из простой импликанты e удалить все подкубы (Z-e), и остается, по крайней мере, одна вершина булева куба, которая содержится в исходном комплексе функции, то оставшиеся вершины является выделенными, или отмеченными.

   Алгоритм нахождения экстремалей также итерационный.

1. Каждая простая импликанта проверяется на наличие в ней выделенной вершины, т.е. вычисляется e#(Z-e), если результат вычитания кубов не пустой, то такая импликанта может быть экстремалью.

   Как правило, вычитание e#(Z-e) сводится в таблицу.

2. Каждый кандидат на экстремаль проверяется на пересечение с комплексом единичных значений функции.

   Если результат пересечения не пустой, значит в L (комплексе единичных значений) имеются обособленные вершины, а e является экстремалью.

   Получаем множество экстремалей нулевого ранга — E₀ = {e}. В смысле Квайна оно соответствует ядру функции.

3. Находим ₁ = Z₀ — E₀
   Т.е. из множества простых импликант удаляем множество экстремалей нулевого ранга.
   Находим L₁ = L₀ # E₀, т.е. находятся все вершины, не покрытые экстремалями.
   ₁ — оставшаяся часть множества простых импликант, неупорядоченное множество простых импликант.

   Операция, которая позволяет сократить в последующем перебор и исключить из _i не максимальные кубы — упорядочивание.

   Пусть u∈₁, v∈₁. Говорят, что u1 удовлетворяет условию u∩L₁ ⊆ v∩L₁.
   ( вершины из L₁, покрываемые u, покрываются и кубов v )

   В этом случае из кубов u,v выбираем при упорядочивание куб v.

   Если кубы разной размерности, а вершины покрывают одинаковые — то оставляем куб большей размерности ( цена = n — r ).

   Таким образом, ₁ => Z₁ (находится Z₁ — упорядоченной множество оставшихся простых импликант), применением процедуры упорядочивания.

4. Остались Z₁ и L₁

   (Z₁,L₁) => E₁ по тому же алгоритму.

   Затем ₂ => Z₂; L₂ = L₁#E₁; (Z₂,L₂) => E₂ и т.д.

Два варианта окончания алгоритма:

1. L = ∅ => покрытие единственное
   E = ∪E_i
2. L ≠ ∅ Если проверка на экстремальность не дает результата, т.е. ни одна простая импликанта не содержит квазеопорных вершин, а операция упорядочивания не дает результата.
   Пример:
   

   В этом случае не остается никакого другого варианта решения, кроме волюнтаристского.

   Берется любая простая импликанта, для которой выдвигается две гипотезы (Алгоритм ветвления):

   1. простая импликанта входит в минимальное покрытие

      e∈E
      находим L_i+1=L_i#{e}, упорядочиваем Z и вновь применяем алгоритм извлечения (возможно еще ветвление).

   2. простая импликанта не входит в минимальное покрытие

      e∉E
      удаляем e из Z_i (находим _i+1), упорядочиваем _i+1 => Z_i+1
      L_i+1 = L_i
      И применяем алгоритм извлечения.

   Таким образом, при ветвление получаем множество покрытий, сравниваем по цене и выбираем наименьшей.

Все вычисления в ручном варианте сводятся к вычислениям над таблицами.

yaffle.github.io

Карты Карно

В другом методе графического отображения булевых функций используют карты Карно — специально организованные таблицы соответствия.

Столбцы и строки таблицы соответствуют всевозможным наборам значений не более 2-х переменных, причем эти наборы расположены в таком порядке, что каждый последующий отличается от предыдущего значением только одной из переменных. Благодаря этому и соседние клетки таблицы по горизонтали и вертикали отличаются только одной переменной. Клетки, расположенные по краям таблицы, также считаются соседними и обладают этим свойством.

Рис. Карты Карно для 2-х и 3-х переменных.

Карты Карно для 4-х переменных.

Как и в обычных таблицах соответствия клетки наборов, на которых функция принимает значение 1, заполняются единицами (нули обычно не вписываются, им соответствуют пустые клетки).

Например, на рис. показана карта Карно для функции, отображение которой дано на 4-х-мерном кубе (см. рис.).

Для упрощения строки и столбцы, соответствующие значениям “1” для некоторой переменной, выделяются фигурной скобкой с обозначением этой переменной.

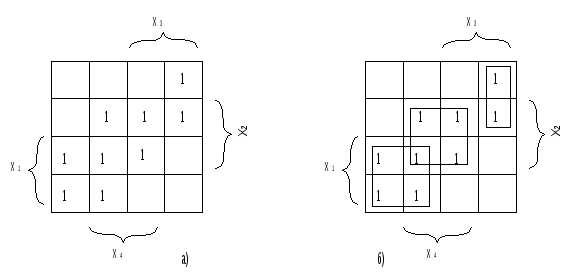
Рис. а) отображение функции четырех переменных;

б) отображение ее минимального покрытия.

Между отображениями функции на n-мерном кубе и на карте Карно имеет место взаимно-однозначное соответствие. На карте Карно S-кубу соответствует совокупность 2-х соседних клеток, размещенных в строке, столбце, квадрате или прямоугольнике. Поэтому все положения, изложенные ранее, справедливы и для карт Карно. Так на рис. б) показано покрытие единиц карты, соответствующее минимальной дизъюнктивной форме

у=, рассматриваемой функции.

Считывание минитермов с карты Карно осуществляется по простому правилу. Клетки, образующие S-куб, дают минитерм (n—S)-го ранга, в который входят те (n—S)-переменные, которые сохраняют одинаковые значения на этом S-кубе, причем значениям “1” соответствуют сами переменные, а значениям “0” их отрицание.

Переменные, которые не сохраняют свои значения на S-кубе, в минитерме отсутствуют. Различные способы считывания приводят к различным представлениям функции в ДНФ.

у=у=

у=

Использование карт Карно требует более простых построений по сравнению с отображением на n-мерном кубе, особенно в случае 4-х переменных.

Для отображения функций 5-ти переменных используют две карты Карно на 4-ре переменные, а для функции 6-ти переменных — четыре таких карты.

При дальнейшем увеличении числа переменных карты Карно становятся практически непригодны.

Метод Мак-Класски (алгебраический метод)

Алгебраический метод известен как метод Мак-Класски, модифицировавшего в 1956 году метод Квайна. Базируется данный метод на следующей теореме.

Теорема. Если в СДНФ функции алгебры логики произвести всевозможные операции неполного склеивания, а затем всевозможные операции элементарного поглощения, то полученная форма функции будет сокращенной.

Элементарную конъюнкцию ранга n будем называть минитермом ранга n.

Элементарная конъюнкция называется импликантой булевой функции, если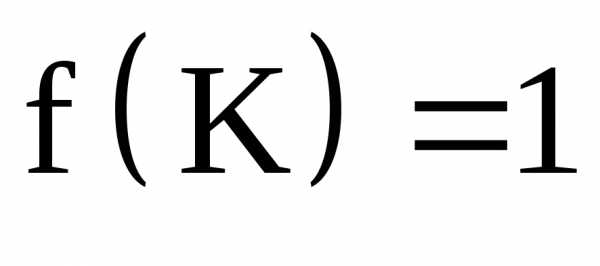, то есть булева функция на данном наборе является константной и равна 1.

Минимизация булевой функции по методу Мак-Класски осуществляется согласно следующей последовательности действий:

1. Записать минитермы в виде их двоичных кодов и разбить их на непересекающиеся группы по числу единиц в этих группах. В i-ю группу войдут только те кодовые комбинации, которые в своей двоичной записи содержат ровно i единиц. Группы располагаются по мере роста i.

2. Попарное сравнение минитермов.

2.1. Произвести попарное сравнение двоичных номеров всех членов группы с индексом i с членами только группы с индексом (i+1).

2.2. Если некоторые два минитерма имеют вид ax_i и 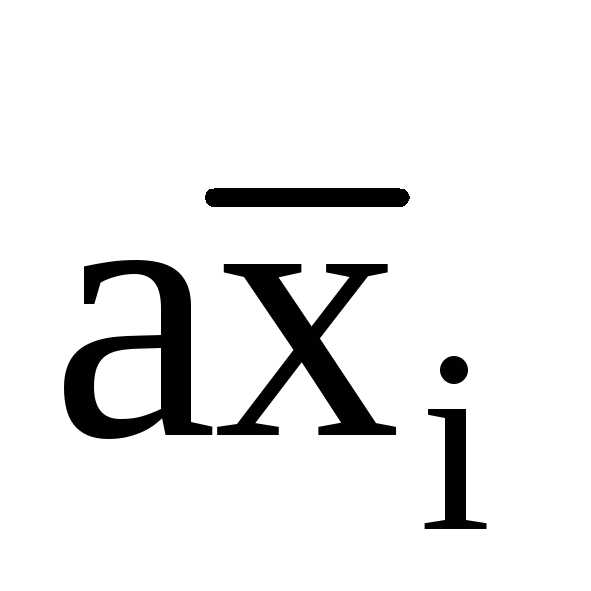, то выписывают конъюнкцию а, которая является минитермом ранга (n-1), то есть если сравниваемы двоичные коды различаются только в одном разряде, то в столбец остатков записывается двоичный код с прочерком “-” на месте этого разряда (этот код соответствует минитерму (n-1)-го ранга.

2.3. Все двоичные коды номеров, участвующих в операции сравнения при условии их склеивания, отмечаются знаком “*”.

2.4. Пункты 2.1-2.3. повторяются для всех групп последовательно в порядке возрастания i. Двоичные коды, не отмеченные знаком “*”, соответствуют простым импликантам.

2.5. После построения всех минитермов (n-1) ранга по пунктам 2.1-2.3, они также сравниваются между собой и получают минитермы ранга (n-2) и т.д. Работа по первому этапу продолжается до тех пор, пока среди двоичных кодов можно будет обнаружить сравнимые, то есть такие укороченные коды, которые содержат прочерки в одних и тех же разрядах и различаются значением одного разряда.

Все неотмеченные минитермы называются первичными или простыми импликантами.

3. Построение импликантной таблицы. Строится таблица, в которой число строк равно числу полученных первичных импликант минимизируемой функции, а число столбцов равно числу минитермов исходной СДНФ. Если в некоторый минитерм исходной СДНФ входит первичная импликанта, то на пересечении строки и столбца ставится метка. Данные импликантной таблицы позволяют определить импликанты, отбросив которые, истинность функции не изменится.

4. Нахождение существенных импликант. Если в каком-либо из столбцов полученной таблицы имеется только одна метка, то первичная импликанта, стоящая в соответствующей строке, называется существенной. Существенная импликанта включается в минимальную ДНФ, а из таблицы исключаются строки, соответствующие существенным импликантам, а также столбцы минитермов, покрываемые этими существенными импликантами. Если в таблице нет столбцов, содержащих только одну метку, то переход на п.7.

5. Вычеркивание лишних столбцов. Если в таблице после четвертого этапа есть два столбца, в которых стоят метки в одинаковых строках, то один из них вычеркивают, так как покрытие оставшегося столбца будет осуществлять покрытие исключенного минитерма.

6. Вычеркивание лишних первичных импликант. Если на пятом этапе появляются строки, в которых нет меток, то первичная импликанта исключается из дальнейшего рассмотрения.

7. Выбор минимального покрытия. Выбирают наименьшее число строк таких, чтобы для каждого столбца из данной таблицы и каждой метки в этом столбце нашлась бы по крайней мере одна строка из множества выбранных строк, которая содержит эту метку.

Дизъюнкция всех простых импликантов покрытия, в том числе и существенных, образует тупиковую форму функции. Из найденных тупиковых форм выбирают минимальную по наименьшему числу дизъюнкций и элементов переменных.

Пример.

.

1) Получение групп кодовых комбинаций. 0011 0100 0101 0111 1001 1011 1100 1101

1 гр. 0100 2 гр. 0011 3 гр. 0111

0101 1011

1001 1101

1100

2) Попарное сравнение минитермов.

Минитермы 3-го ранга: 010-*, -100, 0-11, -011, -101, 10-1, 1-01, 110-*

Минитермы 2-го ранга: -10-.

3) Построение импликантной таблицы и расстановка меток

	0100	0011	0101	1001	1100	0111	1011	1101
-100	*				*
0-11		*				*
-011		*					*
-101			*					*
10-1				*			*
1-01				*				*
-10-	*		*		*			*

4) Нахождение существенных импликант. Столбец, соответствующий кодовой комбинации 0111 содержит единственную метку. Соответствующая этой метке импликанта является существенной, поэтому включаем ее в минимальную ДНФ , а из таблицы согласно п.4 исключаем столбцы и строку, после чего получаем следующую таблицу:

	0100	0101	1001	1100	1011	1101
-100	*			*
-011					*
-101		*				*
10-1			*		*
1-01			*			*
-10-	*	*		*		*

5) и 6) В полученной таблице нет столбцов, в которых стоят метки в одинаковых строках и нет строк, в которых нет меток, поэтому переходим к п.7.

7) Выбор минимального покрытия. Минимальному покрытию соответствует выбор строк -10- и 10-1. Тогда минимизированная ДНФ запишется как .

studfiles.net

iMath Wiki — Минимизация булевых функций. Минимизирующие карты Карно. Метод Куайна-МакКласки

Ясно, что при разработке логических схем, немаловажной является задача минимизации количества используемых элементов (другими словами, логических операций).

В связи с этим, возникает задача минимизации логических функций в некотором классе формул. В частности, в классах ДНФ и КНФ.

Минимальная ДНФ

Такая ДНФ, которая содержит наименьшее общее число вхождений переменных по сравнению со всеми равносильными ей ДНФ.

Минимальная КНФ

Такая КНФ, которая содержит наименьшее общее число вхождений переменных по сравнению со всеми равносильными ей КНФ.

Процесс нахождения минимальных форм, собственно, и называется минимизацией. В простых случаях, для минимизации достаточно тождественных преобразований. В более сложных – используются специальные алгоритмы.

Основным методом минимизации логических функций, представленных в виде СДНФ или СКНФ, является операция попарного неполного склеивания и элементарного поглощения. Операция попарного склеивания осуществляется между двумя членами, содержащими одинаковые переменные, вхождения которых (с отрицанием и без) совпадают для всех переменных, кроме одной. В этом случае все переменные, кроме одной, можно вынести за скобки, а оставшиеся в скобках прямое и инверсное вхождение одной переменной подвергнуть склейке. Например:

\[ \;\overline{x_1}\;x_2x_3x_4 \vee \;\overline{x_1}\;x_2\;\overline{x_3}\;x_4 = \;\overline{x_1}\;x_2x_4 (x_3 \vee\;\overline{x_3}\;) = \;\overline{x_1}\;x_2x_4 \mathbin{\&}1 = \;\overline{x_1}\;x_2x_4. \]

Аналогично для КНФ:

\[ (\;\overline{x_1}\;\vee x_2\vee x_3\vee x_4) (\;\overline{x_1}\;\vee x_2\vee\;\overline{x_3}\;\vee x_4) = \;\overline{x_1}\;\vee x_2\vee x_4\vee x_3\;\overline{x_3}\; = \;\overline{x_1}\;\vee x_2\vee x_4\vee 0 = \;\overline{x_1}\;\vee x_2\vee x_4. \]

Возможность поглощения следует из очевидных равенств

\[ A \vee\;\overline{A}\; = 1 \]\[ A\;\overline{A}\; = 0. \]

Таким образом, главной задачей при минимизации СДНФ и СКНФ является поиск членов, пригодных к склейке с последующим поглощением, что для больших форм может оказаться достаточно сложной задачей.

Карта Карно

Графический способ минимизации булевых функций. Представляет собой операции попарного неполного склеивания и элементарного поглощения. Карты Карно рассматриваются как построенная соответствующим образом таблица истинности функции.

Карты Карно можно рассматривать как определенную плоскую развертку n-мерного булева куба.

Карты Карно были изобретены в 1952 Эдвардом В. Вейчем и усовершенствованы в 1953 Морисом Карно, физиком из «Bell Labs», и были призваны помочь упростить цифровые электронные схемы.

В карту Карно булевы переменные передаются из таблицы истинности и упорядочиваются с помощью кода Грея, в котором каждое следующее число отличается от предыдущего только одним разрядом.

Булевы функции \(N\) переменных, представленные в виде СДНФ или СКНФ, могут иметь в своём составе \(2^N\) различных элементарных членов.

Элементарные члены СДНФ или СКНФ образуют структуру, топологически эквивалентную \(N\)-мерному кубу. Действительно, если рассматривать набор значений функции \(x_1,\,\ldots,\,x_N\) как \(N\)-мерный вектор \(\{x_1,\,\ldots,\,x_N\}\), мы получим набор точек, лежащих на ортах \(N\)-мерной системы координат, и удаленных друг от друга на \(1\). Другими словами, мы получим \(N\)-мерный гиперкуб с ребром \(1\).

Например, для функции двух переменных, заданной таблицей истинности:

можно построить эквивалентный ей квадрат:

001111000110

Или, если обозначить вершины соответствующими элементарными конъюнкциями и выделить вершины, конъюнкции которых входят в СДНФ:

0x̅₁x₂1x₁x₂0x̅₁x̅₂1x₁x̅₂

Или СКНФ:

0x₁∨x̅₂1x̅₁∨x̅₂0x₁∨x₂1x̅₁∨x₂

Можно заметить, что члены, находящиеся на одной стороне квадрата, могут быть склеены. Соответственно, если составляется ДНФ, то операции производятся только над вершинами, в которых функция имеет значение \(1\) (по правилам построения СДНФ). Если же составляется КНФ, то над вершинами, в которых функция имеет значение \(0\) (по правилам построения СКНФ).

При этом, сохраняются переменные, значение которых на стороне постоянно.

В случае функции трёх переменных приходится иметь дело с трёхмерным кубом. Это сложнее и менее наглядно, но технически возможно. На рисунке в качестве примера показана таблица истинности для булевой функции трёх переменных и соответствующий ей куб.

Как видно из рисунка, для трёхмерного случая возможны более сложные конфигурации. Например, четыре члена, принадлежащие одной грани куба, объединяются в один с поглощением двух переменных:

\[ \;\overline{x_1}\;\;\overline{x_2}\;\;\overline{x_3}\; \vee x_1\;\overline{x_2}\;\;\overline{x_3}\; \vee \;\overline{x_1}\;\;\overline{x_2}\;x_3 \vee x_1\;\overline{x_2}\;x_3 =\]

\[ = \;\overline{x_2}\; (\;\overline{x_1}\;\;\overline{x_3}\; \vee\;\overline{x_1}\;x_3 \vee x_1\;\overline{x_3}\; \vee x_1x_3) = \;\overline{x_2}\; (\;\overline{x_1}\; \vee x_1)(\;\overline{x_3}\; \vee x_3) = \;\overline{x_2}\; \]

В общем случае можно сказать, что \(2^K\) членов, принадлежащие одной \(K\)–мерной грани гиперкуба, склеиваются в один член, при этом поглощаются \(K\) переменных.

Карта Карно представляет собой развертку гиперкуба на плоскость. Например, трехмерный куб из предыдущего примера можно развернуть следующим образом:

1x̅₁x̅₂x̅₃1x̅₁x̅₂x₃0x̅₁x₂x̅₃0x̅₁x₂x₃0x₁x₂x₃0x₁x₂x̅₃1x₁x̅₂x₃1x₁x̅₂x̅₃

Карта Карно является представлением такой двумерной развертки в виде таблицы.

\(0\)	\(1\)	\(0\)	\(0\)	\(1\)
\(1\)	\(1\)	\(0\)	\(0\)	\(1\)

В этой карте самые левые ячейки смежны самым правым.

Ясно, что на одной \(K\)-мерной грани могут лежать \(2^K\) вершин. Следовательно, в карте Карно выбираются группы по \(2^K\) смежных ячеек, и в результирующую ДНФ или КНФ входят только те переменные, которые неизменны в рамках данной группы. Общее число членов соответствует числу групп в карте Карно, а число неизменных переменных обратным образом зависит от количества элементов в группе. Как следствие, группы необходимо выбирать как можно более большими. Следует отметить, что одна комбинация переменных может входить в несколько групп.

Для функций четырех переменных, требуется развертка 4-мерного гиперкуба. Карта Карно в таком случае имеет вид:

\(00\)	\(f(0,0,0,0)\)	\(f(0,1,0,0)\)	\(f(1,1,0,0)\)	\(f(1,0,0,0)\)
\(01\)	\(f(0,0,0,1)\)	\(f(0,1,0,1)\)	\(f(1,1,0,1)\)	\(f(1,0,0,1)\)
\(11\)	\(f(0,0,1,1)\)	\(f(0,1,1,1)\)	\(f(1,1,1,1)\)	\(f(1,0,1,1)\)
\(10\)	\(f(0,0,1,0)\)	\(f(0,1,1,0)\)	\(f(1,1,1,0)\)	\(f(1,0,1,0)\)

В данном случае, все крайние ячейки смежны друг другу. Это можно себе представить, натянув эту развертку на тор (“бублик”):

Возможно так же построение карт Карно для функций 5 и 6 переменных, однако работа с ними значительно затрудена. Для числа переменных, большего 6, использование карт Карно попросту непрактично.

Пример

Рассмотрим функцию, имеющую следующую таблицу истинности:

0	0	0	0	1
0	0	0	1	1
0	0	1	0	1
0	0	1	1	0
0	1	0	0	1
0	1	0	1	0
0	1	1	0	1
0	1	1	1	1
1	0	0	0	0
1	0	0	1	0
1	0	1	0	0
1	0	1	1	0
1	1	0	0	0
1	1	0	1	0
1	1	1	0	1
1	1	1	1	1

Перепишем эту таблицу в виде карты Карно:

00	1	1	0	0
01	1	0	0	0
11	0	1	1	0
10	1	1	1	0

Легко выделяются три группы. Исходя из этого, записывается ДНФ:

\(\;\overline{x_1}\;\;\overline{x_2}\;\;\overline{x_3}\;\)\(\vee\)\(\;\overline{x_1}\;\;\overline{x_4}\;\)\(\vee\)\({x_2}{x_3}\)

Метод Куайна-МакКласси строится на основе того же аппарата, что и карты Карно, однако оказывается более практичным для большего количества переменных.

Алгоритм заключается последовательной склейке, и затем редукции результата.

Склейка

Сначала элементарные члены совершенной формы записываются в двоичной форме в таблицу, где группируются по количеству единиц.

Затем, члены, которые отличаются одной переменной (одним битом), могут быть склеены. В таком случае единица заменяется на “-”. Очевидно, что склеены могут быть только члены из соседних групп

Члены, которые нельзя склеить, обозначаются звездочкой «*».

Полученные склеенные члены могут, в свою очередь, так же быть склеены. При этом “-” трактуется как “третье” значение.

Когда никакие члены больше не могут быть склеены, из членов, отмеченных “*”, составляется сокращенная форма, которая не обязательно минимальна. После этого производится редукция.

Редукция

Для редукции, составляется таблица, в строки которой включаются члены сокращенной формы, а в столбцы – члены совершенной.

В ячейках ставится отметка (например, крестик “×”), если соответствующий член сокращенной формы поглощает соответствующий член совершенной формы (т.е. если заголовок строки является частью заголовка столбца).

Выбираются столбцы, содержащие только один “×”. Соответсвтующие им члены сокращенной формы составляют ядро, и должны войти в минимальную форму.

Если ядро не перекрывает все столбцы, то в минимальную форму так же включаются несколько членов сокращенной формы, не входящих в ядро, таким образом, чтобы члены минимальной формы перекрывали все столбцы таблицы.

Пример

Найдем минимальную форму функции

0	0	0	0	0	1
1	0	0	0	1	1
2	0	0	1	0	1
3	0	0	1	1	1
4	0	1	0	0	0
5	0	1	0	1	1
6	0	1	1	0	0
7	0	1	1	1	1
8	1	0	0	0	1
9	1	0	0	1	0
10	1	0	1	0	1
11	1	0	1	1	0
12	1	1	0	0	1
13	1	1	0	1	1
14	1	1	1	0	0
15	1	1	1	1	1

Члены СДНФ в двоичной нотации:

• 0000 = 0
• 0001 = 1
• 0010 = 2
• 0011 = 3
• 0101 = 5
• 0111 = 7
• 1000 = 8
• 1010 = 10
• 1100 = 12
• 1101 = 13
• 1111 = 15

Группировка:

0

1

• 0001 = 1
• 0010 = 2
• 1000 = 8

2

• 0011 = 3
• 0101 = 5
• 1010 = 10
• 1100 = 12

3

4

Склейка 1:

• 0, 1 = 000-
• 0, 2 = 00-0
• 0, 8 = -000
• 1, 3 = 00-1
• 1, 5 = 0-01
• 2, 3 = 001-
• 2,10 = -010
• 8,10 = 10-0
• 8,12 = 1-00
• 3,7 = 0-11
• 5,7 = 01-1
• 5,13 = -101
• 12,13 = 110-
• 7,15 = -111
• 13,15 = 11-1

Группировка 2:

• 0, 1 = 000-
• 2, 3 = 001-
• *12,13 = 110-

---

• 0, 2 = 00-0
• 1, 3 = 00-1
• 8,10 = 10-0
• 5,7 = 01-1
• 13,15 = 11-1

---

• 1, 5 = 0-01
• *8,12 = 1-00
• 3,7 = 0-11

---

• 0, 8 = -000
• 2,10 = -010
• 5,13 = -101
• 7,15 = -111

Склейка 2:

• *0,1,2,3 = 00–
• *0,2,8,10 = -0-0
• *5,7,13,15 = -1-1
• *1,3,5,7 = 0–1

Итого, члены сокращенной формы:

• 12,13 = 110-
• 8,12 = 1-00
• 0,1,2,3 = 00–
• 0,2,8,10 = -0-0
• 5,7,13,15 = -1-1
• 1,3,5,7 = 0–1

Редукция:

12,13									×	×
8,12							×		×
0,1,2,3	×	×	×	×
0,2,8,10	×		×				×	⊗
5,7,13,15					×	×				×	⊗
1,3,5,7		×		×	×	×

Кружком обведены члены ядра.

Ядро, таким образом, включает члены -0-0 и -1-1. Для получения минимальной формы, нам нужно перекрыть дополнительно столбцы 1, 3, 12. Для этого можно взять, например, 0,1,2,3 = 00– и 12,13 = 110-:

\[ f = \;\overline{x_2}\;\;\overline{x_4}\; \vee {x_2}{x_4} \vee \;\overline{x_1}\;\;\overline{x_2}\; \vee {x_1}{x_2}\;\overline{x_3}\; \]

Карта Карно:

00	1		1	1
01	1	1	1
11	1	1	1
10	1			1

wiki.livid.pp.ru

Карты Карно [EXE] — Все для студента

Программа для моделирования электрических цепей любой сложности. Построение АЧХ, ФЧХ. Элементарные навыки работы с осциллографом. В этой программе можно работать с операционными усилителями, логическими элементами (сумматор, генератор слов и некоторые другие).

• 6,67 МБ
• дата добавления неизвестна
• изменен 10.06.2018 07:47

Программа схемотехнического моделирования (симулятор) Micro-Cap может представлять интерес для широкого круга людей, занимающихся или изучающих электронику. В первую очередь эту программу можно рекомендовать студентам электротехнических и радиотехнических специальностей, а также радиолюбителям и инженерам-разработчикам.

• 5,36 МБ
• дата добавления неизвестна
• изменен 13.06.2017 02:36

СПб.: Наука и Техника, 2008. — 544 с. Самоучитель рассказывает секреты микропроцессорной техники, затрагивает основы цифровой логики, принципы программирования. Написан простым, понятным языком, снабжен схемами, иллюстрациями и практическими примерами. После популярной теоретической части автор переходит к практике реализации устройств на микроконтроллерах. В качестве примера…

• 10,32 МБ
• дата добавления неизвестна
• изменен 04.01.2019 06:30

Пер. с англ. Б. И. Копылова. – М.: Лаборатория базовых знаний, 2002. – 832 с. В книге излагаются методы анализа и синтеза современных систем автоматического управления (САУ). Показано, как с использованием принципа обратной связи могут быть созданы высокоэффективные системы управления различного назначения (аэрокосмическая техника, промышленные работы, автомобилестроение,…

• 12,21 МБ
• дата добавления неизвестна
• изменен 19.02.2009 23:26

Автор и выходные данные не указаны. Очень толковое и «по-русски» написанные лекции. Всего их 15. В каждой лекции рассматривается отдельная тема — от самого простого к сложному. Рассматривается всё: определения, применение, примеры построения схем с примерами работы. Базовые понятия цифровой электроники. Микросхемы и их функционирование. Простейшие логические элементы….

• 2,71 МБ
• дата добавления неизвестна
• изменен 20.04.2009 21:23

40 решенных и подробно разобранных задач. Теория вероятности: классическая формула, теоремы сложения и умножения, формула полной вероятности, формула Байеса, формула Бернулли, теоремы Лапласа. Мат. статистика: математическое ожидание, дисперсия и среднее квадратическое отклонение, многоугольник распределения, полигон частот, корреляционная зависимость и т….

• 172,30 КБ
• дата добавления неизвестна
• изменен 19.03.2009 23:04

www.twirpx.com