Асимптоты графика функции. График дробно-линейной функции
Асимптоты графика функции. График дробно-линейной функции.
В этой статье мы рассмотрим, что такое асимптота графика функции, и как ее находить.
Асимптота – это прямая, к которой бесконечно близко приближается график функции.
Асимптоты бывают горизонтальные, вертикальные и наклонные.
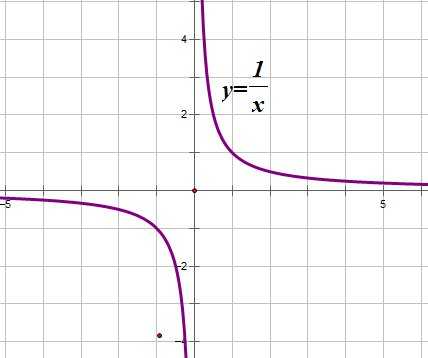
Если мы посмотрим на хорошо известный нам график функции , то увидим, что график этой функции бесконечно близко приближается к прямой (ось ОY) — это вертикальная асимптота, и к прямой (ось ОХ) — это горизонтальная асимптота:
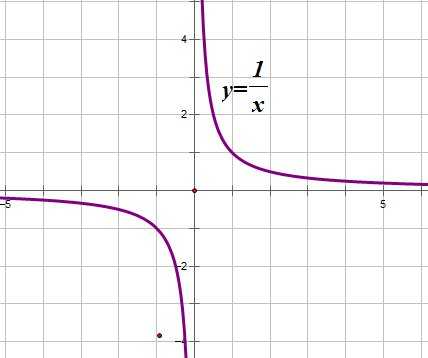
В общем случае горизонтальная асимптота — это прямая, параллельная оси OX. Уравнение горизонтальной асимптоты имеет вид , где — число, к которому стремятся значения функции , когда стремится к .
Вертикальная асимптота — это прямая, параллельная оси OY. Уравнение вертикальной асимптоты имеет вид . Здесь — значение переменной , при котором функция не определена. Как правило, это ноль знаменателя. Если значение стремится к точке, в которой знаменатель равен нулю, то абсолютное значение дроби при этом неограниченно возрастает.
В некоторых случаях для построения графика функции бывает достаточно найти асимптоты графика.
Рассмотрим дробно-линейную функцию. В общем виде уравнение дробно-линейной функции имеет вид: .
График дробно-линейной функции — это гипербола. Как мы знаем, гипербола имеет две асимптоты: горизонтальную и вертикальную.
Заметим, что при знаменатель равен нулю, в этой точке функция не определена. Поэтому прямая — вертикальная асимптота.
Степень в числителе дроби равна степени в знаменателе. Поэтому при числитель и знаменатель растут с одинаковой скоростью, и
и уравнение горизонтальной асимптоты имеет вид .
График дробно-линейной функции — это гипербола, симметричная относительно точки пересечения асимптот графика. Поэтому, чтобы построить график, нам остается только выяснить его расположение относительно этой точки.
Для этого достаточно найти точки пересечения графика с осями координат.
Точка пересечения с осью OX (y=o): .
Точка пересечения с осью OY (x=0): .
Построим график функции . Это дробно-линейная функция и ее график — гипербола.
Найдем горизонтальную и вертикальную асимптоты.
Уравнение горизонтальной асимптоты: ;
уравнение вертикальной асимптоты (ноль знаменателя):
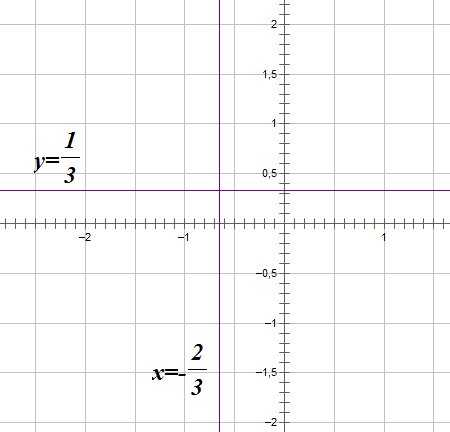
Найдем точки пересечения с осями координат:
С осью ОХ: ;
с осью OY(x=0): .
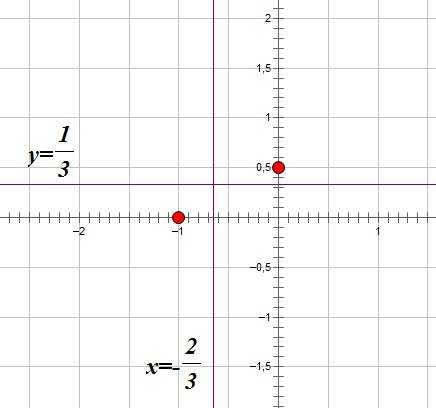
То есть график функции выглядит как-то так:

И, наконец, наклонная асимптота. Наклонная асимптота — это к прямая, к кторой стремится график функции на бесконечности.
Уравнение наклонной асимптоты имеет вид .
Коэффициенты и вычисляются следующим образом:
Найдем асимптоты графика функции
1. Начнем с области определения функции. Функция не определена в точке , следовательно прямая является вертикальной асимптотой.
2. Степень числителя дроби на единицу больше степени знаменателя, поэтому предел этого отношения при отношения равен бесконечности. Следовательно, график функции не имеет горизонтальной асимптоты.
3. Попробуем найти наклонную асимптоту.
(Предел функции равен отношению коэффициентов при максимальных степенях в числителе и знаменателе дроби).
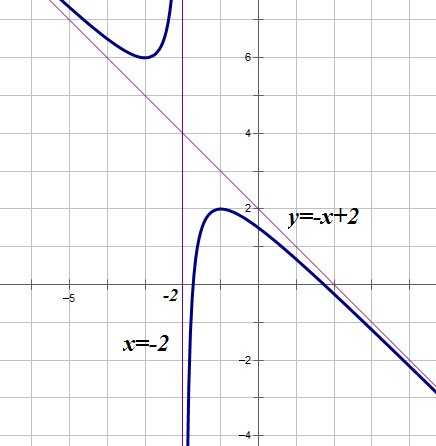
Итак, уравнение наклонной асимптоты:

График функции , построенный с помощью специальной программы, показывает, что асимптоты были найдены верно:
И.В. Фельдман, репетитор по математике.
ege-ok.ru
5.5. Асимптоты графика функции
Построение графика функции значительно облегчается, если знать его асимптоты.
Определение.
Асимптотой кривой называется прямая, расстояние до которой от точки, лежащей на кривой, стремится к нулю при неограниченном удалении от начала координат этой точки по кривой (рис.5.10).
Асимптоты бывают вертикальные (параллельные оси Оу), горизонтальные (параллельные оси Ох) и наклонные.
Рис. 5.10
Вертикальные асимптоты
Определение.
Прямая 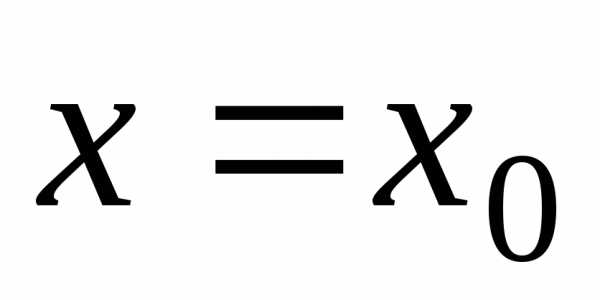 называетсявертикальной
асимптотой графика
функции
называетсявертикальной
асимптотой графика
функции 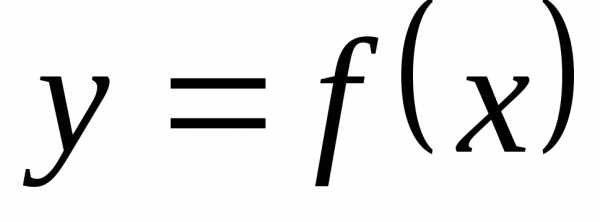 ,
если выполнено одно из условий:
,
если выполнено одно из условий:
или (рис.5.11)
Рис. 5.11
Вертикальные
асимптоты, уравнение которых х=x0 , следует
искать в точках, где функция терпит
разрыв второго рода, или на концах ее
области определения, если концы не равны 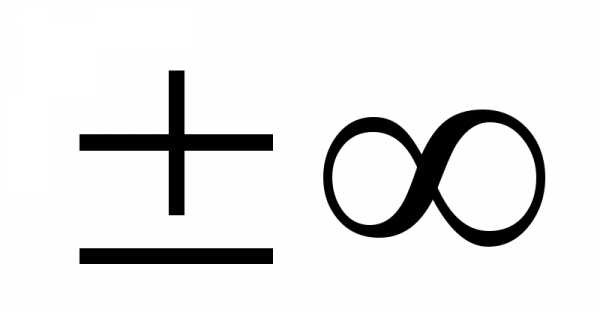 .
Если таких точек нет, то нет и вертикальных
асимптот.
.
Если таких точек нет, то нет и вертикальных
асимптот.
Например, для
кривой 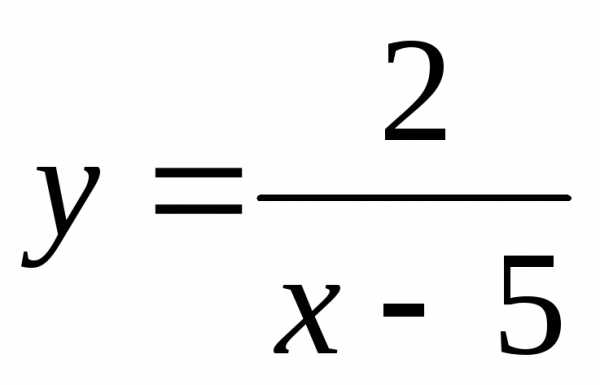 ,
вертикальной асимптотой будет прямая
,
вертикальной асимптотой будет прямая ,
так как
,
так как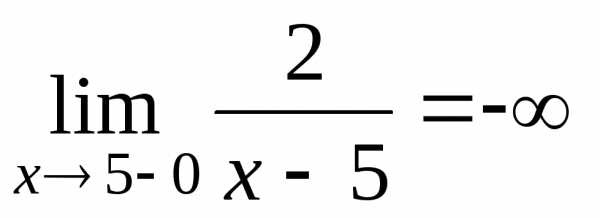 ,
,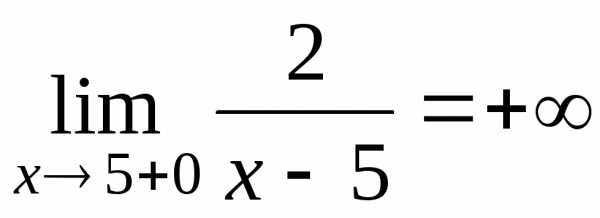 .
Вертикальной асимптотой графика функции
.
Вертикальной асимптотой графика функции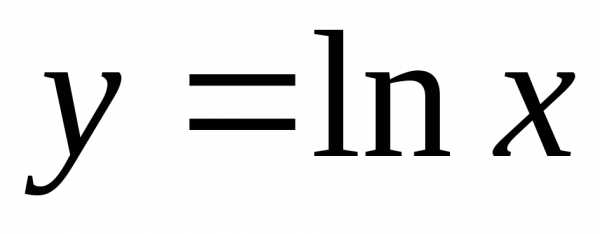 является прямая(осьОу),
поскольку
является прямая(осьОу),
поскольку
.
Горизонтальные асимптоты
Определение.
Если при
()
функция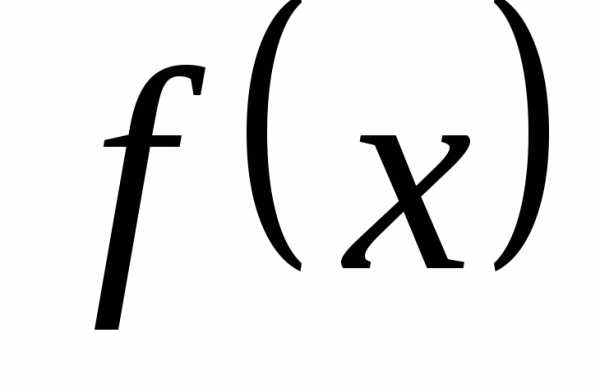 имеет конечный предел, равный числуb:
имеет конечный предел, равный числуb:
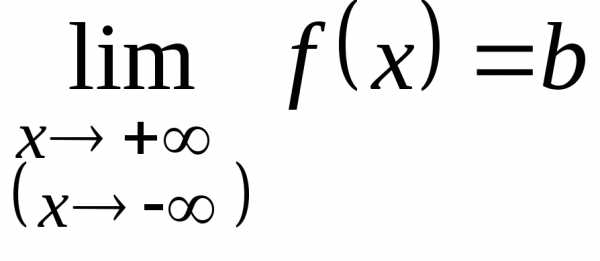 ,
,
то прямая 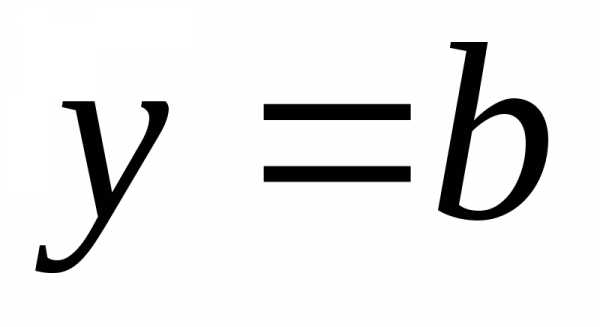 есть горизонтальная асимптота графика
функции
есть горизонтальная асимптота графика
функции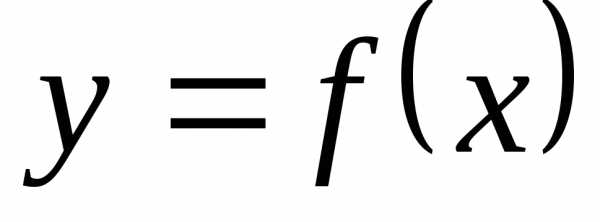
Например, для функции имеем
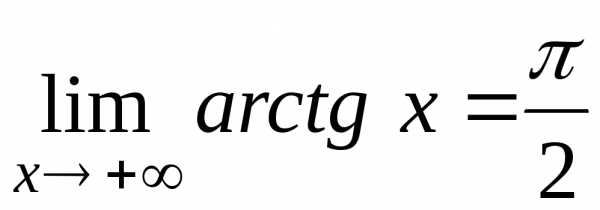 ,
.
,
.
Соответственно,
прямая 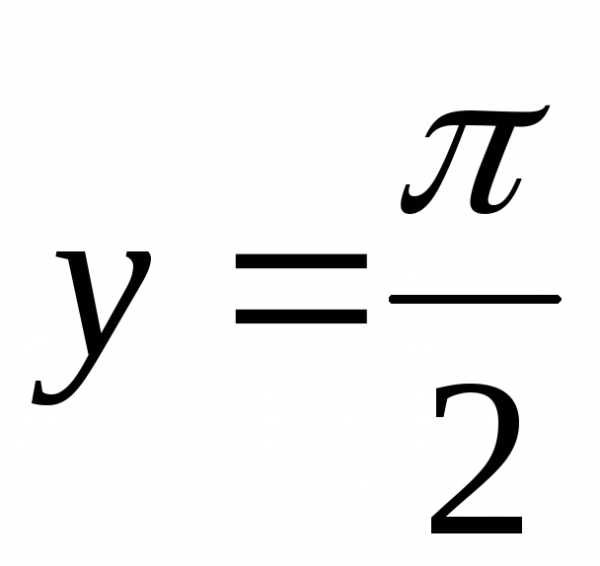 − горизонтальная асимптота для правой
ветви графика функции,
а прямая
− горизонтальная асимптота для правой
ветви графика функции,
а прямая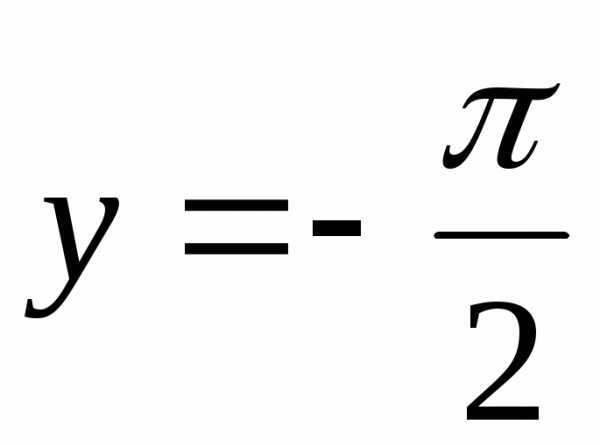 − для левой ветви.
− для левой ветви.
В том случае, если
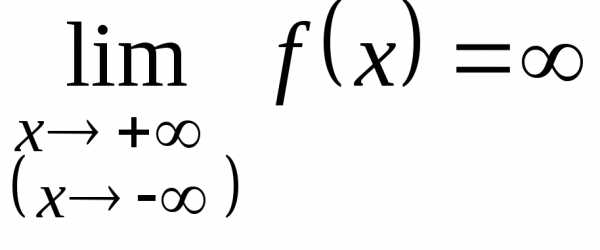 ,
,
график функции не имеет горизонтальных асимптот, но может иметь наклонные.
Наклонные асимптоты
Определение.
Прямая
называетсянаклонной
асимптотой графика функции 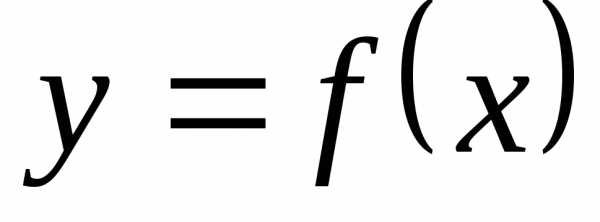 при(),
если выполняется равенство
при(),
если выполняется равенство
.
Наличие наклонной асимптоты устанавливают с помощью следующей теоремы.
Теорема.
Для того, чтобы
график функции 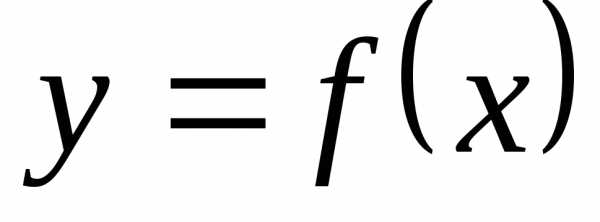 имел при()
наклонную асимптоту,
необходимо и достаточно, чтобы существовали
конечные пределы
имел при()
наклонную асимптоту,
необходимо и достаточно, чтобы существовали
конечные пределы
 и
.
и
.
Если хотя бы один
из этих пределов не существует или равен
бесконечности, то кривая 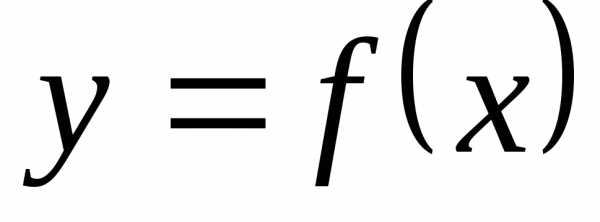 наклонной асимптоты не имеет.
наклонной асимптоты не имеет.
Замечания.
1. При отыскании асимптот следует отдельно рассматривать случаи и.
2. Если
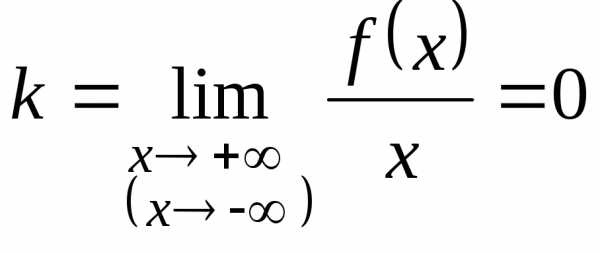 и
и 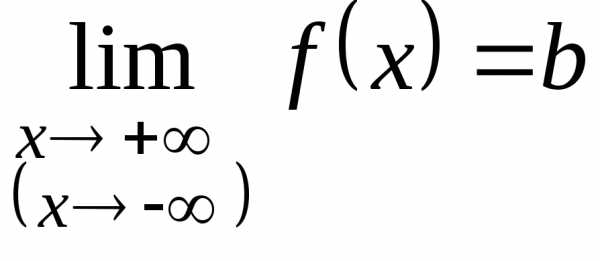 ,
,
то график функции 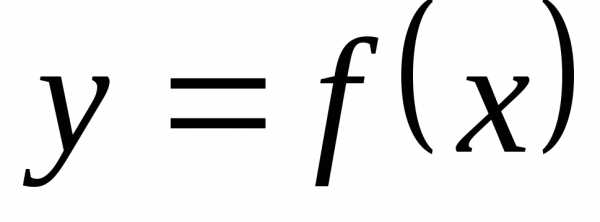
 .
.3. Если
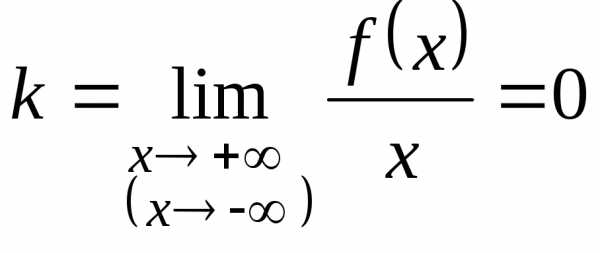 и
,
и
,
то прямая 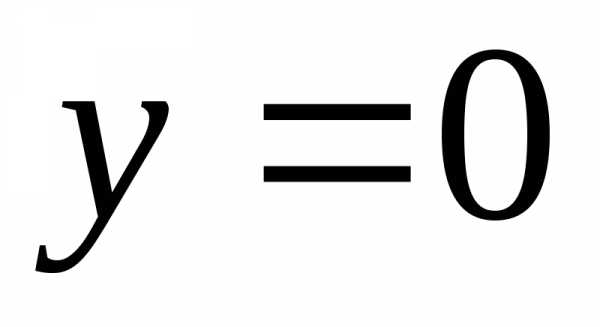 (осьОх)
является горизонтальной асимптотой
графика функции
(осьОх)
является горизонтальной асимптотой
графика функции 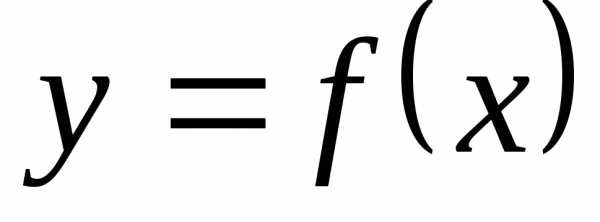 .
.
Из замечаний
следует, что горизонтальную асимптоту
можно рассматривать как частный случай
наклонной асимптоты при 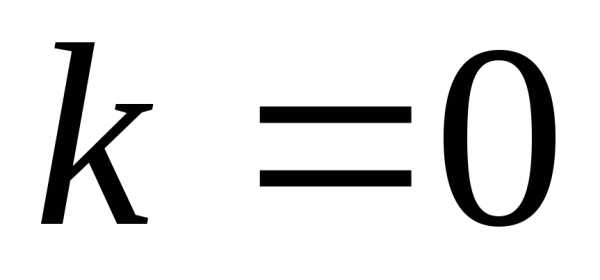 .
Поэтому при отыскании асимптот графика
функции рассматривают лишь два случая:
.
Поэтому при отыскании асимптот графика
функции рассматривают лишь два случая:
1) вертикальные асимптоты,
2) наклонные асимптоты.
Пример
Найти асимптоты
графика функции 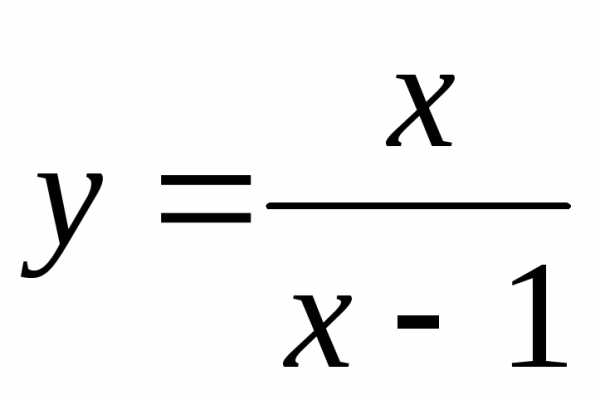
.
1)  − точка разрыва второго рода:
− точка разрыва второго рода:
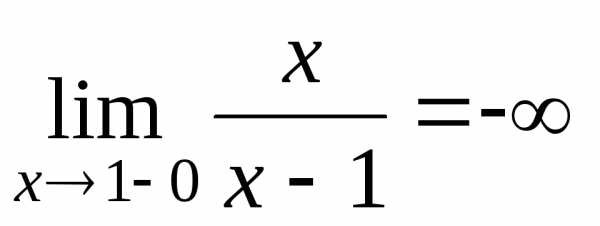 ,
, 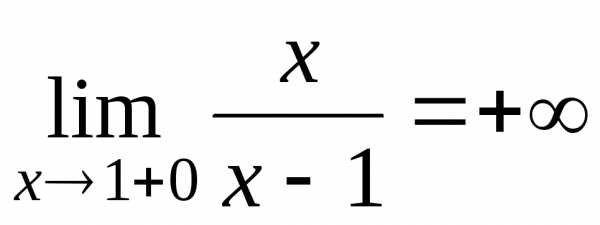 .
.
Прямая  − вертикальная асимптота.
− вертикальная асимптота.
2) ,
,
.
Прямая  − горизонтальная асимптота. Наклонной
асимптоты нет.
− горизонтальная асимптота. Наклонной
асимптоты нет.
5.6. Общая схема исследования функции и построение графика
В предыдущих параграфах было показано, как с помощью производных двух первых порядков изучаются общие свойства функции. Пользуясь результатами этого изучения, можно составить представление о характере функции и, в частности, построить ее график.
Исследование
функции 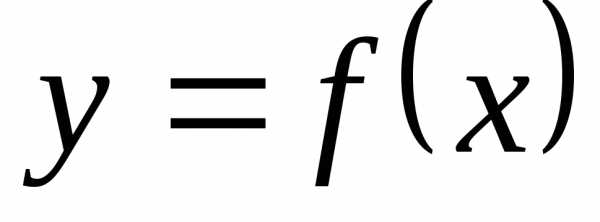 целесообразно проводить по следующей
схеме.
целесообразно проводить по следующей
схеме.
Найти область определения функции.
Исследовать функцию на четность и нечетность.
Исследовать функцию на периодичность.
Найти точки пересечения графика функции с осями координат.
Найти интервалы знакопостоянства функции (интервалы, на которых
 или
или ).
).Найти асимптоты графика функции.
Найти интервалы монотонности и точки экстремума функции.
Найти интервалы выпуклости и вогнутости и точки перегиба графика функции.
Построить график функции.
Пример
Исследовать функцию и построить ее график.
Область определения функции .
Функция нечетная: . График функции симметричен относительно начала координат
Функция непериодическая.
Точки пересечения с осями координат:
С осью Оу: 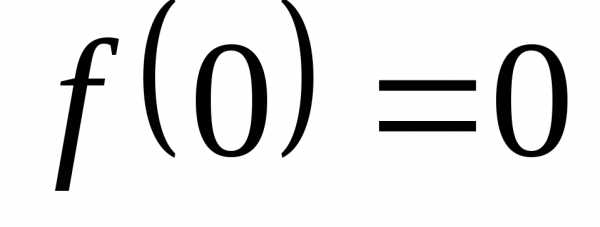 ,
точка
,
точка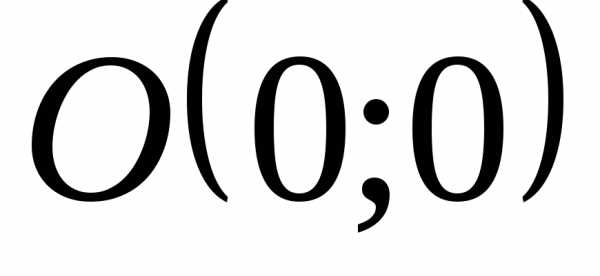 .
.
С осью Ох:
,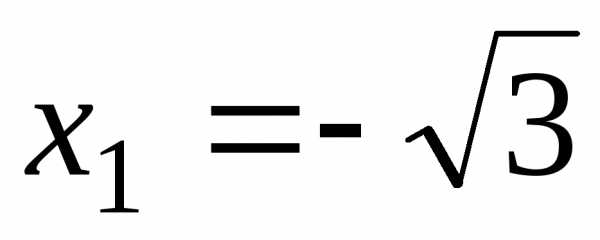 ,
,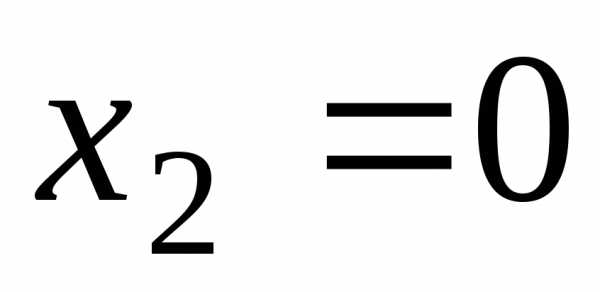 ,
,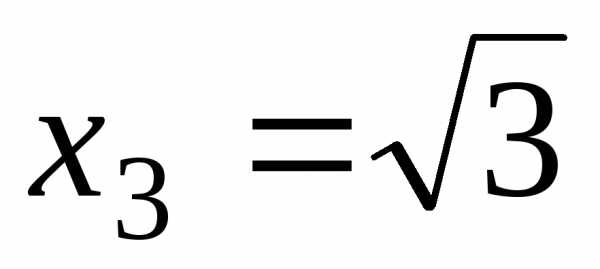 .
.
Точки
 ,
, и
и разбивают осьОх на четыре интервала.
разбивают осьОх на четыре интервала.
 при
;
при
;
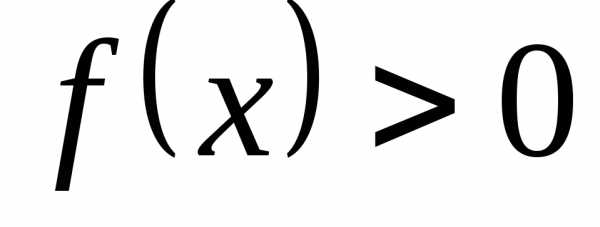 при
;
при
;
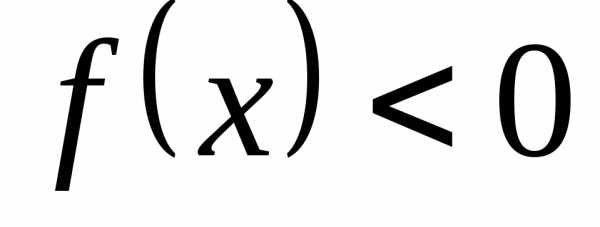 при
при 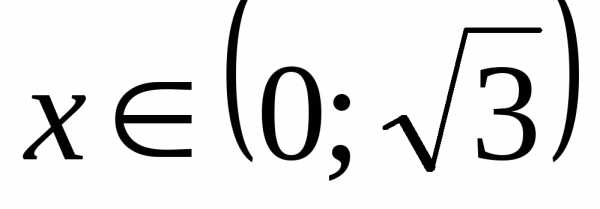 ;
;
 при
.
при
.
Так как функция является непрерывной, то ее график не имеет вертикальных асимптот.
.
Наклонной и горизонтальной асимптот нет.
,
,  ,
,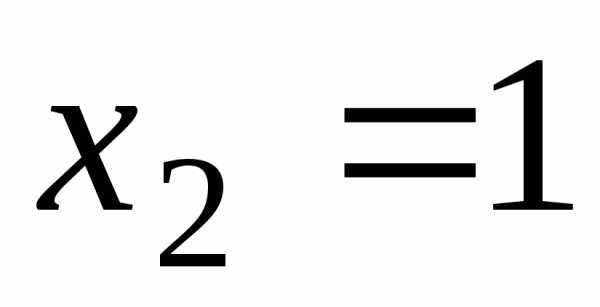 − критические точки.
− критические точки.
 для
«↑»,
для
«↑»,
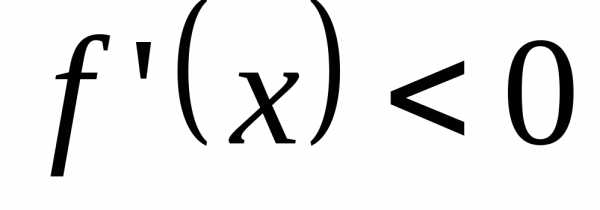 для
«↓»,
для
«↓»,
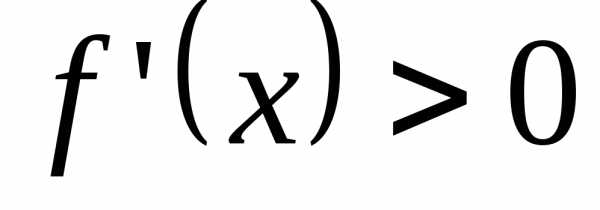 для
«↑».
для
«↑».
Сведем данные в таблицу.
х | | -1 | | 1 | |
| + | 0 | − | 0 | + |
| ↑ (возрастает) | mах 2 | ↓ (убывает) | min -2 | ↑ (возрастает) |
, ;
точка − максимум;
точка 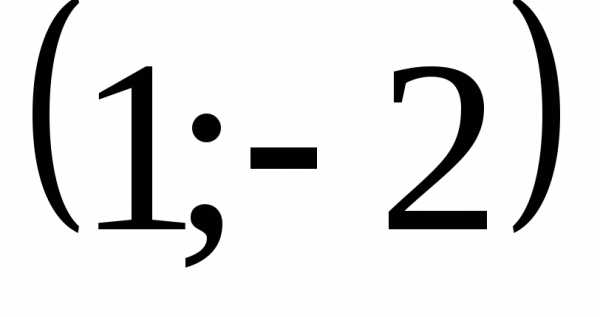 − минимум.
− минимум.
, ,
 ,
, .
.
при
« »;
»;
при
« ».
».
х | | 0 | |
| − | 0 | + |
| (выпуклый) | 0 (точка перегиба) | (вогнутый) |
Точка 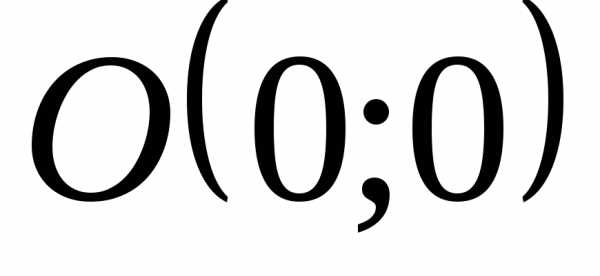 − точка перегиба.
− точка перегиба.
График функции (рис.5.12)
Рис. 5.12
studfiles.net
Как найти асимптоты
Асимптоты обычно находят, когда нужно построить график функции.
Существует несколько видов асимптот по их расположению.
Вертикальную асимптоту можно задать уравнением , где а — любое число.
Наклонная асимптота описывается уравнением прямой с угловым коэффициентом: .
Горизонтальная асимптота является частным случаем наклонной асимптоты, когда угловой коэффициент равен нулю: .
Если требуется найти асимптоты графика функции, значит нужно найти их все. Асимптот у функции может не быть вообще, может быть одна, две и более.
Рассмотрим пример нахождения асимптот.
Пример.
Найдем асимптоты графика функции .
Решение:
Сначала проверим, имеет ли функция вертикальные асимптоты. Для этого проверим, при каких значениях знаменатель дроби будет равен нулю:
Таким образом, функция при не существует.
Определим, является ли прямая вертикальной асимптотой графика функции . Для этого найдем односторонние пределы. Подставим вместо переменной х выражение :
Получили бесконечный левосторонний предел.
Найдем правосторонний предел, чтобы понять, как располагается график функции:
Таким образом, бесконечность односторонних пределов указывает на то, что прямая — вертикальная асимптота графика функции при .
Теперь проверим, имеет ли заданная функция наклонные асимптоты:
При получаем частный случай наклонной асимптоты — горизонтальную асимптоту.
Так как получен конечный первый предел, нужно найти второй предел:
Получили конечный второй предел.
Таким образом, наклонной асимптотой будет:
Ответ. Вертикальная асимптота , горизонтальная асимптота .
ru.solverbook.com
Асимптоты функции
Определение асимптот функции не такое и трудное занятие если Вы хорошо знаете ряд правил и имеете добрые знания вычисления пределов. Если же не умеете находить пределы то наверстывать придется много, но научиться можно.
Прямая называется асимптотой кривой если точка кривой неограниченно приближается к ней при росте абсциссы или ординаты. Асимптоты разделяют на вертикальные, наклонные (горизонтальные) асимптоты.
ВЕРТИКАЛЬНЫЕ АСИМПТОТЫ
График функции при аргументе котрый стремится к точке имеет вертикальную асимптоту, если предел функции в ней бесконечен
Кроме этого точка является точкой разрыва II рода, а уравнение вертикальной асимптоты имеет вид
НАКЛОННЫЕ АСИМПТОТЫ
Уравнение наклонной асимптоты имеет вид
где — пределы, которые вычисляются по правилу
Если оба пределы существуют и конечны то функция имеет наклонную асимптоту, иначе — нет. Следует отдельно рассматривать случаи, когда аргумент стремится к бесконечности () и минус бесконечности ().
ГОРИЗОНТАЛЬНЫЕ АСИМПТОТЫ
Кривая имеет горизонтальную асимптоту только в том случае, когда существует конечный предел функции при и , и эта граница равна
или
Нахождение пределов в некоторых случаях упрощается, если применять правило Лопиталя.
Приведем решения типичных для практики задач на отыскание асимптот.
————————————
Примеры.
Найти асимптоты функций (Дубовик В.П., Юрик И.И. «Высшая математика. Сборник задач»)
І. (5.863)
Решение:
Знаменатель дроби не должен превращаться в ноль
По теореме Виета находим корни квадратного уравнения
Они разбивают область определения на следующие интервалы
Другим выводом является то, что функция имеет две вертикальные асимптоты
Найдем наклонную асимптоту
Первая граница примет вид
Другую определяем по правилу
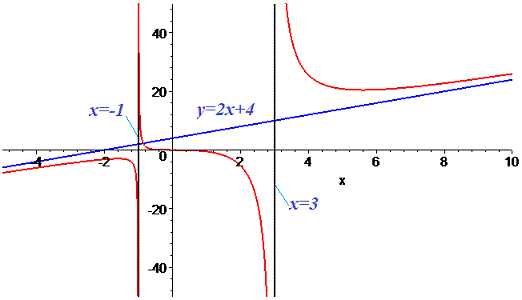
Окончательное уравнение наклонной асимптоты следующее
График функции с асимптотами имеет вид
————————————
ІІ. (5.873)
Решение:
Логарифм функция определена при положительных значениях аргумента и стремится к бесконечности при , это означает
Из этого следует что функция имеет вертикальные асимптоты при
а ее область определения следующая
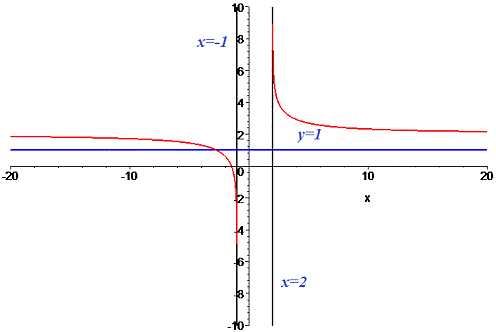
С виду функции следует что функция имеет вертикальную асимптоту
Наклонных асимптот функция не имеет. График функции с асимптотами приведен ниже
————————————
(Клепко В.Ю., Голец В.И. «Высшая математика в примерах и задачах»)
III. (4.71.1)
Решение:
С виду функции следует что она определена во всех точках где знаменатель не превращается в ноль, из этого следует
Эти точки представляют собой вертикальные асимптоты, а также разделяют область определения на интервалы
Наклонных асимптот функция не имеет. Это следует из одного свойства которым я поделюсь с Вами: функции вида «многочлен разделить на многочлен» имеет наклонную асимптоту только в случаях, когда наибольший степень в числителе на единицу больше, чем в знаменателе, т.е.
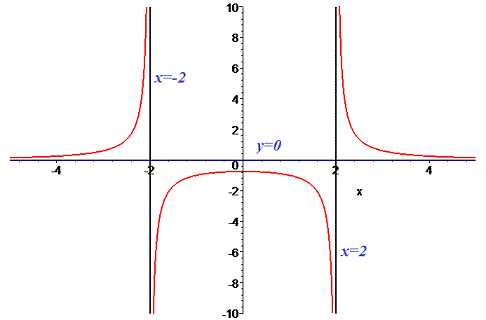
Горизонтальная асимптоту находим с границы
Функция с асимптотами изображена на рисунке
———————————
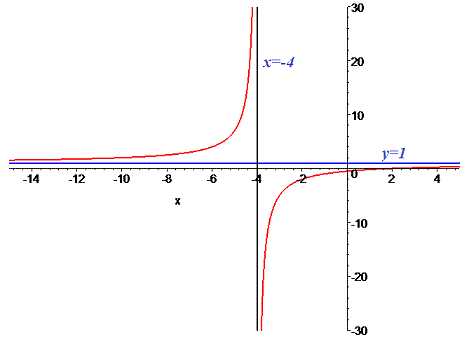
IV. (4.71.2)
Решение:
Область определения функции
При функция имеет вертикальную асимптоту. Наклонных асимптот нет, одна горизонтальная, так как степень числителя и знаменателя равны
Функция будет выглядеть следующим образом
————————————
V. (4.71.3)
Решение:
Областью определения будут два интервала
Точка будет вертикальной асимптотой. Наклонных асимптот нет, горизонтальную находим с предела
Поведение функции изображено на рисунке

—————————————————
VI. (4.71.4)
Решение:
Область определения находим из условия
Точка является вертикальной асимптотой. Наклонную асимптоту находим на основе пределов
Окончательно получим такое уравнение асимптоты
Функция с асимптотами изображена на рисунке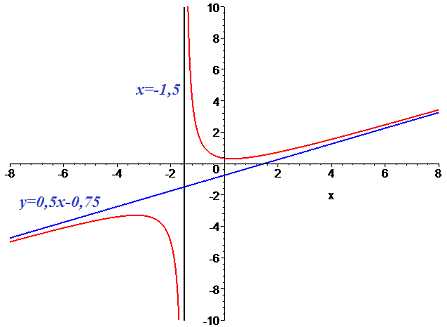
———————————————
VII. (4.71.5)
Решение:
Область определения находим с условия
Точка – вертикальная асимптота. Наклонная асимптота будет известна после вычисления пределов
– уравнение наклонной асимптоты.
График функции следующий

————————————
Подобных примеров можно решить еще много, схема нахождения асимптот при этом не меняется. Бывают
примеры в которых нахождение пределов трудоемкое и занимает более половины объема этой статьи, но
думаю Вам такие в обучении не встретятся.
————————————
Посмотреть материалы:
yukhym.com
19. Асимптоты, их нахождение. Асимптоты оэф. Схема исследования функции и построения ее графика по характерным точкам. Примеры
Определение. Асимптотой графика функции называется прямая, обладающая тем свойством, что расстояние от точкиграфика функции до этой прямой стремится к нулю при неограниченном удалении точки графика от начала координат.
По способам их отыскания выделяют три вида асимптот: вертикальные , горизонтальные, наклонные.
Очевидно, горизонтальные являются частными случаями наклонных (при ).


Нахождение асимптот графика функции основано на следующих утверждениях.
Теорема 1. Пусть функция определена хотя бы в некоторой полуокрестности точкии хотя бы один из ее односторонних пределов в этой точке бесконечен, т.е. равенили. Тогда прямаяявляется вертикальной асимптотой графика функции.
Таким образом, вертикальные асимптоты графика функции следует искать в точках разрыва функции или на концах ее области определения (если это конечные числа).
Теорема 2. Пусть функция определена при значениях аргумента, достаточно больших по абсолютной величине, и существует конечный предел функции. Тогда прямаяесть горизонтальная асимптота графика функции.
Может случиться, что , а, причеми- конечные числа, тогда график имеет две различные горизонтальные асимптоты: левостороннюю и правостороннюю. Если же существует лишь один из конечных пределов или, то график имеет либо одну левостороннюю, либо одну правостороннюю горизонтальную асимптоту.
Теорема 3. Пусть функция определена при значениях аргумента, достаточно больших по абсолютной величине, и существуют конечные пределыи. Тогда прямаяявляется наклонной асимптотой графика функции.
Заметим, что если хотя бы один из указанных пределов бесконечен, то наклонной асимптоты нет.
Наклонная асимптота так же, как и горизонтальная, может быть односторонней.
Пример. Найдите все асимптоты графика функции .
Решение.
Функция определена при . Найдем ее односторонние пределы в точках.
Так как и(два других односторонних предела можно уже не находить), то прямыеиявляются вертикальными асимптотами графика функции.
Вычислим
(применим правило Лопиталя) =.
Значит, прямая — горизонтальная асимптота.
Так как горизонтальная асимптота существует, то наклонные уже не ищем (их нет).
 Ответ:
график имеет две вертикальные асимптоты
и одну горизонтальную.
Ответ:
график имеет две вертикальные асимптоты
и одну горизонтальную.
Общие исследование функции y = f(x).
Область определения функции. Найти ее область определения D(f) . Если это не слишком сложно, то полезно найти также область значений E(f) . (Однако, во многих случаях, вопрос нахождения E(f) откладывается до нахождения экстремумов функции.)
Особые свойства функции. Выяснить общие свойства функции: четность, нечетность, периодичность и т.п. Не любая функция обладает такими свойствами, как четность либо нечетность. Функция заведомо не является ни четной, ни нечетной, если ее область определения несимметрична относительно точки 0 на оси Ox. Точно так же, у любой периодической функции область определения состоит либо из всей вещественной оси, либо из объединения периодически повторяющихся систем промежутков.
Вертикальные асимптоты. Выяснить, как ведёт себя функция при приближении аргумента к граничным точкам области определенияD(f), если такие граничные точки имеются. При этом могут обнаружиться вертикальные асимптоты. Если функция имеет такие точки разрыва, в которых она не определена, то эти точки тоже проверить на наличие вертикальных асимптот функции.
Наклонные и горизонтальные асимптоты. Если область определения D(f) вклоючает в себя лучи вида (a;+) или (−;b), то можно попытаться найти наклонные асимптоты (или горизонтальные асимптоты) при x+или x−соответственно, т.е. найти limxf(x).Наклонные асимптоты: y = kx + b, где k=limx+xf(x) и b=limx+(f(x)−x).Горизонтальны асимптоты: y = b, где limxf(x)=b.
Нахождение точек пересечения графика с осями. Нахождение точки пересечения графика с осью Oy. Для этого нужно вычислить значение f(0). Найти также точки пересечения графика с осью Ox, для чего найти корни уравнения f(x) = 0 (или убедиться в отсутствии корней). Уравнение часто удается решить лишь приближунно, но уже отделение корней помогает лучше уяснить строение графика. Далее, нужно определить знак функции на промежутках между корнями и точками разрыва.
Нахождение точек пересечения графика с асимптотой. В некоторых случаях бывает нужно найти характерные точки графика, которые не были упомянуты в предыдущих пунктах. Например, если функция имеет наклонную асимптоту, то можно попытаться выяснить, нет ли точек пересечения графика с этой асимптотой.
Нахождение интервалов выпуклости и вогнутости. Это делается с помощью исследования знака второй производной f(x). Найти точки перегиба на стыках интервалов выпуклости и вогнутости. Вычислить значение функции в точках перегиба. Если функция имеет другие точки непрерывности (кроме точек перегиба), в которых вторая производная равна 0 либо не существует, то в этих точках также полезно вычислить значение функции. Найдя f(x) , мы решаем неравенство f(x)0. На каждом из интервалов решения функция будет выпуклой вниз. Решая обратное неравенство f(x)0, мы находим интервалы, на которых функция выпукла вверх (то есть вогнута). Определяем точки перегиба как те точки, в которых функция меняет направление выпуклости (и непрерывна).
studfiles.net
Подготовка школьников к ЕГЭ в учебном центре «Резольвента» (Справочник по математике — Элементы математического анализа
Вертикальные асимптоты
Во многих разделах нашего справочника приведены графики различных функций. Для многих функций существуют прямые, к которым графики функций неограниченно приближаются. Такие прямые называют асимптотами, и их точное определение мы дадим чуть позже. Как мы увидим далее, асимптоты бывают вертикальными, горизонтальными и наклонными. С вертикальными и горизонтальными асимптотами графика функции мы уже встречались, в частности, в разделе «Гипербола на координатной плоскости. График дробно-линейной функции». С наклонными асимптотами, за исключением горизонтальных, мы пока еще дела не имели.
Определение 1. Говорят, что x стремится к x0 слева и обозначают
x → x0 – 0 ,
если x стремится к x0 и x меньше x0 .
Говорят, что x стремится к x0 справа и обозначают
x → x0 + 0 ,
если x стремится к x0 и x больше x0 .
Определение 2. Прямую
x = c
называют вертикальной асимптотой графика функции y = f (x) при x , стремящемся к с справа, если функция y = f (x) определена на некотором интервале (с, d) и выполнено соотношение выполнено соотношение
при x → c + 0
Прямую
x = с
называют вертикальной асимптотой графика функции y = f (x) при x , стремящемся к с слева, если функция y = f (x) определена на некотором интервале (d, c) и выполнено соотношение выполнено соотношение
при x → c – 0
Пример 1. Прямая
x = 2
является вертикальной асимптотой графика функции
как справа, так и слева (рис. 1)
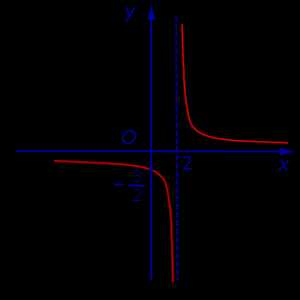
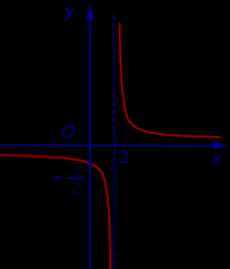
Рис.1
Пример 2. Прямая
x = 0
является вертикальной асимптотой графика функции
y = ln x
при x , стремящемся к 0 справа (рис. 2)
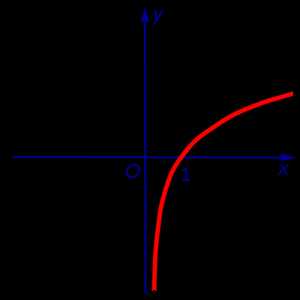

Рис.2
Наклонные асимптоты
Определение 3. Прямую
y = kx + b
называют наклонной асимптотой графика функции y = f (x) при x , стремящемся к , если функция y = f (x) определена на некотором интервале и выполнено соотношение выполнено соотношение
Прямую
y = kx + b
называют наклонной асимптотой графика функции y = f (x) при x , стремящемся к , если функция y = f (x) определена на некотором интервале и выполнено соотношение выполнено соотношение
Горизонтальные асимптоты как частный случай наклонных асимптот
Определение 4. Прямую
y = b
называют горизотальной асимптотой графика функции y = f (x) при x , стремящемся к , если функция y = f (x) определена на некотором интервале и выполнено соотношение выполнено соотношение
Прямую
y = b
называют горизотальной асимптотой графика функции y f (x) при x , стремящемся к , если функция y = f (x) определена на некотором интервале и выполнено соотношение выполнено соотношение
Замечание. Из определений 3 и 5 вытекает, что горизонтальная асимптота является частным случаем наклонной асимптоты y = kx + b, когда угловой коэффициент прямой k = 0 .
Пример 3. Прямая
y = 3
является горизонтальной асимптотой графика функции
как при x , стремящемся к , так и при x , стремящемся к (рис. 3)

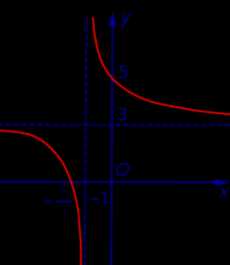
Рис.3
Пример 4. Прямая
y = 0
является горизонтальной асимптотой графика функции
y = 2x
при x , стремящемся к (рис. 4)


Рис.4
Пример 5. График функции y = arctg x (рис.5)
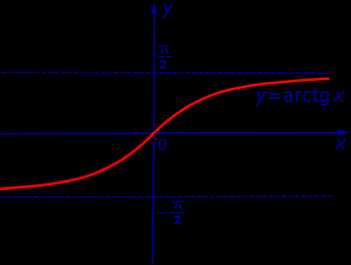
Рис.5
имеет две горизонтальные асимптоты: прямая
является горизонтальной асимптотой графика функции при , а прямая
является горизонтальной асимптотой графика функции при .
Поиск наклонных асимптот графиков функций
Для того, чтобы найти наклонную асимптоту графика функции y = f (x) при (или убедиться, что наклонной асимптоты при не существует), нужно совершить 2 операции.
Первая операция. Вычислим предел предел
| (1) |
Если предел (1) не существует или существует, но равен существует, но равен, то делаем вывод о том, что у графика функции y = f (x) при наклонных асимптот нет.
Если предел (1) существует и равен некоторому числу предел (1) существует и равен некоторому числу, то, обозначив это число буквой k ,
переходим ко второй операции.
Вторая операция. Вычислим предел предел
| (2) |
Если предел (2) не существует или существует, но равен существует, но равен, то делаем вывод о том, что у графика функции y = f (x) при наклонных асимптот нет.
Если предел (2) существует и равен некоторому числу предел (2) существует и равен некоторому числу, то, обозначив это число буквой b ,
делаем вывод о том, что прямая
y = kx + b
является наклонной асимптотой графика функции y = f (x) при .
Совершенно аналогично поступаем для того, чтобы найти наклонную асимптоту графика функции y = f (x) при (или убедиться, что наклонной асимптоты при не существует).
Первая операция. Вычислим предел предел
| (3) |
Если предел (3) не существует или существует, но равен существует, но равен, то делаем вывод о том, что у графика функции y = f (x) при наклонных асимптот нет.
Если предел (3) существует и равен некоторому числу предел (3) существует и равен некоторому числу, то, обозначив это число буквой k ,
переходим ко второй операции.
Вторая операция. Вычислим предел предел
| (4) |
Если предел (4) не существует или существует, но равен существует, но равен, то делаем вывод о том, что у графика функции y = f (x) при наклонных асимптот нет.
Если предел (4) существует и равен некоторому числу предел (4) существует и равен некоторому числу, то, обозначив это число буквой b ,
делаем вывод о том, что прямая
y = kx + b
является наклонной асимптотой графика функции y = f (x) при .
Пример 5. Найти асимптоты графика функции
| (5) |
и построить график этой функции.
Решение. Функция (5) определена для всех и вертикальных асимптот не имеет.
Найдем наклонные асимптоты графика функции (5). При получаем

Отсюда вытекает, что прямая
y = x
– наклонная асимптота графика функции (5) при .
При получаем

Отсюда вытекает, что прямая
y = – x
– наклонная асимптота графика функции (5) при .
Функция (5) является четной функцией, поэтому ее график симметричен относительно оси ординат.
Найдем производную функции (5):
. .
.Итак, y’ > 0 при x > 0 , y’ < 0 при x < 0 , y’ = 0 при x = 0 . Точка x = 0 – стационарная, причем производная функции (5) при переходе через точку x = 0 меняет знак с «–» на «+» . Следовательно, x = 0 – точка минимума функции (5). Других критических точек у функции (5) нет.
Теперь мы уже можем построить график функции (5):

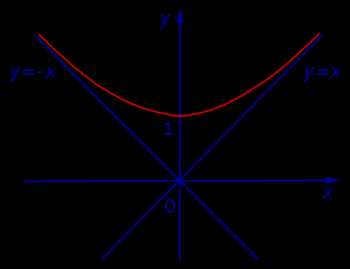
Рис.6
Заметим, что график функции (5) находится выше асимптот y = x и y =v– x , поскольку справедливо неравенство:
.
На нашем сайте можно также ознакомиться с разработанными преподавателями учебного центра «Резольвента» учебными материалами для подготовки к ЕГЭ по математике.
Приглашаем школьников (можно вместе с родителями) на бесплатное тестирование по математике, позволяющее выяснить, какие разделы математики и навыки в решении задач являются для ученика «проблемными». Запись по телефону (495) 509-28-10 |
Для школьников, желающих хорошо подготовиться и сдать ЕГЭ по математике или русскому языку на высокий балл, учебный центр «Резольвента» проводит
У нас также для школьников организованы
МОСКВА, СВАО, Учебный центр «РЕЗОЛЬВЕНТА»
www.resolventa.ru
Разузнай! — Как находить асимптоты функции
|
Процесс нахождения асимптот является одним из базовых этапов исследования функции, который позволяет более подробно изучить её свойства. Для нахождения асимптот различных функций существуют типовые методики, однако, прежде чем их освоить необходимо чётко себе представлять то, какой смысл вкладывается в понятие асимптоты, в силу чего следует чётко сформулировать определение этого понятия.
Асимптотой функции считают такую прямую, к которой бесконечно стремится её график, но никогда с ней не совпадает. Иными словами, основное свойство асимптоты заключается в том, что расстояние от неё до точки графика функции стремится к нулевому значению, при бесконечно большом перемещении данной точки вдоль ветви графика. Следовательно, с их помощью можно определить либо максимально возможное значение непрерывной функции при бесконечном значении аргумента либо наоборот, предельно возможное значение аргумента, при котором график функции стремится к бесконечности. Следует отметить также то, что в зависимости от того либо иного типа графика, асимптоты могут быть трёх основных видов:
- Вертикальные.
- Горизонтальные.
- Наклонные.
Опираясь на всё вышесказанное, можно записать определение различных видов асимптот с помощью языка математики. В этом случае вертикальная асимптота функции y=f(x) будет представлять из себя вертикальную прямую x=a, при том условии, что f(x)→+∞ либо f(x)→-∞ и одновременно x→a.
Используя понятие предела можно записать общее определение вертикальной асимптоты единым выражением вида lim f(x)»x→a»=+-∞. Исходя из этого можно сказать, что вертикальные асимптоты функции, которых как правило две, будет проходить через те точки горизонтальной оси координат, на которых максимально возможное значение функции стремится к плюс либо минус бесконечности.
Более интересным процессом является определение наклонной асимптоты функции, которая по своей сути является прямой линией вида y=kx+b, при том условии, что существуют следующие пределы:
- lim f(x)/x»x→+-∞»=k
- lim (f(x)-kx)»x→+-∞»=b
Резюмируя вышесказанное можно сделать вывод, что определение наклонной асимптоты функции сводится к нахождению двух этих пределов. Необходимо уточнить, что в тех случаях, когда хоть один из вышеуказаных пределов не существует либо неопределён, то наклонной асимптоты такая функция не имеет при абсолютно любых значениях x.
В заключении хотелось бы упомянуть о определении горизонтальной асимптоты, которая является ничем иным, как частным случаем наклонной, при k=0. В общем виде, горизонтальная асимптота представляет из себя прямую линию вида y=b, при том условии, что существует предел lim f(x)»x→+-∞»=b. В силу этого можно утверждать, что определение горизонтальных асимптот сводится к нахождению предельных значений функции при неограниченном возрастании значения аргумента. Интересным является и тот факт, что у любой функции не может быть более двух как наклонных, так и горизонтальных асимптот.
Видео как находить асимптоты функции
- < Как сделать объемную снежинку из бумаги
- Правило буравчика >
razuznai.ru

 или
или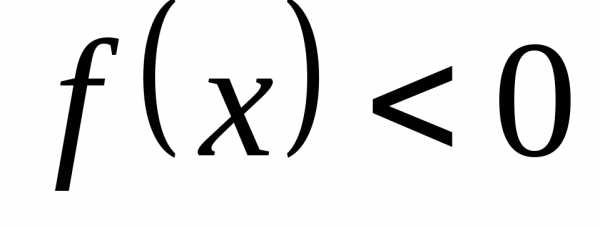 ).
).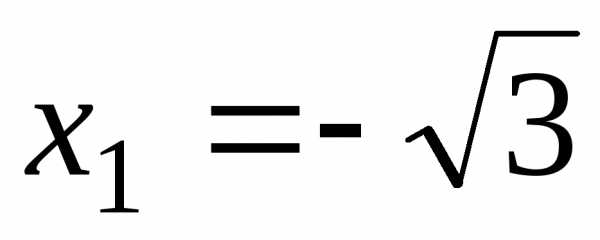 ,
,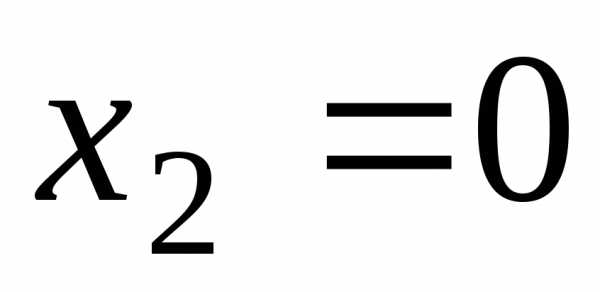 и
и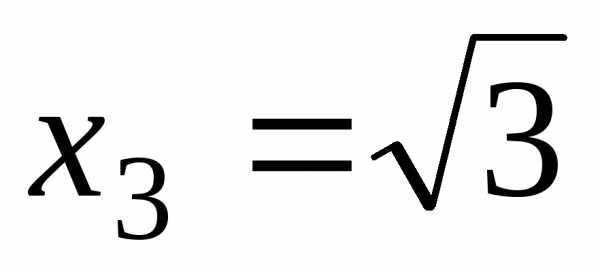 разбивают осьОх на четыре интервала.
разбивают осьОх на четыре интервала.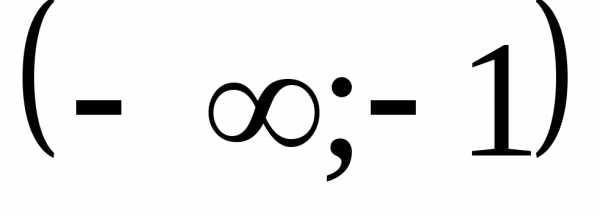


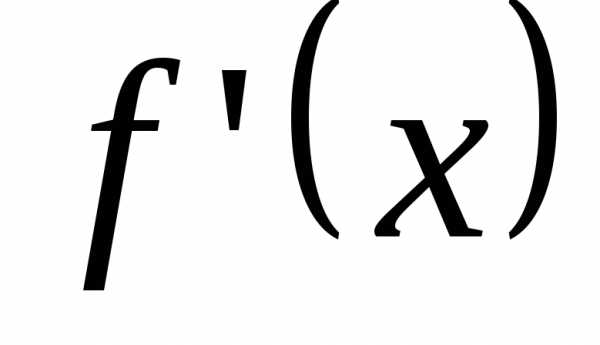
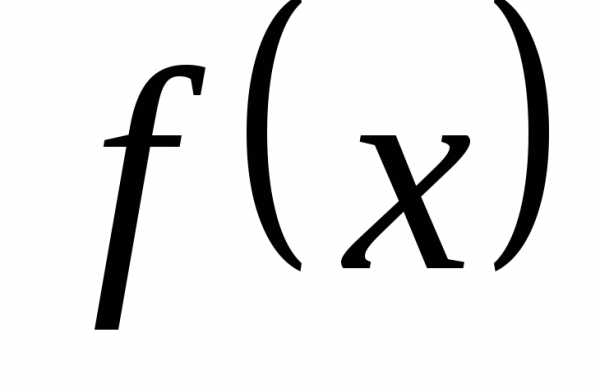
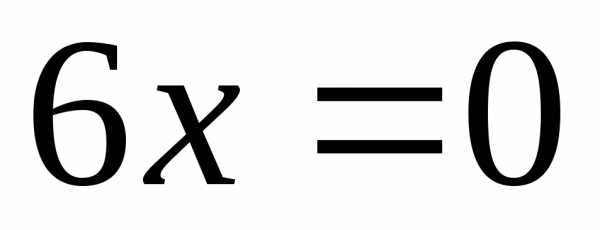 ,
,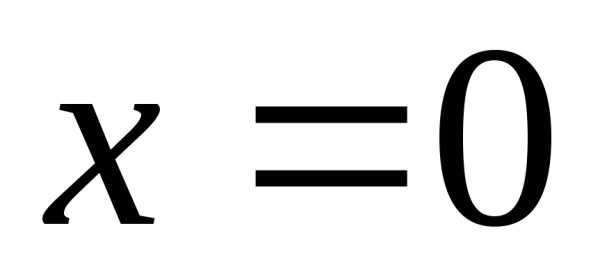 .
.