3.2. Градиент функции | Решение задач по математике и другим предметам!!
При изучении скалярных полей наряду с функций рассматривается некоторый вектор, тесно связанный с этой функцией, — градиент скалярного поля.
Градиентом в точке скалярного поля, заданного дифференцируемой функцией , называется вектор, равный
.
Таким образом, каждой точке скалярного поля, заданного дифференцируемой функцией , соответствует не только значение этой функции, но и вполне определенный вектор .
Между градиентом функции в данной точке и производной по направлению в той же точке имеется связь, которая устанавливается следующей теоремой.
Теорема. Проекция вектора На единичный вектор равна производной функции по направлению :
.
Доказательство. Пусть . Из векторной алгебры известно, что проекция какого-либо вектора на другой вектор равна скалярному произведению этих векторов.
Так как , , то
.
Учитывая, что производная по направлению выражает скорость изменения скалярного поля в этом направлении, можно сказать, что проекция на вектор равна скорости изменения поля в направлении вектора .
Обозначим через угол между единичным вектором и . Тогда .
Поэтому .
Если направления векторов и совпадают (), то производная по направлению имеет, очевидно, наибольшее значение, равное .
Таким образом, есть вектор, указывающий Направление наибольшего возрастания поля в данной точке и имеющий Модуль равный скорости этого возрастания.
Рассмотрим кривую , лежащую на поверхности уровня и проходящую через точку . Градиент функции в точке обладает следующими свойствами: перпендикулярен к вектору , направленному по касательной к кривой в точке .
В случае плоского скалярного поля, заданного дифференцируемой функцией двух переменных , градиент определяется формулой
.
Его связь с производной по направлению выражается равенством
,
Где — угол между единичным вектором и . Вектор перпендикулярен к касательной, проведенной к линии уровня в точке .
Пример 16. Найти наибольшую скорость возрастания функции
в точке .
Решение. Наибольшая скорость возрастания функции равна модулю градиента этой функции. Найдем градиент функции :
,
.
В точке имеем .
Тогда наибольшая скорость возрастания функции равна
.
Пример 17. Найти скорость изменения скалярного поля, определяемого функцией в точке в направлении касательной, проведенной к параболе в этой точке в сторону возрастания координаты , и наибольшую скорость изменения поля в этой точке.
Решение. Скорость изменения скалярного поля в заданном направлении есть производная скалярного поля по направлению вектора , задающего направление.
,
Где ; — направляющие косинусы вектора , . Вектор возьмем на касательной к параболе в , для чего составим уравнение касательной
,
,
— уравнение касательной.
На найденной касательной возьмем точку с любой координатой (), например . Тогда
.
Найдем значения производной по направлению в точке :
,
.
Тогда .
Наибольшая скорость изменения поля в точке есть .
Так как , то
.
Величина наибольшей скорости
.
| < Предыдущая | Следующая > |
|---|
matica.org.ua
МА. Производная по направлению. Градиент
Теоретический минимумПереход от анализа функций одной переменной к анализу функций многих переменных — по крайней мере двух — приводит к значительному
усложнению теории. Помимо прочего теряется наглядность: если функция в общем случае задаёт кривую на плоскости, функция
С другой стороны теоретическое описание функций трёх и большего числа переменных уже принципиально не отличается от описания функций
двух переменных. Поэтому удобно вводить новые понятия именно на основе функций двух переменных, ещё позволяющих наглядно пояснять смысл
нововведений. Так поступим и при определении производной по направлению.
Напомним, что производная функции имеет простой геометрический смысл. Величина в точке равна угловому
коэффициенту касательной к графику этой функции в данной точке. Чем больше этот угловой коэффициент, тем больше угол, который составляет
касательная к графику с осью абсцисс. Чем больше этот угол, тем быстрее меняется функция в малой окрестности рассматриваемой точки. Таким образом,
производная позволяет определять скорость изменения функции.
Теперь обратимся к функции двух переменных. Она, как уже говорилось, определяет поверхность. Выберем точку этой поверхности и зададимся
вопросом о скорости изменения функции в этой точке. Здесь должно быть понятно, что вопрос сформулирован слишком грубо. Когда такой вопрос
ставился в отношении функции одной переменной, то там никаких проблем не было: аргумент мог изменяться только вдоль оси абсцисс. Если же у
функции хотя бы два аргумента, то её изменение определяется уже поведением двух аргументов. В связи с этим в вопрос о скорости изменения
функции следует ввести дополнение, задав направление, в котором будут изменяться её аргументы.
Начнём с частных случаев, а для примера возьмём известную из аналитической геометрии поверхность, которая задаётся уравнением
Поверхность представляет собой т.н. гиперболический параболоид (см. рис. 1).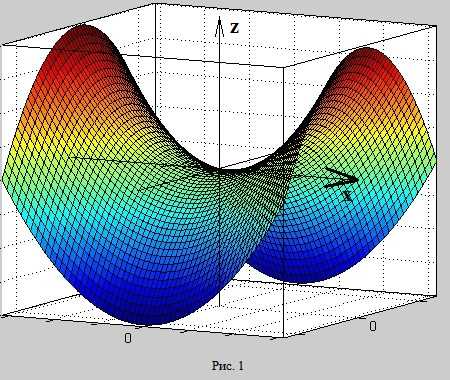
Исследуем поведение функции в точке и её малой окрестности. Например, рассмотрим изменение этой функции
вдоль оси абсцисс. С геометрической точки зрения мы проводим плоскость ; с точки зрения формальной мы фиксируем один аргумент и
фактически переходим к функции одной переменной. А как исследовать функцию одной переменной известно — для этого существует понятие
производной. В терминологии анализа функций нескольких переменных производная функции по одной переменной при фиксированных остальных —
частная производная. Таким образом, в нашем примере скорость изменения функции в точке в направлении оси абсцисс
позволяет определить частная производная . Более того, мы можем расширить возможности этого инструмента. 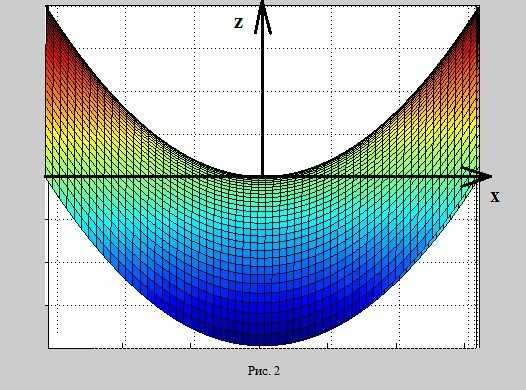
Чтобы пояснить это, рассмотрим сечение параболоида плоскостью (см. рис. 2 — там сечение ограничивает вид поверхности сверху).
Это обычная парабола . Эта функция убывает при отрицательных значениях и возрастает при положительных значениях —
направлению оси абсцисс — и тогда всё будет наоборот! При функция будет убывать, а при — возрастать. А частная производная
в данном случае даёт только правильную количественную характеристику скорости изменения функции, но неправильно определяет
характер монотонности. Это говорит о том, что всё-таки одной частной производной в данном случае недостаточно. Тем более что мы ведь
рассмотрели только удобный частный случай. Есть и второй удобный частный случай: рассмотреть изменение функции в направлении оси ординат —
там главную роль будет играть частная производная . Но как исследовать скорость изменения функции в произвольном направлении,
составляющем с осью абсцисс угол ?
Вот для этого и вводится понятие производной по направлению. Строгое определение таково:
Несложно понять его структуру: она полностью аналогична структуре производной функции одной переменной. Действительно, по своей сути
производная — отношение приращения функции к вызвавшему его приращению аргумента. В случае функции одной переменной рассматривается
одна-единственная возможность изменения аргумента — в направлении оси абсцисс. В анализе функций одной переменной это естественное
направление. Когда аргументов становится больше, например, два, то нужно задать изменение аргумента в произвольном направлении.
Именно так и устроены аргументы у первого слагаемого в числителе дроби. Там написано положение точки, смещённой от точки
по прямой, составляющей с осью абсцисс угол . Таким образом, в числителе дроби под пределом написано приращение функции при
смещении в направлении, составляющем с осью абсцисс угол , в знаменателе находится параметр, описывающий величину смещения
аргументов в этом направлении.
Как обычно, по определению считать производную неудобно, поэтому доказывается следующая простая формула:
.
Обратите внимание: если вычисляем производную в направлении оси абсцисс, то , и получается частная производная по переменной .
Если же мы хотим вычислять производную в противоположном направлении, то , и частная производная приобретает знак минус.
При дифференцировании вдоль оси ординат производная по этому направлению совпадает с частной производной по переменной (угол ).
Теперь можно и обобщить на случай трёх аргументов (а там уже будет ясно обобщение на любое число переменных). В трёхмерном случае направление
определяется направляющими косинусами — косинусами углов, которые направление составляет с осями координат.
.
Заметим, что введение направляющего вектора даёт возможность записать производную по направлению в виде
скалярного произведения:
,
где .
Этот вектор называется градиентом функции . Свойства градиента подробнее рассматриваются в векторном анализе. Здесь остановимся
со смыслом производной функции одного аргумента. Величина производной характеризует скорость изменения функции в данной точке
в данном направлении. В каком-то направлении функция может изменяться быстрее, в каком-то медленнее. В направлении самого быстрого
изменения функции производная будет самая большая по модулю. С другой стороны производная по направлению — скалярное произведение
градиента функции и направляющего вектора данного направления:
.
Наибольшего значения это произведение достигает, когда косинус в правой части становится равным единице. А это возможно при
совпадении направления вектора и градиента функции. Следовательно, направление градиента функции и направлении,
при дифференцировании вдоль которого производная наибольшая, совпадают. Иными словами, градиент направлен в сторону скорейшего
Примеры.
Пример 1. Вычисление производной по направлению.
Найдём производную функции в точке в направлении, составляющем угол 60 градусов с осью абсцисс.
Направляющие косинусы в данном случае , частные производные
.
Таким образом,
.
В качестве несложного упражнения можно вычислить эту производную по определению.
Пример 2. Градиент.
Вычислим градиент модуля радиус-вектора точки, т.е. функции .
Фактически требуется вычислить три частные производные:
.
Заметим, что эту формулу можно записать короче:
.
Она часто используется при вычислениях в векторном анализе.
Пример 3. Геометрический смысл градиента.
Для разнообразия приведём пример из физики, с помощью которого хотелось бы показать, как важно для понимания физических законов
хорошо знать математику. Пример, в действительности, хрестоматийный — закон теплопроводности или закон Фурье. Закон выражает плотность
потока тепла (по модулю это количество теплоты, которое переносится через единичную площадку за единицу времени) через
градиент температуры:
,
где — константа (для изотропной среды), называемая коэффициентом теплопроводности.
Оставляя в стороне количественное соотношение, утверждаемое этим эмпирическим законом, отметим, что в законе чётко прописано направление
переноса тепла. Так как градиент направлен в сторону скорейшего возрастания функции, то градиент, взятый со знаком минус, показывает
направление скорейшего убывания функции. Следовательно, в законе Фурье заложено распространение тепла в направлении скорейшего
убывания температуры.
corum.mephist.ru
Линия уровня функции, градиент и производная : Чулан (М)
Доброго времени суток… подскажите, пожалуйста… немного запутался… Напишу сначала условие задания, потом свое решение и пару вопросов… Заранее спасибо за внимание к теме.Дана функция и точки . а) Построить линию уровня функции, проходящую через точку ; б) найти градиент функции в точке ; в) найти производную функции в направлении вектора .
— собственно функция. Точки: .
Задание А я не совсем знаю как его делать, поэтому напишу его последним. Начну с Б.
б) Для того, что бы найти градиент функции, надо найти частные производные этой функции, сооветственно получаем:
;
;
следовательно градиент равен: или же .
Градиент вроде бы нашел… Теперь буду искать производную функции по направлению:
в)
;
производной функции по направлению будет являтся произведение вектора градиента в начальной точке на вектор направления, тоесть:
.
Теперь подзадание а)
Линией уровня функции является скалярное произведение вектора градиента в начальной точке и вектора направления, приравненные к нулю.
обозначим направление буквой V
Вопрос, что делать дальше? по логике приравнять к нулю… Но как?
dxdy.ru
08.3.2. Градиент | Решение задач по математике и другим предметам!!!
Рассмотрим функцию трех переменных И = F(X, у, Z), дифференцируемую в некоторой точке M(X, Y, Z).
Определение 1. Градиентом функции И = F(X, У, Z) называется вектор, координаты которого равны соответственно частным производным в точке М.
Для обозначения градиента функции используется символ
Аналогично в случае функции двух переменных И = F(X, У) Имеем
Градиент функции характеризует направление и величину максимальной скорости возрастания этой функции в точке.
Для определения геометрического смысла градиента функции введем понятие поверхности уровня. Это понятие аналогично понятию линии уровня, рассмотренному в п. 8.2.
Определение 2. Поверхностью уровня функции И = F(X, у, z) Называется поверхность, на которой эта функция сохраняет постоянное значение
В курсе математического анализа доказывается, что градиент в данной точке ортогонален к этой поверхности.
В случае функции двух переменных все сказанное выше остается в силе, только вместо поверхности уровня будет фигурировать линия уровня. Рассмотрим некоторые примеры.
Пример 5. Найти градиент и его модуль функции Z = в точке М (0, 1).
Решение. По формуле (8.8) имеем для функции двух переменных
При Х = 0 и У = 1 получаем
Пример 6. Найти градиент и его модуль функции И = x2 + у2 — z2 в точке М (1, 1, -2).
Решение. По формуле (8.7) имеем
Подставляя в это выражение координаты точки М, получаем
Пример 7. Найти поверхности уровня функции U = Х2 — 2Х + у2 + 2У — Z.
Решение. Согласно определению поверхности уровня (8.9) имеем
Где С = С + 2. Следовательно, поверхностями уровня данной функции являются параболоиды вращения с осью Х = 1, У = -1, параллельной оси Oz, вершины которых лежат в точках с координатами (1, -1, -С).
| < Предыдущая | Следующая > |
|---|
matica.org.ua
