Как решать графики функций 🚩 как решать функции и графики 🚩 Математика
Автор КакПросто!
Решать графики — задача весьма интересная, но довольно трудная. Чтобы наиболее точно построить график, удобнее пользоваться следующим алгоритмом исследования функции.

Статьи по теме:
Вам понадобится
- Линейка, карандаш, ластик
Инструкция
Для начала обозначьте область определения функции — множество всех допустимых значений переменной.
Далее для облегчения построения графика установите, является ли функция четной, нечетной или индифферентной. График четной функции будет симметричен относительно оси ординат, нечетной функции — относительно начала координат. Поэтому для построения таких графиков достаточно будет изобразить их, например, в положительной полуплоскости, а оставшуюся часть отобразить симметрично. На следующем шаге найдите асимптоты. Они бывают двух видов — вертикальные и наклонные. Вертикальные асимптоты ищите в точках разрыва функции и на концах области определения. Наклонные ищите, найдя угловой и свободный коэффициенты в формуле линейной зависимости. Далее установите экстремумы функции — максимумы и минимумы. Для этого нужно найти производную функции, затем найти ее область определения и приравнять к нулю. В полученных изолированных точках определите наличие экстремума.Определите поведение графика функции с точки зрения монотонности на каждом из полученных промежутков. Для этого достаточно посмотреть на знак производной. Если производная положительна, то функция возрастает, если отрицательна — убывает.
Для более точного исследования функции найдите точки перегиба и интервалы выпуклости функции. Для этого используйте вторую производную функции. Найдите ее область определения, приравняйте к нулю и определите наличие перегиба в полученных изолированных точках. Выпуклость графика определите, исследуя знак второй производной на каждом из полученных интервалов. Функция будет выпукла вверх, если вторая производная отрицательна, и выпукла вниз — если положительна.
Дальше найдите точки пересечения графика функции с осями координат и дополнительные точки. Они понадобятся для более точного построения графика.
Построение графика. Начать следует с изображения осей координат, обозначения области определения и изображения асимптот. Далее нанесите экстремумы и точки перегиба. Отметьте точки пересечения с осями координат и дополнительные точки. Затем плавной линией соедините отмеченные точки в соответствии с направлениями выпуклости и монотонностью.
Полезный совет
Асимптоты лучше изображать пунктиром.
Источники:
- как решать функции и графики
www.kakprosto.ru
Как решать графики функций | Сделай все сам
Решать графики – задача крайне увлекательная, но достаточно сложная. Дабы особенно верно возвести график, комфортнее пользоваться дальнейшим алгорифмом изыскания функции.

Вам понадобится
- Линейка, карандаш, ластик
Инструкция
1. Для начала обозначьте область определения функции – уйма всех возможных значений переменной.
2. Дальше для упрощения построения графика установите, является ли функция четной, нечетной либо индифферентной. График четной функции будет симметричен касательно оси ординат, нечетной функции – касательно начала координат. Следственно для построения таких графиков довольно будет изобразить их, скажем, в правильной полуплоскости, а оставшуюся часть отобразить симметрично.
3. На дальнейшем шаге обнаружьте асимптоты. Они бывают 2-х видов – вертикальные и наклонные. Вертикальные асимптоты ищите в точках обрыва функции и на концах области определения. Наклонные ищите, обнаружив угловой и вольный показатели в формуле линейной зависимости.
4. Дальше установите экстремумы функции – максимумы и минимумы. Для этого надобно обнаружить производную функции, после этого обнаружить ее область определения и приравнять к нулю. В полученных изолированных точках определите присутствие экстремума.
5. Определите поведение графика функции с точки зрения монотонности на всяком из полученных интервалов. Для этого довольно посмотреть на знак производной. Если производная правильна, то функция вырастает, если негативна – убывает.
6. Для больше точного изыскания функции обнаружьте точки перегиба и промежутки выпуклости функции. Для этого используйте вторую производную функции. Обнаружьте ее область определения, приравняйте к нулю и определите присутствие перегиба в полученных изолированных точках. Выпуклость графика определите, изучая знак 2-й производной на всяком из полученных промежутков. Функция будет выпукла вверх, если вторая производная негативна, и выпукла вниз – если правильна.
7. Дальше обнаружьте точки пересечения графика функции с осями координат и добавочные точки. Они потребуются для больше точного построения графика.
8. Построение графика. Начать следует с изображения осей координат, обозначения области определения и изображения асимптот. Дальше нанесите экстремумы и точки перегиба. Подметьте точки пересечения с осями координат и добавочные точки. После этого плавной линией объедините подмеченные точки в соответствии с направлениями выпуклости и монотонностью.
Полезный совет
Асимптоты отличнее изображать пунктиром.
jprosto.ru
Как строить графики функций 🚩 как выглядит график функции 🚩 Образование 🚩 Другое
Автор КакПросто!
Перед построением графика функции необходимо провести полное ее исследование. Поэтому стоит подробнее ознакомиться с тем, как выглядит общий алгоритм исследования функции, а также построения её графика.
Статьи по теме:
Вам понадобится
- Тетрадь, ручка, карандаш, линейка
Инструкция
Найдите область определения функции.Исследуйте функцию на четность, нечетность, периодичность.
Найдите вертикальные асимптоты.
Найдите горизонтальные и наклонные асимптоты.
Найдите точки пересечения графика функции с осями координат («нули функции»). Найдите промежутки монотонности функции (возрастания и убывания). Для этого найдите первую производную функции. Там, где производная положительна, функция возрастает, а там, где производная отрицательна, функция убывает. Точки, в которых функция непрерывна и производная равна нулю, являются точками экстремума. Если при переходе через точку экстремума производная меняет знак с плюса на минус, то это будет точка локального максимума функции. Если же при переходе через точку экстремума производная меняет знак с минуса на плюс, то это точка локального минимума функции. Вычислите значение функции в этих точках. Отметьте эти точки на графике. Схематично изобразите, где функция будет возрастать, а где убывать. Найдите интервалы выпуклости и вогнутости функции. Для этого найдите вторую производную функции, исследуйте знак второй производной. На интервалах, в которых вторая производная больше нуля, функция выпукла вниз. На интервалах, в которых вторая производная меньше нуля, функция выпукла вверх.Точки, в которых вторая производная равна нулю — точки перегиба функции. Найдите точки перегиба функции. Вычислите значение функции в этих точках. Отметьте эти точки на графике. Схематично изобразите промежутки выпуклости и вогнутости функции.
Найдите дополнительные точки функции. Оформите их в виде таблицы: значение аргумента, значение функции.
Учитывая результаты проведенного исследования, постройте график.
Полезный совет
Если необходима высокая точность графика, используйте миллиметровку.
Источники:
- как построить график функции с полным
Для построения графика заданной функции Y=f(X) необходимо провести исследование данного выражения. Строго говоря, в большинстве случаев речь идет о построении эскиза графика, т.е. некоторого фрагмента. Границы этого фрагмента определяются предельными значениями аргумента Х или самого выражения f(X), которые возможно физически отобразить на бумаге, экране и т.д.
Инструкция
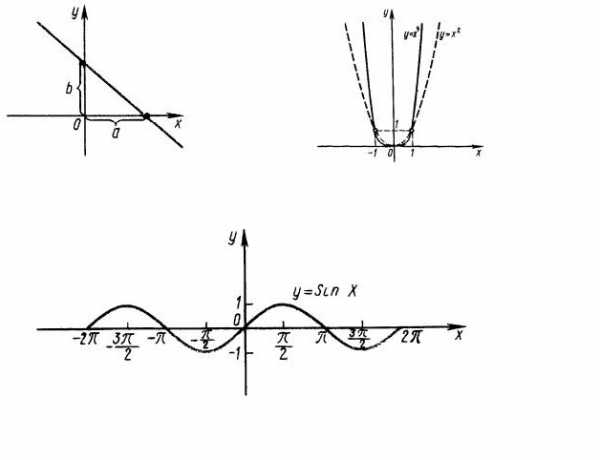
Прежде всего надо выяснить область определения функции, т.е. при каких значениях х выражение f(x) имеет значение. Для примера рассмотрим функции y=x^2, график которой изображен на рис.1. Очевидно, что областью определения функции является вся прямая OX. Областью определения функции y=sin(x) также является вся ось абсцисс (рис.1, снизу). Далее определим область значений функции, т.е. какие значения может принимать у при значениях х, принадлежащих области определения. В нашем примере значение выражения y=x^2 не может быть отрицательным, т.е. область значений нашей функции — множество неотрицательных чисел от 0 до бесконечности.Область значений функции y=sin(x) является отрезок оси OY от -1 до +1, т.к. синус любого угла не может быть больше 1.
Теперь определим четность функции. Функция является четной, если f(x)=f(-x) и нечетной, если f(-x)=-f(x). В нашем случае y=x^2 функция — четная, функция y=sin(x) — нечетная, поэтому достаточно исследовать поведение этих функций только при положительных (отрицательных) значениях аргумента.
Линейная функция у=а*х+b не обладает свойствами четности, поэтому исследовать подобные функции необходимо на всей области их определения.
Следующим шагом будет нахождение точек пересечения графика функции с осями координат.
Ось ординат (ОY) пересекается при х=0, т.е. надо найти f(0). В нашем случае f(0)=0 — графики обеих функций пересекают ось ординат в точке (0;0).
Для нахождения точки пересечения графика с осью абсцисс (нулей функции) необходимо решить уравнение f(x)=0. В первом случае это простейшее квадратное уравнение x^2=0, т.е. х=0, т.е. ось ОХ также пересекается один раз в точке (0;0).
В случае y=sin(x) ось абсцисс пересекается бесконечное число раз с шагом Пи (рис.1, снизу). Этот шаг называется периодом функции, т.е. функция является периодической.
Для нахождения эктремумов (минимальных и максимальных значений) функции можно вычислить ее производную. В тех точках, где значение производной функции равно 0, исходная функция принимает экстремальное значение. В нашем примере производная функции y=x^2 равна 2х, т.е. в точке (0;0) имеется единственный минимум.
Функция y=sin(x) имеет бесконечное число экстремумов, т.к. ее производная y=cos(x) также является периодической с периодом Пи.
После того, как произведено достаточное исследование функции, можно найти значения функции при других значениях ее аргумента для получения дополнительных точек, через которые проходит ее график. Затем все найденные точки можно объединить в таблицу, которая и будет служить основой для построения графика.
Для зависимости y=x^2 определим следующие точки (0;0) — ноль функции и ее минимум, (1;1), (-1;1), (2;4), (-2;4).
Для функции y=sin(x) достаточно будет ее нулей — (0;0), (Пи+n*Пи,0), максимумов — (Пи/2+2*n*Пи; 1) и минимумов — (-Пи/2+2*n*Пи; -1). В этих выражениях n- целое число.
Источники:
- как построить график y x y
www.kakprosto.ru
