Как выглядит равносторонний треугольник – Свойства треугольника. В том числе равенство и подобие, равные треугольники, стороны треугольника, углы треугольника, площадь треугольника — формулы вычисления, прямоугольный треугольник, равнобедренный треугольник, высота треугольника.

Правильный треугольник, площадь правильного треугольника

Правильный треугольник — треугольник, у которого все стороны равны. Каждый угол правильного треугольника равен  градусов.
Правильный треугольник называют еще равносторонним.

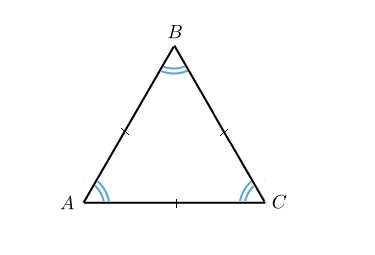
Каждая из высот правильного треугольника является также его медианой и биссектрисой.
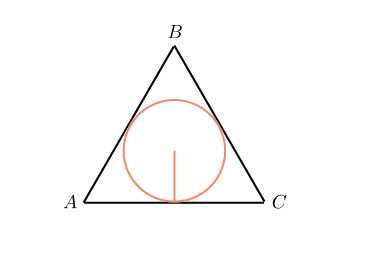
Центры вписанной и описанной окружностей правильного треугольника совпадают.

Пусть сторона правильного треугольника равна .

Высота правильного треугольника:
Радиус окружности, вписанной в правильный треугольник: .
Радиус описанной окружности в два раза больше: .
Площадь правильного треугольника: .

Все эти формулы легко доказать. Если вы нацелены на решение задач части  — докажите их самостоятельно.

. Сторона правильного треугольника равна . Найдите радиус окружности, вписанной в этот треугольник.

Задача решается в одну строчку. Радиус вписанной окружности .

. Найдите радиус окружности, вписанной в правильный треугольник, высота которого равна .

Сравним формулы для высоты правильного треугольника и радиуса вписанной окружности. Очевидно, радиус вписанной окружности равен высоты.

Ответ: .

. Сторона правильного треугольника равна . Найдите радиус окружности, описанной около этого треугольника.

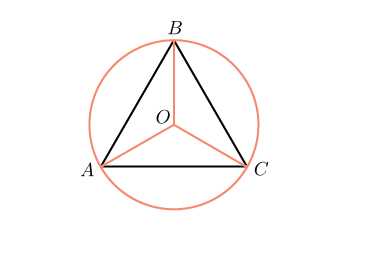
Радиус окружности, описанной вокруг правильного треугольника, равен .

Ответ: .

Звоните нам:

8 (800) 775-06-82 (бесплатный звонок по России)                        +7 (495) 984-09-27 (бесплатный звонок по Москве)

Или нажмите на кнопку «Узнать больше», чтобы заполнить контактную форму. Мы обязательно Вам перезвоним.

ege-study.ru

Равносторонний треугольник Википедия

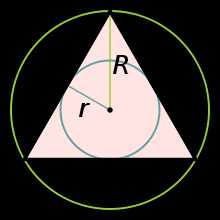Правильный треугольник.

Правильный (равносторонний, или равноугольный) треугольник — это правильный многоугольник с тремя сторонами, простейший из правильных многоугольников. Все стороны правильного треугольника равны между собой, все углы также равны и составляют 60°. В равностороннем треугольнике высота является и биссектрисой, и медианой.

Содержание

• 1 Свойства
• 2 Правильный сферический треугольник
• 3 Теоремы о равностороннем треугольнике или содержащие его
• 4 См. также
• 5 Примечания

Свойства[ | ]

Правильный тетраэдр состоит из четырёх правильных треугольников.

Пусть a — сторона правильного треугольника, R — радиус описанной окружности, r — радиус вписанной окружности.

• Радиус вписанной окружности правильного треугольника, выраженный через его сторону:

r=36a{\displaystyle r={\frac {\sqrt {3}}{6}}a}

• Радиус описанной окружности правильного треугольника, выраженный через его сторону:

R=33a{\displaystyle R={\frac {\sqrt {3}}{3}}a}

• Периметр правильного треугольника:

P=3a=33R=63r{\displaystyle P=3a=3{\sqrt {3}}R=6{\sqrt {3}}r}

• Высоты, медианы и биссектрисы правильного треугольника:

h=m=l=32a{\displaystyle h=m=l={\frac {\sqrt {3}}{2}}a}

• Площадь правильного треугольника рассчитывается по формулам:

S=34a2=334R2=33r2=336P2{\displaystyle S={\frac {\sqrt {3}}{4}}a^{2}={\frac {3{\sqrt {3}}}{4}}R^{2}=3{\sqrt {3}}r^{2}={\frac {\sqrt {3}}{36}}P^{2}}

• Радиус описанной окружности равен двойному радиусу вписанной окружности:

R=2r{\displaystyle R=2r}

ru-wiki.ru

Равнобедренный и равносторонний треугольники. Свойства.

Равнобедренный треугольник

Треугольник называется равнобедренным, если две его стороны равны.

Две равные стороны называют боковыми сторонами, а третью сторону – основанием равнобедренного треугольника.

Теорема: В равнобедренном треугольнике углы при основании равны.

Теорема: В равнобедренном треугольнике биссектриса, проведенная к основанию является медианой и высотой.

Теорема: В равнобедренном треугольнике медиана, проведенная к основанию является биссектрисой и высотой.

Теорема: В равнобедренном треугольнике высота, проведенная к основанию является медианой и биссектрисой.

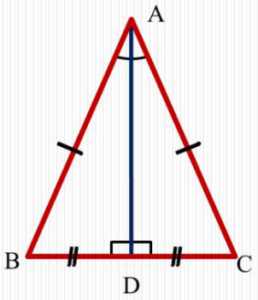
Равносторонний треугольник

Равносторонний треугольник – частный случай равнобедренного треугольника.(т.е. для любого равностороннего треугольника применимы все свойства равнобедренного треугольника)

Треугольник у которого все стороны равны называется равносторонним треугольником.

Признак: В равностороннем треугольнике все углы равны 60°

Свойство: В равностороннем треугольники центры вписанной и описанной окружности совпадают.

По формулам выше можно найти высоту, площадь равностороннего треугольника через сторону, радиус вписанной и радиус описанной окружностей.

bitreit.ru

Равносторонний треугольник — это… Что такое Равносторонний треугольник?



Равносторонний треугольник

Правильный треугольник

Правильный треугольник или равносторонний треугольник — это правильный многоугольник с тремя сторонами, первый из правильных многоугольников. Все стороны правильного треугольника равны между собой, а все углы равны 60° (или π / 3).

В силу определения правильный треугольник также является равнобедренным.

Свойства

Пусть t — сторона правильного треугольника, R — радиус описанной окружности, r — радиус вписанной окружности.

Радиус вписанной окружности правильного треугольника, выраженный через его сторону

.

Радиус описанной окружности правильного треугольника, выраженный через его сторону

.

Периметр правильного треугольника равен

.

Высота правильного треугольника:

,

Площадь правильного треугольника рассчитывается по формулам:

.

Wikimedia Foundation. 2010.

• Равносильность
• Равный-равному

Смотреть что такое «Равносторонний треугольник» в других словарях:

• РАВНОСТОРОННИЙ ТРЕУГОЛЬНИК — РАВНОСТОРОННИЙ ТРЕУГОЛЬНИК, плоская фигура, имеющая три стороны равной длины; три внутренних угла, образуемых сторонами, также равны и составляют 60 °С. см. также ТРЕУГОЛЬНИК …   Научно-технический энциклопедический словарь

• ТРЕУГОЛЬНИК — и (прост.) трёхугольник, треугольника, муж. 1. Геометрическая фигура, ограниченная тремя взаимно пересекающимися прямыми, образующими три внутренних угла (мат.). Тупоугольный треугольник. Остроугольный треугольник. Прямоугольный треугольник.… …   Толковый словарь Ушакова

• Треугольник Серпинского — Треугольник Серпинского  фрактал, один из двумерных аналогов множества Кантора, предложенный польским математиком Серпински …   Википедия

• РАВНОСТОРОННИЙ — РАВНОСТОРОННИЙ, равносторонняя, равностороннее (мат.). Имеющий стороны равной длины. Равносторонний многоугольник. Равносторонний треугольник. Толковый словарь Ушакова. Д.Н. Ушаков. 1935 1940 …   Толковый словарь Ушакова

• Треугольник — Триединая природа вселенной: Небо, Земля, Человек; отец, мать, дитя; человек как тело, душа и дух; мистическое число три; тройка, первая из плоских фигур. Отсюда символ поверхности вообще. Поверхность состоит из треугольников (Платон).… …   Словарь символов

• Треугольник — У этого термина существуют и другие значения, см. Треугольник (значения). Треугольник (в евклидовом пространстве)  это геометрическая фигура, образованная тремя отрезками, которые соединяют три не лежащие на одной прямой точки. Три точки,… …   Википедия

• Треугольник Рёло — Построение треугольника Рёло Треугольник Рёло[* 1] предста …   Википедия

• треугольник — ▲ многоугольник ↑ имеющий, три, угол треугольник простейший многоугольник; задается 3 точками, не лежащими на одной прямой. треугольный. остроугольник. остроугольный. прямоугольный треугольник: катет. гипотенуза. равнобедренный треугольник. ▼… …   Идеографический словарь русского языка

• ТРЕУГОЛЬНИК — Этим геометрическим термином называется музыкальный инструмент, который входит в группу ударных и довольно часто применяется в симфонической и оперной музыке. По форме инструмент представляет собой равносторонний треугольник. Сделан он из… …   Музыкальный словарь

• РАВНОСТОРОННИЙ — РАВНОСТОРОННИЙ, яя, ее. Имеющий равные стороны. Р. треугольник. Толковый словарь Ожегова. С.И. Ожегов, Н.Ю. Шведова. 1949 1992 …   Толковый словарь Ожегова

Книги

• Тетрактис. Символ и ключ, открывающий путь к Истине, Бай-Бал (П. П. Прокопьев), Тетрактис — очень древний и удивительно простой символ, равносторонний треугольник с десятью точками (запятыми) внутри. Несмотря на эту простоту, в ней древние сокрыли величайшие законы… Издатель: Золотое Сечение, Подробнее  Купить за 1341 руб
• Моя первая книга Формы 2 — 4 года, Пиродди К., Эта книга с листами для творчества создана в соответствии с принципами, разработанными выдающимся педагогом и мыслителем Марией Монтессори. Она поможет вашему малышу приобрести важнейшие… Подробнее  Купить за 339 руб
• Формы. Моя первая книга. Система раннего развития Монтессори, Пиродди Кьяра, Эта книга с листами для творчества создана в соответствии с принципами, разработанными выдающимся педагогом и мыслителем Марией Монтессори. Она поможет вашему малышу приобрести важнейшие… Серия: Система раннего развития Монтессори Издатель: Хоббитека, Подробнее  Купить за 312 руб

Другие книги по запросу «Равносторонний треугольник» >>

dic.academic.ru

Треугольник равносторонний: свойства, признаки, площадь, периметр

В школьном курсе геометрии огромное количество времени уделяется изучению треугольников. Ученики вычисляют углы, строят биссектрисы и высоты, выясняют, чем фигуры отличаются друг от друга, и как проще всего найти их площадь и периметр. Кажется, что это никак не пригодится в жизни, но иногда все-таки полезно узнать, например, как определить, что треугольник равносторонний или тупоугольный. Как же это сделать?

Типы треугольников

Три точки, которые не лежат на одной прямой, и отрезки, которые их соединяют. Кажется, что эта фигура — самая простая. Какими могут быть треугольники, если у них всего три стороны? На самом деле вариантов довольно большое количество, и некоторым из них уделяется особое внимание в рамках школьного курса геометрии. Правильный треугольник — равносторонний, то есть все его углы и стороны равны. Он обладает рядом примечательных свойств, о которых речь пойдет дальше.

У равнобедренного равны только две стороны, и он также довольно интересен. У прямоугольного и тупоугольного треугольников, как несложно догадаться, соответственно, один из углов прямой или тупой. При этом они также могут равнобедренными.

Существует и особый вид треугольника, называемый египетским. Его стороны равны 3, 4 и 5 единицам. При этом он является прямоугольным. Считается, что такой треугольник активно использовался египетскими землемерами и архитекторами для построения прямых углов. Есть мнение, что с его помощью были возведены знаменитые пирамиды.

И все-таки все вершины треугольника могут лежать на одной прямой. В этом случае он будет называться вырожденным, в то время как все остальные — невырожденными. Именно они и являются одним из предметов изучения геометрии.

Треугольник равносторонний

Разумеется, правильные фигуры вызывают всегда наибольший интерес. Они кажутся более совершенными, более изящными. Формулы вычисления их характеристик зачастую проще и короче, чем для обычных фигур. Это относится и к треугольникам. Неудивительно, что при изучении геометрии им уделяется достаточно много внимания: школьников учат отличать правильные фигуры от остальных, а также рассказывают о некоторых их интересных характеристиках.

Признаки и свойства

Как нетрудно догадаться из названия, каждая сторона равностороннего треугольника равна двум другим. Кроме того, он обладает рядом признаков, благодаря которым можно определить, правильная ли фигура или нет.

• все его углы равны, их величина составляет 60 градусов;
• биссектрисы, высоты и медианы, проведенные из каждой вершины, совпадают;
• правильный треугольник имеет 3 оси симметрии, он не изменяется при повороте на 120 градусов.
• центр вписанной окружности также является центром описанной окружности и точкой пересечения медиан, биссектрис, высот и срединных перпендикуляров.

Если наблюдается хотя бы один из вышеперечисленных признаков, то треугольник — равносторонний. Для правильной фигуры справедливы все упомянутые утверждения.

Все треугольники обладают рядом примечательных свойств. Во-первых, средняя линия, то есть отрезок, делящий две стороны пополам и параллельный третьей, равна половине основания. Во-вторых, сумма всех углов этой фигуры всегда равна 180 градусам. Кроме того, в треугольниках наблюдается еще одна любопытная взаимосвязь. Так, против большей стороны лежит больший угол и наоборот. Но это, конечно, к равностороннему треугольнику отношения не имеет, ведь у него все углы равны.

Вписанные и описанные окружности

Нередко в курсе геометрии учащиеся также изучают то, как фигуры могут взаимодействовать друг с другом. В частности, изучаются окружности, вписанные в многоугольники или описанные около них. О чем идет речь?

Вписанной называют такую окружность, для которой все стороны многоугольника являются касательными. Описанной — ту, которая имеет точки соприкосновения со всеми углами. Для каждого треугольника всегда можно построить как первую, так и вторую окружность, но только одну каждого вида. Доказательства двух этих

теорем приводятся в школьном курсе геометрии.

Помимо вычисления параметров самих треугольников, некоторые задачи также подразумевают расчет радиусов этих окружностей. И формулы применительно к
равностороннему треугольнику выглядят следующим образом:

r = a/√ ̅3;

R = a/2√ ̅3;

где r — радиус вписанной окружности, R — радиус описанной окружности, a — длина стороны треугольника.

Вычисление высоты, периметра и площади

Основные параметры, вычислением которых занимаются школьники во время изучения геометрии, остаются неизменными практически для любых фигур. Это периметр, площадь и высота. Для простоты расчетов существуют различные формулы.

Так, периметр, то есть длина всех сторон, вычисляется следующими способами:

P = 3a = 3√ ̅3R = 6√ ̅3r, где a — сторона правильного треугольника, R — радиус описанной окружности, r — вписанной.

Высота:

h = (√ ̅3/2)*a, где a — длина стороны.

Наконец, формула площади равностороннего треугольника выводится из стандартной, то есть произведения половины основания на его высоту.

S = (√ ̅3/4)*a², где a — длина стороны.

Также эта величина может быть вычислена через параметры описанной или вписанной окружности. Для этого также существуют специальные формулы:

S = 3√ ̅3r² = (3√ ̅3/4)*R², где r и R — соответственно радиусы вписанной и описанной окружностей.

Построение

Еще один интересный тип задач, касающийся в том числе и треугольников, связан с необходимостью начертить ту или иную фигуру, используя минимальный набор

инструментов: циркуль и линейку без делений.

Для того чтобы построить правильный треугольник с помощью только этих приспособлений, необходимо выполнить несколько шагов.

1. Нужно начертить окружность с любым радиусом и с центром в произвольно взятой точке А. Ее необходимо отметить.
2. Далее нужно провести прямую через эту точку.
3. Пересечения окружности и прямой необходимо обозначить как В и С. Все построения должны проводиться с максимально возможной точностью.
4. Далее надо построить еще одну окружность с тем же радиусом и центром в точке С или дугу с соответствующими параметрами. Места пересечения будут обозначены как D и F.
5. Точки B, F, D необходимо соединить отрезками. Равносторонний треугольник построен.

Решение подобных задач обычно представляет для школьников проблему, но это умение может пригодиться и в обычной жизни.

fb.ru

Правильный треугольник — это… Что такое Правильный треугольник?

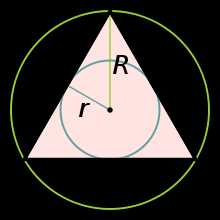Правильный треугольник.

Правильный (или равносторонний) треугольник — это правильный многоугольник с тремя сторонами, первый из правильных многоугольников. Все стороны правильного треугольника равны между собой, а все углы равны 60°.

По определению, правильный треугольник также является равнобедренным.

Свойства

Правильный тетраэдр состоит из четырёх правильных треугольников.

Пусть  — сторона правильного треугольника,  — радиус описанной окружности,  — радиус вписанной окружности.

Радиус вписанной окружности правильного треугольника, выраженный через его сторону

.

Радиус описанной окружности правильного треугольника, выраженный через его сторону

.

Периметр правильного треугольника равен

.

Высоты, медианы и биссектрисы правильного треугольника:

Площадь правильного треугольника рассчитывается по формулам:

.

Радиус описанной окружности равен двойному радиусу вписанной окружности:

Равносторонний треугольник используется при построении правильного 30-угольника.

В Викисловаре есть статья «равносторонний треугольник»

Правильные многоугольники
Основные	Треугольник • Квадрат • Пятиугольник • Шестиугольник • Семиугольник • Восьмиугольник • Девятиугольник • Семнадцатиугольник • 257-угольник • 65537-угольник
См. также	Многоугольник • Теорема Гаусса — Ванцеля

dic.academic.ru

Равносторонний треугольник Википедия

Правильный треугольник.

Правильный (равносторонний, или равноугольный) треугольник — это правильный многоугольник с тремя сторонами, простейший из правильных многоугольников. Все стороны правильного треугольника равны между собой, все углы также равны и составляют 60°. В равностороннем треугольнике высота является и биссектрисой, и медианой.

Свойства

Правильный тетраэдр состоит из четырёх правильных треугольников.

Пусть a — сторона правильного треугольника, R — радиус описанной окружности, r — радиус вписанной окружности.

• Радиус вписанной окружности правильного треугольника, выраженный через его сторону:

r=36a{\displaystyle r={\frac {\sqrt {3}}{6}}a}

• Радиус описанной окружности правильного треугольника, выраженный через его сторону:

R=33a{\displaystyle R={\frac {\sqrt {3}}{3}}a}

P=3a=33R=63r{\displaystyle P=3a=3{\sqrt {3}}R=6{\sqrt {3}}r}

h=m=l=32a{\displaystyle h=m=l={\frac {\sqrt {3}}{2}}a}

• Площадь правильного треугольника рассчитывается по формулам:

S=34a2=334R2=33r2=336P2{\displaystyle S={\frac {\sqrt {3}}{4}}a^{2}={\frac {3{\sqrt {3}}}{4}}R^{2}=3{\sqrt {3}}r^{2}={\frac {\sqrt {3}}{36}}P^{2}}

• Радиус описанной окружности равен двойному радиусу вписанной окружности:

R=2r{\displaystyle R=2r}

• Для равностороннего треугольника T группа движений (самосовмещений) плоскости, переводящих треугольник в себя, состоит из 6 элементов: трёх поворотов на углы 0, ^2π⁄₃ и ^4π⁄₃ вокруг точки O, а также трёх симметрий относительно трёх прямых, на которых лежат биссектрисы треугольника (последние являются также его высотами и медианами).
• На описанной окружности произвольного треугольника ABC{\displaystyle ABC} существуют ровно три точки такие, что их прямая Симсона касается окружности Эйлера треугольника ABC{\displaystyle ABC}, причем эти точки образуют правильный треугольник. Стороны этого треугольника параллельны сторонам треугольника Морлея.
• Равносторонний треугольник является одновременно и равноугольным треугольником, то есть у него равны все внутренние углы.
• Равносторонний треугольник является частными случаем равнобедренного треугольника, а именно: дважды равнобедренным треугольником.

Правильный сферический треугольник

Для любого значения в интервале от 60 до 180 градусов существует правильный сферический треугольник с равными этому значению углами.

Теоремы о равностороннем треугольнике или содержащие его

См. также

Примечания

Многоугольники
Звёздчатые многоугольники
Паркеты на плоскости
Правильные многогранники и сферические паркеты
Многогранники Кеплера — Пуансо
Соты
Четырёхмерные многогранники	{3,3,3} {4,3,3} {3,3,4} {3,4,3} {5,3,3} {3,3,5}

wikiredia.ru