Как найти наибольшее наименьшее значение функции
Автор КакПросто!
Выдающийся немецкий математик Карл Вейерштрасс доказал, что для каждой непрерывной на отрезке функции существуют ее наибольшее и наименьшее значение на этом отрезке. Задача определения наибольшего и наименьшего значения функции имеет широкое прикладное значение в экономике, математике, физике и других науках.
Статьи по теме:
Вам понадобится
- чистый лист бумаги;
- ручка или карандаш;
- учебник по высшей математике.
Инструкция
Пусть функция f(x) непрерывна и определена на заданном отрезке [a; b] и имеет на нем некоторое (конечное) количество критических точек. Первым делом найдем производную функции f'(x) по х. Приравниваем производную функции к нулю, чтобы определить критические точки функции. Не забываем определить точки, в которых производная не существует — они также являются критическими.Из множества найденных критических точек выбираем те, которые принадлежат отрезку [a; b]. Вычисляем значения функции f(x) в этих точках и на концах отрезка.
Из множества найденных значений функции выбираем максимальное и минимальное значения. Это и есть искомые наибольшее и наименьшее значения функции на отрезке.
Видео по теме
Источники:
- Наибольшее и наименьшее значение функции
- как указать наименьшее значение функции
Совет полезен?
Статьи по теме:
Не получили ответ на свой вопрос?
Спросите нашего эксперта:
www.kakprosto.ru
Как найти наибольшее и наименьшее значение функции на интервале? 8 класс
Наибольшее и наименьшее значение функции. С практической точки зрения наибольший интерес представляет использование производной для нахождения наибольшего и наименьшего значения функции. С чем это связано? Максимизация прибыли, минимизация издержек, определение оптимальной загрузки оборудования… Другими словами, во многих сферах жизни приходится решать задачи оптимизации каких-либо параметров. А это и есть задачи на нахождение наибольшего и наименьшего значения функции. Следует отметить, что наибольшее и наименьшее значение функции обычно ищется на некотором интервале X, который является или всей областью определения функции или частью области определения. Сам интервал X может быть отрезком формула, открытым интервалом формула, бесконечным промежутком формула. В этой статье мы будем говорить о нахождении наибольшего и наименьшего значений явно заданной функции одной переменной y=f(x). Навигация по странице. Наибольшее и наименьшее значение функции — определения, иллюстрации. Нахождение наибольшего и наименьшего значения функции на отрезке [a;b]. Нахождение наибольшего и наименьшего значения функции на открытом или бесконечном интервале X. Наибольшее и наименьшее значение функции — определения, иллюстрации. Кратко остановимся на основных определениях. Наибольшим значением функции y=f(x) на промежутке X называют такое значение формула, что для любого формула справедливо неравенство формула. Наименьшим значением функции y=f(x) на промежутке X называют такое значение формула, что для любого формула справедливо неравенство формула. Эти определения интуитивно понятны: наибольшее (наименьшее) значение функции – это самое большое (маленькое) принимаемое значение на рассматриваемом интервале при абсциссе формула. Стационарные точки – это значения аргумента, при которых производная функции обращается в ноль. Для чего нам стационарные точки при нахождении наибольшего и наименьшего значений? Ответ на этот вопрос дает теорема Ферма. Из этой теоремы следует, что если дифференцируемая функция имеет экстремум (локальный минимум или локальный максимум) в некоторой точке, то эта точка является стационарной. Таким образом, функция часто принимает свое наибольшее (наименьшее) значение на промежутке X в одной из стационарных точек из этого промежутка. Также часто наибольшее и наименьшее значение функция может принимать в точках, в которых не существует первая производная этой функции, а сама функция определена. Сразу ответим на один из самых распространенных вопросов по этой теме: «Всегда ли можно определить наибольшее (наименьшее) значение функции»? Нет, не всегда. Иногда границы промежутка X совпадают с границами области определения функции или интервал X бесконечен. А некоторые функции на бесконечности и на границах области определения могут принимать как бесконечно большие так и бесконечно малые значения. В этих случаях ничего нельзя сказать о наибольшем и наименьшем значении функции. Для наглядности дадим графическую иллюстрацию. Посмотрите на рисунки – и многое прояснится. На отрезке изображение На первом рисунке функция принимает наибольшее (max y) и наименьшее (min y) значения в стационарных точках, находящихся внутри отрезка [-6;6]. Рассмотрим случай, изображенный на втором рисунке. Изменим отрезок на [1;6]. В этом примере наименьшее значение функции достигается в стационарной точке, а наибольшее — в точке с абсциссой, соответствующей правой границе интервала. На рисунке №3 граничные точки отрезка [-3;2] являются абсциссами точек, соответствующих наибольшему и наименьшему значению функции. На открытом интервале изображение На четвертом рисунке функция принимает наибольшее (max y) и наименьшее (min y) значения в стационарных точках, находящихся внутри открытого интервала (-6;6). На интервале [1;6) наименьшее значение
Это наибольшее и наименьшее значения y, при наибольшем и наименьшем значениях x, принадлежащих этому интервалу. Например, y наибольшее и наименьшее значения функции y=√x при промежутке [1; 5) yнаиб. =2, yнаим. =1. Чаще всего вычисляется по графику.
touch.otvet.mail.ru
§13 Наибольшее и наименьшее значение функции.
Пусть функция z = f(x,y) определена в некоторой замкнутой области D (т.е. в области с границей ). Требуется найти наибольшее и наименьшее значения функции в этой области. Если какое-либо из этих значений достигается внутри области, то это есть, очевидно, экстремальное значение. Но наибольшее и наименьшее значения могут достигаться и в точках границы. Отсюда следует правило: чтобы найти наибольшее (наименьшее) значение функции в замкнутой области, нужно найти все внутренние критические точки, вычислить значения функции в них и сравнить эти значения с наибольшими ( наименьшими) значениями функции в этой области.
Пример. Найти наибольшее и наименьшее значение функции в замкнутом треугольнике с вершинамиO(0,0) , A(0,1) и B(1,0)
Решение:
1.Ищем
критические точки внутри 
OAB.
—
критическая точка внутри
.
2. Ищем наибольшие и наименьшие значения на границе. Рассматриваем отдельные отрезки.
1)На OA
, 
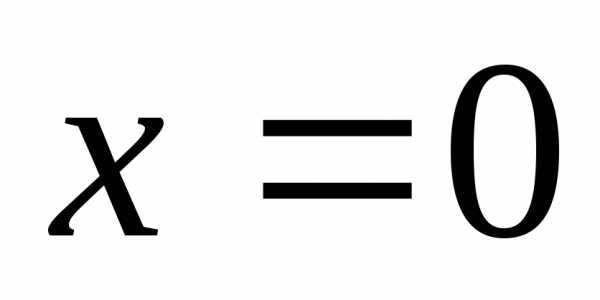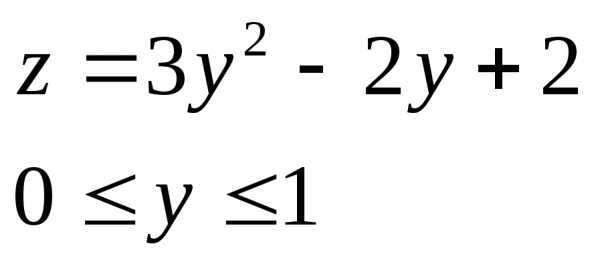— функция одной переменной y
на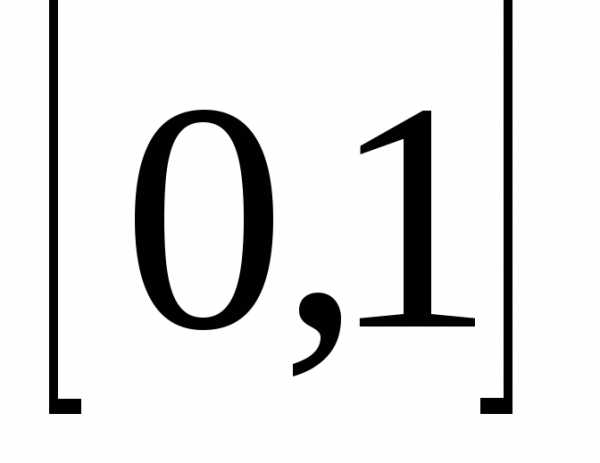 
, 
,
.
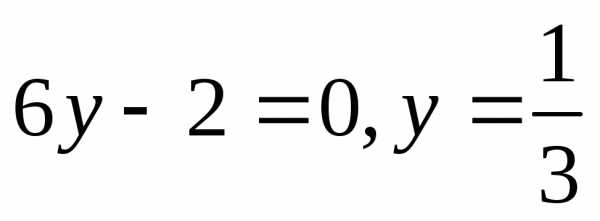Вычислим значения на концах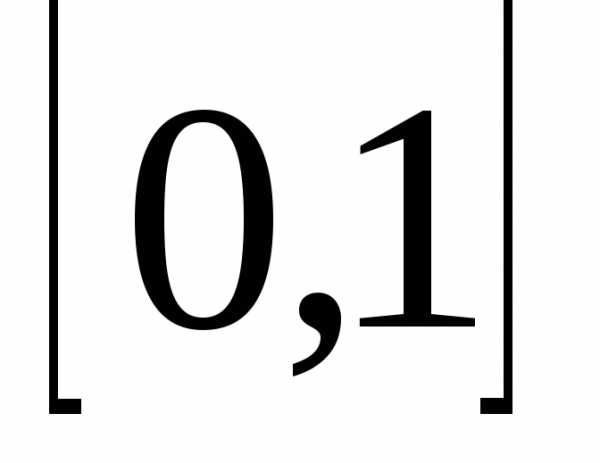 
:
, 
.
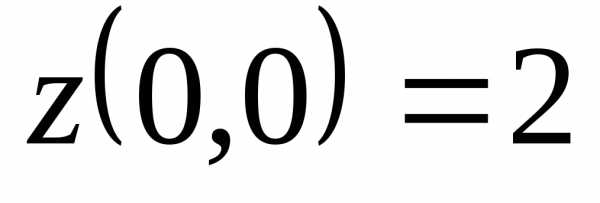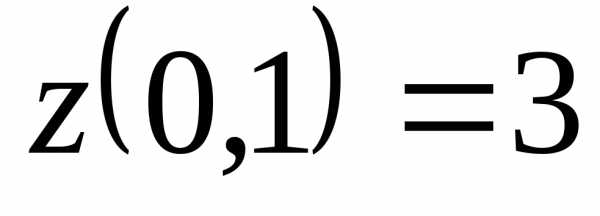2) На OB: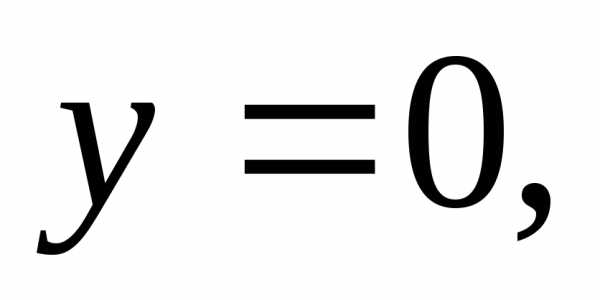 
—
функция одной
переменной
x
на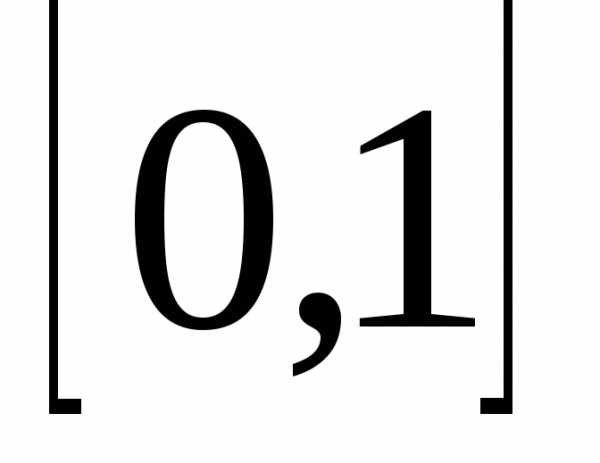 
Аналогично: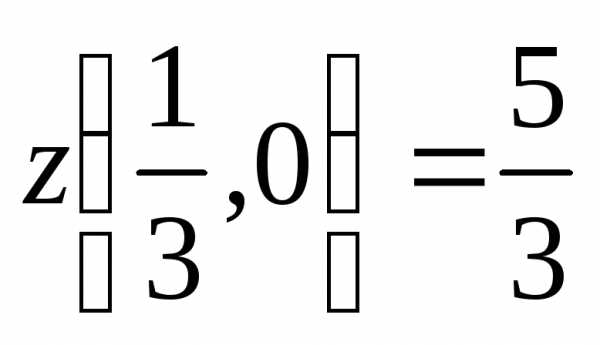 
, 
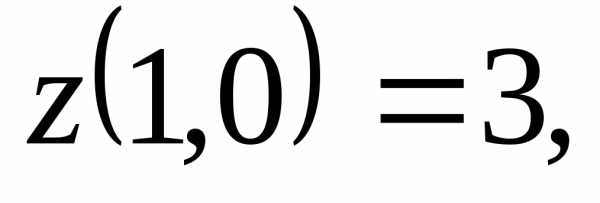
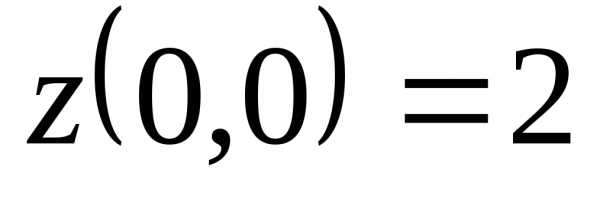
На AB: , Опять имеем функцию одной переменной
на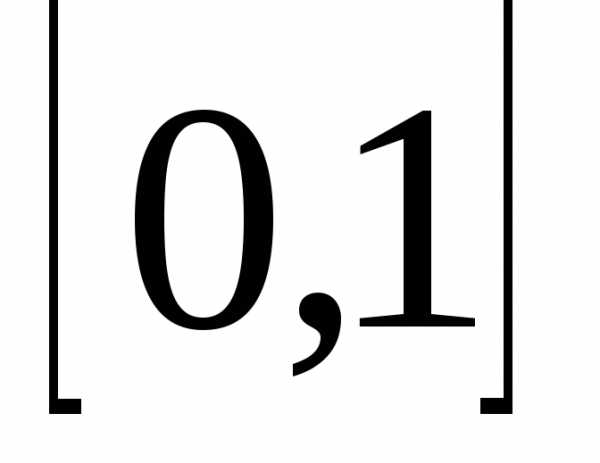 
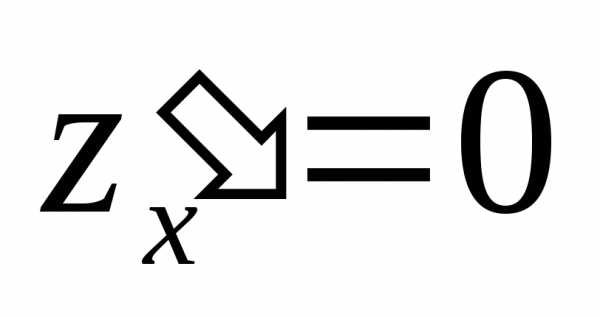при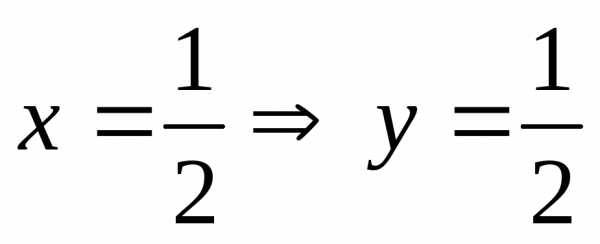
, 
.
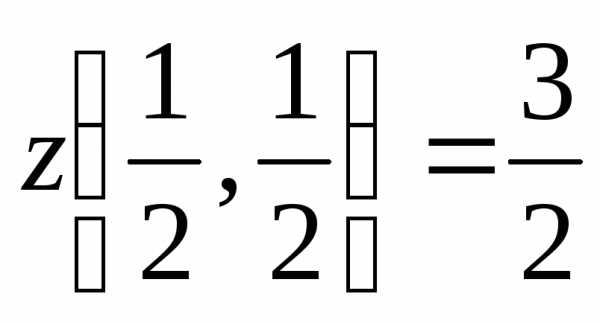В точках A
и B
значения уже вычислялись:.
Итак,
наибольшее значение z
=3 достигается в точках A
и B
, наименьшее значение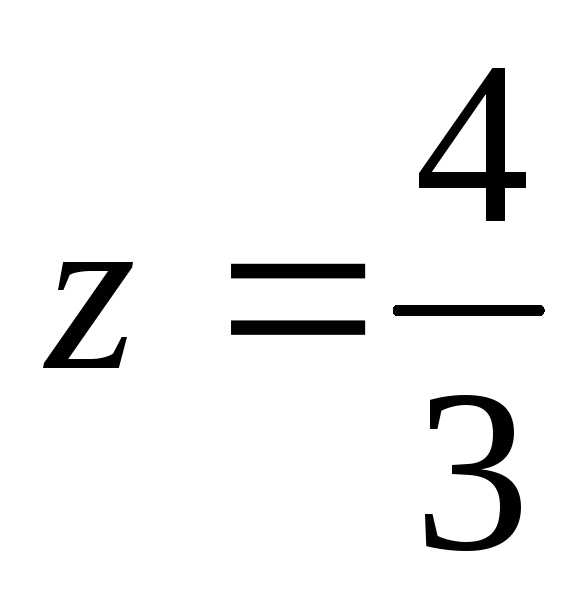 
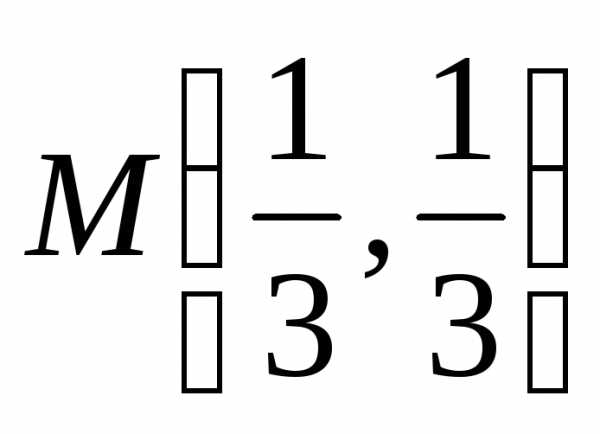.§ 14.Условный экстремум. Метод множителей лангража.
Часто в задачах приходится отыскивать экстремумы функции от нескольких переменных, которые не являются независимыми, а связаны некоторым (или некоторыми) условиями – например, должны удовлетворять одному или нескольким уравнениям (уравнениям связи).
Пример. Нужно изготовить коробку в форме
параллелепипеда
наибольшего объёма 
при заданной площади поверхности 
коробки (площадь имеющегося
материала).
Математически
задача звучит так. Если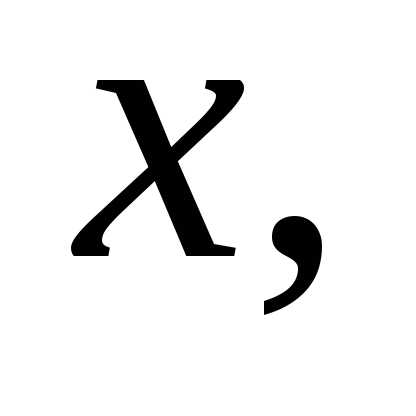 
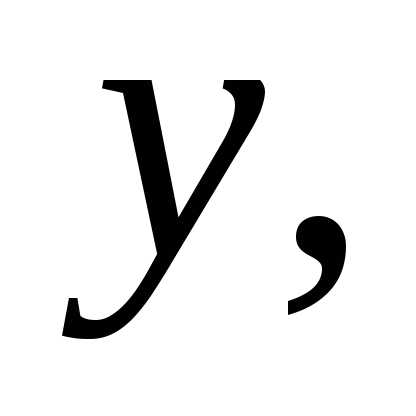z
– длина, ширина, высота коробки, то
,
.Нужно
найти максимум функции 
при дополнительном условии, т.е. это
типичная задача на условный экстремум.
Как решать такие задачи? Рассмотрим сначала вопрос в общем виде.
I. Пусть (1) – функция двух переменных.
(2) – уравнение связи.
1)
Если можно разрешить (2) относительно 
: 
,
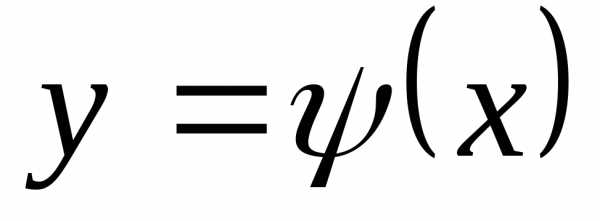то, подставив в (1), получим функцию от
одного переменного: нахождение условного
экстремума сведётся к нахождению
безусловного (обычного) экстремума
функции от этой переменной.
2)
Но можно поступить и иначе (что особенно
ценно, когда (2) разрешить однозначно
нельзя). При тех значениях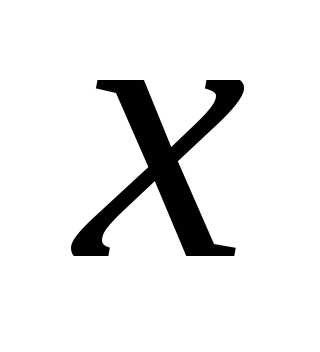 
,
при которых функция
имеет
экстремум, производная от
по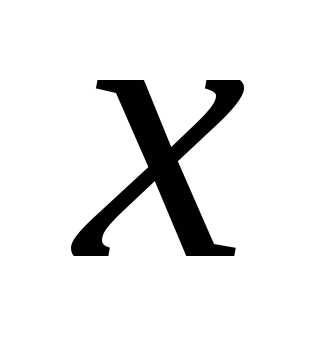
должна обращаться в нуль. Считаем, что
уравнение (2) определяет
как неявную функцию от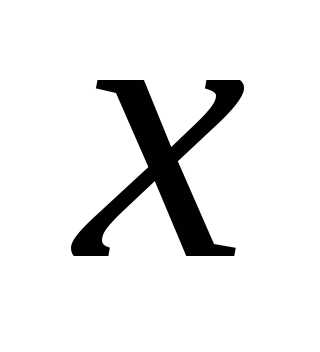
.
Считая, чтоесть функция от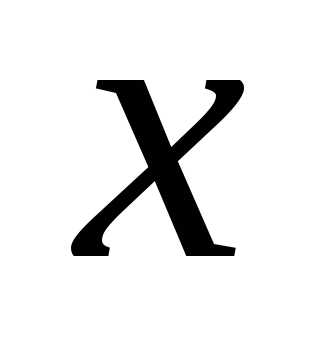
,
из (1) находим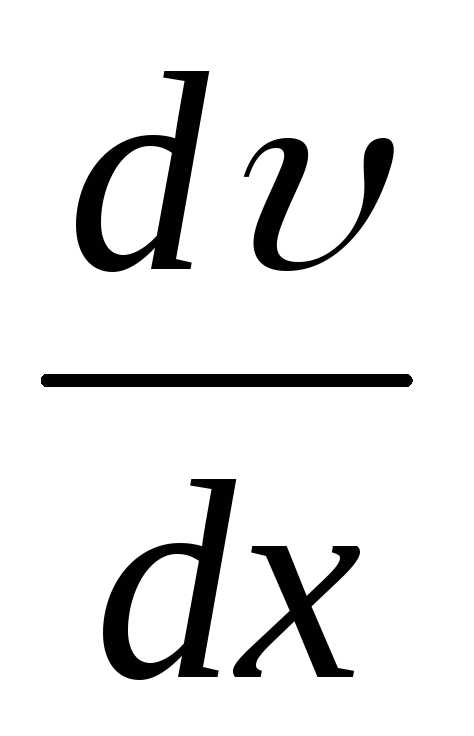
(как полную производную):
.
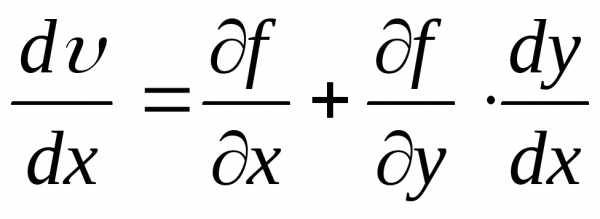Следовательно, в точках экстремума имеем
.
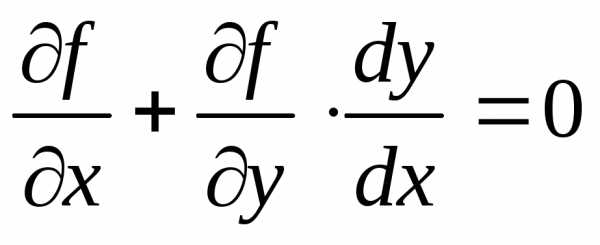(3)
Из
равенства (2) находим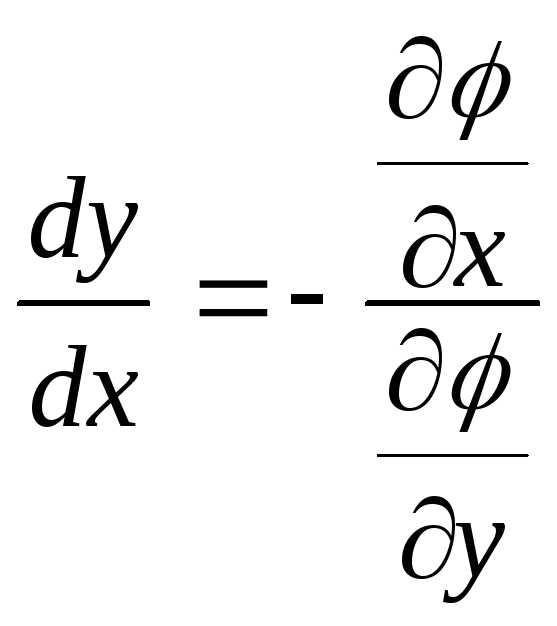 
(считаем
),
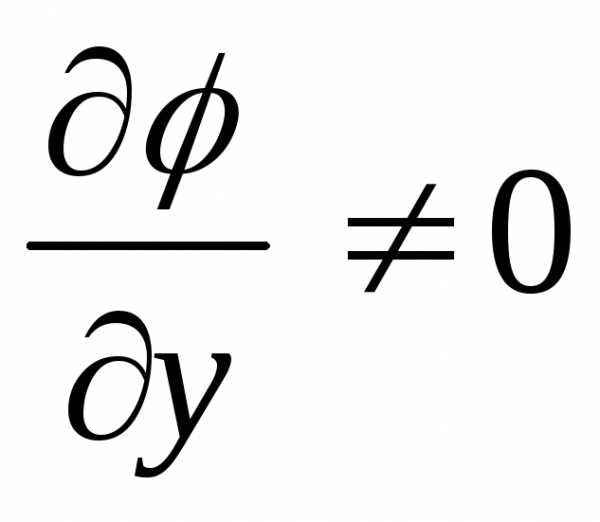откуда
.
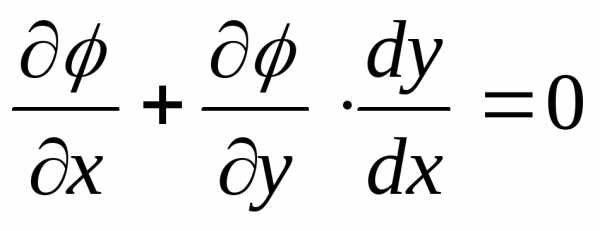(4)
Умножим
члены равенства (4) на неопределённый
пока коэффициент 
(множитель Лагранжа)и сложим почленно
(3) и полученное из (4):
или (5)
((5) удовлетворяется во всех точках экстремума).
Подберём 
так, чтобы для всех значени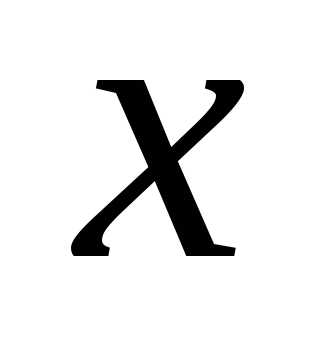й
и
,
соответствующих экстремуму функции
было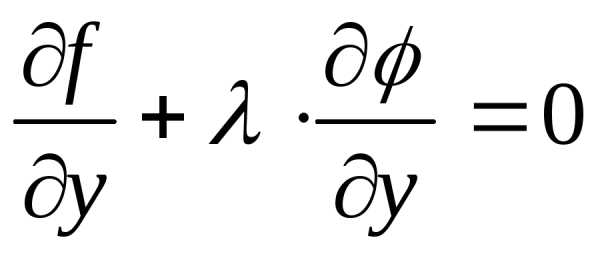
,
тогда и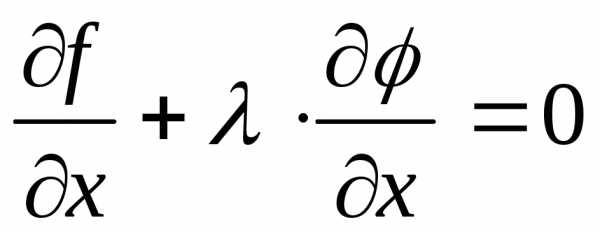
при тех же значениях
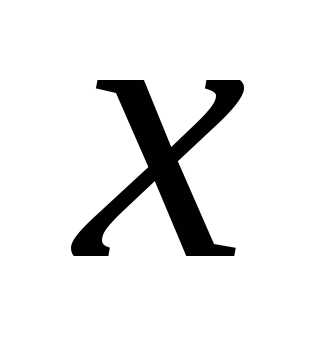и
.
Таким
образом, в точках экстремума должны
одновременно удовлетворяться три
уравнения с тремя неизвестными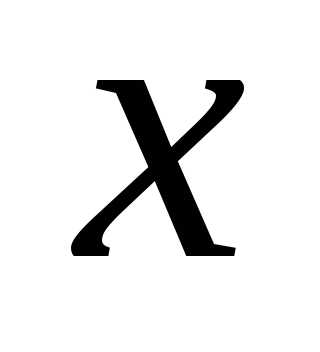 
,
, 
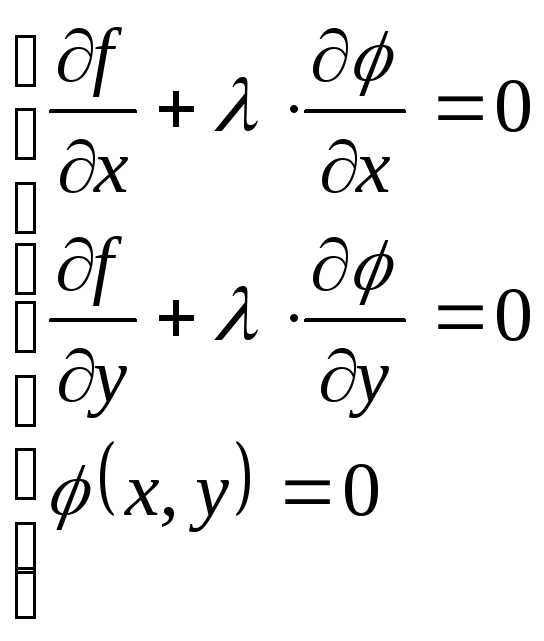(6)
Находим
решение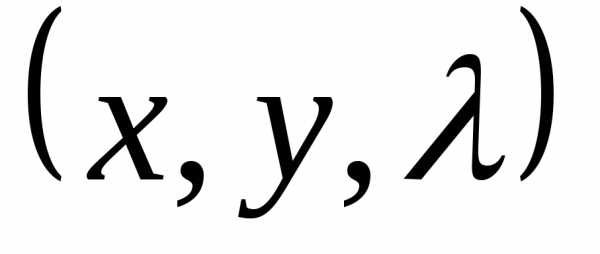 
,
тогда точка (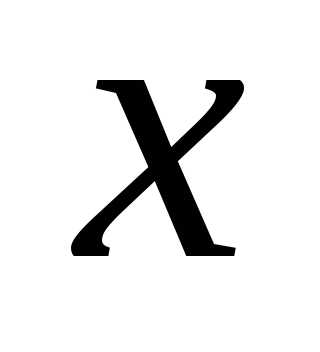
,
)
и будет точкой, подозрительной на
условный экстремум (
больше не нужно!).
Обычно из характера самой задачи можно сказать есть ли в этой точке экстремум и какой?
Для удобства практического применения метода множителей Лагранжа и составления системы (6) сразу рассматривают функцию Лагранжа: .
Тогда
система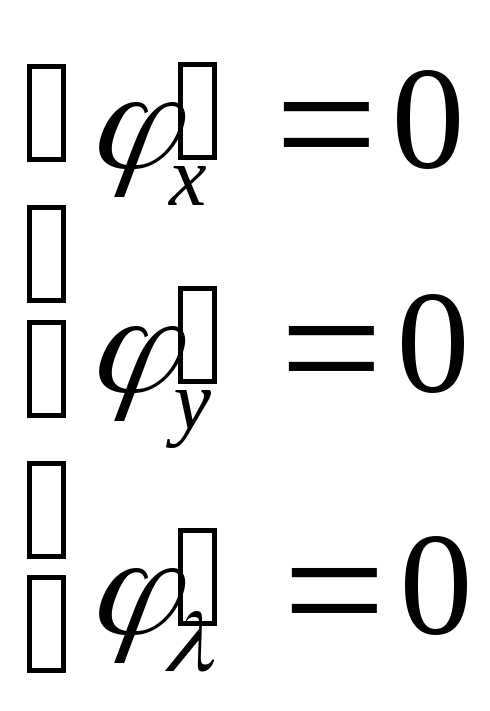 
и даёт систему (6).
II. Рассмотренный метод распространяется и на функции большего числа переменных, с большим числом уравнений связи.
Пусть
нужно найти экстремум функции
при условии, что переменные удовлетворяют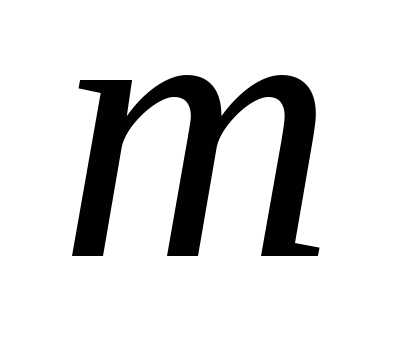
уравнениям связи:
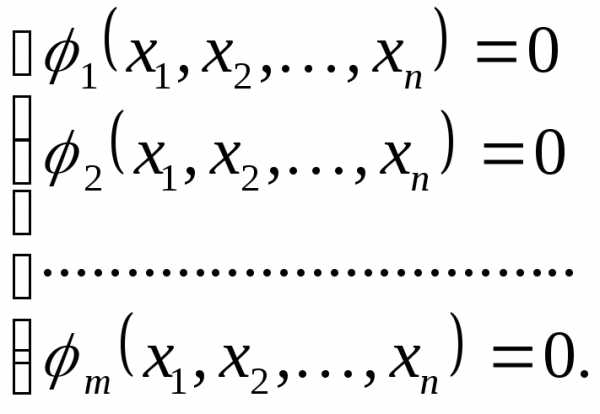
Тогда
– функция Лагранжа. Подозрительные на
экстремум точки, находим, решая систему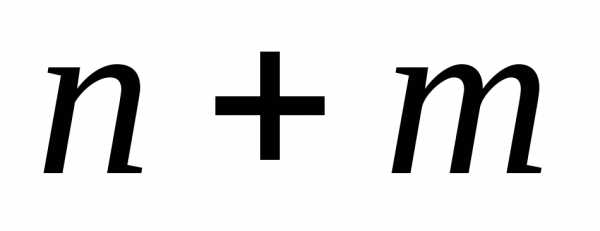
уравнений с
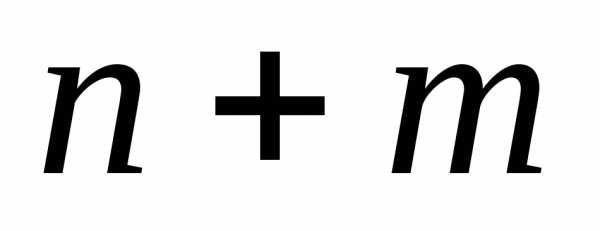неизвестными:
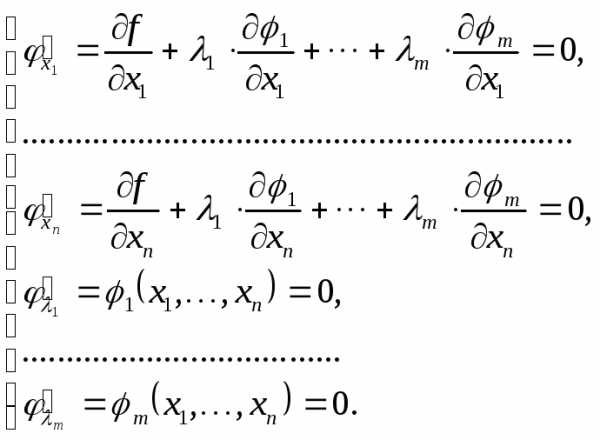
Пример. Найдём решение задачи о коробке, сформулированной вначале.
,
Составим функцию Лагранжа: .
Напишем
систему: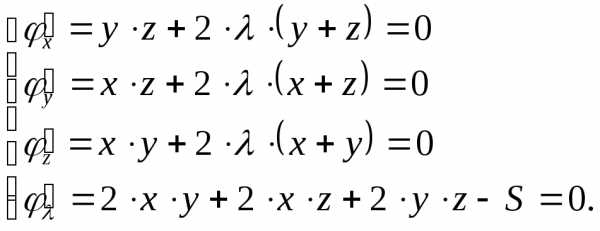 
Домножим первое уравнение на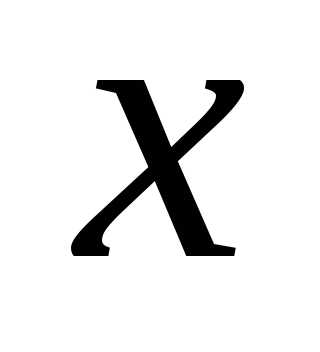 
,
второе – на
,
третье – на
и почленно сложим их.
Получим:
Подставим
это значение
в первые три уравнения, получим:
.
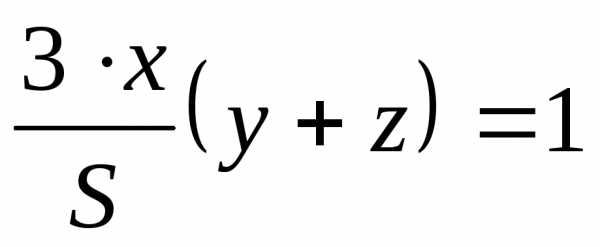
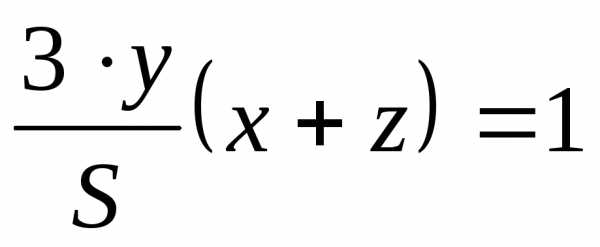
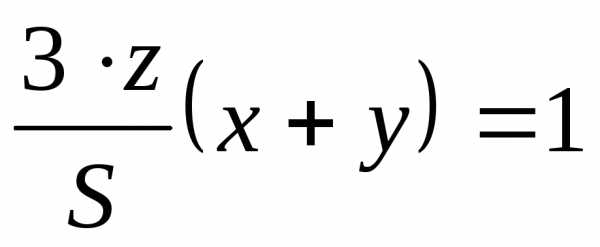
Из четвёртого уравнения тогда имеем: .
Отсюда: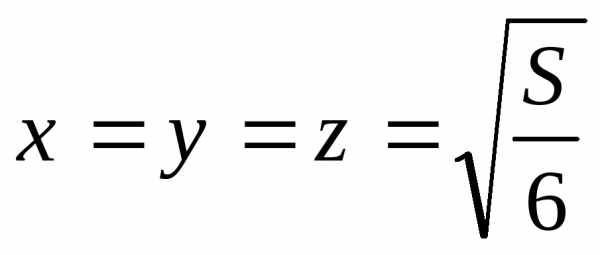 
,
т.е.коробка
должна быть кубом с ребром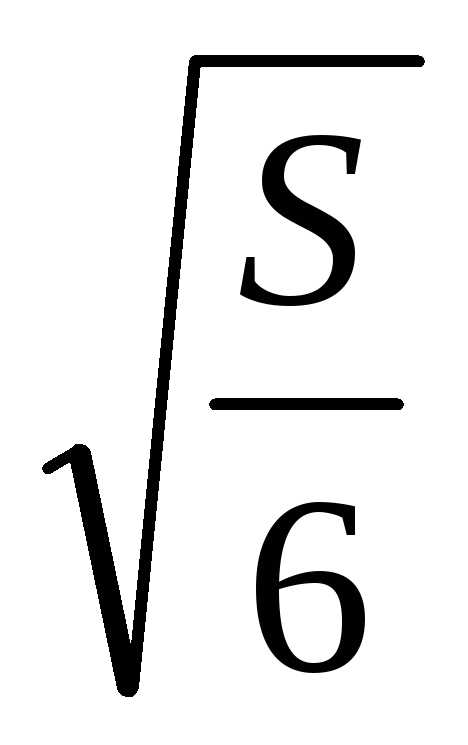 
.
studfiles.net