Разложение в ряд — Калькулятор Онлайн
Чтобы посчитать сумму ряда онлайн выполните следующие действия:
- ввести выражение, для которого нужно вычислить ряд
- указать параметр, по которому будет считать сумма
- указать значение параметра, до которого нужно подсчитать (для бесконечного ряда указываем бесконечность)
Перейти: Найти «сумму числового ряда» →
Разложение в ряд Фурье
Это он-лайн сервис в два шага:
- Ввести функцию, которую необходимо разложить
- Ввести отрезок, на котором необходимо разложить
Перейти: Онлайн «Разложение функции в ряд Фурье» →
Разложение в ряд Тейлора (степенной ряд)
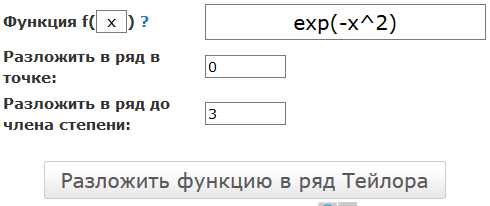
Это он-лайн сервис в три шага:
- Ввести функцию, которую необходимо разложить
- Ввести точку, в окрестности которой необходимо разложить
- Указать до какого члена раскладывать
Перейти: Онлайн «Разложение функции в ряд Тейлора» →
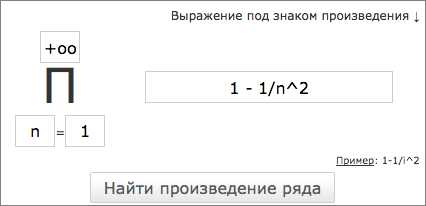
Чтобы посчитать произведение ряда онлайн выполните следующие действия:
- ввести выражение, для которого нужно вычислить произведение ряда
- указать параметр, по которому считать произведение
- указать значение параметра, до которого нужно подсчитать (для бесконечного ряда указываем бесконечность oo)
Перейти: Найти «произведение числового ряда» →
www.kontrolnaya-rabota.ru
Ряд Фурье. Контрольные онлайн
Ряд Фурье
Определение. Коэффициентами Фурье функции называются числа и , определяемые формулами
,
Ряд называется рядом Фурье функции .
В случае разложения в ряд Фурье функции, заданной в интервале , где — произвольное число, формулы принимают вид:
Пример1 Разложить в ряд Фурье функцию на отрезке . Решение.Подставим найденные значения коэффициентов ряда Фурье в формулу:
Пример2 Разложить в тригонометрический ряд Фурье функцию Решение
Если функция задана на интервале , то её ряд Фурье имеет вид ,
где , , .
Заданная функция определена на интервале , следовательно, и ряд Фурье для функции будет иметь вид ,
где , , .
Вычислим коэффициенты ряда Фурье для заданной функции.
Проинтегрировав по частям, получим
Проинтегрировав по частям, получим
Таким образом, в точках дифференцируемости функции
Читать методичку Ряды и интегралы Фурье (pdf)
www.matem96.ru
1.2. Примеры разложений в ряд Фурье
1. Разложить в ряд Фурье в промежутке . Отметим,
что имеет один разрыв на периоде в точке . Имеем ,
В частности, при и мы получаем разложение
,
Из которого заменой следует известная формула
Можно доказать, что
2. Разложить непрерывную в промежутке функцию
В ряд Фурье по синусам. Имеем .
 .
.
Отсюда
Так как числовой ряд обратных квадратов сходится, ряд Фурье сходится абсолютно и мы имеем
3. Разложить ту же функцию в ряд Фурье по косинусам в промежутке . Имеем

Отсюда
При Получаем, в частности
.
4. Разложить в ряд Фурье по косинусам в промежутке . Имеем ,,
Так что .
При Получаем, в частности,
,
А при
.
5. Разложить в ряд Фурье в промежутке .. Здесь Обращается в бесконечность На концах промежутка, оставаясь при этом несобственно интегрируемой, . Ввиду четности функции . Имеем для , используя известный интеграл Эйлера
:
.
Аналогично для , используя выражение для ядра Дирихле (см. 1.3.)
Имеем
Таким образом, окончательно получаем . Это разложение сходится при , что дает равенство
Заменяя на , получаем
.
Формально дифференцируя последний ряд, получаем разложение Фурье (неинтегрируемой!) функции :
.
Это разложение справедливо в смысле теории обобщенных функций (распределений) (см. 2.7.)
В заключение приведем примеры выполнения расчетно-графических заданий.
1. Разложить периодическую с периодом функцию в ряд Фурье.
Имеем .
;
Окончательно,
2. Разложить функцию
В ряд Фурье по синусам. Имеем

Окончательно,
.
| < Предыдущая | Следующая > |
|---|
matica.org.ua
Разложение функции в ряд Фурье
Разложить в тригонометрический ряд Фурье можно непериодическую функцию определенную от минус Пи до Пи —
Разложение кусковой функции в ряд Фурье находят по формуле
где коэффициенты Фурье вычисляют интегрированием
Таким образом, чтобы разложить функцию в ряд Фурье на практике необходимо всего лишь найти коэффициенты Фурье, а для этого нужно хорошо уметь интегрировать. На деле это занимает много времени и сил и многим бывает не под силу. В этом Вы сейчас наглядно убедитесь.
Пример: 6.9 Разложить функцию в тригонометрический ряд Фурье:
Вычисления: Заданная функция непереодическая. Для вычисления коэффициентов Фурье используем формулы 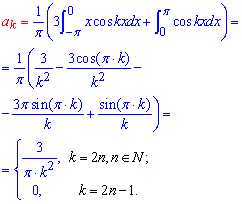
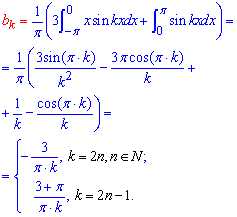
Сложность заключается в том, что для конечной формулы разложения ряда коэффициенты Фурье с четными и нечетными индексами надо свести в один.
Это требует определенных умений, однако реализовать это может научиться каждый. Кроме того, Вы должны безупречно знать что sin(0)=sin(Pi)=0, cos(0)=1, cos(Pi)=-1.
После всех манипуляций разложение функции в ряд Фурье должно принять вид
Если в результате вычислений Вы получили что-то отменное от этого, значит Вы где-то допустили ошибку.
Пример: 6.12 Найти разложение функции в тригонометрический ряд Фурье
Вычисления: Интегрированием функции с тригонометрическими множителями и без них находим коэффициенты Фурье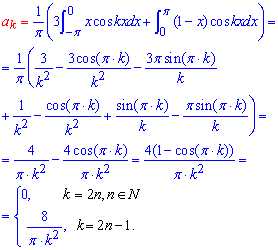
Составляем формулы коэффициентов Фурье и записываем разложение функции в тригонометрический ряд
Пример: 6.18 Найти разложение функции в тригонометрический ряд Фурье:
Вычисления: Находим коэффициенты Фурье интегрированием
Интегралы по силам каждому, для вычисления меж необходимы лишь знания значений синуса и косинуса в -Pi 0, Pi. Подставляем полученные коэффициенты в ряд Фурье и получаем следующее разложение функции
Пример: 6.20 Найти разложение функции в тригонометрический ряд Фурье:
Вычисления: Интегрированием находим коэффициенты Фурье a0, ak, bk
Далее для коэффициентов составляем общие формулы и подставляем в формулу разложения функции в тригонометрический ряд Фурье
Пример 6.30 Разложить функцию в тригонометрический ряд Фурье:
Вычисления: Определим интегрированием коэффициенты Фурье:
Вычисления достаточно громоздки, поэтому хорошо разберите формулы и для себя изучите методику интегрирования.
При сворачивании коэффициентов Фурье получим искомое разложение функции в ряд Фурье
Как Вы могли убедиться разложить функцию в ряд Фурье по силам не каждому студенту. Умение интегрировать и знания рядов Вам в этом будут хорошими помощниками.
yukhym.com
Числовые ряды, ряды фурье и преобразование Фурье
Задание 1
Исследовать на сходимость числовые ряды.
А)
Б)
Решение
А) Исследуем ряд на абсолютную сходимость. Рассмотри ряд из модулей:
При n→∞: →0, поэтому применим формулу при , тогда получим ряд , а этот ряд сходится как сумма геометрической прогрессии.
— следовательно, на основании второго (предельного) признака сравнения заключаем, что исходный ряд сходится абсолютно.
Б) Воспользуемся интегральным признаком Коши:
Следовательно, исходный ряд расходится, так как расходится соответствующий несобственный интеграл.
Задание 2
Исследовать знакочередующийся ряд На абсолютную и условную сходимость.
Решение
1) Исследуем ряд на абсолютную сходимость:
;
Используем 2й признак сравнения:
Так как ряд расходится как обобщённый гармонический. Следовательно, данный ряд не сходится абсолютно.
Исследуем ряд на условную сходимость.
Так как ряд сходится по признаку Лейбница (,) , то сходится условно по 2му признаку сравнения и ряд
Следовательно, данный ряд сходится условно.
Задание 3
Найти интервал сходимости степенного ряда. Исследовать поведение ряда на концах интервала сходимости.
Решение
Найдём интервал сходимости ряда ,
Тогда или , .
Ряд сходится абсолютно на интервале (-8;-2)
Исследуем поведение ряда на концах интервала сходимости:
При x=-8 исходный ряд примет вид , данный ряд является знакопеременным, исследуем его на абсолютную сходимость:
Воспользуемся вторым признаком сравнения: , , . Следовательно и сходятся или расходятся одновременно, а так как ряд расходится (Так как ряд Дирихле
Расходится при р<1), то ряд не сходится абсолютно.
Данный ряд сходится условно по признаку Лейбница: И .
При х=-2 исходный ряд примет вид . Как мы убедились выше этот ряд расходится.
Значит степенной ряд имеет интервал абсолютной сходимости: . В т. х=-8 ряд сходится условно.
Задание 4
Разложить функцию в ряд Тейлора по степеням . Указать область сходимости полученного ряда. Найти , если Варианта.
А)
Б)
Решение
А) Преобразуем исходное выражение:
Тогда используем стандартное разложение:
, тогда
Используем стандартное разложение:
, тогда
Подставим:
Б) Преобразуем исходную функцию к виду:
Воспользуемся стандартным разложением:
Имеем окончательно:
Задание 5
Используя признак Вейерштрасса, доказать равномерную сходимость функционального ряда на указанном промежутке.
Решение
Исходя из неравенств
на
Максимум числителя при n=2, то есть , 3/2<2
Минимум знаменателя на при ,
Имеем: — мажорирующий ряд.
Если мажорирующий ряд сходится, то функциональный ряд сходится равномерно.
Ряд сходится как сумма геометрической прогрессии.
Следовательно, мажорирующий ряд сходится.
А значит сходится и функциональный ряд на промежутке .
Задание 6
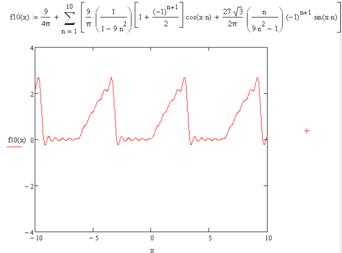
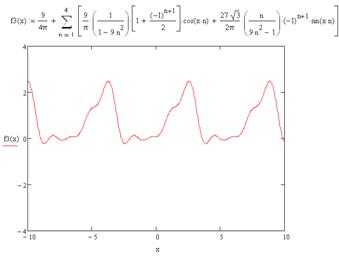
А) Разложить функцию , заданную па полупериоде , в ряд Фурье по косинусам. Построить графики второй, третьей, десятой частичных сумм. Написать равенство Парсеваля для полученного ряда. Сумму какого числового ряда можно отыскать с помощью полученного равенства?
Б) Разложить функцию , заданную на полупериоде , в ряд Фурье по синусам. Построить графики второй, третьей, десятой частичных сумм. Указать тип сходимости полученного ряда.
В) Разложить функцию в ряд Фурье, продолжая ее па полупериод функцией, равной 0. Построить графики второй, четвертой, десятой частичных сумм. Указать тип сходимости полученного ряда.
Решение
а) Доопределим функцию на промежутке чётным образом и продолжим её на всю числовую ось как периодическую с периодом, равным 2. — чётная функция. Тригонометрический ряд Фурье содержит только косинусы. Вычислим коэффициенты Фурье этой функции.
, следовательно
 ,
,
Так как рассматриваемая функция непрерывна всюду, то сумма её ряда Фурье равна данной функции при всех х и .
При Имеем и
Равенство Парсеваля:
, так как , то
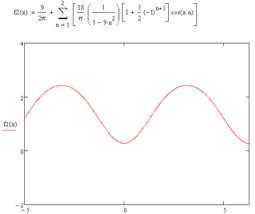
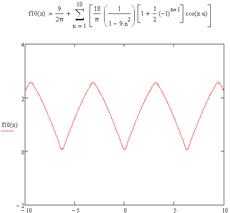
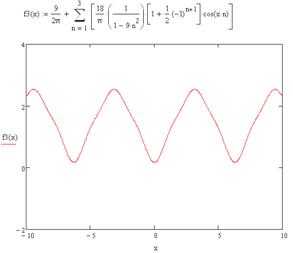
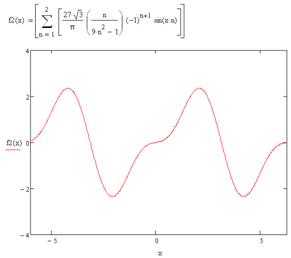
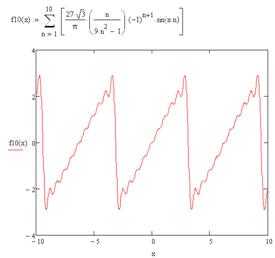
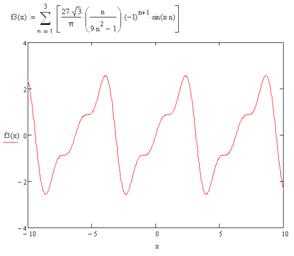
Б) Доопределим функцию на промежутке нечётным образом, а значение в т : и продолжим её на всю числовую ось как периодическую с периодом, равным 2. Согласно теореме Дирихле тригонометрический ряд Фурье такой функции будет сходиться к этой функции во всех точках непрерывности. Вычислим коэффициенты Фурье этой функции.
Так как рассматриваемая функция непрерывна всюду, то сумма её ряда Фурье равна данной функции при всех х и .
Так как функция кусочно-дифференцируема на то ряд Фурье сходится в среднем на
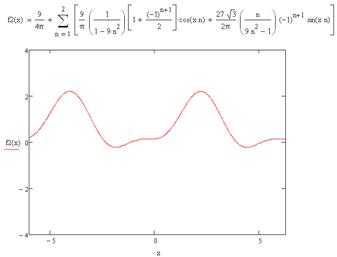
В) Разложим в ряд Фурье функцию
Т=2
Вычислим коэффициенты Фурье этой функции
, следовательно
 ,
,
Ряд Фурье имеет вид:
Ряд Фурье сходится в среднем (аналогично пункту б)
Задание 7
Методом Фурье найти решение уравнения колебания струны длины , закреплённой на концах и удовлетворяющей следующим
Начальным условиям: ,
,
Решение
Решение ищем в виде ряда
, где l=2 по условию.
Так как , а По условию, то решение имеет вид:
, где
 Окончательно:
Окончательно:
Задание 8
Найти приближённое решение задачи Коши ; ;
Решение задачи Коши ищется в виде степенного ряда , коэффициенты которого вычисляются последовательно. Ограничиваясь суммой , содержащей N + 1 член рада, получаем приближенное решение. Оценка погрешности этого решения в работе облегчается тем, что получающиеся степенные ряды знакочередующиеся. Требуется, чтобы эта погрешность не превосходила 0,001 при .
Решение
Ищем решение в виде: , тогда
,
,
Используя начальные условия, найдём значения двух коэффициентов ; .
Подставим ряды в заданное уравнение и приводим подобные члены. Получаем:
Приравнивая все коэффициенты ряда, стоящего в первой части, к нулю (только при таком условии ряд будет тождественно равен нулю), получим систему:
,, , , тогда из которой определяем следующие значения всех остальных коэффициенов
, ,,…,,…
Таким образом искомый частный интеграл данного уравнения есть степенной ряд
, который сходится при любом значении x (согласно признаку Даламбера )
Оценим погрешность. Она не должна превосходить 0,001 при
Так как , то достаточно взять первые 2 члена ряда
Задание 9
Приближенно вычислить определенный интеграл
Для вычисления интеграла функцию f(x) разлагают на отрезке интегрирования в степенной ряд, который интегрируют почленно. Ограничившись несколькими первыми слагаемыми полученного таким образом числового ряда, имеем приближенное значение интеграла. В работе погрешность приближения не должна превышать 0.0001, и оценка этой погрешности упрощается по тем же причинам, что и в задаче 8.
Решение
Воспользуемся разложением функции в ряд Маклорена
, при
Тогда
Имеем
 Получен знакочередующийся ряд, слагаемое меньше чем 0.0001. Отбрасывая это слагаемое, получим приближённое значение интеграла с заданной точностью
Получен знакочередующийся ряд, слагаемое меньше чем 0.0001. Отбрасывая это слагаемое, получим приближённое значение интеграла с заданной точностью
Задание 10
А) Найти преобразование Фурье (спектральную плотность S(u)) следующих функций (сигналов).
Б) Продолжить периодически функцию (сигнал) с интервала [0,Т] (или [-Т/2,Т/2], см. рисунок) на всю числовую прямую, разложить в ряд Фурье. Построить графики второй и третьей частичных сумм.
Решение
а) Найдём функцию, по рисунку. Прямая проходит через 2 точки: И . Запишем уравнение искомой прямой: . Имеем:
Следовательно, исходный сигнал описывается следующей формулой:
Спектральную плотность S(u) найдем с помощью прямого преобразования Фурье:
Первый интеграл берем по частям: U=t dU=dt dV=e-jutdt V=-(e-jut)/(ju),
Б) Продолжим функцию нечётным образом, тогда

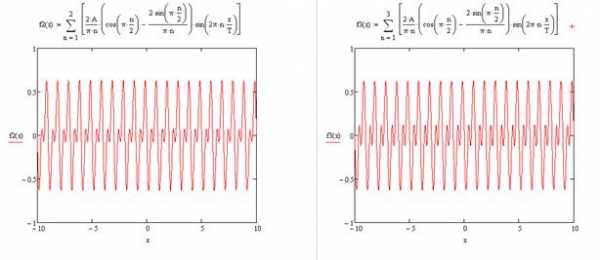
Ряд Фурье имеет вид:
Графики частичных сумм:
| < Предыдущая | Следующая > |
|---|
matica.org.ua
Ряды Фурье Решение Онлайн
Ряды Фурье
На данный момент ведётся работа над созданием конспектов по проведённым консультациям. Все уже созданные…
Vor 7 years
Ряд Фурье
Методические рекомендации к онлайн решению. math.semestr.ru/tau/fourier.php Разложить в ряд Фурье функцию f (x) …
Vor 3 years
de-film.com
Как разложить функцию в ряд Фурье
Разложение функций в ряды Фурье используется достаточно часто, поскольку в таком виде их удобно дифференцировать, интегрировать, использовать сдвиг функции по аргументу, а также свёртку функций. Несмотря на то, что процедура разложения функции в ряд Фурье даже в самом простом случае может быть достаточно трудоёмкой, система Вольфрам Альфа, как правило, легко справляется с этой задачей.Ряды Фурье представляются в тригонометрической и экспоненциальной (комплексной) форме:
В первом варианте в качестве базиса разложения используется система синусов и косинусов. Но при работе с рядами Фурье вместо них бывает удобнее использовать экспоненты мнимого аргумента. Видимо поэтому, Вольфрам Альфа отдает предпочтение второму варианту.
Самый простой способ разложить функцию в ряд Фурье — отправить в Вольфрам Альфа запрос вида Fourier series [функция, аргумент, количество членов ряда]. Например,
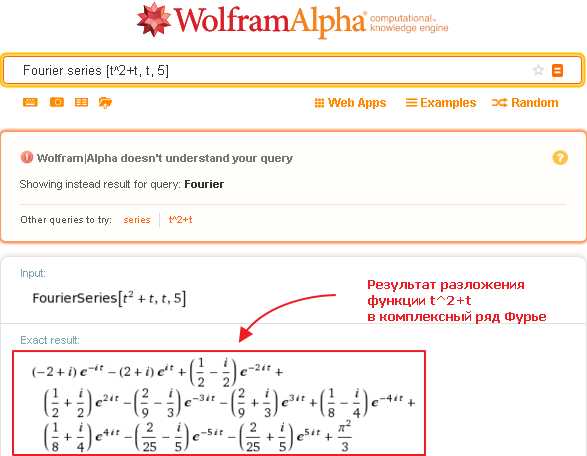
В полученном результате, как и требуется, представлены члены разложения до 5-го номера включительно; коэффициенты при сопряженных степенях экспоненты являются комплексно-сопряженными числами.
Одновременно Вольфрам Альфа дает графическое представление аппроксимации заданной функции рядом Фурье (здесь центральная часть графика аппроксимирует заданную параболу):
Еще более отчетливо особенности Фурье-аппроксимации можно видеть в результатах следующего запроса (где ряд Фурье аппроксимирует прямую):
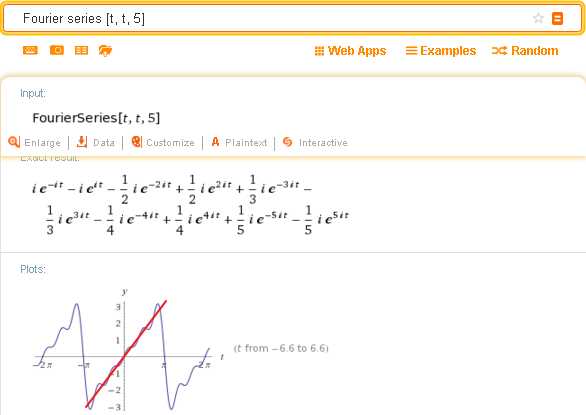
Представление заданной функции рядом Фурье в тригонометрической форме выводится в самой нижней части выдачи (здесь — для второго примера):
Кстати, несмотря на то, что выше в выдаче системы было: «Wolfram|Alpha doesn’t understand your query. Showing instead result for query: Fourier», — что означает «Система не понимает ваш запрос. Показан результат, соответствующий запросу: Fourier», не ведитесь на это 😉 По запросу «Fourier», который предлагает использовать система, будут выведены либо биографические сведения об ученом-математике Jean-Baptiste-Joseph Fourier (mathematician), либо преобразование Фурье данной функции Fourier[t^2+t]; зависит от того, поставите ли вы между словом «Fourier» и скобкой пробел или нет.
Если в запросе Fourier series не указывать явно количество членов разложения n, то система Вольфрам Альфа по умолчанию выводит четыре варианта для значений n от 0 до 3, и только для комплексной формы ряда Фурье:
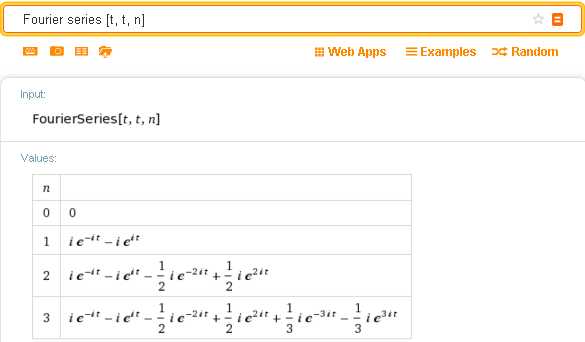
Дополнительные варианты разложения для n больше 3 можно получить тут же с помощью кнопки «More». Но это относится только к графическому представлению результатов:
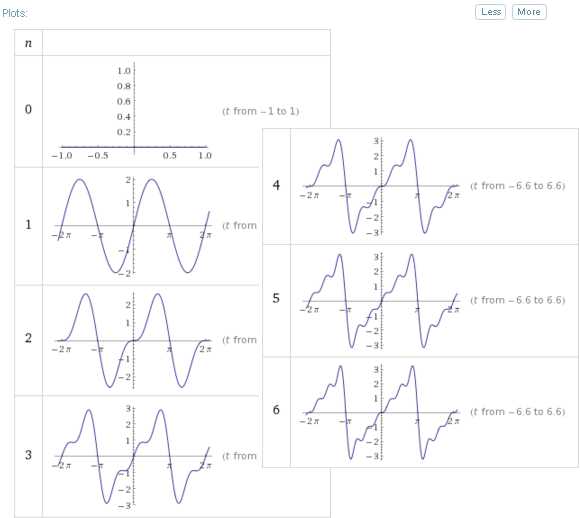
Таким образом, чтобы получить разложение функции в тригонометрический ряд Фурье, нужно в запросе Fourier series явно указывать количество членов разложения.
Что делать, если стоит задача найти не разложение в ряд Фурье, а коэффициенты ряда Фурье?
Прежде всего, можно использовать запрос FourierCoefficient[выражение, аргумент, n], по которому система Вольфрам Альфа выводит n-й коэффициент разложения выражения в комплексный ряд Фурье.
Например, 5-й коэффициент разложения выражения (t^2+t) в ряд Фурье можно получить так:
FourierCoefficient[t^2+t, t, 5]
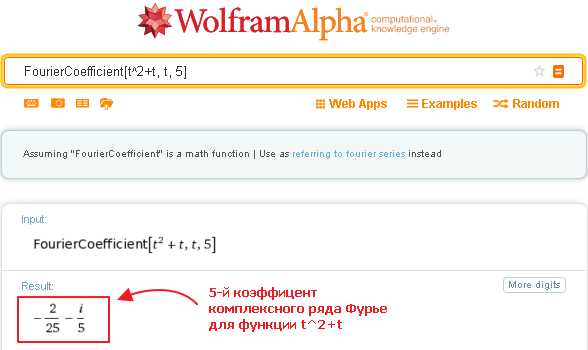
Если же при не указывать явно n, то данный запрос выведет общее выражение для n-го коэффициента ряда Фурье данного выражения:
FourierCoefficient[t^2+t, t, n]
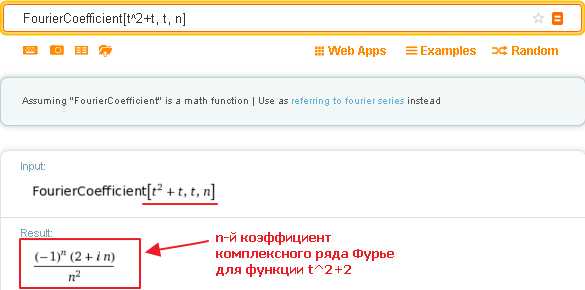
Кроме этого, Вольфрам Альфа тут же выводит также таблицу коэффициентов комплексного ряда Фурье (до 15-го члена включительно, если нажать «More»):
В этом кратком обзоре я не упомянул, как разложить функцию в ряд Фурье по синусам и косинусам или как использовать калькулятор рядов Фурье системы Вольфрам Альфа, а также ничего не сказал о двумерных рядах Фурье. Все это — темы моих будущих постов. Следите за блогом.
Если этот пост решил вашу проблему или просто понравился вам, поделитесь ссылкой на него со своими друзьями в социальных сетях.
www.wolframalpha-ru.com
