Комплексные числа в тригонометрической форме — Мегаобучалка
Действия над комплексными числами, записанными в алгебраической форме
Алгебраической формой комплексного числа z = (a, b).называется алгебраическое выражение вида
z = a + bi.
Арифметические операции над комплексными числами z1= a1+ b1i и z2= a2+ b2i, записанными в алгебраической форме, осуществляются следующим образом.
1. Сумма (разность) комплексных чисел
z1± z2= (a1± a2) + (b1±b2)∙i,
т.е. сложение (вычитание) осуществляются по правилу сложения многочленов с приведением подобных членов.
2. Произведение комплексных чисел
z1∙z2= (a
т.е. умножение производится по обычному правилу умножения многочленов, с учетом того, что i2=1.
3. Деление двух комплексных чисел осуществляется по следующему правилу:
, (z2 ≠ 0),
т.е. деление осуществляется умножением делимого и делителя на число, сопряженное делителю.
Возведение в степень комплексных чисел определяется следующим образом:
.
Легко показать, что
Примеры.
1. Найти сумму комплексных чисел z1= 2 – i и z2= –4 + 3i.
z1+ z2= ( 2 + (–1)∙i )+ (–4 + 3i ) = ( 2 + (–4)) + ((–1) + 3 ) i = –2+2i.
2. Найти произведение комплексных чисел z1= 2 – 3i и z2= –4 + 5i.
= ( 2 – 3i ) ∙ (–4 + 5i ) = 2 ∙(–4) + (-4) ∙(–3i)+ 2∙5i – 3i∙5i =7+22i.
3. Найти частное z от деления z1= 3 – 2на z2 = 3 – i.
z = .
4. Решить уравнение: , x и y Î R.
(2x + y ) + ( x + y )i = 2 + 3i.
В силу равенства комплексных чисел имеем:
откуда x = –1 , y = 4.
5. Вычислить: i2, i3, i4, i5, i6, i-1 , i-2.
6. Вычислить , если .
.
7. Вычислить число обратное числу z =3-i.
.
Комплексные числа в тригонометрической форме
Комплексной плоскостью называется плоскость с декартовыми координатами (x, y), если каждой точке с координатами (a, b) поставлено в соответствие комплексное число z = a + bi. При этом ось абсцисс называется действительной осью, а ось ординат – мнимой. Тогда каждое комплексное число a + bi геометрически изображается на плоскости как точка A ( a, b ) или вектор .
Следовательно, положение точки А ( и, значит, комплексного числа z) можно задать длиной вектора | | = r и углом j , образованным вектором | | с положительным направлением действительной оси. Длина вектора называется модулем комплексного числа и обозначается | z |=r, а угол j называется аргументом комплексного числа и обозначается j = arg z .
Ясно, что | z | ³ 0 и | z |
= 0 Û z = 0.Из рис. 2 видно, что .
Аргумент комплексного числа определяется неоднозначно, а с точностью до 2pk, k Î Z.
Из рис. 2 видно также, что если z=a+bi и j=arg z, то
cosj = , sinj = , tgj = .
Если zÎ Rи z > 0,то arg z = 0 +2pk;
если z Î Rи z < 0,то arg z = p + 2pk;
если z = 0, arg z не определен.
Главное значение аргумента определяется на отрезке 0 £ arg z £ 2p,
либо -p £ arg z £ p.
Примеры:
1. Найти модуль комплексных чисел z1 = 4 – 3i и z2 = –2–2i.
;
.
2. Определить на комплексной плоскости области, задаваемые условиями:
1) | z | = 5; 2) |
Решения и ответы:
1) | z | = 5 Û Û — уравнение окружности радиусом 5 и с центром в начале координат.
2) Круг радиусом 6 с центром в начале координат.
3) Круг радиусом 3 с центром в точке z0 = 2 + i.
4) Кольцо, ограниченное окружностями с радиусами 6 и 7 с центром в точке z0 = i.
3. Найти модуль и аргумент чисел: 1) ; 2) .
1) ; а = 1, b = Þ ,
Þ j1 = .
2) z2 = –2 – 2i; a = –2, b = -2 Þ ,
.
Указание: при определении главного аргумента воспользуйтесь комплексной плоскостью.
Используя формулы можно перейти от алгебраической формы записи комплексных чисел к тригонометрической форме (формула Муавра):
.
Комплексные числа в тригонометрической форме равны тогда и только тогда, когда равны их модули, а аргументы отличаются на целое число кратное 2p.
4. Записать числа в тригонометрической форме.
1) , 2) , 3) , 4) .
1) , ,
.
(За значение угла берем наименьшее неотрицательное из возможных значений аргумента.)
Таким образом: z1 = .
2) , r2 = 1, j2 = , .
3) , r3 = 1, j3 = , .
4) , r4 = 1, j4 = , .
megaobuchalka.ru
Тригонометрическая форма комплексного числа — ПриМат
Зададим декартову систему координат на плоскости. Изобразим комплексное число в его геометрической форме.
Угол — аргумент числа .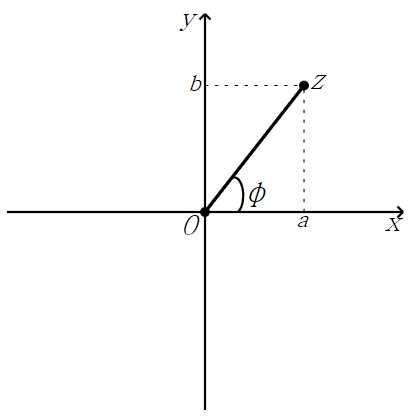
Между координатами точки существует взаимосвязь, которая верна при различных расположениях точек на плоскости:
Эта взаимосвязь получена из определения геометрического представления комплексного числа.
Применив полученные формулы к алгебраической форме комплексного числа , мы получим: , таким образом:
— тригонометрическая форма комплексного числа .
Замечание!
Следует различать запись числа в тригонометрической форме и форме на него похожей:
— не тригонометрическая форма комплексного числа;
— не тригонометрическая форма комплексного числа;
— не тригонометрическая форма комплексного числа;
Умножение
Деление
=
Возведение в степень (Формула Муавра)
, , :
Доказательство
Проверим для:
:
Математическая индукция.
1.База индукции:
,
2.Шаг индукции:
Предположим, что формула верна для , . Докажем справедливость формулы для
:
:
Таким образом можно заключить, что формула справедлива для всех целых .
Тригонометрическое представление комплексных чисел
Лимит времени: 0
Информация
Вы уже проходили тест ранее. Вы не можете запустить его снова.
Тест загружается…
Вы должны войти или зарегистрироваться для того, чтобы начать тест.
Вы должны закончить следующие тесты, чтобы начать этот:
| Место | Имя | Записано | Результат | |
|---|---|---|---|---|
| Таблица загружается | ||||
| Нет данных | ||||
- С ответом
- С отметкой о просмотре
Задание 1 из 4
Количество баллов: 1 Какая запись является записью числа в его тригонометрической форме?
ib.mazurok.com
3 Вопрос. Различные формы записи комплексных чисел. Умножение и деление комплексных чисел, записанных в тригонометрической форме. Алгебраическая форма комплексного числа
Запись вида называется алгебраической или координатной формой комплексного числа .
При этом действительное число называется действительной частью числа : , а действительное число — его мнимой частью
Величина называется мнимой единицей и удовлетворяет равенству .
Тригонометрическая форма комплексного числа
Пусть задано комплексное число . Как известно, его можно изобразить на комплексной плоскости точкой, абсцисса которой равна действительной части этого числа, то есть , а ордината — мнимой части .
Абсциссу и ординату комплексного числа можно выразить через модуль и аргумент следующим образом:
В данном случае и удовлетворяют соотношениям:
Тогда
Таким образом, для всякого комплексного числа справедливо равенство
которое называется тригонометрической формой комплексного числа .
То есть, если — модуль комплексного числа , а его аргумент, то тригонометрической формой комплексного числа называется выражение
Умножение комплексных чисел в тригонометрической форме
Зададим два комплексных числа в тригонометрической форме и и перемножим их по правилу умножения двучленов:
или
Получили новое число , записанное в тригонометрической форме: , для которого .
Правило умножения. При умножении комплексных чисел, заданных в тригонометрической форме, их модули перемножаются, а аргументы складываются:
В результате умножения чисел может получиться аргумент произведения, не являющийся главным значением.
Деление комплексных чисел в тригонометрической форме
Рассмотрим частное комплексных чисел , заданных в тригонометрической форме. Из определения частного имеем и, применяя к произведению правило умножения, получаем .
Правило деления. Модуль частного, полученного в результате деления чисел, заданных в тригонометрической форме, равен частному от деления модуля числителя на модуль знаменателя, а аргумент частного равен разности аргументов делимого и делителя:
В результате деления чисел по формуле может получиться аргумент частного, не являющийся главным значением.
Показательная форма комплексного числа Формула Эйлера
Пусть — некоторое комплексное число. По определению полагают, что
Если число — действительное, то есть , то
Если число — чисто мнимое, то есть , то
Таким образом, имеем равенство
которое называется формулой Эйлера.
Рассмотрим произвольное комплексное число, записанное в тригонометрической форме: . По формуле Эйлера
а тогда
Следовательно, любое комплексное число можно представить в так называемой показательной форме:
Операции с комплексными числами в показательной форме
Такая форма представления позволяет дать наглядную интерпретацию операциям умножения комплексных чисел, их деления и возведения комплексного числа в степень. Например, умножение комплексного числа на комплексное число выглядит следующим образом:
То есть, чтобы найти произведение комплексных чисел, нужно перемножить их модули и сложить аргументы.
Аналогично можно довольно легко найти частное от деления комплексного числа на комплексное число :
Отсюда получаем правило, что для того чтобы найти частное двух комплексных чисел, надо поделить их модули и отнять аргументы.
Для возведения комплексного числа в целую степень нужно представить это число в показательной форме, модуль возвести в степень, а аргумент увеличить в раз:
studfiles.net
1.2.Тригонометрическая форма комплексного числа.
С каждым комплексным числом на плоскости связывается точка с координатами. Положение этой точки однозначно определяется расстоянием от начала координати угломмежду положительным направлением вещественной оси и лучем, проведенным из начала координат в эту точку. Если угол отсчитывается в положительном направлении, то ему приписывается знак «+», а в противном случае знак «-». Комплексное число 0=0+0iоднозначно определяется расстоянием (равным 0) от начала координат, а потому ему значение угла не приписывается. Числоназываетсямодулем комплексного числа, а указанный выше уголназываетсяаргументом и обозначается. Аргумент комплексного числа определяется с точностью до слагаемого, кратного.
Из рисунка видно, что . Так что мы имеем следующий вид тригонометрической формы комплексного числа
.
А число, комплексно сопряженное к z,имеет такую тригонометрическую форму. Теперь, используя формулы для синуса и косинуса суммы (разности) двух углов, получаем
При возведении комплексного числа в степень с натуральным показателем можно воспользоваться следующей формулой, которая называется формулой Муавра.
.
Для представления комплексного числа в тригонометрической форме очень полезно изобразить соответствующую этому числу точку (это избавит вас от ошибки в определении аргумента числа).
При решении задач часто используется следующий результат.
где .
Приведем примеры решения некоторых задач.
Формула Муавра.
еорема. (Формула Муавра, 1707 г.)
Для любого целого числа n и любого действительного числа имеет место следующее равенство:
. (1)
Доказательство. Разобьем доказательство на 3 этапа.
1) Пусть – натуральное число. Так как комплексное число имеет модуль , то справедливость формулы Муавра в этом случае следует из следствия 2 теоремы об умножении комплексных чисел в тригонометрической форме записи.
2) Пусть теперь . Тогда
, ч.т.д.
3) Пусть , где – натуральное число. Тогда по свойству целых степеней, которые справедливы в любом поле, в том числе и вполе комплексных чисел, имеем:
.
Здесь мы использовали уже доказанные случаи формулы Муавра возведения в натуральную степень и в степень, равную (–1).
Теорема доказана.
Следствие. (О целых степенях комплексного числа.)
Пусть . Тогда
.
Доказательство предоставляется читателю.
п.2. Деление комплексных чисел в тригонометрической форме записи.
Теорема. (О делении комплексных чисел в тригонометрической форме)
Пусть , где и , где – два произвольных комплексных числа записанных в тригонометрической форме. Тогда
. (2)
Доказательство. Воспользуемся следствием формулы Муавра и правилом умножения комплексных чисел в тригонометрической форме записи. Получаем:
, ч.т.д.
Пример 1. Запишите комплексные числа и в тригонометрической форме и найдите их произведение и частное .
Решение. 1) Комплексное число на комплексной плоскостинаходится во второй четверти, поэтому
, .
2) Комплексное число на комплексной плоскости находится во четвертой четверти, поэтому
, .
3)
.
Ответ: , .
Пример 2. Вычислить .
Решение. Комплексное число на комплексной плоскостинаходится в третьей четверти, поэтому ,
Применим формулу Муавра:
.
Корені п-ого степеня з комплексного числа, корні з одиниці.
п.3. Корни из комплексных чисел.
Определение. Пусть и . Корнем n-й степени из комплексногочисла z называется комплексное число , такое, что .
Теорема. (Формула корней из комплексного числа.)
Для любого ненулевого комплексного числа
, где , существует ровно n корней n-й степенииз комплексного числа z и все они могут быть найдены по формуле
, (3)
где , – арифметический корень n-й степени из положительного числа .
Доказательство. Обозначим
(4)
и докажем, что данное множество исчерпывает все множество корней n-й степени из комплексного числа z.
Доказательство проведем в 3 этапа. Сначала мы докажем, что всеэлементы множества (4) являются корнями n-й степени из комплексногочисла z. Затем мы покажем, что среди корней множества (4) нет равных. И, наконец, мы покажем, что любой корень n-й степени из комплексногочисла z является элементом множества (4).
1) По следствию 2 формулы Муавра
, ч.т.д.
2) Допустим, что , где и . Тогда по теореме о равенстве двух комплексных чисел в тригонометрическойформе записи следует, что равны их аргументы.
Но, аргумент числа может отличаться от числа на числократное числу (т.е. на целое число оборотов) и аналогично для аргумента числа . Отсюда следует, что , где . Умножим это равенство на n: . Отсюда следует, что и т.к. по нашему предположению , то , чего не может быть, т.к. и . Получили противоречие. Следовательно, среди корней вмножестве (10) нет равных, ч.т.д.
3) Пусть теперь комплексное число является корнем n-й степени из комплексного числа z, т.е. . Так как . Отсюда, из тех же соображений, что и во второй части доказательства, следуют равенства и , где . Из первого равенства получаем, что , а из второго следует .
Далее, разделим целое число t на n с возможным остатком: , где , а остаток r также является целым числом, но . Отсюда
и
. Таким образом,корень является корнем из множества корней (4), ч.т.д.
Теорема доказана.
Пример. Вычислить .
Решение. Запишем число в тригонометрической форме записи: . Тогда
, где
, .
Ответ: , где
,
,
п.4. Расположение корней на комплексной плоскости.
Перепишем формулу (3) в виде
, где ,.
Заметим, что
. (5)
Из этой формулы мы видим, что аргументы корней образуют арифметическую прогрессию.
Так как модульу всех корней одинаковый, то на комплексной плоскости они удалены от началакоординатна одинаковое расстояние. Отсюда делаем вывод, что все корни на комплексной плоскости изображаются точками, лежащими наокружностирадиусас центром в начале координат. Из формулы (5) мы видим, чтоуголмеждутакимидвумясоседнимиточкамиодинаковый. Отсюда делаем вывод, что все корни располагаются наокружностиравномерно. Если соединить все соседние точки (корни) отрезками прямой, то получим правильный n-угольник.
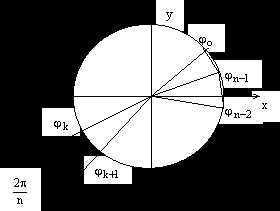
рис.1.
При изображении корней на комплексной плоскости около точки, с которой отождествляется кореньпроставляется только его аргумент, поскольку модули у всех корней одинаковые.
Пример. Изобразить все корни на комплексной плоскости.
Решение. Сами корни мы уже вычислили (см. предыдущий пример). Изображаем координатные оси, проводим окружность радиуса с центром в началекоординати отмечаем на ней точки полярныйуголкоторых равен:
, ,.
Соединим построенные точки отрезками прямыхи получаем правильный треугольник.
прямоугольная выноска: » width=»83″>
рис.2.
п.5. Корни из единицы.
Пусть – натуральное число. По формуле корней изкомплексногочисла, существует ровно n корней изкомплексногочисла. Для вычисления этих корней запишем единицу втригонометрическойформе:
, т.е. ,.
Обозначим все множество корней через . По формуле корней получаем:
, (6)
, . (7)
В частности, ,
. (8)
Заметим, что верна формула:
. (9)
Действительно, равенство(9) сразу же получается по формуле Муавра:
.
Теперь мы все множество корней из 1 можем записать так:
(10)
Теорема. Множество всех корней из 1 является коммутативной группой.
Доказательство. Сначала мы должны показать, что множество замкнуто относительно умножения. Пусть– два произвольных корня из 1, т.е.. Найдем их произведение:
.
Замечаем, что
. (11)
Отсюда следует, что , если. В противном случае,. Обозначим черези. Тогда
, ч.т.д.
Таким образом, на множествеопределена операция умножения и т.к. она ассоциативна и коммутативна вполекомплексныхчисел, то она ассоциативна и коммутативна и намножестве. Далее,. Покажем, что любой элемент изимеет обратный элемент также принадлежащий множеству:
.
Действительно, по условию . Тогда
, т.е. .
Теорема доказана.
Пример. Построить таблицу умножения для группы .
Решение. Обозначим для простоты
. Тогда, где.
Заполняем таблицу Кэли (таблицу умножения):
Изобразим все корни третьей степенииз 1 на комплексной плоскости. Т.к. ихмодульравен 1, то все они лежат натригонометрической(т.е. единичной) окружности:
рис.3.
Здесь, ,.
Многочлени. Дії над многочленами, теорема про ділення з остачею.
studfiles.net
Представить в тригонометрической форме комплексные числа
Представить в тригонометрической форме комплексные числа сможем, для начала вспомнив, что такое комплексные числа.
Рассмотрим число в виде z=a+bi, которое называется комплексным. Изобразить его можно на комплексной плоскости с помощью точки, абсцисса которой (число а) — это действительная часть данного числа, а ордината (число b) — мнимая часть.
Абсцисса а и ордината b рассматриваемого комплексного числа выражается с помощью модуля и аргумента таким образом:
При тригонометрические функции можно выразить так:
Тогда можно записать:
Таким образом, равенство является \textbf{тригонометрической формой комплексного числа z}.
Рассмотрим пример.
Пример.
Дано число z=-13i. Представим его в тригонометрической форме.
Решение.
Для данного комплексного числа его действительная часть а=0, а мнимая часть b=-13.
Запишем модуль данного числа:
Найдем тригонометрические функции:
Найдем значение : .
Получаем тригонометрическую форму данного комплексного числа:
Ответ. .
ru.solverbook.com
Умножение комплексных чисел в тригонометрической форме записи » Аналитическая геометрия f(x)dx.Ru
п.5. Умножение комплексных чисел в тригонометрической форме записи. Свойства модуля комплексных чисел.
Теорема. (Об умножении комплексных чисел в тригонометрической форме записи.)
Пусть , где и , где – два произвольных комплексных числа записанных в тригонометрической форме. Тогда
. (13)
Доказательство.
, ч.т.д.
Теорема доказана.
Отсюда вытекает правило умножения комплексных чисел в тригонометрической форме записи.
Для того, чтобы перемножить два комплексных числа в тригонометрической форме записи нужно перемножить их модули, а аргументы сложить.
Следствие 1. Пусть k натуральное число и . Пусть далее , где – произвольные n комплексных чисел записанных в тригонометрической форме записи. Тогда
.
Доказательство проводится индукцией по числу сомножителей и предоставляется читателю.
Следствие 2. Пусть n натуральное число и – произвольное комплексное число в тригонометрической форме записи. Тогда
.
Доказательство сразу же следует из Следствия 1.
Теорема. (Свойства модуля комплексного числа.)
Пусть – произвольные комплексные числа и соответствующие точки на комплексной плоскости. Тогда:
1) и . Т.е. модуль произведения комплексных чисел равен произведению их модулей и модули противоположных чисел равны;
2) расстояние между точками и комплексной плоскости равно модулю разности соответствующих комплексных чисел: ;
3) ;
4) ;
Доказательство. 1) По предыдущей теореме имеем:
, где и ,
т.е. .
Таким образом, равенства и есть тригонометрическая форма записи числа , следовательно, по теореме о равенстве комплексных чисел в тригонометрической форме записи, имеем , ч.т.д.
Далее, т.к. , то по только что доказанному свойству , ч.т.д.
Заметим, что последнее равенство можно получить и из других соображений.
Противоположные числа на комплексной плоскости изображаются точками симметричными относительно начала координат. Действительно, пусть . Тогда и точки , имеют противоположные декартовые координаты. Значит, в силу симметрии, расстояния от этих точек до начала координат равны, т.е. , ч.т.д. Заметим, также, что такой же результат можно получить с помощью формулы (12) вычисления модуля комплексного числа.
2). Пусть , . Тогда и по формуле (12) имеем:
. (14)
С другой стороны, рассмотрим числа и как точки на комплексной плоскости. Тогда точка имеет декартовые координаты , а и искомое расстояние между ними вычисляется по формуле (14), ч.т.д.
3) Рассмотрим на комплексной плоскости точки , и начало координат О. В общем случае эти три точки являются вершинами треугольника :
рис.6.
Воспользуемся известным свойством треугольника: длина стороны треугольника не превосходит суммы длин двух его других сторон.
Мы только что доказали, что длина стороны этого треугольника равна , а длины сторон и равны по определению модулям чисел и : , . Отсюда и получаем, что .
Заменим в последнем неравенстве число на противоположное число , тогда получаем:
, ч.т.д.
Заметим, что равенство в этих неравенствах достигается тогда и только тогда, когда треугольник вырождается в отрезок прямой, т.е. когда все три точки О, и лежат на одной прямой.
4) , откуда следует
. Поменяв местами и , получаем
, откуда и следует доказываемое неравенство.
Теорема доказана.
Теория комплексных чисел имеет много приложений в различных областях математики. Не могу удержаться от искушения привести хотя бы один такой пример, относящийся к области теории чисел.
Определение. Говорят, что натуральное число n представимо в виде суммы двух квадратов, если существуют такие целые числа х и у, что выполняется равенство:
.
Теорема. Если два числа представимы в виде суммы двух квадратов, то их произведение также представимо в виде суммы двух квадратов.
Доказательство. Пусть и , где .
Нам нужно доказать, что найдутся два целых числа а и b такие, что .
С этой целью рассмотрим два комплексных числа и .
Тогда и по формуле (12) имеем: .
С другой стороны, , . Так как , то или , то отсюда получаем равенство: , где , ч.т.д.
Теорема доказана.
Возможно найдутся ответы здесь:
fxdx.ru
Действия над комплексными числами в тригонометрической форме
Сложение и вычитание удобнее производить над комплексными числами в алгебраической форме, а умножение и деление – в тригонометрической форме.
1. Умножений. Пусть даны два комплексных числа, записанных в тригонометрической форме: z1 = r1(cos1 + isin1) z2 = r2(cos2 + isin2).
z1z2 = r1r2(cos1cos2 – sin1sin2) + i(cos1sin2 + sin1cos2) = = r1r2(cos(1 + 2) + isin(1 + 2)).
Итак, модуль |z1z2| = r1r2, аргумент arg(z1z2) = arg z1 + arg z2.
Пример 1.13. Для z1 = 2(cos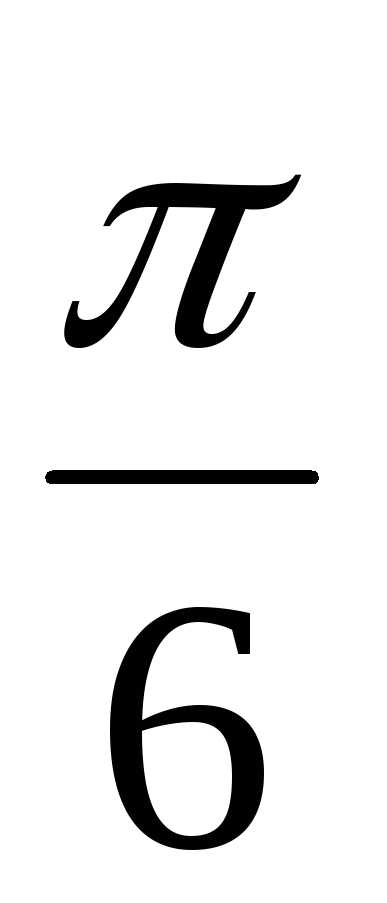 + isin
+ isin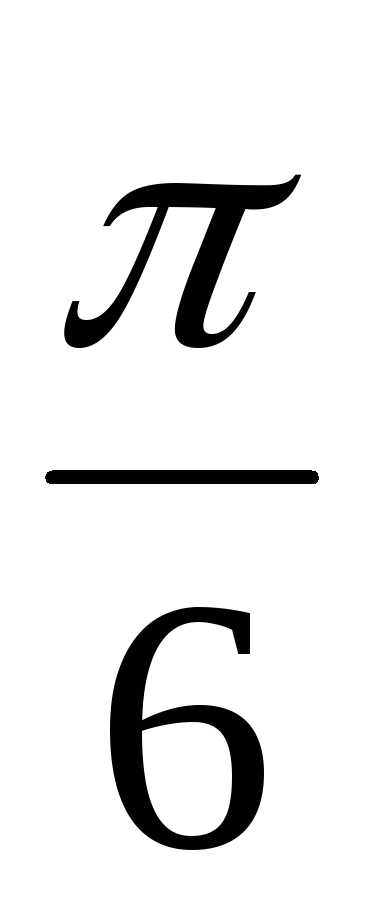 )
и z2 = 3(cos
)
и z2 = 3(cos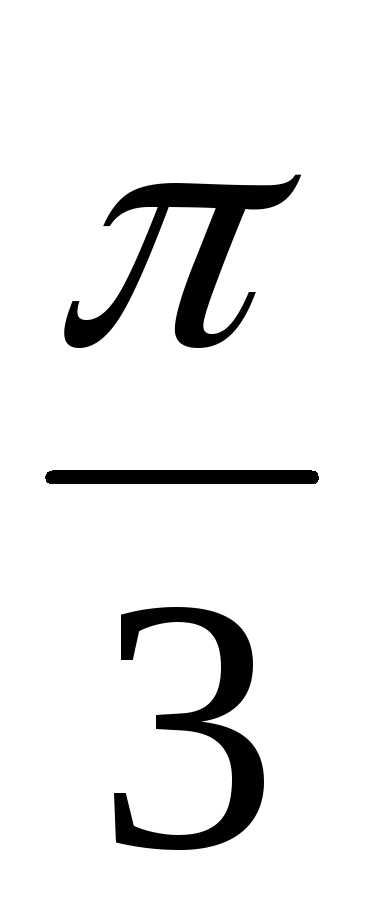 + isin
+ isin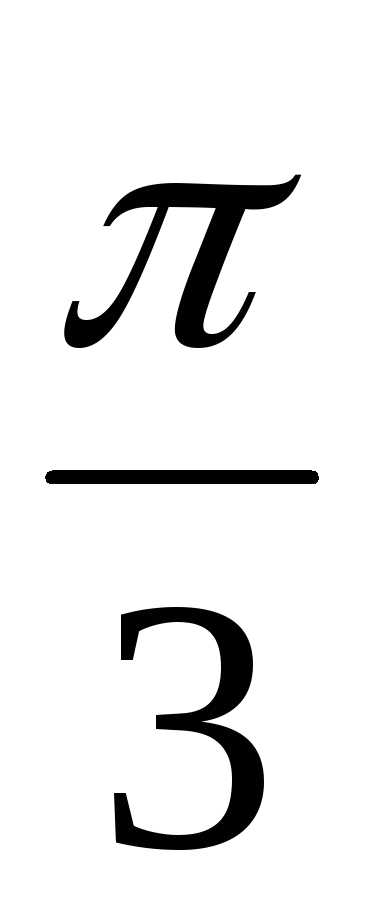 )
найти их произведение z1z2.
)
найти их произведение z1z2.
Решение.
Применяем формулу для нахождения
произведения двух комплексных чисел,
записанных в тригонометрической форме. z1z2 = 23(cos( +
+ 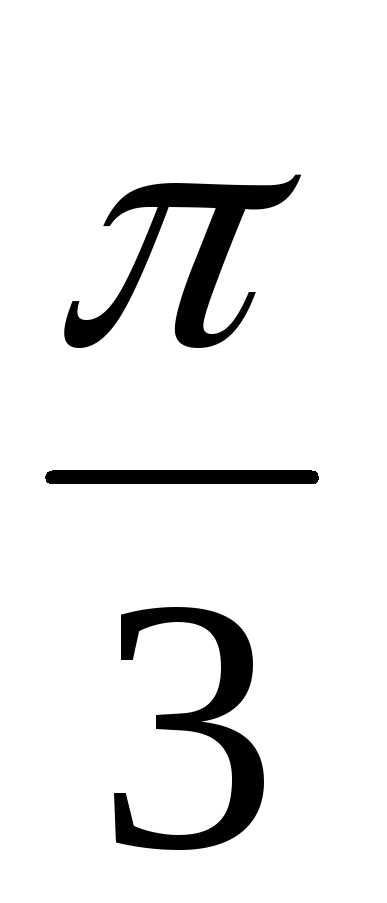 ) + isin(
) + isin(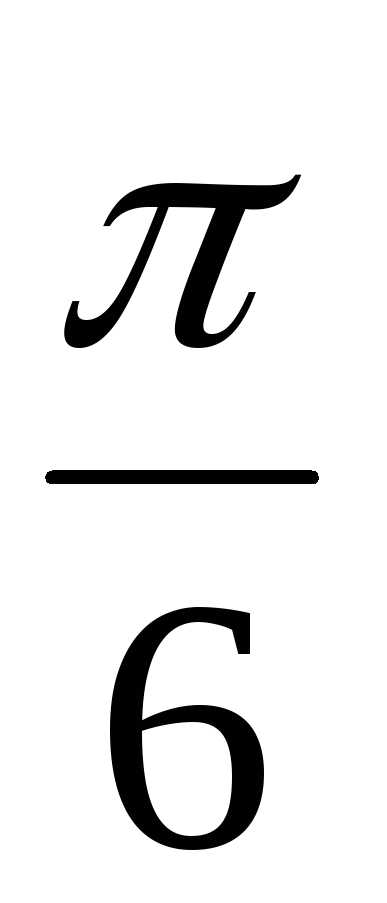 +
+ 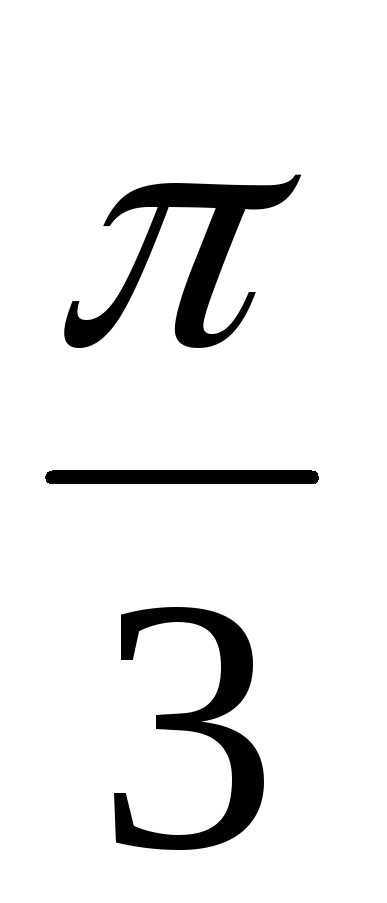 )) = 6(cos
)) = 6(cos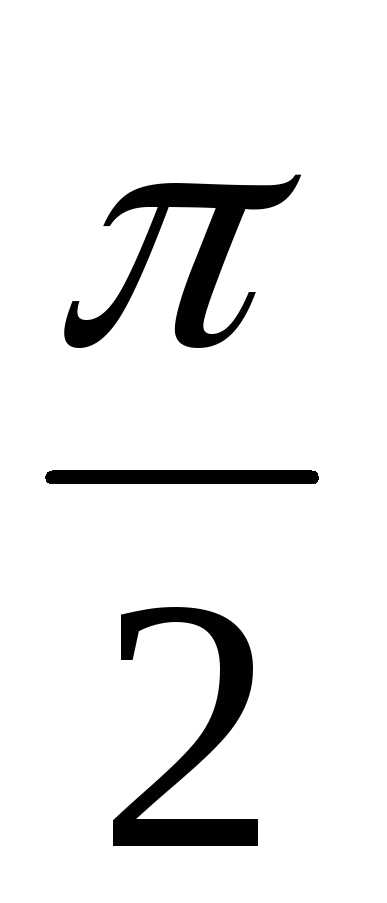 + isin
+ isin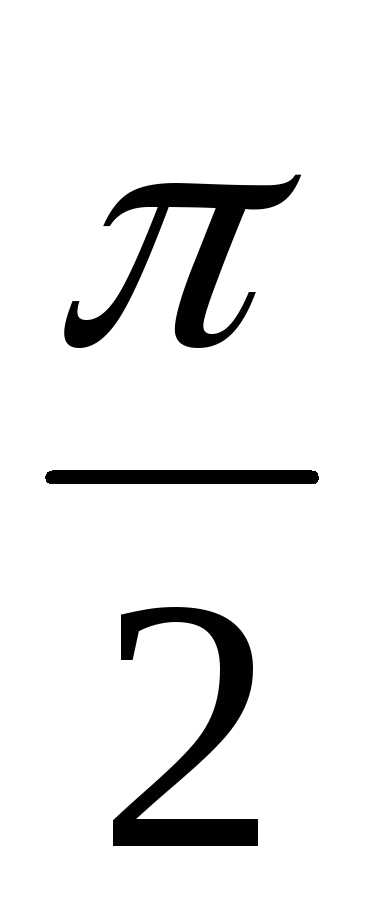 )
– тригонометрическая форма произведения
чисел z1 и z2 или в алгебраической форме z1z2 = 6i.
)
– тригонометрическая форма произведения
чисел z1 и z2 или в алгебраической форме z1z2 = 6i.
2. Деление. 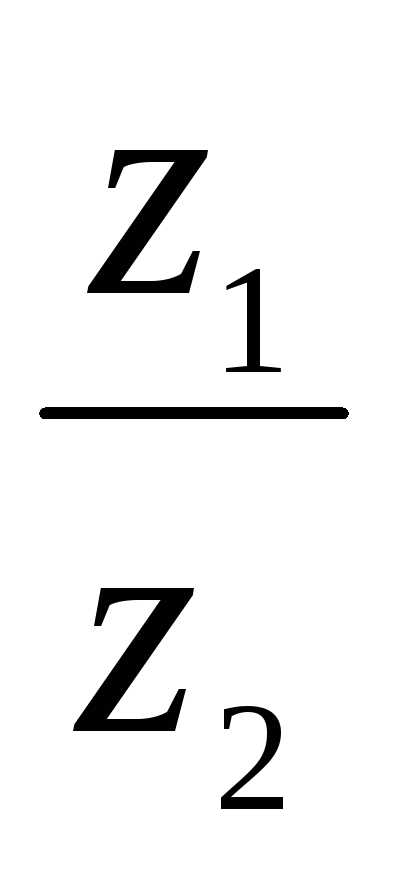 =
=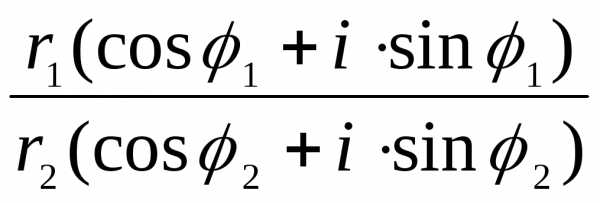 =
= =
=
= 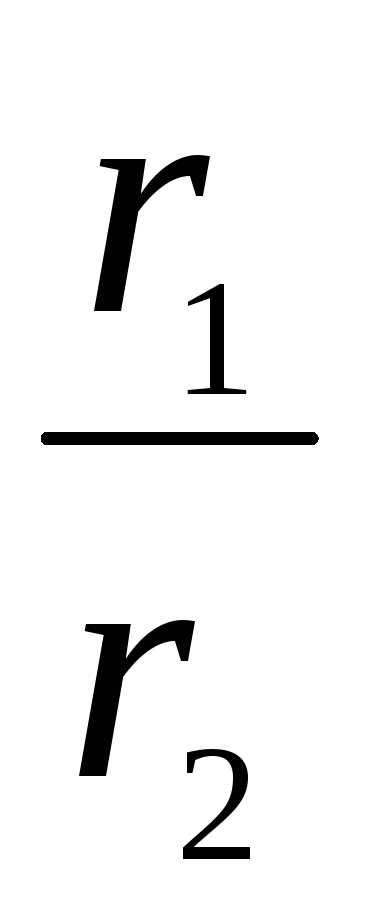 =
=
= 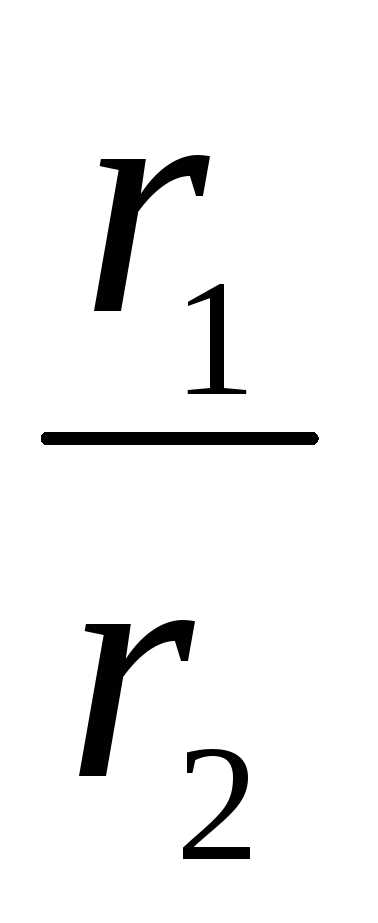 ( cos(1 – 2) + isin(1 – 2))
( cos(1 – 2) + isin(1 – 2))
Итак,
модуль
|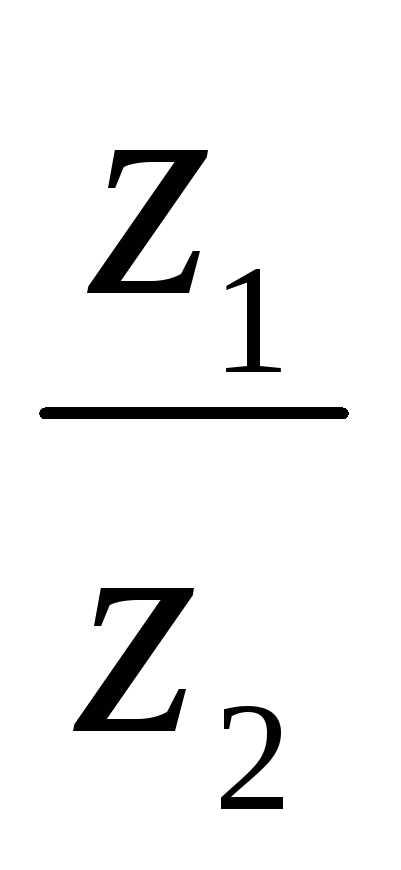 | =
| = 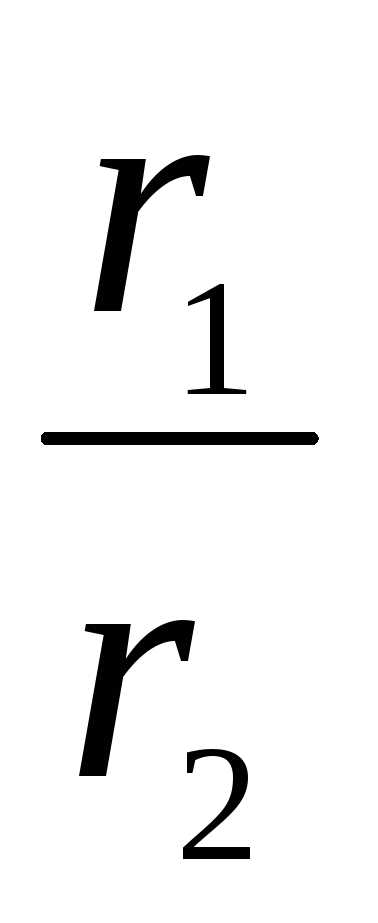 ,
аргумент arg(
,
аргумент arg(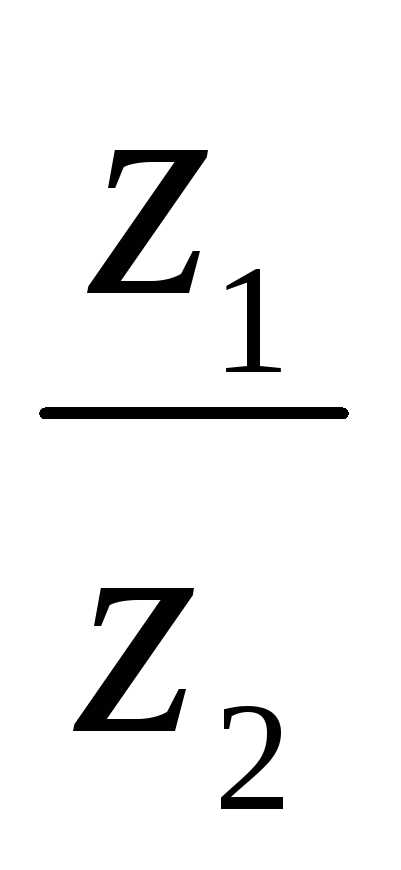 ) = arg z1 – arg z2.
) = arg z1 – arg z2.
Пример 1.14. Для z1 = 10(cos45 + isin45)
и z2 = 5(cos60 + isin60)
найти их частное от деления 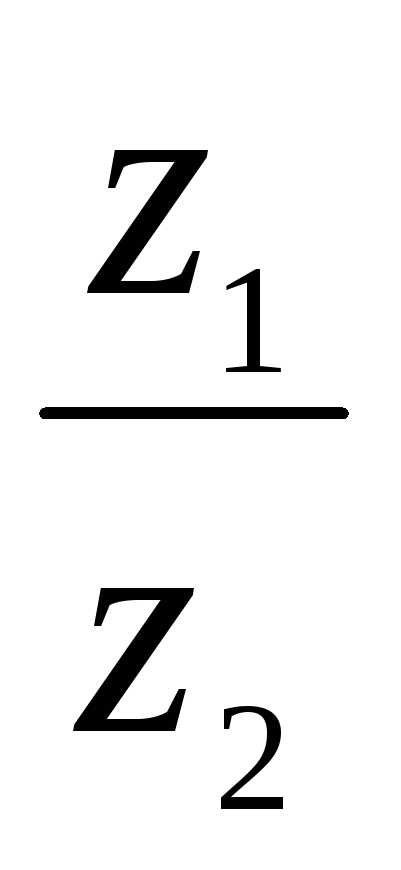 .
.
Решение.
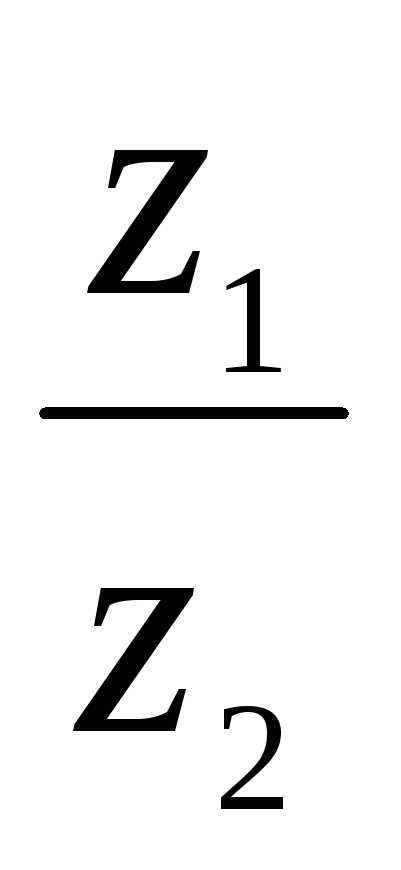 =
= 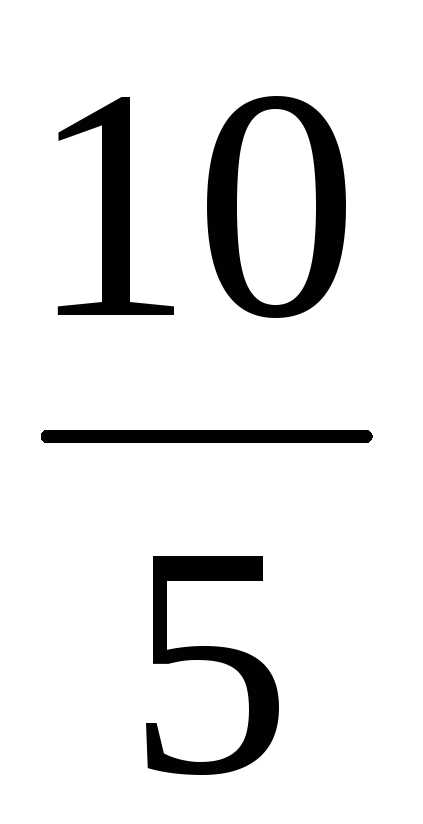 (cos(45 – 60) + isin(45 – 60)) = 2(cos(–15) + isin(–15))
– тригонометрическая форма частного
чисел z1 и z2.
Заметим, что если данное выражение
записать в виде равносильного выражения 2(cos15 – isin15),
то это не будет уже тригонометрической
формой записи комплексного числа.
(cos(45 – 60) + isin(45 – 60)) = 2(cos(–15) + isin(–15))
– тригонометрическая форма частного
чисел z1 и z2.
Заметим, что если данное выражение
записать в виде равносильного выражения 2(cos15 – isin15),
то это не будет уже тригонометрической
формой записи комплексного числа.
3. Возведение в степень.
Если z = r(cos + isin), то zn = rn(cos(n) + isin(n)), где n Z. Данная формула называется формулой Муавра9.
Пример 1.15. Для z = 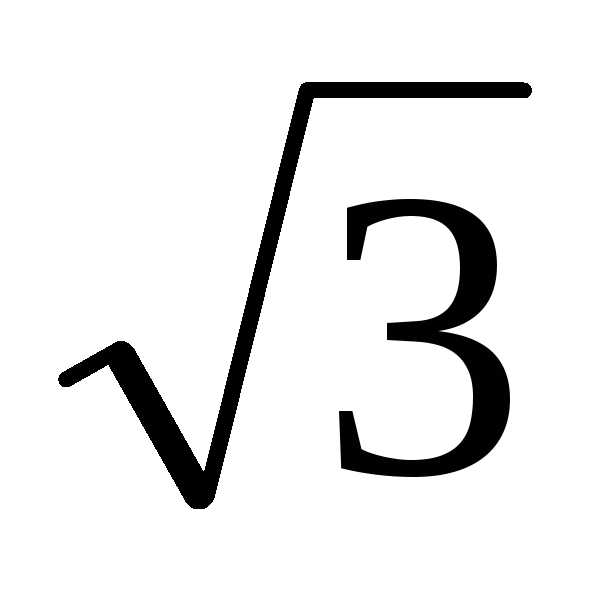 – i,
найти z4.
– i,
найти z4.
Решение.
Воспользуемся формулой Муавра, но для
начала надо это комплексное число
записать в тригонометрической форме.
В примере 1.12 мы это уже находили z = 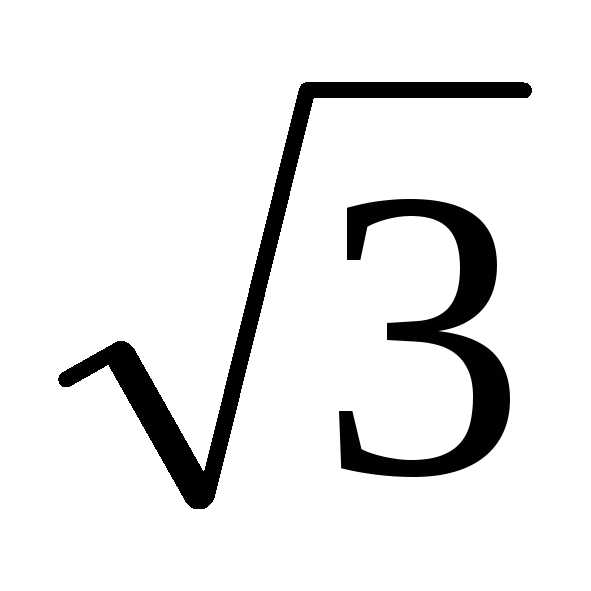 – i = 2(cos
– i = 2(cos + isin
+ isin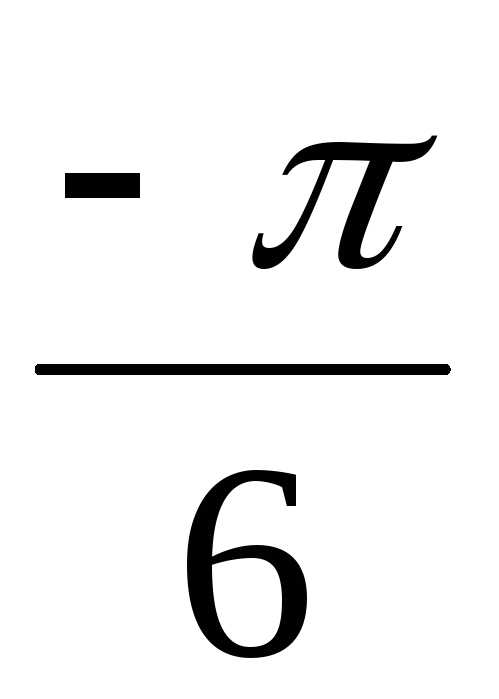 ).
Тогда z4 = (
).
Тогда z4 = (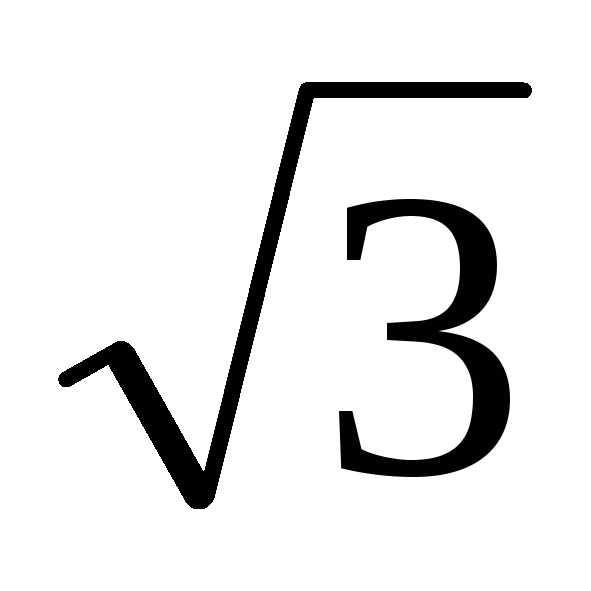 – i)4 = (2(cos
– i)4 = (2(cos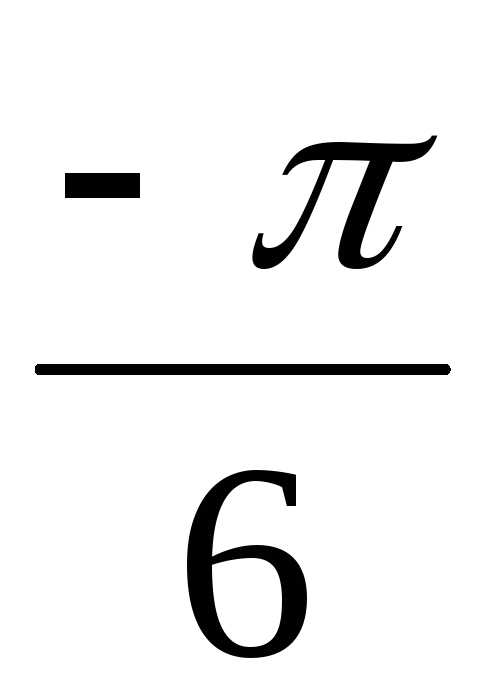 + isin
+ isin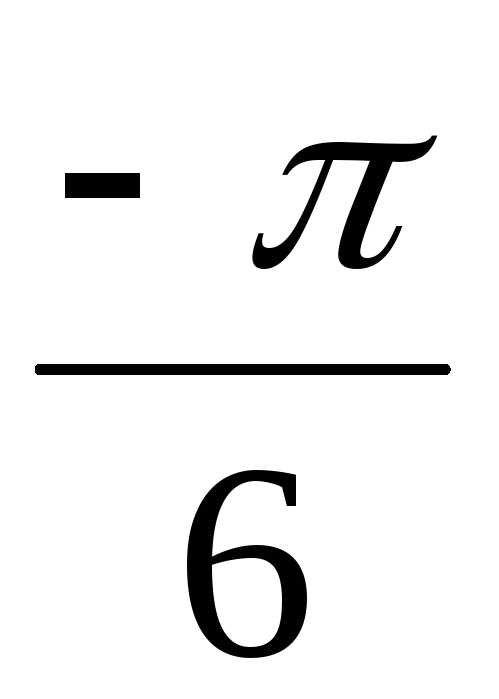 ))4 = 24(cos
))4 = 24(cos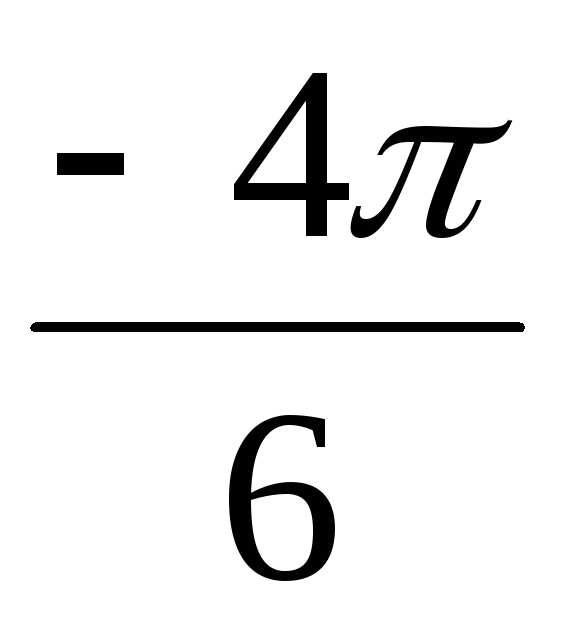 + isin
+ isin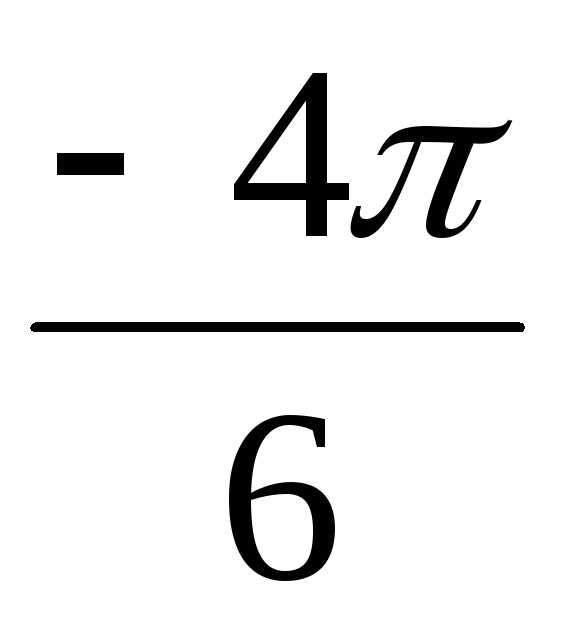 ) =
= 16(cos
) =
= 16(cos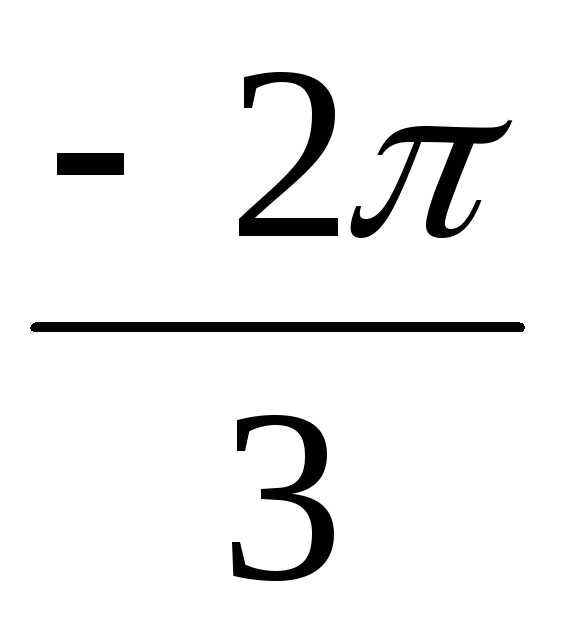 + isin
+ isin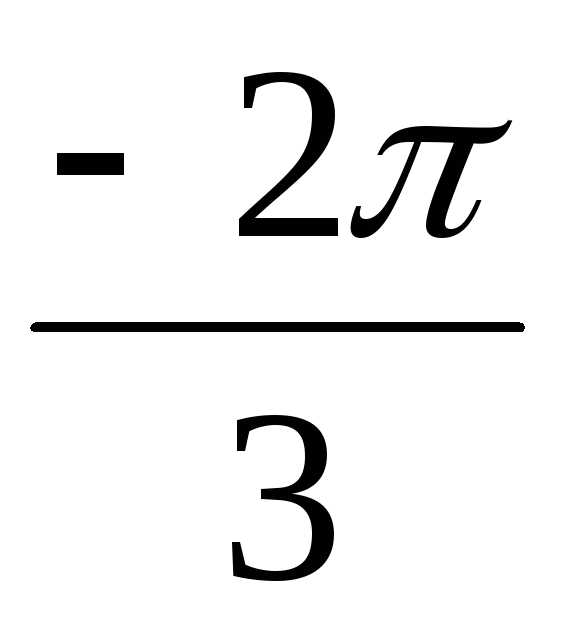 )
– тригонометрическая форма результата
возведения в четвертую степень данного
комплексного числа. Найдем также и
алгебраическую форму записи числа z4. z4 = 16(cos
)
– тригонометрическая форма результата
возведения в четвертую степень данного
комплексного числа. Найдем также и
алгебраическую форму записи числа z4. z4 = 16(cos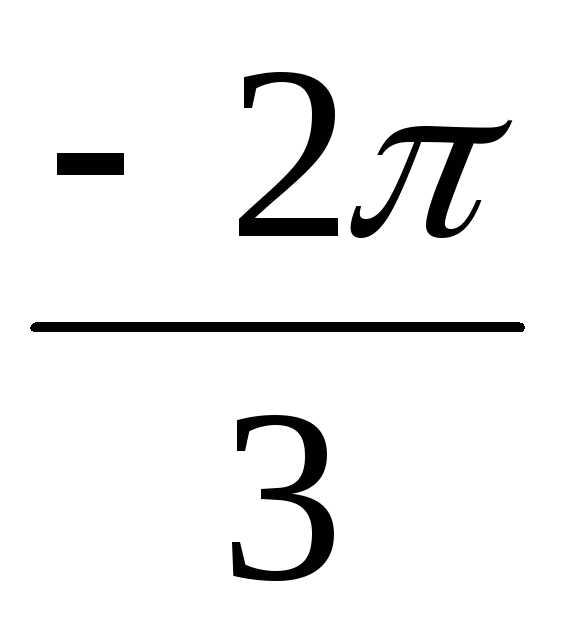 + isin
+ isin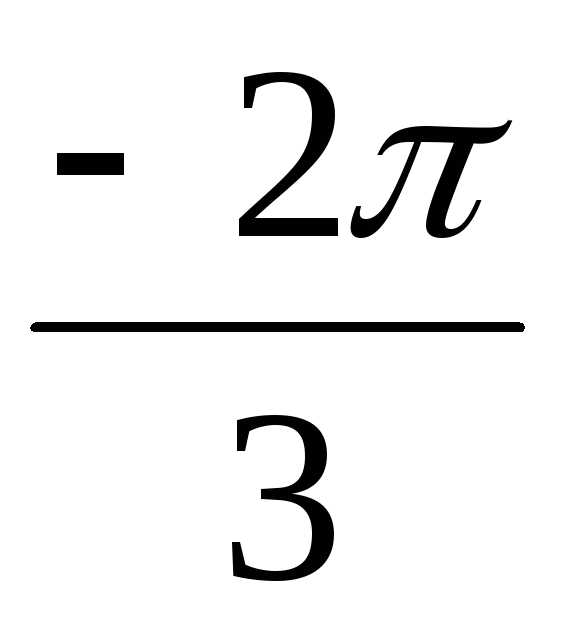 ) = 16(cos
) = 16(cos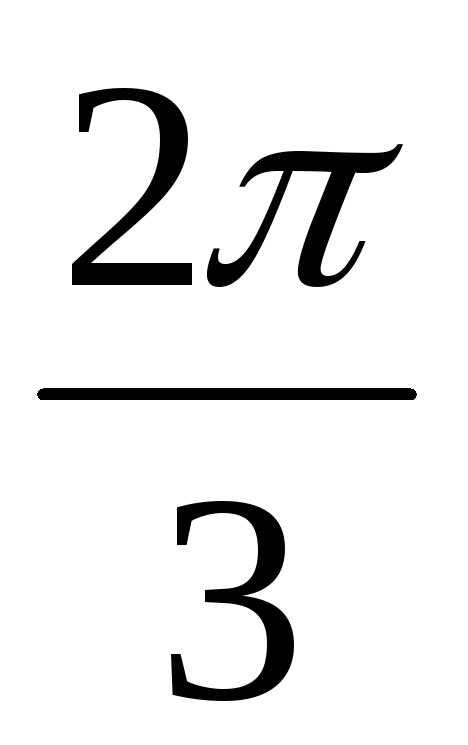 – isin
– isin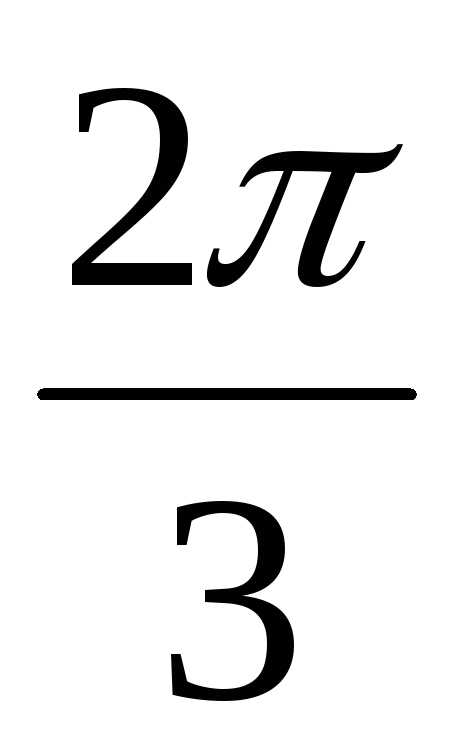 ) = 16(
) = 16(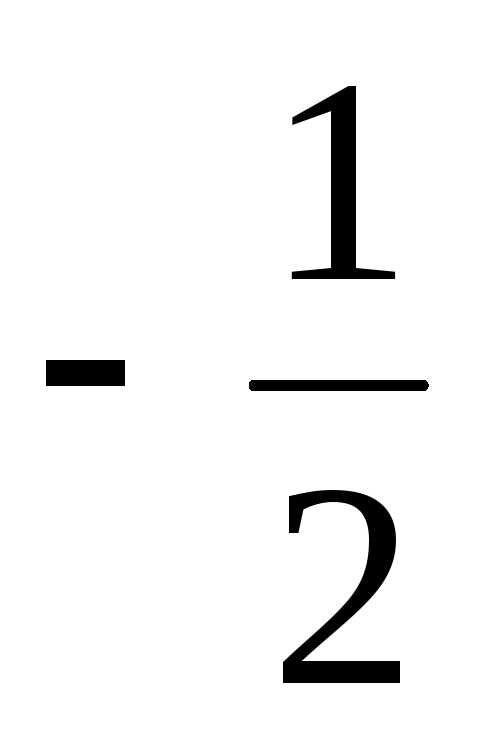 – i
– i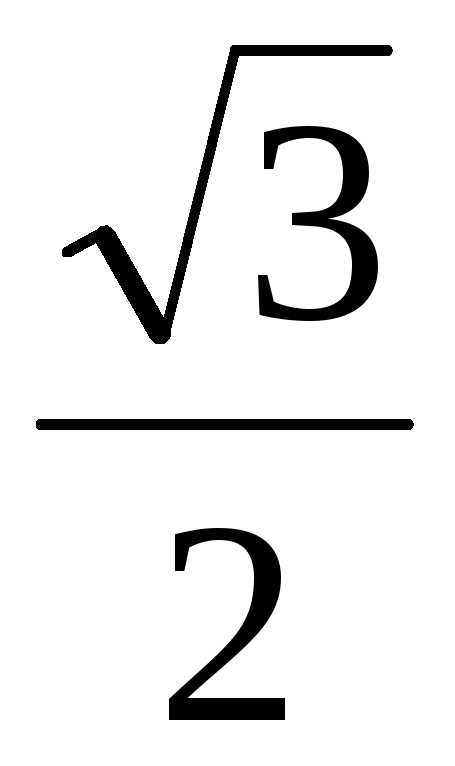 ) =
= –8 – 8
) =
= –8 – 8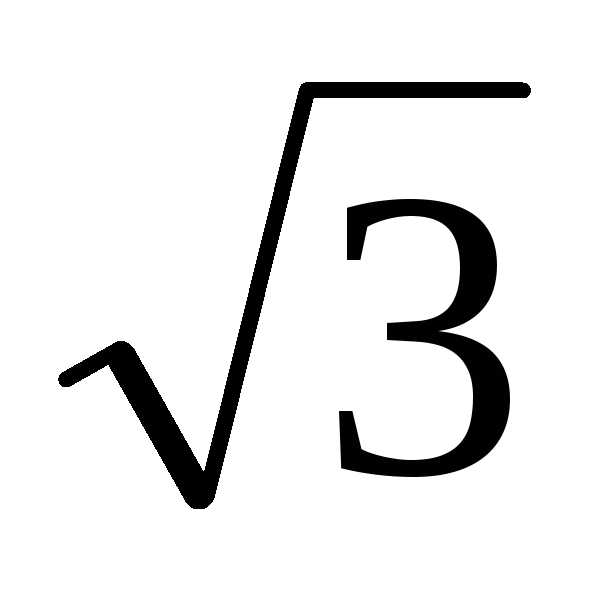 i.
i.
4. Извлечение корня n-ой степени.
Можно показать, что каждое комплексное число, отличное от нуля, имеет ровно n корней n-й степени.
Если z = r(cos + isin), то
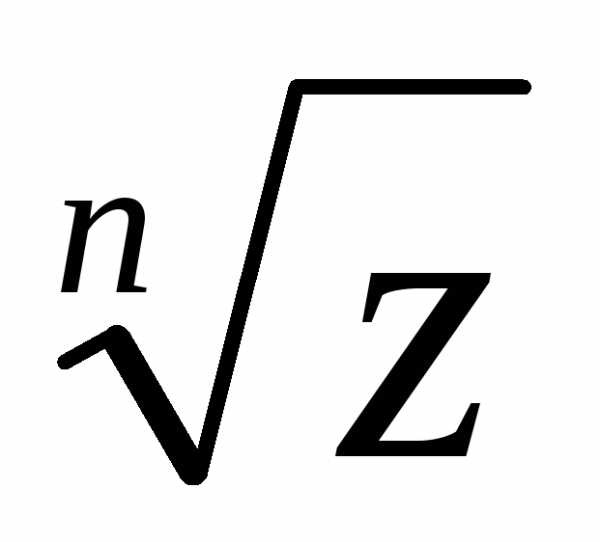 = =
= =
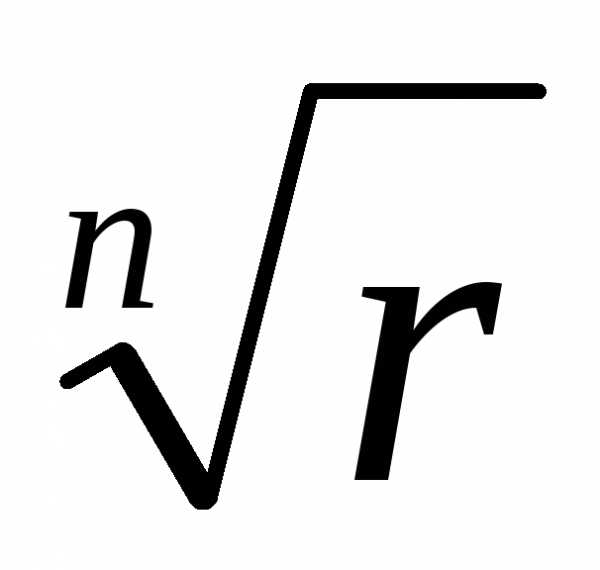 (cos
(cos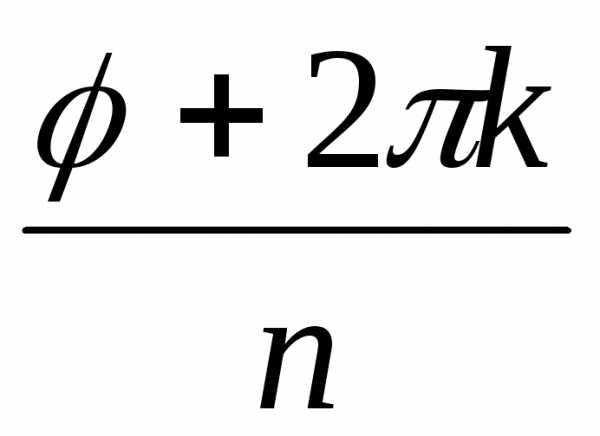 + isin
+ isin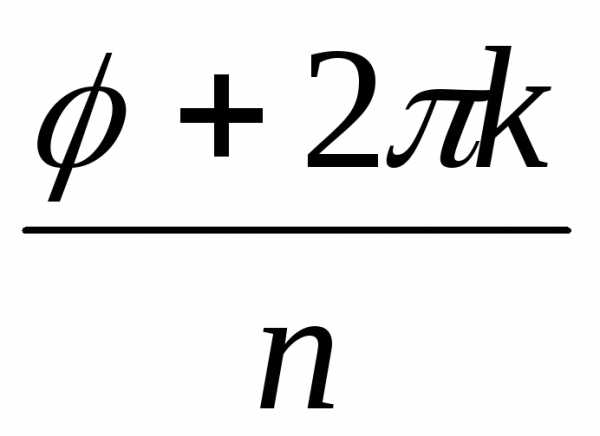 ),
гдеk = 0,
1, …, n – 1.
),
гдеk = 0,
1, …, n – 1.
Пример 1.16. Найти 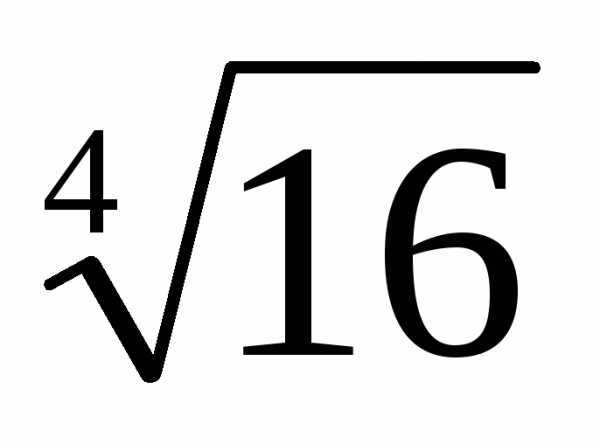 .
.
Решение.
Пусть z = 16,
найдем сначала тригонометрическую
форму данного комплексного числа. Имеем z = 16
a = 16, b = 0
r = 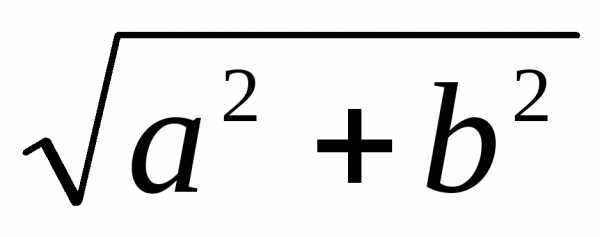 =
=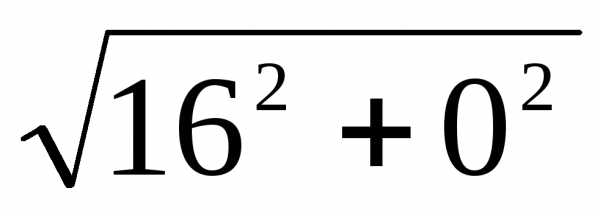 = 16;т. к. a = 16 > 0,
то
=
= 16;т. к. a = 16 > 0,
то
= 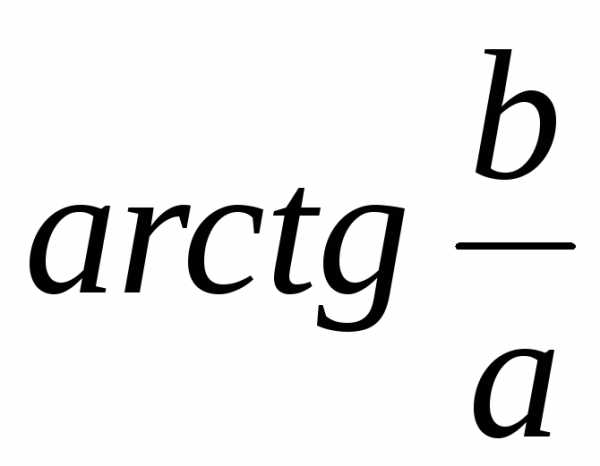 =
= 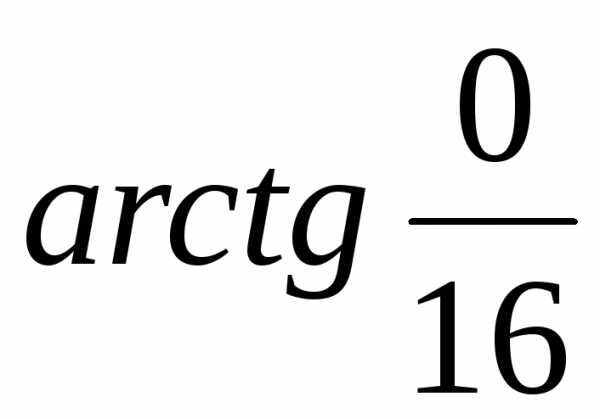 =
=
=
=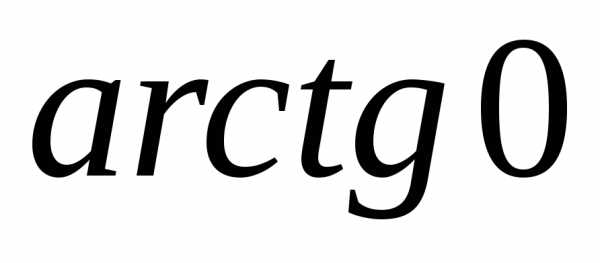 = 0.Тогда z = 16 = r(cos + isin) = 16(cos0 + isin0).
= 0.Тогда z = 16 = r(cos + isin) = 16(cos0 + isin0).
Применяем формулу для нахождения корня n-ой степени.
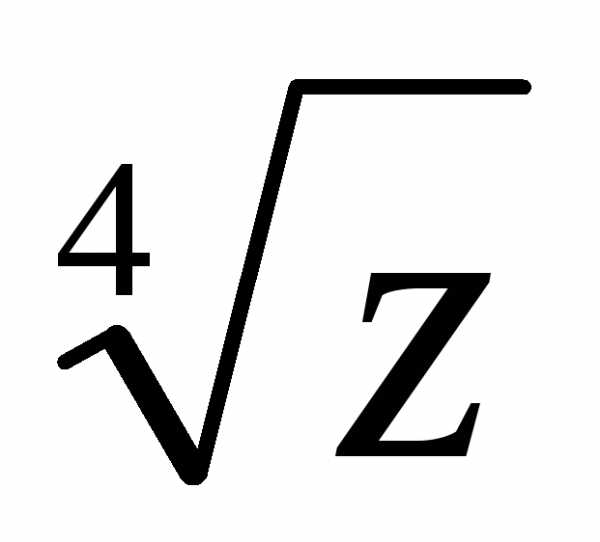 =
= 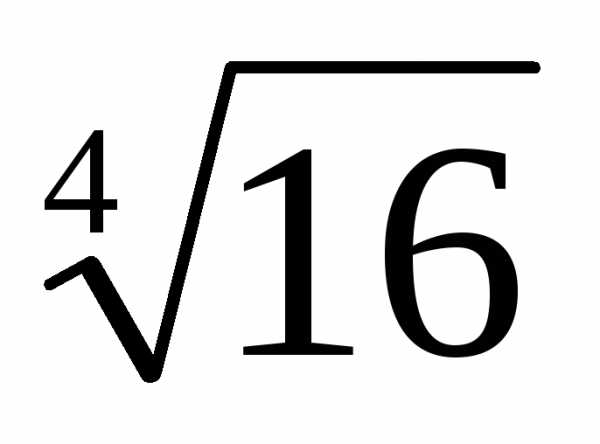 ==
==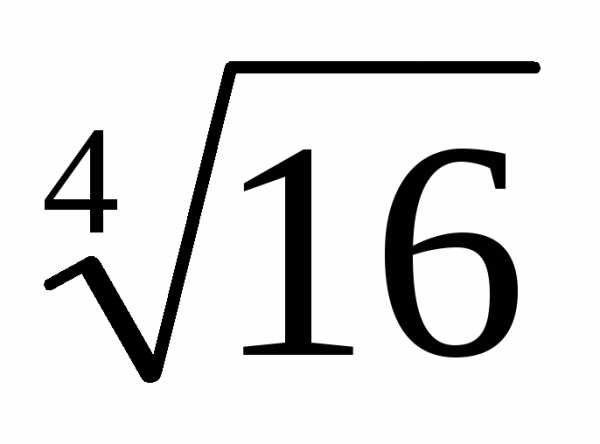 (cos
(cos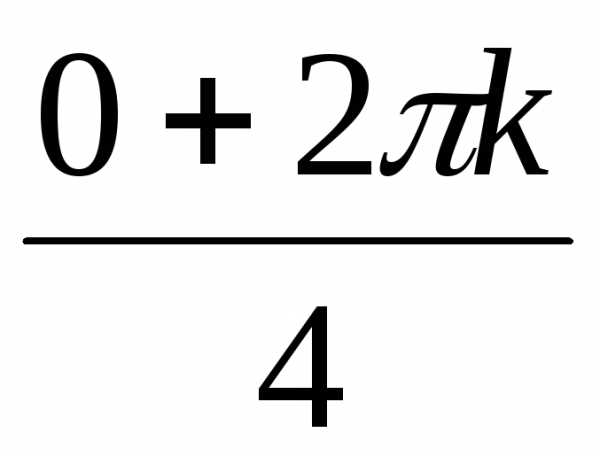 + isin
+ isin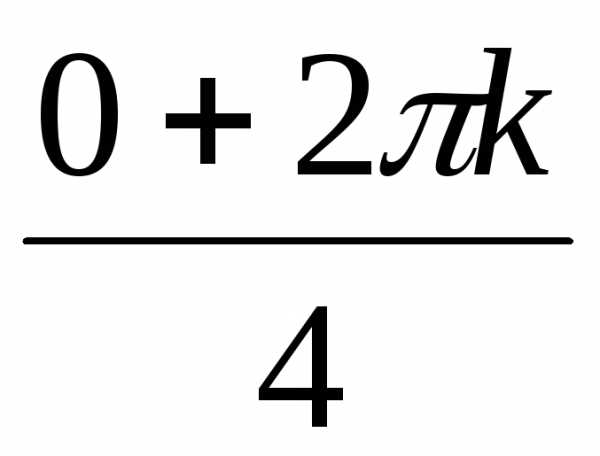 ) =
) =
= 2(cos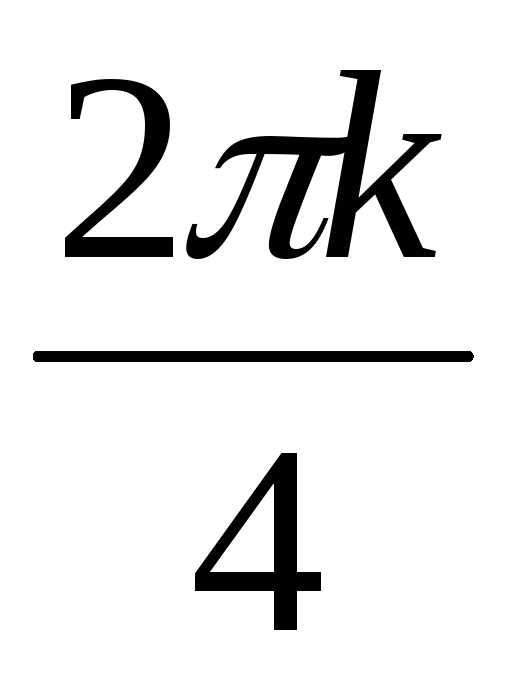 + isin
+ isin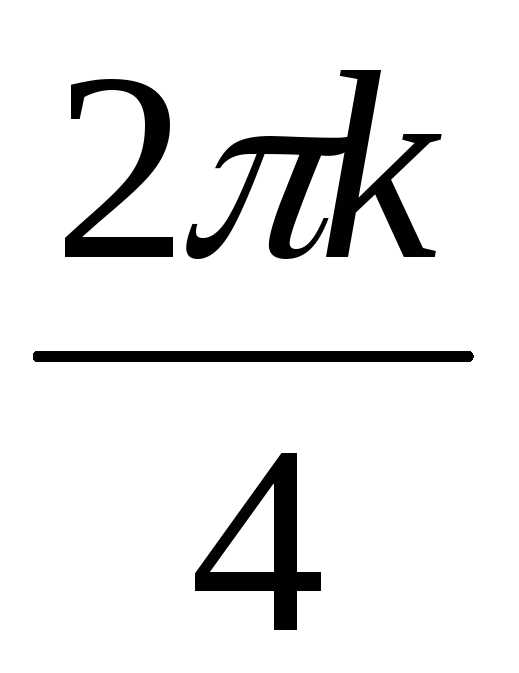 ) ,где k = 0,
1, 2, 3. Найдем
все четыре корня:
) ,где k = 0,
1, 2, 3. Найдем
все четыре корня:
k = 0
0 = 2(cos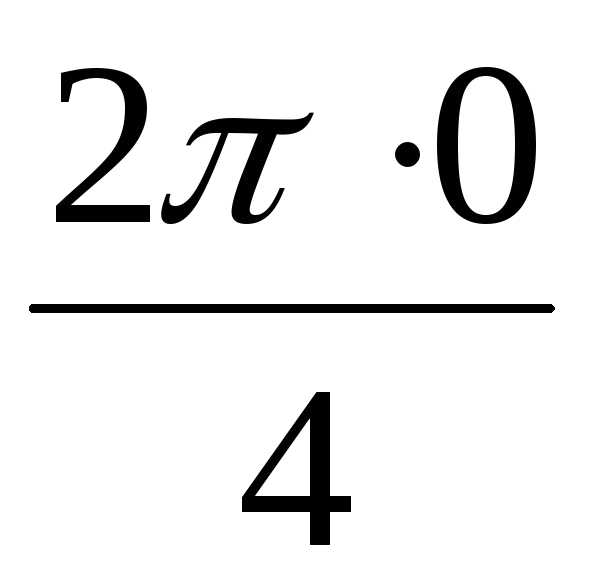 + isin
+ isin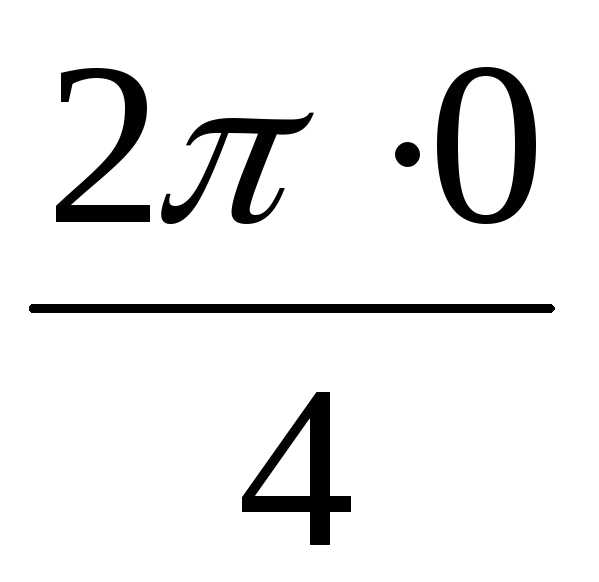 ) = 2
(cos0 + isin0) = 2,
) = 2
(cos0 + isin0) = 2,
k = 1
1 = 2(cos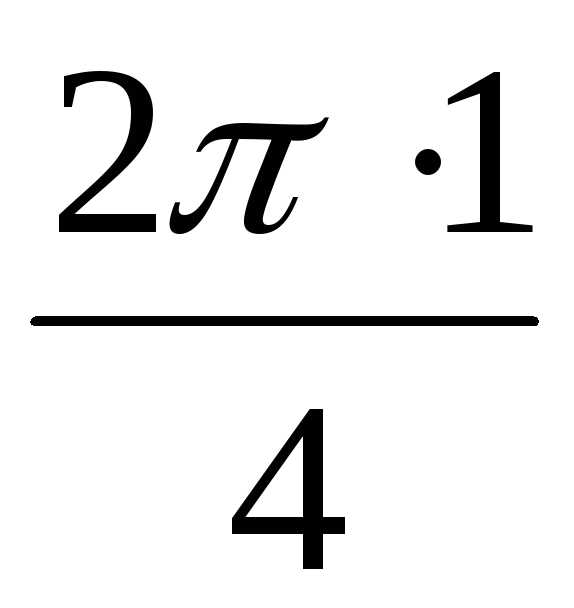 + isin
+ isin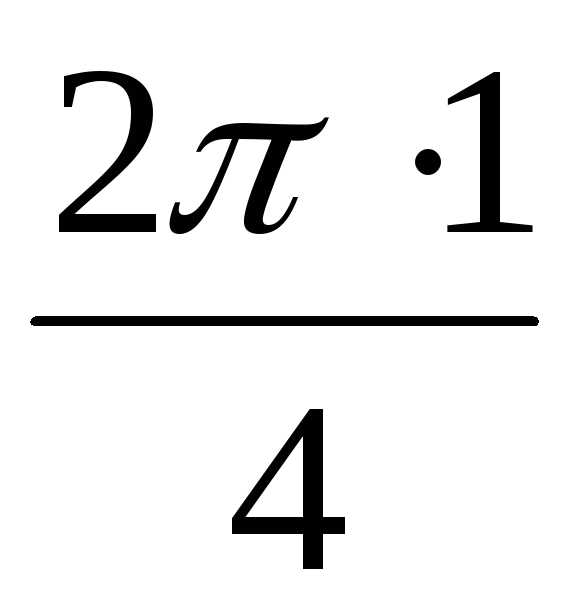 ) = 2(cos
) = 2(cos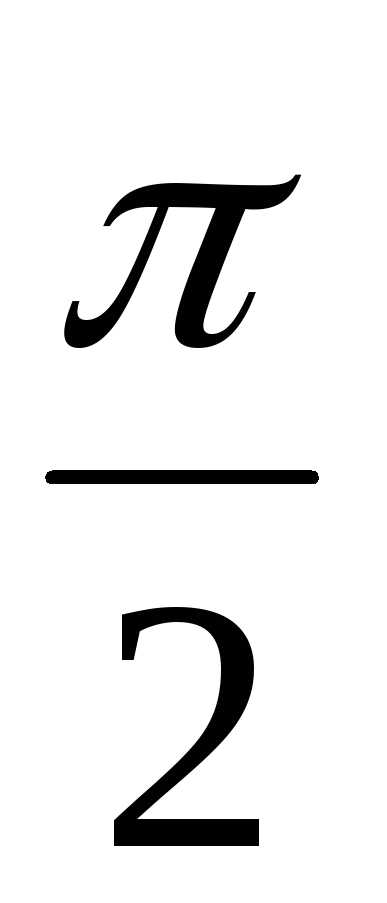 + isin
+ isin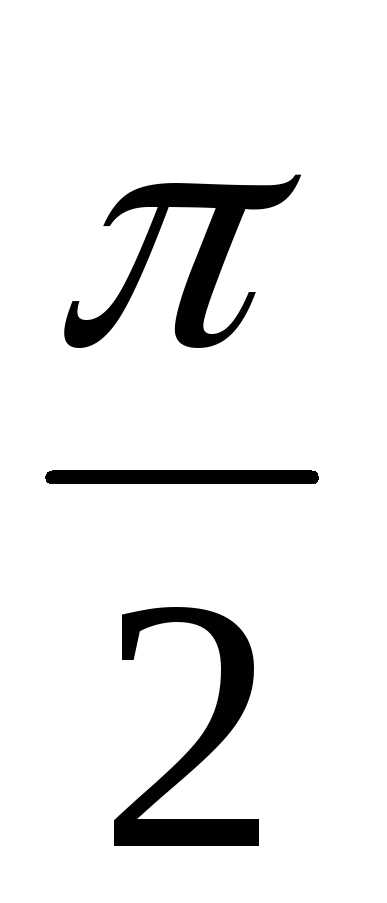 ) = 2(0 +i1) = 2i,
) = 2(0 +i1) = 2i,
k = 2
2 = 2(cos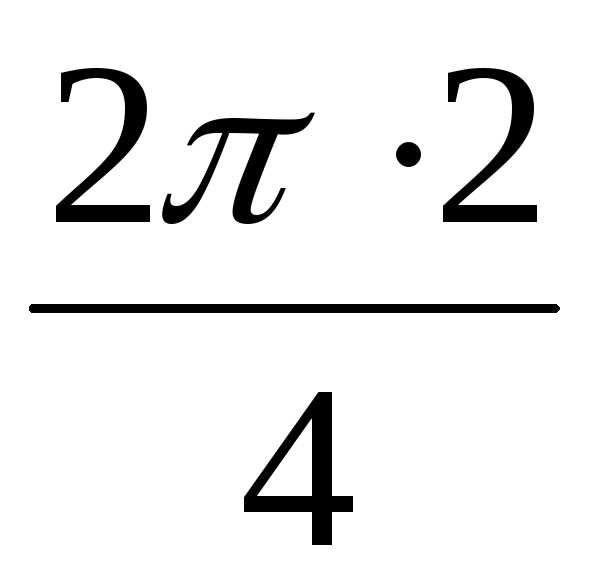 + isin
+ isin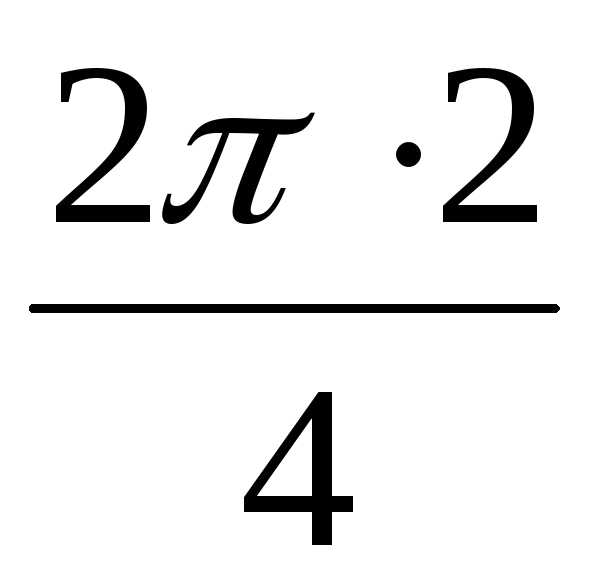 ) = 2(cos + isin) = 2(–1 + i0) = –2,
) = 2(cos + isin) = 2(–1 + i0) = –2,
k = 3
3 = 2(cos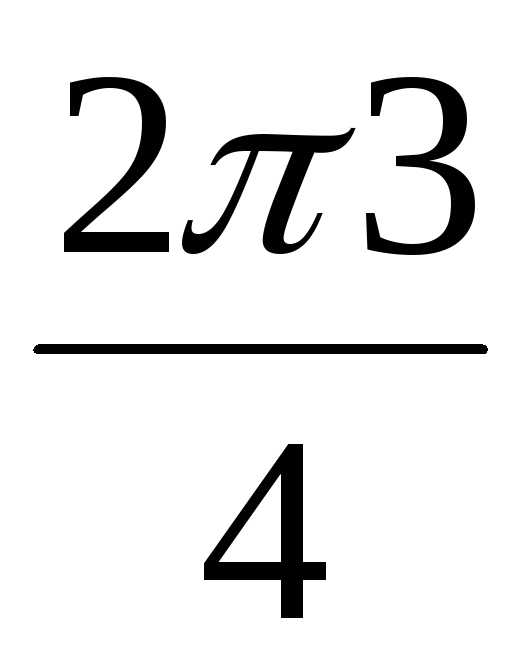 + isin
+ isin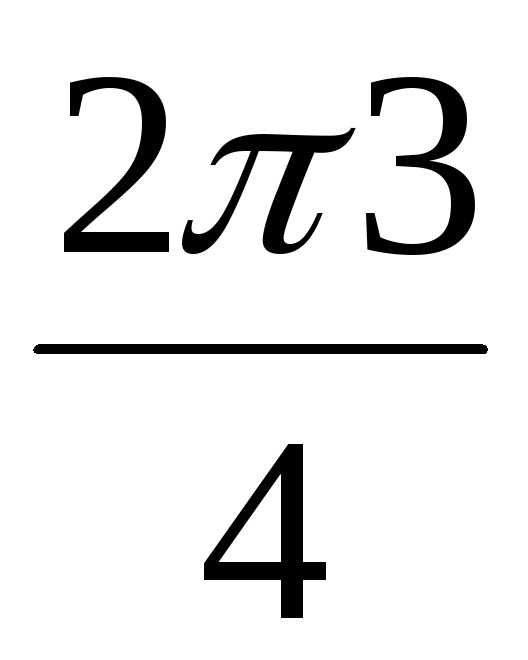 ) = 2(cos
) = 2(cos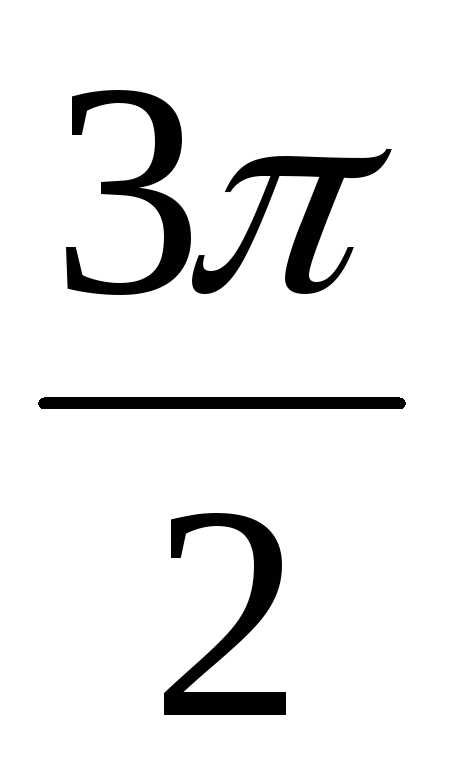 + isin
+ isin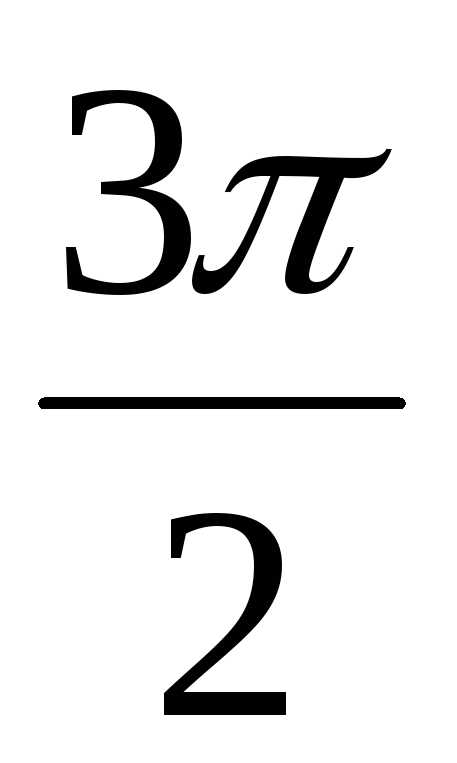 ) = 2(0 –i)) = –2i.
) = 2(0 –i)) = –2i.
Замечание. Геометрически все n значений корней n-ой
степени из комплексного числа r(cos + isin)
изображаются точками, лежащими на
окружности с центром в начале координат,
радиус которой равен 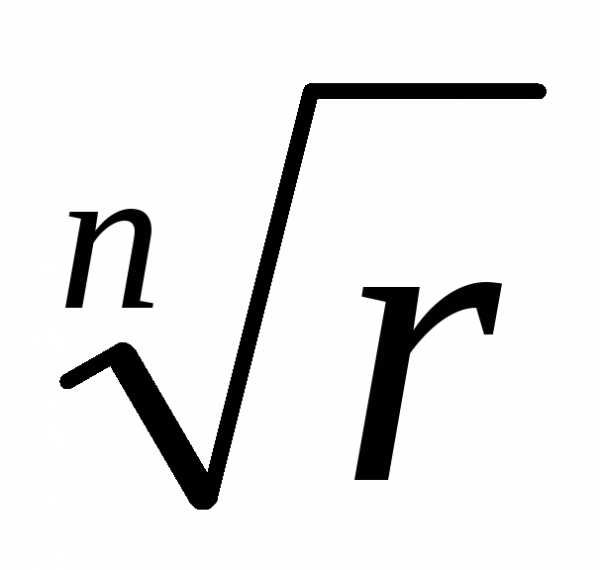 .
Если эти точки соединить, то в результате
получится правильный n-угольник.
.
Если эти точки соединить, то в результате
получится правильный n-угольник.
studfiles.net
