теория и примеры решений задач
Представим себе следующую ситуацию. До опыта о его услових можно было сделать ряд гипотез (в литературе можно также встретить их обозначение не буквой B, а буквой H), несовместных и образующих полную группу.
Вероятности гипотез до опыта (называемые также априорными вероятностями) заданы и равны
.
Теперь предположим, что опыт произведён и в его результате появилось событие A.
Как нужно пересмотреть вероятности гипотез с учётом этого факта?
Формула Байеса позволяет найти вероятность каждой из гипотез о том, в результате какого из событий, образующих полную систему, наступило событие A (или как часто говорят, найти апостериорные вероятности).
Поэтому формула Байеса представляет собой отношение
произведения вероятности одного из событий системы на условную вероятность этого
события относительно соответствующего события системы к полной вероятности наступления
события
То есть, по формуле Байеса вероятность, как и в самых простых случаях, вычисляется как отношение «одного ко всем»:
.
Видим, что знаменатель в этой формуле — ничто иное, как полная вероятность события A, а числители для каждого отдельного случая равны первому, второму, и так далее до n-го слагаемому суммы, находящейся в знаменателе.
Формула Байеса может быть также записана в виде
.
Пример 1. Имеются три урны; в первой 3 белых шара и 1 чёрный, во второй — 2 белых шара и 3 чёрных, в третьей — три белых шара. Некто подходит наугад к одной из урн и вынимает из неё один шар. Этот шар оказался белым. Найти послеопытные (апостериорные) вероятности того, что этот шар вынут из первой, второй, третьей урны.
Решение. Гипотезы:
— выбрана первая урна;
— выбрана вторая урна;
— выбрана третья урна.
Так как урна выбирается наугад, то априорные вероятности гипотез раны:
.
В результате опыта появилось событие A — из выбранной урны вынут белый шар.
Условные вероятности события A относительно каждой из гипотез:
, , .
Применяя формулу Байеса, находим апостериорные вероятности гипотез:
;
;
.
Пример 2.
Решение. Итак, для каждой из гипотез в числителе должно быть произведение вероятности одного из событий системы на условную вероятность этого события относительно соответствующего события системы, а в знаменателе — полная вероятность собыия A.
Вероятность того, что купленная лампочка изготовлена на первом
заводе и стандартна:
.
Вероятность того, что купленная лампочка изготовлена на втором
заводе и стандартна:
.
Вероятность того, что купленная лампочка изготовлена на третьем
заводе и стандартна:
Вычисляя по формуле Байеса, получаем:
— вероятность того, что купленная стандартная лампочка изготовлена на первом заводе
;
— вероятность того, что купленная стандартная лампочка изготовлена на втором заводе
;
— вероятность того, что купленная стандартная лампочка изготовлена на третьем заводе
.
: {документ подготовил первый чиновник}
: {документ подготовил второй чиновник}
: {документ подготовил третий чиновник}
A: {в документе допущена ошибка}
Событие |
||||
0,40 |
0,04 |
0,0160 |
0,36 |
|
0,35 |
0,06 |
0,0210 |
0,47 |
|
0,25 |
0,03 |
0,0075 |
0,17 |
|
Всего |
1,00 |
— |
0,0445 |
1,00 |
По формуле Байеса находим:
Итак, вероятность того, что ошибку допустил первый чиновник, составляет 0,36, второй – 0,47, третий – 0,17.function-x.ru
Формулы полной вероятности и Байеса. Примеры
Для случайных событий при вычислении их вероятности используются формулы полной вероятности и Байеса. Они не столь сложны в понимании и вычислении, и приведенный ниже теоретический и практический материал поможет Вам быстро его изучить.
Пусть в условиях эксперимента событие появляется совместно с одним из группы несовместных событий (гипотез) , образующих полную группу , известны или можно установить априорные вероятности каждой из гипотез и условные вероятности события при условии, что осуществилась та или иная гипотеза, тогда вероятность события определяется по формуле полной вероятности:
где – вероятность гипотезы ; – условная вероятность события при выполнении гипотезы . Приведенная формула называется формулой полной вероятности.
—————————————
Задача 1. В магазине три холодильника в которых заканчивается мороженое. В первом 4 белых и 6 шоколадных, во втором — 2 белых и 8 шоколадных, в третьем — 3 белых и 7 шоколадных. Наугад выбирают холодильник и вынимают из него мороженое. Определить вероятность того, что оно белое.
Решение. Обозначим события следующим образом: – выбрано — й холодильник, – выбрано белое мороженое
Тогда имеем:
Вероятности, что из каждого холодильника можно извлечь белое мороженое будут равны
Используя формулу полной вероятности находим:
Таким образом вероятность вытащить белое мороженое равна 0,3 или 30%.
—————————————
Задача 2. В офисе есть четыре ноутбука изготовленных компанией , 6 компанией , 8 компанией и два, которые производит . Гарантии, что ноутбуки этих компаний будут работать в течение гарантийного срока без ремонта составляют 70%, 80%, 85%, и 55% для каждой из них. Нужно найти вероятность, что выбранный ноутбук будет работать без ремонта в течение гарантийного срока.
Решение. Обозначим события следующим образом: – выбрано ноутбук компании, – ноутбук проработает без ремонта.
Вероятности выбора ноутбука каждой из компаний считаем равносильными их количеству, на основе этого вероятности примут значения:
Вероятности, что они будут работать без ремонта равны
Здесь мы просто переводим проценты в вероятность.
Применяем формулу полной вероятности:
Вероятность безремонтной работы ноутбука равна 0,775.
———————————
ФОРМУЛА БАЙЕСА
Пусть события образуют полную группу несовместных событий () и пусть событие происходит обязательно с одним из них . Предположим событие произошло, тогда вероятность того, что оно произошла именно с определяется формулой:
Рассмотрим практическую сторону применения формулы Байеса
——————————-
Задача 3. Заданны условия первой задачи. Нужно установить вероятность того, что мороженое извлекли из второго холодильника.
Решение. Выпишем результаты первой задачи, необходимые для вычислений
и подставим в формулу Байеса
Как можно видеть, вычисления по формуле несложные, главное понять, что и как определяется.
——————————-
Задача 4. Для задачи 2 нужно установить вероятность того, что исправный ноутбук принадлежит к компаниям , .
Решение. Выпишем предварительно найдены вероятности
и проведем вычисления по формуле Байеса
——————————-
Задача 5. На склад поступают телефоны трех заводов, причем доля телефонов первого завода составляет 25%, второго — 60%, третьего — 15%. Известно также, что средний процент телефонов без брака для первой фабрики составляет 2%, второй — 4%, третьей — 1%. Найти вероятность того, что:
а) наугад взят телефон окажется с браком;
б) телефон изготовлен на первом заводе, если он бракованный;
в) на каком заводе скорее был изготовлен телефон, если он сделан качественно ?
Решение.
а) Введем для ясности обозначения:
– наугад выбранный телефон оказался бракованным;
Предположение: – телефон изготовлен на первой, – второй и –третий фабрике соответственно. Собития попарно несовместимы и образуют полную группу. Вероятность каждого предположения определяем делением процентной доли продукции ко всей (100%)
Подобным образом определяем условные вероятности события
Применим формулу полной вероятности для определения возможности выбора бракованного телефона
б) для отыскания вероятности применим формулу Байеса
в) чтобы определить, на каком заводе скорее был изготовлен рабочий телефон необходимо сравнить между собой вероятности предположений:
где событие (вытащили телефон без брака) противоположна . Для противоположных событий используют формулу
По подобной формуле определяем условные вероятности события , если только справедливы предположения
По формуле Байеса находим вероятности
Наибольшую вероятность имеет второе предположение, поэтому телефон скорее всего был изготовлен на втором заводе.
——————————-
Задач на нахождение полной вероятности и применения формулы Байеса в литературе и интернете множество. Стоит ввести в гугле нужный запрос и вам тут же будет предложено множество материалов к выбору. Поэтому освоить данный материал не трудно, стоит лишь внимательно (без паники) разобраться с приведенными примерами и подобными. Все остальные решаются по аналогичной схеме.
yukhym.com
Формула полной вероятности —
На практике часто необходимо определить вероятность интересующего события, которое может произойти с одним из событий, образующих полную группу. Следующая теорема, являющаяся следствием теорем сложения и умножения вероятности, приводит к выводу важной формулы для вычисления вероятности подобных событий. Эта формула называется формулой полной вероятности.
Пусть H1, H2, … , Hn есть n попарно несовместных событий, образующих полную группу:
1) все события попарно несовместны: Hi ∩ Hj = ; i, j = 1,2, … , n; i j;
2) их объединение образует пространство элементарных исходов W:
Такие события иногда называют гипотезами. Пусть совершается событие А, которое может наступить только при условии наступления одного из событий Hi (i = 1, 2, … , n). Тогда справедлива теорема.
| Рис. 1.19 |
Теорема. Формула полной вероятности. Вероятность события А, которое может насту-пить лишь при условии появления одного из n попарно несовместных событий H1, H2, … , Hn, образующих полную группу, равна сумме парных произведений вероятностей каждого из событий Hi (i = 1, 2, … , n) на условную вероятность события А / Hi, т.е.
(1.14)
Доказательство. Действительно, по условию событие А может наступить, если наступает одно из несовместных событий H1, H2 … Hn,т.е. появление события А означает осуществление одного из событий H1 ∙А, H2 ∙ А, … , Hn ∙ А. Последние события также несовместны, т.к. из H
=.
Это равенство хорошо иллюстрируется рис. 1.19. Из теоремы сложения следует. Но по теореме умножения справедливо равенст-во при любом i, 1 ≤ i ≤ n. Следовательно, фор-мула полной вероятности (1.14) справедлива. Теорема доказана.
Замечание. Вероятности событий (гипотез) H1, H2, … , Hn, которые входят в формулу (1.14) при решении конкретных задач или заданы или же они должны быть вычислены в процессе решения. В последнем случае правильность вычисления р(Hi) (i = 1, 2, … , n) проверяется по соотношению = 1 и расчёт р(Hi) выполняется на первом этапе решения задачи. На втором этапе рассчитывается р(А).
При решении задач на применении формулы полной вероятности удобно придерживаться следующей методики.
Методика применения формулы полной вероятности
а). Ввести в рассмотрение событие (обозначим его А), вероятность которого необходимо определить по условию задачи.
б). Ввести в рассмотрение события (гипотезы) H1, H2, … , Hn, которые образуют полную группу.
в). Выписать или вычислить вероятности гипотез р(H1), р(H2), … , р(Hn). Контроль правильности вычисления р(Hi) проверяется по условию В большем числе задач вероятности р(Hi) задаются непосредственно в условии задачи. Иногда эти вероятности, а также вероятности p(А/H1), p(А/H2), …, p(А/Hn) умножены на 100 (заданы числа в процентах). В этом случае заданные числа надо поделить на 100.
г). Вычислить искомую вероятность р(А) по формуле (1.14).
Пример. Экономист рассчитал, что вероятность роста стоимости акции его компании в следующем году составит 0,75, если экономика страны будет на подъёме, и 0,30, если будет финансовый кризис. По мнению экспертов, вероятность экономического подъёма равна 0,6. Оценить вероятность того, что акции компании в следующем году поднимутся в цене.
Решение. В начале условие задачи формализуется по вероятности. Пусть А – событие ” акции поднимутся в цене” ( по вопросу задачи). По условию задачи выделяются гипотезы: H1 – “экономика будет на подъёме”, H2 – “экономика вступит в полосу кризиса”. H1, H2 – образуют полную группу, т.е. H1 ∙ H2 = , H1 + H2 = . Вероятность p(H1) = 0,6, следовательно, p(H2) = 1 – 0,6 = 0,4. Условные вероятности p(А/H1) = 0,75, p(А/H2) = 0,3. Используя формулу (1.14), получим:
p(А) = p(H1) ∙ p(А/H1) + p(H2) ∙ p(А/H2) = 0,75 ∙ 0,6 + 0,3 ∙ 0,4 = 0,57.
einsteins.ru
Формула полной вероятности и формула Бейеса Байеса и их применение
Сибирский государственный университет телекоммуникаций и информатики
Кафедра высшей математики
РЕФЕРАТ
по дисциплине : «Теория вероятностей и математическая статистика»
на тему:
«Формула полной вероятности и формула Бейеса(Байеса) и их применение»
Выполнил:
Руководитель: профессор Б.П.Зеленцов
Новосибирск, 2010
Содержание
Введение 3
1. Формула полной вероятности 4-5
2. Формула Байеса(Бейеса) 5-6
3. Задачи с решениями 7-11
4. Основные сферы применения формулы Байеса(Бейеса) 11
Заключение 12
Литература 13
Введение
Теория вероятностей является одним из классических разделов математики. Она имеет длительную историю. Основы этого раздела науки были заложены великими математиками. Назову, например, Ферма, Бернулли, Паскаля.
Позднее развитие теории вероятностей определились в работах многих ученых.
Большой вклад в теорию вероятностей внесли ученые нашей страны:
П.Л.Чебышев, А.М.Ляпунов, А.А.Марков, А.Н.Колмогоров. Вероятностные и статистические методы в настоящее время глубоко проникли в приложения. Они используются в физике, технике, экономке, биологии и медицине. Особенно возросла их роль в связи с развитием вычислительной техники.
Например, для изучения физических явлений производят наблюдения или опыты. Их результаты обычно регистрируют в виде значений некоторых наблюдаемых величин. При повторении опытов мы обнаруживаем разброс их результатов. Например, повторяя измерения одной и той же величины одним и тем же прибором при сохранении определенных условий (температура, влажность и т.п.), мы получаем результаты, которые хоть немного, но все же отличаются друг от друга. Даже многократные измерения не дают возможности точно предсказать результат следующего измерения. В этом смысле говорят, что результат измерения есть величина случайная. Еще более наглядным примером случайной величины может служить номер выигрышного билета в лотерее. Можно привести много других примеров случайных величин. Все же и в мире случайностей обнаруживаются определенные закономерности. Математический аппарат для изучения таких закономерностей и дает теория вероятностей.
Таким образом, теория вероятностей занимается математическим анализом случайных событий и связанных с ними случайных величин.
Пусть имеется группа событий H 1 , H 2 ,…, Hn , обладающая следующими свойствами:
1) все события попарно несовместны: Hi
Hj =Æ; i , j =1,2,…,n ; i ¹ j ;2) их объединение образует пространство элементарных исходов W:
W =
.В этом случае будем говорить, что H 1 , H 2 ,…,Hn образуют полную группу событий . Такие события иногда называют гипотезами .
Пусть А – некоторое событие: А ÌW (диаграмма Венна представлена на рисунке 8). Тогда имеет место формула полной вероятности:
P (A ) = P (A /H 1 )P (H 1 ) + P (A /H 2 )P (H 2 ) + …+P (A /Hn )P (Hn ) =
Доказательство. Очевидно: A =
, причем все события (i = 1,2,…,n ) попарно несовместны. Отсюда по теореме сложения вероятностей получаемP (A ) = P (
) + P () +…+ P (Если учесть, что по теореме умножения P (
) = P (A/H i )P (H i ) (i = 1,2,…,n ), то из последней формулы легко получить приведенную выше формулу полной вероятности.Пример . В магазине продаются электролампы производства трех заводов, причем доля первого завода — 30%, второго — 50%, третьего — 20%. Брак в их продукции составляет соответственно 5%, 3% и 2%. Какова вероятность того, что случайно выбранная в магазине лампа оказалась бракованной.
Пусть событие H 1 состоит в том, что выбранная лампа произведена на первом заводе, H 2 на втором, H 3 — на третьем заводе. Очевидно:
P (H 1 ) = 3/10, P (H 2 ) = 5/10, P (H 3 ) = 2/10.
Пусть событие А состоит в том, что выбранная лампа оказалась бракованной; A/Hi означает событие, состоящее в том, что выбрана бракованная лампа из ламп, произведенных на i -ом заводе. Из условия задачи следует:
P (A / H 1 ) = 5/10; P (A / H 2 ) = 3/10; P (A / H 3 ) = 2/10
По формуле полной вероятности получаем
Пусть H 1 ,H 2 ,…,Hn — полная группа событий и А Ì W – некоторое событие. Тогда по формуле для условной вероятности
(1)Здесь P (Hk /A ) – условная вероятность события (гипотезы) Hk или вероятность того, что Hk реализуется при условии, что событие А произошло.
По теореме умножения вероятностей числитель формулы (1) можно представить в виде
P = P = P (A /Hk )P (Hk )
Для представления знаменателя формулы (1) можно использовать формулу полной вероятности
P (A )
Теперь из (1) можно получить формулу, называемую формулой Байеса :
По формуле Байеса исчисляется вероятность реализации гипотезы Hk при условии, что событие А произошло. Формулу Байеса еще называют формулой вероятности гипотез. Вероятность P (Hk ) называют априорной вероятностью гипотезы Hk , а вероятность P (Hk /A ) – апостериорной вероятностью.
Теорема. Вероятность гипотезы после испытания равна произведению вероятности гипотезы до испытания на соответствующую ей условную вероятность события, которое произошло при испытании, деленному на полную вероятность этого события.
Пример. Рассмотрим приведенную выше задачу об электролампах, только изменим вопрос задачи. Пусть покупатель купил электролампу в этом магазине, и она оказалась бракованной. Найти вероятность того, что эта лампа изготовлена на втором заводе. Величина P (H 2 ) = 0,5 в данном случае это априорная вероятность события, состоящего в том, что купленная лампа изготовлена на втором заводе. Получив информацию о том, что купленная лампа бракованная, мы можем поправить нашу оценку возможности изготовления этой лампы на втором заводе, вычислив апостериорную вероятность этого события.
Выпишем формулу Байеса для этого случая
Из этой формулы получаем: P (H 2 /A ) = 15/34. Как видно, полученная информация привела к тому, что вероятность интересующего нас события оказывается ниже априорной вероятности.
3. Задачи с решениями.
Задача 1. В магазин поступила новая продукция с трех предприятий. Процентный состав этой продукции следующий: 20% — продукция первого предприятия, 30% — продукция второго предприятия, 50% — продукция третьего предприятия; далее, 10% продукции первого предприятия высшего сорта, на втором предприятии — 5% и на третьем — 20% продукции высшего сорта. Найти вероятность того, что случайно купленная новая продукция окажется высшего сорта.
Решение. Обозначим через В событие, заключающееся в том, что будет куплена продукция высшего сорта, через
обозначим события, заключающиеся в покупке продукции, принадлежащей соответственно первому, второму и третьему предприятиям.Можно применить формулу полной вероятности, причем в наших обозначениях:
Подставляя эти значения в формулу полной вероятности, получим искомую вероятность:
Задача 2. Один из трех стрелков вызывается на линию огня и производит два выстрела. Вероятность попадания в мишень при одном выстреле для первого стрелка равна 0,3, для второго — 0,5; для третьего — 0,8. Мишень не поражена. Найти вероятность того, что выстрелы произведены первым стрелком.
Решение. Возможны три гипотезы:
— на линию огня вызван первый стрелок, — на линию огня вызван второй стрелок, — на линию огня вызван третий стрелок.mirznanii.com
Формула полной вероятности. Формула Байеса. Примеры решения задач
Формула полной вероятности. Формула Байеса.
Формула полной вероятности
,
где B1, B2 ,…, Bn — полная группа попарно несовместных событий.
Формула Байеса
,
где B1, B2, …, Bn — полная группа событий.
Задача 1.
Фирма имеет три источника поставки комплектующих – фирмы А,В,С. На долю фирмы А приходится 50 % общего объема поставок, В – 30% и С – 20%. Из практики известно, что 10% поставляемых фирмой А деталей – бракованные, фирмой В – 5% и С – 6%.
Найти вероятность того, что наудачу выбранная деталь будет бракованной.Решение. Производится испытание – извлекается одна деталь.
Событие А – появилась бракованная деталь.
Гипотеза Н1 – деталь фирмы А.
Гипотеза Н2 – деталь фирмы В.
Гипотеза Н3 – деталь фирмы С.
Тогда, согласно формуле полной вероятности, искомая вероятность равна:
Задача 2.
В центральную бухгалтерию корпорации поступили пачки накладных для проверки и обработки. 90 % пачек были признаны удовлетворительными: они содержали только 1 % неправильно заполненных накладных. Остальные 10 % пачек были признаны неудовлетворительными, так как содержали 5 % неверно оформленных накладных. Взятая наугад из пачки накладная оказалась оформленной неверно. Учитывая это, какова вероятность того, что вся пачка накладных будет признана несоответствующей стандарту? Решение. Испытание – проверяется пачка накладных.
Событие А – взятая наугад накладная оказалась неверной.
Гипотеза Н1 – пачка не соответствует стандарту.
Гипотеза Н2 – пачка соответствует стандарту.
Необходимо узнать вероятность гипотезы Н1 при условии, что событие А произошло. Согласно формуле Бейеса имеем:
Задача 3.
Имеется три урны с различным составом шаров в каждой. В первой - 5 белых и 5 черных, во второй - 3 белых и 3 черных, в третьей - 2 белых и 4 черных. Из случайно выбранной урны извлекается шар. Он оказался белым. Определить вероятность того, что он был вынут из третьей урны.Решение: Введем обозначения для рассматриваемых событий.
Пусть А — извлечен белый шар. — выбрана первая урна.
— выбрана вторая урна. — выбрана третья урна.
— вероятность извлечения белого шара из первой урны.
— вероятность извлечения белого шара из второй урны.
— вероятность извлечения белого шара из третьей урны.
Определим вероятности, соответствующие этим событиям . Так как все урны одинаковы, то
.
, , .
Тогда, используя формулу полной вероятности, получим:
.
Пересчитаем вероятность третьей гипотезы с условием, что произошло рассматриваемое событие, используя формулу Байеса.
www.matem96.ru
Формула полной себестоимости и примеры
Понятие себестоимости и ее виды
Цена на любой товар находится в зависимости от его начальной себестоимости, рассчитываемой по специальной формуле при учете определенных затрат.
Формула полной себестоимости представляет собой сумму всех издержек, в том числе коммерческие затраты.
В соответствии с полным объемом затрат на производство себестоимость может быть:
- Цеховая себестоимость, состоящая из всех типов затрат на каждом этапе производственного цикла;
- Производственная себестоимость, которая определяется суммированием цеховых и общих затрат предприятия;
- Полная себестоимость, учитывающая не только производственные затраты, но и затраты на продажу и транспортировку товара.
Существует множество видов себестоимости в соответствии с особенностями производства и способами реализации продукции.
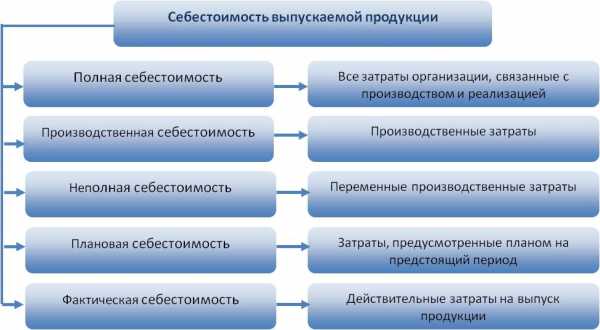
Формула полной себестоимости
Формула полной себестоимости чаще всего применяется при оценке эффективности деятельности компании. Она включает в себя все затраты на производство товара, а также последующие расходы на его транспортировку и реализацию. В общем виде формула полной себестоимости выглядит следующим образом:
Сполн=ПЗ+РЗ
Здесь Сполн- полная себестоимость продукции,
ПЗ – затраты на производство,
РЗ – затраты на реализацию продукции.
Все остальные виды себестоимости являются частью полной себестоимости, поскольку она включает в себя более полный состав затрат на производство и коммерческие расходы компании.
Производственная себестоимость продукции представляет собой сумму, затраченную на ее производство. Эта сумма включает в себя:
- природные ресурсы,
- материалы и сырье,
- амортизация основных средств,
- энергию и топливо,
- оплату труда персонала (в том числе отчисления) и др.
Что показывает полная себестоимость
Себестоимость представляет собой стоимостной показатель, который отражает, какие затраты несет предприятие на изготовление определенного объема продукции или изготовление единицы продукции. Руководство любого предприятия при помощи формулы полной себестоимости может выявить самый затратный вид товара, а также уменьшить издержки производства.
При анализе полной себестоимости можно сделать выводы об убыточности или прибыльности выпускаемой или реализуемой продукции, а также возможности ее производства в перспективе.
Достоинствами поной себестоимости можно назвать:
- полное соответствие действующим нормативным актам налогообложения и финансового учета,
- корректную оценку стоимости запаса готовой продукции.
Недостатками метода расчета по полной себестоимости являются:
- включение затрат, которые не связаны с производством продукции, в результате чего искажается показатель рентабельности;
- невозможно провести анализ, контроль и планирование затрат по причине невнимания к характеру их поведения в зависимости от производственных объемов.
Примеры решения задач
ru.solverbook.com
Полная формула — Большая Энциклопедия Нефти и Газа, статья, страница 1
Полная формула
Cтраница 1
Полная формула будет нужна во второй главе. [1]
Полные формулы углеводородов получатся после дополнения схем углеродных скелетов необходимым числом атомов водорода. [2]
Полные формулы углеводородов получаются после дополнения схем углеродных скелетов необходимым числом атомов водорода. [3]
Полная формула комплексной частицы перечисляет все лиганды внутренней координационной сферы и указывает способ их присоединения. [4]
Полная формула пересчета видимой плотности в относительную плотность учитывает величину потери веса пикнометром в возцухе. [5]
Более строгие и полные формулы для модуля упругости будут приведены без вывода. [6]
Наиболее полные формулы ошибок различных элементов сплошных сетей даны К. Л. Проворовым [13, 14] для ряда триангуляции, выделенного из сети ( рис. III. [7]
Полную формулу Мюллера мы не приводим, потому что для нас важно лишь выяснить, как изменяется процесс коагуляции в полидисперсных золях. Полная формула сложнее, и ее трудно применять. [8]
Существуют более полные формулы, приводимые в справочниках, учитывающие конечную толщину металлических пластин. [10]
Приведение полной формулы ввиду ее громоздкости здесь нецелесообразно. Фактически, мы построили алгоритм нахождения весовых коэффициентов оптимального портфеля, сформировав его последовательными шагами. Последующее использование вычислительной техники превращает интересующую инвестора проблему в разряд технической. [11]
Вместо полных формул, выведенных выше, на практике пользуются приближенными формулами. В дальнейшем изложении на нескольких частных примерах мы покажем, какая степень приближения достигается при таком способе расчета. [12]
Определение полной формулы комплексной частицы чаще всего удается, если частица длительное время существует в растворе или в кристаллическом соединении в виде стабильного образования. [13]
Для получения полной формулы отказов секции следует добавить отказы всех выключателей ( включая секционный или шино-соединительный) в неподвижном состоянии, отказы шинных разъединителей при оперативных переключениях, повреждения изоляции шин. Однако перечисленные дополнительные отказы составляют незначительную часть вышеприведенных повреждений, отраженных в формуле, и с ними практически можно не считаться. [15]
Страницы: 1 2 3 4
www.ngpedia.ru
