Линейные и квадратные уравнения
Определение
Уравнение (с одной переменной) — это некоторое равенство двух выражений, содержащее неизвестную (переменную). \[f(x)=g(x) \qquad \qquad (1)\]Пусть для определенности все дальнейшие уравнения содержат переменную, обозначенную буквой \(x\).
Замечание
Заметим, что \(x\) — это просто некоторое число, значение которого неизвестно.
Определение
Областью определения (или областью допустимых значений, сокращенно ОДЗ) любого уравнения вида \((1)\) будем называть множество значений переменной \(x\), при которых определены (то есть не теряют смысла) функции \(f(x)\) и \(g(x)\).
Пример
Уравнение \(\dfrac {10}{x-1}=5\) определено при всех значениях переменной \(x\), кроме \(x=1\), потому что в этом случае знаменатель дроби в левой части равенства обращается в ноль. Значит, ОДЗ уравнения \(x\in (-\infty;1)\cup(1;+\infty)\).
Определение
Корнем уравнения называется то числовое значение \(x\), при котором уравнение обращается в верное равенство.
Иногда корни уравнения называют решением этого уравнения.
Например, корнем уравнения из предыдущего примера является число \(x=3\), потому как тогда уравнение принимает вид \(\dfrac{10}{3-1}=5\) или, что то же самое, \(5=5\), что является верным равенством.
Замечание
1) Заметим, что уравнение может как иметь корни, так и не иметь корней. Например, уравнение \(\dfrac 1x=0\) ни при каких значениях \(x\) не может быть верным, потому что дробь равна нулю, когда ее числитель равен нулю, а знаменатель при этом не теряет смысла. У нашей дроби числитель \(1\ne 0\).
2) Фраза “решить уравнение” означает найти все корни данного уравнения или доказать, что корней нет.
Определение
Два уравнения равносильны (или эквивалентны), если они имеют одинаковые решения.Например, уравнения \(x=3\) и \(3x=6+x\) эквивалентны, т.к. оба имеют единственное решение \(x=3\).
Эквивалентность уравнений обозначается так: \(x=3 \quad \Leftrightarrow \quad 3x=6+x\).
Свойства уравнений
1. В любом уравнении можно переносить слагаемые из одной части равенства в другую, при этом меняя их знак на противоположный. При этом полученное уравнение равносильно исходному.
Например, уравнение \(x+4=2x^2\) можно переписать в виде \(x+4-2x^2=0\).
2. В любом уравнении можно правую и левую части умножать или делить на одно и то же число, не равное нулю. При этом полученное уравнение равносильно исходному.
Например, уравнение \(0,5x=-2\) равносильно уравнению \(x=-4\), которое получено из исходного путем умножения обеих частей на \(2\).
3. В любом уравнении можно к правой и левой частям прибавлять одно и то же число. При этом полученное уравнение равносильно исходному.
Например, уравнение \(x+2=5x^2\) после прибавления к обеим частям \(-2\) примет вид \(x=5x^2-2\).
\[{\Large{\text{Линейные уравнения}}}\] Линейное уравнение – это уравнение вида \[ax + b = 0\qquad \qquad (2)\] где \(a\ne 0,b\) – числа, или уравнение, к нему сводящееся.
ОДЗ линейного уравнения \((2)\) — все \(x \in\mathbb{R}\).
Линейное уравнение \(ax+b=0\) преобразуется в \(ax=-b\) и всегда имеет единственное решение \(x=-\dfrac ba\).
Например, \(2x-4=0\) имеет корень \(x=2\).
Замечание: при переносе слагаемых из одной части равенства в другую знак слагаемого меняется на противоположный. Например, выражение \(x-5=8\) преобразуется в выражение \(x=8+5\).
Знак, стоящий перед слагаемым – это и есть его знак, то есть в выражении \(x-5\) два слагаемых: \(x\) и \(-5\). Если перед слагаемым не стоит никакого знака, то подразумевается, что перед ним стоит знак “\(+\)”.
\[{\Large{\text{Квадратные уравнения}}}\] Квадратное уравнение – это уравнение вида \[ax^2+bx+c=0 \qquad \qquad (3)\] где \(a, b, c\) – числа, причем \(a\ne 0\), или уравнение, к нему сводящееся.
Число \(a\) называется старшим (первым) коэффициентом, число \(b\) – вторым коэффициентом, число \(c\) – свободным членом.
Замечание
1) Заметим, что если \(a=0\), то уравнение \((3)\) становится линейным; именно поэтому в определении \(a\ne 0\).
2) Выражение \(ax^2+bx+c\) называется квадратичным (квадратным) трехчленом.
ВАЖНО! Обращаем ваше внимание на то, что, например, в квадратном трехчлене \(7-x^2+2x\) коэффициент \(a=-1\), \(b=2\) и \(c=7\)! Так как \(7-x^2+2x=-x^2+2x+7\), а по определению \(a\) – коэффициент перед \(x^2\), \(b\) – коэффициент перед \(x\), \(c\) – свободный член.
Определение
Дискриминантом квадратного уравнения \((3)\) называется выражение \(D=b^2-4ac\).
Корни квадратного уравнения
1) Если дискриминант квадратного уравнения больше нуля (\(D>0\)), то оно имеет два различных корня \[x_1=\dfrac{-b-\sqrt D}{2a} \qquad \text{и} \qquad x_2=\dfrac{-b+\sqrt D}{2a}\]
2) Если дискриминант квадратного уравнения равен нулю (\(D=0\)), то оно имеет два совпадающих корня (часто говорят, что оно имеет один корень) \[x=-\dfrac b{2a}\]
3) Если дискриминант квадратного уравнения меньше нуля (\(D<0\)), то оно не имеет корней.
Пример:
Решите уравнение \[3x^2 — 33x + 90 = 0.\]
Решение.
Найдём дискриминант данного уравнения: \[D = 33^2 — 4\cdot 3\cdot 90 = 9\] Следовательно, уравнение имеет два различных корня, равных \[x_1=\dfrac{33 + 3}{6} = 6 \qquad \text{и} \qquad x_2=\dfrac{33 —
3}{6} = 5\]
Теорема Виета
Пусть квадратное уравнение \(ax^2 + bx + c = 0\), \(a\neq 0\), имеет два корня \(x_1\) и \(x_2\) (возможно, совпадающих), то есть \(D\geqslant 0\). Тогда их сумма равна \[x_1+x_2=-\dfrac{b}{a}\] а их произведение равно \[x_1\cdot x_2=\dfrac{c}{a}\]
Доказательство
Сумма корней этого уравнения равна \[\dfrac{-b + \sqrt{D}}{2a} + \dfrac{-b — \sqrt{D}}{2a} = -\dfrac{2b}{2a} = -\dfrac{b}{a}\] Произведение корней этого уравнения равно \[\dfrac{-b + \sqrt{D}}{2a} \cdot \dfrac{-b — \sqrt{D}}{2a} = \dfrac{(-b + \sqrt{D})(-b — \sqrt{D})}{4a^2} = \dfrac{b^2 — D}{4a^2} = \dfrac{4ac}{4a^2} = \dfrac{c}{a}\]
Определение
Квадратное уравнение называется приведенным, если старший коэффициент \(a=1\).
Любое квадратное уравнение можно сделать приведенным: для этого необходимо разделить уравнение на \(a\).
Следствие
Для приведенного квадратного уравнения \(x^2+px+q=0\) теорема Виета выглядит следующим образом: \[x_1+x_2=-p, \qquad \qquad x_1\cdot x_2=q\]
Теорема: разложение на множители квадратного трехчлена
Пусть уравнение \(ax^2 + bx + c = 0\), \(a\neq 0\), имеет два корня (возможно, совпадающих), то есть \(D\geqslant 0\). Тогда при любом значении \(x\) выполнено \[ax^2 + bx + c = a(x — x_1)(x — x_2),\] где \(x_1\) и \(x_2\) – корни уравнения \(ax^2 + bx + c = 0\) (возможно, совпадающие).
Доказательство
Сделаем преобразования: \[\begin{aligned} &a(x-x_1)(x-x_2)=a\left(x — \dfrac{-b + \sqrt{D}}{2a}\right)\left(x — \dfrac{-b — \sqrt{D}}{2a}\right) =a\left(x^2 — x\left(\dfrac{-b + \sqrt{D}}{2a} + \dfrac{-b — \sqrt{D}}{2a}\right) + \dfrac{b^2 — D}{4a^2}\right)=\\[2ex] &=a\left(x^2-x\cdot \left(-\dfrac ba\right)+\dfrac{b^2-(b^2-4ac)}{4a^2}\right) =a(x^2+\dfrac ba x+\dfrac ca)=ax^2+bx+c \end{aligned}\]
Пример
Разложить на множители квадратный трехчлен \(3x^2-2x-1\).
Решение.
Рассмотрим уравнение \(3x^2-2x-1=0\) и найдем его корни.
\(D=(-2)^2-4\cdot 3\cdot (-1)=16\), значит
\[x_1=\dfrac{2-4}{2\cdot 3}=-\dfrac 13 \qquad \qquad x_2=\dfrac{2+4}{2\cdot 3} =1\]
Таким образом, \(3x^2-2x-1=3(x-1)(x+\frac13)=(x-1)(3x+1)\).
\[{\Large{\text{Простейшие кубические уравнения}}}\] \(\bullet\) Кубический корень из числа \(a\) – это такое число \(b\), которое при возведении в куб равно \(a\): \[\sqrt[3] a=b\quad \text{то же самое, что }\quad a=b^3\] \(\bullet\) Таблица кубов чисел от 1 до 10: \[\begin{array}{|ll|}
\hline
1^3=1 & \quad6^3=216 \\
2^3=8 & \quad7^3=343\\
3^3=27 & \quad8^3=512\\
4^3=64 & \quad9^3=729\\
5^3=125 & \quad10^3=1000\\
\hline \end{array}\] \(\bullet\) Простейшие кубические уравнения – уравнения, сводящиеся к виду \[x^3=a\] Для любого числа \(a\) такие уравнения имеют единственный корень \[x=\sqrt[3]a\] Пример:
1) решением уравнения \(x^3=-8\) является \(x=\sqrt[3]{-8}=-2\).
2) решением уравнения \(x^3=64\) является \(x=4\).
shkolkovo.net
Как решать линейные уравнения?
Линейное уравнение – это алгебраическое уравнение, полная степень многочленов которого равна единице. Решение линейных уравнений – часть школьной программы, причем не самая сложная. Однако некоторые все же испытывают затруднения при прохождении данной темы. Надеемся, прочитав данный материал, все трудности для вас останутся в прошлом. Итак, давайте разбираться. как решать линейные уравнения.
Общий вид
Линейное уравнение представляется в виде:
- ax + b = 0, где a и b – любые числа.
Несмотря на то, что a и b могут быть любыми числами, их значения влияют на количество решений уравнение. Выделяют несколько частных случаев решения:
- Если a=b=0, уравнение имеет бесконечное множество решений;
- Если a=0, b≠0, уравнение не имеет решения;
- Если a≠0, b=0, уравнение имеет решение: x = 0.
В том случае, если оба числа имеют не нулевые значения, уравнение предстоит решить, чтобы вывести конечное выражения для переменной.
Как решать?
Решить линейное уравнение – значит, найти, чему равна переменная. Как же это сделать? Да очень просто – используя простые алгебраические операции и следуя правилам переноса. Если уравнение предстало перед вами в общем виде, вам повезло, все, что необходимо сделать:
- Перенести b в правую сторону уравнения, не забыв изменить знак (правило переноса!), таким образом, из выражения вида ax + b = 0 должно получиться выражение вида: ax = -b.
- Применить правило: чтобы найти один из множителей (x — в нашем случае), нужно произведение (-b в нашем случае) поделить на другой множитель (a — в нашем случае). Таким образом, должно получиться выражение вида: x = -b/а.
Вот и все – решение найдено!
Теперь давайте разберем на конкретном примере:
- 2x + 4 = 0 – переносим b, равное в данном случае 4, в правую сторону
- 2x = –4 – делим b на a (не забываем о знаке минус)
- x = –4/2 = –2
elhow.ru
Как решать линейные уравнения? | Александр Будников
Линейные уравнения – довольно безобидная и понятная тема школьной математики. Но, как это ни странно, количество ошибок на ровном месте при решении линейных уравнений лишь немногим меньше, чем в других темах – квадратных уравнениях, логарифмах, тригонометрии и прочих. Причины большинства ошибок – банальные тождественные преобразования уравнений. В первую очередь, это путаница в знаках при переносе слагаемых из одной части уравнения в другую, а также ошибки при работе с дробями и дробными коэффициентами. Да-да! Дроби в линейных уравнениях тоже встречаются! Сплошь и рядом. Чуть ниже такие злые уравнения мы с вами тоже обязательно разберём.)
Ну что, не будем тянуть кота за хвост и начнём разбираться, пожалуй? Тогда читаем и вникаем.)
Что такое линейное уравнение? Примеры.
Обычно линейное уравнение имеет следующий вид:
ax + b = 0,
где a и b – любые числа. Какие угодно: целые, дробные, отрицательные, иррациональные – всякие могут быть!
Например:
7х + 1 = 0 (здесь a = 7, b = 1)
x – 3 = 0 (здесь a = 1, b = -3)
x/2 – 1,1 = 0 (здесь a = 1/2, b = -1,1)
В общем, вы поняли, я надеюсь.) Всё просто, как в сказке. До поры до времени… А если присмотреться к общей записи ax+b=0 более пристально, да немного призадуматься? Ведь a и b – любые числа! А если у нас, скажем, a = 0 и b = 0 (любые же числа можно брать!), то что у нас тогда получится?
0 = 0
Но и это ещё не все приколы! А если, допустим, a = 0, b = -10? Тогда уже совсем какая-то ахинея получается:
0 = 10.
Что весьма и весьма напрягает и подрывает завоёвываемое потом и кровью доверие к математике… Особенно на контрольных и экзаменах. А ведь из этих непонятных и странных равенств ещё и икс найти нужно! Которого нету вообще! И вот тут даже хорошо подготовленные ученики, порой, могут впасть, что называется, в ступор… Но не переживайте! В данном уроке все такие сюрпризы мы тоже рассмотрим. И икс из таких равенств тоже обязательно отыщем.) Причём этот самый икс ищется очень и очень просто. Да-да! Удивительно, но факт.)
Ну хорошо, это понятно. Но как же можно узнать по внешнему виду задания, что перед нами именно линейное уравнение, а не какое-либо ещё? К сожалению, только по внешнему виду распознать тип уравнения возможно далеко не всегда. Дело всё в том, что линейными называются не только уравнения вида ax+b=0, но и любые другие уравнения, которые тождественными преобразованиями, так или иначе, сводятся к такому виду. А как тут узнаешь, сводится оно или нет? Пока пример почти не решишь – почти никак. Это огорчает. Но для некоторых типов уравнений можно при одном беглом взгляде сразу с уверенностью сказать, линейное оно или нет.
Для этого ещё разок обратимся к общей структуре любого линейного уравнения:
ax + b = 0
Обратите внимание: в линейном уравнении всегда присутствует только переменная икс в первой степени и какие-то числа! И всё! Больше ничего. При этом нету иксов в квадрате, в кубе, под корнем, под логарифмом и прочей экзотики. И (что особенно важно!) нет дробей с иксом в знаменателях! А вот дроби с числами в знаменателях или деление на число – запросто!
Например:
Это линейное уравнение. В уравнении присутствуют только иксы в первой степени да числа. И нету иксов в более высоких степенях – в квадрате, в кубе и так далее. Да, здесь есть дроби, но при этом в знаменателях дробей сидят только числа. А именно — двойка и тройка. Иными словами, в уравнении нету деления на икс.
А вот уравнение
уже нельзя назвать линейным, хотя здесь тоже присутствуют только числа и иксы в первой степени. Ибо, помимо всего прочего, здесь есть ещё и дроби с иксами в знаменателях. И после упрощений и преобразований такое уравнение может стать каким угодно: и линейным, и квадратным – всяким.
Как решать линейные уравнения? Примеры.
Так как же решать линейные уравнения? Читайте дальше и удивляйтесь.) Всё решение линейных уравнений базируется всего на двух основных вещах. Перечислим их.
1) Набор элементарных действий и правил математики.
Это использование скобок, раскрытие скобок, работа с дробями, работа с отрицательными числами, таблица умножения и так далее. Эти знания и умения необходимы не только для решения линейных уравнений, а для всей математики вообще. И, если с этим проблемы, вспоминайте младшие классы. Иначе несладко вам придётся…
2) Базовые тождественные преобразования уравнений.
Их всего два. Да-да! Более того, эти самые базовые тождественные преобразования лежат в основе решения не только линейных, а вообще любых уравнений математики! Одним словом, решение любого другого уравнения – квадратного, логарифмического, тригонометрического, иррационального и т.д. – как правило, начинается с этих самых базовых преобразований. А вот решение именно линейных уравнений, собственно, на них же (преобразованиях) и заканчивается. Готовым ответом.) Так что не поленитесь и прогуляетесь по ссылке.) Тем более, что там линейные уравнения тоже детально разбираются.
Что ж, я думаю, пора приступать к разбору примеров.
Для начала, в качестве разминки, рассмотрим какую-нибудь элементарщину. Безо всяких дробей и прочих наворотов. Например, такое уравнение:
х – 2 = 4 – 5х
Это классическое линейное уравнение. Все иксы максимум в первой степени и деления на икс нигде нету. Схема решения в таких уравнениях всегда едина и проста до ужаса: все члены с иксами надо собрать слева, а все члены без иксов (т.е. числа) собрать справа. Вот и приступаем к сбору.
Для этого запускаем в ход первое тождественное преобразование. Нам нужно перенести -5х влево, а -2 перенести вправо. Со сменой знака, ясное дело.) Вот и переносим:
х + 5х = 4 + 2
Ну вот. Полдела сделано: иксы собрали в кучку, числа – тоже. Теперь слева приводим подобные, а справа – считаем. Получаем:
6х = 6
Чего теперь нам не хватает для полного счастья? Да чтобы слева чистый икс остался! А шестёрка – мешает. Как от неё избавиться? Запускаем теперь второе тождественное преобразование – делим обе части уравнения на 6. И – вуаля! Ответ готов.)
х = 1
Разумеется, пример совсем примитивный. Чтобы общую идею уловить. Что ж, решим что-нибудь посущественнее. Например, разберём вот такое уравнение:
Детально разберём.) Это тоже линейное уравнение, хотя, казалось бы, тут есть дроби. Но в дробях есть деление на двойку и есть деление на тройку, а вот деления на выражение с иксом – нету! Так что – решаем. Используя всё те же тождественные преобразования, да.)
Что вначале делать будем? С иксами — влево, без иксов – вправо? В принципе, можно и так. Лететь в Сочи через Владивосток.) А можно пойти по кратчайшему пути, сразу воспользовавшись универсальным и мощным способом. Если знать тождественные преобразования, разумеется.)
Для начала задаю ключевой вопрос: что вам сильнее всего бросается в глаза и больше всего не нравится в этом уравнении? 99 человек из 100 скажут: дроби! И будут правы.) Вот и избавимся сначала от них. Безопасно для самого уравнения.) Поэтому начнём сразу со второго тождественного преобразования – с домножения. На что надо помножить левую часть, чтобы знаменатель благополучно сократился? Правильно, на двойку. А правую часть? На тройку! Но… Математика – дама капризная. Она, понимаешь, требует умножать обе части только на одно и то же число! Каждую часть помножать на своё число – не катит… Что делать будем? Что-что… Искать компромисс. Чтобы и наши хотелки удовлетворить (избавиться от дробей) и математику не обидеть.) А помножим-ка обе части на шестёрку!) То есть, на общий знаменатель всех дробей, входящих в уравнение. Тогда одним махом и двойка сократится, и тройка!)
Вот и домножаем. Всю левую часть и всю правую часть целиком! Посему используем скобочки. Вот так выглядит сама процедура:
Теперь раскрываем эти самые скобочки:
Теперь, представив 6 как 6/1, помножим шестёрку на каждую из дробей слева и справа. Это обычное умножение дробей, но, так уж и быть, распишу детально:
А вот здесь – внимание! Числитель (х-3) я взял в скобки! Это всё потому, что при умножении дробей числитель умножается весь, целиком и полностью! И с выражением х-3 надо работать как с одной цельной конструкцией. А вот если вы запишете числитель вот так:
6х – 3,
то это будет ошибкой. Дальше можно уже не решать, да…
Но у нас всё правильно и надо дорешивать. Что дальше делать? Раскрывать скобки в числителе слева? Ни в коем случае! Мы с вами домножали обе части на 6, чтобы от дробей избавиться, а не для того чтобы париться с раскрытием скобок. На данном этапе нам надо сократить наши дроби. С чувством глубокого удовлетворения сокращаем все знаменатели и получаем уравнение безо всяких дробей, в линеечку:
3(х-3) + 6х = 30 – 4х
А вот теперь и оставшиеся скобки можно раскрыть:
3х – 9 + 6х = 30 – 4х
Уравнение становится всё лучше и лучше! Вот теперь вновь вспоминаем про первое тождественное преобразование. С каменным лицом повторяем заклинание из младших классов: с иксами – влево, без иксов – вправо. И применяем это преобразование:
3х + 6х + 4х = 30 + 9
Приводим подобные слева и считаем справа:
13х = 39
Осталось поделить обе части на 13. То есть, вновь применить второе преобразование. Делим и получаем ответ:
х = 3
Готово дело. Как вы видите, в данном уравнении нам пришлось один раз применить первое преобразование (перенос слагаемых) и дважды – второе: в начале решения мы использовали домножение (на 6) с целью избавиться от дробей, а в конце решения использовали деление (на 13), чтобы избавиться от коэффициента перед иксом. И решение любого (да-да, любого!) линейного уравнения состоит из комбинации этих самых преобразований в той или иной последовательности. С чего именно начинать – от конкретного уравнения зависит. Где-то выгоднее начинать с переноса, а где-то (как в этом примере) – с домножения (или деления).
Работаем от простого – к сложному. Рассмотрим теперь откровенную жесть. С кучей дробей и скобок. А я уж подскажу, как не надорваться.)
Например, вот такое уравнение:
Минуту смотрим на уравнение, ужасаемся, но всё-таки берём себя в руки! Основная проблема – с чего начинать? Можно сложить дроби в правой части. Можно выполнить вычитание дробей в скобках. Можно обе части на что-нибудь домножить. Или поделить… Так что же всё-таки можно? Ответ: всё можно! Ни одно из перечисленных действий математика не запрещает. И какую бы последовательность действий и преобразований вы бы ни выбрали, ответ получится всегда один – правильный. Если, конечно, на каком-то шаге не нарушить тождественность ваших преобразований и, тем самым, не наляпать ошибок…
А, чтобы не наляпать ошибок, в таких навороченных примерах, как этот, всегда полезнее всего оценить его внешний вид и в уме прикинуть: что можно такое сделать в примере, чтобы максимально упростить его за один шаг?
Вот и прикидываем. Слева стоят шестёрки в знаменателях. Лично мне они не нравятся, а убрать их очень легко. Домножу-ка я обе части уравнения на 6! Тогда шестёрки слева благополучно сократятся, дроби в скобках пока никуда не денутся. Ну и ничего страшного. С ними чуток позже расправимся.) А вот справа у нас сократятся знаменатели 2 и 3. Именно при этом действии (умножении на 6) у нас за один шаг достигаются максимальные упрощения!
После умножения всё наше злое уравнение станет вот таким:
Кто не понял, как именно получилось это уравнение, значит, вы плохо усвоили разбор предыдущего примера. А я старался, между прочим…
Что дальше можно сделать? Дальше удобнее всего раскрыть все скобки справа. Причём правильно раскрыть, соблюдая основы! В правой части перед обеими скобками стоит знак плюс, поэтому все знаки при раскрытии сохраняются.
Итак, раскрываем:
Теперь самым логичным шагом было бы уединить дроби слева, а 5х отправить в правую часть. Заодно и подобные в правой части приведём. Получим:
Уже гораздо лучше. Теперь левая часть сама собой подготовилась к умножению. На что надо домножить левую часть, чтобы сразу и пятёрка сократилась, и четвёрка? На 20! Но ещё у нас присутствуют минусы в обеих частях уравнения. Поэтому удобнее всего будет умножать обе части уравнения не на 20, а на -20. Тогда одним махом и минусы исчезнут, и дроби.
Вот и умножаем:
Кому до сих пор непонятен этот шаг – значит, проблемы не в уравнениях. Проблемы – в основах! Вновь вспоминаем золотое правило раскрытия скобок:
Если число умножается на какое-то выражение в скобках, то это число надо последовательно умножить на каждое слагаемое этого самого выражения. При этом если число положительно, то знаки выражений после раскрытия сохраняются. Если отрицательно – меняются на противоположные:
a(b+c) = ab+ac
-a(b+c) = -ab-ac
Минусы у нас исчезли после домножения обеих частей на -20. И теперь скобки с дробями слева мы умножаем на вполне себе положительное число 20. Стало быть, при раскрытии этих скобок все знаки, что были внутри них, сохраняются. А вот откуда взялись скобки в числителях дробей, я уже подробно объяснял в предыдущем примере.
А вот теперь дроби и сократить можно:
4(3-5х)-5(3х-2) = 20
Раскрываем оставшиеся скобки. Опять же, правильно раскрываем. Первые скобки умножаются на положительное число 4 и, стало быть, все знаки при их раскрытии сохраняются. А вот вторые скобки умножаются на отрицательное число -5 и, поэтому, все знаки меняются на противоположные:
12 — 20х — 15х + 10 = 20
Остались сущие пустяки. С иксами влево, без иксов – вправо:
-20х – 15х = 20 – 10 – 12
-35х = -2
Вот почти и всё. Слева нужен чистый икс, а число -35 мешает. Вот и делим обе части на (-35). Напоминаю, что второе тождественное преобразование разрешает нам умножать и делить обе части на какое угодно число. В том числе и на отрицательное.) Лишь бы не на ноль! Смело делим и получаем ответ:
x = 2/35
На сей раз икс получился дробным. Ничего страшного. Такой уж пример.)
Как мы видим, принцип решения линейных уравнений (даже самых накрученных) довольно простой: берём исходное уравнение и тождественными преобразованиями последовательно упрощаем его прямо до получения ответа. С соблюдением основ, разумеется! Главные проблемы здесь именно в несоблюдении основ (скажем, перед скобками стоит минус, а знаки при раскрытии поменять забыли), а также в банальной арифметике. Так что не пренебрегайте основами! Они – фундамент всей остальной математики!
Некоторые приколы при решении линейных уравнений. Или особые случаи.
Всё бы ничего. Однако… Попадаются среди линейных уравнений и такие забавные перлы, которые в процессе их решения могут и в сильный ступор вогнать. Даже отличника.)
Например, вот такое безобидное с виду уравнение:
7х + 3 = 4х + 5 + 3х — 2
Широко позёвывая и слегка скучая, собираем все иксы слева, а все числа справа:
7х-4х-3х = 5-2-3
Приводим подобные, считаем и получаем:
0 = 0
Вот-те раз! Выдал примерчик фокус! Само по себе это равенство возражений не вызывает: ноль действительно равен нулю. Но икс-то пропал! Бесследно! А мы обязаны записать в ответе, чему равен икс. Иначе решение не считается, да.) Что же делать?
Без паники! В таких нестандартных случаях спасают самые общие понятия и принципы математики. Что такое уравнение? Как решать уравнения? Что значит решить уравнение?
Решить уравнение – это значит, найти все значения переменной икс, которые при подстановке в исходное уравнение дадут нам верное равенство (тождество)!
Но верное равенство у нас уже получилось! 0=0, вернее некуда!) Остаётся догадаться, при каких именно иксах у нас получается это равенство. Какие же такие иксы можно подставлять в исходное уравнение, если при подстановке все они всё равно посокращаются в полный ноль? Неужели ещё не догадались?
Ну, конечно же! Иксы можно подставлять любые!!! Совершенно любые. Какие хотите, такие и подставляйте. Хоть 1, хоть -23, хоть 2,7 – какие угодно! Они всё равно сократятся и в результате останется чистая правда. Попробуйте, поподставляйте и убедитесь лично.)
Вот вам и ответ:
х – любое число.
В научной записи это равенство пишется так:
Читается эта запись так: «Икс – любое действительное число.»
Или в другой форме, через промежутки:
Как вам больше нравится, так и оформляйте. Это верный и совершенно полноценный ответ!
А теперь я изменю в нашем исходном уравнении всего одно число. Вот такое уравнение теперь решим:
7х + 2 = 4х + 5 + 3х – 2
Опять переносим слагаемые, считаем и получаем:
7х – 4х – 3х = 5 – 2 – 2
0 = 1
И как вам этот прикол? Было обычное линейное уравнение, а стало непонятное равенство
0 = 1…
Говоря научным языком, мы получили неверное равенство. А по-русски неправда это. Бред сивой кобылы. Ахинея.) Ибо ноль никак не равен единице!
А теперь опять соображаем, какие же иксы при подстановке в исходное уравнение дадут нам верное равенство? Какие? А никакие! Какой икс ни подставляй, всё равно всё посокращается и останется лажа.)
Вот и ответ: решений нет.
В математической записи такой ответ оформляется вот так:
Читается: «Икс принадлежит пустому множеству.»
Такие ответы в математике тоже встречаются довольно часто: далеко не всегда у какого-либо уравнения имеются корни в принципе. Какие-то уравнения могут и вовсе не иметь корней. Совсем.
Вот такие вот два сюрприза. Надеюсь, что теперь внезапная пропажа иксов в уравнении не поставит вас навечно в тупик. Дело вполне знакомое.)
И тут слышу закономерный вопрос: а в ОГЭ или ЕГЭ они будут? На ЕГЭ сами по себе в качестве задания – нет. Слишком уж простенькие. А вот в ОГЭ или в текстовых задачках – запросто! Так что теперь – тренируемся и решаем:

Ответы (в беспорядке): -2; -1; любое число; 2; нет решений; 7/13.
Всё получилось? Отлично! У вас неплохие шансы на экзамене.
Что-то не сходится? Гм… Печалька, конечно. Значит, где-то пока есть пробелы. Либо в основах, либо в тождественных преобразованиях. Либо же дело в банальной невнимательности. Перечитайте урок ещё раз. Ибо не та это тема, без которой можно вот так легко обойтись в математике…
Удачи! Она вам обязательно улыбнётся, поверьте!)
abudnikov.ru
Как решить линейное уравнение? Уравнение прямой?
ТЕОРЕТИЧЕСКАЯ ЧАСТЬ
Линейное уравнение — это уравнение вида ax+b=0,
где a и b некоторые числа,
x – переменная стоящая в числителе, находящаяся в первой степени.
Хочешь готовиться к экзаменам бесплатно? Репетитор онлайн бесплатно. Без шуток. ЗДЕСЬ
Что является решением уравнения?
Решением уравнения является нахождение всех его корней или доказательство их отсутствия.
Примеры линейных уравнений:
3x+5=0
x+1=5
2x=0
7x=7
3x+1=x
Нелинейные уравнения:
Чем отличаются линейные уравнения от не линейных?
У линейных уравнений x всегда находится в первой степени в числители. Если одно из условий не выполняется то уравнение нелинейное.
Как решаются линейные уравнения?
Все что связано с переменной x переносим в одну сторону, а обычные числа в другую. Это называется: “Неизвестные в одну сторону известные в другую”. В итоге корень уравнения будет равен x=-b/a. Рассмотрим на примере:
Как построить прямую? Как построить график прямой или линейной функции? Можно узнать здесь.
ПРАКТИЧЕСКАЯ ЧАСТЬ
Пример №1:
2x+2=0 (здесь неизвестное это 2x его мы оставляем в левой стороне, а 2 переносим через равно в правую сторону, при переносе через равно знак с + меняется на -)
2x=-2 | : 2 (далее нам нужно получить просто x без коэффициента 2, поэтому мы все уравнение делим на 2, получим 2x:2=-2:2 )
x=-1 (получили корень уравнения)
2x+2=0 (здесь неизвестное это 2x его мы оставляем в левой стороне, а 2 переносим через равно в правую сторону, при переносе через равно знак с + меняется на -)
2x=-2 | : 2 (далее нам нужно получить просто x без коэффициента 2, поэтому мы все уравнение делим на 2, получим 2x:2=-2:2 )
x=-1
Сделаем проверку уравнения подставим вместо переменной x полученный корень:
2*(-1)+2=0
-2+2=0
0=0
Решено верно
Ответ: -1
Пример №2:
2x-6=4x (здесь неизвестное это 2x и 4x. 4х нужно перенести в левую часть уравнения, а -6 переносим через равно в правую сторону, при переносе через равно знак у -6 меняется с – на +, а у 4х знак меняется с + на -)
2x-4x=6 (при вычитании 2x-4x=-2x)
-2x=6 | : (-2) (далее нам нужно получить просто x без коэффициента -2, поэтому мы все уравнение делим на -2, получим -2x:(-2)=6:(-2) )
x= -3
Сделаем проверку уравнения подставим вместо переменной x полученный корень:
2*(-3)-6=4*(-3)
-6-6=-12
-12=-12
Решено верно
Ответ: -3
Пример №3:
x-3=x-3
x-x=3-3
0=0
Ответ: x может быть любое число
Пример №4:
2x+7=2x-3
2x-2x=-7-3
0=-10
Ответ: корней нет
tutomath.ru
Как решать квадратное уравнение
Как решать квадратные уравнения
Алгоритм решения квадратного уравнения
Речь идет о поиске только действительных корней квадратного уравнения.
Шаг 1: Записываем уравнение в стандартном виде
В общем виде квадратное уравнение можно записать так:
Здесь — любое ненулевое число, — любые числа, a — то число, которое необходимо найти. Такой вид уравнения называют стандартным. Например, — квадратное уравнение в стандартном виде, причем , и . Число называют старшим коэффициентом, число — свободным коэффициентом. А все выражение вида называют квадратным трехчленом.
Типичная ошибка: считать, что , то есть забыть про знак «-«.
Cтоит заметить, что все коэффициенты уравнения можно уменьшить в раза. Уравнение примет вид . Числа , и , естественно, изменились (уменьшились!). Зато корни уравнения остались прежними. Поэтому всегда стоит проверять, а нельзя ли таким образом упростить уравнение, чтобы легче было далее находить корни.
Итак, первым делом необходимо привести квадратное уравнение к стандартному виду. Для этого можно раскрывать скобки, приводить подобные слагаемые, переносить слагаемые из одной части уравнения в другую (при этом слагаемые меняют знак). Например, . Раскрываем скобки: . Приводим подобные слагаемые: . Переносим все слагаемые из правой части в левую: (повторю: такие слагаемые меняют свой знак). И опять приводим подобные слагаемые: . Получим квадратное уравнение в стандартном виде. Причем , и .
Типичная ошибка: забыть поменять знак слагаемого при переносе.
Типичная ошибка: перепутать слагаемые местами и неправильно определить коэффициенты. Например, . И кажется, что , и . На самом деле, , и .
Интересный случай: предположим, что получилось уравнение . Чему равно ? На этот вопрос не каждый может ответить уверенно. Ответ: .
Интересный случай: дано уравнение . Мы смело раскрываем скобки и переносим и из правой части в левую. Но после приведения подобных слагаемых получается уравнение . Нет ! Ни о каком стандартном виде квадратного уравнения здесь не может быть и речи просто потому, что это не квадратное уравнение, а совсем другая история под названием «Линейное уравнение».
Замечание: опытные в квадратных уравнениях математики советуют всегда делать коэффициент положительным. Для этого левую и правую части уравнения всегда можно домножить на . Например, заменим на . По-простому говоря, каждое слагаемое меняет знак. Да, это другое уравнение и коэффициенты другие. Но корни у него такие же, как и у исходного уравнения. Поэтому далее спокойно можно работать с новым. Зачем делать положительным? Например, затем, чтобы было меньше арифметических ошибок, когда будем находить дискриминант. Что такое дискриминант, узнаем в следующем шаге.
Шаг 2: Находим дискриминант.
У нас есть квадратное уравнение в виде . Вычисляем число , которое называется дискриминантом квадратного уравнения. Например, для уравнения дискриминант равен .
Типичная ошибка: часто вместо пишут , то есть забывают скобки, но это уже , а не .
Типичная ошибка: неправильно определяют коэффициенты , и
Типичная ошибка: в слагаемом неправильно определяют окончательный знак. Например, в все-таки в итоге получается , а не .
Редкая ошибка: дискриминант пишут с большой буквы, видимо, из уважения или считая, что это фамилия.
Шаг 3: Находим корни уравнения
У нас есть дискриминант . Далее все зависит от его знака.
Если , то корней у уравнения нет. Ответ: корней нет. Вот так внезапно решение закончилось. Например, в уравнении дискриминант равен . Поэтому корней нет. Кстати, что это значит? Это значит, что какое бы число вы не выбрали, подстановка его в выражение вместо никогда не даст . Проверим число , например: . Не ноль. То есть — не корень. Аналогично с любым другим числом: ноль никогда не получится.
Если , то . Числа и — это как раз те коэффициенты из стандартной записи уравнения. Например, в уравнении дискриминант . Тогда . Ответ: .
Типичная ошибка: неправильно подставляют в формулу . Ошибаются со знаком. Ведь если , например, то .
Если . То в ответе будет два корня, которые можно найти по формулам и . Например, в уравнении дискриминант . Тогда и . Так как , то и . Ответ: .
Замечание: часто для сокращения пишут две формулы в одной: .
Замечание: иногда дискриминант может оказаться «некрасивым», например, . Такое может быть, и терять самообладание не стоит. Совет один: перепроверить решение и, если ошибка не найдена, со спокойной совестью решать дальше. Чаще всего задачи придумывают так, чтобы дискриминант были полным квадратом (кстати, полезно выучить таблицу квадратов чисел от 1 до 20). Но иногда попадаются ответы вида .
Типичная ошибка: неправильно находят . Например, считают, что . На самом деле, . Отрицательным выражение быть не может (по определению арифметического квадратного корня).
Вот и весь алгоритм. Конечно, есть еще много деталей. Например, есть неполные квадратные уравнения, когда лучше решать способами без дискриминанта. Есть еще уравнения, сводящиеся к квадратным. Есть еще поиск комплексных корней квадратного уравнения (для ЕГЭ это излишне). Кстати, проверить свое решение квадратного уравнения всегда можно здесь. Далее стоит изучить теорему Виета, понять, а как возникает формула для дискриминанта, как быть с уравнением третьей степени.
Полный пример решения квадратного уравнения.
Условие
Решить уравнение
Решение
Согласно алгоритму, раскрываем скобки: .
На всякий случай, расписал все подробно. Но вообще такие действия надо научиться делать почти устно. Более того, лучше заметить, что к первому слагаемому применима формула сокращенного умножения, точнее, разность квадратов. Такие формулы позволяют значительно экономить время и силы (потренироваться можно здесь).
Но продолжим решение: . Приводим подобные слагаемые и переносим в левую часть уравнения: .
Изменим знак : .
Находим дискриминант. Так как , и , то . Дискриминант , поэтому у уравнения два корня: и .
Осталось заметить, что корни можно упростить, ведь .
Получаем окончательный ответ, который запишем одной формулой: .
Как видите, малейшая неточность в арифметических вычислениях — и весь труд в итоге напрасен.
Поэтому стоит потренироваться выполнять арифметические вычисления устно и без ошибок.
Ответ:
Задачи для самостоятельного решения
Номера 41, 42, 43, 51, 52, 53 (ответы находятся после условий)
все статьи по математике
www.itmathrepetitor.ru
Как решать квадратное уравнение | Подготовка к ЕГЭ по математике
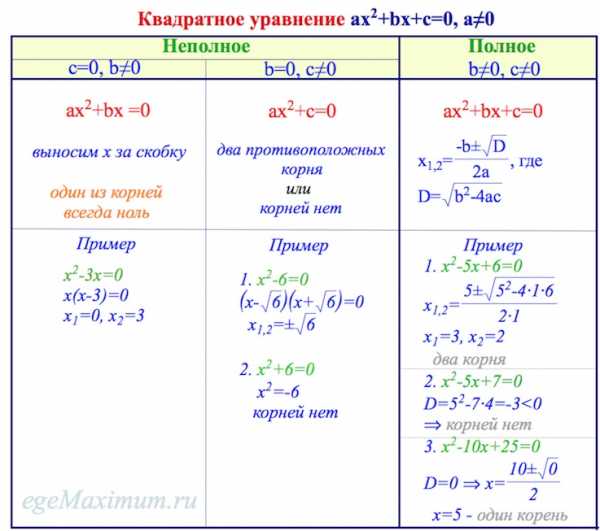
Надеюсь, вы внимательно изучили таблицу, приведенную выше. Если все еще есть вопросы, – давайте разбираться.
Во первых, почему рассматриваются только случаи при ? Просто потому, что при у нас уже будет не квадратное уравнение, а линейное.
Формулу дискриминанта знают практически все, но почему же тогда возникают все же сложности с решением уравнений?
Начнем с того, что иногда происходит путаница с коэффициентами , и . Ни в коем случае мы не считаем, что – это тот коэффициент, что стоит на первом месте! Но – тот, что при . Давайте договоримся, что будем приводить всякое квадратное уравнение к стандартному виду, ставя на первое место слагаемое, содержащее , на последнее – свободный от член (если таковой имеется). Например, уравнение будем переписывать так .
Далее, некоторых может сбить с толку минусовой коэффициент при старшем члене (то есть ). В этом случае советую домножать обе части уравнения на -1. Например, встречая уравнение , переписывать его в таком виде , и только потом высчитывать дискриминант, находить корни.
И, наконец, замечу, находятся и такие товарищи, которые, встречая, например, уравнение , спешат выносить за скобку, путая это уравнение с неполным. Нет, это обычное полное квадратное уравнение, которое после переноса влево примет вид , – решаем мы его через дискриминант.
Поэтому, давайте договоримся всякое уравнение приводить к такому виду, чтобы справа стоял только ноль и ничего больше.
Плавно перешли к неполным квадратным уравнениям. Если мы будем придерживаться последного совета, то мы не сможем спутать неполное уравнение с полным уж это точно. Справа будет два слагаемых (вырожденный случай – одно), а не три как у полного уравнения. Можно, конечно, и такие уравнения решать через дискриминант,но проще поступить иначе.
У нас в случае неполного уравнения будет всегда получаться либо уравнение с двумя , либо с одним . Что делать, в случае, если у нас оба слагаемых содержат (например, )? Ну, конечно, выносить его за скобку (), в этом случае будем всегда получать, что произведение двух множителей равно . Когда такое возможно? Конечно, когда один из множителей равен нулю (либо , либо ). В этом случае у нас всегда один из корней будет нулевым.
Во втором же случае, неполное уравнение будет содержать лишь одно слагаемое с (например, или ). Если свободный член отрицательный (как в первом случае, ), то мы всегда сможем разложить левую часть на множители по формуле разность квадратов ( для уравнения имеем , далее ). Если же свободный член положителен, то уравнение не имеет корней (действительно, в уравнении первое слагаемое должно бы быть равным -3, чтобы в сумме с 3 дать 0, но такое невозможно).
В общем, каждое отдельно взятое квадратное уравнение мы решам одним из трех способов, – выбор не велик.
Заметим, также, что в случае полного квадратного уравнения в зависимости от того, какой дискриминант мы получаем, – на выходе разное количество корней. Если , то будем иметь два корня, если , то имеем один корень (или два совпавших), наконец, если , то корней нет.
Смотрите также статью «Что делать, если дискриминант громоздкий?»
egemaximum.ru
Линейные и квадратные уравнения. | Социальная сеть работников образования
проверочный тест по теме: «Решение линейных уравнений» Вариант 1.
- -6х – 4 = -9х + 11
1) 3 2) 12 3) 5 4) 1
- 6 – 5х = 2х +5
1) 8 2) 7 3) 4)
- 10(х – 9) = 7
1) 9,7 2) 0,87 3) 4) -0,97
- 5(2х + 4) = 6х – 10 Ответ: ______
- 7(-3 + х) – 2х = -6 Ответ: ______
- 2(х — 3) — 5 = 4х Ответ: ______
- -5 (7 – х) + 2х = -7 Ответ: ______
- Ответ: ______
- Ответ: ______
- 9 + 3(1 – 2х) = 6х – 4 Ответ: ______
- Ответ: ______
- Ответ: ______
- Ответ: ______
14) 3 – 3(х + 2) = 5 — 5х Ответ: ______
15) 1 + 8х +3(5 – х) = -4х – 2 Ответ: ______
16) -10х – 6(-1 + 6х) = -6х – 4 Ответ: ______
Проверочный тест по теме: «Решение линейных уравнений» Вариант 2.
- 10х + 4 = 7х + 19
1) 1 2) -5 3) 12 4) 5
- 9 – 6х = 8х + 7
1) 2) 3) 1 4) — 5
- 5(х + 2) = 1
1) 1,8 2) 3) -4 4) -1,8
- 7(2х + 3) = 12х + 11 Ответ: ______
- 7(-4 + х) + 3х = 4 Ответ: ______
- 2(х + 7) – 9 = -2х Ответ: ______
- -3 (5 – х) = 11 + 2х Ответ: ______
- Ответ: ______
- Ответ: ______
- Ответ: ______
- Ответ: ______
- Ответ: ______
- Ответ: _____
- -3 + 4( х – 1) = 5 – 2х Ответ: _____
- 2х – 3 + 2(х — 1) = 3х – 11 Ответ: _____
- 9х – 7(-10 — 3х) = х — 17 Ответ: ______
Ответы к проверочному тесту по теме: «Решение линейных уравнений».
Вариант 1.
1) 3
2)
3) 1
4) – 7, 5
5) 3
6) – 5,5
7) 4
8) – 0,6
9) — 7
10) 1,75
11) – 1,5
12)
13) 7
14) 4
15) – 2
16) 0,25
Ответы к проверочному тесту по теме: «Решение линейных уравнений».
Вариант 2.
1) 4
2) 2
3) 4
4) – 5
5) 3,2
6) – 1,25
7) 26
8) – 3
9) 1,8
10) 3
11) 2
12)
13)
14) 2
15) – 6
16) – 3
Проверочный тест по теме: «Решение квадратных уравнений»
Вариант 1.
1) Решите уравнение: х2 + 4х = 0
1) 0; 4 2) 4 3) 0; -4 4) 1; -4
2) Решите уравнение: 1 – 9у2= 0
Ответ: ________
3) Решите уравнение: –у2 + 3 = 0
Ответ: ________
4) Решите уравнение: х2 – 7х + 12 = 0
1) -3; 4 2) -3; -4 3) 3; -4 4) 3; 4
5) Найдите наименьший корень уравнения:
у2 + 8у + 15 = 0
Ответ: _______
6) Решите уравнение: 2х2 – 7х + 5 = 0
Ответ: _______
7) Найдите сумму корней уравнения:
х2 – 13х + 40 = 0
Ответ: ________
8) Найдите наибольший корень уравнения:
х2 = -15х – 56
Ответ: ________
9) Найдите произведение корней уравнения:
х2 + 16х = — 63
Ответ: ________
10) Соотнесите квадратные уравнения и их корни:
а) х2 + 3х -4 = 0 б) х2 – 9 = 0 в) х2 — 10х + 25 =0
1) х1=-3, х2 = 3 2) х = 5
3) х1=-4, х2= 1 4) нет корней
Ответ:
11) Найдите корни уравнения: 4х +1= — 4х2
Ответ: ________
12) Решите уравнение:
Ответ: ________
13) Решите уравнение: 5(х – 2) = (3х +2)(х – 2)
Ответ: ________
14) Решите уравнение:
Ответ: ________
Проверочный тест по теме: «Решение квадратных уравнений»
Вариант 2.
1) Решите уравнение: 3х2 — х = 0
1) — 2) 0; 3 3) 0; 1 4)
2) Решите уравнение: 1 – 16у2= 0
Ответ: ____
3) Решите уравнение: –у2 + 8 = 0
Ответ:_______
4) Решите уравнение: х2 — 8х + 15 = 0
1) 3; 5 2) -3; -5 3) -3; 5 4) 3; -5
5) Найдите наибольший корень уравнения:
2х2 + 3х + 1 = 0
Ответ: ________
6)Решите уравнение: 4х2 — 7х + 3 = 0
Ответ: ________
7) Найдите сумму корней уравнения:
х2 – 17х + 42 =0
Ответ: ________
8) Найдите наименьший корень уравнения:
х2 = 7х + 18
Ответ: ________
9) Найдите произведение корней уравнения:
х2 + 9х = — 14
Ответ: ________
10) Соотнесите квадратные уравнения и их корни:
а) х2 — х — 2 = 0 б) х2 – х = 0 в) х2 + 25 =0
1) х1=-1, х2 = 1 2) х1 = 0, х2 = 1
3) х1=-1, х2= 2 4) нет корней
Ответ:
11) Найдите корни уравнения: 1 +4у = 5у2
Ответ: ________
12) Решите уравнение:
Ответ: ________
13) Решите уравнение: (х + 3)2 – 16 = (1 – 2х)2
Ответ: ________
14) Решите уравнение:
Ответ: ________
Ответы к проверочному тесту по теме: «Решение квадратных уравнений».
Вариант 1.
1) 3
2)
3)
4) 4
5) -5
6) 1; 2,5
7) 13
8) -7
9) 63
10)
11) -0,5
12) -0,75; 2,5
13) 1; 2
14) -4,8; 2
Ответы к проверочному тесту по теме: «Решение квадратных уравнений».
Вариант 2.
1) 4
2) -0,25; 0,25
3)
4) 1
5) -0,5
6) 0,75; 1
7) 17
8) -2
9) 14
10)
11) -0,2; 1
12) -0,25;
13)
14) -0,8; 3
nsportal.ru
