Квадратные уравнения с корнями – Иррациональные уравнения. Подробная теория с примерами.

Квадратные уравнения (способы решения)

Разделы: Математика

---

Необходимость решать уравнения не только первой, но и второй степени ещё в древности была вызвана потребностью решать задачи, связанные с нахождением площадей земельных участков и с земляными работами военного характера, а также с развитием астрономии и самой математики.

Квадратные уравнения умели решать около 2000 лет до нашей эры в Вавилоне. Применяя современную алгебраическую запись, можно сказать, что в их книгописных текстах встречаются, кроме неполных, и такие, как полные квадратные уравнения.

Определение

Уравнение вида ax² + bx + c = 0, где a, b, c — действительные числа, причем a ≠ 0, называют квадратным уравнением.

Если a = 1 , то квадратное уравнение называют приведенным; если a ≠ 1, то неприведенным .

Числа a, b, c носят следующие названия: a — первый коэффициент, b — второй коэффициент, c — свободный член.

Корни уравнения ax2 + bx + c = 0 находят по формуле

Выражение D = b²— 4ac называют дискриминантом квадратного уравнения.

• если D < 0, то уравнение не имеет действительных корней;
• если D = 0, то уравнение имеет один действительный корень;
• если D > 0, то уравнение имеет два действительных корня.

В случае, когда D = 0, иногда говорят, что квадратное уравнение имеет два одинаковых корня.

Формулы

Полное квадратное уравнение

Неполные квадратные уравнения

Если в квадратном уравнении ax² + bx + c = 0 второй коэффициент b или свободный член c равен нулю, то квадратное уравнение называется неполным.

Неполные уравнения выделяют потому, что для отыскания их корней можно не пользоваться формулой корней квадратного уравнения — проще решить уравнение методом разложения его левой части на множители.

Способы решения неполных квадратных уравнений:

1. c = 0, то уравнение примет вид
   ax² + bx = 0.
   x(ax + b) = 0 ,
   x = 0 или ax + b = 0, x = —b : a.
2. b = 0, то уравнение примет вид
   ax² + c = 0,
   x² = —c / a,
   x_{1, 2} = ±√(-c / a).
3. b = 0 и c = 0 , то уравнение примет вид
   ax² = 0,
   x = 0

Решение неполного квадратного уравнения

Квадратные уравнения с комплексными переменными

Сначала рассмотрим простейшее квадратное уравнение z² = a, где a-заданное число, а z-неизвестное. На множестве действительных чисел это уравнение:

1. имеет один корень z = 0, если а = 0;
2. имеет два действительных корня z_{1, 2} = ±√a
3. Не имеет действительных корней, если a < 0

Решение квадратных уравнений с помощью графиков

Не используя формул квадратное уравнение можно решить графическим способом. Например x² + x + 1 = 0.
Решим уравнение. Для этого построим два графика y = x²; y

= x + 1.

y = x², квадратичная функция, график парабола.
y = x + 1, линейная функция, график прямая.

Графики пересекаются в двух точках, уравнение имеет два корня.
Ответ: x ≈ -0,6; x ≈ 2,6.

Решение задач с помощью квадратных уравнений

Процессы	Скорость км/ч	Время ч.	Расстояние км.
Вверх по реке	10 — x	35 / (10 — x)	35
Вверх по протоку	10 — x + 1	18 / (10 — x + 1)	18
V течения	x
V притока	x + 1

Зная, что скорость в стоячей воде равна 10 км/ч, составим уравнение.

ОДЗ: ∀ x ≠ 9, 10.

Практикум

т.к. D₁
Ответ: корней нет.
Ответ: x = 2,5.

Заключение

Ещё в древности люди пользовались ими не зная, что это – квадратные уравнения.

В наше время невозможно представить себе решение как простейших, так и сложных задач не только в математике, но и в других точных науках, без применения решения квадратных уравнений.

Надеюсь и вы открыли для себя что-нибудь новое

Презентация

20.06.2009

Поделиться страницей:

urok.1sept.ru

Вывод формулы корней полного квадратного уравнения. Решение приведенных квадратных уравнений и уравнений с четным вторым коэффициентом

Разделы: Математика

---

Устный счет:

1. При каком значении Х , выражение принимает минимальное значение

а) ; б)
2. Зависимость y(x) выражается формулой y = 13x + 1 выразить x(y)

3. Не решая уравнения, определить, равносильны ли они:

4. Выделить полный квадрат:

5. Вычислить пары чисел , удовлетворяющих условиям

а) m + n = 4 mn = 4

б) m + n = –3 mn = –18

1. Какое уравнение называется полным?
2. Что такое корни квадратного уравнения?
3. Сколько корней может иметь квадратное уравнение?

Теорема. Квадратное уравнение не может иметь более двух различных корней.

Доказательство:

Предположим, что уравнение три различных корня:

Если уравнение имеет корень, то после подстановки его в уравнение получится верное числовое равенство:

(1)
(2)
(3)

из (2) отнимаем (1)

–

_____________________

В каком случае произведение равно 0?

Так как = > 0 = > a+ b = 0. (4)

Из (3) вычтем (2)

–

_________________

= > a+ b = 0 (5)

Из (4) отнимем (5)

–

________________

а0 = > = > ,
а по условию пришли к противоречию.

Давайте решим уравнение

:

Самостоятельно:

a)

Вместе:

б)

Нравится ли этот способ? Нет! Тогда будем рассуждать иначе:

(формулу для нахождения корней квадратного уравнения учить проговаривать словами).

– дискриминант квадратного уравнения.

По теореме, доказанной нами , уравнение не может иметь более двух корней.

Количество корней зависит от D.

1). D > 0
2). D = 0

3). D < 0 – уравнение действительных корней не имеет.

Решить уравнения:

1)
– корней нет.

2)
D = 49–48 = 1

3)
D = 25 + 12 = 37

Если в уравнении b = 2k ,то уравнение имеет вид

D =

Диктант(один ученик на внутренней доске, в это время двое по карточкам)

1) Вычислить дискриминант квадратного уравнения D = 100
2) Найти корни квадратного уравнения х = 3 и
3) При каком условии полное квадратное уравнение имеет один корень D = 0
4) При каком условии полное квадратное уравнение не имеет корней.
5) Решить уравнение D < 0.

После диктанта ребята меняются тетрадями и проверяют задание , исправляют ошибки и задают вопросы ученику у доски.

Все проверяют работу учеников на доске, которым были даны карточки.

1)

а) Решить уравнение

б) При каком m можно представить в виде квадрата двучлена выражение

а)

б)

2)

1. Решить уравнение

2. При каком а уравнение имеет один корень

Этим учащимся задаются вопросы и ставится оценка.

Итог урока

– Какие уравнения мы сегодня решали?
– Сколько корней может иметь квадратное уравнение?
– С помощью чего мы их решали?

Когда D = 0, то …
D < 0, то …
D > 0, то …

3.03.2008

Поделиться страницей:

urok.1sept.ru

Квадратные уравнения и его корни

Квадратные уравнения – это фундамент, на котором покоится величественное здание алгебры. Квадратные уравнения находят широкое применение при решении тригонометрических, показательных, иррациональных уравнений и неравенств. Решение многих задач математики, физики и практики сводится к решению алгебраических уравнений.

В школьном курсе математики изучаются формулы корней квадратных уравнений, с помощью которых можно решать любые квадратные уравнения.

Однако имеются и другие приёмы решения квадратных уравнений, которые позволяют очень быстро и рационально решать квадратные уравнения.

Данные приёмы решения заслуживают внимания, поскольку они не отражены в школьных учебниках математики.

Овладение данными приёмами поможет мне экономить время и эффективно решать уравнения.

Потребность в быстром решении обусловлена применением тестовой системы вступительных экзаменов.

Квадратным уравнением называется уравнение ах² + bх + с = 0, где а≠0, а, b,с – заданные числа числа, х – неизвестное.

Коэффициенты а, b,с квадратного уравнения называют так: а- первым или старшим коэффициентом, b-вторым коэффициентом, с-свободным членом.

Неполное квадратное уравнение

Квадратное уравнение ах² + bх + с = 0 называют неполным, если хотя бы один из коэффициентов b или с равен нулю.

1) ах² = 0, х=0

2) ах² + с = 0, ах² = -с

1. если с>0, то нет действительных корней

2. если с

3) ах² + bх = 0, х(ах+в)=0 х=0 или ах=- в х=- в/а

Пример1: 5х²=0 х=0

Ответ: х= 0

Пример2: 3х² — 27 = 0

3х²=27 х²=9 х 1,2=

Ответ: х1,2 =

Пример3: х²+7=0 х²=-7

Ответ: нет действительных корней

Пример4: х²- 6х=0 х(х-6)=0 х1=0 или х2=6

Ответ: х1=0; х2=6

3. История квадратных уравнений.

Квадратные уравнения в Древнем Вавилоне.

Необходимость решать уравнения не только первой, но и второй степени ещё в древности была вызвана потребность решать задачи, связанные с нахождением площадей земельных участков и с земляными работами военного характера, а также с развитием астрономии и самой математики. Квадратные уравнения умели решать около 2000 лет назад до н. э. вавилоняне. Применяя современную алгебраическую запись, можно сказать, что в их клинописных текстах встречаются, кроме неполных, и такие, например, полные квадратные уравнения:

Правило решения этих уравнений, изложено в вавилонских текстах, совпадает по существу с современным, однако неизвестно, каким образом дошли вавилоняне до этого правила. Почти все найденные до сих пор клинописные тексты переводят только задачи с решениями, изложенными в виде рецептов, без указаний относительно того, каким образом они были найдены.

Несмотря на высокий уровень развития алгебры в Вавилоне, в клинописных текстах отсутствуют понятие отрицательного числа и общие методы решения квадратных уравнений.

Как составлял и решал Диофант квадратные уравнения.

В “Арифметике” Диофант нет систематического изложения алгебры, однако в ней содержится систематизированный ряд задач, сопровождаемых объяснениями и решаемых при помощи составления уравнений разных степеней.

При составлении уравнений Диофант для упрощения решения умело выбирает неизвестные.

Вот, к примеру, одна из его задач.

Задача 11. “Найти два числа, зная, что их сумма равна 20, а произведение – 96”.

Диофант рассуждает следующим образом: из условия задачи вытекает, что искомые числа не равны, так если бы они были равны, то их произведение равнялось бы не96, а 100. Таким образом, одно из них будет больше половины их суммы, т. е. 10 – x. Разность между ними 2x. Отсюда уравнение

(10 + x) (10 – x) = 96, или же

100 – x² = 96, x² – 4 = 0 (1)

Отсюда x = 2. Одно из искомых чисел равно 12, другое 8. Решение x = -2 для Диофанта не существует, так как греческая математика знала только положительные числа.

Если мы решим эту задачу, выбирая в качестве неизвестного одно из искомых чисел, то мы придем к решению уравнения y (20 – y) = 96 y² – 20y + 96 = 0 (2)

Ясно, что, выбирая в качестве неизвестного полуразность искомых чисел, Диофант упрощает решение; ему удаётся свести задачу к решению не полного квадратного уравнения(1).

Квадратные уравнения в Индии

Задачи на квадратные уравнения встречаются уже в 499г. В Древней Индии были распространены публичные соревнования в решении трудных задач. В одной из старинных индийских книг говорится по поводу таких соревнований следующее:

«Как солнце блеском своим затмевает звёзды, так ученый человек затмит славу другого в народных собраниях, предлагая и решая алгебраические задачи».

Одна из задач знаменитого индийского математика XIIв. Бхаскары:

Решение Бхаскары свидетельствует о том, что он знал о двузначности корней квадратных уравнений. Часть страницы из алгебры Бхаскары (вычисление корней).

Квадратные уравнения у ал-Хорезми

В алгебраическом трактате ал-Хорезми даётся классификация линейных уравнений и квадратных уравнений. Автор насчитывает 6 видов уравнений, выражая их следующим образом:

1) “Квадраты равны корнями”, т. е. ax² = bx.

2) “Квадраты равны числу”, т. е. ax²= c.

3) “Корни равны числу”, т. е. ax = c

4) “Квадраты и числа равны корням”, т. е. ax² + c = bx/

5) “Квадраты и корни равны числу”, т. е. ax² + bx = c.

6) “Корни и числа равны квадратам”, т. е. bx + c + ax²

Для ал-Хорезми, избегавшего употребления отрицательных чисел, члены каждого из этих уравнений слагаемые, а не вычитаемые. При этом заведомо не берутся во внимание уравнения, у которых нет положительных решений. Автор излагает способы решения указанных уравнений, пользуясь приёмами ал-джабар и ал-мукабала. Его решения, конечно, не совпадает полностью с нашим. Уже не говоря о том, что оно чисто риторическое, следует отметить, например, что при решении неполного квадратного уравнения первого вида ал-Хорезми, как и все математики до 17 века, не учитывает нулевого решения, вероятно, потому, что в конкретных практических задачах оно не имеет значения. При решении полных квадратных уравнений ал-Хорезми на частных числовых примерах излагает правила решения, а затем их геометрические доказательства.

Квадратные уравнения в Европе XIII — XVIIв. в.

Формулы решения квадратных уравнений по образцу ал-Хорезми в Европе были впервые изложены в книге “Книге абака”, написанной в 1202 г. Итальянским математиком Леонардо Фибоначчи. Этот объёмистый труд, в котором отражено влияние математики как стран ислама, так и Древней Греции, отличается и полнотой, и ясностью изложения. Автор разработал самостоятельно некоторые новые алгебраические примеры задач и первый в Европе подошёл к введению отрицательных чисел. Его книга способствовала распространению алгебраических знаний не только в Италии, но и в Германии, Франции и других стран Европы. Многие задачи из “Книги абака” переходили почти во все европейские учебники 16 – 17 веков и частично 18 века.

Общие правило решения квадратных уравнений, приведённых к единому каноническому виду x² + bx = c, при всевозможных комбинациях знаков коэффициентов b, c было сформулировано в Европе лишь в 1544 г. М. Штифелем.

Вывод формулы решения квадратного уравнения в общем виде имеется у Виета, однако Виет признавал только положительные корни. Итальянские математики Тарталья, Кардано, Бомбелли среди первых в 16 веке учитывают, помимо положительных, и отрицательные корни. Лишь в 17 веке благодаря трудам Жирара, Декарта, Ньютона и других учёных способов решения квадратных уравнений принимает современный вид.

4. Решение квадратных уравнений.

4. 1 Метод выделения полного квадрата

Пример1: решить квадратное уравнение х² + 2х – 3=0

➢ Преобразуем это уравнение так: х² + 2х = 3, х² + 2х +1= 3+1,

(х + 1)² = 4.

Следовательно, х+1=2 или х+1= -2, откуда х1=1, х2= -3.

Решая уравнение, мы преобразовали его так, что в левой части получился квадрат двучлена, а правая часть не содержит неизвестное.

4. 2 Решение квадратных уравнений по формуле.

ах² + bх + с = 0

D=b²- 4ac

Если D =0,то х=

Если D>0,то

Если D

Пример1: х² — 4х +5 =0

D=16-4·1·5

D

Пример2: 2х² + 3х + 1 = 0

D=9-4·2·1=1 х1=

Ответ: -1; — ½

4. 3 Теорема Виета

Если — корни уравнения х² + bх + c = 0, то справедливы формулы

Т. е. сумма корней приведенного квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену.

Пример1: х² — 14х – 15 =0

Ответ: 15; -1

Теорема Виета aх² + bх + c = 0 x1 + x2 = — b/a x1· x2 = c/a

По праву достойна в стихах быть воспета

О свойствах корней теорема Виета.

Что лучше, скажи, постоянства такого:

Умножишь ты корни – и дробь уж готова?

В числителе с , в знаменателе а.

А сумма корней тоже дроби равна.

Хоть с минусом дробь, что за беда.

В числителе в, b знаменателе а.

5. Приёмы устного решения квадратного уравнения.

1. Свойства коэффициентов квадратного уравнения:

Если в квадратном уравнении ах² + bх + с = 0 сумма коэффициентов а + в + с = 0, то х1 = 1; х2 = с/а.

Пример: 5х² — 8х +3 = 0

Так как 5 – 8 + 3 = 0, то х1 = 1; х2 = 0,6

Если в квадратном уравнении ах² + bх + с = 0 выполняется равенство а + с = в, то х1 = -1; х2 = — с/а.

Пример: 5х² + 8х +3 = 0

Так как 5 + 3 = 8, то х1 = — 1; х2 = — 0,6

Пример. Решить уравнения с большими коэффициентами:

5. 2 Приём «Переброски»:

Пример1:

2х² — 11х +5=0 х²-11х+10=0

делим на 2

Пример2:

6х² — 7х – 3 = 0 х² — 7х -18 = 0

делим на 6

Ответ:1,5; -1/3

6. Комплексные числа.

Решение многих задач физики и техники приводит к квадратным уравнениям с отрицательным дискриминантом. Эти уравнения не имеют решения в области действительных чисел. Но решение многих таких задач имеет вполне определенный физический смысл. Значение величин, получающихся в результате решения указанных уравнений, назвали комплексными числами. Комплексные числа широко использовал отец русской авиации Н. Е. Жуковский (1847 – 1921) при разработке теории крыла, автором которой он является. Комплексные числа и функции от комплексного переменного находят применение во многих вопросах науки и техники.

Цель настоящей работы знакомство с историей появления комплексных чисел, с действиями с комплексными числами, решение уравнений с комплексным переменным.

7. Действия с комплексными числами.

Рассмотрим решение квадратного уравнения х²+1=0. Отсюда х²=-1. Число х, квадрат которого равен –1, называется мнимой единицей и обозначается i. Таким образом i²=-1, откуда i=. Решение квадратного уравнения, например, х² –8х+25=0, можно записать следующим образом: х=4=4=4=

=43=43i.

Числа вида 4+3i и 4-3i называют комплексными числами. В общем виде комплексное число записывается а+bi, где a и b- действительные числа, а i – мнимая единица. Число а называется действительной частью комплексного числа, bi-мнимой частью этого числа, b- коэффициентом мнимой части комплексного числа.

Сложение комплексных чисел. Суммой двух комплексных чисел z1=a+bi и z2=c+di называется комплексное число z=(a+c)+(b+d)i. Числа a+bi и a-bi называются сопряженными. Их сумма равна действительному числу 2а, (а+bi)+(а-bi)=2а. Числа а+bi и -a-bi называются противоположными. Их сумма равна нулю. Комплексные числа равны, если равны их действительные части и коэффициенты мнимых частей: а+bi=c+di, если a=c, b=d. Комплексное число равно нулю тогда, когда его действительная часть и коэффициент мнимой части равны нулю, т. е. z=a+bi=0, если a=0,b=0. Действительные числа являются частным случаем комплексных чисел. Если b=0, то a+bi=a — действительное число. Если а=0, b0, то a+bi=bi – чисто мнимое число. Для комплексных чисел справедливы переместительный и сочетательный законы сложения. Их справедливость следует из того, что сложение комплексных чисел по существу сводится к сложению действительных частей и коэффициентов мнимых частей, а они являются действительными числами, для которых справедливы указанные законы.

Вычитание комплексных чисел определяется как действие, обратное сложению: разностью двух комплексных чисел a+ bi и c+di называется комплексное число х+уi, которое в сумме с вычитаемым дает уменьшаемое. Отсюда, исходя из определения сложения и равенства комплексных чисел получим два уравнения, из которых найдем, что х=а-с, у=b-d. Значит, (а+bi)-(c+di)=(a-c)+ (b-d)i.

Произведение комплексных чисел z1=a+bi и z2=c+di называется комплексное число z = (ac-bd)+(ad+bc)i, z1z2= (a+bi)(c+di)=(ac-bd)+(ad+bc)i. Легко проверить, что умножение комплексных чисел можно выполнять как умножение многочленов с заменой i2 на –1. Для умножения комплексных чисел также справедливы переместительный и сочетательный законы, а также распределительный закон умножения по отношению к сложению.

Из определения умножения получим, что произведение сопряженных комплексных чисел равно действительному числу: (a +bi)(a-bi)=a2+b2

Деление комплексных чисел, кроме деления на нуль, определяется как действие, обратное умножению. Конкретное правило деления получим, записав частное в виде дроби и умножив числитель и знаменатель этой дроби на число, сопряженное со знаменателем:(a+bi):(c+di) =. = = +i.

Степень числа i является периодической функцией показателя с периодом 4. Действительно, i2 =-1, i3 =-i, i4 = 1, i4n = (i4)n = 1n = 1, i4n+1=i, i4n+2 =-1, i4n+3 =-i.

Квадратное уравнение с комплексным неизвестным.

Рассмотрим сначала простейшее квадратное уравнение z2=a, где а — заданное число, z — неизвестное.

На множестве действительных чисел это уравнение:

1) имеет один корень z=0, если а=0;

2) имеет два действительных корня z1,2=, если а>0;

3) не имеет действительных корней, если а

На множестве комплексных чисел это уравнение всегда имеет корень.

Задача 1. Найти комплексные корни уравнения z2=a, если:

1) а = -1; 2) а = -25; 3) а = -3.

1)z2 = -1. Так как i2 = -1, то это уравнение можно записать в виде z2 = i2, или z2- i2 = 0. Отсюда, раскладывая левую часть на множители, получаем

(z-i)(z+i)=0, z1=i, z2=-i.

Ответ. z1,2=i.

2) z2 = -25. Учитывая, что i2 = -1,преобразуем это уравнение: z2=(-1)25, z2=i252, z2-52i=0, (z-5i)(z+5i)=0, откуда z1=5i, z2=-5i.

Ответ. z 1,2=5i.

3) z2=-3, z2=i2()2, z2-()2i2=0, (z-i)(z+i)=0, z1 =i, z 2=-i.

Ответ. z1,2=i.

Вообще уравнение z2=a, где а

Используя равенство i2=-1, квадратные корни из отрицательных чисел принято записывать так: =i, =i=2i, = i.

Итак, определен для любого действительного числа а (положительного, отрицательного и нуля). Поэтому любое квадратное уравнение az2+bz+c=0, где а,b,с- действительные числа, а0, имеет корни. Эти корни находятся по известной формуле:

Задача 2. Решить уравнение z2-4z+13=0. По формуле находим: z1,2= = = = =23i.

Заметим, что найденные в этой задаче корни являются сопряженными: z1=2+3i и z2=2-3i. Найдем сумму и произведение этих корней: z1+z2=(2+3i)+(2-3i)=4, z1z2=(2+3i)(2-3i)=13.

Число 4 — это 2-й коэффициент уравнения z2-4z+13=0, взятый с противоположным знаком, а число 13 — свободный член, то есть в этом случае справедлива теорема Виета. Она справедлива для любого квадратного уравнения: если z1 и z2 — корни уравнения az2+bz+c=0, z1+z2= -, z1z2=.

Задача 3. Составить приведенное квадратное уравнение с действительными коэффициентами, имеющее корень z1=-1-2i.

Второй корень z2 уравнения является числом, сопряженным с данным корнем z1, то есть z2=-1+2i. По теореме Виета находим

P=-(z1+z2)=2, q=z1z2=5. Ответ z²+2z+5=0.

8. Заключение.

В данной работе рассмотрены способы решения квадратных уравнений. А также рассмотрены приёмы решения квадратных уравнений, которые позволяют очень быстро и рационально решать квадратные уравнения.

Данные приёмы решения заслуживают внимания, поскольку они не отражены в школьных учебниках математики. Овладение данными приёмами поможет мне экономить время и эффективно решать уравнения. Потребность в быстром решении обусловлена применением тестовой системы вступительных экзаменов.

В настоящем работе дано понятие комплексных чисел, история их возникновения. Рассмотрены примеры действий с комплексными числами. Приведены примеры решения уравнений с комплексным переменным, что позволяет решить любые квадратные уравнения, даже с отрицательным дискриминантом.

Таким образом, цели работы — рассмотреть способы решения квадратных уравнений: метод выделения полного квадрата, решение квадратных уравнений по формуле, теорема Виета; изучить приёмы устного решения квадратного уравнения; рассмотреть решение квадратного уравнения с комплексными неизвестными — достигнуты.

www.hintfox.com

Формулы корней квадратных уравнений | Учеба-Легко.РФ

 

Пусть дано квадратное уравнение ах² + bх + с = 0. 
Применим к квадратному трехчлену ах² + bх + с те же преобразования, которые мы выполняли в § 13, когда доказывали теорему о том, что графиком функции у = ах² + bх + с является парабола. 
Имеем

Обычно выражение b² — 4ас обозначают буквой D и называют дискриминантом квадратного уравнения ах² + bх + с = 0 (или дискриминантом квадратного трехчлена ах + bх + с).

Таким образом

Значит, квадратное уравнение ах² + их + с = О можно переписать в виде

Любое квадратное уравнение можно преобразовать к виду (1), удобному, как мы сейчас убедимся, для того, чтобы определять число корней квадратного уравнения и находить эти корни.

Доказательство. Если D < 0, то правая часть уравнения (1) — отрицательное число; в то же время левая часть уравнения (1) при любых значениях х принимает неотрицательные значения. Значит, нет ни одного значения х, которое удовлетворяло бы уравнению (1), а потому уравнение (1) не имеет корней.

Пример 1. Решить уравнение 2x² + 4х + 7 = 0. 
Решение. Здесь а = 2, b = 4, с = 7, 
D = b²-4ac = 4². 4. 2. 7 = 16-56 = -40. 
Так как D < 0, то по теореме 1 данное квадратное уравнение не имеет корней.

Доказательство. Если D = 0, то уравнение (1) принимает вид

   — единственный корень уравнения.

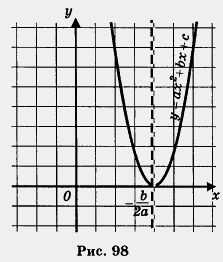
Замечание 1. Помните ли вы, что х = —  — абсцисса вершины параболы, которая служит графиком функции у = ах² + их + с? Почему именно это 
значение оказалось единственным корнем квадратного уравнения ах² + их + с — 0? «Ларчик» открывается просто: если D — 0, то, как мы установили ранее,

Графиком же функции  является парабола с вершиной в точке  (см., например, рис. 98). Значит, абсцисса вершины параболы и единственный корень квадратного уравнения при D = 0 — одно и то же число.

 

Пример 2. Решить уравнение 4x² — 20x + 25 = 0. 
Решение. Здесь а = 4, b = -20, с = 25, D = b² — 4ас = (-20)² — 4 • 4 • 25 = 400 — 400 = 0.

Так как D = 0, то по теореме 2 данное квадратное уравнение имеет один корень. Этот корень находится по формуле

Ответ: 2,5. 

Замечание 2. Обратите внимание, что 4х² — 20х +25 — полный квадрат: 4х² — 20х + 25 = (2х — 5)². 
Если бы мы это заметили сразу, то решили бы уравнение так: (2х — 5)² = 0, значит, 2х — 5 = 0, откуда получаем х = 2,5. Вообще, если D = 0, то

ах² + bх + с =  — это мы отметили ранее в замечании 1. 
Если D > 0, то квадратное уравнение ах² + bх +  с = 0 имеет два корня, которые находятся по формулам

 

Доказательство. Перепишем квадратное уравнение ах² + ^Ьх + с = 0 в виде (1)

Положим 
По условию, D > 0, значит, правая часть уравнения положительное число. Тогда из уравнения (2) получаем, что

Итак, заданное квадратное уравнение имеет два корня:

Замечание 3. В математике довольно редко бывает так, чтобы введенный термин не имел, образно выражаясь, житейской подоплеки. Возьмем новое 
понятие — дискриминант. Вспомните слово «дискриминация». Что оно означает? Оно означает унижение одних и возвышение других, т.е. различное отноше- 
ние к различным пюдям. Оба слова (и дискриминант, и дискриминация) происходят от латинского discriminans — «различающий». Дискриминант различает квадратные уравнения по числу корней.

Пример 3. Решить уравнение Зх² + 8х — 11 = 0. 
Решение. Здесь а = 3, b = 8, с = — 11, 
D = b² — 4ас = 8² — 4 • 3 • (-11) = 64 + 132 = 196. 
Так как D > 0, то по теореме 3 данное квадратное уравнение имеет два корня. Эти корни находятся по формулам (3)

Фактически мы с вами выработали следующее правило:

Правило решения уравнения 
ах² + bх + с = 0

Это правило универсально, оно применимо как к полным, так и к неполным квадратным уравнениям. Однако неполные квадратные уравнения обычно по этому правилу не решают, их удобнее решать так, как мы это делали в предыдущем параграфе.

Пример 4. Решить уравнения:

а) х² + Зх — 5 = 0;            б) — 9x² + 6х — 1 = 0;            в) 2х²-х + 3,5 = 0.

Р е ш е н и е. а) Здесь а = 1, b = 3, с = — 5, 
D = b² — 4ас = З² — 4 • 1 • (- 5) = 9 + 20 = 29.

Так как D > 0, то данное квадратное уравнение имеет два корня. Эти корни находим по формулам (3)

б) Как показывает опыт, удобнее иметь дело с квадратными уравнениями, у которых старший коэффициент положителен. Поэтому сначала умножим обе части уравнения на -1, получим

9x² — 6x + 1 = 0. 
Здесь а = 9, b = -6, с = 1, D = b² — 4ас = 36 — 36 = 0. 
Так как D = 0, то данное квадратное уравнение имеет один корень. Этот корень находится по формуле х = — . Значит, 

Это уравнение можно было решить по-другому: так как 
9х² — 6x + 1 = (Зх — IJ, то получаем уравнение (Зх — I)² = 0, откуда находим Зх — 1 = 0, т. е. х = .

в) Здесь а = 2, b = — 1, с = 3,5, D = b² — 4ас = 1 — 4 • 2 • 3,5= 1 — 28 = — 27. Так как D < 0, то данное квадратное уравнение не имеет корней.

Математики — люди практичные, экономные. Зачем, говорят они, пользоваться таким длинным правилом решения квадратного уравнения, лучше сразу написать общую формулу:

Если окажется, что дискриминант D = b² — 4ас — отрицательное число, то записанная формула не имеет смысла (под знаком квадратного корня находится отрицательное число), значит, корней нет. Если же окажется, что дискриминант равен нулю, то получаем

т. е. один корень (говорят также, что квадратное уравнение в этом случае имеет два одинаковых корня:

Наконец, если окажется, что b² — 4ас > 0, то получаются два корня х₁и х₂, которые вычисляются по тем же формулам (3), что указаны выше.

Само число  в этом случае положительно (как всякий квадратный корень из положительного числа), а двойной знак перед ним означает, что в одном случае (при отыскании х₁ ) это положительное число прибавляется к числу — b, а в другом случае (при отыскании х₂) это положительное число вы-
читается из числа — b.

У вас есть свобода выбора. Хотите —- решайте квадратное уравнение подробно, используя сформулированное выше правило; хотите — запишите сразу формулу (4) и с ее помощью делайте необходимые выводы.

Пример 5. Решить уравнения: 

Решение, а) Конечно, можно использовать формулы (4) или (3), учитывая, что в данном случае  Но зачем выполнять действия с дробями, когда проще и, главное, приятнее иметь дело с целыми числами? Давайте освободимся от знаменателей. Для этого нужно умножить обе части уравнения на 12, т. е. на наименьший общий знаменатель дробей, служащих коэффициентами уравнения. Получим

откуда 8х² + 10x — 7 = 0.

А теперь воспользуемся формулой (4)

б) Мы снова имеем уравнение с дробными коэффициентами: а = 3, b = — 0,2, с = 2,77. Умножим обе части уравнения на 100, тогда получим уравнение с целыми коэффициентами: 
300x² — 20x + 277 = 0. 
Далее воспользуемся формулой (4):

Простая прикидка показывает, что дискриминант (подкоренное выражение) — отрицательное число. Значит, уравнение не имеет корней.

Пример 6. Решить уравнение 
Решение. Здесь, в отличие от предыдущего примера, предпочтительнее действовать по правилу, а не по сокращенной формуле (4).

Имеем а = 5, b = -, с = 1, D = b² — 4ас = (- ) ² — 4 • 5 • 1 = 60 — 20 = 40. Так как D > 0, то квадратное уравнение имеет два корня, которые будем искать по формулам (3)

Пример 7. Решить уравнение 
х² — (2р + 1)x +(р²+р-2) = 0

Решение. Это квадратное уравнение отличается от всех рассмотренных до сих пор квадратных уравнений тем, что в роли коэффициентов выступают не конкретные числа, а буквенные выражения. Такие уравнения называют уравнениями с буквенными коэффициентами или уравнениями с параметрами. В данном случае параметр (буква) р входит в состав второго коэффициента и свободного члена уравнения. 
Найдем дискриминант:

Пример 8. Решить уравнение рx² + (1 — р) х — 1 = 0. 
Решение. Это также уравнение с параметром р, но, в отличие от предыдущего примера, его нельзя сразу решать по формулам (4) или (3). Дело в том, что указанные формулы применимы к квадратным уравнениям, а про заданное уравнение мы этого пока сказать не можем. В самом деле, а вдруг р = 0? Тогда 
уравнение примет вид 0 • x²+ (1-0)x- 1 = 0, т. е. х — 1 = 0, откуда получаем х = 1. Вот если точно известно, что , то можно применять формулы корней квадратного уравнения:

uclg.ru