Базис (Лекция №17)
ЛИНЕЙНЫЕ ОПЕРАЦИИ НАД ВЕКТОРАМИ В КООРДИНАТНОЙ ФОРМЕ
- При умножении вектора на число все его координаты
умножаются на это число, т.е. если .
Действительно, используя свойства операций умножения вектора на число и сложении векторов будем иметь
.
При сложении векторов их соответствующие координаты складываются, т.е. если .
Доказательство очевидно.
Условие коллинеарности двух векторов в коорднинатной форме.
Два вектора коллинеарны тогда и только тогда, когда их соответствующие координаты пропорциональны. Т.е. если , то.
Доказательство:
- Пусть вектор коллинеарен , тогда найдется λ такое, что . Значит, и . Поскольку разложение вектора по элементам базиса единственно, то .
- Пусть выполняется равенство . Обозначим коэффициент пропорциональности через λ. Тогда и, следовательно,
, т.е. . Теорема доказана.
- Даны векторы . Найти вектор .
.
- Найти координаты вектора в базисе, образованном
векторами , , .
Обозначим координаты вектора в новом базисе . Тогда в новом базисе будем иметь:

Итак, .
Рассмотрим две произвольные точки и . Найдем координаты вектора .
Очевидно, что . Но по определению координат вектора и . Следовательно,
Таким образом, чтобы найти координаты вектора , нужно из координат его конца вычесть соответствующие координаты начала.
Примеры.
- Заданы точкиA(1; -2; 3), B(2; 0; -1). Найти вектор .
- Даны A(-2; 3; 1), В(-1; 2; 0), С(0; 1; 1). Найти .
- Известно, что. Найти координаты точки D, если
А(3; -4; -1), В(-4; 4; 1), С(-3; -5; 4).
Пусть тогда
. С другой стороны . Следовательно, должно выполняться равенство (x+3; y+5; z-4)=(5;10;-8). Отсюда
x=2, y=5, z=-4, т.е. точка D имеет координаты D(2; 5; -4).
- Даны векторы . Найти вектор .
СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ И ЕГО СВОЙСТВА
Мы рассмотрели умножение вектора на число. Однако во многих задачах механики и физики встречается операция умножения вектора на вектор. Но при этом результат может быть как числом, так и вектором. Поэтому рассматривают два вида умножения векторов: скалярное и векторное.
Пусть даны два вектора и , угол между, которыми равен .
Скалярным произведением векторов и называется число, равное произведению длин этих векторов на косинус угла между ними. Скалярное произведение обозначается . Итак, .
Если один из векторов нулевой, то угол не определен, и скалярное произведение по определения считается равным нулю.
Рассмотрим свойства скалярного произведения.
- Скалярное произведение двух
векторов подчиняется коммутативному закону, т.е. для любых векторов и .
Очевидно, из определения скалярного произведения:
.
- Для любого числа λ и любых векторов имеем:
.
Доказательство. Ограничимся случаем, когда λ > 0. В этом случае угол между векторами и совпадает с углом между векторами и , .
Поэтому . Откуда
Аналогично доказывается и равенство .
Случай λ <0 рассмотреть самостоятельно.
- Для любых векторов выполняется равенство . Доказательство. Используя определение скалярного произведения и свойства проекций вектора на ось, будем иметь
- Для любого вектора выполняется
соотношение.
Действительно, так как , то .
Из этого свойства в частности следует .
- Скалярное произведение двух
векторов равно нулю тогда и только тогда,когда равен нулю один из сомножителей или векторы перпендикулярны.
Это свойство очевидно из определения скалярного произведения.
Таким образом, необходимым и достаточным условием ортогональности двух векторов является равенство нулю их скалярного произведения.
Пример. Дан вектор . Известно, что
Найти .
Имеем, т.е. .
Найдем:
Следовательно, .
Рассмотрим, как находится скалярное произведение векторов, если они заданы в координатной форме. Пусть даны два вектора и .
Рассмотрим сначала все возможные скалярные произведения векторов друг на друга.
Поэтому
Итак, скалярное произведение векторов равно сумме произведений соответствующих координат: .
Это соотношение позволяет вычислить длину вектора через его координаты:
.
Далее из определения скалярного произведения находим
.
Выражая скалярное произведение и длины векторов через их координаты,получим формулу для нахождения косинуса угла между векторами
.
Условие ортогональности двух векторов:
или .
Т.о., для того чтобы два вектора были перпендикулярны необходимо и достаточно, чтобы сумма произведений соответствующих координат этих векторов была равна нулю.
Примеры.
- Пусть А(-1; 1; 0), B(3; 1; -2), . Найти:
- ;
- и ;
- .
- .
- .
- .
- Найти в , если известны координаты его вершин A(1; 5; 6),
B(5; 3; 10), C(2; 1; 14).
- При каком значении m векторы и перпендикулярны?
Условие ортогональности двух векторов .
. Следовательно, m = 15.
ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ И ЕГО СВОЙСТВА
Введем сначала понятие ориентации тройки векторов.
Пусть даны три некомпланарных вектора с общим началом, перечисленных в определенном порядке: первый – , второй – , третий – .
Тройка некомпланарных векторов называется правоориентированной
или просто правой, если из конца
третьего вектора кратчайший поворот от первого ко второму виден против часовой
стрелки. В противном случае тройку векторов называют
Векторным произведением векторов и называется новый вектор , удовлетворяющий условиям:
- Длина вектора равна площади параллелограмма, построенного на векторах и .
- Вектор перпендикулярен плоскости этого параллелограмма.
- Он направлен так, что векторы и образуют правую тройку векторов.
Векторное произведение векторов и обозначается символом . Если хотя бы один из сомножителей равен нулю, то векторное произведение по определению считают равным нулю
Векторное произведение обладает следующими свойствами:
- Из определения следует, что
длина векторного произведения численно равна площади параллелограмма,
построенного на векторах, и, следовательно, находится по формуле:
.
Таким образом, и .
- При перестановке
сомножителей векторное произведение меняет свой знак .
Действительно из определения векторного произведения следует, что векторы и имеют одинаковые модули, расположены на одной прямой, но направлены в противоположные стороны. Поэтому, векторы и являются противоположными векторами и поэтому .
- Скалярный множитель можно
выносить за знак векторного произведения, т.е. для
любого числа λ и любых векторов
.
Доказательство этого свойства непосредственно следует из определения векторного произведения. Докажем для λ > 0. В этом случае . Тогда по определению векторного произведения
Вектор перпендикулярен векторам и . Вектор также векторам и , т.к. векторы и , и лежат в одной плоскости. Следовательно, векторы и коллинеарны. Очевидно, что направления их также совпадают. Т. к. , и следовательно, , то .
Поэтому .
Аналогично проводится доказательство для случая λ < 0.
- Для любых векторов имеет место
равенство
.
Примем без доказательства.
- Векторное произведение двух
векторов равно нулевому вектору тогда и только тогда, когда один из
сомножителей равен нулю или векторы коллинеарны.
Действительно, если векторы коллинеарны, то , т.е. площадь параллелограмма, построенного на данных векторах,равна нулю.
Таким образом, для того чтобы два ненулевых вектора были коллинеарны, необходимо и достаточно, чтобы их векторное произведение равнялось нулевому вектору.
В частности .
Примеры.
- Раскрыть скобки
.
- Найти площадь треугольника,
построенного на векторах и , если известно, что и .
.
Найдем ..
Можно показать, что если и , то координаты векторного произведения векторов и находятся по формуле:
.
Примеры.
- Найти векторное произведение векторов и .
.
- Найти площадь , если A(2; 3; 1), B(-1; -2; 0), C(-3; 0; 1).
- Даны векторы . Найти параметры n, p, q если известно, что векторы и коллинеарны, а
векторы и ортогональны.
Так как векторы и коллинеарны, то . Векторы и ортогональны, поэтому . Итак, получили систему уравнений
toehelp.ru
I уровень
1.1.Даны векторыи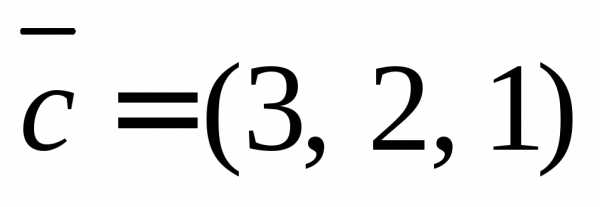
1)
2)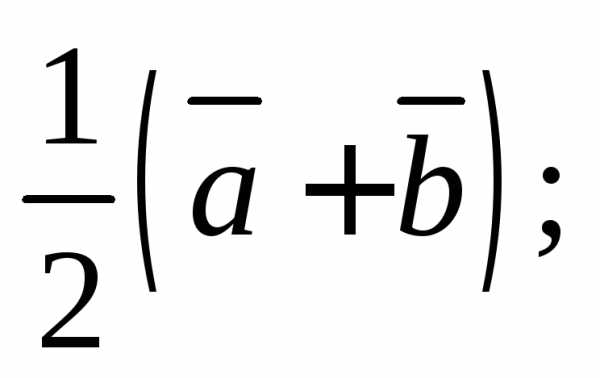 3)
3)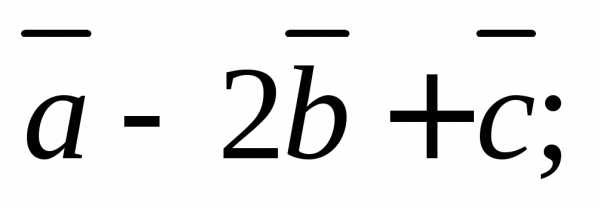 4)
4)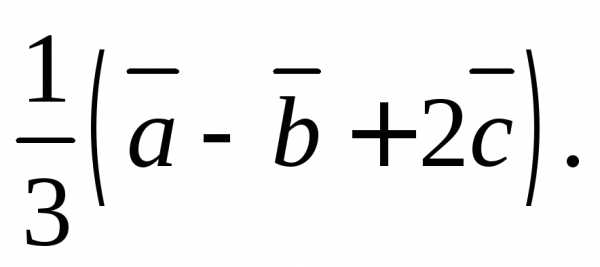
1.2. Найдите прямоугольные декартовы
координаты вектора 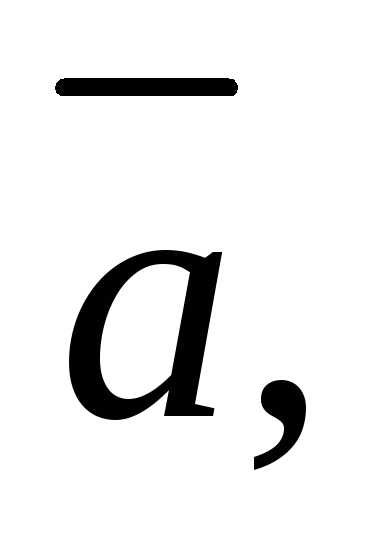 если известны углы
если известны углы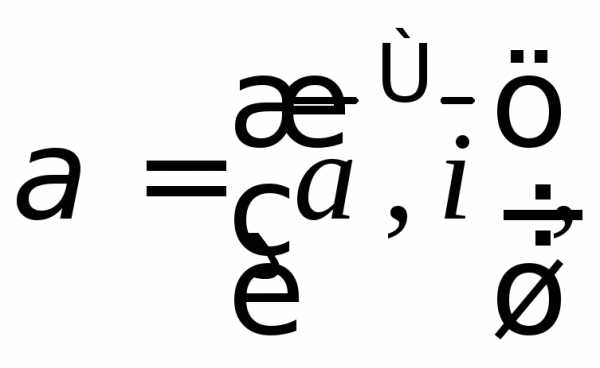
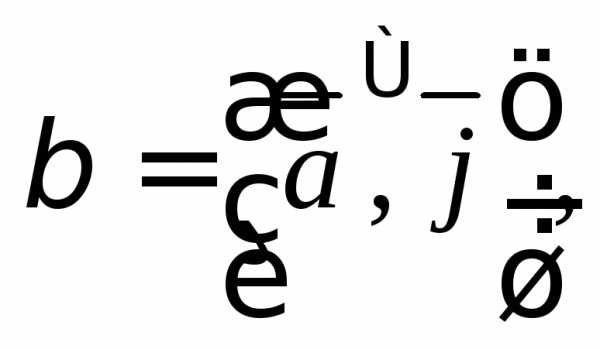
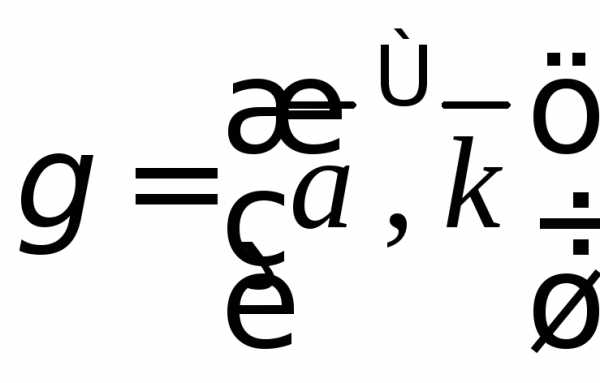 и на
и на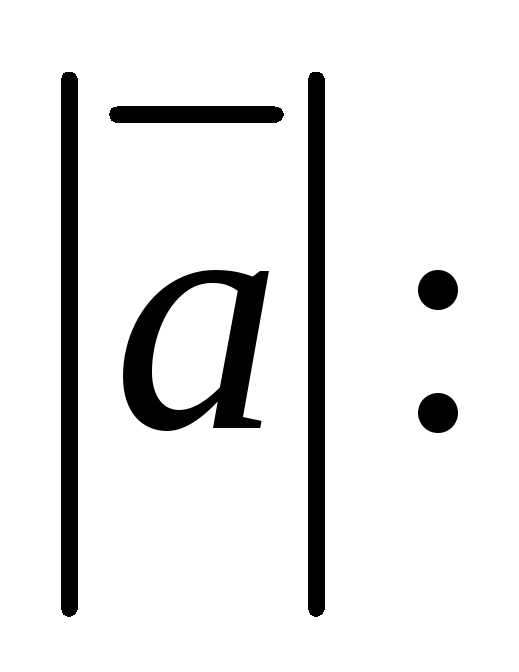
1) 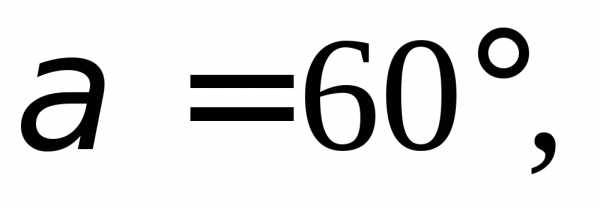
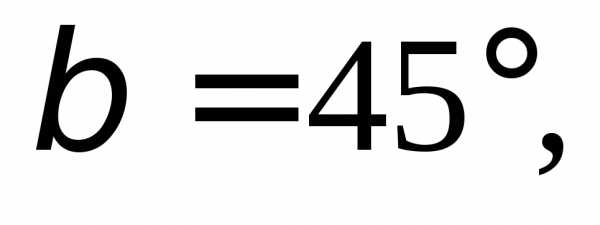
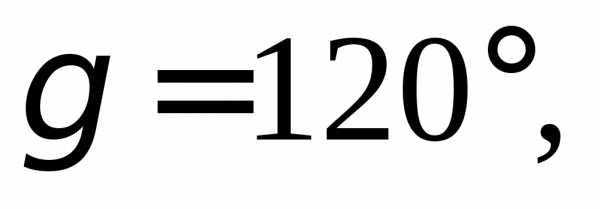
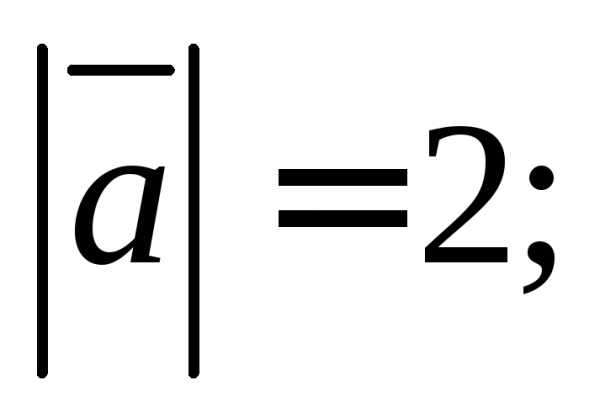
2) 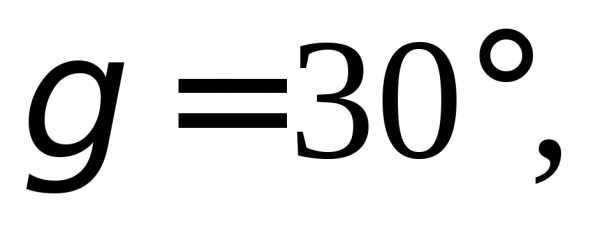
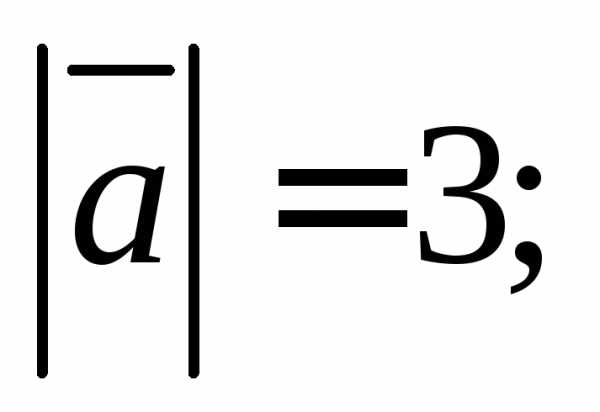
3) 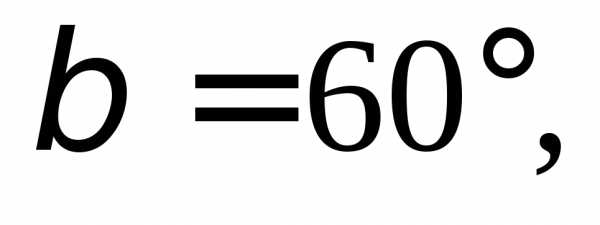
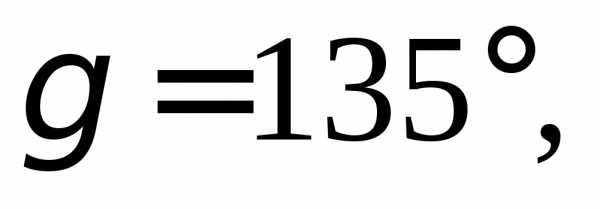
4) 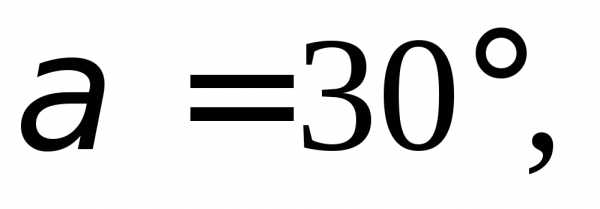
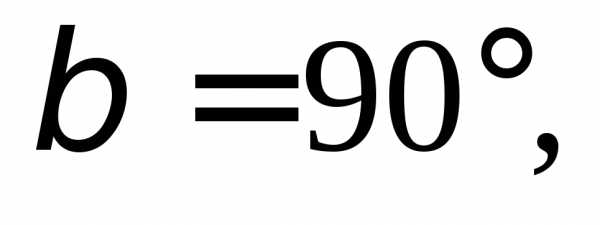
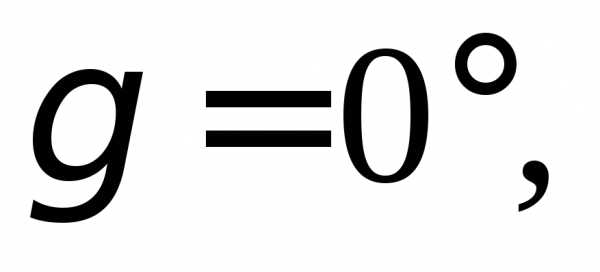
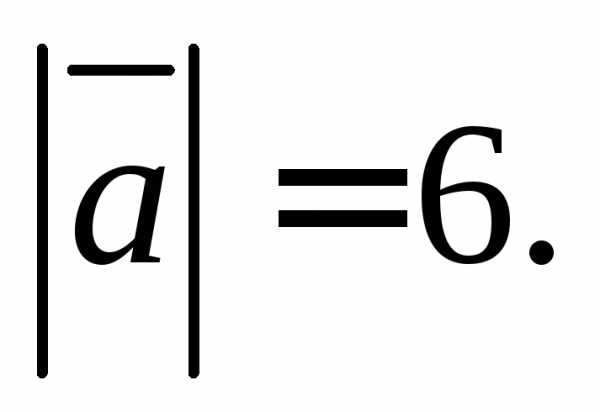
1.3.Заданы векторыиНайдите:
1) 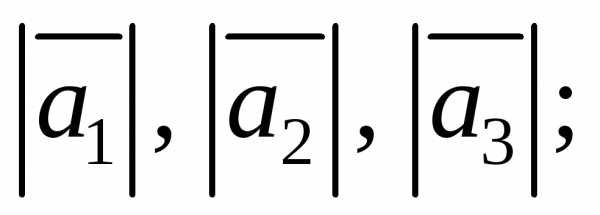 2)
2) 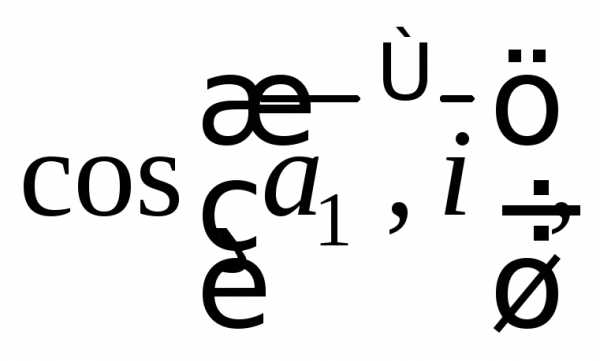
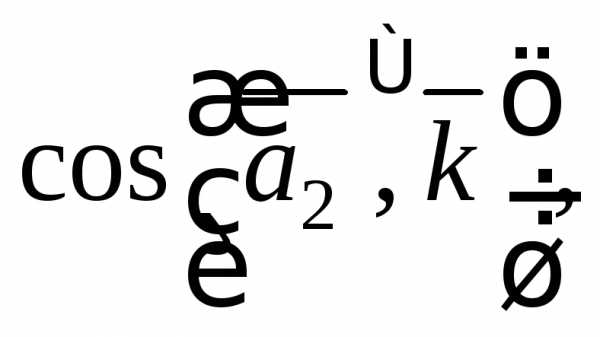
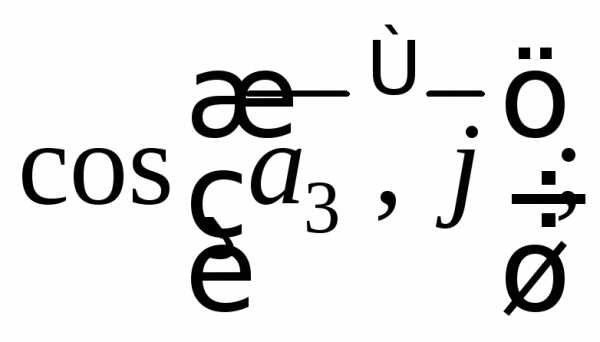
3)
координаты вектора 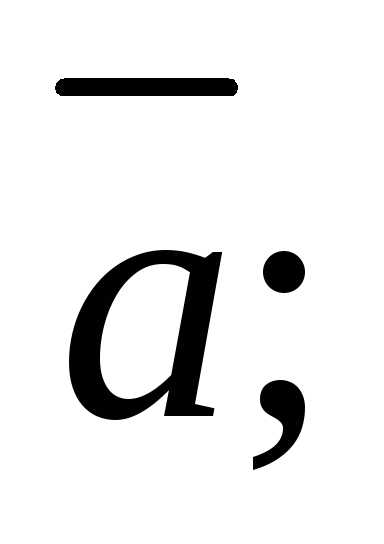 4)
4)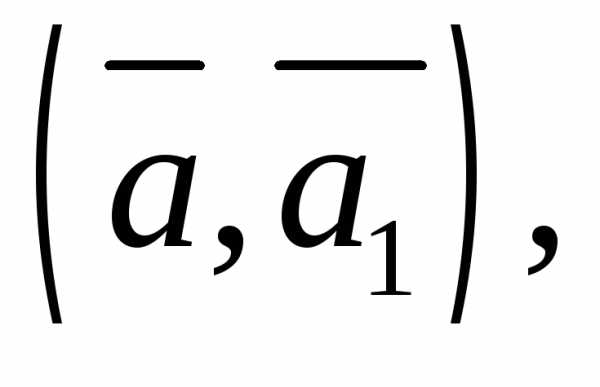
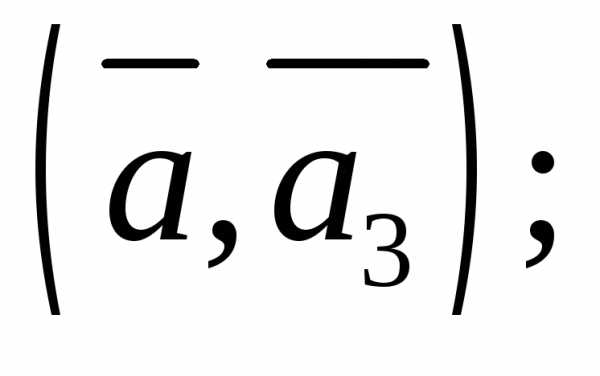
5) 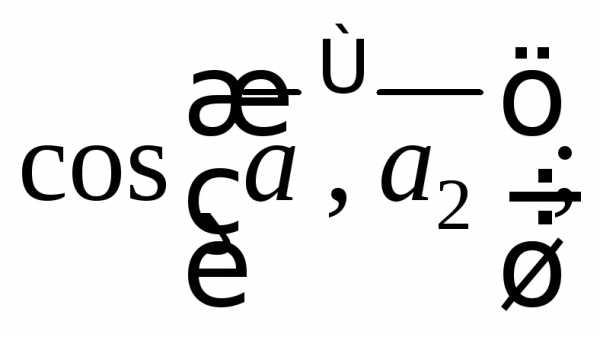 6)
6)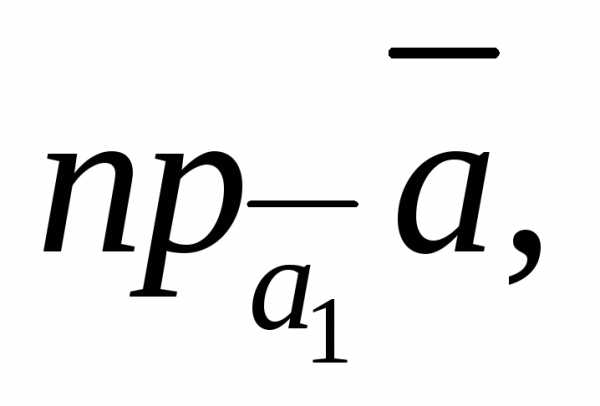
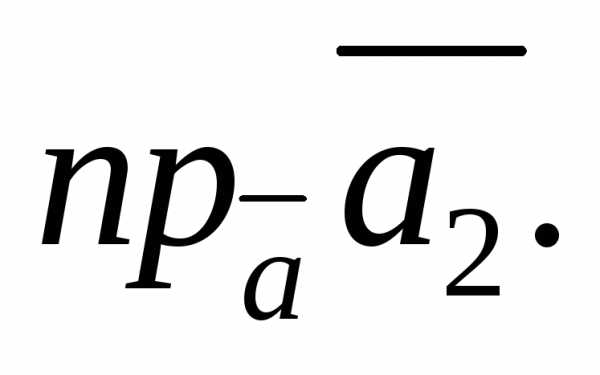
1.4.Найдите значение числаλ, при котором векторыиперпендикулярны.
1.5.Вычислите работу, произведенную силойпри перемещении ее точки приложения из начала в конец вектора
II уровень
2.1.Даны векторыПодберите числа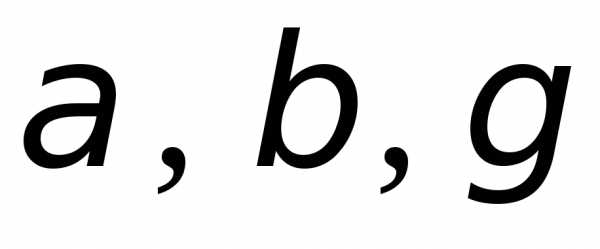 такие, чтобы векторыобразовали замкнутую ломаную.
такие, чтобы векторыобразовали замкнутую ломаную.
2.2.Покажите,
что векторы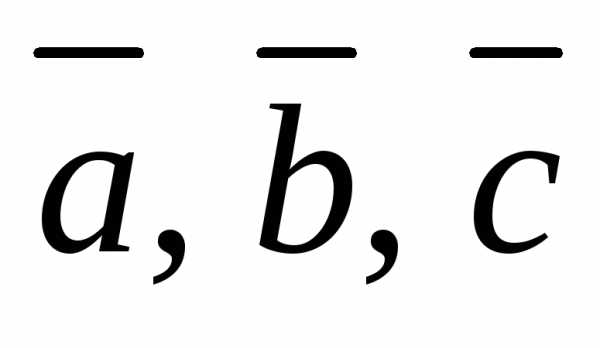 образовывают в пространстве базис и
найдите координаты вектора
образовывают в пространстве базис и
найдите координаты вектора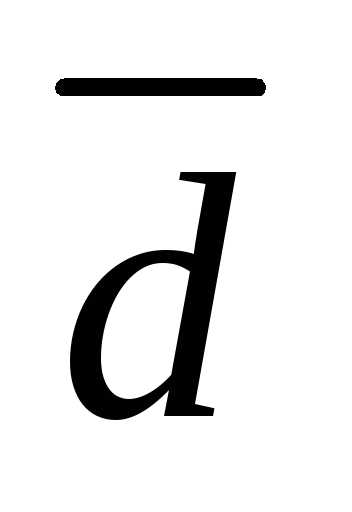 в этом базисе:
в этом базисе:
1)
2) 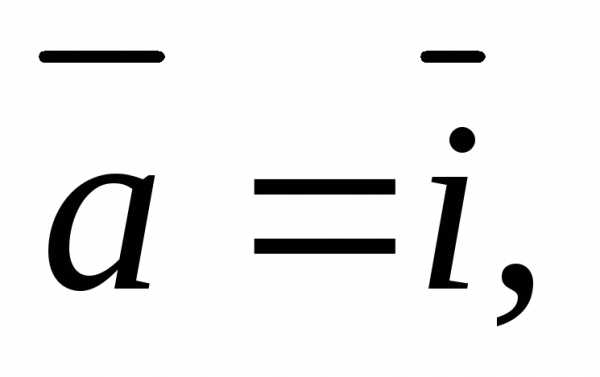
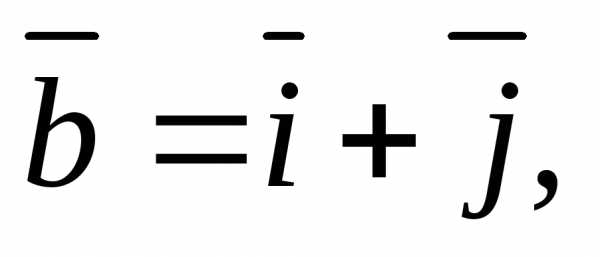
2.3.Найдите
вектор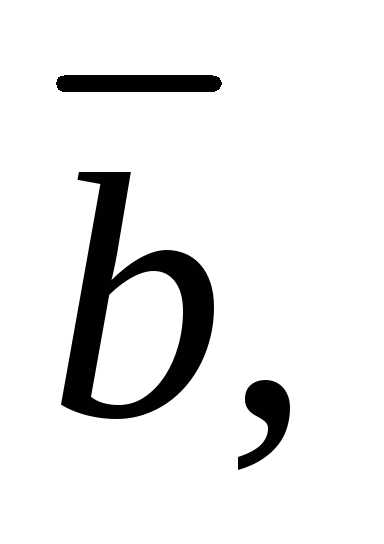 коллинеарный векторуобразующий с вектором
коллинеарный векторуобразующий с вектором острый угол и имеющий длину
острый угол и имеющий длину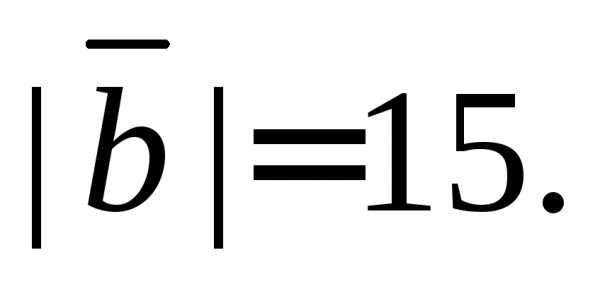
2.4.Найдите
вектор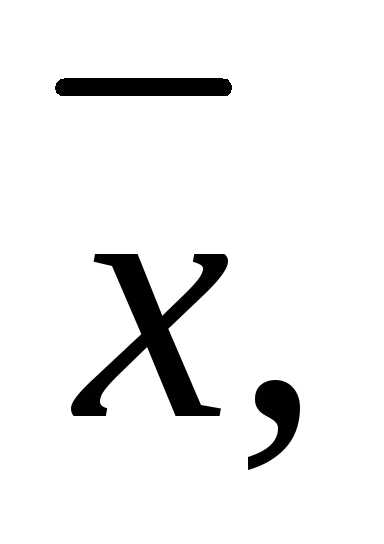 образующий со всеми тремя базисными
векторами
образующий со всеми тремя базисными
векторами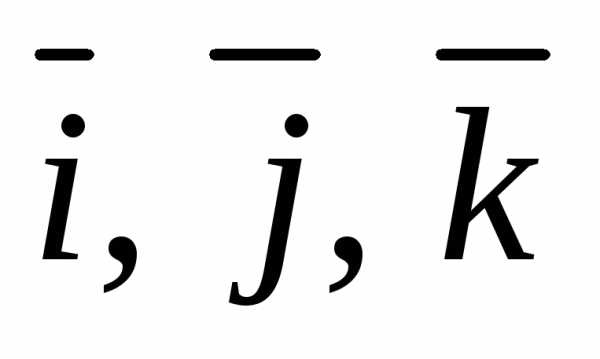 равные острые углы, если
равные острые углы, если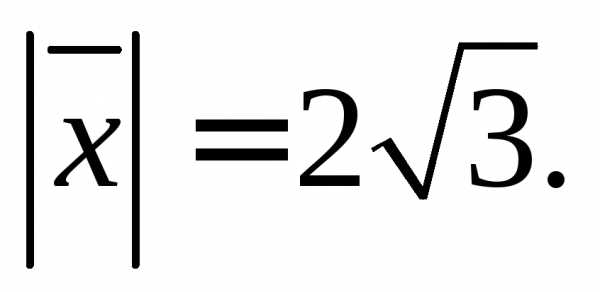
2.5.Найдите
вектор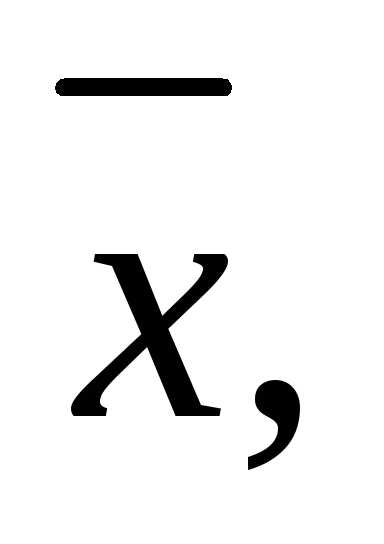 образующий с ортом
образующий с ортом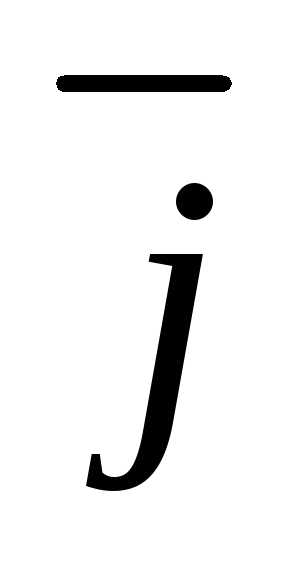 угол 60°, с ортом
угол 60°, с ортом – угол 120°, если
– угол 120°, если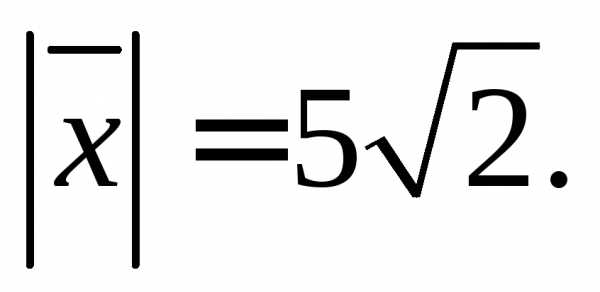
2.6.Вычислите
координаты вектора, длина которого
равна 8, зная, что с вектором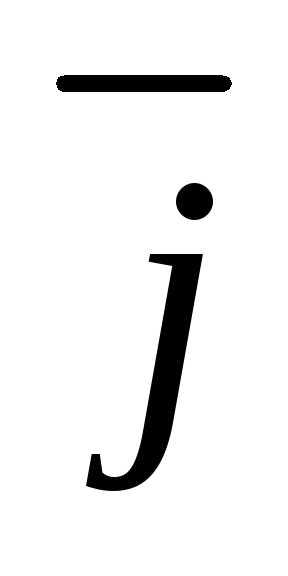 он образует угол 45°, с вектором
он образует угол 45°, с вектором – угол 60°, с вектором
– угол 60°, с вектором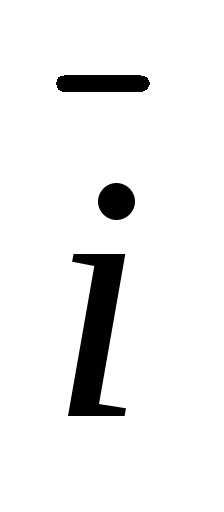 – тупой угол.
– тупой угол.
2.7.Определите координаты концов отрезка, который точкамиC(2, 0, 2) иD(5, –2, 0) разделен на три равные части.
2.8.Вычислите скалярное произведение векторов:
1) и
2) и
2.9.Найдите угол между векторами
1) и
2)
и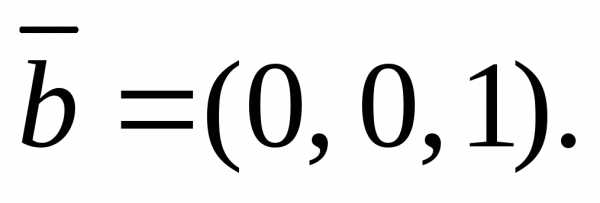
2.10. Для векторов
и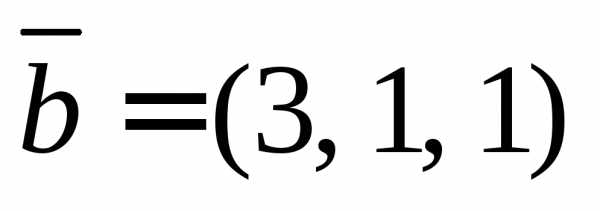 найдите вектор
найдите вектор удовлетворяющий условиям
удовлетворяющий условиям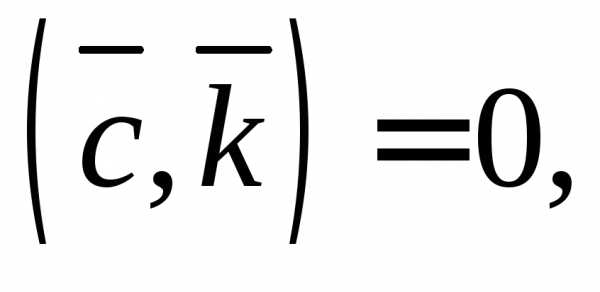
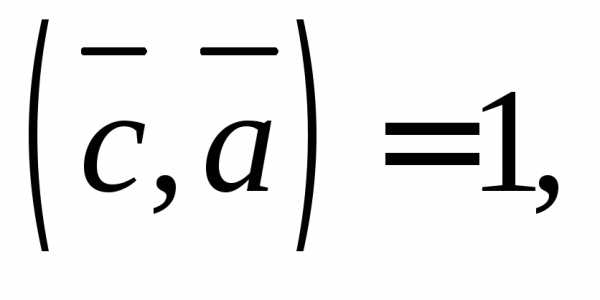
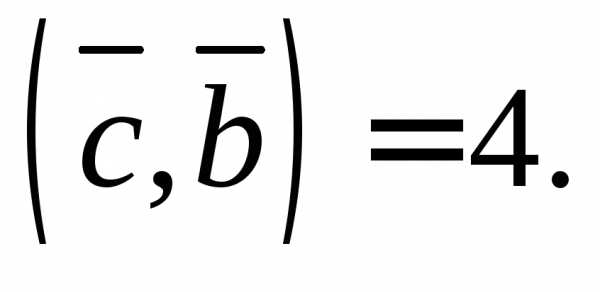
III уровень
3.1. Даны три некомпланарных вектора 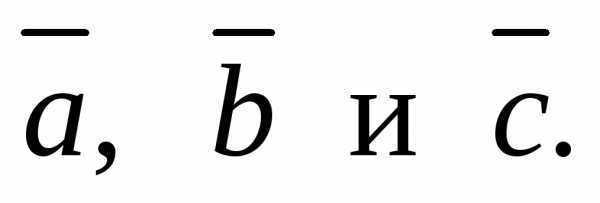 Вычислите значенияλ,
при которых векторы
Вычислите значенияλ,
при которых векторы  компланарны.
компланарны.
3.2.Даны три вершиныA(3, – 4, 7),B(–5, 3, 2) иC(1, 2, –3) параллелограммаABCD. Найдите его четвертую вершинуD.
3.3.Даны вершины треугольникаA(3, –1, 5),B(4, 2, –5) иС(–4, 0, 3). Найдите длину медианы, проведенной из вершиныA.
3.4.Даны вершиныA(1, –1, –3),B(2, 1, –2) иC(–5, 2, –6) треугольникаABC. Вычислите длину биссектрисы его внутреннего угла при вершинеA.
3.5. Треугольник задан координатами своих вершин A(3, –2 1), B(3, 1, 5) и C(4, 0, 3). Вычислите расстояние от начала координат до точки пересечения медиан этого треугольника.
3.6. В вершинах треугольника A(1, –1, 2), B(0, 4, 2) и C(2, –1, 1)сосредоточены массы 1, 2, 3 соответственно. Найдите координаты центра масс этой системы.
У
к а з а н и е. Из функции известно, что
для пары масс m1 и m2,
сосредоточенных в точках A и B,
центр находится в точке, делящей отрезок AB в отношении 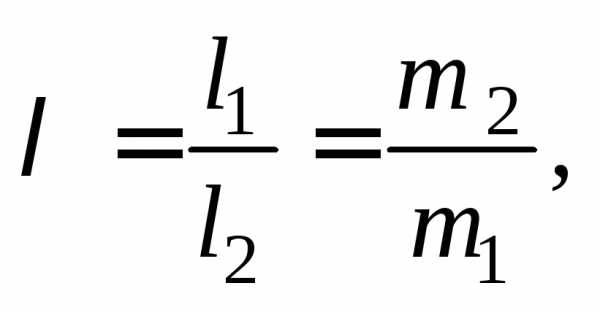 где
где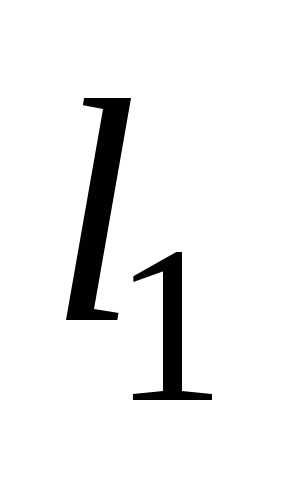 и
и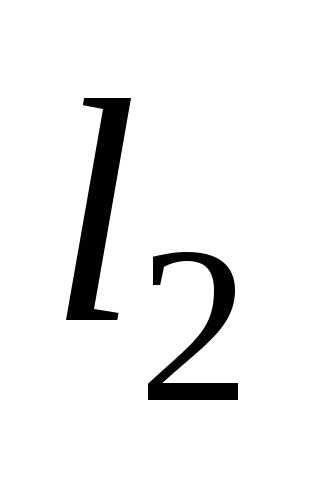 – расстояние от соответствующих точек
до их центра.
– расстояние от соответствующих точек
до их центра.
3.7.Даны два
вектора:иНайдите вектор компланарный векторам
компланарный векторам и
и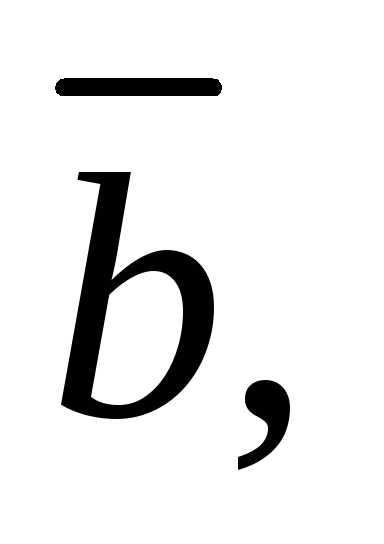 перпендикулярный вектору
перпендикулярный вектору равный ему по длине и образующий с
вектором
равный ему по длине и образующий с
вектором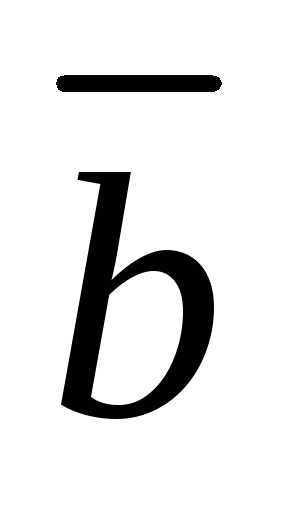 тупой угол.
тупой угол.
3.8.Векторы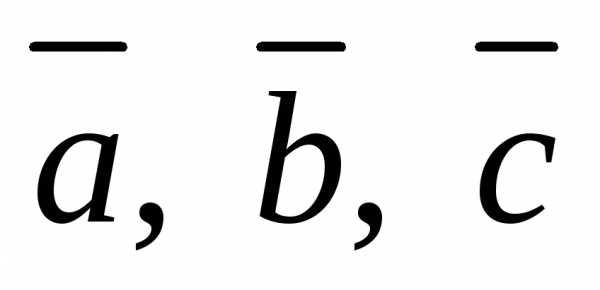 имеют равные длины и образуют попарно
равные углы. Найдите координаты вектора
имеют равные длины и образуют попарно
равные углы. Найдите координаты вектора если
если
3.9.Выразите
координаты вектора в базисечерез координаты в базисе
в базисечерез координаты в базисе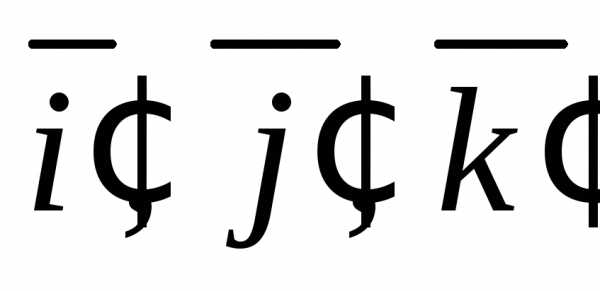 и наоборот, если
и наоборот, если
14.3. Векторное произведение
Векторным
произведением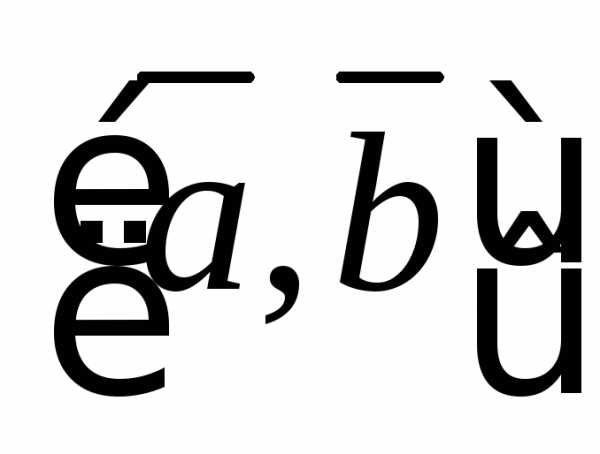 двух векторов
двух векторов и
и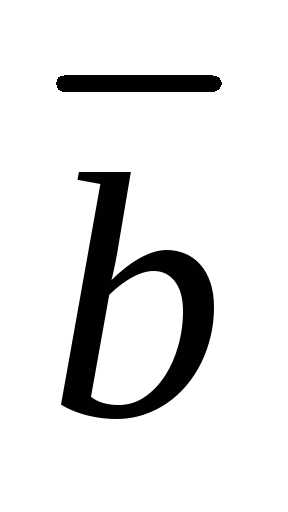 называется вектор, удовлетворяющий
следующим условиям:
называется вектор, удовлетворяющий
следующим условиям:
1)
2) 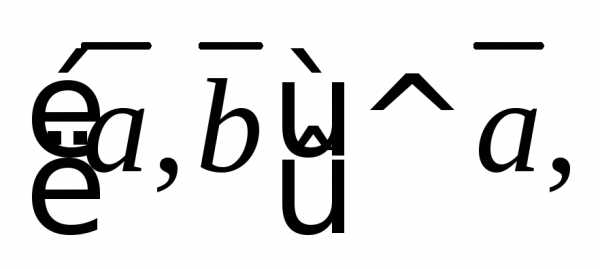
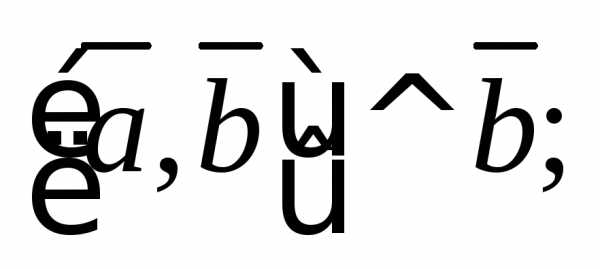
3) тройка векторов  – правая.
– правая.
Векторное
произведение обозначают также 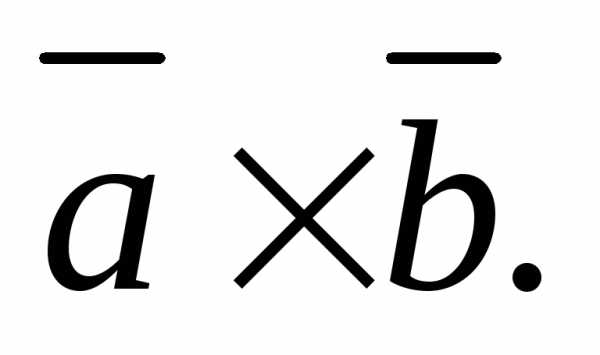
Если хотя бы один
из векторов  или
или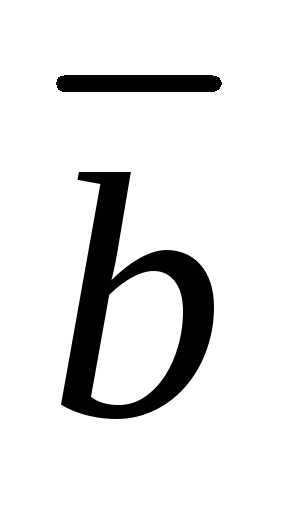 нулевой, то
нулевой, то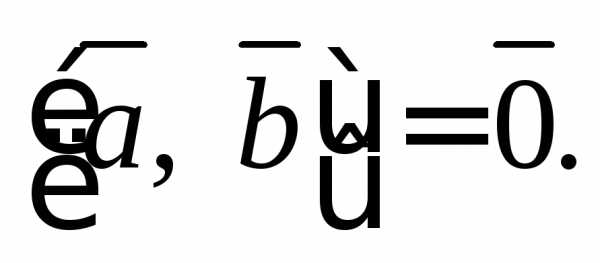
Геометрический
смыслвекторного произведения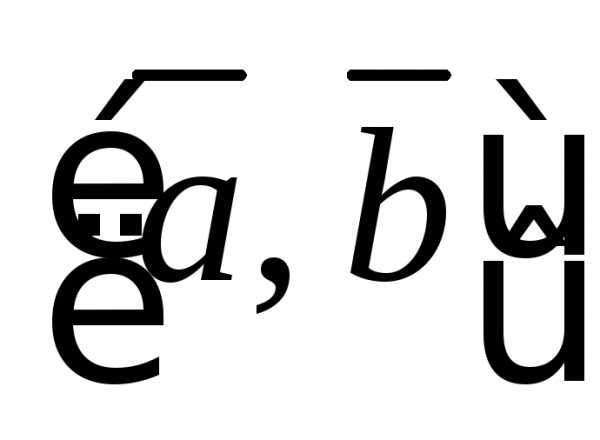 состоит в том, что длина этого вектора
численно равна площади параллелограмма,
который построен на векторах
состоит в том, что длина этого вектора
численно равна площади параллелограмма,
который построен на векторах и
и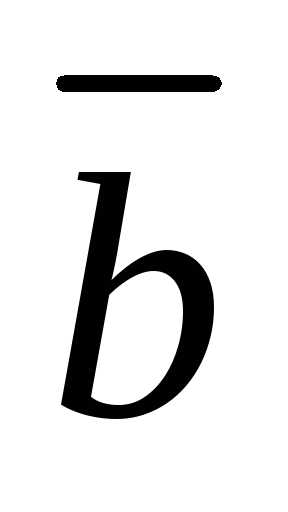 ,
приведенных к общему началу,
,
приведенных к общему началу,
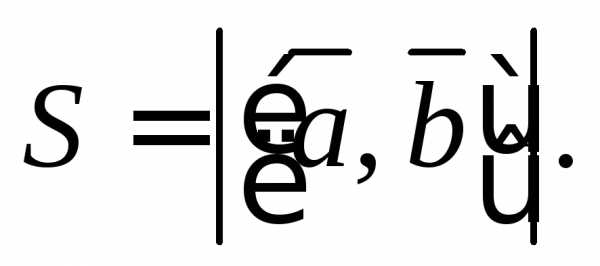
Физический
смыслвекторного произведения
состоит в том, что момент силы
силы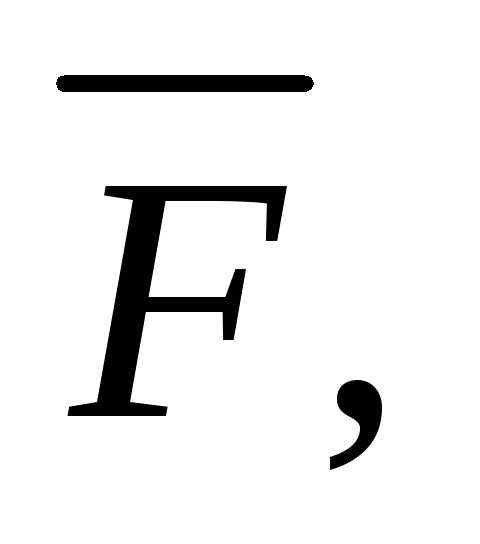 приложенной к точкеAотносительно точкиO,
есть векторное произведение векторов
приложенной к точкеAотносительно точкиO,
есть векторное произведение векторов и
и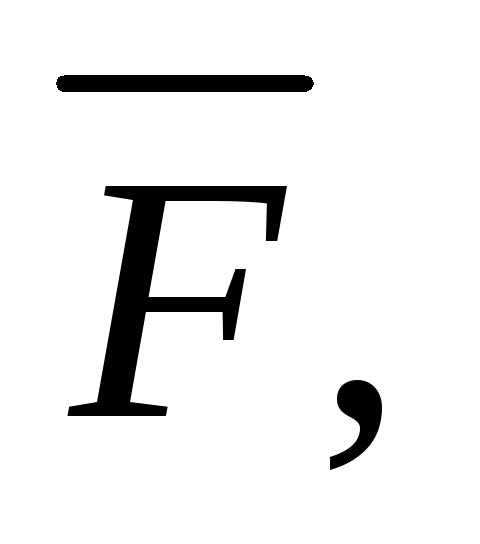 т. е.
т. е.
Свойства векторного произведения
1.
2.
3.
4. 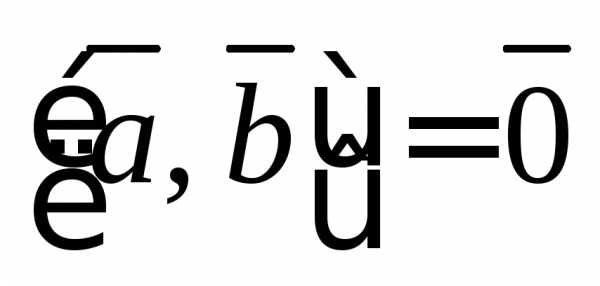 при
при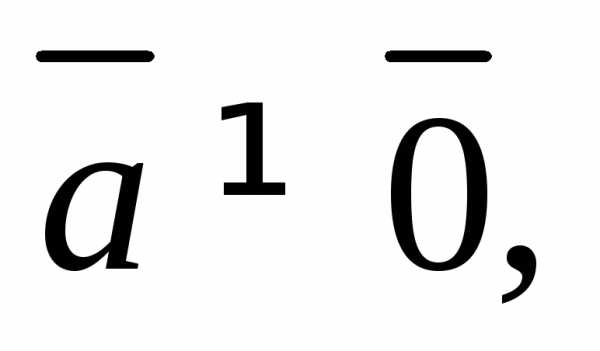
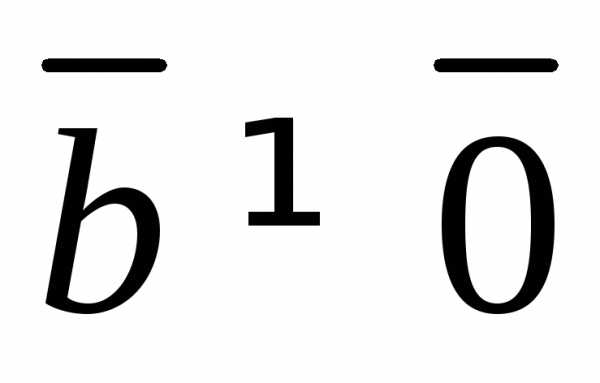 тогда и только тогда, когда векторы
тогда и только тогда, когда векторы и
и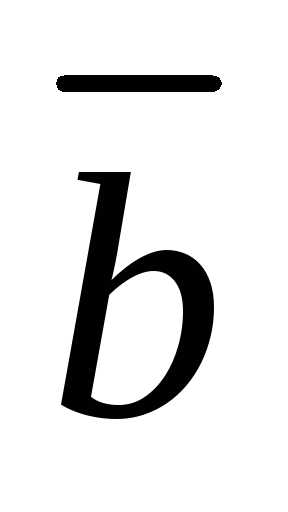 коллинеарны.
коллинеарны.
Если векторы  и
и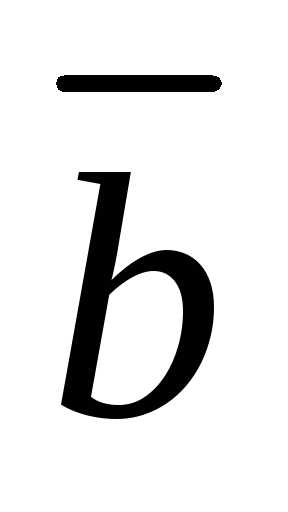 заданы в ортонормированном базисе иито
заданы в ортонормированном базисе иито
Последнюю формулу удобно записать в виде формального определителя третьего порядка
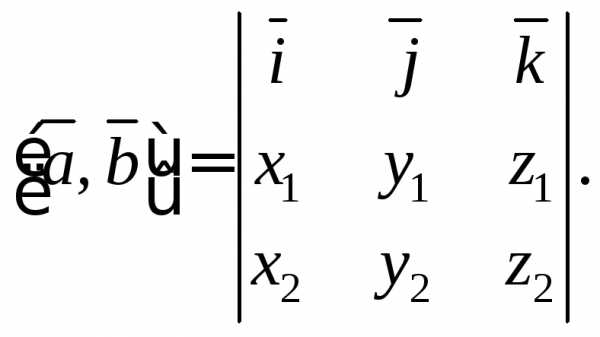
Пример
1. Пусть 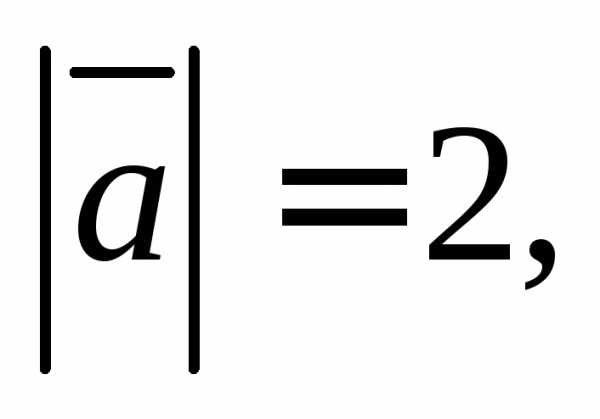

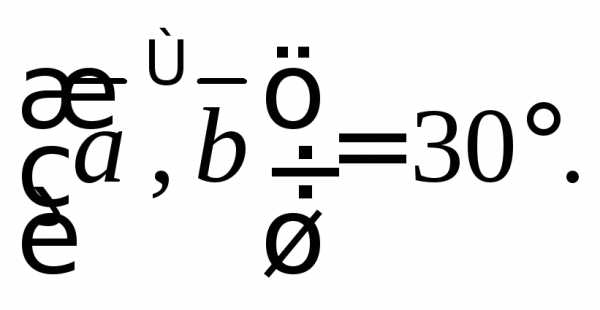 Найти:
Найти:
1) 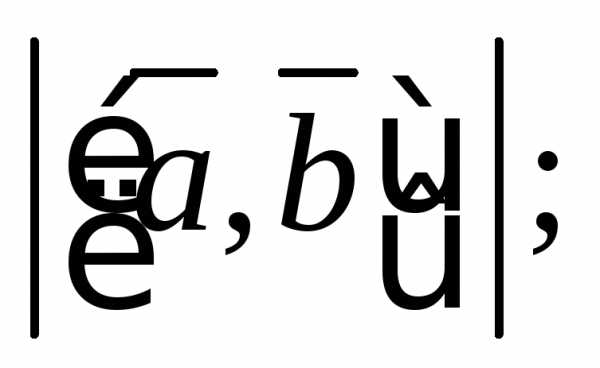 2)
2)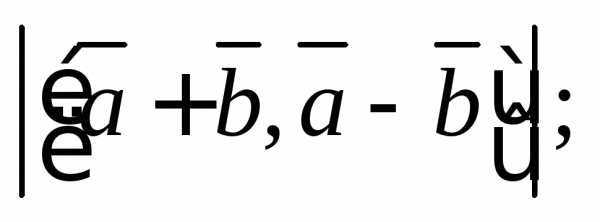 3)
3)
Решение. 1) По определению
векторного произведения векторов  и
и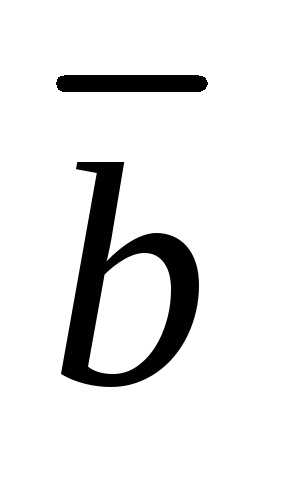 его длина
его длина
2) Используя алгебраические свойства векторного произведения, имеем:
Значит,
3) Используя свойства векторного произведения и условие задачи, получим:
Пример 2. Упростить выражение:
1)
2)
Решение. Воспользуемся
равенствами 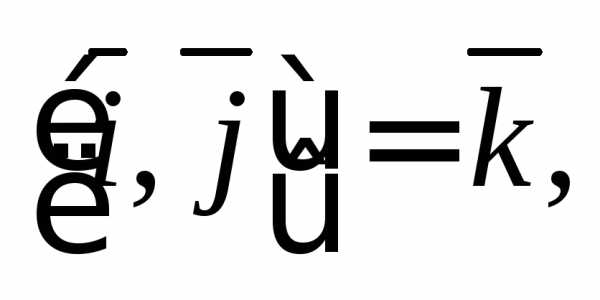
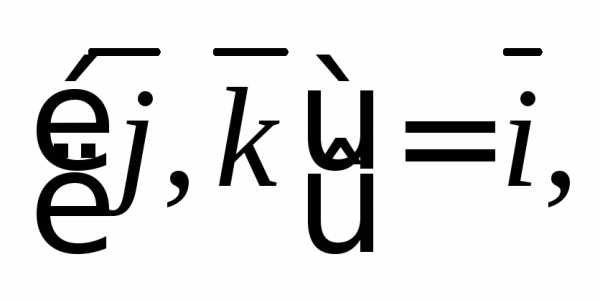
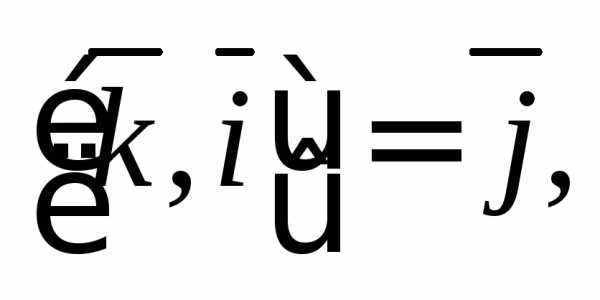
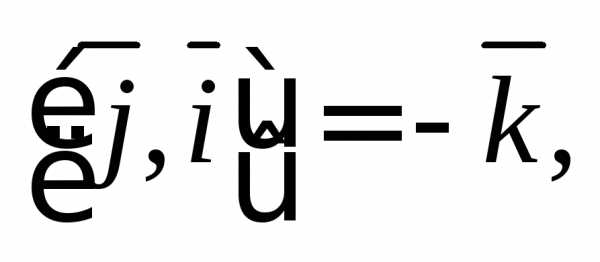
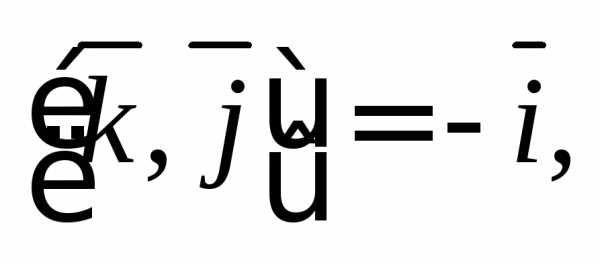
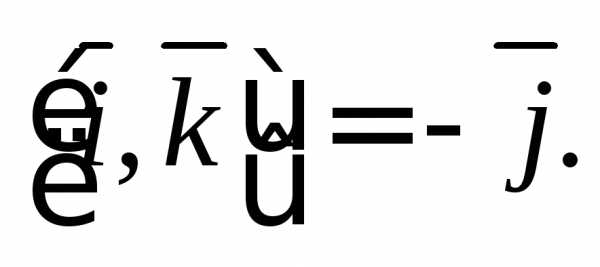
Тогда имеем:
1)
2)
Пример
3. Вычислить площадь параллелограмма,
диагоналями которого служат векторы 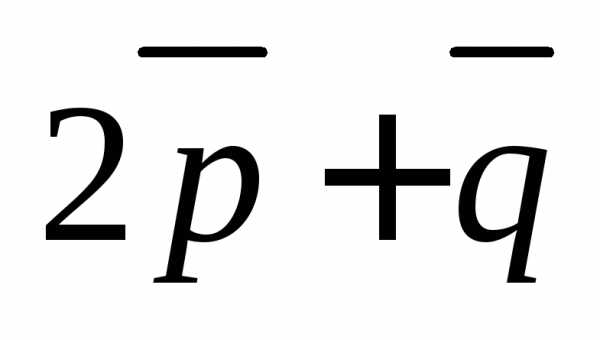 и
и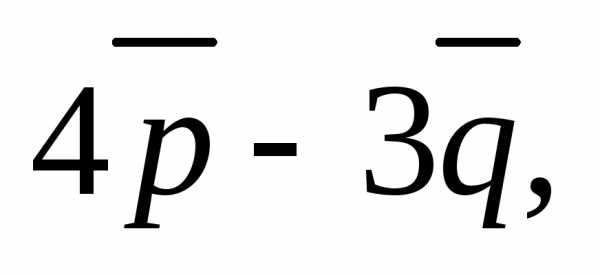 где
где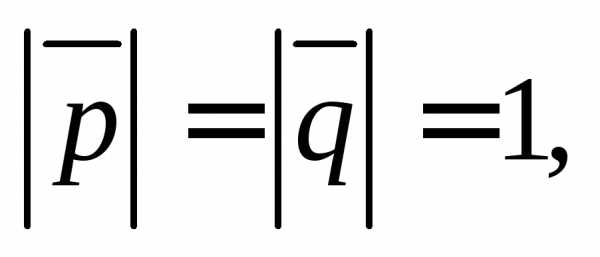
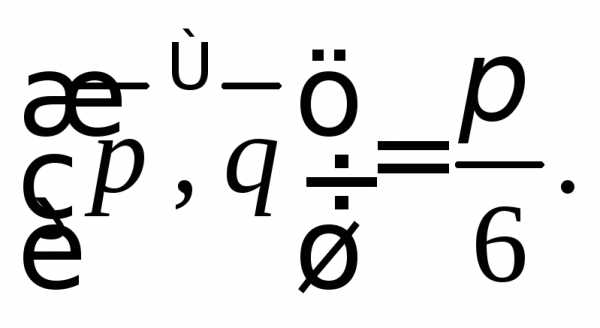
Решение. Используем известную из планиметрии формулу площади параллелограмма и геометрический смысл векторного произведения:
где
Тогда по свойствам векторного произведения получим:
Пример 4. Вычислить площадь треугольника ABC и его высоту, опущенную из вершины A к стороне BC, если A(1, 1, 1), B(4, 2, –1), C(2, 3, 0).
Решение. Используем тот факт, что 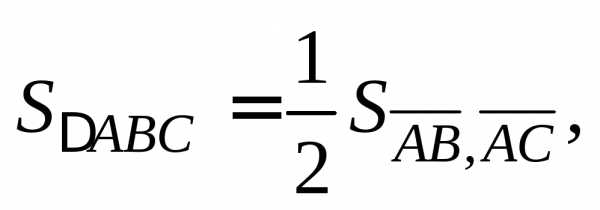 где
где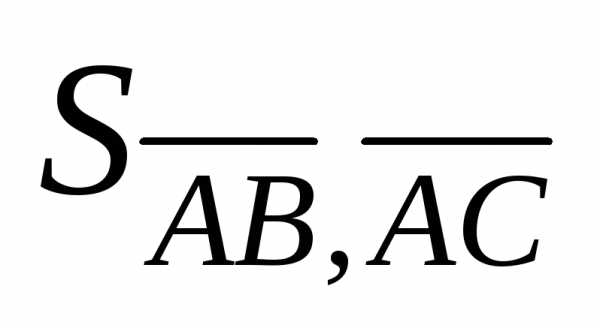 – площадь параллелограмма, построенного
на векторах
– площадь параллелограмма, построенного
на векторах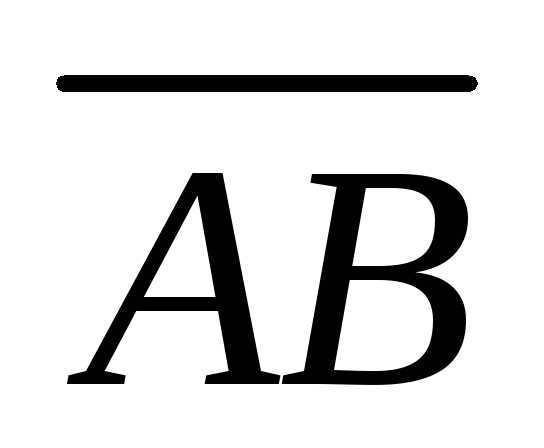 и
и .
Так какнайдем сначала
.
Так какнайдем сначала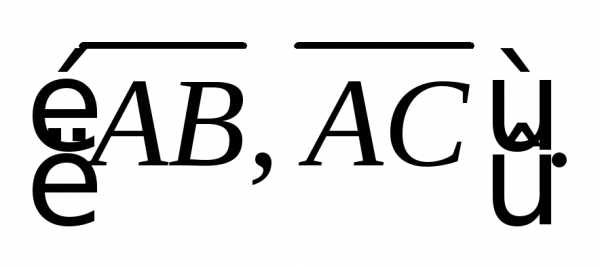
Вычисляем векторное произведение в координатной форме:
Тогда
Значит, 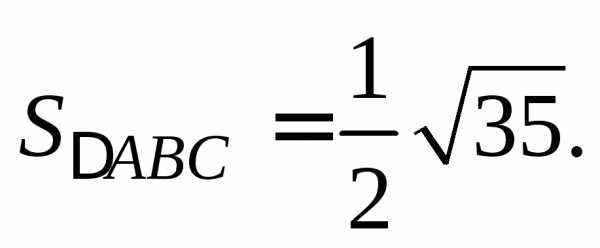
Для
нахождения высоты h треугольника ABC воспользуемся формулой 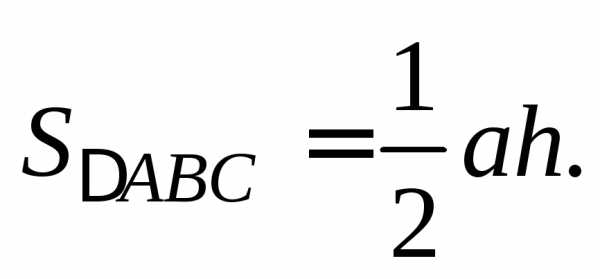 Тогда
Тогда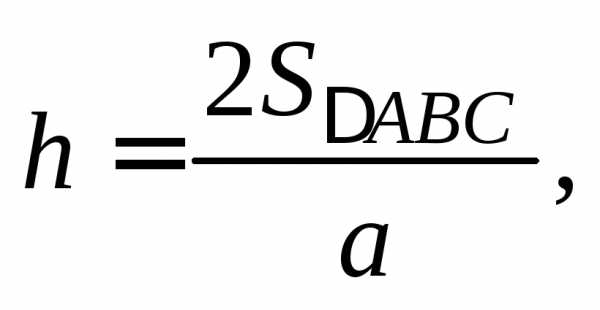 здесь
здесь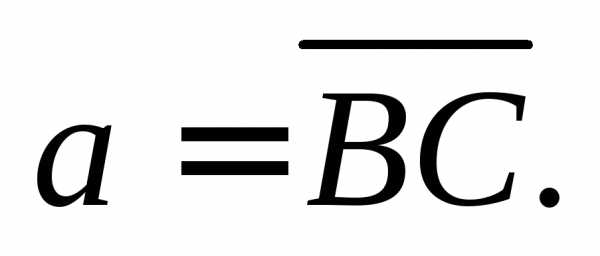
Значит
Пример 5. Даны три силы: приложенные к точкеA(–1, 4, 2). Определить величину и направляющие косинусы момента равнодействующей этих сил относительно точки O(2, 3, –1).
Решение. Пусть сила  – равнодействующая сил
– равнодействующая сил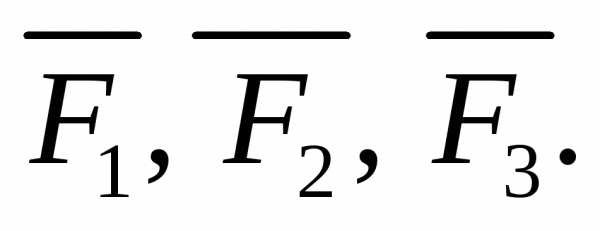 ТогдаЗначит момент
ТогдаЗначит момент этой силы равен
этой силы равен
Вычисляем Для нахождения направляющих косинусов используем формулы (14.9):
Задания
studfiles.net
§7. Примеры решения типовых задач
В данном параграфе рассмотрим задачи, связанные с различными системами координат, делением отрезка в заданном отношении.
Пример 1.
Даны координаты точек: А(4; 3), В(7; 6), С(2; 11). Докажем, что треугольник АВС прямоугольный.
Найдем длины сторон треугольника АВС. С этой целью используем формулу, позволяющую находить расстояние между двумя точками на плоскости:
.
Длины сторон будут равны:
,
,
.
Учитывая, что для сторон данного треугольника выполняется теорема Пифагора
,
то треугольник АВС – прямоугольный.
Пример 2.
Даны точки А(2; 1) и В(8; 4). Найдем координаты точки М(х; у), которая делит отрезок в отношении 2:1.
Напомним, что точка М(х; у) делит отрезок АВ, где A(xA, yA), B(xB, yB), в отношении λ : μ, если ее координаты удовлетворяют условиям:
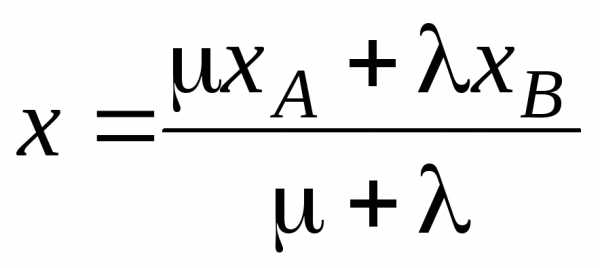 ,
,  .
.
Найдем точку М для данного отрезка
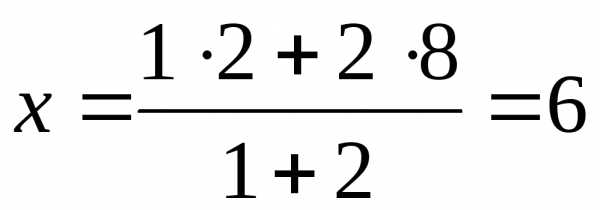 ,
, 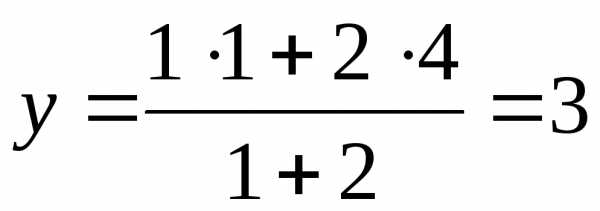 .
.
Таким образом, точка М(6; 3) делит отрезок АВ в отношении 2:1.
Пример 3.
Найдем прямоугольные
координаты точки А(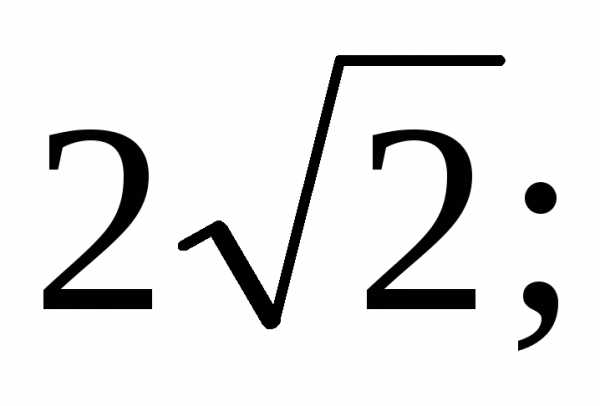 3π/4),
если полюс совпадает с началом координат,
а полярная ось направлена по оси абсцисс.
3π/4),
если полюс совпадает с началом координат,
а полярная ось направлена по оси абсцисс.
Учитывая формулы перехода от полярной к прямоугольной системе координат
x = r cosφ, y = r sinφ,
получаем
,
.
В прямоугольной декартовой системе координат координаты точки А(–2; 2).
Пример 4.
Найдем полярные координаты точек, имеющих следующие прямоугольные координаты:
А(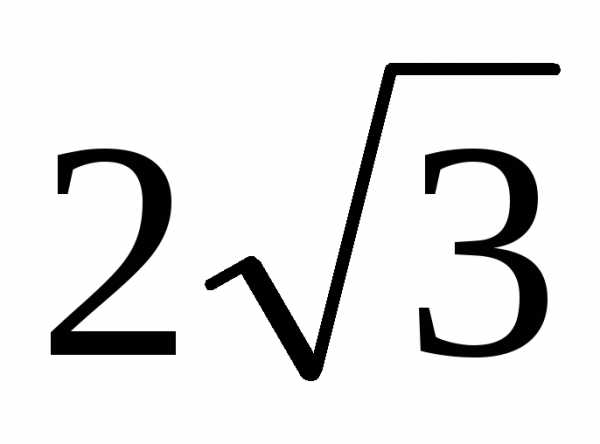 ;
2),В(–4;
4), С(–7;
0).
;
2),В(–4;
4), С(–7;
0).
Используем формулы перехода от прямоугольных координат к полярным:
,
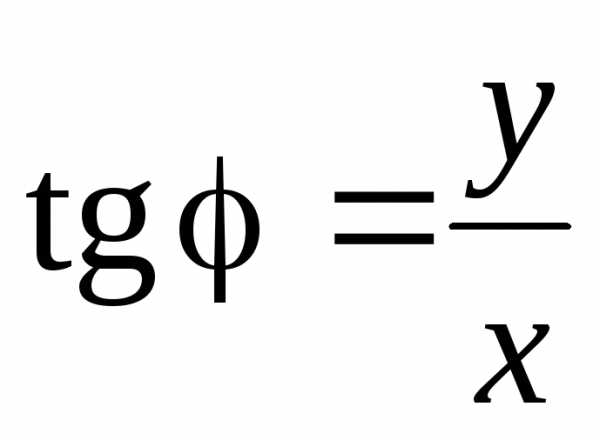 .
.
Получим координаты для точки А:
,
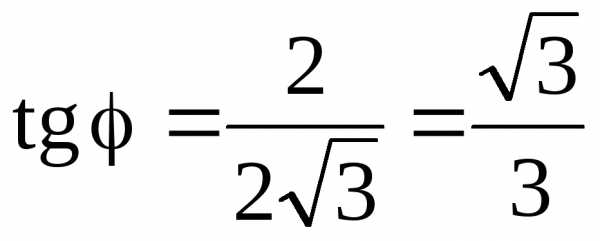 ,
,  .
.
Таким образом А(4; π/6) – полярные координаты (рис. 15).
Для точки В (рис. 16) имеем
,
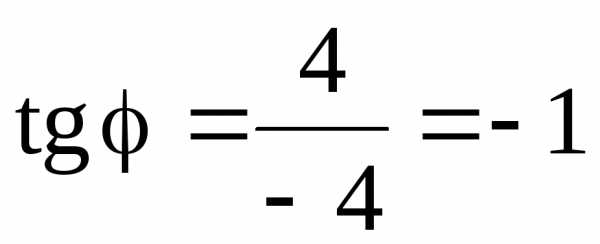 ,
, 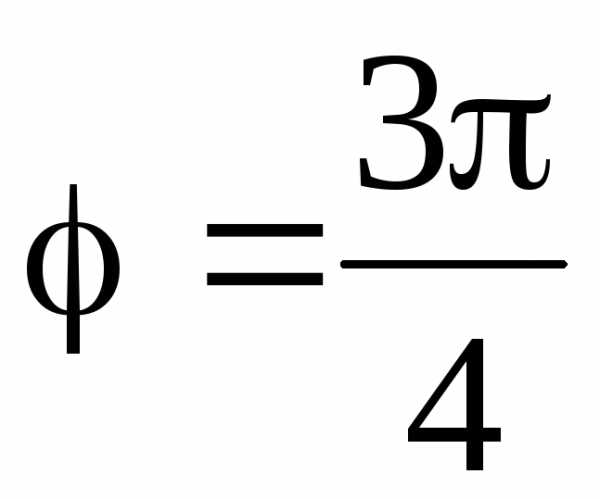 .
.
Следовательно,
полярные координаты точки В(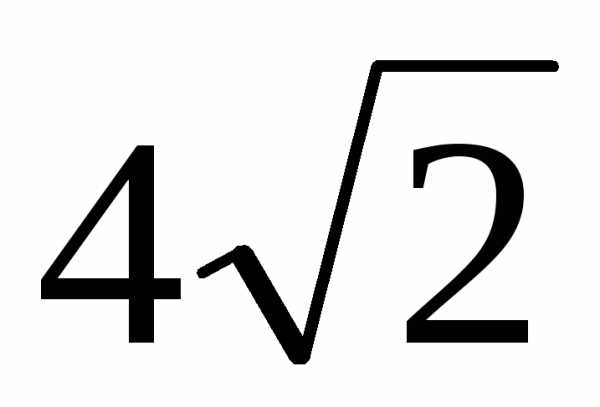 ,
3π/4).
,
3π/4).
Рассмотрим точку С(–7; 0) (рис. 17). В этом случае
,
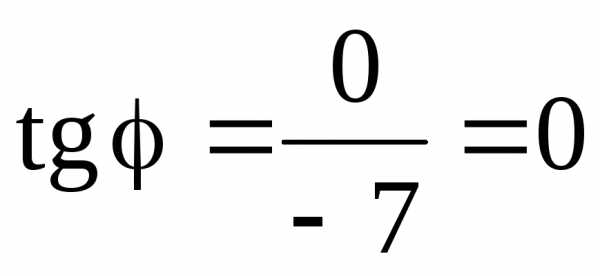 ,
, 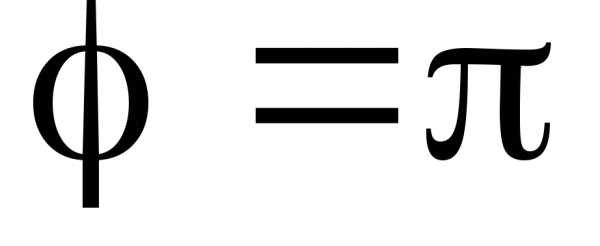 .
.
Можно записать полярные координаты точки С(7; π).
Пример 5.
Найдем длину вектора a = 20i + 30j – 60k и его направляющие косинусы.
Напомним, что направляющие косинусы – это косинусы углов, которые вектор a(a1, a2, a3) образует с осями координат:
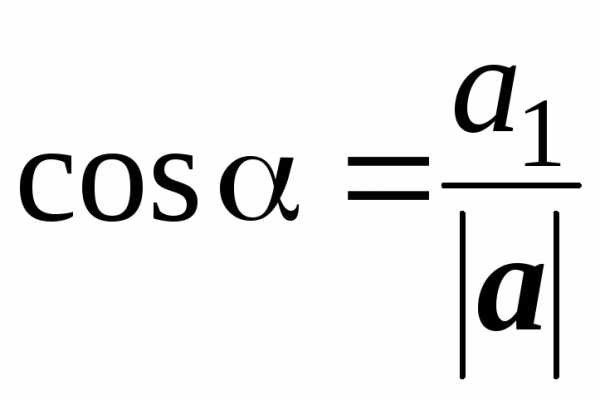 ,
, 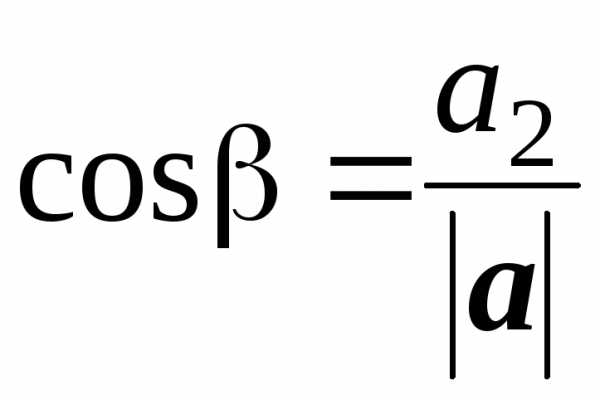 ,
,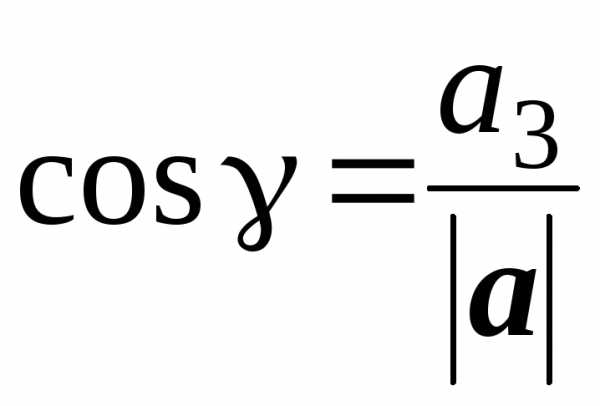 ,
,
где .
Применим эти формулы к данному вектору, получим
,
,
.
Пример 6.
Нормируем вектор a = 3i + 4j – 12k.
Нормировать
вектор – это найти вектор единичной
длины а0,
направленный также как и данный вектор.
Для произвольного вектора a(a1, a2, a3)
соответствующий вектор единичной длины
можно найти, умножив a на дробь 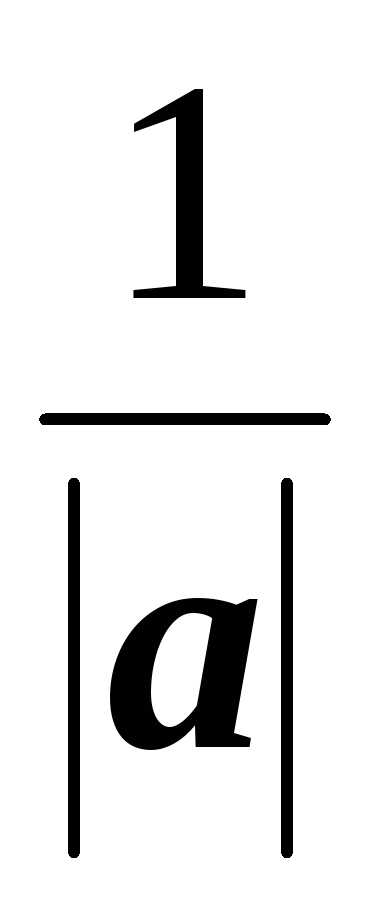 .
.
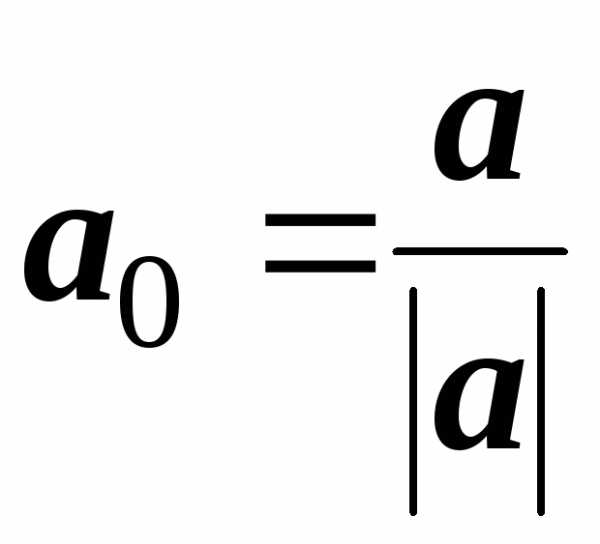 .
.
В нашем случае и вектор единичной длины:
.
Пример 7.
Найдем скалярное произведение векторов
a = 4i + 5j + 6k и b = 3i – 4j + k.
Для того чтобы найти скалярное произведение векторов, нужно умножить соответствующие координаты и полученные произведения сложить. Так, для векторов a = a1i + a2j + a3k и b = b1i + b2j + b3k скалярное произведение имеет вид:
(a, b) = a1b1 + a2b2 + a3b3.
Для данных векторов получаем
(a, b) = 4∙3 + 5∙(–4) + 6∙1 = 12 – 20 + 6 = –2.
Пример 8.
Покажем, что векторы a = 2i – 3j + 5k и b = i + 4j + 2k перпендикулярны.
Два вектора перпендикулярны, если их скалярное произведение равно нулю.
Найдем скалярное произведение:
(a, b) = 2∙1 + (–3)∙4 + 5∙2 = 2 – 12 + 10 = 0.
Таким образом, векторы а и b перпендикулярны.
Пример 9.
Выясним, при каком значении параметра m векторы a = 2i + 3j + mk и b = 3i + mj – 2k перпендикулярны.
Найдем скалярное произведение векторов а и b:
(a, b) = 2∙3 + 3∙m – 2∙m = 6 + m.
Векторы перпендикулярны, если их скалярное произведение равно нулю. Приравниваем к нулю произведение (а, b):
6 + m = 0.
При m = – 6 векторы а и b перпендикулярны.
Пример 10.
Найдем скалярное произведение (3а + 4b, 2а – 3b), если |a| = 2, |b| = 1 и угол φ между а и b равен π/3.
Воспользуемся свойствами скалярного произведения:
(αa, βb) = αβ(a, b),
(a + b, c) = (a, c) + (b, c),
(a, b) = (b, a)
(a, a) = |a|2,
а также определением скалярного произведения (a, b) = |a|∙|b|∙cosφ. Перепишем скалярное произведение в виде
(3a + 4b, 2a – 3b) = 6(a, a) – 9(a, b) + 8(b, a) – 12(b, b) =
= 6|a|2 – (a, b) – 12|b|2 = 6∙22 – 2∙1∙cos(π/3) – 12∙12 = 11.
Пример 11.
Определим угол между векторами
a = i + 2j + 3k и b = 6i + 4j – 2k.
Для нахождения угла воспользуемся определением скалярного произведения двух векторов
(a, b) = |a|∙|b|∙cosφ,
где φ – угол между векторами а и b. Выразим cosφ из этой формулы
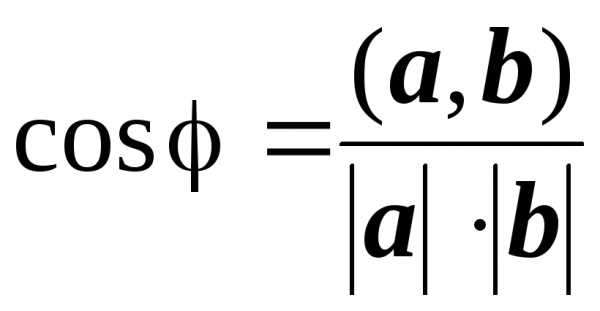 .
.
Учитывая, что (а, b) = 1∙6 + 2∙4 + 3∙(–2) = 8, ,, получаем:
.
Следовательно, 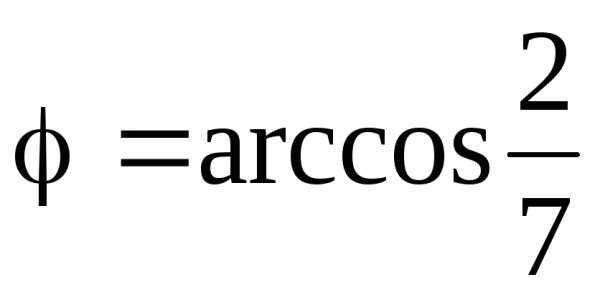 .
.
Пример 12.
Найдем векторное произведение векторов
a = 5i – 2j + 3k и b = i + 2j – 4k.
Известно, что векторное произведение векторов a = a1i + a2j + a3k и b = b1i + b2j + b3k находится по формуле
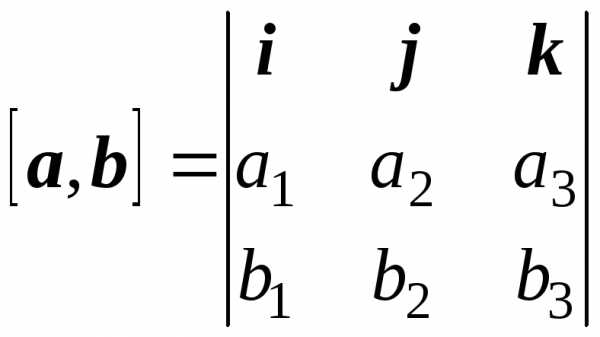 .
.
Следовательно, для данных векторов
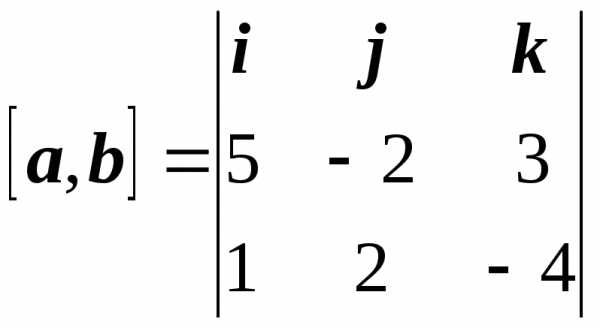
= 2i + 23j + 12k.
Рассмотрим пример, где для нахождения модуля векторного произведения будет использоваться определение векторного произведения, а не выражение его через координаты сомножителей, как было в предыдущем примере.
Пример 13.
Найдем модуль векторного произведения векторов а + 2b и 2а – 3b, если |a| = 1, |b| = 2 и угол между векторами а и b равен 30°.
Из определения векторного произведения видно, что для произвольных векторов а и b его модуль равен
|[a, b] | = |a| ∙ |b| ∙ sin φ.
Учитывая свойства векторного произведение
[a, b] = – [b, a],
[a, a] = 0,
[αa + βb, c] = α[a, c] + β[b, c],
получаем
[a + 2b, 2a – 3b] = 2[a, a] – 3[a, b] + 4[b, a] – 6[b, b] = –7[a, b].
Значит, модуль векторного произведения равен
|[a + 2b, 2a – 3b]| = |–7[a, b]| = 7 ∙ |a| ∙ |b| ∙ sin 30° = 7∙1∙2∙0,5 = 7.
Пример 14.
Вычислим площадь параллелограмма, построенного на векторах
a = 6i + 3j – 2k и b = 3i – 2j + 6k.
Известно, что модуль векторного произведения двух векторов равен площади параллелограмма, построенного на этих векторах. Найдем векторное произведение по формуле:
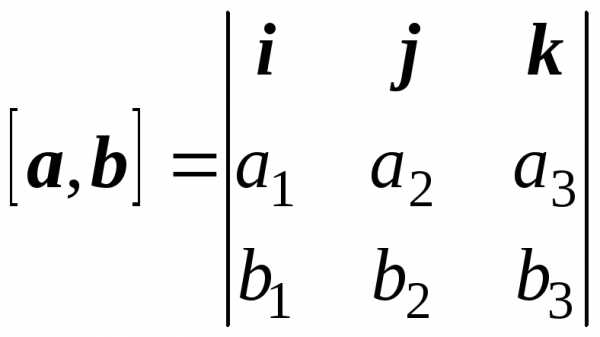 ,
,
где a = a1i + a2j + a3k и b = b1i + b2j + b3k. Затем вычислим его модуль.
Для данных векторов получаем
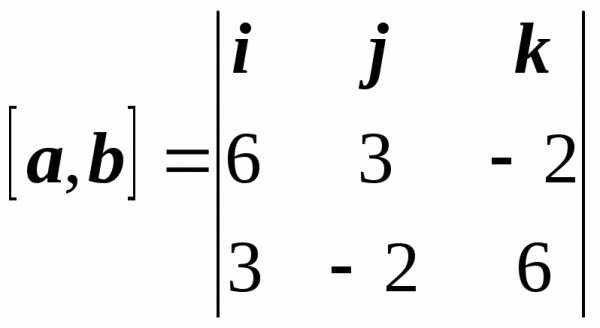
= 14i – 42j – 21k.
Следовательно, площадь параллелограмма равна
S = |[a, b]| = (кв. ед.).
Пример 15.
Вычислим площадь треугольника с вершинами А(1;2;1), В(3;3;4), С(2;1;3).
Очевидно,
что площадь треугольника АВС равна половине площади параллелограмма,
построенного на векторах 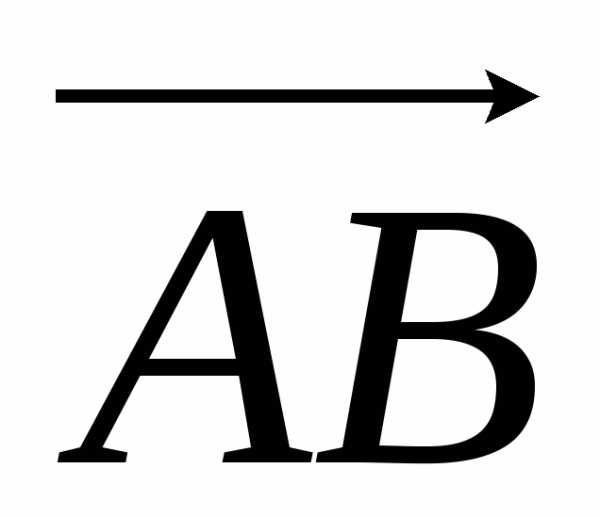 и
и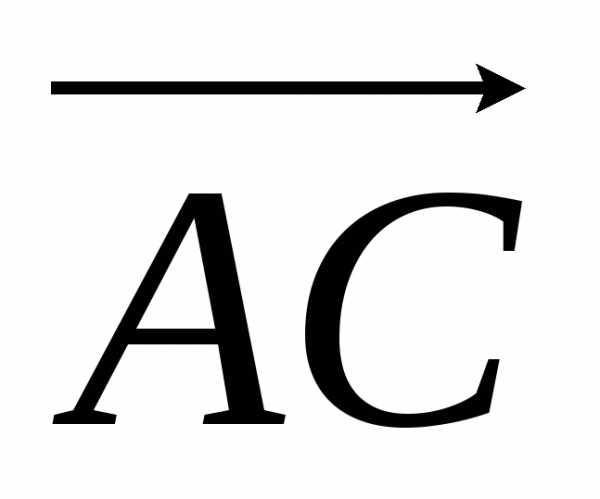 .
.
В свою очередь,
площадь параллелограмма, построенного
на векторах 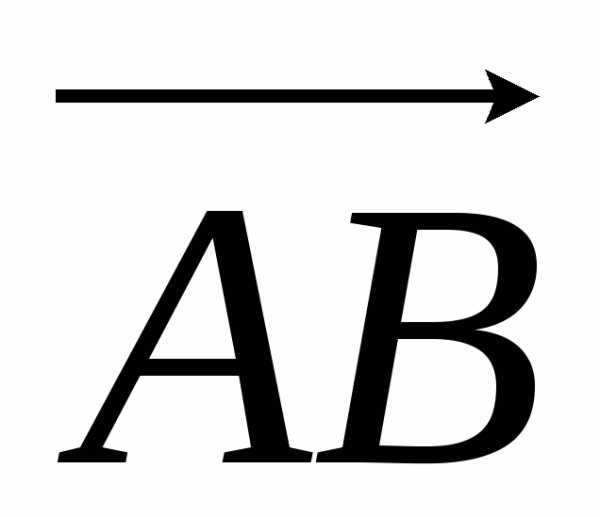 и
и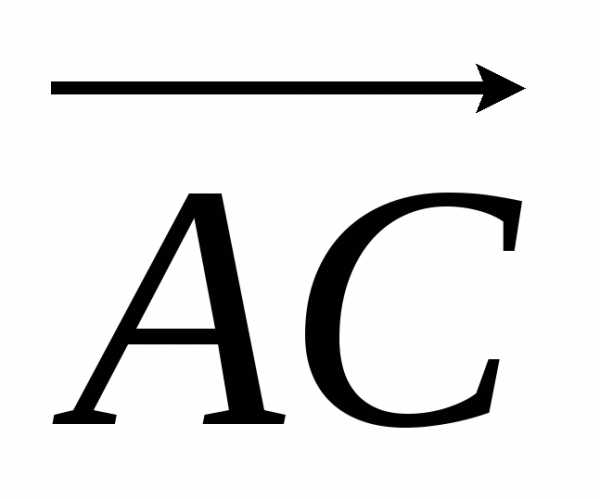 ,
равна модулю векторного произведения
[
,
равна модулю векторного произведения
[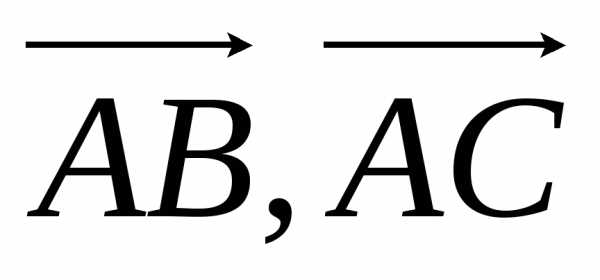 ].
Таким образом
].
Таким образом
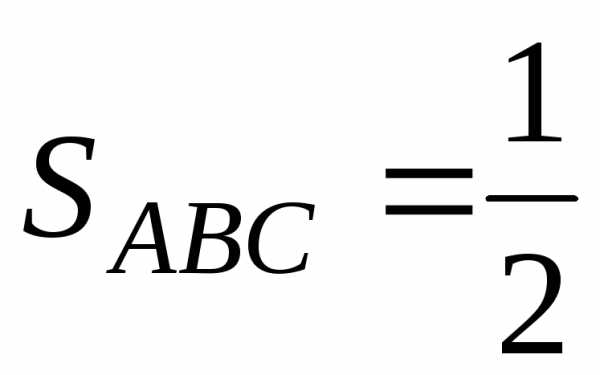 |[
|[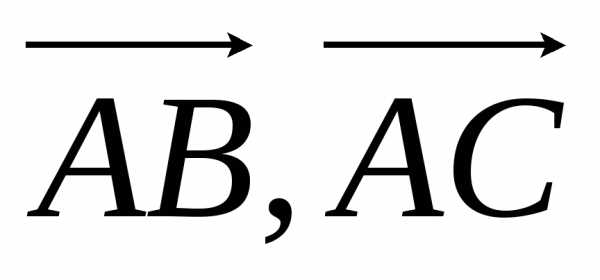 ]|.
]|.
Найдем координаты
векторов 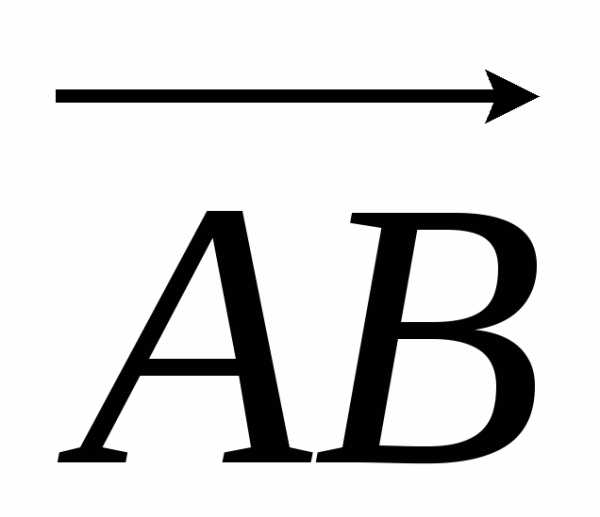 и
и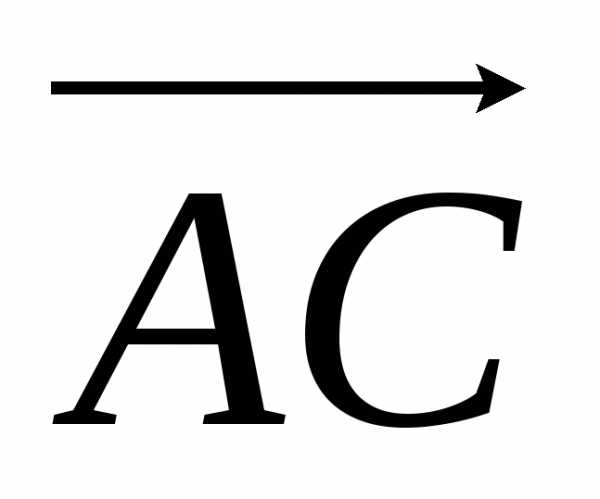 ,
вычитая из координат конца вектора
соответствующие координаты начала,
получим
,
вычитая из координат конца вектора
соответствующие координаты начала,
получим
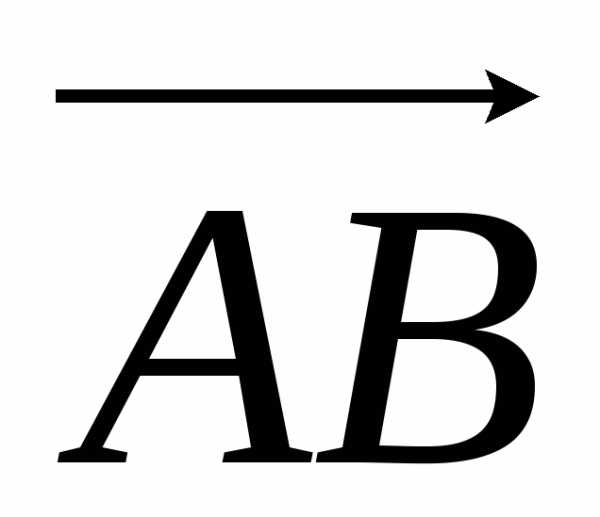 = (3 –
1)i + (3 – 2)j + (4 – 1)k = 2i + j + 3k,
= (3 –
1)i + (3 – 2)j + (4 – 1)k = 2i + j + 3k,
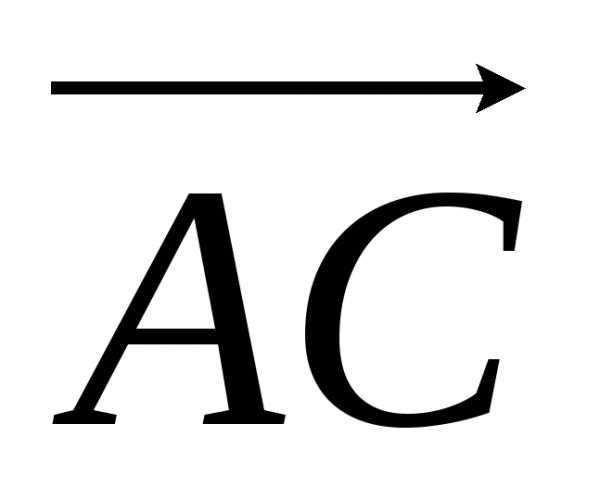 = (2 –
1)i + (1 – 2)j + (3 – 1)k = i – j + 2k.
= (2 –
1)i + (1 – 2)j + (3 – 1)k = i – j + 2k.
Найдем векторное произведение:
[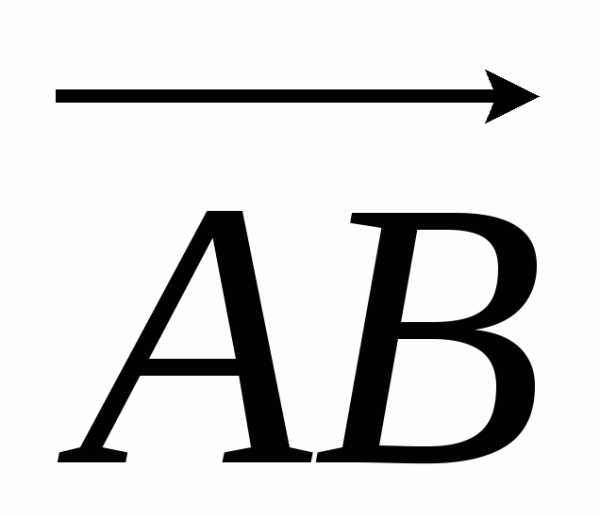 ,
,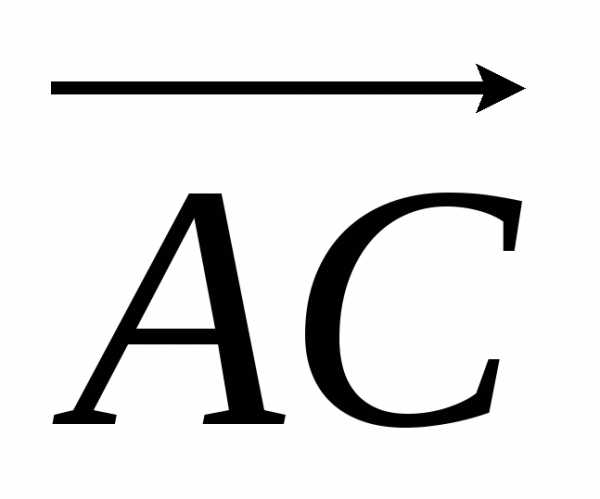 ]
=
]
=  5i – j – 3k.
5i – j – 3k.
Найдем модуль векторного произведения:
|[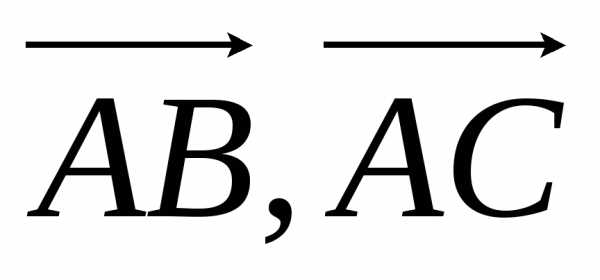 ]|
=
.
]|
=
.
Следовательно, можем получить площадь треугольника:
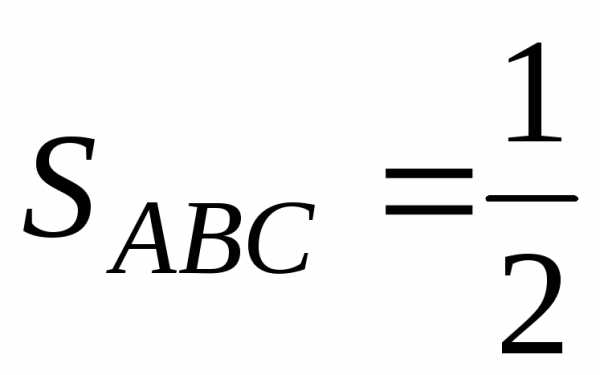
 (кв. ед.).
(кв. ед.).
Пример 16.
Вычислим площадь параллелограмма, построенного на векторах a + 3b и 3a – b, если |a| = 2, |b| = 1 и угол между а и b равен 30°.
Найдем модуль векторного произведения, используя его определение и свойства, указанные в примере 13, получим
[a + 3b, 3a – b] = 3[a, a] – [a, b] + 9[b, a] – 3[b, b] = –10[a, b].
Значит, искомая площадь равна
S = |[a + 3b, 3a – b]| = |–10[a, b]| = 10 ∙ |a| ∙ |b| ∙ sin 30° =
= 10∙2∙1∙0,5 = 10 (кв. ед.).
Следующие примеры будут связаны с использованием смешанного произведения векторов.
Пример 17.
Показать, что векторы a = i + 2j – k, b = 3i + k и с = 5i + 4j – k компланарны.
Векторы компланарны, если их смешанное произведение равно нулю. Для произвольных векторов
a = a1i + a2j + a3k, b = b1i + b2j + b3k, c = c1i + c2j + c3k
смешанное произведение находим по формуле:
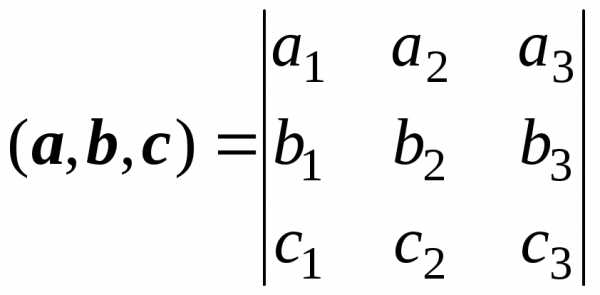 .
.
Для данных векторов получаем
.
Таким образом, данные векторы компланарны.
Пример18.
Найдем объем треугольной пирамиды с вершинами А(1;1;1), В(3;2;1), С(2;4;3), D(5;2;4).
Найдем
координаты векторов 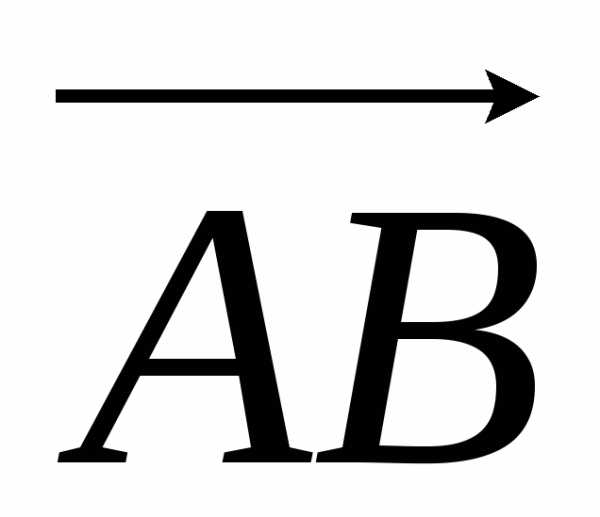 ,
,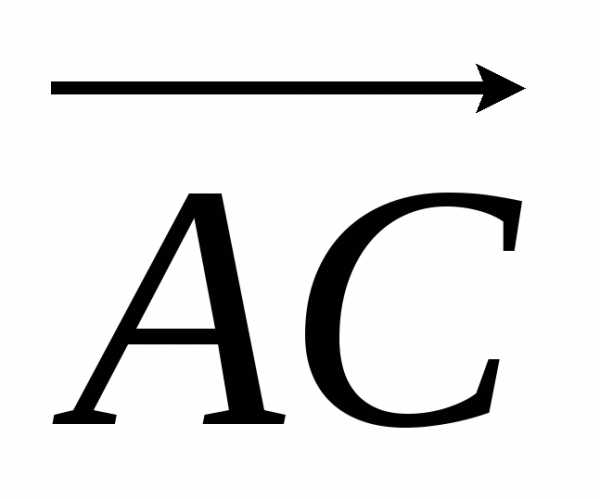 и
и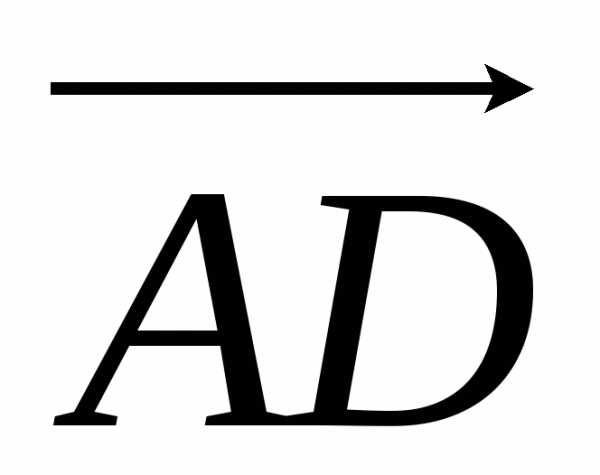 ,
совпадающих с ребрами пирамиды. Вычитая
из координат конца вектора соответствующие
координаты начала, получаем
,
совпадающих с ребрами пирамиды. Вычитая
из координат конца вектора соответствующие
координаты начала, получаем
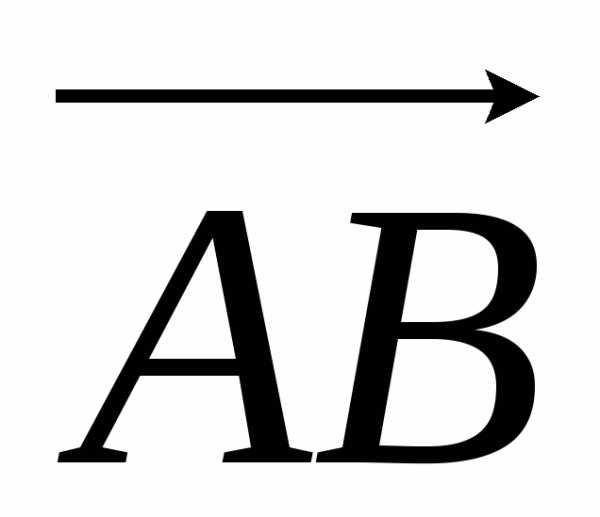 = 2i + 3j,
= 2i + 3j,
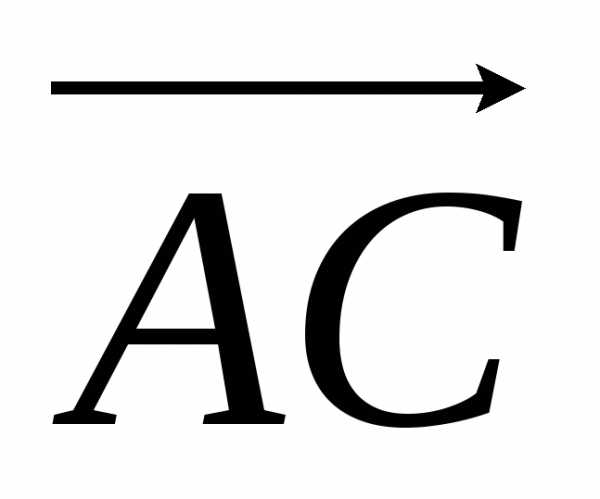 = i + 3j + 2k,
= i + 3j + 2k,
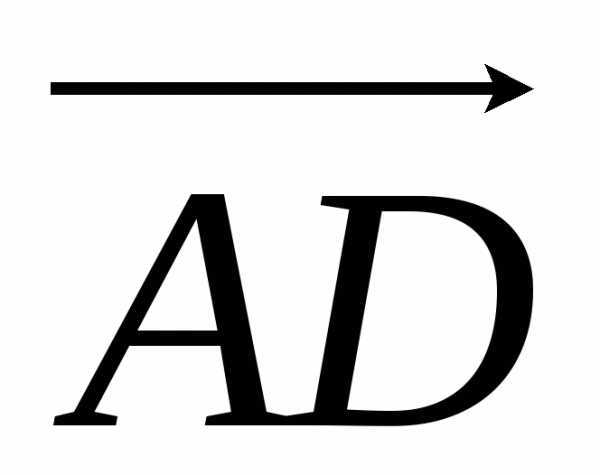 = 4i + j + 3k.
= 4i + j + 3k.
Известно, что объем
пирамиды равен 1/6 объема параллелепипеда,
построенного на векторах 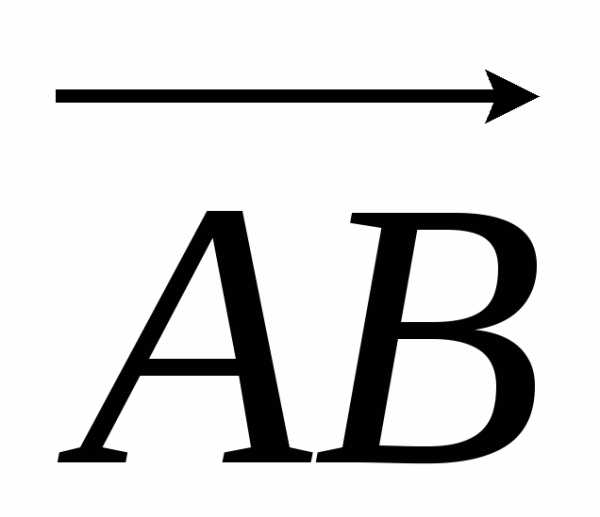 ,
,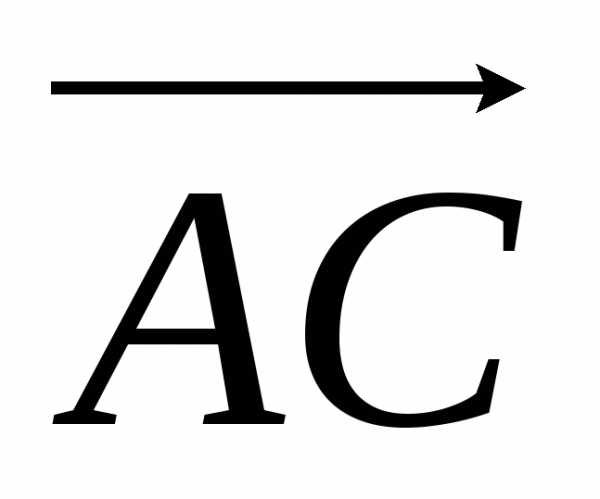 и
и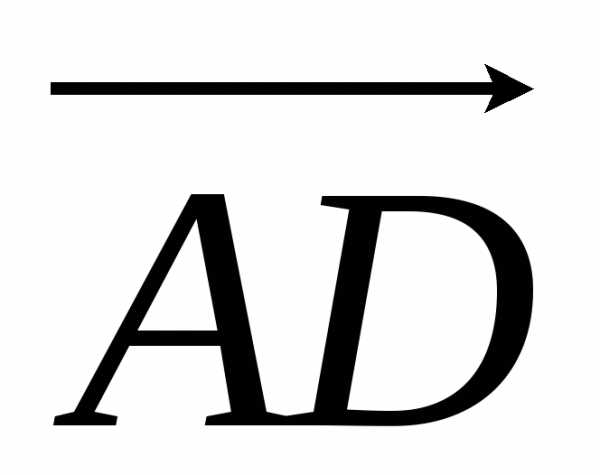 .
Таким образом,
.
Таким образом,
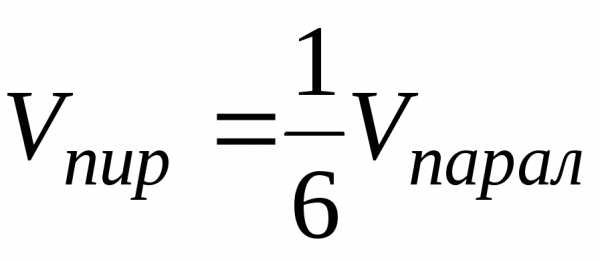 .
.
В свою очередь, объем параллелепипеда равен модулю смешанного произведения
Vпарал = |(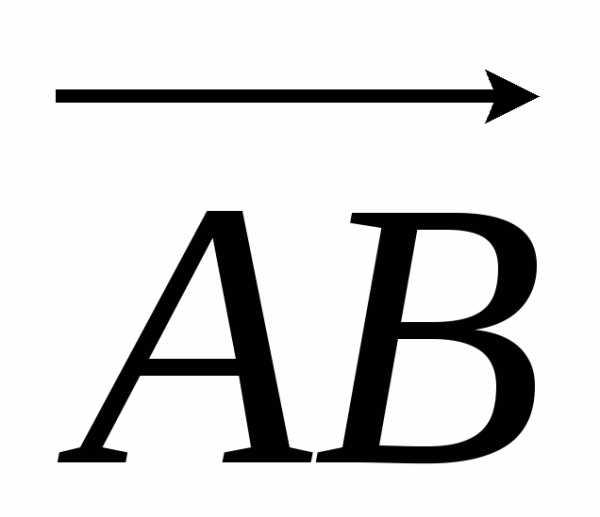 ,
,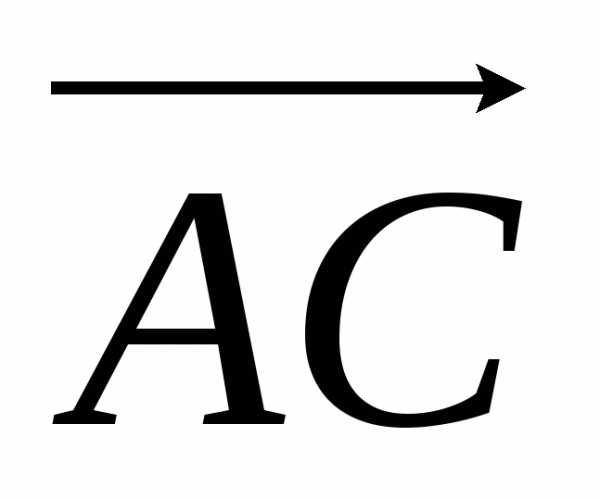 ,
,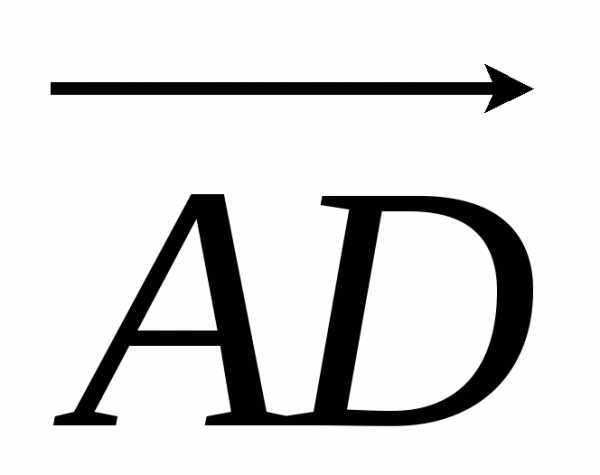 )|.
)|.
Найдем смешанное произведение
(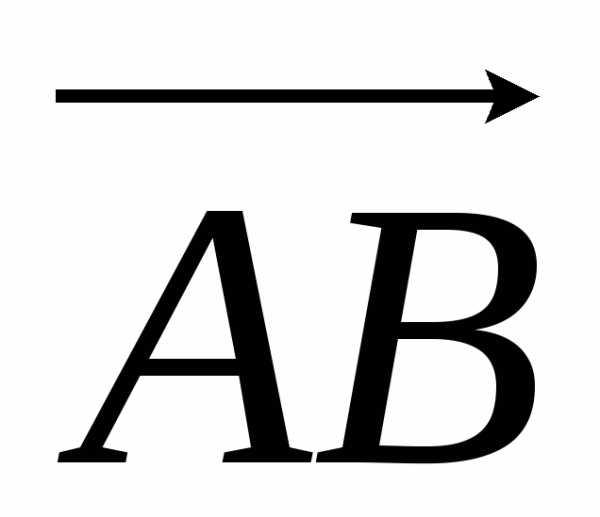 ,
,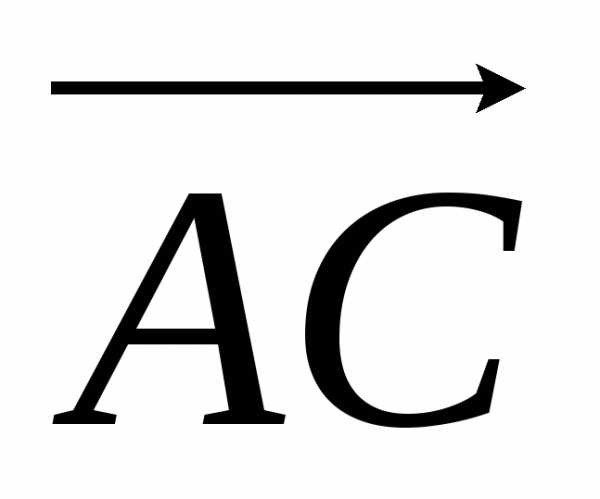 ,
,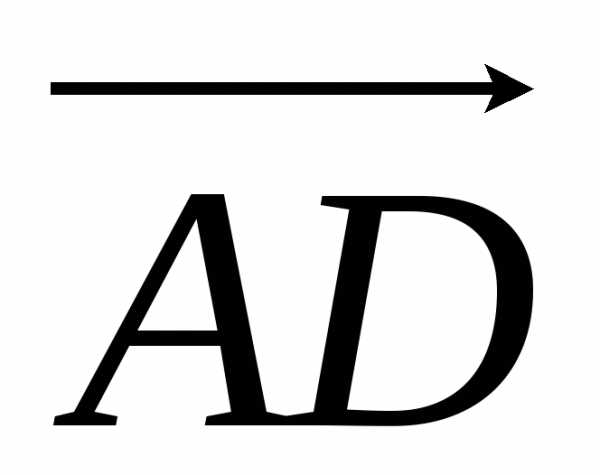 )
=
)
= 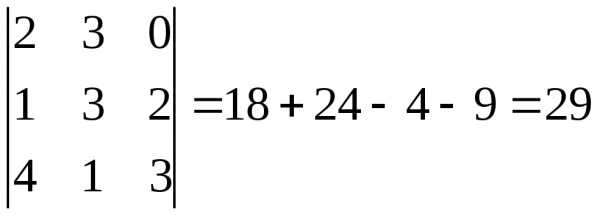 .
.
Итак, объем пирамиды равен
(куб. ед.).
В следующих примерах покажем возможное применение векторной алгебры.
Пример 19.
Проверим, являются ли коллинеарными вектора 2а + b и а – 3b, где a = 2i + j – 3k и b = i + 2j + 4k.
Найдем координаты векторов 2а + b и а – 3b:
2а + b = 2(2i + j – 3k) + i + 2j + 4k = 5i + 4j – 2k,
а – 3b = 2i + j – 3k – 3(i + 2j + 4k) = –i – 5j – 15k.
Известно, что у коллинеарных векторов пропорциональные координаты. Учитывая, что
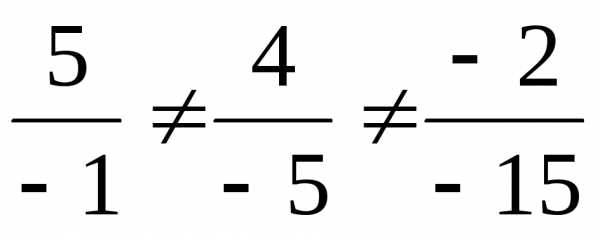 ,
,
получаем, что вектора 2а + b и а – 3b неколлинеарны.
Эту задачу можно было решить и другим способом. Критерием коллинеарности векторов является равенство нулю векторного произведения:
[2a + b, a – 3b] = 2[a, a] – 6[a, b] + [b, a] – 3[b, b] = –7[a, b].
Найдем векторное произведение векторов а и b:
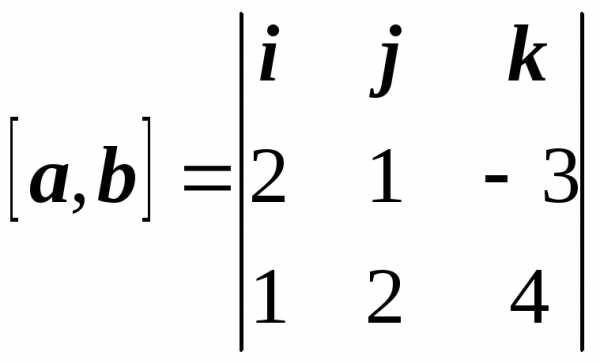
= 10i – 11j + 3k ≠ 0.
Следовательно,
[2a + b, a – 3b] = –7[a, b] ≠ 0
и векторы 2а + b и а – 3b неколлинеарны.
Пример 20.
Найдем работу силы F(3; 2; 1), когда точка ее приложения А(2; 4;–6), двигаясь прямолинейно, перемещается в точку В(5; 2; 3).
Известно,
что работа силы – это скалярное
произведение силы F на вектор перемещения 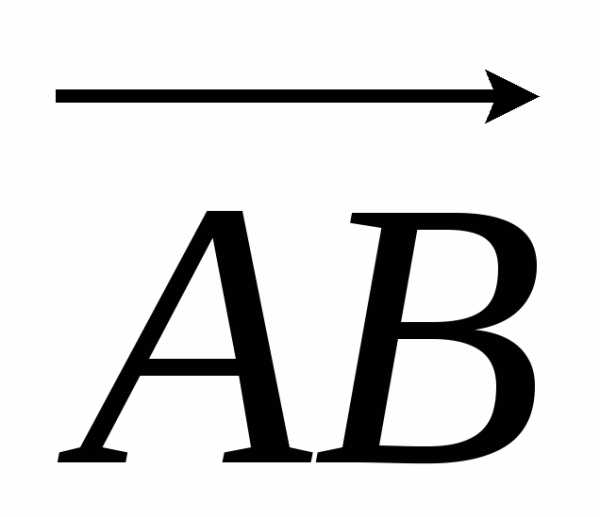 .
.
Найдем
координаты вектора 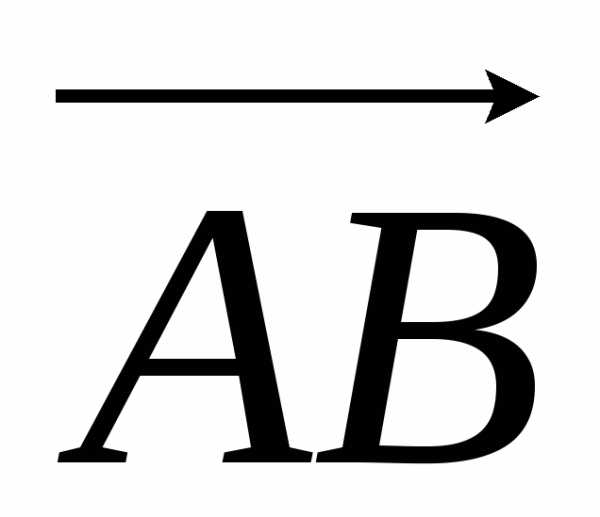 :
:
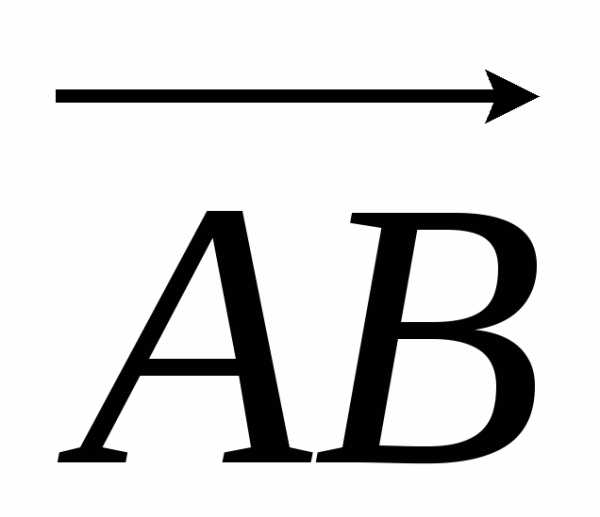 = 3i – 2j + 9k.
= 3i – 2j + 9k.
Следовательно, работа силы F по перемещению точки А в точку В будет равна скалярному произведению
(F, 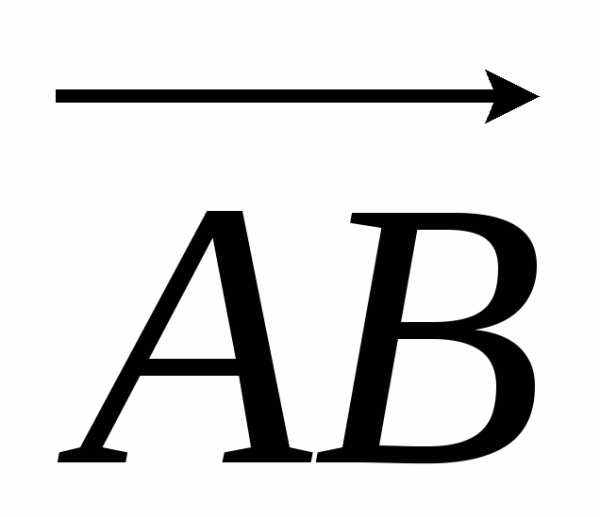 )
= 3∙3 + 2∙(–2) + 1∙9 = 9 – 4 + 9 = 14.
)
= 3∙3 + 2∙(–2) + 1∙9 = 9 – 4 + 9 = 14.
Пример 21.
Пусть сила F( 2;3;–1) приложена к точке А(4;2;3). Под действием силы F точка А перемещается в точку В(3;1;2). Найдем модуль момента силы F относительно точки В.
Известно,
что момент силы равен векторному
произведению силы на перемещение. Найдем
вектор перемещения 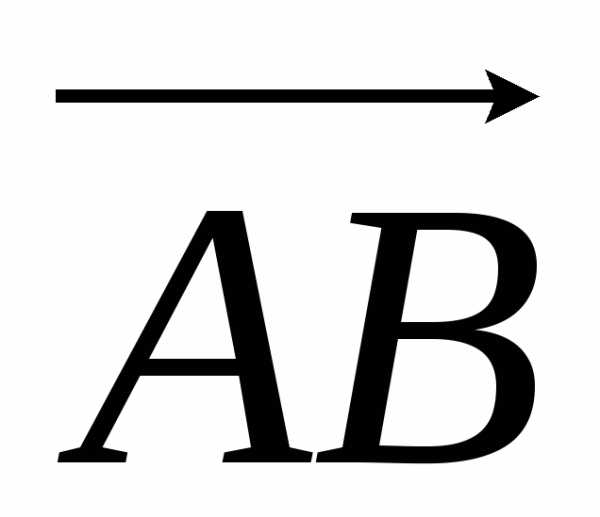 :
:
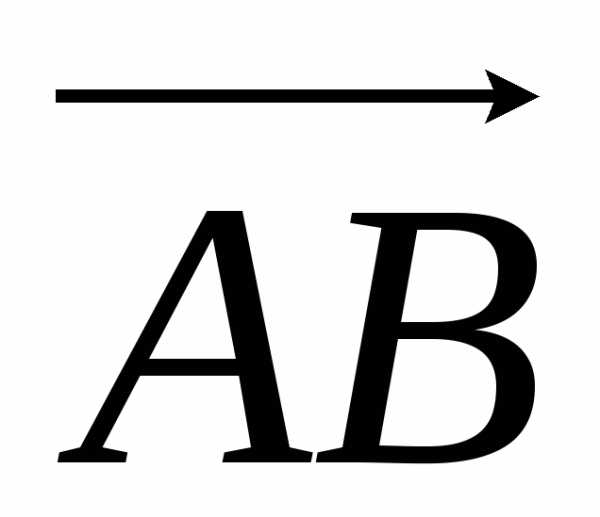 = (3 –
4)i +
(1 – 2)j + (2 – 3)k = – i – j – k.
= (3 –
4)i +
(1 – 2)j + (2 – 3)k = – i – j – k.
Найдем момент силы как векторное произведение:
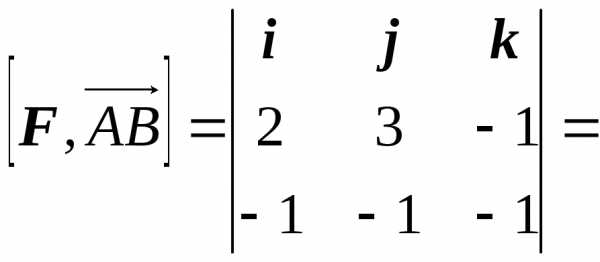
= – 4i + 3j + k.
Следовательно, модуль момента силы равен модулю векторного произведения:
|[F, 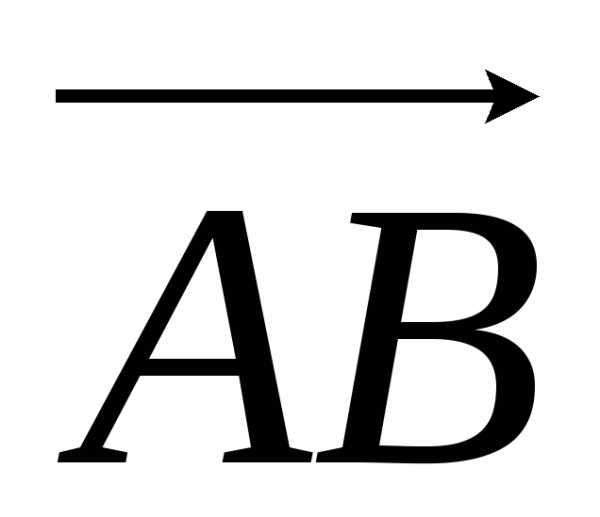 ]|
=
.
]|
=
.
studfiles.net
Задачи с векторами
Задачи с векторами на ЕГЭ. Дорогие друзья! Вы знаете, что в состав экзамена по математике входят такие задания. Не факт, что такая задача попадёт именно вам, но готовиться к этому и понимать тему в любом случае нужно. На блоге мы уже рассмотрели несколько задач на сумму (разность) векторов, длину вектора, в этой же статье есть необходимая теория. Посмотрите её, прежде чем рассматривать задачи представленные ниже.
Также загляните в справочник на блоге. Если нужно вспомнить, что такое абсцисса и ордината точки, тогда посмотрите эту статью. Кратко повторим:
Чтобы найти координаты вектора, нужно из координат его конца вычесть соответствующие координаты начала:
Формула для определения длины вектора, если известны координаты его начала и конца:
Формула для определения длины вектора, если известны его координаты:
27725. Вектор АВ с началом в точке A(2;4) имеет координаты (6;2). Найдите ординату точки B.
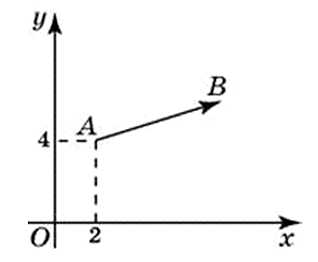
Как уже сказано координаты вектора находятся следующим образом: из соответствующих координат конца вычитаются координаты начала вектора. То есть:
Координаты вектора нам даны, координаты его начала тоже, значит:
Следовательно можем найти координаты точки В:
х2 – 2 = 6 у2 – 4 = 2
х2 = 8 у2 = 6
Таким образом, ордината точки В равна 6.
Ответ: 6
27726. Вектор АВ с началом в точке A(3;6) имеет координаты (9;3). Найдите сумму координат точки B.
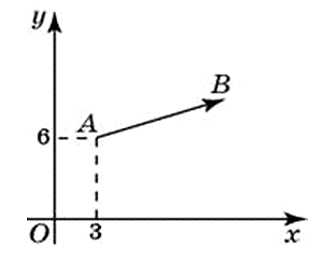
Задача по процессу решения такая же как и предыдущая, но иначе поставлен вопрос. Вычисления так же находятся в пределах устного счёта. Ещё раз запишем координаты вектора, когда известны координаты его начала и конца:
Координаты вектора и координаты его начала даны, значит:
Можем найти координаты точки В:
х2 – 3 = 9 у2 – 6 = 3
х2 = 12 у2 = 9
Таким образом, сумма координат точки В равна 21.
Ответ: 21
27727. Вектор АВ с концом в точке B (5;3) имеет координаты (3;1). Найдите абсциссу и ординату точки A, также сумму её координат.
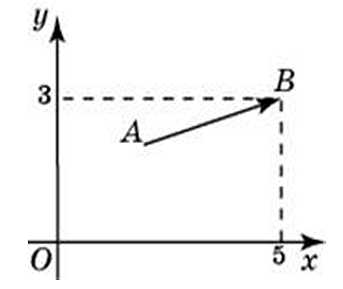
Нам известны координаты вектора и координаты его конца, значит:
Можем найти координаты точки А:
5 – х1 = 3 3 – у1 = 1
х1 = 2 у1 = 2
Таким образом, абсцисса точки А равна двум, ордината тоже равна двум, а сумма координат равна 2+2 = 4.
Ответ: 4
27731 Найдите квадрат длинны вектора a+b.
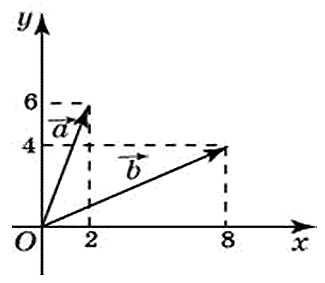
В данной задаче необходимо найти координаты вектора, который является суммой указанных векторов, затем найти его длину и возвести её в квадрат. Запишем формулу длины вектора, если известны его координаты:
Или в другой форме:
Найдём координаты вектора, который является суммой данных векторов. Для этого сначала найдём координаты данных векторов.
Рассмотрим вектор:
Рассмотрим вектор:
*Можно было глядя на эскиз сразу их записать, так как точки их начал совпадают с началом координат.
Теперь найдём координаты вектора являющегося их суммой:
(2 + 8; 6 + 4) = (10;10)
Таким образом, длина вектора являющегося суммой векторов a и b равна:
Следовательно квадрат длины будет равен 200.
*Имея опыт в решении подобных задач, можно сразу записывать:
Как видите, вычисления можно осуществить устно. Здесь для вас умышленно представлено подробное решение.
Ответ: 200
27733. Найдите квадрат длины вектора a – b.

Задача аналогична предыдущей. Необходимо найти координаты вектора, который является разностью представленных векторов, затем найти его длину и результат возвести в квадрат.
Координаты данных векторов нам уже известны (из предыдущей задачи):
Теперь найдём координаты вектора, который является их разностью:
(2 – 8; 6 – 4) = (–6;2)
Таким образом, длина вектора, который является разностью векторов
Следовательно квадрат её длины будет равен 40.
*Можно сразу записывать и вычислять:
Ответ: 40
27723. Найдите сумму координат вектора АВ.
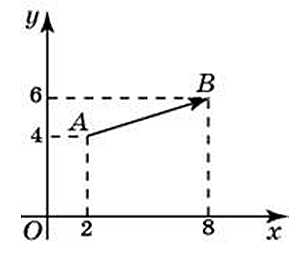
Посмотреть решение
27724.Вектор АВ с началом А(2;4) имеет координаты (6;2) Найдите абсциссу точки В.
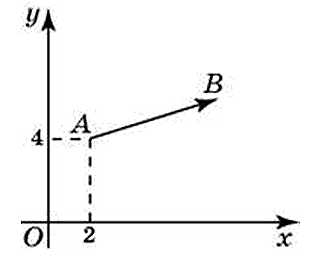
Посмотреть решение
27730. Найдите сумму координат вектора а + b.

Посмотреть решение
27732. Найдите сумму координат вектора а–b.

Посмотреть решение
27736. Найдите сумму координат вектора а + b
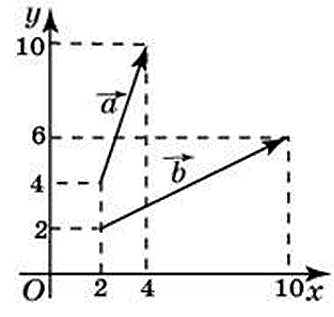
Посмотреть решение
27739. Найдите квадрат длины вектора а–b.

Посмотреть решение
Вы убедились, что задачи с векторами на ЕГЭ это одни из самых простых заданий. Есть, конечно, задания со скалярным произведением векторов, но о они сложности не представляют, нужно лишь знать формулу скалярного произведения. Такие задачи мы также рассмотрим, не пропустите!
На этом всё. Если что-то непонятно, пишите. Успеха Вам!
С уважением, Александр Крутицких
Уроки сделаны… Мама охрипла… Сын оглох … Соседи выучили всё наизусть, собака пересказала!!!..
P.S: Делитесь этой статьёй в сетях.
matematikalegko.ru

