Квантили
Квантили — величины, разделяющие совокупность на определенной количество равных по численности элементов частей.
Самый известный квантиль – медиана, делящая совокупность на две равные части. Кроме медианы часто используются квартили, делящие ранжированный ряд на 4 равные части, децили -10 частей и перцентили — на 100 частей.
Квартили
Квартили представляют собой значение признака, делящее ранжированную совокупность на четыре равные по количеству элементов части. Различают квартиль первого порядка (нижний квартиль) и квартиль третьего порядка (верхний квартиль). Первый (нижний) квартиль отсекает от совокупности ¼ часть единиц с минимальными значениями, а третий (верхний) отсекает ¼ часть единиц с максимальными значениями, второй квартиль является медианой. Для расчёта квартили надо поделить вариационный ряд медианой на две равные части, а затем в каждой из них найти медиану.
К примеру, если выборка состоит из 6 элементов, тогда за начальную квартиль выборки принимается второй элемент, а за нижнюю квартиль пятый элемент.
1 квартиль
2 квартиль
медиана
В случае, если вариационный ряд состоит к примеру, из 9 элементов, тогда за верхнюю квартиль принимают арифм. среднее 2-го и 3-го элеметов, а за нижнюю арифм. среднее 7-го и 8-го элементов.
1 квартиль 3 квартиль
Расчет квартилей для дискретного ряда:
Пример . Расчет медианы и квартилей.
Фирма по продаже сувениров желает узнать рабочую выработку. В данном списке представлено количество сувениров, сделанных каждым рабочим за какой-то день:
92, 100, 89, 98, 101, 84, 113, 93, 81, 14, 113, 86, 98, 99, 105, 88, 101, 89, 93, 102, 101, 99, 87, 109, 92, 99, 111, 98, 102, 95
В вариационном ряду 30 значений: 14, 81 84, 86, 87, 88, 89, 89, 92, 92, 93, 93, 95, 98, 98, ↓, 98, 99, 99, 99, 100, 101, 101, 101, 102, 102, 105, 109, 111, 113, 113.
Найдём верхнюю и нижнюю квартили. Медиана делит вариационный ряд на 15 значений (условное значение обозначено стрелкой). Верняя квартиль – 8-е значение, нижняя — 23-е значение. Q1= 89, Q2= 101 (шт)
Расчет квартилей для дискретного ряда:
В дискретном ряду сначала определяют номера (позиции) квартилей:
позиция 1-го квартиля
позиция 3-го квартиля
2. Если номер квартиля – целое число, то значение квартиля будет равно величине элемента ряда, которое обладает накопленной частотой равной номеру квартиля. Например, если квартиль находится в 20-й позиции, его значение будет равно значению 20-го наблюдения.
Если номер квартиля – нецелое число, то квартиль попадает между двумя наблюдениями. Значением квартиля будет сумма значения элемента, для которого накопленная частота равна целому значению номера квартиля, и указанной части (нецелая часть номера квартиля) разности между этим наблюдением и следующим. Например, если позиция квартиля равна 20,25, квартиль попадает между 20-м и 21-м наблюдениями, и его значение будет равно значению 20-го наблюдения плюс 1/4 разности между значением 20-го и 21-го наблюдений.
Расчет квартилей для интервального ряда:
Для расчета квартилей для интервального ряда
Определяем номер квартиля,
Определяем квартильный интервал,
Рассчитываем квартиль по формуле:
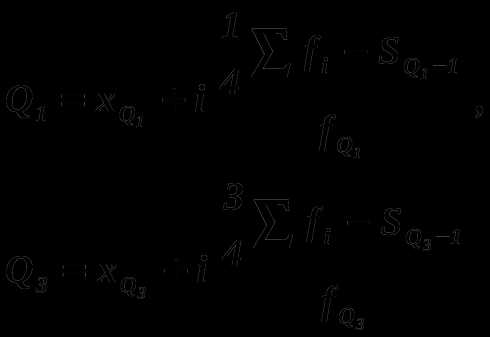
Где:
— нижняя граница интервала, содержащего нижний квартиль. Интервал определяется по сумме накопленных частот, не превышающей 25 % от суммы всех частот, — нижняя граница интервала, содержащего верхний квартиль. Интервал определяется по сумме накопленных частот, превышающей 75 % от суммы всех частот. — ширина интервала — накопленные частоты интервала, предшествующего интервалу, содержащему нижний квартиль — накопленные частоты интервала, предшествующего интервалу, содержащему верхний квартиль — частота интервала, содержащего нижний квартиль — частота интервала, содержащего верхний квартиль
Децили
Децили – варианты, делящие ранжированный ряд на десять равных частей. Первый дециль отсекает 1/10 часть совокупности, а девятый дециль отсекает 9/10 частей. Таким образом, различают 9 децилей.
Рассчитываются децили по аналогичным формулам:
Определяем номер дециля по формуле:
Если номер дециля – целое число, то значение дециля будет равно величине элемента ряда, которое обладает накопленной частотой равной номеру дециля. Например, если дециль находится в 20-й позиции, его значение будет равно значению 20-го наблюдения. Если номер дециля – нецелое число, то дециль попадает между двумя наблюдениями. Значением дециля будет сумма значения элемента, для которого накопленная частота равна целому значению номера дециля, и указанной части (нецелая часть номера дециля) разности между этим наблюдением и следующим. Например, если позиция дециля равна 20,25, дециль попадает между 20-м и 21-м наблюдениями, и его значение будет равно значению 20-го наблюдения плюс 1/4 разности между значением 20-го и 21-го наблюдений.
Для интервального ряда:
– значение j-го дециля, — нижняя граница децильного интервала; — ширина децильного интервала; – сумма всех частот, -накопленная частота интервала, предшествующего децильному; — частота децильного интервала.
studfiles.net
Квартили в статистике | univer-nn.ru
Интервалы | Диапазон по продолжительности жизни | Число стран (частота), f | Накопленная частота, f |
1 | 60,8 — 63,53 | 6 | 6 |
2 | 63,53 – 66,25 | 19 | |
3 | 66,25 – 68,98 | 12 | 31 |
4 | 68,98 – 71,70 | 18 | 49 |
5 | 71,70 — 74,43 | 37 | 86 |
6 | 74,43 — 77,15 | 22 | 108 |
| 7 | 77,15 — 79,88 | 27 | 135 |
8 | 79,88 — 82,60 | 15 | 150 |
Аналогично определению медианы вычисляются значения признака, делящие совокупность на 4 равные по численности части – квартили, которые обозначаются заглавной латинской буквой Q с подписным значком номера квартиля. Для первого и третьего квартилей приводим формулы и расчет:
Первый квартиль
Значение квартиля Q1 находится в интервале 68,98 – 71,70, соответствующего частоте fQ1 = 150:4 = 37,5
Третий квартиль
Значение квартиля находится в интервале 68,98 – 71,70, соответствующего частоте fQ3 = (3*150):4 = 112,5
Примеры работ
Материалы сайта
Обращаем Ваше внимание на то, что все материалы опубликованы для образовательных целей.
univer-nn.ru
Квартиль 2019
Что такое «квартиль»
Квартал — это статистический термин, описывающий разделение наблюдений на четыре определенных интервала, основанные на значениях данных и их сравнении со всем набором наблюдений ,
Старайтесь не путать четверть с квартикой.
BREAKING DOWN ‘Quartile’
Чтобы понять квартиль, важно понять медиану как меру центральной тенденции. Медиана в статистике — это среднее значение набора чисел. Это точка, в которой ровно половина данных лежит ниже и выше центрального значения. Итак, учитывая набор из 13 чисел, медиана будет седьмым числом. Шесть чисел, предшествующих этому значению, являются наименьшими числами в данных, а шесть чисел после медианы являются наивысшими числами в приведенном наборе данных. Поскольку медиана не зависит от экстремальных значений или выбросов в распределении, иногда это бывает предпочтительнее среднего.
В то время как медиана является надежной оценкой местоположения, она ничего не говорит о том, как данные по обе стороны от ее значения распространяются или распределяются. Квартал измеряет распространение значений выше и ниже среднего, разделив распределение на четыре группы. Точно так же, как медиана делит данные на половину, так что 50% измерения лежит ниже медианы и 50% лежит над ней, квартиль разбивает данные на четверти, так что 25% измерения меньше, чем нижняя квартиль, 50 % меньше среднего, а 75% меньше, чем верхний квартиль.
Квартал делит данные на три точки — более низкий квартиль, медианный и верхний квартиль — для формирования четырех групп набора данных. Нижняя квартиль или первый квартиль обозначаются как Q1, а среднее число находится между наименьшим значением набора данных и медианной. Второй квартиль Q2 также является медианным. Верхний или третий квартиль, обозначенный как Q3, является центральной точкой, которая находится между медианным и наибольшим числом распределения. Теперь мы можем отобразить четыре группы, сформированные из квартилей. Первая группа значений содержит наименьшее число до Q1; вторая группа включает Q1 в медиану; третий набор является медианным для Q3; и четвертая категория включает Q3 в самую высокую точку данных всего набора.
Каждый квартиль содержит 25% от общего количества наблюдений. Как правило, данные распределяются от самых маленьких до крупнейших, причем эти наблюдения падают ниже 25% от всех проанализированных данных, выделенных в 1-м квартиле, наблюдения падают между 25. 1% и 50% и распределяются во 2-м квартиле, тогда наблюдения падают между 51% и 75% выделены в 3-м квартиле и, наконец, остальные наблюдения, выделенные в 4-м квартиле.
Пример квартили
Давайте работать с примером.Предположим, что распределение математических баллов в классе из 19 учеников в порядке возрастания:
59, 60, 65, 65, 68, 69, 70, 72, 75, 75, 76, 77, 81, 82, 84 , 87, 90, 95, 98
Сначала отмет
ru.toptipfinance.com
Пояснения к таблицам
| Минимальный уровень: | наименьшее значение заработной платы в изучаемом массиве. |
| Максимальный уровень: | наибольшее значение заработной платы в изучаемом массиве. |
| Мода: | наиболее часто встречающееся значение заработной платы в изучаемом массиве. |
| Медиана, или Средний квартиль: | значение заработной платы, расположенное в середине изучаемого массива, упорядоченного по возрастанию. |
| Нижний квартиль: | значение заработной платы, ниже которого в упорядоченном по возрастанию массиве находится четверть (25%) данных о заработных платах. |
| Верхний квартиль: | значение заработной платы, выше которого в упорядоченном по возрастанию массиве находится четверть (25%) данных о заработных платах. |
| Среднее арифметическое: | сумма всех значений заработных плат исследуемого массива, деленная на количество заработных плат, содержащихся в массиве. |
Показатели, на которые следует ориентироваться при определении среднерыночной стоимости специалиста
Наиболее распространенным видом среднего значения заработной платы является среднее арифметическое. Однако среднее арифметическое довольно чувствительно к влиянию экстремальных значений (слишком малые или слишком большие зарплаты) и его значение смещается в сторону этих экстремальных значений, поэтому ориентироваться на данный показатель в случае большого разброса данных особого смысла не имеет.
При решении вопроса о соответствии зарплаты специалиста среднему рыночному значению, следует руководствоваться значением медианы, которая в отличие от среднего арифметического не чувствительна к влиянию экстремальных значений.
Для понимания того, находится ли интересующее Вас значение заработной платы в рыночном коридоре, следует ориентироваться на диапазон зарплат между нижним и верхним квартилями, в котором сосредоточены 50% исследуемых данных.
Мода это наиболее часто встречающееся значение. В то время как любой исследуемый массив данных по заработным платам всегда обладает одним средним арифметическим и одной медианой, у набора данных может быть одна мода, ни одной моды или несколько мод. Мода полезна в том случае, когда нужно узнать какие значения зарплат по исследуемой позиции наиболее популярны.
Приводимые значения, характеризующие исследуемый массив, а также таблица соответствия диапазонов зарплат и требований к специалисту, позволяют устанавливать и корректировать зарплату специалиста с учетом его профессиональных навыков и опыта работы, а также разрабатывать и применять схемы материального поощрения персонала компании.
Пример расчета приводимых показателей
Для наглядности демонстрации расчета показателей для абстрактной позиции ограничимся, например, размером исследуемого массива заработных плат n = 25, где 13 значений зарплат соответствуют предложениям работодателей, а 12 значений − ожиданиям Соискателей.
Пусть указаны следующие значения заработных плат (в долларах):
в предложениях работодателей: 1300; 1000; 800; 700; 800; 500; 1100; 700; 600; 800; 1200; 900; 600;
в ожиданиях Соискателей: 900; 600; 1000; 800; 1100; 800; 700; 1100; 900; 500; 900; 800.
Таким образом, изучаемый массив зарплат:
1300; 1000; 800; 700; 800; 500; 1100; 700; 600; 800; 1200; 900; 600; 900; 600; 1000; 800; 1100; 800; 700; 1100; 900; 500; 900; 800.
Для удобства восприятия расположим зарплаты в порядке возрастания:
500; 500; 600; 600; 600; 700; 700; 700; 800; 800; 800; 800; 800; 800; 900; 900; 900; 900; 1000; 1000; 1100; 1100; 1100; 1200; 1300.
Определение позиций квартилей в массиве:
нижний квартиль: (n+1)/4= (25+1)/4= 6.5,
т.е. значение квартиля находится между 6 и 7 элементами массива;
средний квартиль: (n+1)/2= (25+1)/2= 13,
т.е. значение квартиля соответствует 13-ому элементу массива;
верхний квартиль: 3*(n+1)/4=3*(25+1)/4=19.5,
т.е. значение квартиля находится между 19 и 20 элементами массива.
| Минимальное значение | 500$ |
| Максимальное значение | 1300$ |
| Мода | 800$ |
| Медиана | 800$ |
| Нижний квартиль | 700$ |
| Верхний квартиль | 1000$ |
| Среднее арифметическое | 844$ |
Таким образом, зарплаты, сосредоточенные вблизи значения нижнего квартиля, соответствуют оплате труда специалиста с минимально необходимыми навыками работы, имеющим базовое образование. Данный уровень чаще всего применим для молодых специалистов с небольшим опытом работы.
Медиана характеризует среднерыночный уровень оплаты труда специалистов с уверенными профессиональными навыками, имеющими опыт работы не менее двух-трех лет по данной позиции, базовое образование, дополненное курсами, тренингами и т.п.
Зарплаты, сосредоточенные в интервале от верхнего квартиля и выше, соответствуют оплате труда специалистов с отличными профессиональными навыками, имеющими опыт самостоятельной работы по данному профилю, опыт руководства и развития новых направлений.
Индекс востребованности оценивает количество резюме, размещенных в базе портала Superjob.ru в конкретном регионе / городе, приходящихся на одну соответствующую вакансию. Значение индекса, близкое к единице, означает, что спрос регионального рынка труда на таких специалистов не удовлетворен. Существенное превышение индекса над единицей означает переизбыток данных специалистов на анализируемом рынке труда.
Подписка на результаты новых исследований
© Перепечатка в любых СМИ, в том числе в Интернете, возможна при условии прямой активной ссылки на портал Superjob.ru.
www.superjob.ru
Квартили и интерквартильный интервал (IQR) в MS EXCEL. Примеры и методы
Для вычисления квартилей в MS EXCEL существует специальная функция КВАРТИЛЬ(). В этой статье дадим определение квартилей и научимся их вычислять для выборки и для непрерывного распределения. Также вычислим интерквартильный интервал.
Квартили (Quartiles) — значения, которые делят выборку (набор значений) на четыре части, содержащие приблизительно равное количество наблюдений (по 25%).
Поясним определение квартиля на примере.
Пусть имеется выборка, состоящая из 50 значений в ячейках А7:А56 (см. файл примера, лист Квартиль-выборка). Для наглядности отсортируем значения по возрастанию и построим гистограмму.
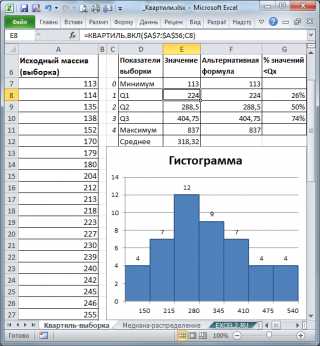
Чтобы разделить выборку на 4 части достаточно 3-х квартилей.
Первый квартиль (или нижний квартиль, Q1) делит выборку, на 2 части: примерно 25% значений в выборке меньше Q1, остальные 75% — больше. Для вычисления 1-го квартиля используйте формулу =КВАРТИЛЬ.ВКЛ(A7:A56;1). Для нашей выборки формула вернет значение 224. Значения 224 нет в выборке, формула произвела интерполяцию на основе 2-х соседних значений 223 и 227.
Примечание: Функция КВАРТИЛЬ.ВКЛ() появилась в MS EXCEL 2010. В более ранних версиях использовалась аналогичная ей функция КВАРТИЛЬ().
Чтобы убедиться, что примерно 25% значений меньше, чем 224, используем формулу =СЧЁТЕСЛИ(A7:A56;»<«&224)/СЧЁТ(A7:A56). В результате получим, что 26% меньше, чем 1-й квартиль.
Чем в выборке больше значений и меньше повторов, тем точнее деление выборки квартилями на четверти.
Примечание: Первый квартиль — это то же самое, что и 25-я процентиль. Подробнее см. статью про процентили.
Второй квартиль (или медиана, Q2) также делит выборку, на 2 равные части: половина чисел множества больше, чем медиана, а половина чисел меньше, чем медиана. Для вычисления 2-го квартиля используйте формулу =КВАРТИЛЬ.ВКЛ(A7:A56;2) или =МЕДИАНА(A7:A56)
Третий квартиль (или верхний квартиль, Q3) делит выборку, на 2 части: примерно 75% значений в выборке меньше Q3, остальные 25% — больше. Для вычисления 3-го квартиля используйте формулу =КВАРТИЛЬ.ВКЛ(A7:A56;3) или =ПРОЦЕНТИЛЬ.ВКЛ(A7:A56;0,75)
Примечание: Третий квартиль — это то же самое, что и 75-я процентиль.
Второй аргумент функции КВАРТИЛЬ.ВКЛ() может также принимать значения 0 и 4. В первом случае функция вернет минимальное значение, во втором – максимальное.
Интерквартильный размах
Интерквартильным размахом или интерквартильным интервалом (InterQuartile range, IQR) называется разность между третьим и первым квартилями (Q3 — Q1). Интерквартильный размах является характеристикой разброса значений в выборке.
Примечание: Характеристикой разброса значений в выборке является также дисперсия и стандартное отклонение.
Интерквартильный размах, а также квартили используются при построении Блочной диаграммы, которая полезна для оценки разброса значений (variation) в небольших выборках или для сравнения нескольких выборок имеющих сходные распределения.

Подробнее о построении Блочной диаграммы см. статью Блочная диаграмма в MS EXCEL.
Квартили непрерывного распределения
Если функция распределения F(х) случайной величины х непрерывна, то 1-й квартиль является решением уравнения F(х)=0,25, второй — F(х)=0,5, а третий F(х)=0,75.
Примечание: Подробнее о Функции распределения см. статью Функция распределения и плотность вероятности в MS EXCEL.
Если известна функция плотности вероятности p(х), то 1-й квартиль можно найти из уравнения:
Например, решив аналитическим способом это уравнение для Логнормального распределения lnN(μ; σ2), получим, что медиана (2-й квартиль) вычисляется по формуле eμ или в MS EXCEL =EXP(μ). При μ=1, медиана равна 2,718.

Обратите внимание на точку Функции распределения, для которой F(х)=0,5 (см. картинку выше или файл примера, лист Квартиль-распределение). Абсцисса этой точки равна 2,718. Это и есть значение 2-го квартиля (медианы), что естественно совпадает с ранее вычисленным значением по формуле eμ.
Примечание: Напомним, что интеграл от функции плотности вероятности по всей области задания случайной величины равен единице:
Поэтому, линии квартилей (х=квартиль) делят площадь под графиком функции плотности вероятности на 4 равные части.
Квартили в MS EXCEL
Чтобы вычислить в MS EXCELквартили заданного распределения необходимо использовать соответствующую обратную функцию распределения.
При вычислении квартилей в MS EXCEL используются обратные функции распределения: НОРМ.СТ.ОБР(), ЛОГНОРМ.ОБР(), ХИ2.ОБР(), ГАММА.ОБР() и т.д. Подробнее о распределениях, представленных в MS EXCEL, можно прочитать в статье Распределения случайной величины в MS EXCEL.
Например, в MS EXCEL 1-й квартиль для логнормального распределения LnN(1;1) можно вычислить по формуле =ЛОГНОРМ.ОБР(0,25;1;1), а 3-й квартиль для стандартного нормального распределения по формуле =НОРМ.СТ.ОБР(0,75).
excel2.ru
Квартили и децили.
По аналогии с нахождением медиан в вариационных рядах можно отыскать значение признака у любой по порядку единицы ранжированного ряда. Так в частности можно найти значение у единиц делящих ряд на 4 равные части на 10 и т.п.
Варианты, которые делят ранжированный ряд на 4, называют квартилями.
При этом различают: нижний (или первый) квартиль (Q1) – значение признака у единицы у единицы ранжированного ряда, делящей совокупность в соотношении ¼ к ¾ и верхний (или третий) квартиль(Q3) – значение признака у единицы ранжированного ряда, делящий совокупность в соотношении ¾ к ¼.
Второй квартиль, есть медиана Q2 = Ме нижний и верхний квартили в интервальном ряду рассчитывается по формуле аналогично медиане.
для нижнего
для верхнего
где xo – нижняя граница интервала, содержащего квартиль (нижний и верхний)
f1Q1-1 – накопленная частота интервала, предшествующего интервалу, содержащему нижний квартиль.
f1Q3-1 – то же для вернего квартиля.
FQ1; FQ3 – частоты квартильных интервалов (нижнего и верхнего).
Интервалы, в которых содержатся Q1 и Q3 определяют по положенным частотам (или частостям).
Пример.
Вал.прод., т.р. х | Число предприятий f | Накопленная частота f1 |
До 50 50-100 100-150 150-200 200-250 250-300 > 300 | 3 6 10 21 33 18 9 | 3 9 19 40 73 91 100 |
Из примера находим первый квартиль
Q1 =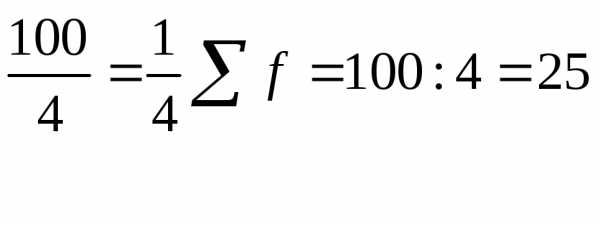 т.е.
интервал 150-200
т.е.
интервал 150-200
это означает, что у ¼ всех предприятий выпуск продовольствия не превышает 164,3 т.р.
кроме квартилей рассчитывают децили – варианты, делящие ранжированный ряд на 10 равных частей.
Обозначаются они через D, первый дециль D1 делит ряд в соотношении 1/10 и 9/10, второй D2 – 2/10 и 8/10

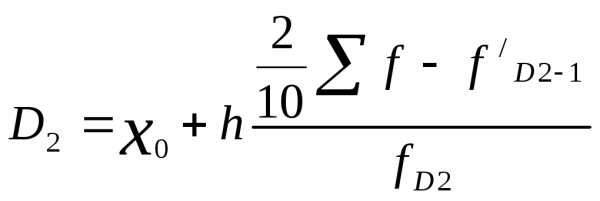
и медиана, и квартили, и децили принадлежат к так называемым порядковым статистикам, под которым понимают вариант, занимающий определенное порядковое место в ранжированном ряду.
Понятие о моментах распределения.
В математической статистике моментом k-того прядка называется средняя арифметическая из k- той степени отложений отдельных вариантов от некоторой постоянной величины А, т.е. если обозначить момент к-того порядка
Через Мк, то в общем виде

в статистике находят применение моменты первых четырех.
Теоретические кривые распределения.
Графическое изображение вариационного ряда дает представление о форме распределения. Однако судить о закономерностях данного эмпирического распределения по полигону или гистограмме рискованно, т.к. оно зависит от ряда причин, и частности от числа исследованных единиц.
Характерные черты распределения проявляются при росте числа наблюдений.
По мере увеличения числа наблюдений и уменьшения величины интервала для непрерывных признаков ступенчатость гистограммы или ломанность полигона будут сглаживаться и приближаться к некоторой плановой кривой.
Имея графическое изображение эмпирического вариационного ряда, можно представить тот предел в виде сплошной плавной линии, к которой стремится данная гистограмма или полигон при увеличении числа наблюдений и уменьшение величины интервала.
Этот предел в виде сплошной плавной линии называют кривой распределения.
Кривая распределения может рассматриваться как некая теоретическая (вероятностная) форма распределения, свойственная той или иной совокупности в конкретных условиях места и времени. Если кривая описана математически, т.е. выражена уравнением с определенными параметрами, то она более точно отражает закономерности того или иного распределения.
Имея дело с эмпирическими распределениями можно предположить, что данному эмпирическому распределению соответствует характерное для него теоретическая кривая.
Знание формы теоретической кривой может быть использовано в различных практических расчетах, прогнозах. Поэтому при изучении закономерностей распределение нужно определить тип кривой распределения, установить по эмпирическим данным ее параметры, рассчитать по найденному уравнению
Теоретические частоты (построить эту теоретическую кривую), проверить на сколько эмпирические частоты близки к предполагаемым теоретическим.
Кривая нормального распределения и ее построение по эмпирическим данным.
Среди различных кривых распределения особое место занимает нормальное распределение.
Нормальное распределение на графике представляет собой симметрическую колоколообразную кривую, имеющую максимум в точке соответствующей средней арифметической ряда. Эта же точка является модой и медианой ряда.
Точки перегиба у нормальной кривой на расстоянии от средней арифметической.
график
Кривая нормального распределения выражается следующим уравнением:
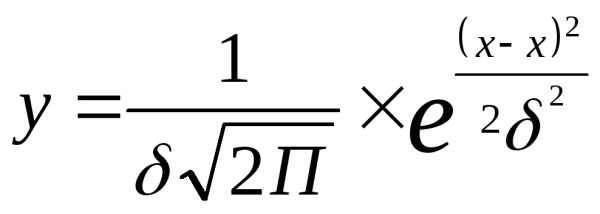
где у ордината кривой распределения П=3,14 е = 2,182… -основание натурального логарифма.
Отклонение отдельных
вариантов от средней арифметической
нормируют по 
и именуют нормированным отклонением

если в приведенной выше формуле кривой нормального распределения произвести соответственную замену, то уравнение примет вид
Как видно из
уравнения, два параметра – средняя
арифметическая  и средне квадратическое отклонение
и средне квадратическое отклонение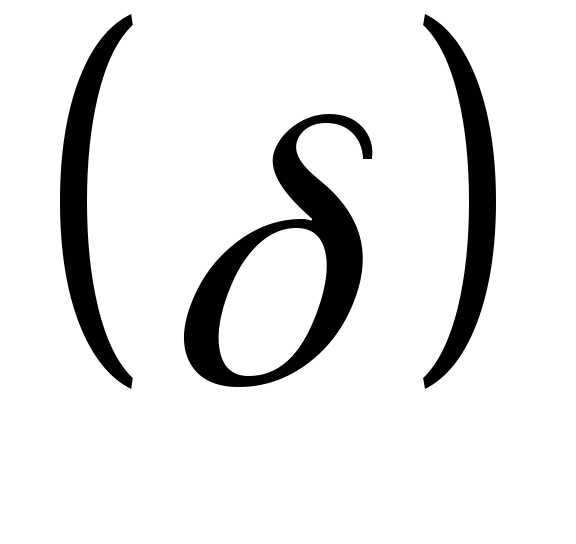 — определяют очертание симметричной
кривой нормального распределения.
— определяют очертание симметричной
кривой нормального распределения.
В зависимости от их значения она может иметь разный центр группирования, быть более удлиненной или сжатой.
Если площадь, ограниченную кривой нормального распределения, принять за 1 или за 100%, то можно рассчитать площадь, заключенную между кривой и е двумя ординатами.
Установлено, что
площадь между ординатами, проведенными
на расстояние 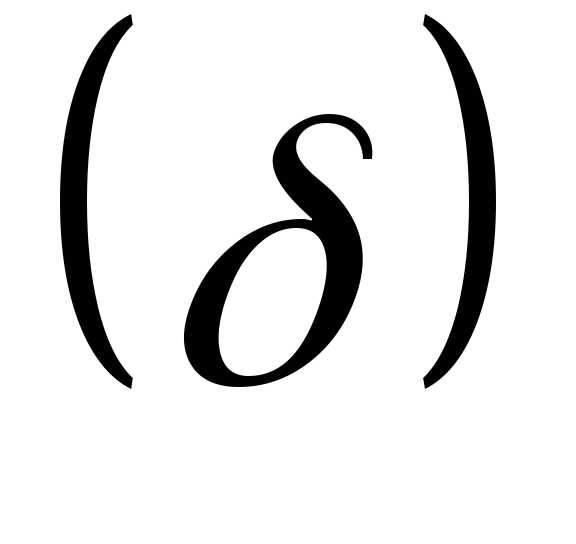 с каждой стороны от средней арифметической,
составляет 0,683 всей площади.
с каждой стороны от средней арифметической,
составляет 0,683 всей площади.
Это означает, что
68,3% всех исследованных единиц (частот)
отклоняются от средней арифметической
не более чем на 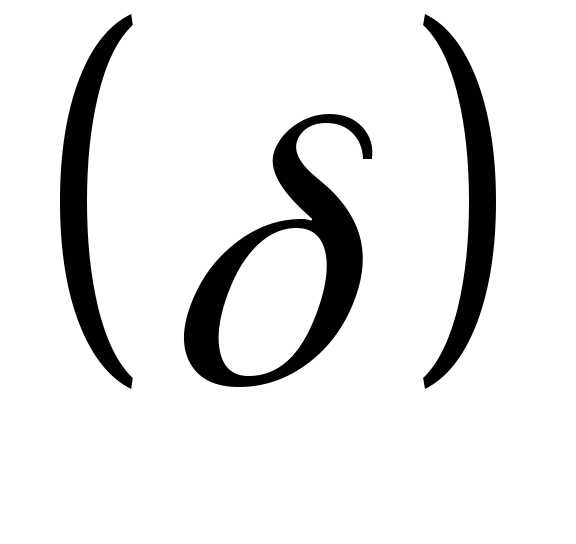 ,
т.е. находятся в пределах (
,
т.е. находятся в пределах ( ).
).
S,
заключенная между ординатами, проведенными
на расстояние 2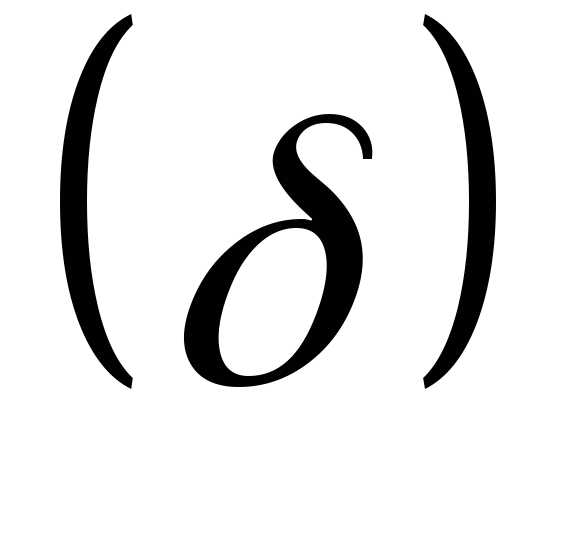 в одну другую сторону от средней
арифметической, составляет 0,954, т.е. всех
единиц совокупности находятся в пределах
в одну другую сторону от средней
арифметической, составляет 0,954, т.е. всех
единиц совокупности находятся в пределах .
Это так называемое правило 3-сигментов,
характерное для нормального распределения.
.
Это так называемое правило 3-сигментов,
характерное для нормального распределения.
Нормальное распределение характерно для явлений в области биология и техники.
В экономике чаще встречаются умеренно ассиметричные распределения.
Тем не менее кривая нормального распределения имеет определенное значение в анализе вариационных рядов и в теории выборочного метода.
Есть несколько способов построения кривой нормального распределения по эмпирическим данным, если есть основание предположить близость данного распределение к нормальному. По одному из этих способов теоретические частоты (m1) отыскивается
где  —
табулированная величина, отыскиваемая
по отклонениям t, а Nh/
—
табулированная величина, отыскиваемая
по отклонениям t, а Nh/ — константа, на к умножаются значения
— константа, на к умножаются значения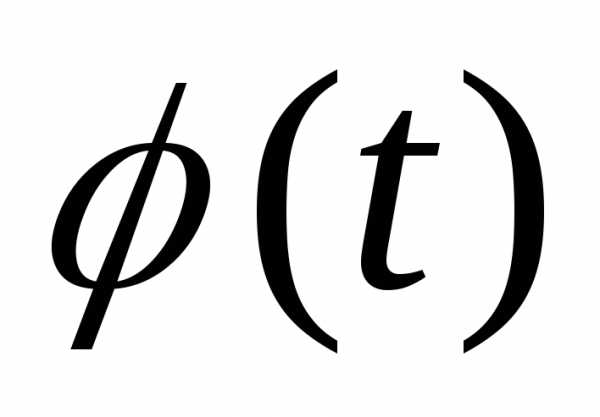 и которая определяет теоретические
частоты исходя из общей численности
единиц совокупности и числа выделяемых
групп. Последовательность расчета
следующая:
и которая определяет теоретические
частоты исходя из общей численности
единиц совокупности и числа выделяемых
групп. Последовательность расчета
следующая:
1 находим 
2 находим 
3 находим нормированное
отклонение каждого варианта от средней
арифметической 
4 для найденных t
по таблице определяем 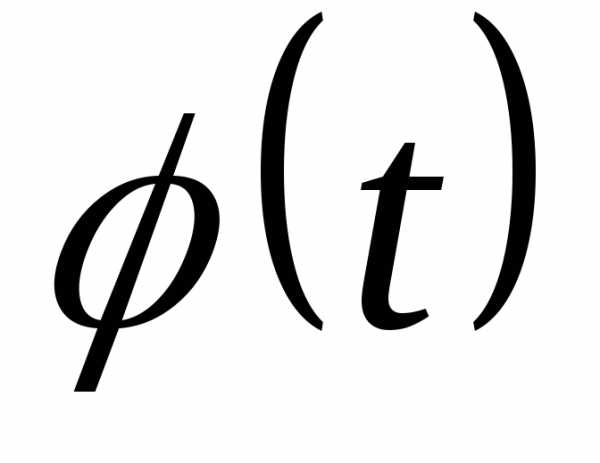
5 расчитаем константу 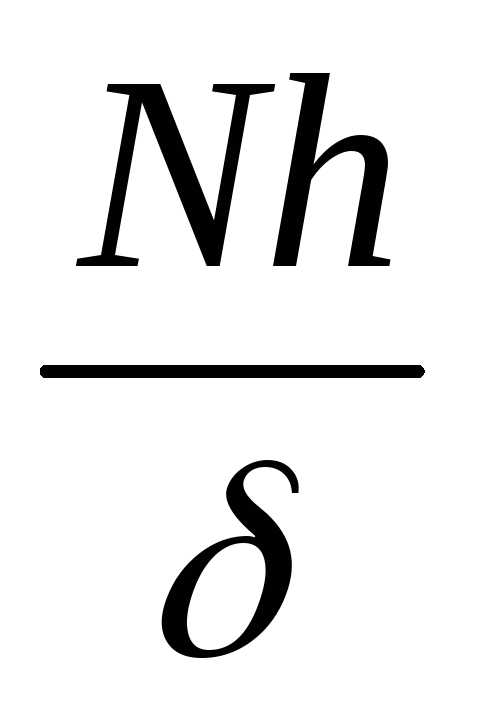
6 каждое значение 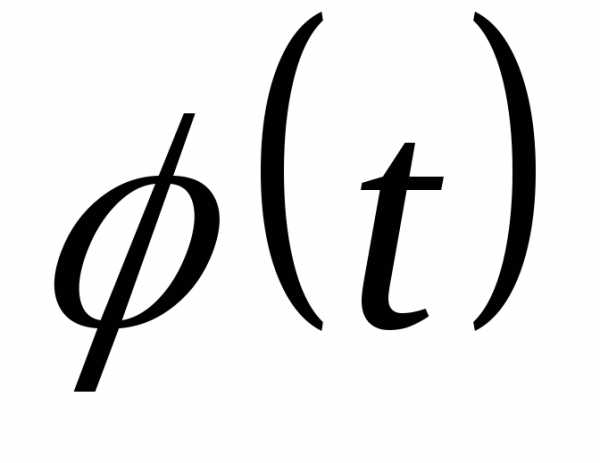 умножаем на константу
умножаем на константу
результаты умножения (после округления до целых чисел) будут искомыми частотами (m/) теоретической кривой нормального распределения.
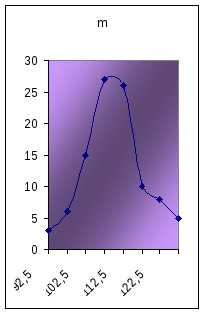
Пример 100предприятиц по % выполнения плана по валовой продукции (х). показано на рис распределение и теоретическое, и эмпирическое.
Середина интервала х | m |
|
| | 63 |
92,5 97,5 102,5 107,5 112,5 117,5 122,5 127,5 | 3 6 15 27 26 10 8 5 | -17,7 -12,7 -7,7 -2,5 2,5 7,3 12,3 17,3 | -2,21 -1,59 -0,96 -0,31 0,29 0,91 1,54 2,16 | 0,0347 0,1127 0,2516 0,3802 0,3825 0,2637 0,1219 0,0387 | 2,1861 2 7,1001 7 15,85 16 23,95 24 24,097 24 16,61 17 7,68 8 2,44 2 |
Итого | 100 |
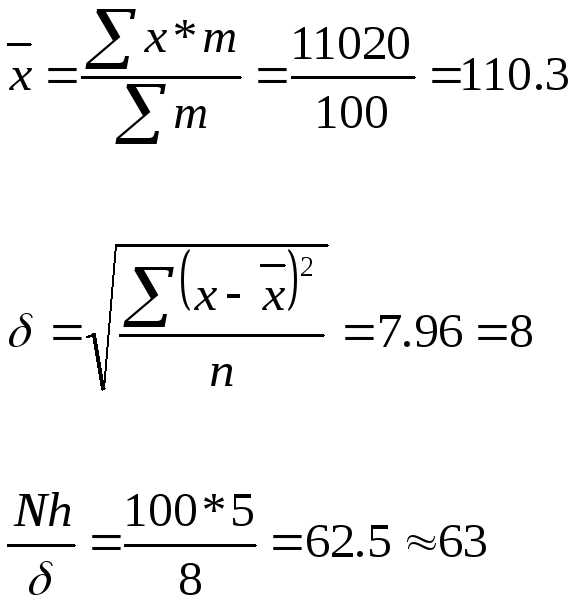
studfiles.net
КВАРТИЛЬ (функция КВАРТИЛЬ) — Служба поддержки Office
Возвращает квартиль множества данных. Квартиль часто используются при анализе продаж для разбиения генеральной совокупности на группы. Например, можно воспользоваться функцией КВАРТИЛЬ, чтобы найти среди всех предприятий 25 процентов наиболее доходных.
Важно: Эта функция была заменена одной или несколькими новыми функциями, которые обеспечивают более высокую точность и имеют имена, лучше отражающие их назначение. Хотя эта функция все еще используется для обеспечения обратной совместимости, она может стать недоступной в последующих версиях Excel, поэтому мы рекомендуем использовать новые функции.
Дополнительные сведения о новых функциях см. в разделах Функция КВАРТИЛЬ.ИСКЛ и Функция КВАРТИЛЬ.ВКЛ.
Синтаксис
КВАРТИЛЬ(массив;часть)
Аргументы функции КВАРТИЛЬ описаны ниже.
-
Массив Обязательный. Массив или диапазон ячеек с числовыми значениями, для которых определяется значение квартиля.
-
Часть Обязательный. Значение, которое требуется вернуть.
Если часть равна | КВАРТИЛЬ возвращает |
|---|---|
|
0 |
Минимальное значение |
|
1 |
Первую квартиль (25-ю персентиль) |
|
2 |
Значение медианы (50-ю персентиль) |
|
3 |
Третью квартиль (75-ю персентиль) |
|
4 |
Максимальное значение |
Замечания
-
Если массив пуст, функция КВАРТИЛЬ возвращает значение ошибки #ЧИСЛО!.
-
Если значение аргумента «часть» не является целым числом, то оно усекается.
-
Если часть < 0 или часть > 4, функция КВАРТИЛЬ возвращает значение ошибки #ЧИСЛО!.
-
Функции МИН, МЕДИАНА и МАКС возвращают то же значение, что и функция КВАРТИЛЬ, если аргумент «часть» равен соответственно 0, 2 или 4.
Пример
Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.
Данные | ||
|---|---|---|
|
1 |
||
|
2 |
||
|
4 |
||
|
7 |
||
|
8 |
||
|
9 |
||
|
10 |
||
|
12 |
||
|
Формула |
Описание (результат) |
Результат |
|
=КВАРТИЛЬ(A2:A9;1) |
Первая квартиль (25-я процентиль) для приведенных выше данных (3,5) |
3,5 |
support.office.com

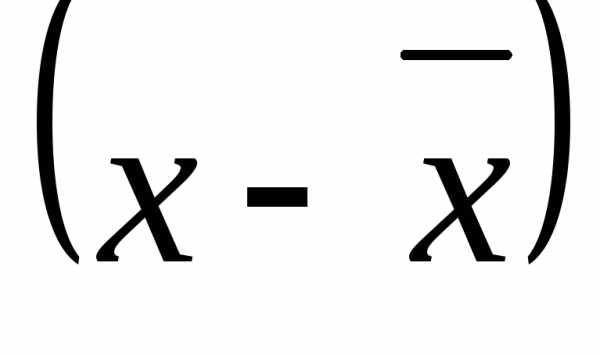
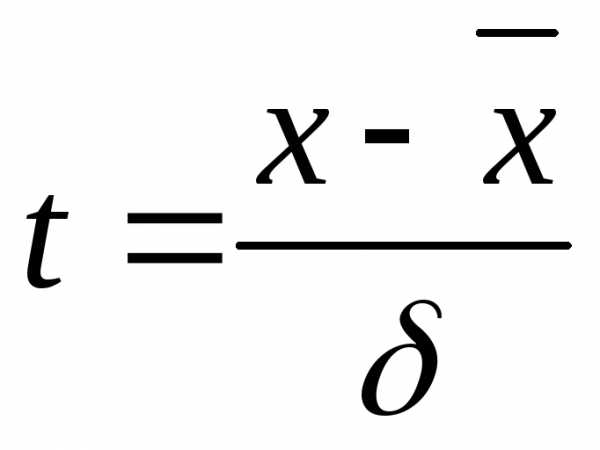

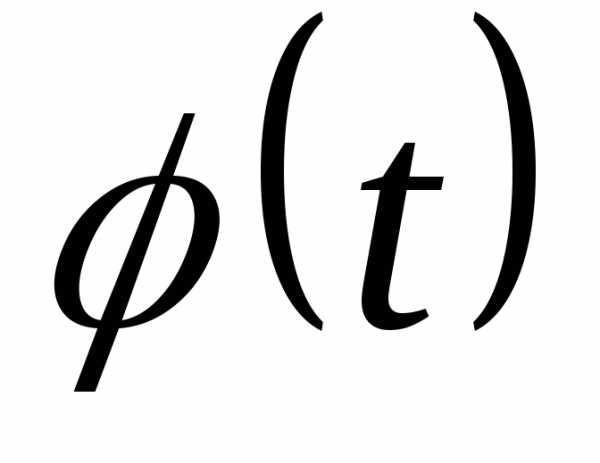 =m/
=m/