Собственные значения и собственные векторы матрицы
13
I. Теоретическая часть
Основные вопросы:
Характеристическая матрица и характеристический многочлен
Собственные значения и собственные векторы матрицы
Нахождение собственных векторов
1. Характеристическая матрица и характеристический многочлен
Рассмотрим квадратную матрицу п-го порядка:
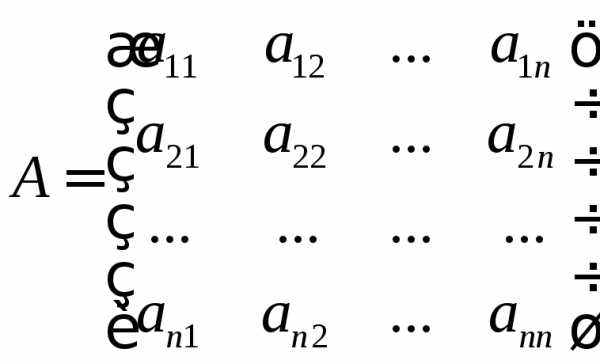 . (1)
. (1)
Умножим единичную матрицу того же порядка на число и вычтем её из матрицы А.
Определение. Матрица вида
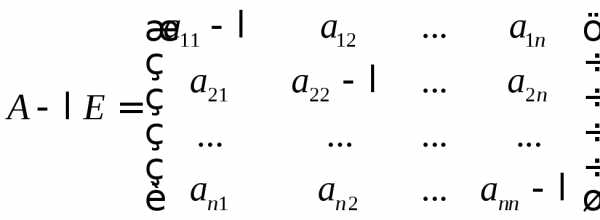 , (2)
, (2)
где λ − независимая переменная, называется
Определение. Определитель характеристической матрицы (2)
(3)
называется характеристическим многочленом матрицы А.
Действительно, выражение (3) является многочленом относительно λ, в чём легко убедиться, вычислив определитель любым способом, например, разложением по первой строке. Степень характеристического многочлена матрицы равна порядку этой матрицы, в данном случае эта степень равна n.
Определение. Следом матрицы А называется сумма её диагональных элементов:
. (4)
Найдём характеристические многочлены для квадратных матриц 2-го и 3-го порядков.
1. Для матрицы 2-го порядка
,
. (5)
где 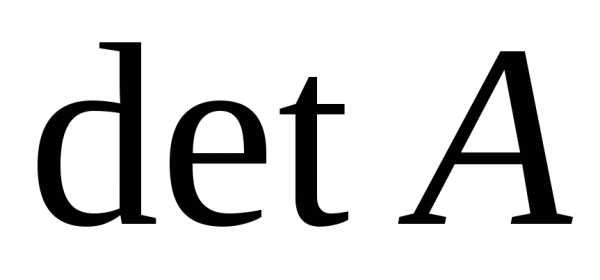 ,
или
,
или − величина определителя матрицыА.
− величина определителя матрицыА.
2. Для матрицы 3-го порядка
,
. (6)
Доказательство. Разложим определитель по первой строке:
=
=
, ч.т.д.
В общем виде характеристический многочлен можно записать в виде:
. (7)
Если положить λ =
0, то 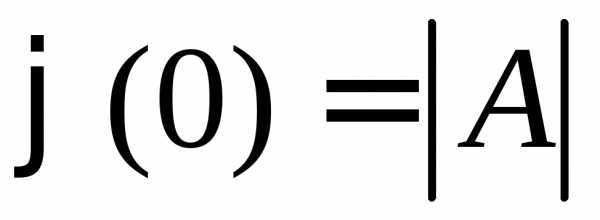 есть свободный член многочлена, равный
определителю матрицыА. Это видно и
из формулы (2).
есть свободный член многочлена, равный
определителю матрицыА. Это видно и
из формулы (2).
Пример 1. Найти характеристический многочлен
матрицы 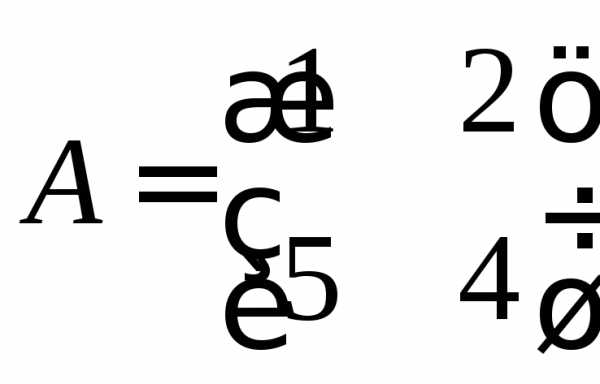 .
.
Решение.
.
Пример 2. Найти характеристический многочлен
матрицы 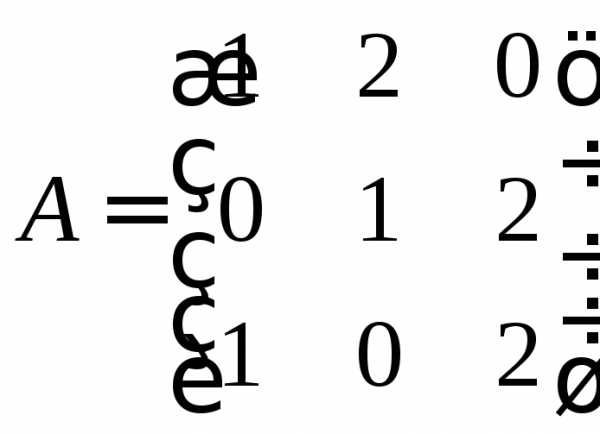 .
.
Решение. Характеристический многочлен найдём, разложив определитель по первой строке:
.
Проверим правильность вычисления коэффициентов по формуле (6):
.
;
.
2. Собственные значения и собственные векторы матрицы
Определение. Рассмотрим квадратную матрицу  .
Пусть для некоторого ненулевого вектора
.
Пусть для некоторого ненулевого вектора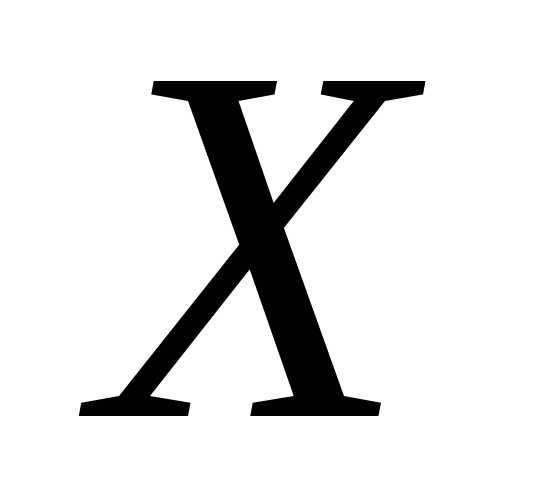
АХ = λХ. (8)
Тогда вектор 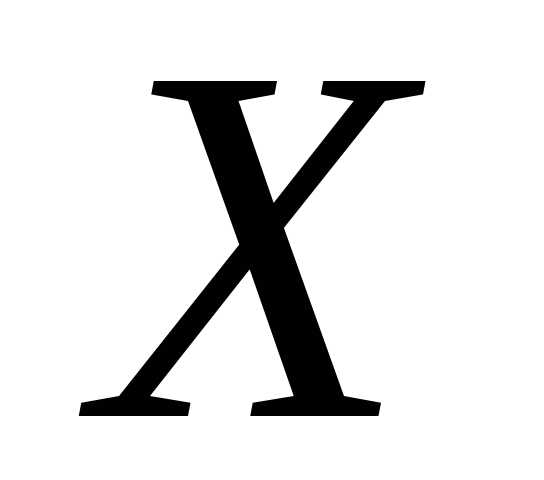 называетсясобственным
вектором матрицы А, а
число называется собственным значением этой матрицы.
называетсясобственным
вектором матрицы А, а
число называется собственным значением этой матрицы.
Определение. Уравнение называется характеристическим уравнением.
Определение. Корнем многочлена называется значение переменной, обращающее этот многочлен в нуль. Корнем матричного многочлена будет матрица, обращающая этот многочлен в нулевую матрицу.
Теорема 1. Собственные значения матрицы А являются корнями характеристического многочлена.
Верно и обратное: каждый корень характеристического многочлена матрицы А
Теорема 2. Если – собственные значения матрицыА, то:
1) 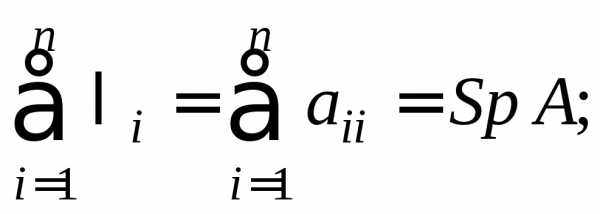
2) 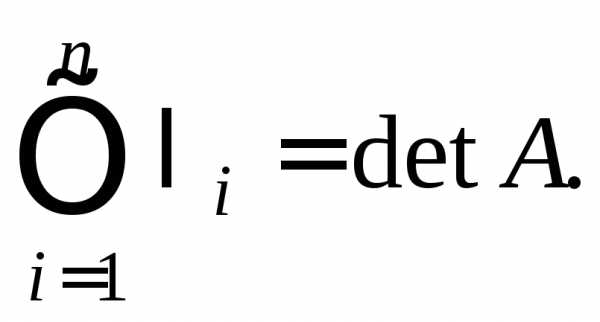
Эти равенства можно использовать в качестве проверки вычисленных собственных значений.
Теорема 3. (Теорема Гамильтона – Кэли).
Любая квадратная
матрица является корнем своего
характеристического многочлена, т. е. 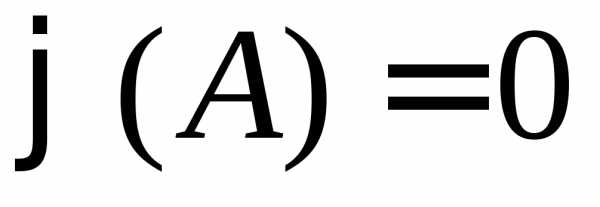 ,
где под нулём понимается нулевая матрица,
а под свободным членом характеристического
многочлена – этот свободный член,
умноженный на единичную матрицу.
,
где под нулём понимается нулевая матрица,
а под свободным членом характеристического
многочлена – этот свободный член,
умноженный на единичную матрицу.
Пример 1. Найти
собственные значения матрицы 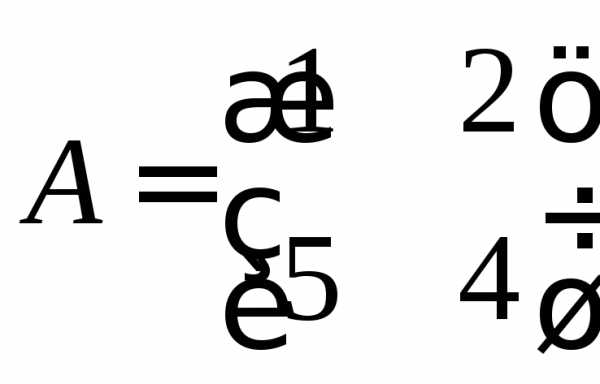
Решение. Чтобы найти собственные значения, приравняем к нулю характеристический многочлен:
=0.
Корни квадратного уравнения: .
Сумма корней ; произведение корней.
Подставим матрицу А в характеристический многочлен:
.
В результате получили нулевую матрицу. Это и означает, что матрица является корнем своего характеристического многочлена.
Пример 2. Показать, что матрица 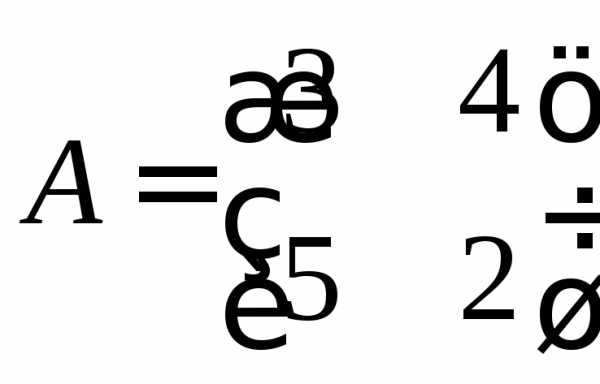 является корнем своего характеристического
многочлена.
является корнем своего характеристического
многочлена.
Решение. ;
Найдём характеристический многочлен матрицы:
.
Вычислим  ,
для этого нужно найти
,
для этого нужно найти
, 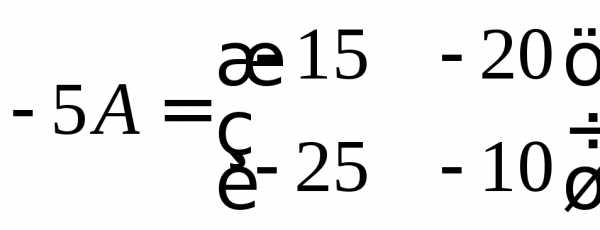 и
и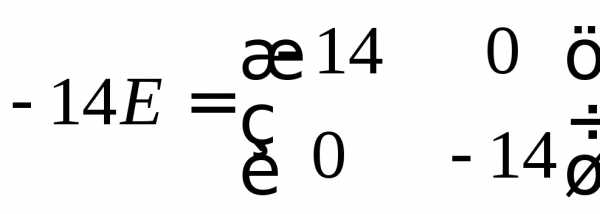 .
.
Тогда
.
studfiles.net
собственные значения и собственные векторы
Собственные векторы и собственные
значения линейного оператора
Определение 1. Собственным
вектором оператора  называют
ненулевой вектор
называют
ненулевой вектор  ,
удовлетворяющий равенству:
,
удовлетворяющий равенству: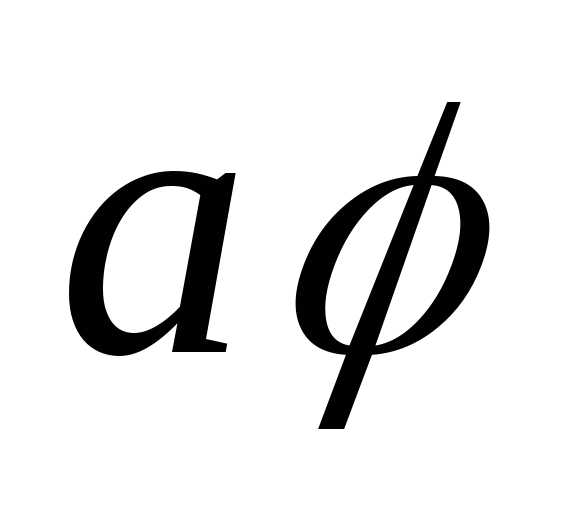 =
=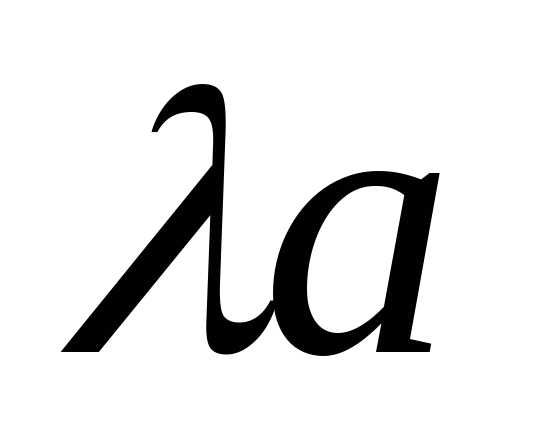 .
.
Определение 2. Собственным
значением оператора  называют
число
называют
число  ,
для которого выполняется равенство:
,
для которого выполняется равенство: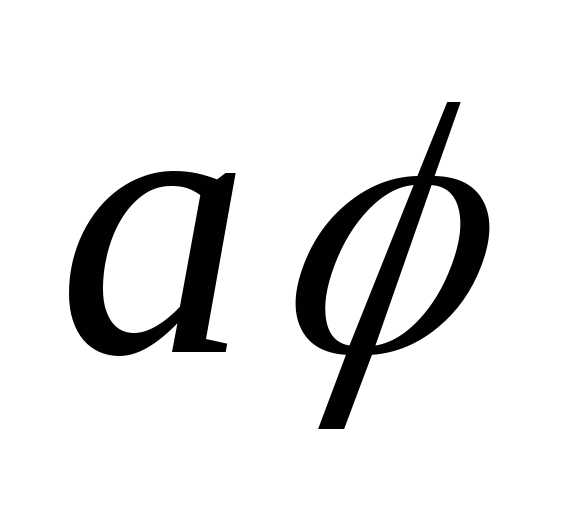 =
=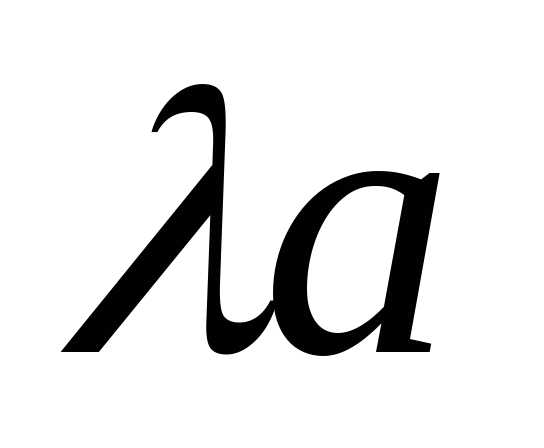
 — ненулевой вектор.
— ненулевой вектор.
| (1) |
(2) |
Решив последнее
уравнение относительно  ,
найдем собственные значения матрицы.
Уравнение (5.8) называютхарактеристическим
уравнением матрицы
,
найдем собственные значения матрицы.
Уравнение (5.8) называютхарактеристическим
уравнением матрицы  .
Найдя корни характеристического
уравнения, последовательно подставляя
их в систему (1) и решая получаемые
системы, найдем собственные векторы
матрицы
.
Найдя корни характеристического
уравнения, последовательно подставляя
их в систему (1) и решая получаемые
системы, найдем собственные векторы
матрицы
Рассмотрим несколько примеров, в каждом из которых будем выполнять последовательность действий решения задачи об отыскании собственных значений и собственных векторов матрицы.
Пример 1.
Найти собственные
значения и собственные векторы матрицы  .
Дать геометрическую интерпретацию
полученного решения.
.
Дать геометрическую интерпретацию
полученного решения.
Матрица имеет размерность 2
 2,
то есть является представлением
линейного оператора в пространстве
2,
то есть является представлением
линейного оператора в пространстве
 .
.Составим уравнение для отыскания собственных векторов в матричном виде:


3. Перепишем матричное уравнение в виде системы уравнений:
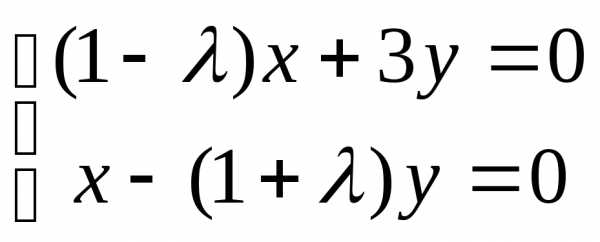
Однородная система имеет ненулевые решения тогда и только тогда, когда определитель ее главной матрицы равен 0. Получаем характеристическое уравнение системы и решаем его:
.
Собственные
значения матрицы  :
: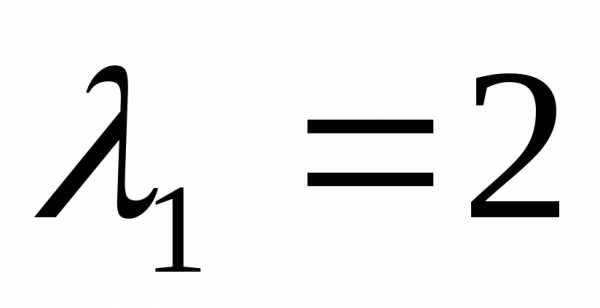 ,
,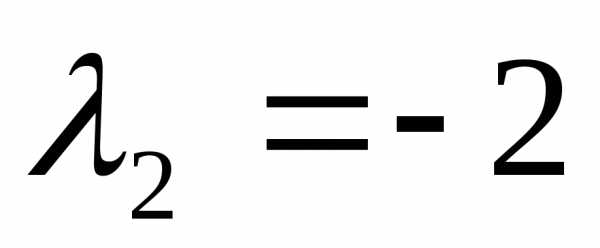 .
.
Найдем собственные векторы для каждого собственного значения:
Пример
2.Найти собственные значения и
собственные векторы линейного оператора
, заданного в некотором базисе матрицейА=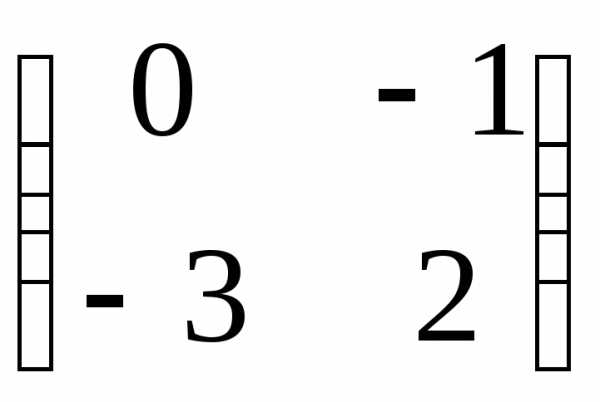 .
.
Составим и решим характеристическое уравнение .
В нашей задаче .
Тогда характеристическое уравнение принимает вид:
, или ,
,
,
— собственные значения линейного оператора.
Найдем собственные векторы, соответствующие собственному значению
 ,
решая матричное уравнение:
,
решая матричное уравнение:
х=0или, т.е.
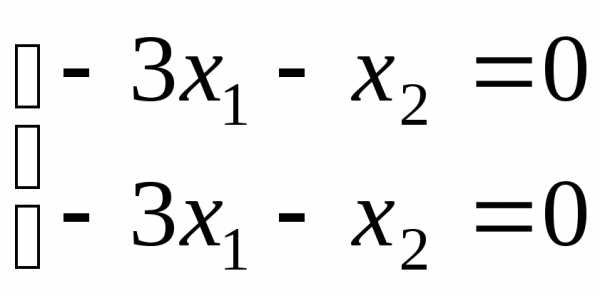 .
.
Полагая в последнем
равенстве 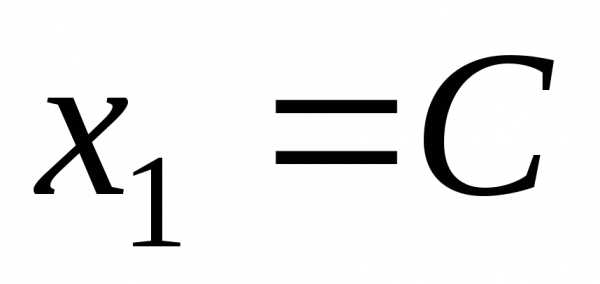 ,
получим
,
получим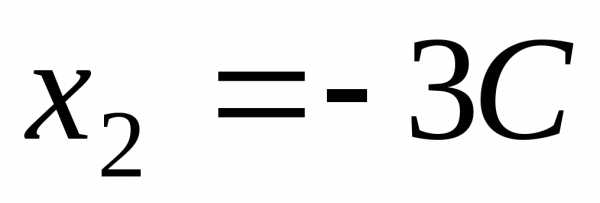 .
.
Откуда собственные
векторы, соответствующие собственному
значению 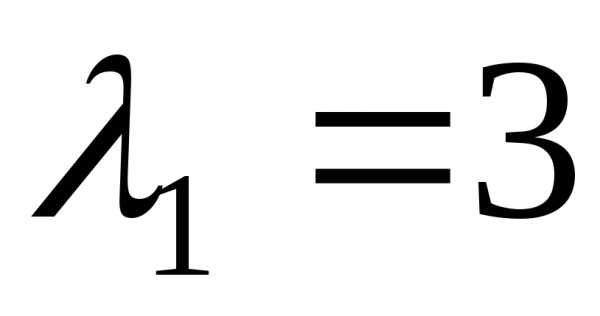 ,
имеют видх1=
,
имеют видх1=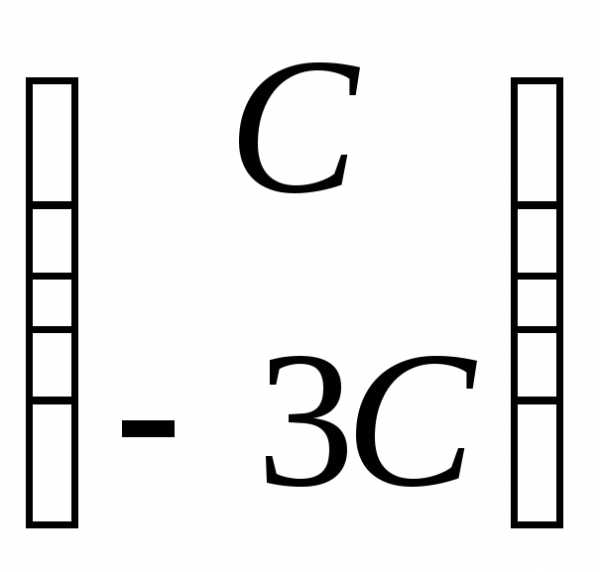 .
.
Найдем собственные векторы, соответствующие собственному значению
 ,
решая матричное уравнение:
,
решая матричное уравнение:
х=0или, т.е.
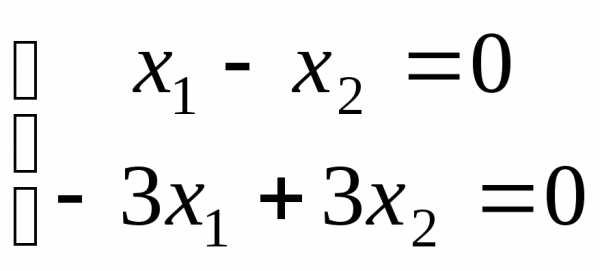 .
.
Полагая в последнем
равенстве  ,
получим
,
получим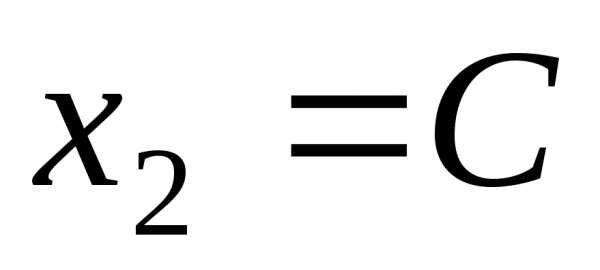 .
.
Откуда собственные
векторы, соответствующие собственному
значению 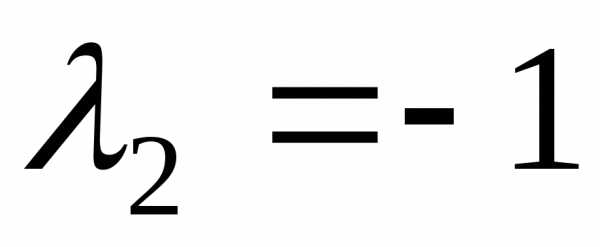 ,
имеют видх2=
,
имеют видх2=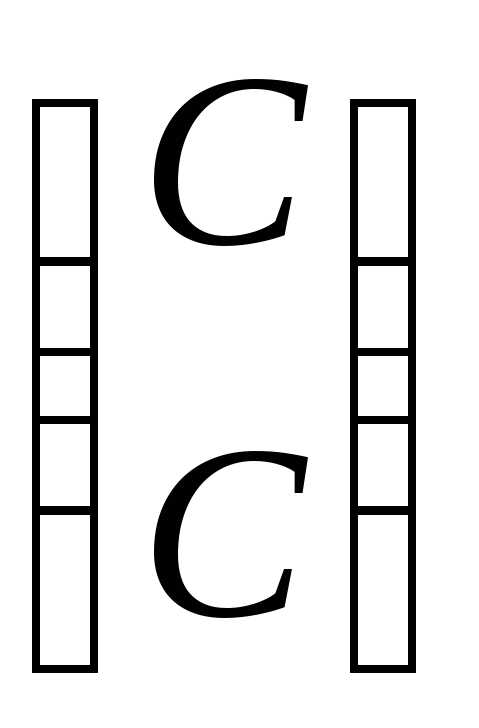 .
.
Ответ. Собственному
значению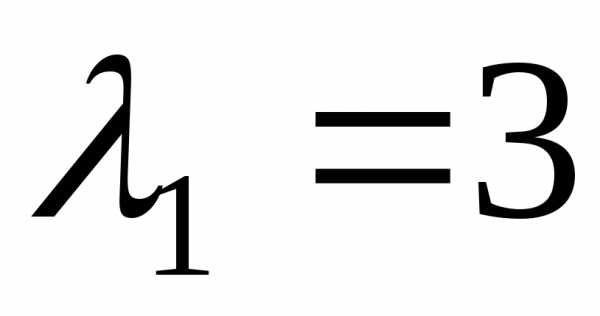 соответствуют собственные векторых1=
соответствуют собственные векторых1=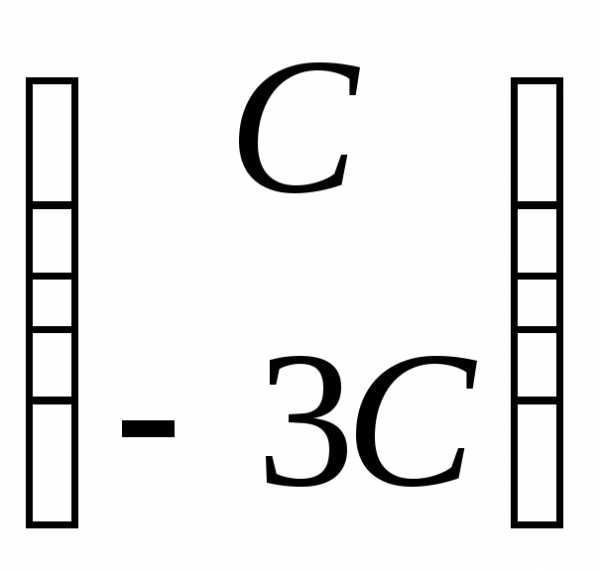 ,
а собственному значению
,
а собственному значению собственные векторы
собственные векторы
х2=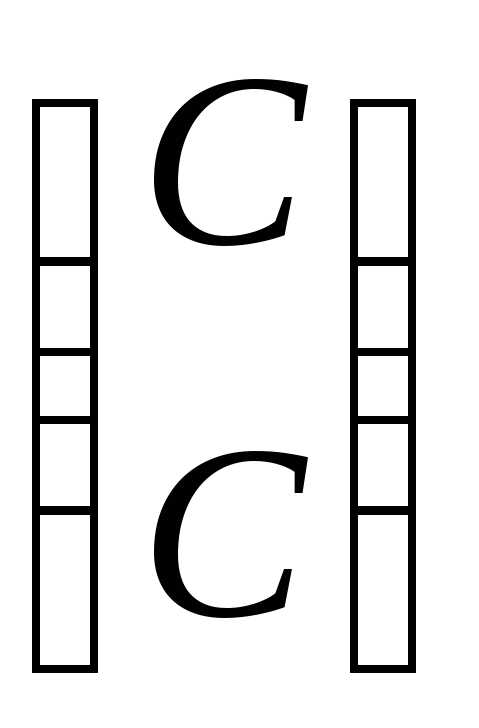 .
.
Пример
3.Найти собственные значения и
собственные векторы линейного оператора
, заданного в некотором базисе матрицейА= .
.
Найдем собственные значения линейного оператора. Для этого составим характеристическое уравнение и найдем его корни:
.
,
,
,
,
, ,
 ,
— собственные значения линейного
оператора.
,
— собственные значения линейного
оператора.
Найдем собственные векторы, соответствующие собственному значению
 .
Исходя из соотношениях=0или в нашем случае
.
Исходя из соотношениях=0или в нашем случае
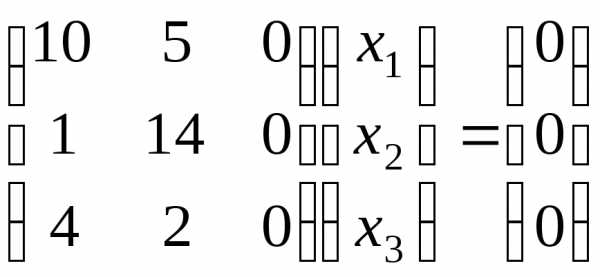 ,
запишем систему:
,
запишем систему:
 Решая методом
Гаусса, получаем
Решая методом
Гаусса, получаем
Поскольку ранг
матрицы системы (r=2)
меньше количества неизвестных, то
система имеет бесконечное множество
решений. Записывая преобразованную
систему и решая ее, получим,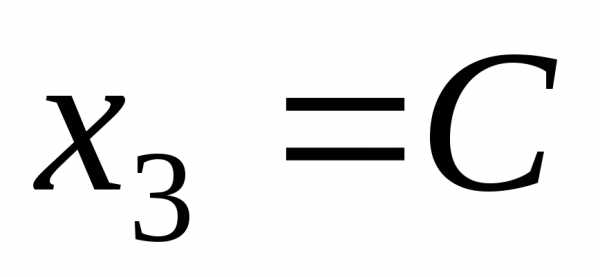 .
.
Таким образом,
собственные векторы, соответствующие
собственному значению 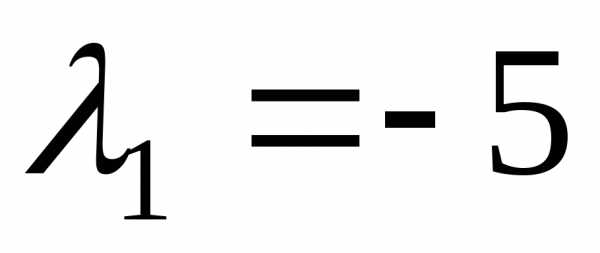 ,
имеют вид:Х1=
,
имеют вид:Х1=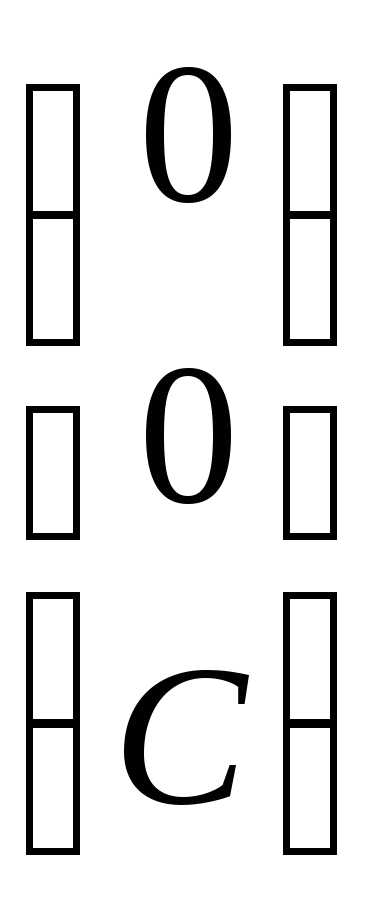 .
.
Найдем собственные векторы, соответствующие собственному значению
 .
Исходя из соотношениях=0или в нашем случае
.
Исходя из соотношениях=0или в нашем случае
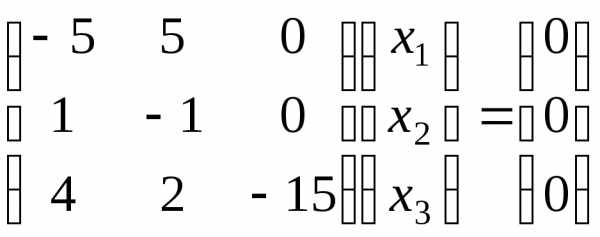 ,
т.е.
,
т.е.
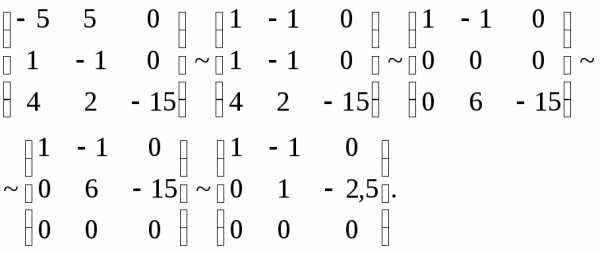
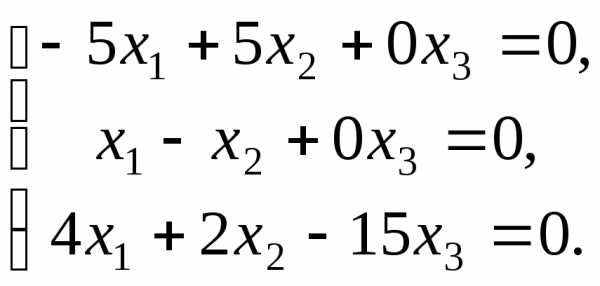 Решая методом
Гаусса, получаем
Решая методом
Гаусса, получаем
откуда, система
принимает вид 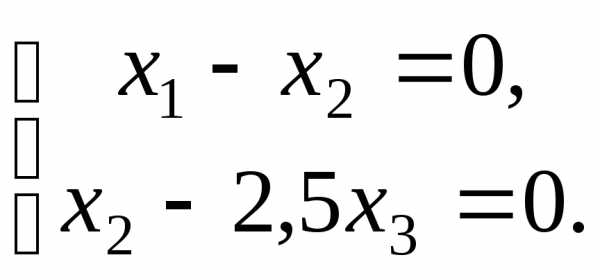
Полагая 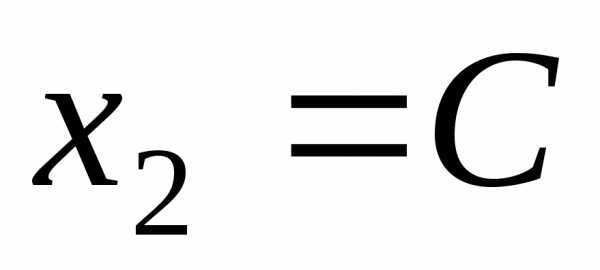 ,
получим
,
получим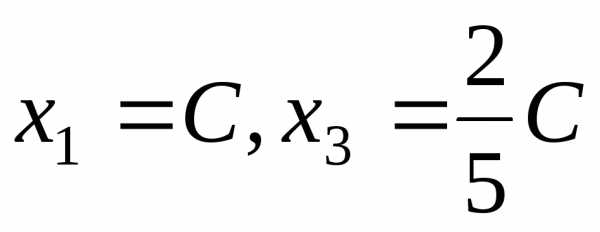 .
.
Таким образом,
собственные векторы, соответствующие
собственному значению  ,
имеют вид:Х2=
,
имеют вид:Х2=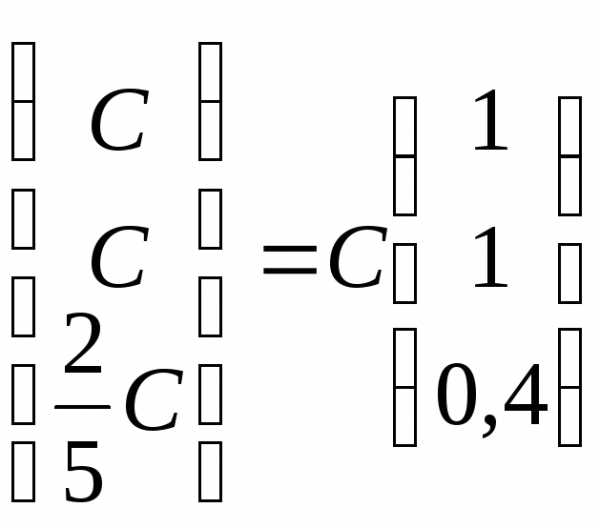 .
.
Найдем собственные векторы, соответствующие собственному значению
 .
Исходя из соотношениях=0или в нашем случае
.
Исходя из соотношениях=0или в нашем случае
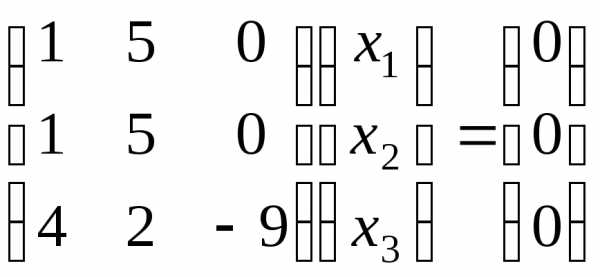 ,
т.е.
,
т.е.
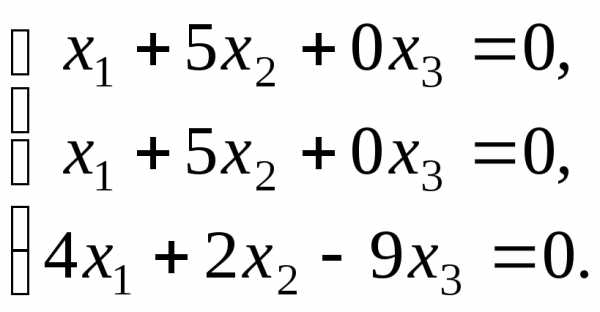 Решая методом
Гаусса, получаем
Решая методом
Гаусса, получаем
,
откуда, система
принимает вид 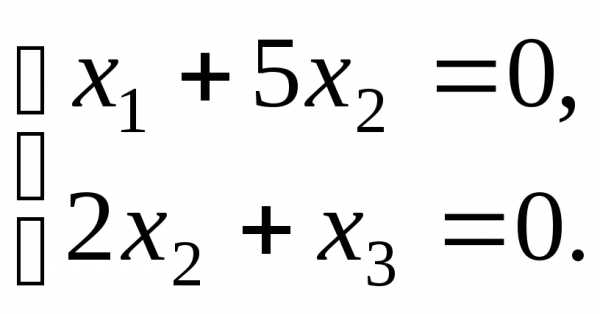
Полагая 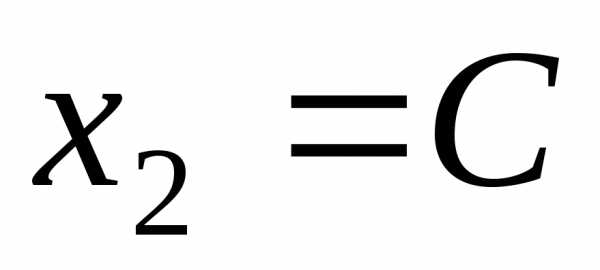 ,
получим.
,
получим.
Таким
образом, собственные векторы,
соответствующие собственному значению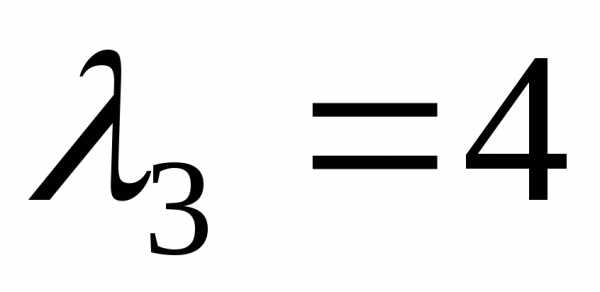 ,
имеют вид:Х3=
,
имеют вид:Х3=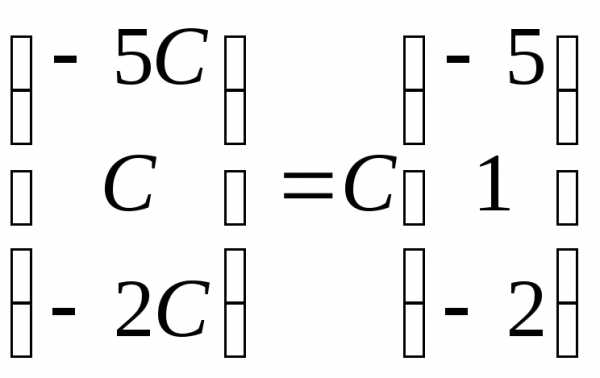 .
.
studfiles.net
Собственные векторы и собственные значения матрицы.
Характеристическим
уравнением матрицы А
= 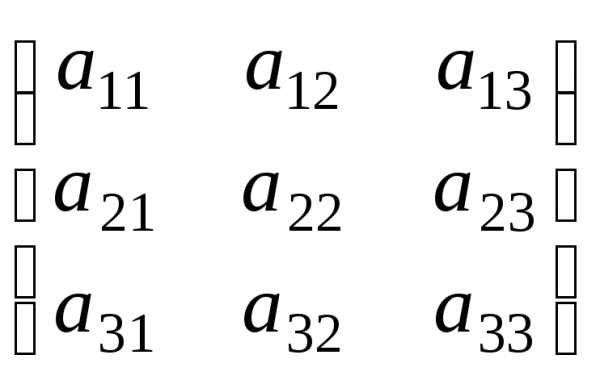 называется уравнение,
т.е.
называется уравнение,
т.е.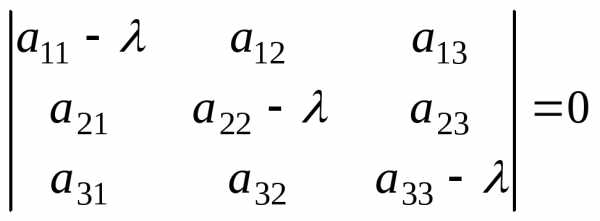 .
.
Корни этого уравнения 1, 2, 3 называются характеристическими числами матрицы А или собственными значениями матрицы А, эти числа действительные, если матрица является симметрической.Если элементы квадратной матрицы удовлетворяют условию аij = aji, то матрица называется симметрической.
Ненулевой
вектор х называется
собственным
вектором квадратичной матрицы А,
принадлежащим ее собственному значению
совпадает с множеством всех ненулевых
решений системы однородных уравнений
( )х = 0, записанных в векторно-матричной
форме.
)х = 0, записанных в векторно-матричной
форме.
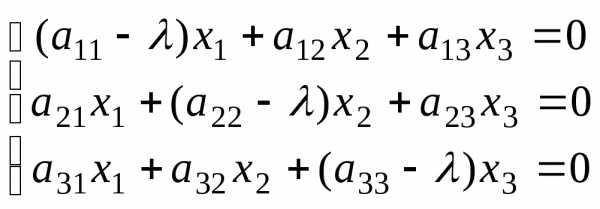
в которой имеет одно из значений 1, 2, 3 и определитель которой в силу этого равен нулю, определяет тройку чисел соответствующую данному собственному значению который и является искомым собственным вектором.
Пример.
Дана матрица 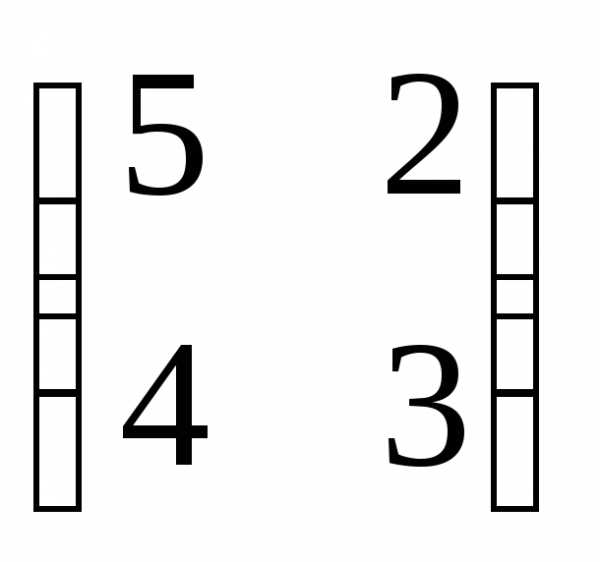 .
Найти собственные значения и собственные
векторы.
.
Найти собственные значения и собственные
векторы.
Решение:
Составим
характеристическое уравнение 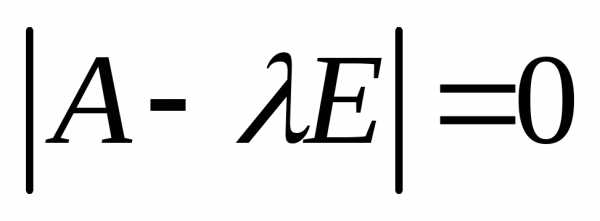
 =0
=0
(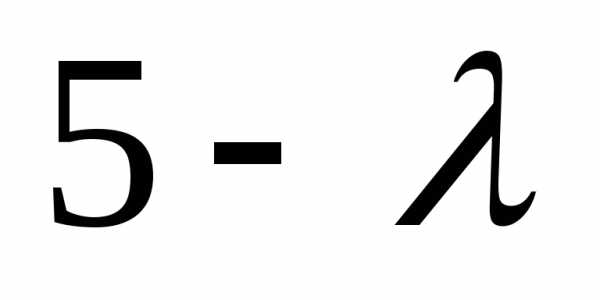 )(
)(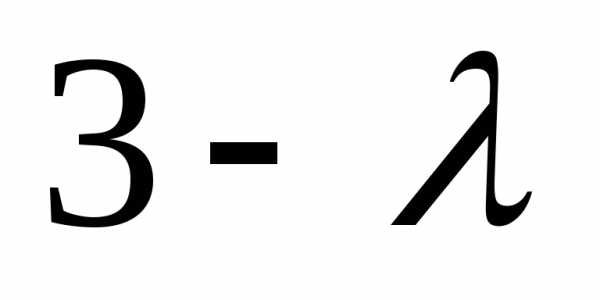 )
– 8 = 0
)
– 8 = 0
2 — 8 + 7 = 0
1=7, 2 = 1.
Находим собственный вектор, соответствующий первому собственному значению
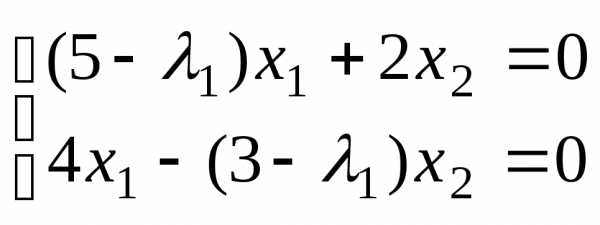 ;
;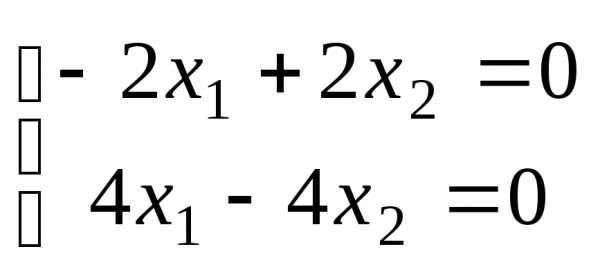 х1 = х2
— собственный вектор, соответствующий
собственному числу1=7
х1 = х2
— собственный вектор, соответствующий
собственному числу1=7
Находим собственный вектор, соответствующий второму собственному значению
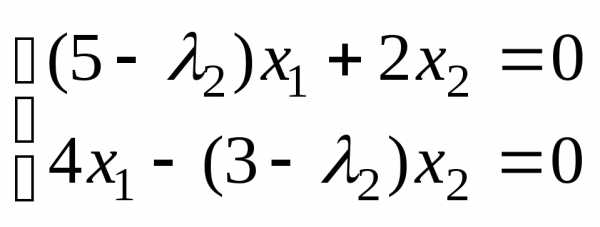 ;
;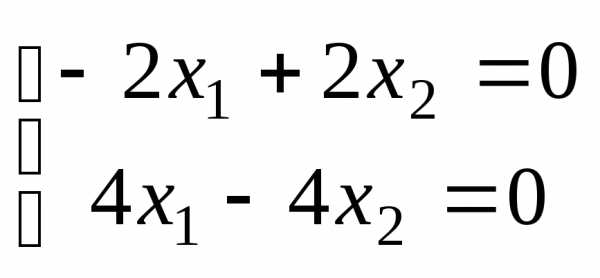
2х1 =- х2 х1 =
2х1 =- х2 х1 =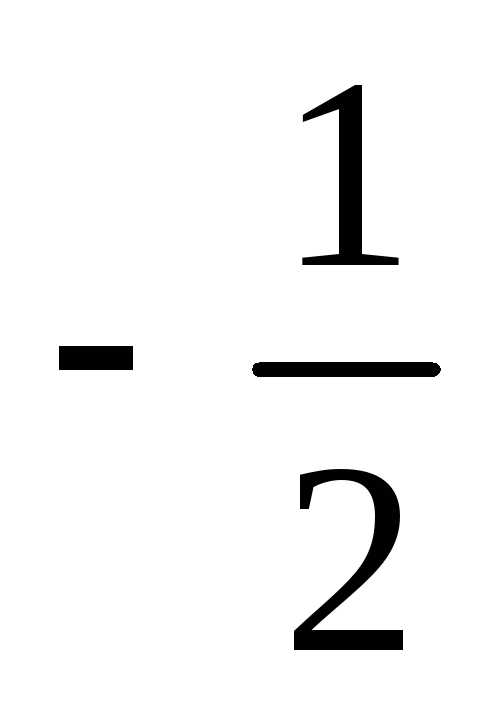 х2
х2  — собственный вектор, соответствующий
собственному числу2 = 1
— собственный вектор, соответствующий
собственному числу2 = 1
II. Векторная алгебра.
Различают два рода величин: скалярные и векторные.
Если некоторая величина определяется только ее числовым значением, то ее называют скалярной. Если при определении некоторой величины для ее полной характеристики, кроме числового значения, надо знать и ее направление, то такая величина называется векторной, или вектором. Длина вектора называется также его модулем, или абсолютной величиной. Вектор равен нулю, если его модуль равен нулю. Такой вектор называется нулевым.
Два
вектора 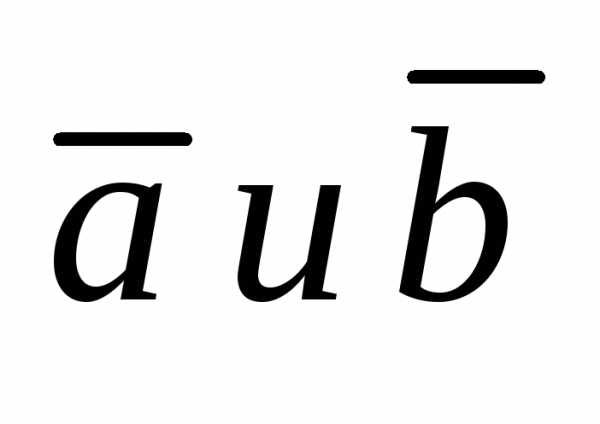 называются равными, если равны их
модули, они параллельны и сонаправлены.
называются равными, если равны их
модули, они параллельны и сонаправлены.
При
умножении вектора 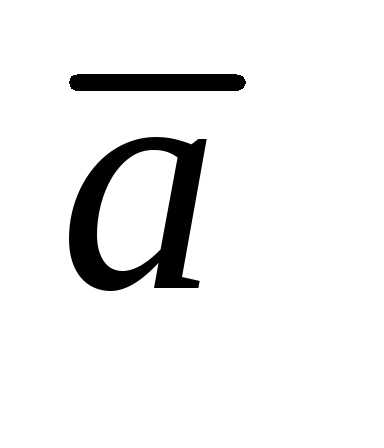 на
скаляр k получается вектор
на
скаляр k получается вектор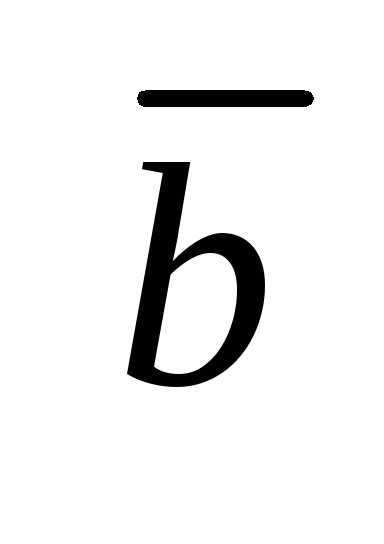 модуль которого равен модулю вектора
модуль которого равен модулю вектора 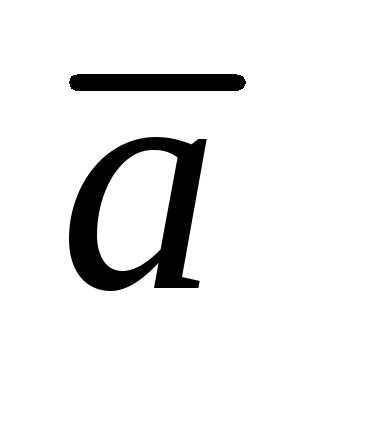 ,
умноженному на k. Направления
векторов
,
умноженному на k. Направления
векторов  совпадают,
если k > 0, и они противоположны, если k < 0.
совпадают,
если k > 0, и они противоположны, если k < 0.
Два вектора, лежащие на параллельных прямых называются коллинеарными.
Единичным вектором, или ортом данного вектора, называется вектор, совпадающий по направлению с данным вектором и имеющий модуль, равный единице. Прямоугольные координаты
Если в пространстве задана прямоугольная система координат Оxyz, то точка М пространства, имеющая координаты x (абсцисса), y (ордината), z (аппликата), обозначается М(x, y, z).
Расстояние между двумя точками А(х1, у1, z1) и В(х2 , у2, z2) определяется по формуле . В частности, расстояние от точкиМ(x, y, z) от начала координат О определяется по формуле
Если х1, у1, z1-координаты
точки А, а х2,у2, z2—
координаты точки В, то координаты х и у точки С,
делящей отрезок АВ в отношении 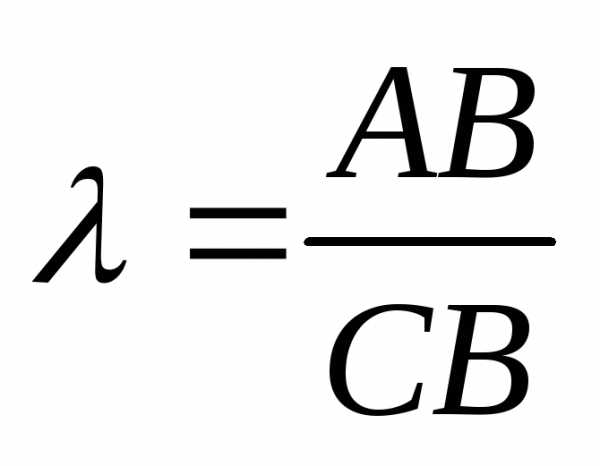 определяются
по формулам
определяются
по формулам
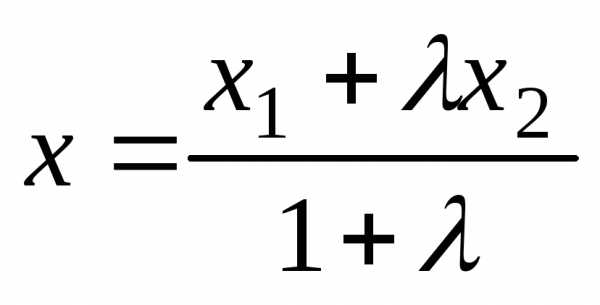 ;
; 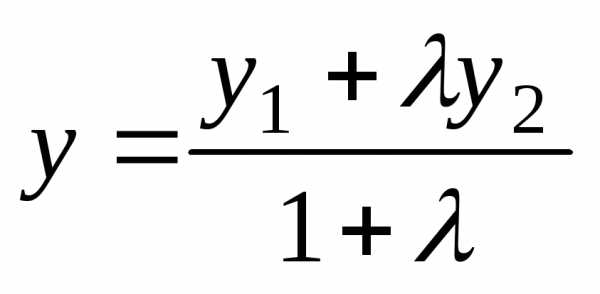 ;
;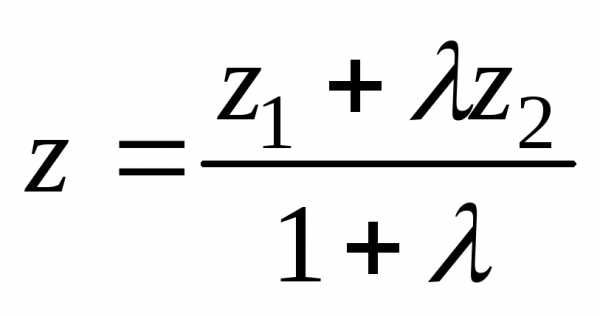
Если λ == 1, то точка С(х, у,z) делит отрезок АВ пополам, и тогда координаты х и у средины отрезка А В определятся по формулам
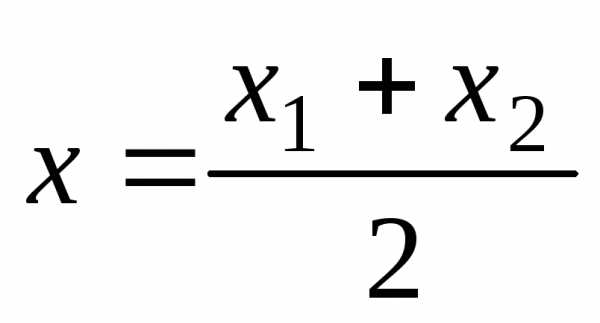 ;
; 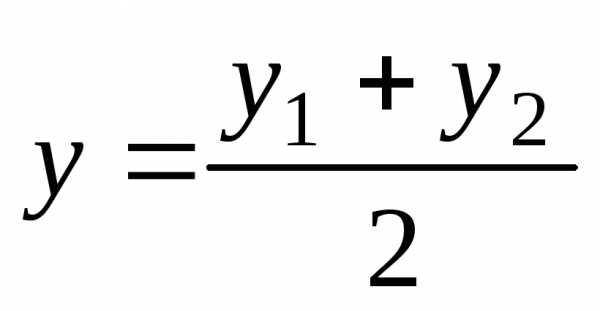 ;
;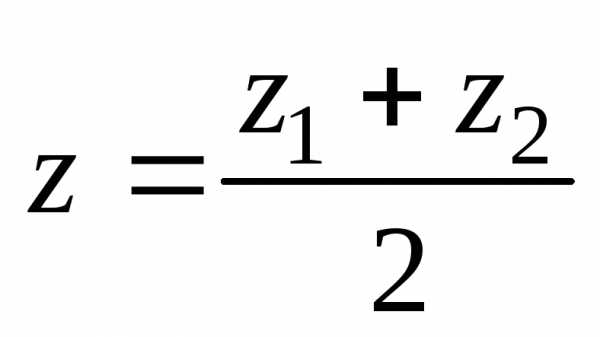
Площадь
треугольника на плоскости по известным
координатам его вершин А
(х1,
у1), В(х2, y2),
С (х3, у3) вычисляется по формуле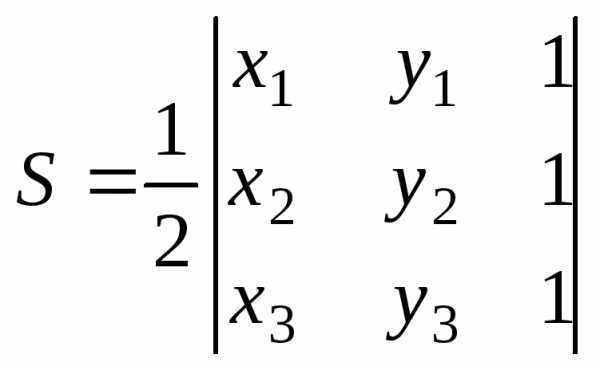 .
. Полученное
с помощью этой формулы число следует
взять по абсолютной величине. ЕслиS = 0, то значит три точки лежат на одной
прямой.
Полученное
с помощью этой формулы число следует
взять по абсолютной величине. ЕслиS = 0, то значит три точки лежат на одной
прямой.
Пример. Найти координаты точки С—средины отрезка, соединяющего точки
А (—2, 4) и В (—4, 10).
Решение. В формулах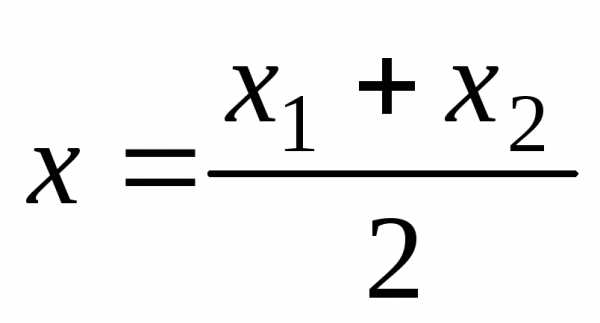 и
и 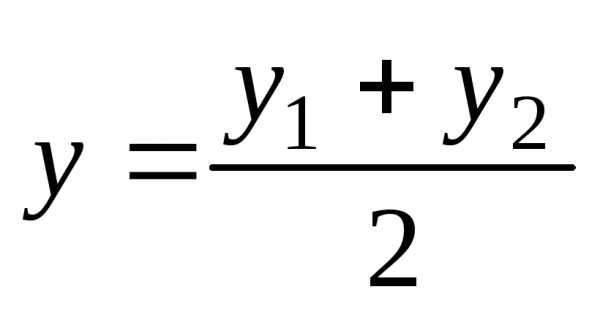 возьмем х1 = — 2; х2 = — 4;
возьмем х1 = — 2; х2 = — 4;
у1=
4;  =
10. Тогда абсцисса средины отрезкаАВ
х =-3; ордината
— у= 7.
=
10. Тогда абсцисса средины отрезкаАВ
х =-3; ордината
— у= 7.
Пример. Найти площадь треугольника, вершины которого находятся в точках А (2, — 3), В(1, 1), С(- 6, 5).
Решение: Задачу решим, воспользовавшись формулой площади треугольника
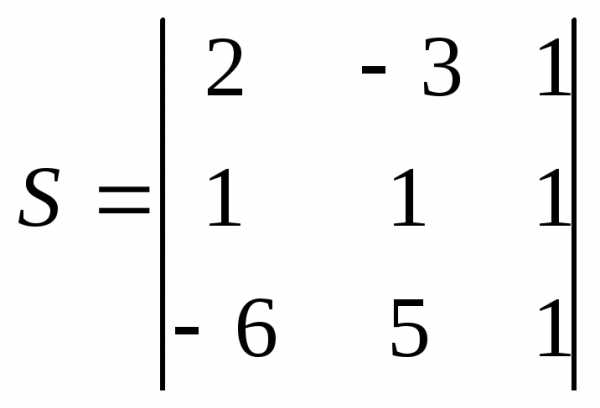 =
12
=
12
Ответ. S = 12 кв. ед.
Скалярное произведение.
Скалярным
произведением двух векторов  называется число, равное произведению
их модулей на косинус угла φ между ними. Скалярное произведение
векторов
называется число, равное произведению
их модулей на косинус угла φ между ними. Скалярное произведение
векторов 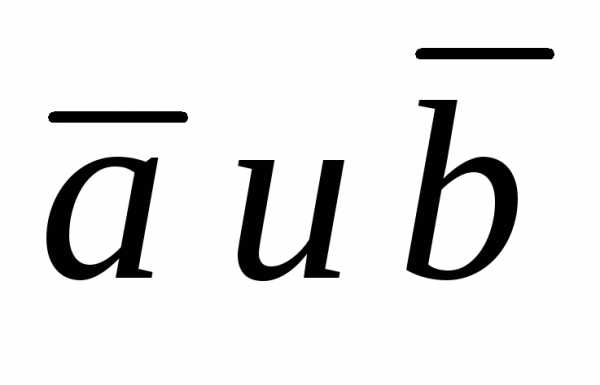 обозначается символом
обозначается символом 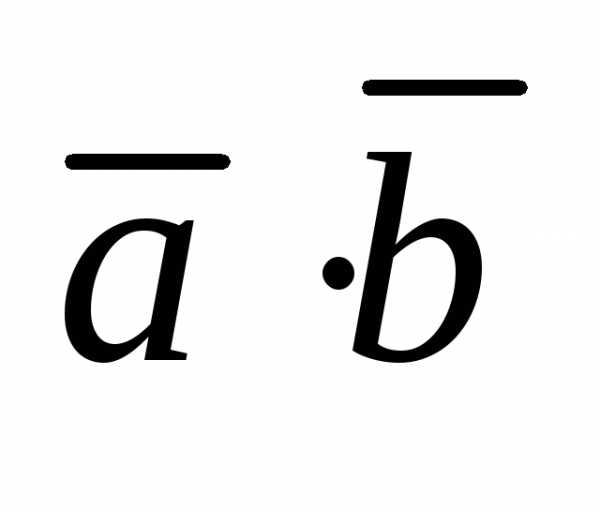 .
.
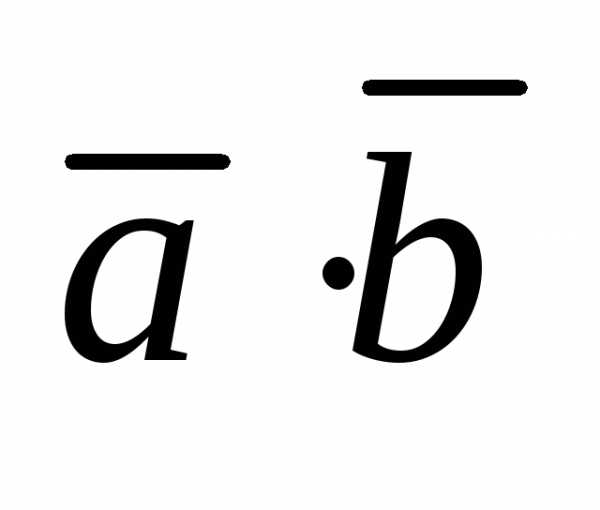 =
= cosφ.
cosφ.
Свойства скалярного произведения:
 =
=  (переместительный
закон)
(переместительный
закон) = 0, если
= 0, если  (скалярное произведение двух
перпендикулярных векторов равно нулю)
или какой-либо из перемножаемых векторов
является нулевым.
(скалярное произведение двух
перпендикулярных векторов равно нулю)
или какой-либо из перемножаемых векторов
является нулевым.
(распределительный закон)
Скалярное
произведение ортов осей координат: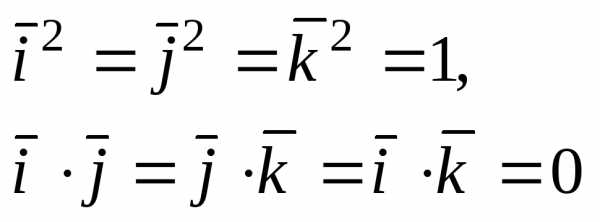
Если
векторы 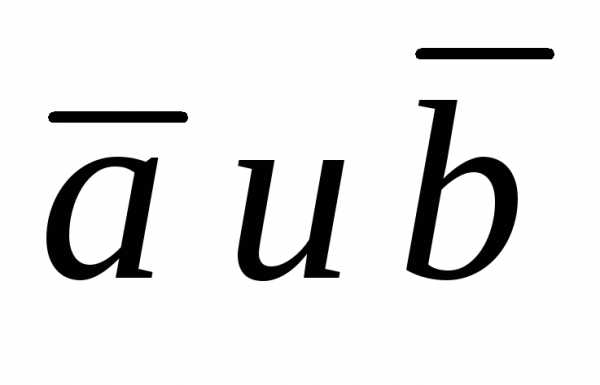 заданы своими координатами:
заданы своими координатами: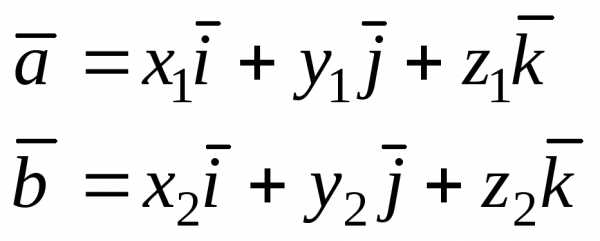 ,
то их скалярное произведение вычисляется
по формуле
,
то их скалярное произведение вычисляется
по формуле 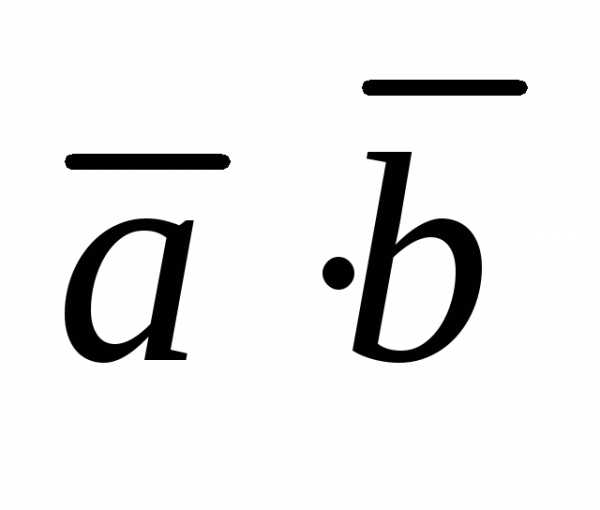 =x1x2 +y1y2+z1z2.
=x1x2 +y1y2+z1z2.
Векторное произведение.
Векторным
произведением векторов  называется вектор
называется вектор  ,
который определяется следующими
условиями:
,
который определяется следующими
условиями:
1)
Его модуль равен 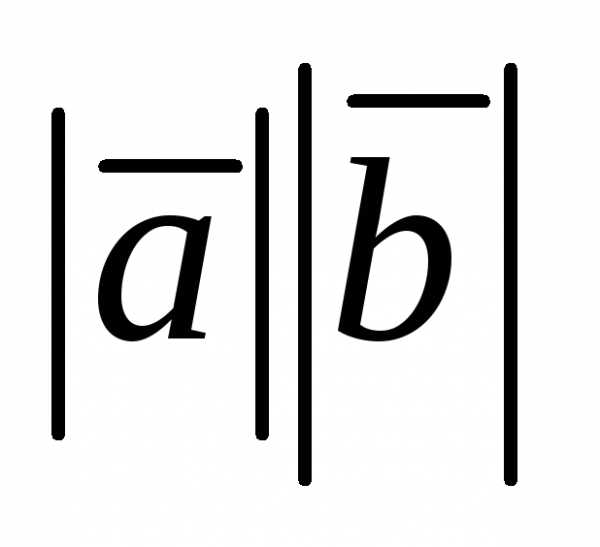 sinφ,где φ — угол между векторами
sinφ,где φ — угол между векторами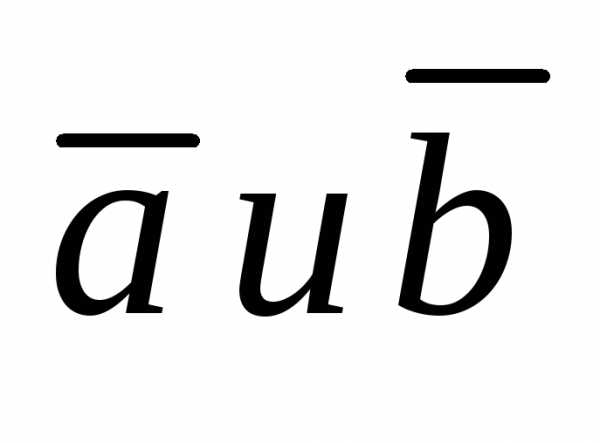 .
.
Модуль
вектора  равен площади параллелограмма,
построенного на векторах
равен площади параллелограмма,
построенного на векторах 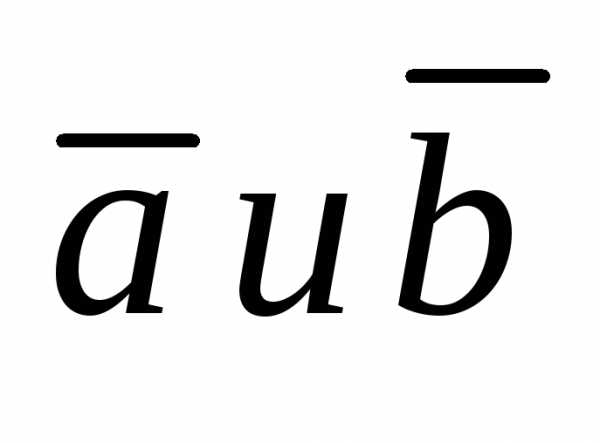
3) 

Основные свойства векторного произведения:
1)
Векторное произведение 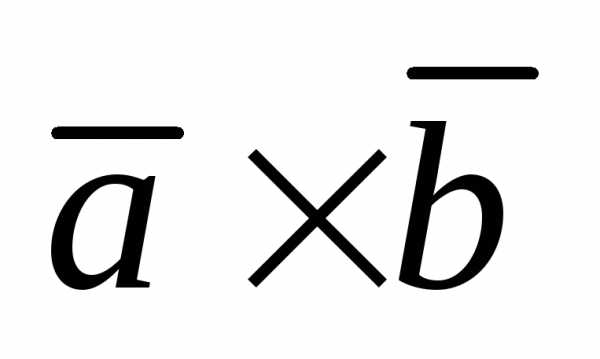 равно
нулю, если векторы
равно
нулю, если векторы 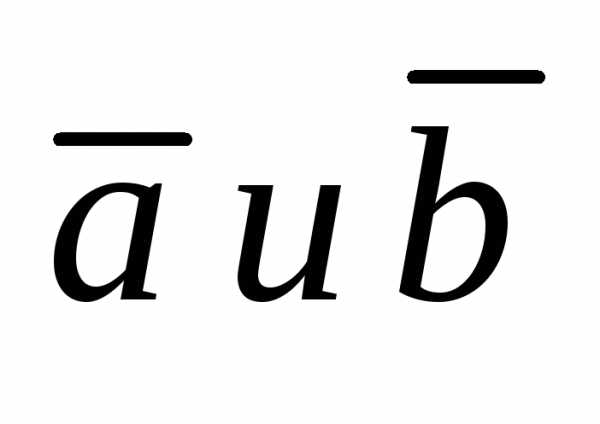 коллинеарны
или какой-либо из перемножаемых векторов
является нулевым.
коллинеарны
или какой-либо из перемножаемых векторов
является нулевым.
2)
При перестановке местами векторов
сомножителей векторное произведение
меняет знак на противоположный 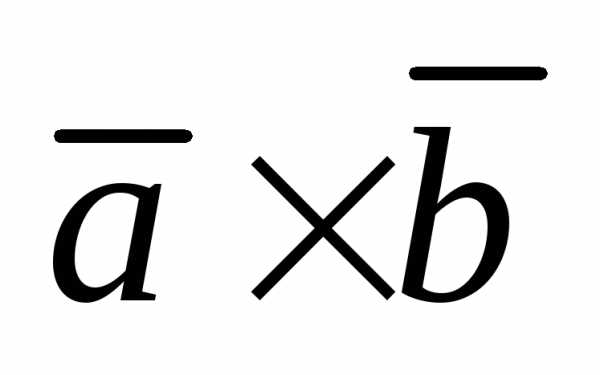 =
=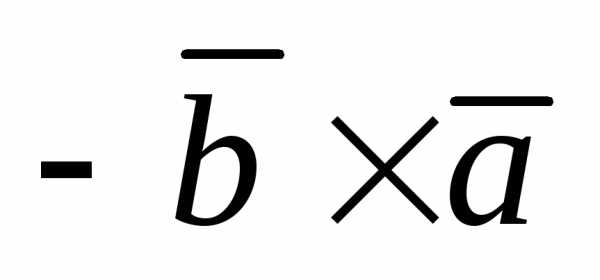 ;
;
3)(  )
) =(распределительное свойство)
=(распределительное свойство)
Если
векторы  заданы своими координатами:
заданы своими координатами: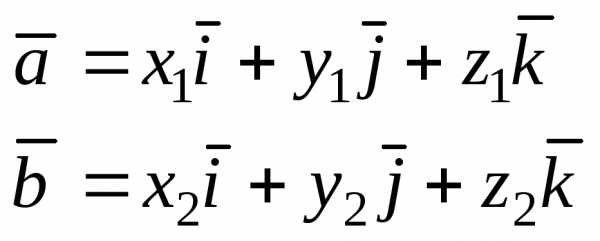 ,
то векторное произведение находим по
формуле:
,
то векторное произведение находим по
формуле:
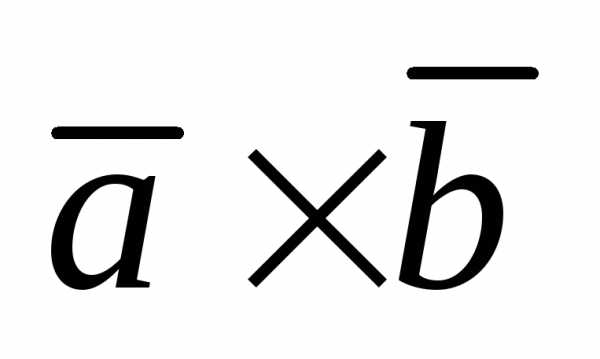 =
= 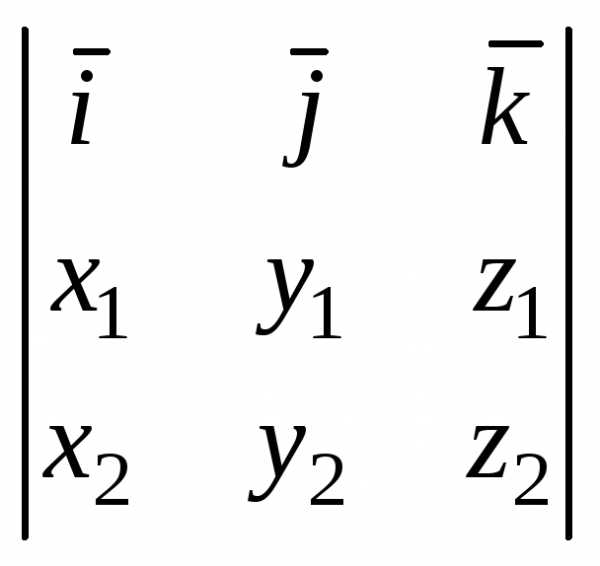
Площадь
параллелограмма и треугольника,
построенного на векторах  ,соответственно
равны
,
,соответственно
равны
,
Смешанное произведение
Векторно-скалярное
произведение трех векторов 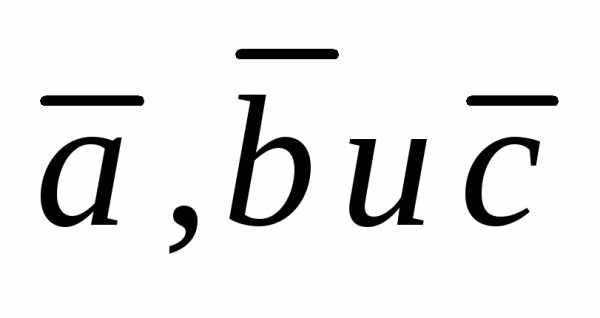 или смешанное их произведение вычисляется по формуле
или смешанное их произведение вычисляется по формуле
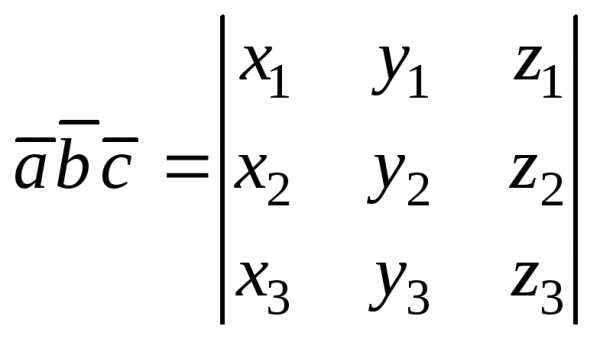 ,
если векторы
,
если векторы 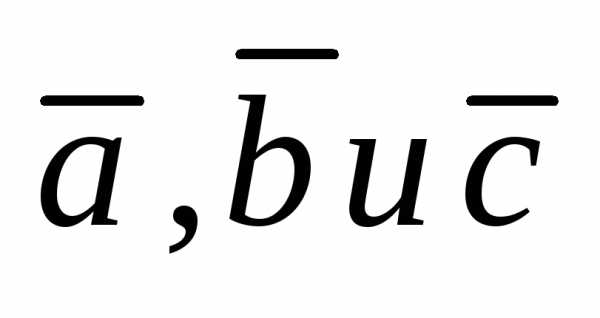 заданы своими координатами:
заданы своими координатами: .
.
Абсолютная
величина смешанного произведения равна
объему параллелепипеда, построенного
на векторах 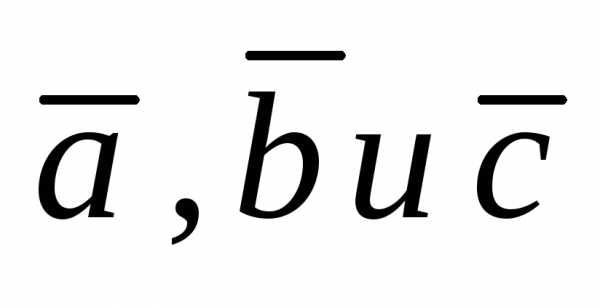 .
.
Объем
пирамиды, построенной на векторах 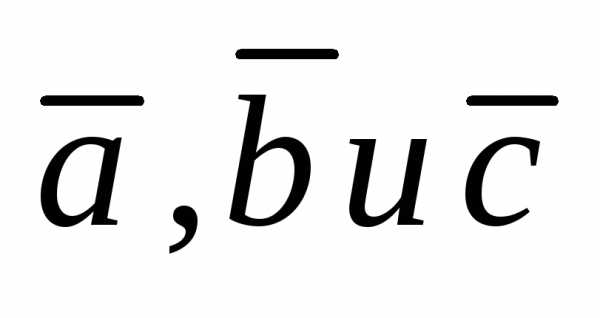 , получим по формуле
, получим по формуле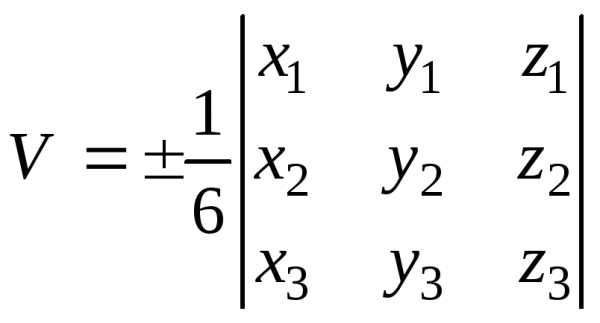 причем знак перед определителем должен
быть выбран так, чтобы объемV был положительным.
причем знак перед определителем должен
быть выбран так, чтобы объемV был положительным.
Три
вектора 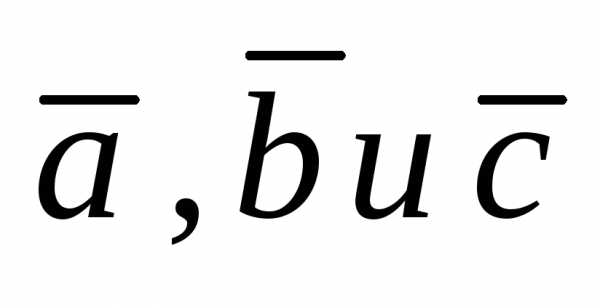 называются
компланарными, если они лежат в одной
плоскости или параллельны одной и той
же плоскости. Для того, чтобы три вектора
были компланарны, необходимо и
достаточно, чтобы их смешанное произведение
было равно нулю.
называются
компланарными, если они лежат в одной
плоскости или параллельны одной и той
же плоскости. Для того, чтобы три вектора
были компланарны, необходимо и
достаточно, чтобы их смешанное произведение
было равно нулю.
Пример. Начти объем пирамиды, если координаты ее вершин А(х1, у1, z1) и В(х2 , у2, z2)
Решение: Рассмотрим векторы,на которых построена пирамида.
Зная координаты начала и конца каждого вектора, найдем проекции этих векторов на оси прямоугольной системы координат:
,,для объема пирамиды получаем на основании
формулы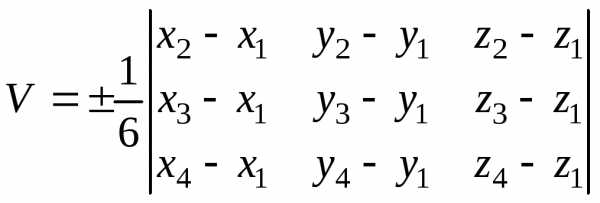
studfiles.net
4. Собственные значения и собственные векторы подобных матриц.
Если имеет место
равенство
,
то матрицы и
и подобные (см. глава 6).
подобные (см. глава 6).
Докажем, что подобные матрицы имеют одинаковый спектр.
Теорема. Характеристические многочлены подобных матриц совпадают.
►Пусть матрицы  и
и подобные. Тогда существует такая
невырожденная матица
подобные. Тогда существует такая
невырожденная матица ,
что.
,
что.
Покажем, что
характеристические многочлены подобных
матриц  и
и совпадают.
совпадают.
.◄
Следствие 1. Характеристические уравнения подобных матриц совпадают .
Следствие 2. Собственные значения подобных матриц совпадают.
Следствие 3.
Для подобных матриц  и
и и.
и.
Замечание. Из равенств
ине всегда следует подобие матриц и
и .
.
Например,
матрицы 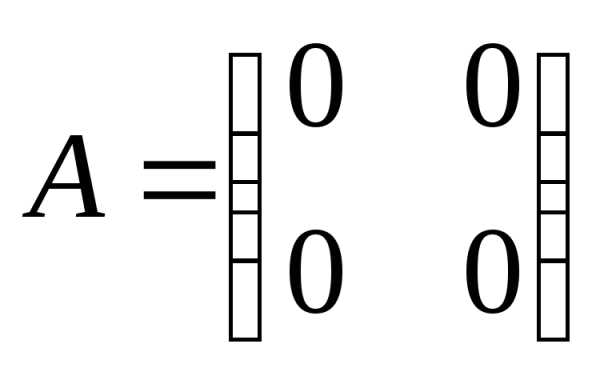 и
и имеют одинаковые следы и одинаковые
определители, но не являются подобными.
имеют одинаковые следы и одинаковые
определители, но не являются подобными.
►Действительно,
для любой невырожденной матрицы второго
порядка  выражение,
откуда следует, что матрицы
выражение,
откуда следует, что матрицы и
и не
являются подобными.◄
не
являются подобными.◄
Теорема. Если и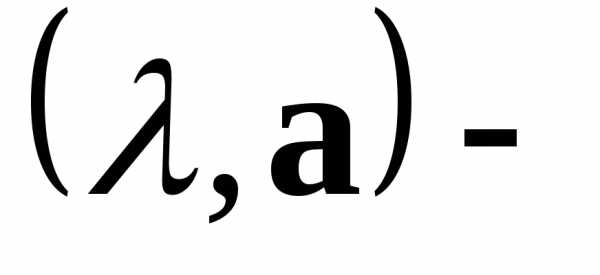 собственная пара матрицы
собственная пара матрицы ,
то
,
то —
собственная пара матрицы
—
собственная пара матрицы .
.
► Так как 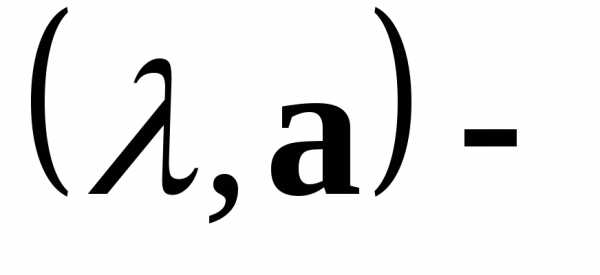 собственная пара матрицы
собственная пара матрицы ,
то.
Умножаяслева на
,
то.
Умножаяслева на ,
имеем,
с
другой стороны,,
откуда.
Последнее означает, что
,
имеем,
с
другой стороны,,
откуда.
Последнее означает, что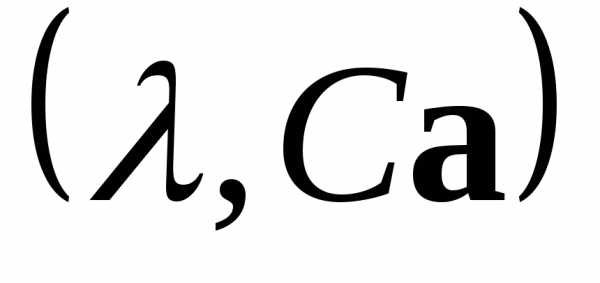 — собственная пара матрицы
— собственная пара матрицы .◄
.◄
Замечание. Если
и матрица диагональная, то собственными значениямиматрицы
диагональная, то собственными значениямиматрицы  являются
диагональные элементы
являются
диагональные элементы  ,
а собственными векторами — единичные
векторы
,
а собственными векторами — единичные
векторы .
Тогда в силу доказанной теоремы
собственному значению
.
Тогда в силу доказанной теоремы
собственному значению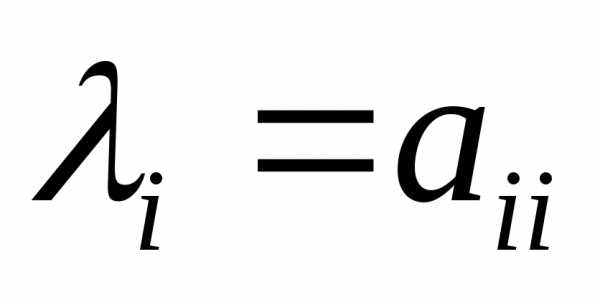 матрицы
матрицы соответствует собственный вектор
соответствует собственный вектор (
( -ый
столбец матрицы
-ый
столбец матрицы ).
).
● Пример 9.
Могут ли матрицы =
= и
и 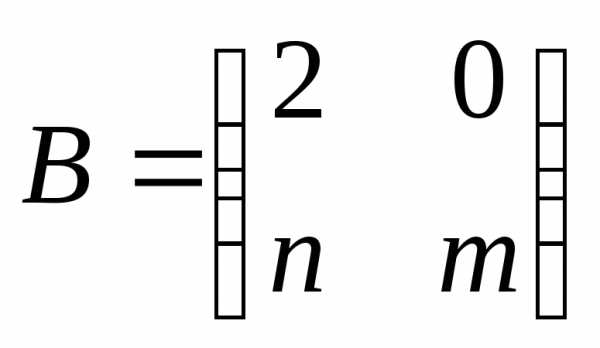 быть подобными?
быть подобными?
Решение. Если
матрицы подобны, то
и .
.
Система 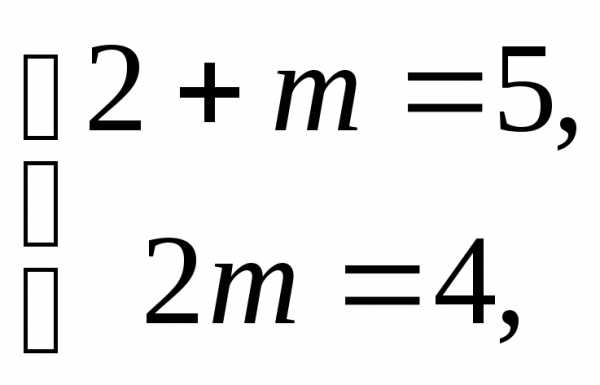 несовместна, откуда следует, что
несовместна, откуда следует, что
матрицы  и
и не могут быть подобными.●
не могут быть подобными.●
● Пример
10. Для
любознательных. Доказать,
что матрицы 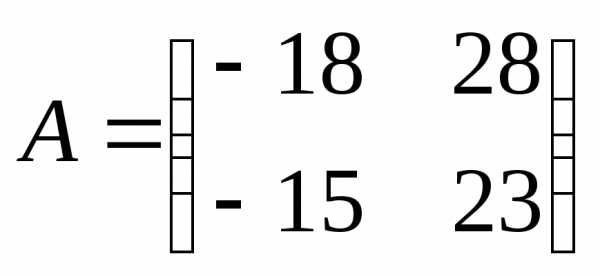 и
и 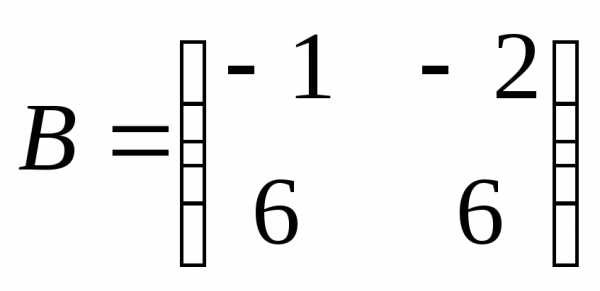 подобны.
подобны.
Решение.
Если
матрицы  и
и подобны, то существует хотя бы одна
невырожденная матрица
подобны, то существует хотя бы одна
невырожденная матрица ,
что,
и собственной паре
,
что,
и собственной паре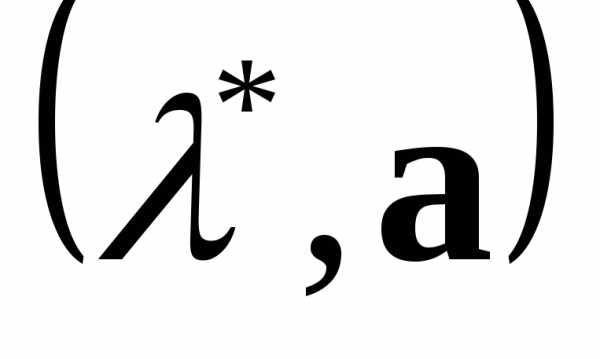 матрицы
матрицы соответствует собственная пара
соответствует собственная пара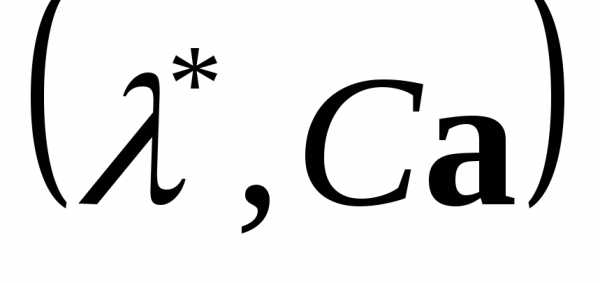 матрицы
матрицы .
.
и
,
откуда следует, что собственные значения
матриц и
и совпадают. Характеристическое
уравнение матрицы
совпадают. Характеристическое
уравнение матрицы  ,
а, следовательно, и матрицы
,
а, следовательно, и матрицы имеет вид,
корни которого
имеет вид,
корни которого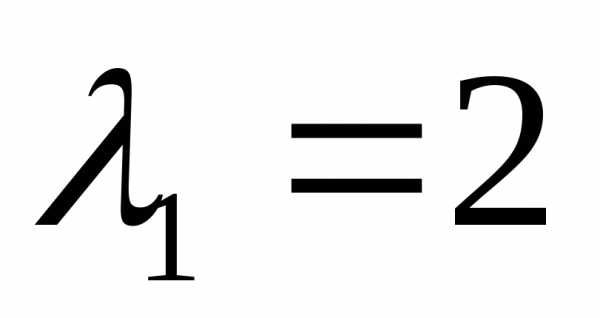 и
и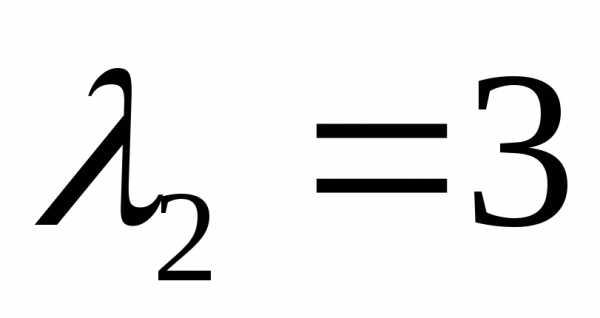 .
Нетрудно проверить, чтои- собственные векторы матрицы
.
Нетрудно проверить, чтои- собственные векторы матрицы ,
соответствующие собственным значениям
,
соответствующие собственным значениям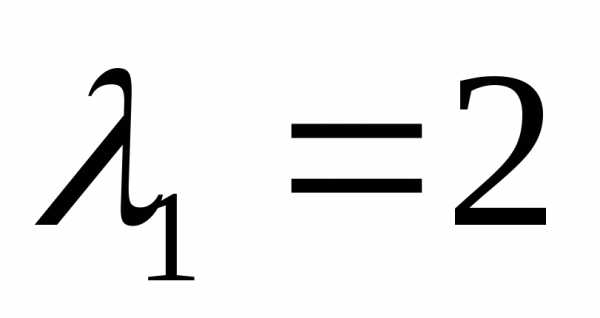 и
и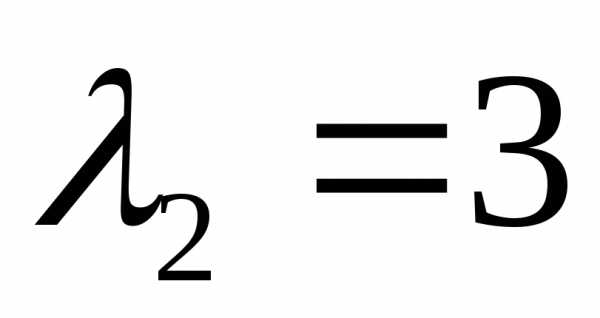 .
Если существует такая матрица
.
Если существует такая матрица ,
что,
то
,
что,
то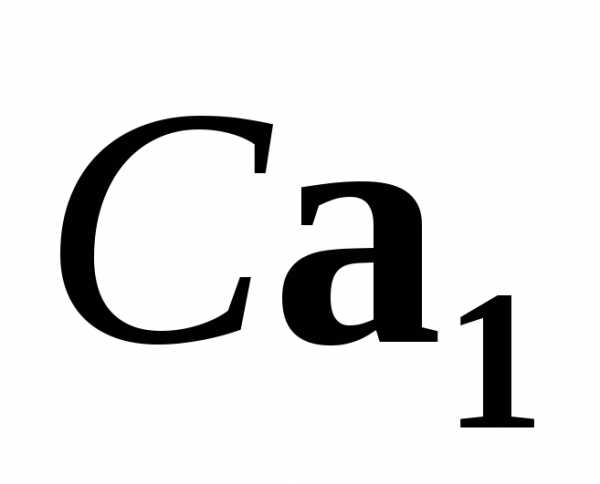 и
и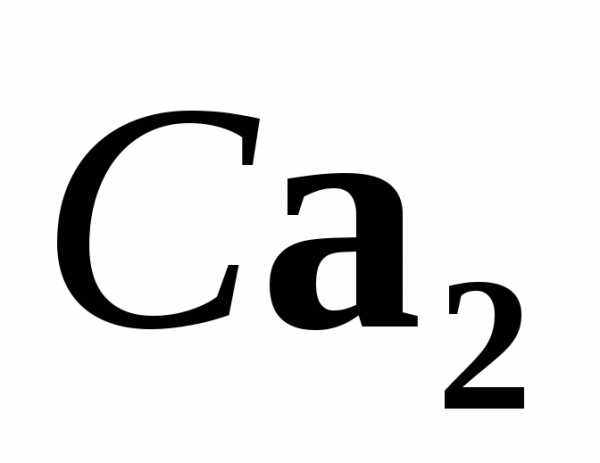 — собственные векторы матрицы
— собственные векторы матрицы ,
соответствующие
,
соответствующие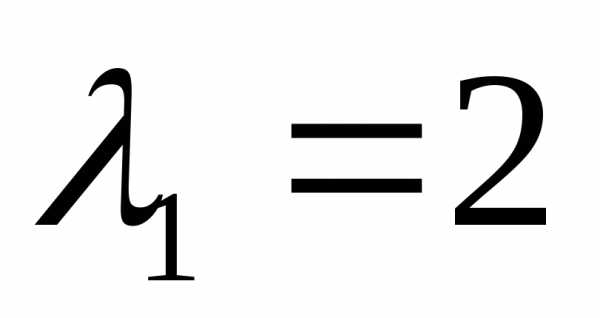 и
и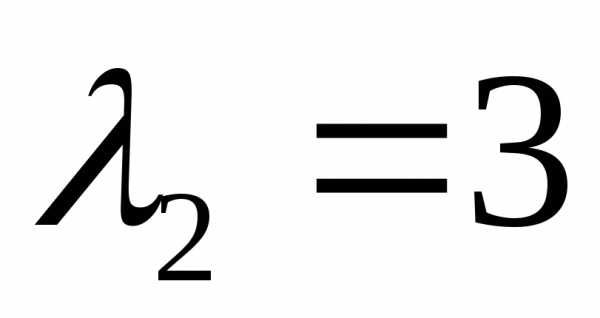 .
Собственные векторы
.
Собственные векторы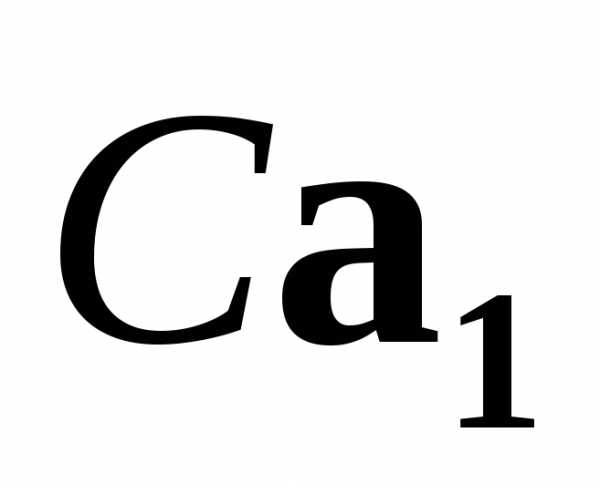 и
и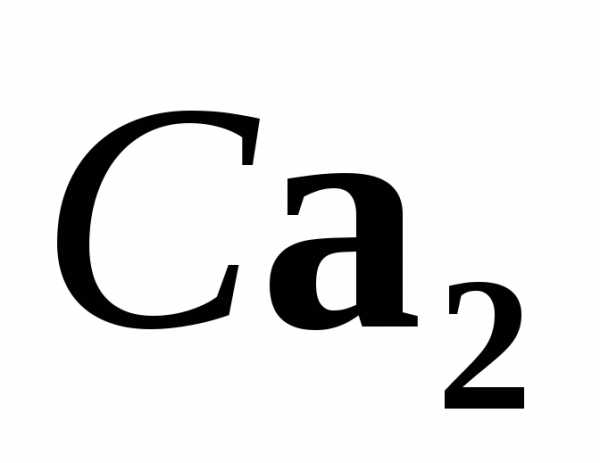 удовлетворяют системами.
удовлетворяют системами.
Пусть  .
Тогда предыдущие уравнения могут быть
записаны в виде,.
.
Тогда предыдущие уравнения могут быть
записаны в виде,.
Первое матричное уравнение эквивалентно одному скалярному уравнению , второе — уравнению.
Для нахождения  ,
,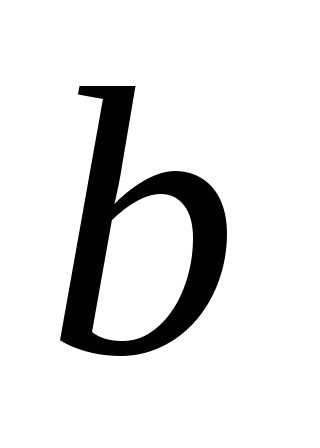 ,
, и
и имеем систему уравнений
имеем систему уравнений
ранг матрицы
которой равен двум (минор второго порядка 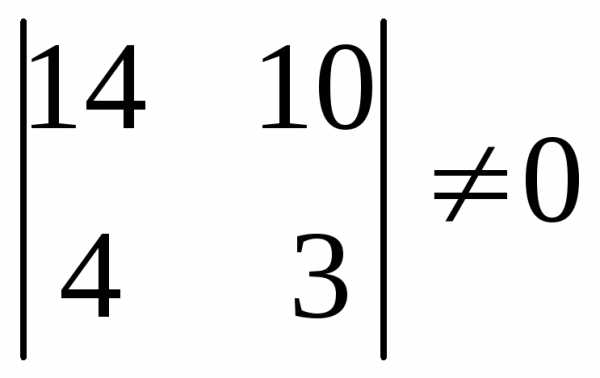 ).
Две неизвестные можно задать произвольно.
Чтобы получитьнетривиальное решение необходимо хотя бы одну
неизвестную задать отличной от нуля.
).
Две неизвестные можно задать произвольно.
Чтобы получитьнетривиальное решение необходимо хотя бы одну
неизвестную задать отличной от нуля.
Пусть 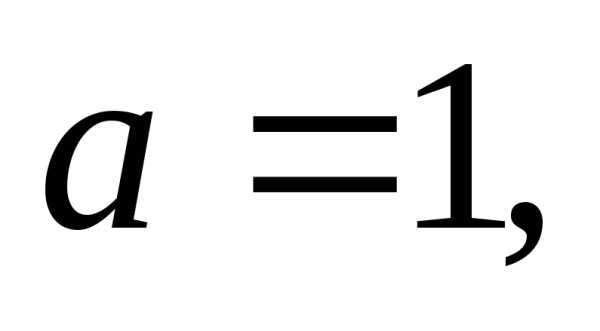
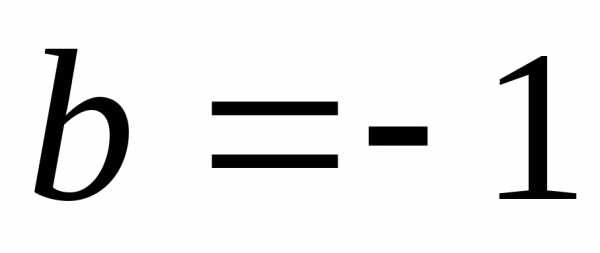 ,
тогда
,
тогда 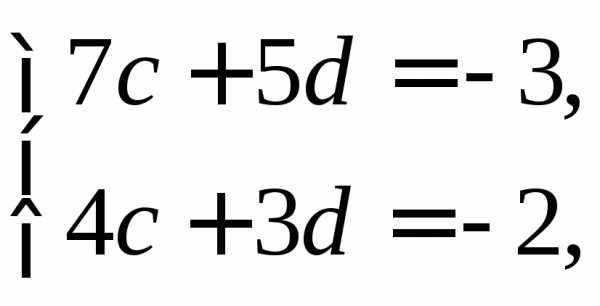
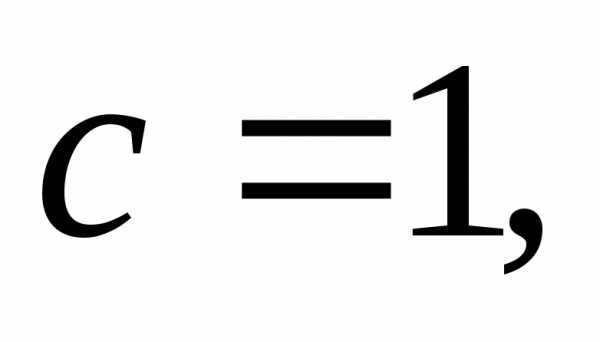
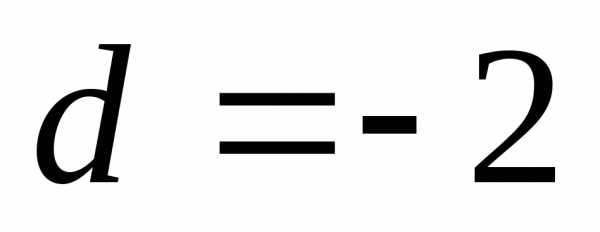 ,матрица
,матрица 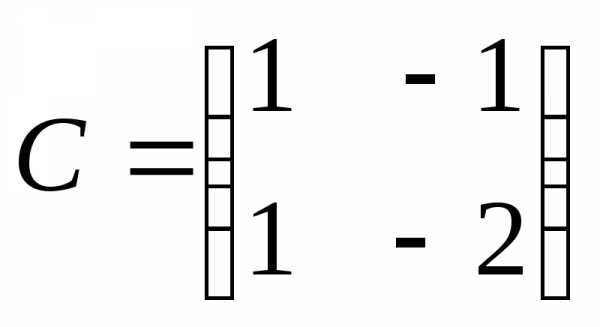 .
.
Следовательно,
существует невырожденная матрица  такая, чтои матрицы
такая, чтои матрицы и
и подобны.●
подобны.●
Замечание.
Из произвольности выбора неизвестных
следует, что можно подобрать бесконечное
множество матриц  ,
таких, что.
,
таких, что.
5. Собственные значения и собственные векторы симметрической матрицы.
Теорема. Собственные значения симметрической матрицы действительные числа.
► Предположим
противное.
Пусть комплексное число 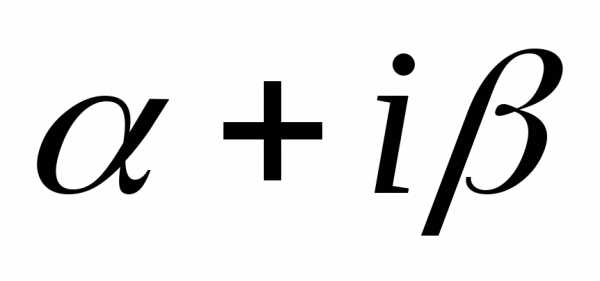
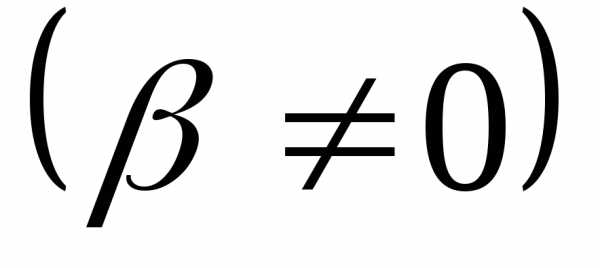 — собственное значение симметрической
матрицы
— собственное значение симметрической
матрицы ,
а вектор
,
а вектор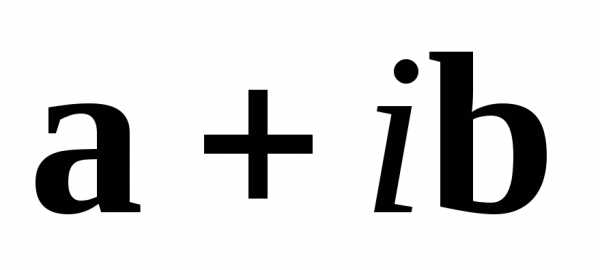 собственный вектор, соответствующий
указанному собственному значению, т.е.. Тогда,
откуда
собственный вектор, соответствующий
указанному собственному значению, т.е.. Тогда,
откуда
, (8.9)
(8.10)
Умножая (8.9) слева
на 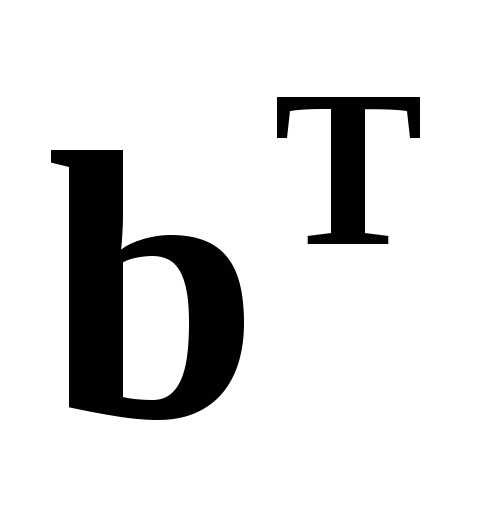 ,
учитывая равенство
,
учитывая равенство 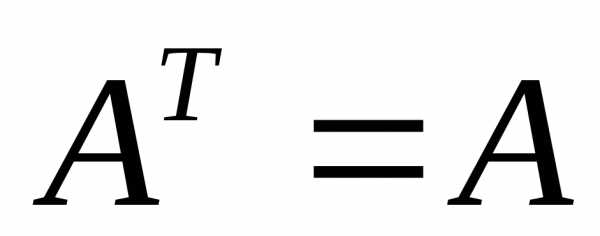 и используя (8.10), имеем,,,, откуда,
а это противоречит тому, что
и используя (8.10), имеем,,,, откуда,
а это противоречит тому, что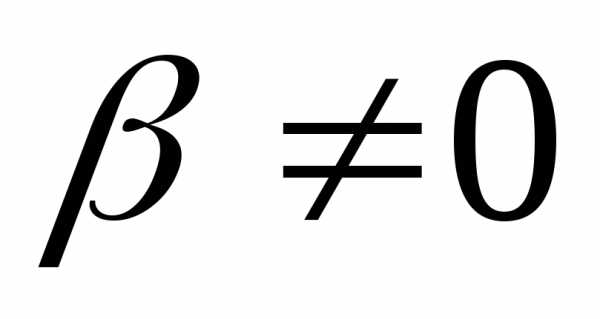 и
.
Противоречие доказывает теорему.◄
и
.
Противоречие доказывает теорему.◄
Теорема. Собственные векторы симметрической матрицы, соответствующие различным собственным значениям, взаимно перпендикулярны.
►Пусть  собственный вектор матрицы
собственный вектор матрицы ,
соответствующий собственному значению
,
соответствующий собственному значению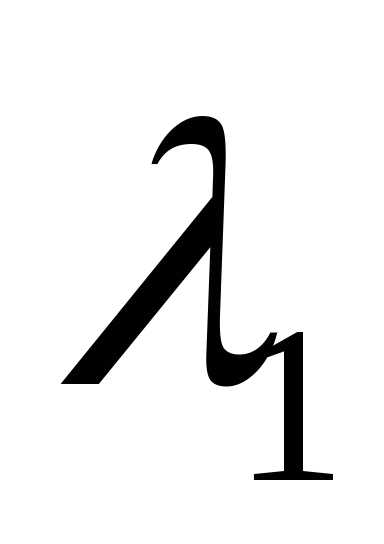 и
и —
собственный вектор, соответствующий
собственному значению
—
собственный вектор, соответствующий
собственному значению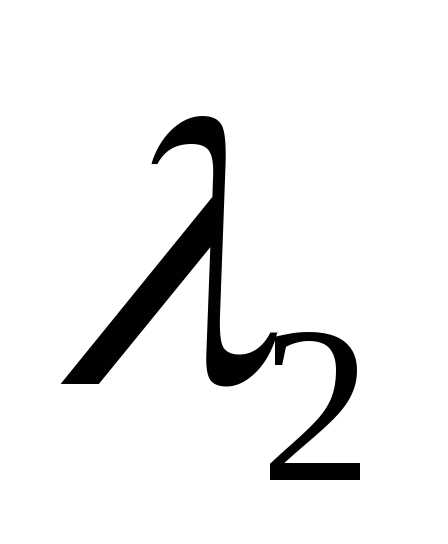
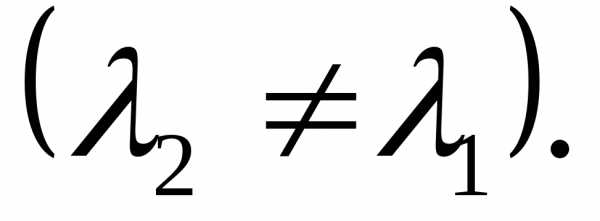
 (8.11)
(8.11)
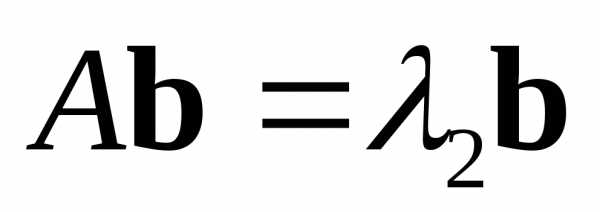 (8.12)
(8.12)
Умножая
равенство (8.11) слева на 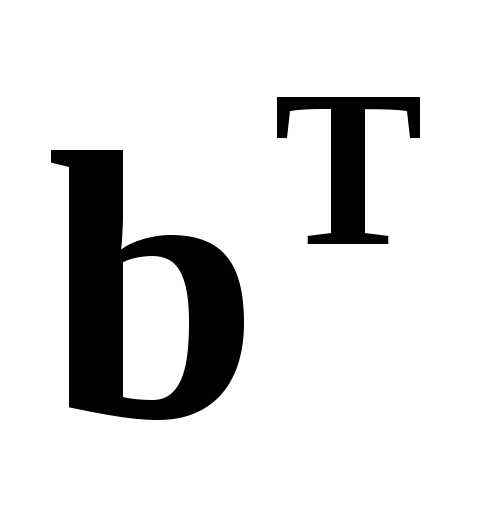 ,
учитывая равенство
,
учитывая равенство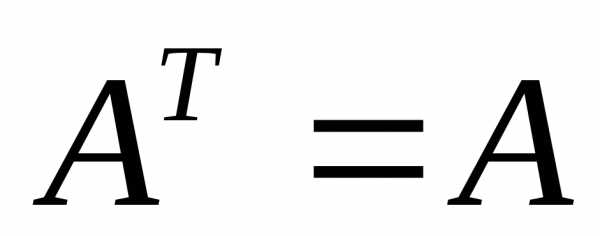 и используя (8.12), имеем,
откуда
и используя (8.12), имеем,
откуда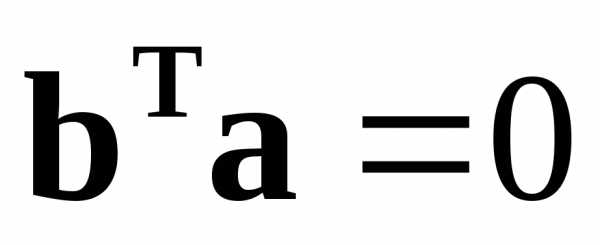 ,
т.е. векторы
,
т.е. векторы  и
и  взаимно перпендикулярны.◄
взаимно перпендикулярны.◄
● Пример 11. При каком значении  векторявляется собственным вектором матрицы
векторявляется собственным вектором матрицы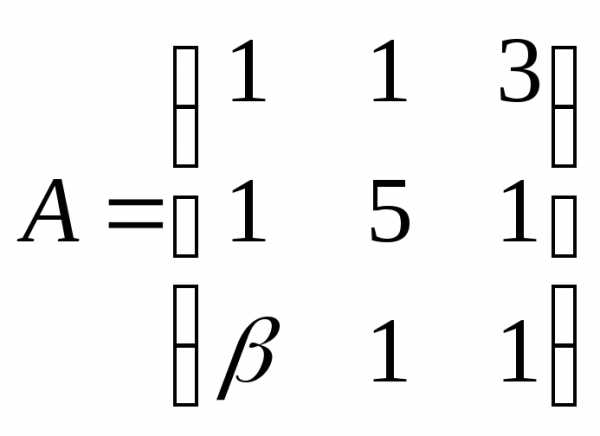 ?
?
Показать, что при
найденном значении  вектор
также является собственным вектором
этой
матрицы. Найти все собственные пары
этой матрицы при найденном
вектор
также является собственным вектором
этой
матрицы. Найти все собственные пары
этой матрицы при найденном  .
.
Решение. 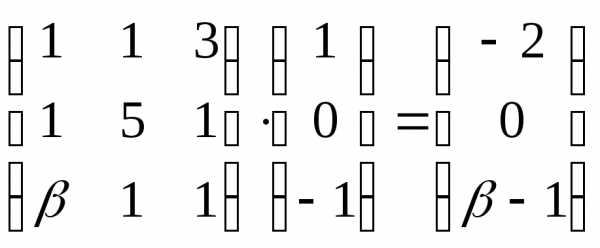 .
Так каксобственный вектор матрицы
.
Так каксобственный вектор матрицы ,
то
,
то
 ,
откуда
,
откуда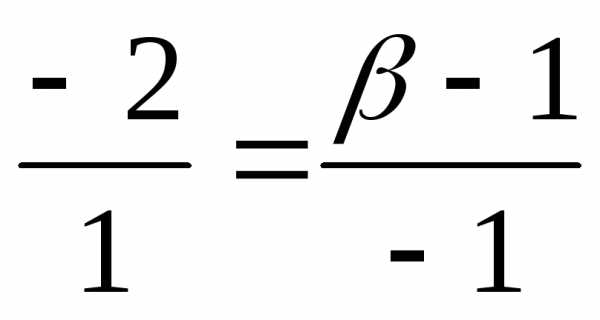 ,
, .
При найденном
.
При найденном
 =-2
=-2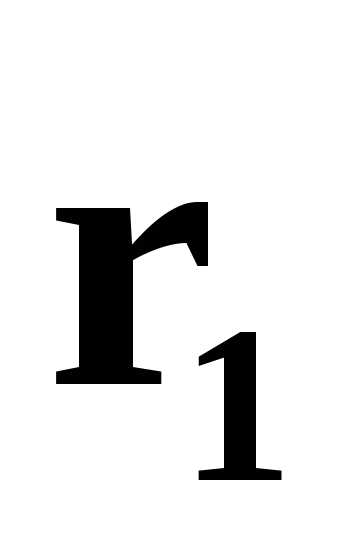 и
и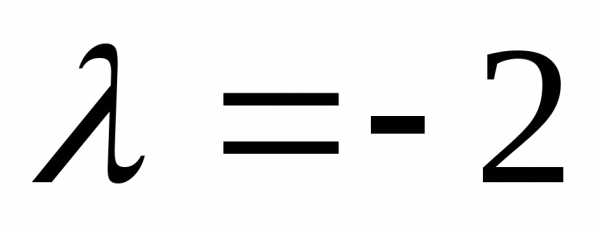 .
.
Найдем собственное значение, соответствующее собственному вектору .
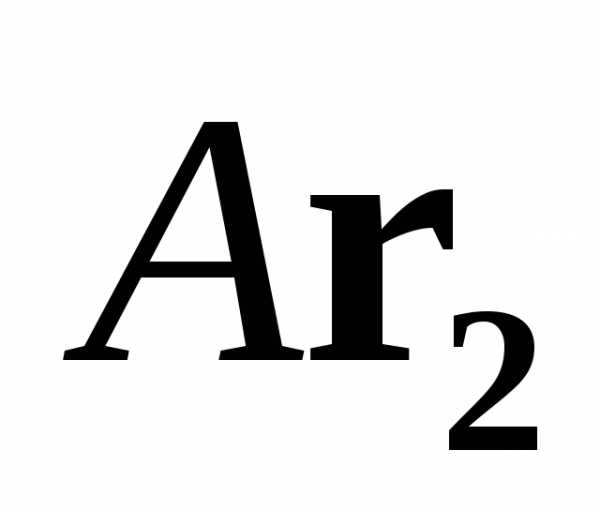 =
=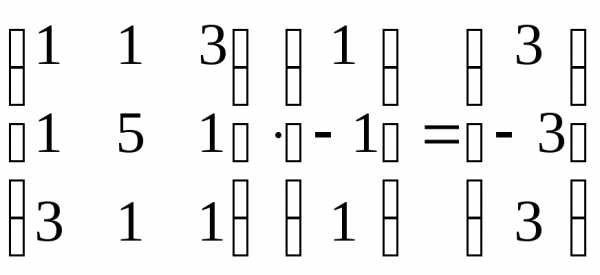 =3
=3 ,
откуда следует, что векторсобственный вектор матрицы
,
откуда следует, что векторсобственный вектор матрицы ,
который соответствует собственному
значению
,
который соответствует собственному
значению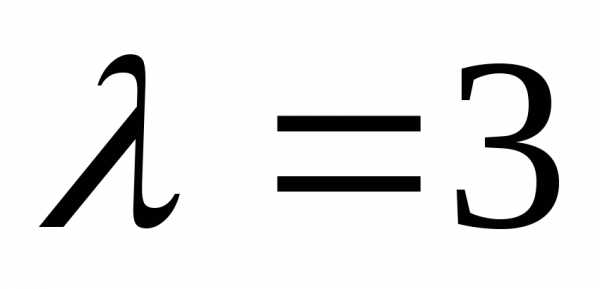 .
.
При найденном  матрица
матрица симметрическая, поэтому собственные
векторы, отвечающие различным собственным
значениям, взаимно перпендикулярны.
Третий собственный вектор
симметрическая, поэтому собственные
векторы, отвечающие различным собственным
значениям, взаимно перпендикулярны.
Третий собственный вектор найдем как вектор, перпендикулярный
векторам
найдем как вектор, перпендикулярный
векторам 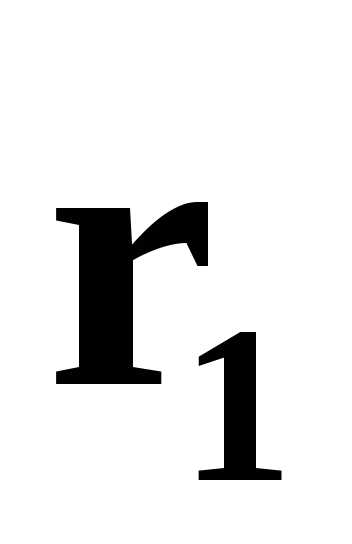 и
и 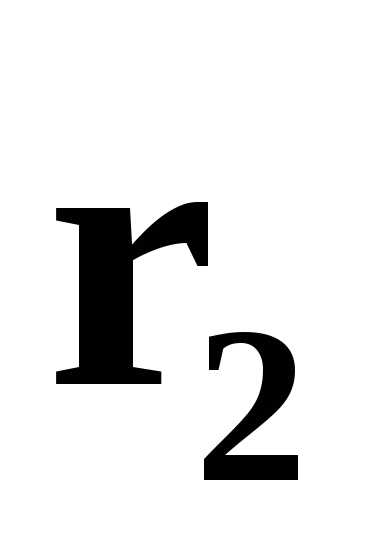 .
Вектор
перпендикулярен векторам
.
Вектор
перпендикулярен векторам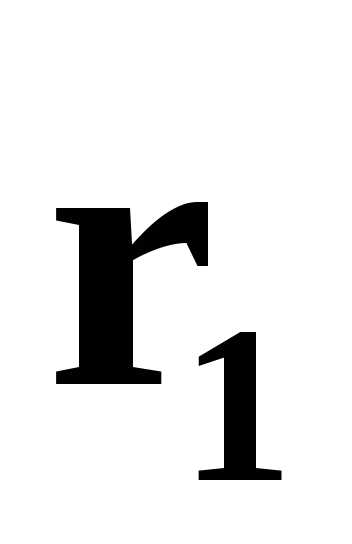 и
и  .
Проверим, что
— собственный вектор этой матрицы и
найдем соответствующее ему собственное
значение.
.
Проверим, что
— собственный вектор этой матрицы и
найдем соответствующее ему собственное
значение.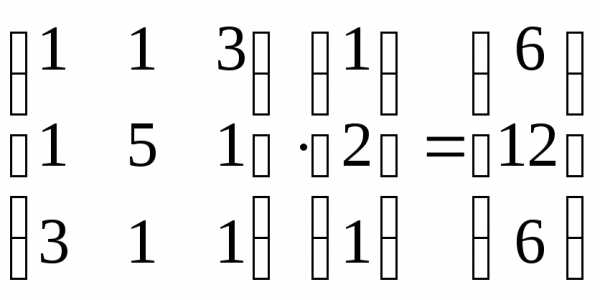 ,
откуда следует, что
,
откуда следует, что =6
=6 ,
а вектор
при
,
а вектор
при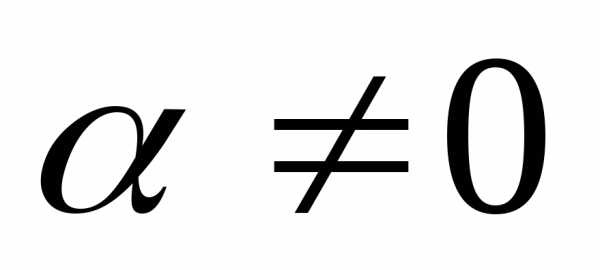 —
собственный вектор матрицы,
который соответствует собственному
значению
—
собственный вектор матрицы,
который соответствует собственному
значению .
.
Ответ: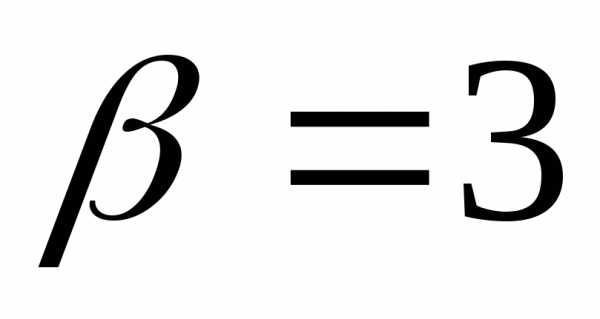 ;
;
при 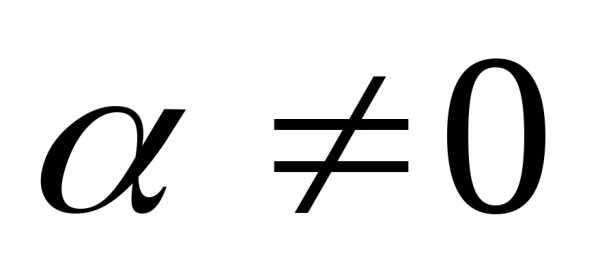 (-2,)
,(3,),
(-2,)
,(3,),
(6, ) — собственные пары матрицы.
studfiles.net
14. Собственные векторы и собственные значения матрицы.
Определение. Число называется собственным значением квадратной матрицы А, если найдется вектор такой, что А·=·. Вектор называется собственным вектором матрицы А, соответствующим данному собственному значению.
Теорема 1. Собственные значения матрицы А являются решениями уравнения
.
Это уравнение называется характеристическим уравнением матрицы А.
Теорема 2. Число различных собственных значений квадратной матрицы не превосходит ее порядка. Собственные векторы, отвечающие различным собственным значениям, линейно независимы.
15. Системы линейных уравнений.
Определение 1. Система вида
называется системой m линейных уравнений с n неизвестными, где x1, x2, …, xn — неизвестные, aij, i=,j= — коэффициенты при неизвестных, b1, b2, …, bm — свободные члены.
Определение 2. Если все свободные члены равны нулю, то система называется однородной, и неоднородной — в противном случае.
Определение 3. Решением системы называется совокупность из n чисел с1, с2, …, сn, при подстановке которой в систему вместо неизвестных будет получено m числовых тождеств.
Определение 4. Система называется совместной, если она имеет хотя бы одно решение, и несовместной в противном случае.
Определение 5. Совместная система называется определенной, если она имеет единственное решение, и неопределенной — в противном случае.
При изучении систем исследуют три вопроса:
1) совместна система или нет;
2) если система совместна, то является ли она определенной или неопределенной;
3) нахождение единственного решения в случае определенной системы и всех решений в случае неопределенной.
16. Совместность неоднородной системы.
Рассмотрим неоднородную систему:
Рассмотрим матрицы:
и .
Матрица называется расширенной матрицей системы.
Теорема (теорема Кронекера — Капелли). Неоднородная система линейных уравнений совместна тогда и только тогда, когда ранг матрицы, составленной из коэффициентов при неизвестных, равен рангу расширенной матрицы.
Доказательство. Необходимость. Пусть система совместна, тогда найдутся числа с1, с2, …, сn, при подстановке которых в систему мы получим m тождеств, которые можно записать в виде одного векторного тождества:
.
Следовательно, вектор-столбец свободных членов является линейной комбинацией векторов-столбцов матрицы А, тогда добавление его к системе векторов-столбцов матрицы А не меняет ранга системы. Отсюда r(A)=.
Достаточность. Пусть r(A)==r. Следовательно, существует линейно независимая подсистема из r векторов-столбцов матрицы A. Она же будет содержатся и в матрице . Так как эта система максимальна, то вектор-столбец свободных членов будет выражаться через эти r векторов-столбцов. Следовательно, вектор-столбец свободных членов можно представить в виде линейной комбинации всех векторов-столбцов матрицы А, т.е. найдутся числа с1, с2, …, сnтакие, что вектор-столбец будет представлен в виде
.
Следовательно, числа с1, с2, …, сn являются решением системы, т.е. она совместна.
17. Решение систем методом Крамера и с помощью обратной матрицы.
Рассмотрим неоднородную систему n линейных уравнений с n неизвестными:
Теорема (теорема Крамера). Если определитель матрицы, составленной из коэффициентов при неизвестных, отличен от нуля (), то система имеет единственное решение, которое можно найти по формулам Крамера:
, где — главный определитель, — j-й вспомогательный определитель, который получен из определителя заменой j-го столбца столбцом свободных членов.
Если главный определитель равен нулю и хотя бы один их вспомогательных определителей отличен от нуля, то система решений не имеет.
Если главный определитель и все вспомогательные определители равны нулю, то система имеет бесконечно много решений.
studfiles.net
5.1.3. Собственные числа и собственные векторы матрицы
Вектор Х называется Собственным вектором матрицы А, если найдется такое число L, что выполняется равенство: АХ = LХ, то есть результатом применения к Х линейного оператора, задаваемого матрицей А, является умножение этого вектора на число L. Само число L называется Собственным числом матрицы А.
Подставив в формулы (3) X’J = LXj, получим систему уравнений для определения координат собственного вектора:
Отсюда
.
Эта линейная однородная система будет иметь нетривиальное решение только в случае, если ее главный определитель равен 0 (правило Крамера). Записав это условие в виде:
Получим уравнение для определения собственных чисел L, называемое Характеристическим уравнением. Кратко его можно представить так:
Поскольку в его левой части стоит определитель матрицы А-LЕ. Многочлен относительно L | A — LE| называется Характеристическим многочленом матрицы А.
Свойства характеристического многочлена:
1) Характеристический многочлен линейного преобразования не зависит от выбора базиса.
Доказательство.
(см. (11.4)), но Следовательно, . Таким образом, не зависит от выбора базиса. Значит, и |A—LE| не изменяется при переходе к новому базису.
2) Если матрица А линейного оператора является Симметрической (т. е. АIj=Aji), то все корни характеристического уравнения (11.6) – действительные числа.
Свойства собственных чисел и собственных векторов:
1) Если выбрать базис из собственных векторов Х1, х2, х3, соответствующих собственным значениям λ1, λ2, λ3 матрицы А, то в этом базисе линейное преобразование А имеет матрицу диагонального вида:
Доказательство этого свойства следует из определения собственных векторов.
2) Если собственные значения оператора А различны, то соответствующие им собственные векторы линейно независимы.
3) Если характеристический многочлен матрицы А имеет три различных корня, то в некотором базисе матрица А имеет диагональный вид.
Пример 1.
Найдем собственные числа и собственные векторы матрицы
Составим характеристическое уравнение:
(1- L)(5 — L)(1 — L) + 6 — 9(5 — L) — (1 — L) — (1 — L) = 0,
L³ — 7L² + 36 = 0, L1 = -2, L2 = 3, L3 = 6.
Найдем координаты собственных векторов, соответствующих каждому найденному значению L. Из (5) следует, что если Х(1)={X1,X2,X3} – собственный вектор, соответствующий L1=-2, то
Совместная, но неопределенная система. Ее решение можно записать в виде Х(1)=(A,0,-A), где А – любое число. В частности, если потребовать, чтобы |X(1)|=1,
Подставив в систему (5) L2=3, получим систему для определения координат второго собственного вектора — X(2)=(Y1,Y2,Y3):
Откуда Х(2)=(B,-B,B) или, при условии |X(2)|=1,
Для L3 = 6 найдем собственный вектор X(3)=(Z1, Z2, Z3):
X(3)={C,2C,C} или в нормированном варианте
Можно заметить, что Х(1)Х(2) = Ab – Ab = 0, X(1)X(3) = Ac – Ac = 0, X(2)X(3) = Bc — 2Bc + Bc = 0. Таким образом, собственные векторы этой матрицы попарно ортогональны.
| < Предыдущая | Следующая > |
|---|
matica.org.ua
Собственные векторы и собственные значения
Вектор называется собственным вектором линейного оператора , если действие этого оператора на сводится к растяжению вектора в раз, т.е.
| . |
Число при этом называют собственным значением оператора .
Из данного определения следует схема получения и . Перепишем или и так как , то
| . |
В развернутом виде получим однородную систему:
| (20) |
которая называется характеристической, и будет иметь ненулевое решение, если ее определитель обращается в нуль:
| (21) |
Уравнение (21) называется характеристическим (или вековым) и служит для получения собственных значений . После раскрытия определителя приходим к алгебраическому уравнению 3-й степени вида:
| (22) |
где – след матрицы ; – алгебраические дополнения, – определитель матрицы .
Пусть уравнение (22) имеет три действительных корня . Тогда из системы (20) находим координаты собственных векторов . Составим матрицу , по столбцам которой стоят координаты этих векторов. Это матрица перехода от стандартного базиса к базису из собственных векторов и тогда линейный оператор в этом базисе будет иметь матрицу вида:
| , |
причем диагональную, по главной диагонали которой стоят собственные значения , т.е.
.
Это справедливо только для случая различных действительных корней.
Предлагаем студентам проверить это самостоятельно.
Замечание. Если матрица линейного оператора симметрическая , то ее собственные значения действительные и различные, а собственные векторы ортогональны.
Предлагаем студентам проверить это самостоятельно.
Пример 14
Найти собственные векторы и собственные значения линейного оператора, заданного в некотором базисе симметрической матрицей
.
Решение
Искомый собственный вектор удовлетворяет характеристической системе
Собственные значения удовлетворяют уравнению .
После раскрытия определителя получаем алгебраическое уравнение 3-й степени: , где ,
, , ,
.
Приходим к уравнению вида:
Получаем собственные значения – все действительные и различные.
Строим собственные векторы. Значение подставляем в характеристическую систему:
Ее определитель равен нулю, и, следовательно, ранг системы (т.к. минор ). Система равносильна системе:
или
, , .
По правилу Крамера . Полагаем и получаем 1-й собственный вектор . Можно взять и тогда .
Аналогично значение подставляем в характеристическую систему:
Вновь система равносильна двум уравнениям:
т. к. минор и . Находим решения системы по формулам Крамера:
; ; .
Получаем координаты второго собственного вектора: . Полагаем и , . Можно взять и тогда .
Далее берем и подставляем в характеристическую систему:
, ,
. Получим 3-й собственный вектор . Можно взять , тогда .
Ответ: , , , .
Заметим, что построенные векторы взаимно перпендикулярны в пространстве, т. к. , , .
Собственные векторы можно нормировать:
, , – эти три вектора образуют ортонормированный базис в 3-х мерном пространстве.
Показать, что матрица линейного оператора в базисе из собственных векторов будет иметь диагональную форму: .
Приведение квадратичной формы к каноническому виду
Пусть задана квадратичная форма от двух переменных вида:
Значит, матрица квадратичной формы является симметрической.
Пример 15
Для ,
т.е. .
Матрица квадратичной формы в базисе из собственных векторов будет диагональной, т.е. .
Действительно, составим характеристическую систему
Ее определитель равен нулю: или
, где , .
Получим характеристическое уравнение , корни которого
, .
Решим систему при :
или .
Полагаем и получаем 1-й собственный вектор .
Аналогично, для :
или .
Полагаем и получаем 2-й собственный вектор .
Заметим, что , т. к. .
Строим матрицу перехода , ее определитель .
Обратная матрица существует: , и в базисе из собственных векторов получаем вид матрицы квадратной формы:
.
Тогда квадратичная форма в базисе из собственных векторов примет канонический вид:
или .
При этом «новые» и «старые» координаты связаны между собой формулой
или
Замечание. Аналогично для квадратичной формы от 3-х переменных
.
Матрица (квадратичной формы)
| – симметрическая. |
Например, ,
т. к. .
В базисе из собственных векторов квадратичная форма примет вид:
, где – собственные значения симметрической матрицы . При собственные векторы ортогональны.
Замечание об евклидовых пространствах
В линейном –мерном пространстве вводим скалярное произведение по правилу:
| . |
Такая операция над векторами обладает следующими свойствами:
1) – коммутативность;
2) – дистрибутивность;
3) – ассоциативность по умножению на скаляр;
4) при и при .
–мерное векторное пространство, в котором задано скалярное произведение векторов, удовлетворяющее указанным четырем свойствам, называется евклидовым пространством.
Длиной (нормой) вектора в этом пространстве называется
| , | (25) |
для которой выполняются свойства:
1) , если ;
2) при любом ;
3) – неравенство Коши–Буняковского;
4) – неравенство треугольника.
Угол между векторами и в евклидовом пространстве определяется из формулы:
| (26) |
Определение корректно, т.к. согласно неравенству Коши–Буняковского
, т. е. .
Два вектора называется ортогональными, если , откуда .
Векторы –мерного пространства образуют ортонормированный базис, если при любых и при .
Теорема 4. Во всяком –мерном евклидовом пространстве существует ортонормированный базис.
Например, в : , , .
infopedia.su


 2,
то есть является представлением
линейного оператора в пространстве
2,
то есть является представлением
линейного оператора в пространстве
 .
.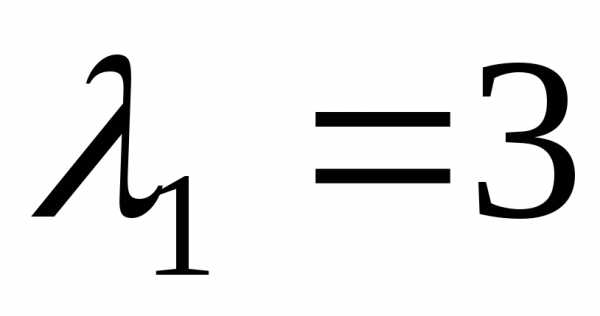 ,
решая матричное уравнение:
,
решая матричное уравнение: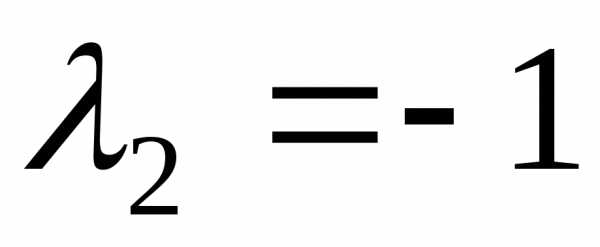 ,
решая матричное уравнение:
,
решая матричное уравнение: .
Исходя из соотношениях=0или в нашем случае
.
Исходя из соотношениях=0или в нашем случае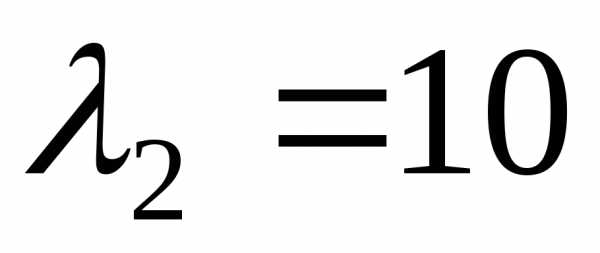 .
Исходя из соотношениях=0или в нашем случае
.
Исходя из соотношениях=0или в нашем случае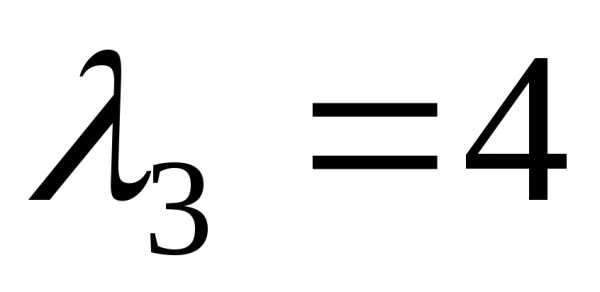 .
Исходя из соотношениях=0или в нашем случае
.
Исходя из соотношениях=0или в нашем случае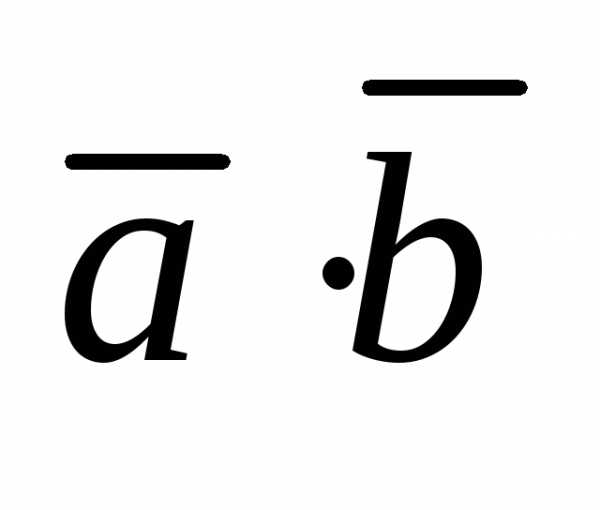 =
= 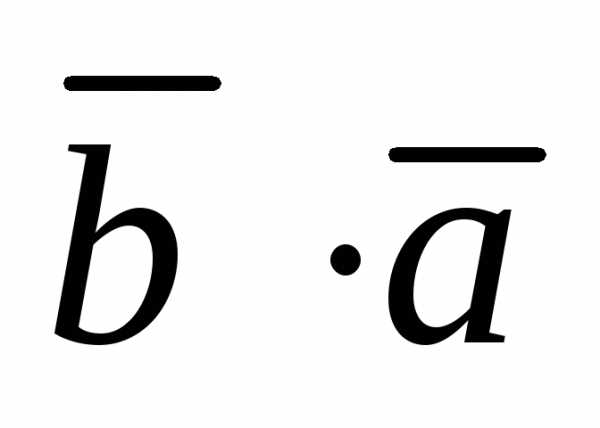 (переместительный
закон)
(переместительный
закон)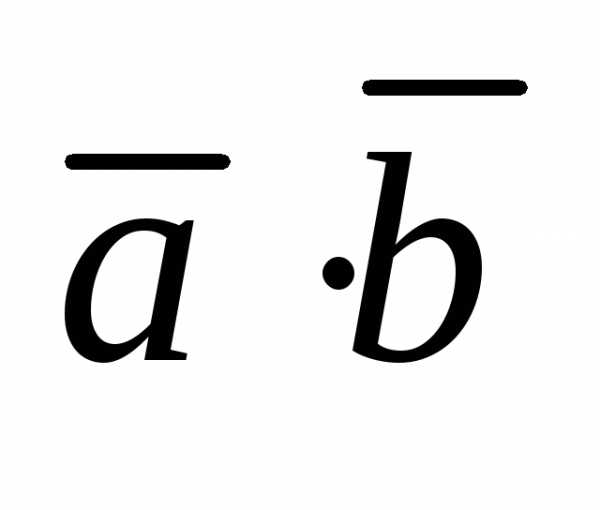 = 0, если
= 0, если 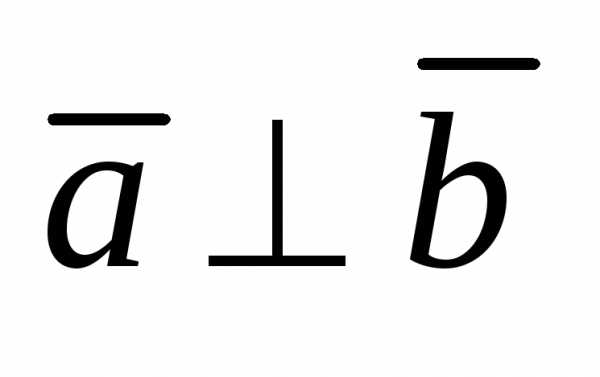 (скалярное произведение двух
перпендикулярных векторов равно нулю)
или какой-либо из перемножаемых векторов
является нулевым.
(скалярное произведение двух
перпендикулярных векторов равно нулю)
или какой-либо из перемножаемых векторов
является нулевым.