Нормальное распределение гаусса для чайников – , —

Нормальное распределение — Электронный учебник K-tree

 КАЛЬКУЛЯТОР ТАБЛИЦА |

Вероятность

Вероятность, что подброшенная монета упадёт орлом вверх 50%, что при броске шестигранного кубика выпадет 4 — 16,7%, что завтра на кого-нибудь упадёт метеорит — 0.00000000294%. Это простые примеры, достаточно разделить количество желаемых событий на общее количество случаев и мы получаем вероятность события, но когда результаты эксперимента могут быть не только орлом или решкой (что эквивалентно да/нет), а большим набором данных. Например, вес батона хлеба, если мы возьмём в магазине 1000 буханок хлеба и взвесим каждую, то мы узнаем, что на самом деле батон не весит 400 грамм, результаты будут варьироваться в диапазоне 384-416 грамм (допуск разброса веса предусмотрен ГОСТом). Если Вы построите график «Количество буханок — Вес», то график будет иметь форму напоминающую колокол, что-то похожее на следующий график:

Плотность вероятности нормального распределения

Такую форму график получит потому, что большинство значений близко к 400. Это — пример нормального распределения, множество событий имеют закон нормального распределения, например, вес или рост для определённого возраста, или среднее время Вашего похода до магазина и многие другие события также подчиняются закону нормального распределения.

Вот так работают маркетологи: проводят опрос 1000 человек и получают представление о всём населении

В случае таблицы Вы имеете дело с дискретными данными, т.е. для каждого веса есть определённая вероятность, но в случае графика дело немного меняется, теперь мы говорим не о 1000 буханок, которые мы взвесили, а обо всех буханках в мире сразу! Зачем? Что бы не взвешивать все буханки. Имея закон распределения, который мы получили взвесив 1000 буханок (мы могли взвесить 100, 200, 500, сколько угодно), мы можем предположить, что сколько бы мы буханок не взяли, замерив их, мы получим ту же форму колокола. Используя термины статистики, все буханки хлеба — это генеральная совокупность, 1000 замеренных буханок — выборка.

Теперь, возьмём одну буханку хлеба, какова вероятность, что её вес будет между 390г и 400г?

Вероятность события между a и b:

P(a ≤ X ≤ b) = P(X ≤ b) — P(X ≤ a)

Распределение вероятности — это функция, в которой для каждого события Х присваивается вероятность p, что событие произойдёт

Распределение Гаусса

Нормальное распределение получило своё название абсолютно справедливо: по статистике, большинство событий происходят именно с вероятностью нормального распределения, но что это значит? Это означает, например, что когда Вы видите на упаковке хлеба обозначение «Вес: 400±16г» — вес батона имеет нормальное распределение со средним значением 400г и стандартным отклонением 16г.

Таблица нормального распределения

Таблица нормального распределения — это затабулированные значения функции нормального распределения.

Для нахождения вероятности события Z₀ можно воспользоваться таблицей нормального распределения ниже. На пересечении строк (n) и столбцов (m) находится значение вероятности n+m.

Z0	0.00	0.01	0.02	0.03	0.04	0.05	0.06	0.07	0.08	0.09
0	0.500	0.504	0.508	0.512	0.516	0.520	0.524	0.528	0.532	0.536
0.1	0.540	0.544	0.548	0.552	0.556	0.560	0.564	0.568	0.571	0.575
0.2	0.579	0.583	0.587	0.591	0.595	0.599	0.603	0.606	0.610	0.614
0.3	0.618	0.622	0.625	0.629	0.633	0.637	0.641	0.644	0.648	0.652
0.4	0.655	0.659	0.663	0.666	0.670	0.674	0.677	0.681	0.684	0.688
0.5	0.692	0.695	0.699	0.702	0.705	0.709	0.712	0.716	0.719	0.722
0.6	0.726	0.729	0.732	0.736	0.739	0.742	0.745	0.749	0.752	0.755
0.7	0.758	0.761	0.764	0.767	0.770	0.773	0.776	0.779	0.782	0.785
0.8	0.788	0.791	0.794	0.797	0.799	0.802	0.805	0.808	0.811	0.813
0.9	0.816	0.819	0.821	0.824	0.826	0.829	0.832	0.834	0.837	0.839
1	0.841	0.844	0.846	0.849	0.851	0.853	0.855	0.858	0.860	0.862
1.1	0.864	0.867	0.869	0.871	0.873	0.875	0.877	0.879	0.881	0.883
1.2	0.885	0.887	0.889	0.891	0.892	0.894	0.896	0.898	0.900	0.901
1.3	0.903	0.905	0.907	0.908	0.910	0.911	0.913	0.915	0.916	0.918
1.4	0.919	0.921	0.922	0.924	0.925	0.926	0.928	0.929	0.931	0.932
1.5	0.933	0.934	0.936	0.937	0.938	0.939	0.941	0.942	0.943	0.944
1.6	0.945	0.946	0.947	0.948	0.950	0.951	0.952	0.953	0.954	0.955
1.7	0.955	0.956	0.957	0.958	0.959	0.960	0.961	0.962	0.963	0.963
1.8	0.964	0.965	0.966	0.966	0.967	0.968	0.969	0.969	0.970	0.971
1.9	0.971	0.972	0.973	0.973	0.974	0.974	0.975	0.976	0.976	0.977
2	0.977	0.978	0.978	0.979	0.979	0.980	0.980	0.981	0.981	0.982
2.1	0.982	0.983	0.983	0.983	0.984	0.984	0.985	0.985	0.985	0.986
2.2	0.986	0.986	0.987	0.987	0.988	0.988	0.988	0.988	0.989	0.989
2.3	0.989	0.990	0.990	0.990	0.990	0.991	0.991	0.991	0.991	0.992
2.4	0.992	0.992	0.992	0.993	0.993	0.993	0.993	0.993	0.993	0.994
2.5	0.994	0.994	0.994	0.994	0.995	0.995	0.995	0.995	0.995	0.995
2.6	0.995	0.996	0.996	0.996	0.996	0.996	0.996	0.996	0.996	0.996
2.7	0.997	0.997	0.997	0.997	0.997	0.997	0.997	0.997	0.997	0.997
2.8	0.997	0.998	0.998	0.998	0.998	0.998	0.998	0.998	0.998	0.998
2.9	0.998	0.998	0.998	0.998	0.998	0.998	0.999	0.999	0.999	0.999
3	0.999	0.999	0.999	0.999	0.999	0.999	0.999	0.999	0.999	0.999
3.1	0.999	0.999	0.999	0.999	0.999	0.999	0.999	0.999	0.999	0.999
3.2	0.999	0.999	0.999	0.999	0.999	0.999	0.999	0.999	0.999	1.000
Таблица 1. Таблица нормального распределения. Красным выделены часто используемые значения при выборе критической области

Не только. График нормального распределения построен для среднего значения ноль и стандартного отклонения единица, т.е. 0±1. Но если Ваши среднее и отклонение отличаются от нуля и единицы, то к Вашим услугам следующая формула:

Z = (X — μ) / σ

Где μ и σ — среднее значение и стандартное отклонение для Вашего распределения соответственно, а X — величина, для которой Вы хотите узнать вероятность. Возвращаясь к примеру с батоном хлеба — для того, что бы узнать, какова вероятность, что батон будет весить меньше 396 грамм — необходимо подставить в формулу значения X=396, μ = 400, σ = 16:

Z = (396 — 400) / 16 = -0.25

Далее, по таблице необходимо найти значение для Z. Как для Z = -0.25, так и для Z = 0.25 это будет 0,5987 (нормальное распределение симметрично, поэтому значение вероятности определяется для абсолютного значения Z: график симметричен относительно оси Y, поэтому значение вероятности не зависит от знака X)

Свойства функции распределения

• Симметрична относительно центра (среднее значение — математическое ожидание μ)
• Мода и медиана равны математическому ожиданию μ

Функция распределения

Функция распределения предназначена для того, что бы определить, какова вероятность, что величина X меньше или равна некоторого числа x.

На примере батона из первого абзаца: если мы хотим узнать, какова вероятность, что батон будет весить меньше 410 грамм, то, воспользовавшись формулой приведения, получим Z=0.63 и значение P(X

Среднее значение нормального распределения (μ)

Математическое ожидание (среднее значение) для стандартного нормального распределения равно нулю: μ = 0

Нормальное распределение в excel

Что бы получить значение нормального распределения в эксель, существует формула «НОРМ.РАСП» (в старых версиях НОРМРАСП), в которую передаётся значение события X, например, какова вероятность попасть в интервал [-0.5;0.5]?

=НОРМРАСП(0,5;0;1;1) = 0,35
=НОРМ.РАСП(0,5;0;1;1) = 0,35

Синтаксис команды следующий: НОРМРАСП(событие Х, среднее, отклонение, интегральная). Так, Вы можете найти значение нормального распределения без приведения значений:

=НОРМ.РАСП(396;400;16;1) = 0.4

Для поиска значения Z, при наличии вероятности, например, для 95%, можно воспользоваться формулой «НОРМОБР»:

=НОРМОБР(0,95;0;1) = 1,64

Тесты

1. Нормальное распределение

k-tree.ru

Нормальное распределение (распределение Гаусса)

7

Аппарат математической статистики достаточно хорошо разработан применительно к условию, когда распределение случайной величины подчиняется закону нормального распределения (закон Гаусса).

Исследованиями в технологии машиностроения установлено, что большинство характеристик технологических процессов подчиняется именно этому закону.

Нормальный закон распределения играет исключительно важную роль во всех областях техники и технологии и занимает особое положение среди других законов распределения.

Нормальное распределение случайной величины возникает в тех случаях, когда результат испытаний является следствием влияния большого количества факторов, среди которых нет доминирующих, а объем наблюдений достаточно велик. Многие непрерывные наблюдения при увеличении объема испытаний стремятся к нормальному распределению.

Случайная величина распределена по нормальному закону, если уравнение плотности распределения вероятности имеет вид:

				(Y−Y	)2
		1	−	o
				2σo2
	ϕ(Y )=	σo 2πe			.
Параметрами	закона	нормального			распределения		являются

среднеквадратическое отклонение σ0 и среднее значение Yо .

Точную формулу для функции распределения, подчиненного нормальному закону, получить нельзя, так как выражение плотности вероятности представляет неинтегрируемую функцию. Для расчета вероятности попадания случайной величины в какой-либоинтервал используется функция Лапласа. Значения функции Лапласа табулированы и представлены в справочниках и учебниках по теории вероятности.

ϕ(Y) 1σo 2π

±2σo

±3σo

Кривая закона нормального распределения

8

Теоретическая кривая закона нормального распределения имеет колоколообразный вид, симметричный относительно перпендикуляра к оси абсцисс, проходящего через точку на оси абсцисс с координатой Yо, достигает максимума в этой точке (1σ0 2π ) и асимптотически приближается к нулю

при ± ∞.

Математическое ожидание: M(Y) = Y0 . Дисперсия: D(Y) = σ02 .

Площадь под кривой, ограниченная интервалом Y1≤Y0≤Y2, соответствует вероятности того, что результаты эксперимента попадут в данный интервал. В пределах ±3σ0 отY0 находится99,73% площади под кривой.

Поэтому на практике для нормального распределения применяют «правило трех сигм». Для закона нормального распределения на основании «правила трех сигм» поле рассеянияр случайной величины составляет:

p= (Yo+3σo) −(Yo−3σo) = 6σo.

Всвязи с тем, что оценивать σ0 их0 можно с помощью характеристикS иx выборки, практическое поле рассеяния определяют по формуле:

p = 2 l S,

где l – табличное значение коэффициента, взятое при данном объеме выборки дляα=0,95 (причемl рассчитано из условия, что количество значений случайных величин, находящихся в пределах практического поля рассеяния, составляет 99,73 %).

Примерами нормального закона распределения могут служить:

–распределение погрешности измерительных приборов;

–характеристики измерения показателя в партии одинаковых изделий;

–погрешности позиционирования станков с ЧПУ, роботов и т.п.

studfiles.net

Распределение Гаусса — это… Что такое Распределение Гаусса?

Нормальное распределение, также называемое распределением Гаусса, — распределение вероятностей, которое играет важнейшую роль во многих областях знаний, особенно в физике. Физическая величина подчиняется нормальному распределению, когда она подвержена влиянию огромного числа случайных помех. Ясно, что такая ситуация крайне распространена, поэтому можно сказать, что из всех распределений в природе чаще всего встречается именно нормальное распределение — отсюда и произошло одно из его названий.

Нормальное распределение зависит от двух параметров — смещения и масштаба, то есть является с математической точки зрения не одним распределением, а целым их семейством. Значения параметров соответствуют значениям среднего (математического ожидания) и разброса (стандартного отклонения).

Стандартным нормальным распределением называется нормальное распределение с математическим ожиданием 0 и стандартным отклонением 1.

Моделирование нормальных случайных величин

Простейшие, но неточные методы моделирования основываются на центральной предельной теореме. Именно, если сложить много независимых одинаково распределённых величин с конечной дисперсией, то сумма будет распределена примерно нормально. Например, если сложить 12 независимых базовых случайных величин, получится грубое приближение стандартного нормального распределения. Тем не менее, с увеличением слагаемых распределение суммы стремится к нормальному.

Использование точных методов предпочтительно, поскольку у них практически нет недостатков. В частности, преобразование Бокса — Мюллера является точным, быстрым и простым для реализации методом генерации.

Статистическая проверка принадлежности нормальному распределению

Поскольку нормальное распределение часто встречается на практике, то для него разработаны специальные статистические критерии проверки на «нормальность»:

• Критерий Пирсона
• Критерий Колмогорова-Смирнова
• Критерий Андерсона-Дарлинга(англ.)
• Критерий Жака-Бера(англ.)
• Критерий Шапиро-Вилка(англ.)
• «График нормальности»(англ.) — не столько критерий, сколько графическая иллюстрация: точки специально построенного графика должны лежать почти на одной прямой.

Заключение

Нормальное распределение наиболее часто встречается в природе, нормально распределёнными являются следующие случайные величины:

• отклонение при стрельбе
• ошибки при измерениях
• рост человека

Такое широкое распространение закона связано с тем, что он является предельным законом, к которому приближаются многие другие (например, биномиальный). Доказано, что сумма очень большого числа случайных величин, влияние каждой из которых близко к 0, имеет распределение, близкое к нормальному. Этот факт является содержанием предельной теоремы Ляпунова.

См. также

Wikimedia Foundation. 2010.

dic.academic.ru

Нормальное распределение Гаусса

Поделись с друзьями

В большинстве практических случаев при чисто случайных разбросах результатов отдельных измерений относительно истинного значения измеряемой величины функция распределения имеет вид, получивший название нормального распределения Гаусса.

Если причины, вызывающие отклонения результатов измерения от истинного значения, настолько разнообразны и многоплановы, что невозможно выделить какую-либо доминанту, функция распределения всегда имеет вид экспоненты с определенными параметрами. К этому утверждению следует относиться как к аксиоме физики, т. е. мир устроен так, что при случайном выпадении многократных результатов повторяющихся событий функция распределения будет иметь вид экспоненты. В метрологии, как и в физике вообще, встречается достаточно много аксиом, например постоянство скорости света, корпускулярно-волновой дуализм, токи смещения в уравнениях Максвелла, принцип относительности и т. д. Аналитическую зависимость функции нормального распределения можно отнести к категории таких принципов или аксиом. В метрологии и в технике измерений получение такой зависимости неоценимо в определении достоверности, правильности и точности измерений. Предложенная Гауссом зависимость дифференциальной функции распределения результатов повторяющихся случайных событий оказалась настолько ценной, что в Германии, например, формула нормального распределения считается одним из самых крупных достижений науки.

Нормальное распределение выпадения определенного результата в повторяющихся случайных событиях это такое распределение, дифференциальная функция распределения которого имеет вид:

(3.42)

где δ = х — mF; здесь: х — результат однократного измерения; mF — математическое ожидание результата измерения так, что

(3.43)

где σx — среднее квадратическое отклонение результатов измерения.

При записи в таком виде кривые нормального распределения зависят от среднего квадратического отклонения. При увеличении σ распределение все более расплывается, т. е. вероятность появления больших отклонений от математического ожидания увеличивается, а вероятность меньших погрешностей сокращается (рис.).

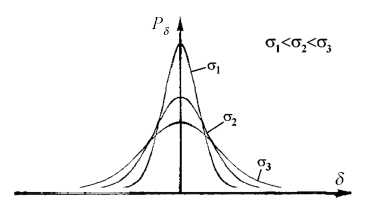
Для того чтобы сделать аналитическую зависимость нормального дифференциального распределения более универсальной, делают замену переменных, выражая отклонения величины х от математического ожидания mF в единицах среднего квадратического отклонения:

(3.44)

где х — результат отдельного измерения; x1 — минимальное возможное значение измерения; x2 — максимальное возможное значение измерения. После такой замены переменных вероятность попадания результата измерения в некоторый заданный интервал (x1 ; x2 ] выражается как:

(3.45)

Интегралы в скобках не выражаются в элементарных функциях. Их вычисляют с помощью так называемого нормированного нормального распределения с дифференциальной функцией

(3.46)

график которой изображен на рис.

.

Функция p(t) не зависит от параметров распределения, в силу чего может быть затабулирована. Интегральная функция нормального распределения имеет вид:

(3.47)

По физическому смыслу это есть вероятность того, что погрешность измерения будет меньше или равна величине z, т. е.

(3.48)

Интегральная функция нормального распределения также затабулирована. Используя интегральную функцию нормального распределения, можно определить вероятность попадания результата измерения в интервал (x1 , x2 ] как

(3.49)

При этом справедливо тождество:

(3.50)

Подчеркнем, что все сказанное справедливо, если погрешности случайные, распределение можно считать нормальным с известной дисперсией σx2 . Тогда на основании формулы (3.44) имеем:

(*)

Обычно значения t1 и t2, выбирают симметрично по обе стороны от максимума распределения так, что t1 = t2 = tp. Формула для вероятности попадания результата в заданный интервал приобретает вид:

(3.52)

Меняя х и mF местами в этом неравенстве, получим:

(3.53)

Если систематические погрешности исключены и mF = Q, то

(3.54)

Это означает, что истинное значение измеряемой величины с доверительной вероятностью Р = 2Ф(tp) -1 находится между границами интервала . Интервал от -tpσx до +tpσx называется доверительным интервалом погрешности измерения, а половина интервала tpσx называется доверительной границей случайного отклонения результатов наблюдения, соответствующей доверительной вероятности Р.

Для определения доверительной границы задаются доверительной вероятностью Р и по (*) находят из таблиц параметр tp. После этого вычисляют доверительное отклонение tpσx . Если известно среднее квадратическое отклонение результатов измерения, то легко определить погрешность измерения при заданной доверительной вероятности.

Задача может быть поставлена иначе, а именно: какова доверительная вероятность попадания результата измерения в заданный доверительный интервал, если известно среднее квадратическое отклонение серии измерений? В этом случае определяют параметр tp делением доверительного интервала на среднеквадратическое отклонение tp= (tpσx ) /σx . Затем из таблиц значений интегральной функции нормального распределения находят величину Ф(tp), после чего вычисляют доверительную вероятность как 2Ф(tp) -1.

Из приведенных определений понятий, определяющих нормальное распределение вероятности получения определенных результатов измерения можно кратко сформулировать следующие выводы:

1. Погрешности измерения (интервалы допустимой погрешности) зависят от того, с какой вероятностью мы хотим получить достоверный результат.

2.      Для определения погрешности при заданном доверительном интервале и для определения этого интервала при заданной доверительной вероятности необходимо знать среднее квадратическое отклонение результатов измерения.

3.      Функции нормального распределения дают связь между вероятностью попадания результатов измерения (доверительной вероятностью) в заданный интервал и величиной самого интервала, называемого доверительной границей случайного отклонения.

students-library.com

Нормальное распределение непрерывной случайной величины

Нормальное распределение вероятностей непрерывной случайной величины (иногда — распределение Гаусса) можно назвать колоколообразным из-за того, что симметричная относительно среднего функция плотности этого распределения очень похожа на разрез колокола.

На рисунке ниже представлена функция плотности нормального распределения, график которой получен при рассчёте некоторой выборки данных в пакете программных средств STATISTICA. На ней столбцы гистограммы представляют собой интервалы значений выборки, распределение которых близко (или, как принято говорить в статистике, незначимо отличаются от) к собственно графику функции плотности нормального распределения, который представляет собой кривую красного цвета. На графике видно, что эта кривая действительно колоколообразная.

Для увеличения рисунка можно щёлкнуть по нему левой кнопкой мыши.

Нормальное распределение во многом ценно благодаря тому, что зная только математическое ожидание непрерывной случайной величины и стандартное отклонение, можно вычислить любую вероятность, связанную с этой величиной.

Примерами случайных величин, распределённых по нормальному закону, являются рост человека, масса вылавливаемой рыбы одного вида. Нормальность распределения означает следующее: существуют значения роста человека, массы рыбы одного вида, которые на интуитивном уровне воспринимаются как «нормальные» (а по сути — усреднённые), и они-то в достаточно большой выборке встречаются гораздо чаще, чем отличающиеся в бОльшую или меньшую сторону.

Вероятность встретить в выборке те или иные значение равна площади фигуры под кривой и в случае нормального распределения мы видим, что под верхом «колокола», которому соответствуют значения, стремящиеся к среднему, площадь, а значит, вероятность, больше, чем под краями. Таким образом, получаем то же, что уже сказано: вероятность встретить человека «нормального» роста, поймать рыбу «нормальной» массы выше, чем для значений, отличающихся в бОльшую или меньшую сторону. В очень многих случаях практики ошибки измерения распределяются по закону, близкому к нормальному.

Функцию плотности нормального распределения непрерывной случайной величины можно найти по формуле:

,

где x — значение изменяющейся величины, — среднее значение, — стандартное отклонение, e=2,71828… — основание натурального логарифма, =3,1416…

Свойства функции плотности нормального распределения

• для всех значений аргумента функция плотности положительна;
• если аргумент стремится к бесконечности, то функция плотности стреится к нулю;
• функция плотности симметрична относительно среднего значения: ;
• наибольшее значение функции плотности — у среднего значения: ;
• кривая функции плотности выпукла в интервале и вогнута на остальной части;
• мода и медиана нормального распределения совпадает со средним значением;
• при нормальном распределении коэффициенты ассиметрии и эксцесса равны нулю (подробнее рассмотрим это свойство в следующем параграфе о приближенном методе проверки нормальности распределения).

Изменения среднего значения перемещают кривую функции плотности нормального распределения в направлении оси Ox. Если возрастает, кривая перемещается вправо, если уменьшается, то влево.

Если меняется стандартное отклонение, то меняется высота вершины кривой. При увеличении стандартного отклонения вершина кривой находится выше, при уменьшении — ниже.

Уже в этом параграфе начнём решать практические задачи, смысл которых обозначен в заголовке. Разберём, какие возможности для решения задач предоставляет теория. Отправное понятие для вычисления вероятности попадания нормально распределённой случайной величины в заданный интервал — интегральная функция нормального распределения.

Интегральная функция нормального распределения:

.

Однако проблематично получить таблицы для каждой возможной комбинации среднего и стандартного отклонения. Поэтому одним из простых способов вычисления вероятности попадания нормально распределённой случайной величины в заданный интервал является использование таблиц вероятностей для стандартизированного нормального распределения.

Стандартизованным или нормированным называется нормальное распределение, среднее значение которого , а стандартное отклонение .

Функция плотности стандартизованного нормального распределения:

.

Интегральная функция стандартизованного нормального распределения:

.

На рисунке ниже представлена интегральная функция стандартизованного нормального распределения, график которой получен при рассчёте некоторой выборки данных в пакете программных средств STATISTICA. Собственно график представляет собой кривую красного цвета, а значения выборки приближаются к нему.

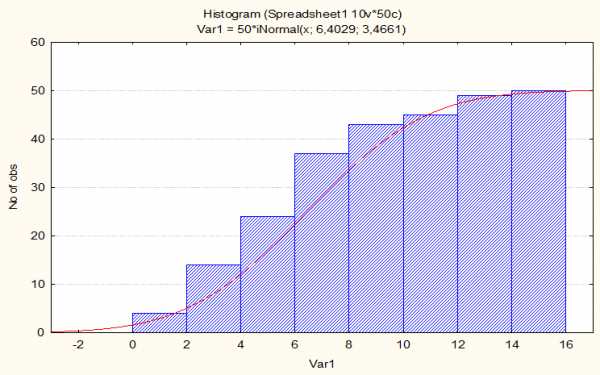
Для увеличения рисунка можно щёлкнуть по нему левой кнопкой мыши.

Стандартизация случайной величины означает переход от первоначальных единиц, используемых в задании, к стандартизованным единицам. Стандартизация выполняется по формуле

.

На практике все возможные значения случайной величины часто не известны, поэтому значения среднего и стандартного отклонения точно определить нельзя. Их заменяют средним арифметическим наблюдений и стандартным отклонением s. Величина z выражает отклонения значений случайной величины от среднего арифметического при измерении стандартных отклонений.

Открытый интервал

Таблица вероятностей для стандартизированного нормального распределения, которая есть практически в любой книге по статистике, содержит вероятности того, что имеющая стандартное нормальное распределение случайная величина Z примет значение меньше некоторого числа z. То есть попадёт в открытый интервал от минус бесконечности до z. Например, вероятность того, что величина Z меньше 1,5, равна 0,93319.

Пример 1. Предприятие производит детали, срок службы которых нормально распределён со средним значением 1000 и стандартным отклонением 200 часов.

Для случайно отобранной детали вычислить вероятность того, что её срок службы будет не менее 900 часов.

Решение. Введём первое обозначение:

— искомая вероятность.

Значения случайной величины находятся в открытом интервале. Но мы умеем вычислять вероятность того, что случайная величина примет значение, меньшее заданного, а по условию задачи требуется найти равное или большее заданного. Это другая часть пространства под кривой плотности нормального распределения (колокола). Поэтому, чтобы найти искомую вероятность, нужно из единицы вычесть упомянутую вероятность того, что случайная величина примет значение, меньше заданного 900:

Теперь случайную величину нужно стандартизировать.

Продолжаем вводить обозначения:

z = (X ≤ 900);

x = 900 — заданное значение случайной величины;

μ = 1000 — среднее значение;

σ = 200 — стандартное отклонение.

По этим данным условия задачи получаем:

.

По таблицам стандартизированной случайной величине (границе интервала) z = −0,5 соответствует вероятность 0,30854. Вычтем ее из единицы и получим то, что требуется в условии задачи:

.

Итак, вероятность того, что срок службы детали будет не менее 900 часов, составляет 69%.

Эту вероятность можно получить, используя функцию MS Excel НОРМ.РАСП (значение интегральной величины — 1):

P(X≥900) = 1 — P(X≤900) = 1 — НОРМ.РАСП(900; 1000; 200; 1) = 1 — 0,3085 = 0,6915.

О расчётах в MS Excel — в одном из последующих параграфах этого урока.

Пример 2. В некотором городе среднегодовой доход семьи является нормально распределённой случайной величиной со средним значением 300000 и стандартным отклонением 50000. Известно, что доходы 40 % семей меньше величины A. Найти величину A.

Решение. В этой задаче 40 % — ни что иное, как вероятность того, что случайная величина примет значение из открытого интервала, меньшее определённого значения, обозначенного буквой A.

Чтобы найти величину A, сначала составим интегральную функцию:

По условию задачи

μ = 300000 — среднее значение;

σ = 50000 — стандартное отклонение;

x = A — величина, которую нужно найти.

Составляем равенство

.

По статистическим таблицам находим, что вероятность 0,40 соответствует значению границы интервала z = −0,25.

Поэтому составляем равенство

и находим его решение:

A = 287300.

Ответ: доходы 40 % семей менее 287300.

Закрытый интервал

Во многих задачах требуется найти вероятность того, что нормально распределённая случайная величина примет значение в интервале от z1 до z2. То есть попадёт в закрытый интервал. Для решения таких задач необходимо найти в таблице вероятности, соответствующие границам интервала, а затем найти разность этих вероятностей. При этом требуется вычитать меньшее значение из большего. Примеры на решения этих распространённых задач — следующие, причём решить их предлагается самостоятельно, а затем можно посмотреть правильные решения и ответы.

Пример 3. Прибыль предприятия за некоторый период — случайная величина, подчинённая нормальному закону распределения со средним значением 0,5 млн. у.е. и стандартным отклонением 0,354. Определить с точностью до двух знаков после запятой вероятность того, что прибыль предприятия составит от 0,4 до 0,6 у.е.

Правильное решение и ответ.

Пример 4. Длина изготавливаемой детали представляет собой случайную величину, распределённую по нормальному закону с параметрами μ=10 и σ=0,071. Найти с точностью до двух знаков после запятой вероятность брака, если допустимые размеры детали должны быть 10±0,05.

Подсказка: в этой задаче помимо нахождения вероятности попадания случайной величины в закрытый интервал (вероятность получения небракованной детали) требуется выполнить ещё одно действие.

Правильное решение и ответ.

Функция

позволяет определить вероятность того, что стандартизованное значение Z не меньше -z и не больше +z, где z — произвольно выбранное значение стандартизованной случайной величины.

Приближенный метод проверки нормальности распределения значений выборки основан на следующем свойстве нормального распределения: коэффициент асимметрии β1 и коэффициент эксцесса β2 равны нулю.

Коэффициент асимметрии β1 численно характеризует симметрию эмпирического распределения относительно среднего. Если коэффициент асимметрии равен нулю, то среднее арифметрического значение, медиана и мода равны: и кривая плотности распределения симметрична относительно среднего. Если коэффициент асимметрии меньше нуля (β1 < 0), то среднее арифметическое меньше медианы, а медиана, в свою очередь, меньше моды () и кривая сдвинута вправо (по сравнению с нормальным распределением). Если коэффициент асимметрии больше нуля (β1 > 0), то среднее арифметическое больше медианы, а медиана, в свою очередь, больше моды () и кривая сдвинута влево (по сравнению с нормальным распределением).

Коэффициент эксцесса β2 характеризует концентрацию эмпирического распределения вокруг арифметического среднего в направлении оси Oy и степень островершинности кривой плотности распределения. Если коэффициент эксцесса больше нуля, то кривая более вытянута (по сравнению с нормальным распределением) вдоль оси Oy (график более островершинный). Если коэффициент эксцесса меньше нуля, то кривая более сплющена (по сравнению с нормальным распределением) вдоль оси Oy (график более туповершинный).

Коэффициент асимметрии можно вычислить с помощью функции MS Excel СКОС. Если вы проверяете один массив данных, то требуется ввести диапазон данных в одно окошко «Число».

Коэффициент эксцесса можно вычислить с помощью функции MS Excel ЭКСЦЕСС. При проверке одного массива данных также достаточно ввести диапазон данных в одно окошко «Число».

Итак, как мы уже знаем, при нормальном распределении коэффициенты асимметрии и эксцесса равны нулю. Но что, если мы получили коэффициенты асимметрии, равные -0,14, 0,22, 0,43, а коэффициенты эксцесса, равные 0,17, -0,31, 0,55? Вопрос вполне справедливый, так как практически мы имеем дело лишь с приближенными, выборочными значениями асимметрии и эксцесса, которые подвержены некоторому неизбежному, неконтролируемому разбросу. Поэтому нельзя требовать строгого равенства этих коэффициентов нулю, они должны лишь быть достаточно близкими к нулю. Но что значит — достаточно?

Требуется сравнить полученные эмпирические значения с допустимыми значениями. Для этого нужно проверить следующие неравенства (сравнить значения коэффициентов по модулю с критическими значениями — границами области проверки гипотезы).

Для коэффициента асимметрии β1:

,

где

— квантиль стандартного нормального распределения уровня ,

— среднеквадратическое отклонение для выборки с числом наблюдений n.

Для коэффициента асимметрии β2:

,

где

— квантиль стандартного нормального распределения уровня ,

— среднеквадратическое отклонение для выборки с числом наблюдений n.

Так как коэффициенты асимметрии и эксцесса могут оказаться и положительными, и отрицательными, то в приближенном методе проверки нормальности распределения используется двусторонний квантиль стандартного нормального распределения; он задаёт интервал, в который случайная величина попадает с определённой вероятностью. Приведём значения двусторонних квантилей стандартного нормального распределения определённых уровней (слева — уровень, справа — значение квантиля):

• 0,90: 1,645
• 0,95: 1,960
• 0,975: 2,241
• 0,98: 2,326
• 0,99: 2,576
• 0,995: 2,807
• 0,999: 3,291
• 0,9995: 3,481
• 0,9999: 3,891

Например, для выборки с числом наблюдений n = 50 и α = 0,05, пользуясь этими значениями и ранее приведёнными формулами, можно получить границу области принятия гипотезы для коэффициента асимметрии 0,62 и для коэффициента эксцесса 1,15. Поэтому приведённые ранее примеры эмпирических значений коэффициента асимметрии -0,14, 0,22, 0,43 попадают в область принятия гипотезы. То же самое относится к значениям коэффициента эксцесса 0,17, -0,31, 0,55. Следовательно, если получены такие эмпирические значения, то с вероятностью 95% данные выборки подчиняются нормальному закону распределения.

Значения функции плотности f(x) и интегральной функции F(x) нормального распределения можно вычислить при помощи функции MS Excel НОРМ.РАСП. Окно для соответствующего расчёта показано ниже (для увеличения нажать левой кнопкой мыши).

MS Excel требует ввести следующие данные:

• x — значение изменяющегося признака;
• среднее значение;
• стандартное отклонение;
• интегральная — логическое значение: 0 — если нужно вычислить функцию плотности f(x) и 1 — если вероятность F(x).

Решить задачу самостоятельно, а затем посмотреть решение

Пример 5. Определить с точностью до двух знаков после запятой вероятность попадания при стрельбе в полосу шириной 3,5 м, если ошибки стрельбы подчиняются нормальному закону распределения со средним значением 0 и σ = 1,9.

Правильное решение и ответ.

Решим ещё одну задачу вместе

Пример 6. О случайной величине X известно, что она нормально распределена, а вероятности того, что она составит 10 или меньше и больше 25, соответственно и . Найти среднее значение (математическое ожидание) случайной величины и её дисперсию.

Решение. Используем данные в условии задачи вероятности:

Пользуясь статистическими таблицами, находим:

Составляем систему из полученных равенств:

Решая систему, находим:

.

Начало темы «Теория вероятностей»

function-x.ru

Нормальное распределение (закон Гаусса, кривая Гаусса)

1. Общие положения

Непрерывная случайная величина Х имеет нормальное распределение, если ее плотность вероятности имеет вид:

(3.20)

где а – произвольный, а – положительный параметры.

Закон (распределение) Гаусса имеет огромное значение в теории вероятностей и её приложениях. Основное отличие этого закона от рассмотренных выше законов заключается в том, что он является предельным законом, к которому при некоторых условиях приближаются другие законы распределения. Нормальное распределение считается заданным, если заданы его параметры a, σ. Оно позволяет анализировать случайные погрешности измерений изготовленных изделий, осуществлять контроль технологических процессов, анализировать ошибки стрельбы, исследовать различные классы шумов радиотехнических устройств и др. В частности, это распределение позволяет определять вероятность попадания нормальной случайной величины в заданный интервал, определять вероятность отклонения размеров изделий от их средних значений (математических ожиданий), вычислять интервалы, в которых будут заключаться размеры изделий, если задана некоторая вероятность, и другие задачи – прямые и обратные, связанные с использованием формулы (3.20) и вытекающих из неё других формул.

Покажем, что функция f(x) удовлетворяет основному свойству плотности распределения – условию нормировки: .

Кроме того, f(x) > 0 в силу свойства показательной функции и f(x) – непрерывна при . Кривая, соответствующая (3.20) называется кривой Гаусса, и она имеет вид, показанный на рисунке 3.22.

Рис. 3.22

Функция распределения имеет вид .

Параметр a характеризует сдвиг кривой Гаусса вправо (a > 0) или влево (a < 0). Если a = 0, а σ = 1, то точка максимума располагается на оси OY, и нормальное распределение тогда называется стандартным. Для такого распределения плотность выражается формулой: . В этом случае совпадает с функцией Гаусса, которая использовалась ранее при вычислении вероятности по формулам Лапласа (см. подраздел 2.6.2).

Установим смысл параметров a и σ, определяющих нормальное распределение. С этой целью необходимо найти M(x) и D(x) с использованием функции f(x) .

Таким образом, a = M(x). (Первый интеграл в преобразуемом выражении равен нулю в силу нечетности функции и симметрии пределов интегрирования относительно начала координат).

Аналогично вычисляется и дисперсия, соответствующая нормальному распределению с f(x) (3.20).

Таким образом, , а – среднеквадратичное отклонение ( как параметр нормального распределения равен σ как среднеквадратичному отклонению).

Замечание. Начальный момент, равный медиане, для нормального распределения равен a, а коэффициент асимметрии A = 0 и коэффициент «островершинности» E = 0. Поэтому кривая Гаусса симметрична относительно прямой x = a.

2. Исследование поведения функции f(x) нормального распределения

1) Функция f(x) > 0 при всех , т.е. график f(x) расположен выше оси абсцисс.

2) , т.е. ось абсцисс является горизонтальной асимптотой f(x).

3) при x=a и при x<a, при x>a. Таким образом, в точке x = a реализуется максимум f(x) и точка максимума есть (см. рисунок 3.23).

4) Как было отмечено выше, график функции f(x) симметричен относительно прямой x=a т.к. разность x – a в формуле для f(x) возведена в квадрат.

5) ;

Таким образом, в точках , расположенных симметрично относительно прямой x = a, функция f(x) имеет перегиб, т.е. точками перегиба являются

.

6) Влияние изменения параметров a и на поведение кривой f(x).

Изменение параметра а не изменяет форму кривой Гаусса, а приводит только к сдвигу ее вдоль оси (рисунок 3.23 a).

Рис. 3.23

Параметр σ изменяет точку максимума (см. п.3) , т.е. чем больше σ, тем ближе расположена точка максимума к оси Ox. Кроме того, чем меньше параметр σ, тем ближе расположены точки перегиба к прямой x = a и тем выше эти точки (рисунок 3.23 б).

einsteins.ru

Нормальное распределение

Одномерное нормальное распределение

Графики плотности нормального распределения

Вычисления процентных точек нормального распределения

Двумерное нормальное распределение 

Графики плотности двумерного распределения

Нормальное распределение (normal distribution) – играет важную роль в анализе данных.

Иногда вместо термина нормальное распределение употребляют термин гауссовское распределение в честь К. Гаусса (более старые термины, практически не употребляемые в настоящее время: закон Гаусса, Гаусса-Лапласа распределение).

Одномерное нормальное распределение

Нормальное распределение имеет плотность::

      (*)

В этой формуле ,  фиксированные параметры,  – среднее, – стандартное отклонение.

Графики плотности при различных параметрах приведены ниже.

Характеристическая функция нормального распределения имеет вид:

Дифференцируя характеристическую функцию и полагая t = 0, получаем моменты любого порядка.

Кривая плотности нормального распределения симметрична относительно  и имеет в этой точке единственный максимум, равный 

Параметр стандартного отклонения  меняется в пределах от 0 до ∞.

Среднее  меняется в пределах от -∞ до +∞.

При увеличении параметра  кривая растекается вдоль оси х, при стремлении  к 0 сжимается вокруг среднего значения (параметр  характеризует разброс, рассеяние).

При изменении  кривая сдвигается вдоль оси х (см. графики).

Варьируя параметры  и , мы получаем разнообразные модели случайных величин, возникающие в телефонии.

Типичное применение нормального закона в анализе, например, телекоммуникационных данных – моделирование сигналов, описание шумов, помех, ошибок, трафика.

Графики одномерного нормального распределения

Рисунок 1. График плотности нормального распределения: среднее равно 0, стандартное отклонение 1

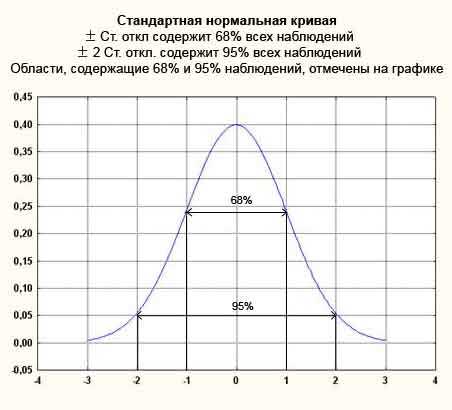
Рисунок 2. График плотности стандартного нормального распределения с областями, содержащими 68% и 95% всех наблюдений

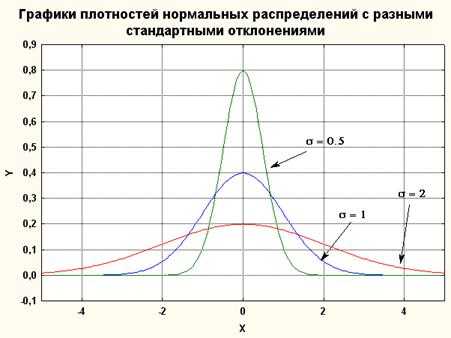
Рисунок 3. Графики плотностей нормальных распределений c нулевым средним и разными отклонениями (=0.5, =1, =2)

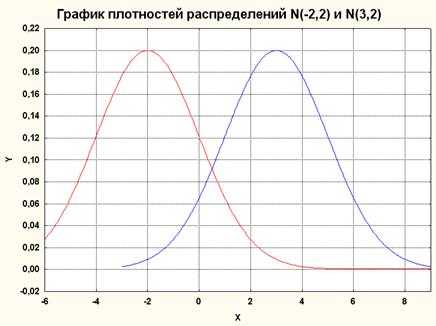
Рисунок 4 Графики двух нормальных распределений N(-2,2) и N(3,2).

Заметьте, центр распределения сдвинулся при изменении параметра .

Замечание

В программе STATISTICA под обозначением N(3,2) понимается нормальный или гауссов закон с параметрами: среднее  = 3 и стандартное отклонение =2.

В литературе иногда второй параметр трактуется как дисперсия, т.е. квадрат стандартного отклонения.

Вычисления процентных точек нормального распределения с помощью вероятностного калькулятора STATISTICA

С помощью вероятностного калькулятора STATISTICA можно вычислить различные характеристики распределений, не прибегая к громоздким таблицам, используемым в старых книгах.

Шаг 1. Запускаем Анализ / Вероятностный калькулятор / Распределения.

В разделе распределения выберем нормальное.

Рисунок 5. Запуск калькулятора вероятностных распределений

Шаг 2. Указываем интересующие нас параметры.

Например, мы хотим вычислить 95% квантиль нормального распределения со средним 0 и стандартным отклонением 1.

Укажем эти параметры в полях калькулятора (см. поля калькулятора среднее и стандартное отклонение).

Введем параметр p=0,95.

Галочка «Обратная ф.р». отобразится автоматически. Поставим галочку «График».

Нажмем кнопку «Вычислить» в правом верхнем углу.

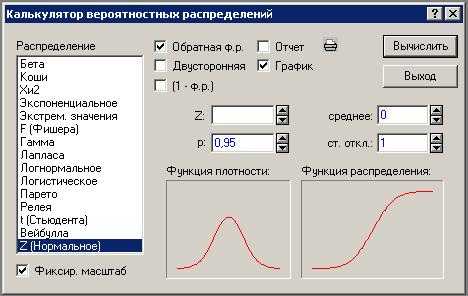
Рисунок 6. Настройка параметров

Шаг 3. В поле Z получаем результат: значение квантиля равно 1,64 (см. следующее окно).

Рисунок 7. Просмотр результата работы калькулятора

Далее автоматически появится окно с графиками плотности и функции распределения нормального закона:

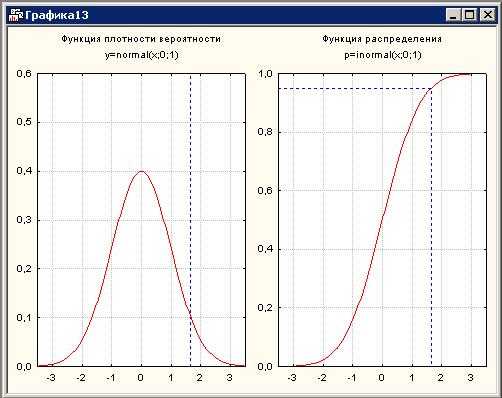
Рисунок 8. Графики плотности и функции распределения. Прямая x=1,644485

  

  

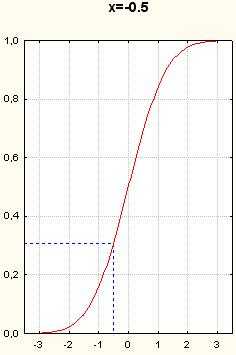
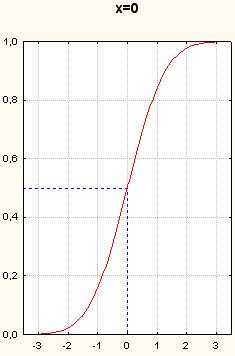
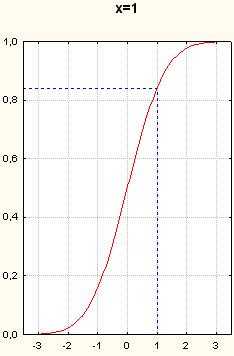
Рисунок 9. Графики функции нормального распределения. Вертикальные пунктирные прямые- x=-1.5, x=-1, x=-0.5, x=0

     

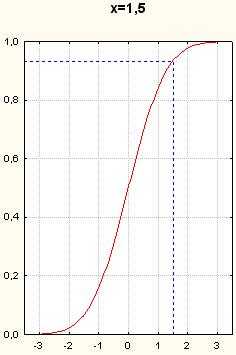
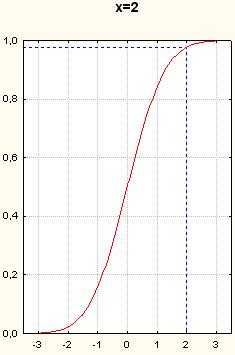
Рисунок 10. Графики функции нормального распределения. Вертикальные пунктирные прямые- x=0.5, x=1, x=1.5, x=2 

Оценка параметров нормального распределения

Значения нормального распределения можно вычислить с помощью интерактивного калькулятора.

Двумерное нормальное распределение

Одномерное нормальное распределение естественно обобщается на двумерное нормальное распределение.

Например, если вы рассматриваете сигнал только в одной точке, то вам достаточно одномерного распределения, в двух точках – двумерного, в трех точках – трехмерного и т.д.

Общая формула для двумерного нормального распределения имеет вид:

Где  – парная корреляция между X₁ и X₂;

– среднее и стандартное отклонение переменной X₁соответственно;

– среднее и стандартное отклонение переменной X₂соответственно.

Если случайные величины Х₁ и Х₂ независимы, то корреляция равна 0,  = 0,  соответственно средний член в экспоненте зануляется, и мы имеем:

f(x₁,x₂) = f(x₁)*f(x₂)

Для независимых величин двумерная плотность распадается в произведение двух одномерных плотностей.

Графики плотности двумерного нормального распределения

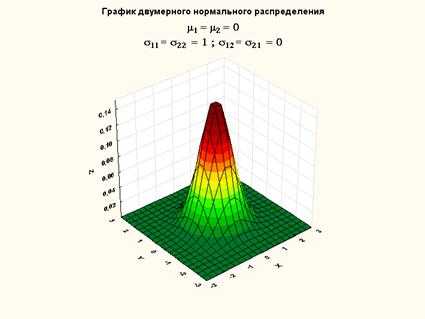
Рисунок 11. График плотности двумерного нормального распределения (нулевой вектор средних, единичная ковариационная матрица)

Рисунок 12. Сечение графика плотности двумерного нормального распределения плоскостью z=0.05

Рисунок 13. График плотности двумерного нормального распределения (нулевой вектор мат. ожидания, ковариационная матрица с 1 на главной диагонали и 0.5 на побочной)

Рисунок 14. Сечение графика плотности двумерного нормального распределения (нулевой вектор мат. ожидания, ковариационная матрица с 1 на главной диагонали и 0.5 на побочной) плоскостью z= 0.05

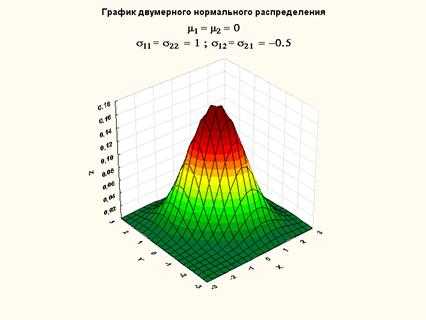
Рисунок 15. График плотности двумерного нормального распределения (нулевой вектор мат. ожидания, ковариационная матрица с 1 на главной диагонали и -0.5 на побочной)

Рисунок 16. Сечение графика плотности двумерного нормального распределения (нулевой вектор мат. ожидания, ковариационная матрица с 1 на главной диагонали и -0.5 на побочной) плоскостью z=0.05

Рисунок 17. Сечения графиков плотностей двумерного нормального распределения плоскостью z=0.05

Для лучшего понимания двумерного нормального распределения попробуйте решить следующую задачу.

Задача. Посмотрите на график двумерного нормального распределения. Подумайте, можно ли его представить, как вращение графика одномерного нормального распределения? Когда нужно применить прием деформации?

Читайте далее — многомерное нормальное распределение

Связанные определения:
Cтандартное нормальное распределение
Критерий Колмогорова-Смирнова
Нормальное распределение
Шапиро-Уилка W критерий

В начало

Содержание портала

statistica.ru