Лекция 12. Предел функции
Лекция 12. Предел функции.
12.1. Определения предела функции.
Пусть задана
функция 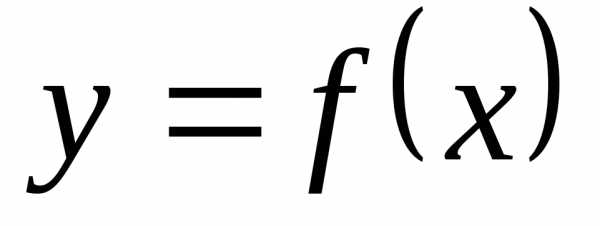 ,
определённая на множестве
,
определённая на множестве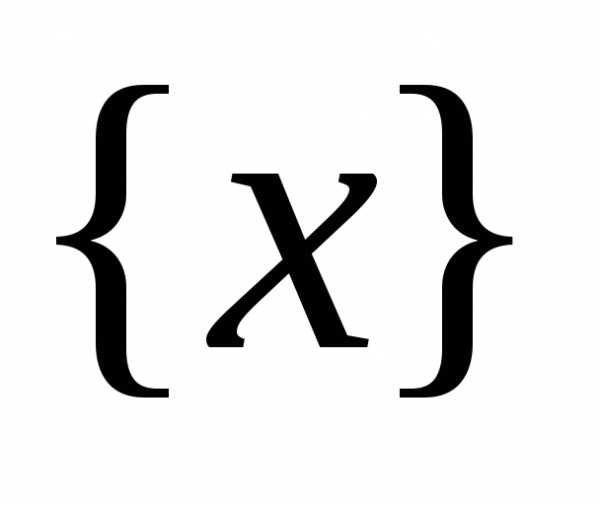 .
Пусть имеется точкаa,
быть может и не принадлежащая
.
Пусть имеется точкаa,
быть может и не принадлежащая 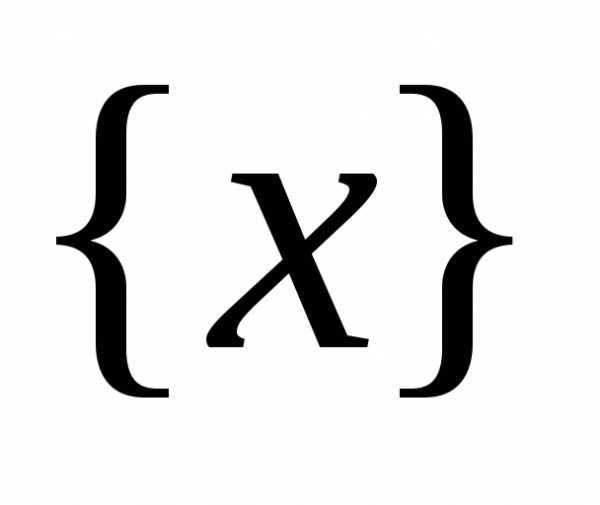 ,
но такая, что в любой
,
но такая, что в любой -окрестности
точкиa имеются точки множества
-окрестности
точкиa имеются точки множества 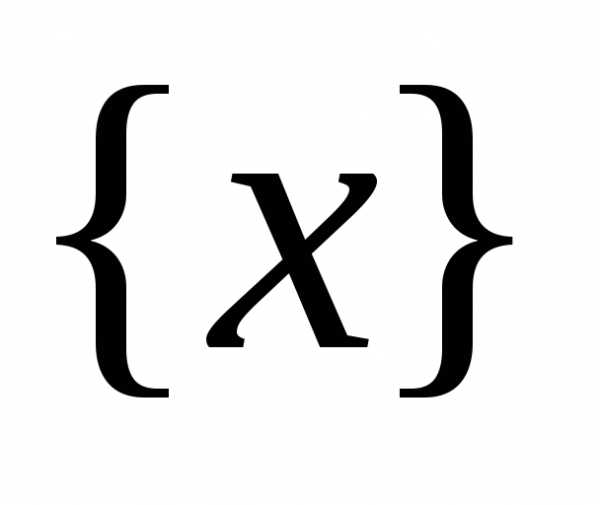 ,
отличные отa.
Например:
,
точкаa не принадлежит
,
отличные отa.
Например:
,
точкаa не принадлежит 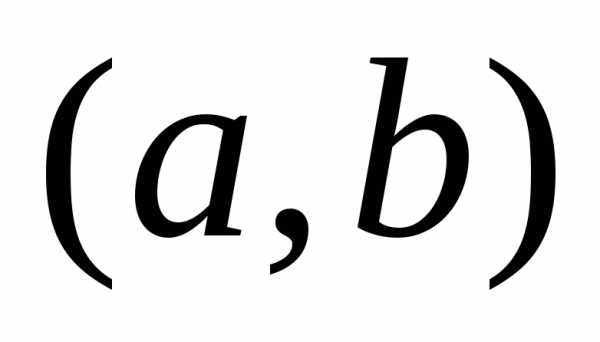 ,
но любая
,
но любая
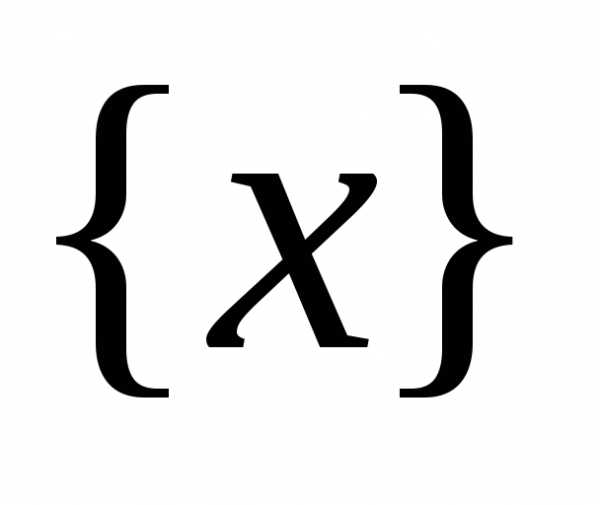 и отличные отa.
и отличные отa. Определение 12.1 (определение
предела функции по Гейне). Число b называется пределом (или предельным
значением) функции 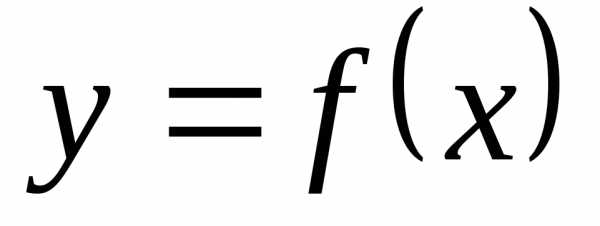 в точке a (или при
),
если для любой последовательности
значений аргумента,
сходящейся кa и состоящей из чисел
в точке a (или при
),
если для любой последовательности
значений аргумента,
сходящейся кa и состоящей из чисел 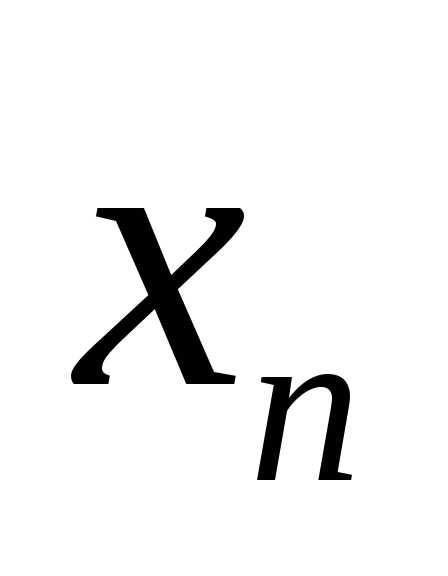 ,
отличных отa,
соответствующая последовательность
значений функции
сходится к числуb.
,
отличных отa,
соответствующая последовательность
значений функции
сходится к числуb.
Определение 12.2 (определение предела функции по Коши). Число b называется
пределом функции в точке a,
если для любого сколь угодно малого
положительного числа
в точке a,
если для любого сколь угодно малого
положительного числа  найдётся отвечающее ему положительное
число
найдётся отвечающее ему положительное
число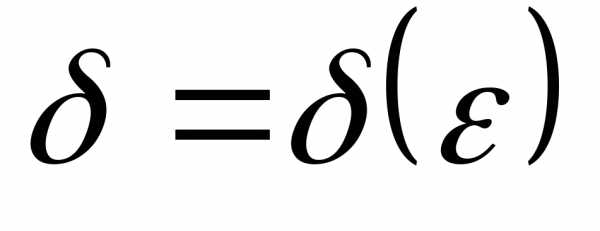 такое, что для всех значений аргументаx,
удовлетворяющих условию
,
справедливо неравенство.
такое, что для всех значений аргументаx,
удовлетворяющих условию
,
справедливо неравенство.Обозначается предел функции следующим образом:
 или
или 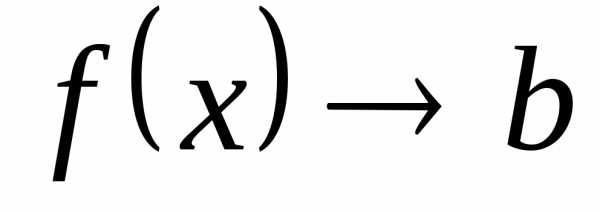 при.
при.
♦ Утверждение 12.1. Определения 12.1 и 12.2 эквивалентны.
☼ Замечание 12.1. Элементы последовательности 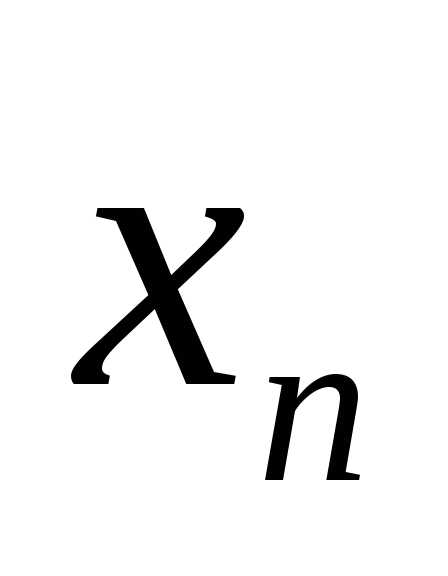
 может быть не определена в точке a.
Определение 12.1 явно содержит это
требование, в определении 12.2 неравенство
может быть не определена в точке a.
Определение 12.1 явно содержит это
требование, в определении 12.2 неравенство 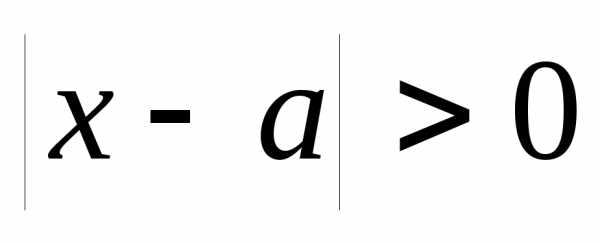 означает
означает  . ☼
. ☼ Пример 12.1. 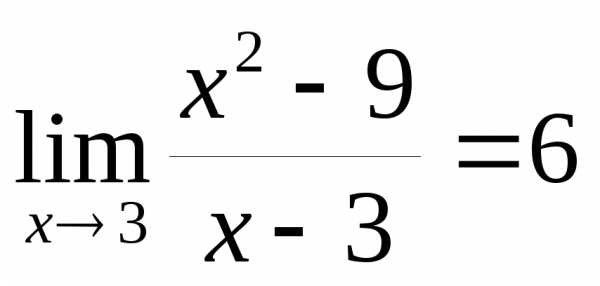 .
.
☼ Замечание 12.2.
Функция  может иметь в точке a только один предел, так как имеется
единственный предел последовательности
может иметь в точке a только один предел, так как имеется
единственный предел последовательности 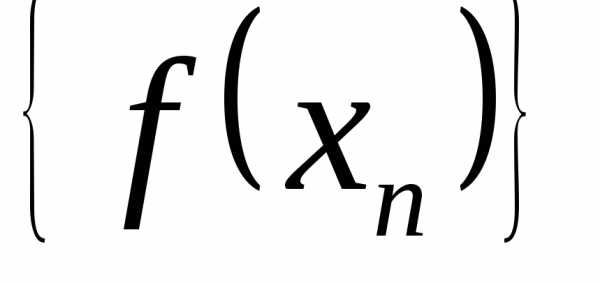 в определении 12.1, а определение 12.2
эквивалентно определению 12.1.☼
в определении 12.1, а определение 12.2
эквивалентно определению 12.1.☼
Пример 12.2. 1) 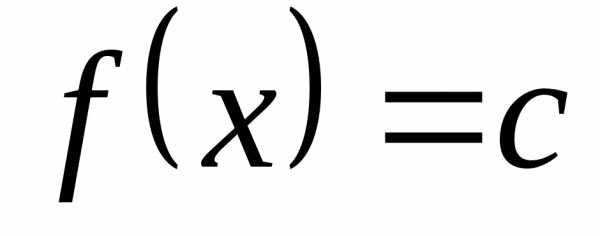
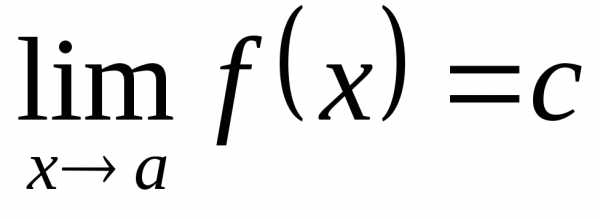 ,
так как любая последовательность ,
сходящаяся к числу a,
порождает последовательность
.
,
так как любая последовательность ,
сходящаяся к числу a,
порождает последовательность
. 2) 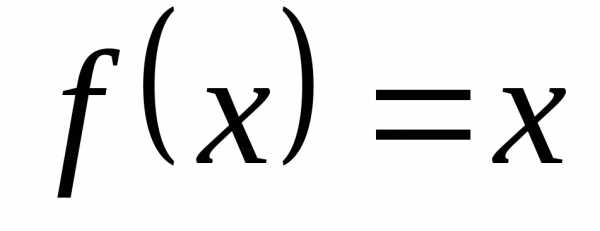 .
.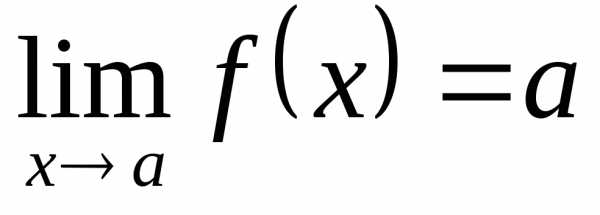 ,
так как последовательности и совпадают.
,
так как последовательности и совпадают.
3) 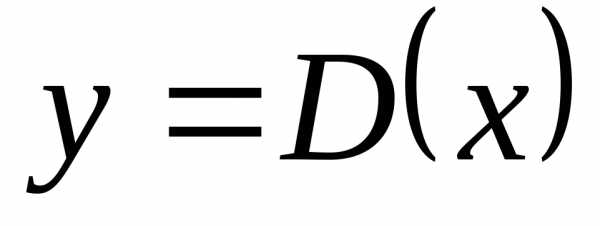 – функция Дирихле, – не имеет предела:
для рациональных чисел при,
для иррациональных при
– функция Дирихле, – не имеет предела:
для рациональных чисел при,
для иррациональных при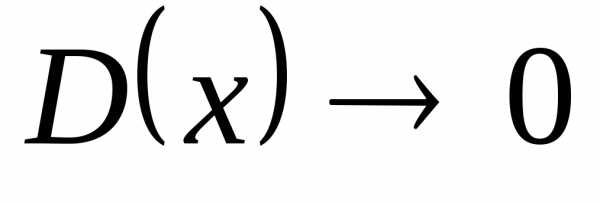 .
Это противоречит определению 12.1.
.
Это противоречит определению 12.1.
Определение 12.3. Число b называется правым
(левым) предельным значением функции 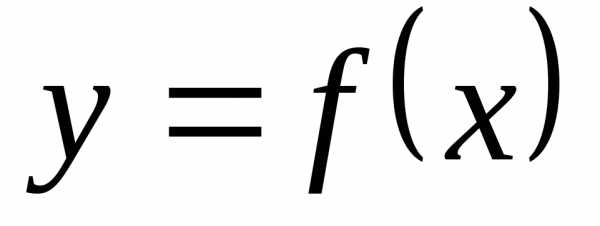
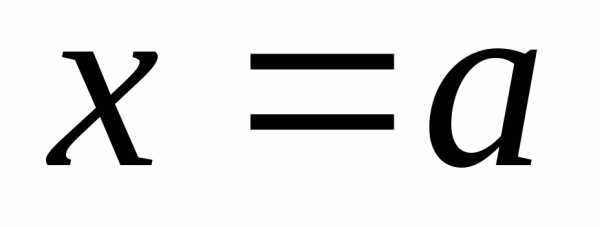 ,
если для любой последовательности
значений аргумента ,
сходящейся к a,
элементы
,
если для любой последовательности
значений аргумента ,
сходящейся к a,
элементы 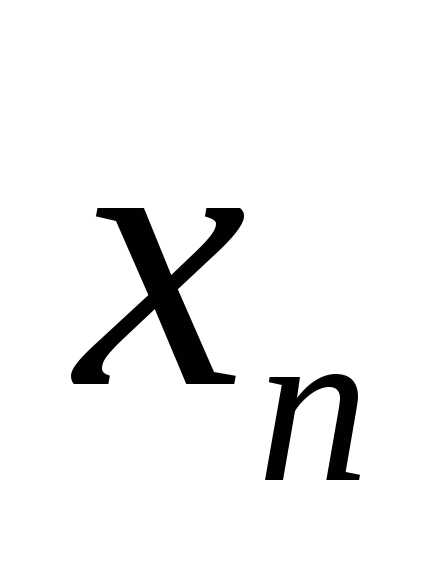 которой больше (меньше)a,
соответствующая последовательность значений функции сходится к b.
которой больше (меньше)a,
соответствующая последовательность значений функции сходится к b.Обозначения: илидля правого предельного значения,
или для левого предельного значения.
Пример 12.3. Для функции правое предельное значениеи левое предельное значение.
♦ Утверждение 12.2. Если в
точке a правое и левое предельные значения
функции 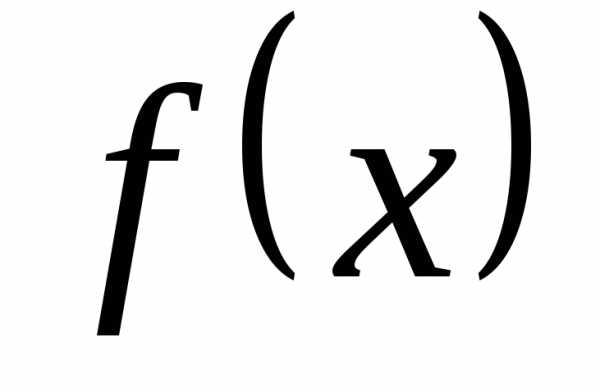 равны, то в точкеa существует предельное значение этой
функции, равное указанным односторонним
предельным значениям.
равны, то в точкеa существует предельное значение этой
функции, равное указанным односторонним
предельным значениям.
Доказательство. Пусть
последовательность 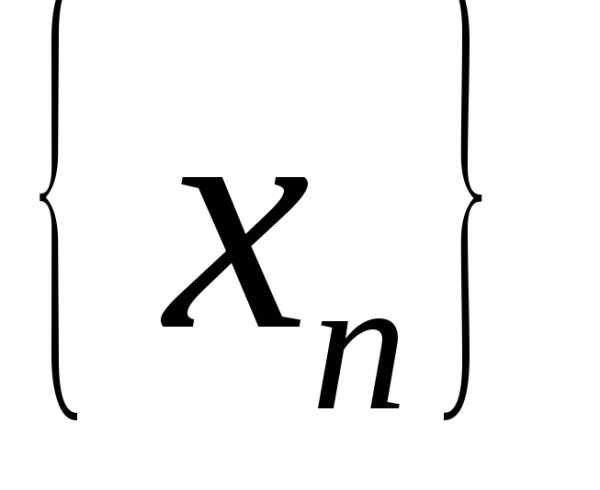 :
: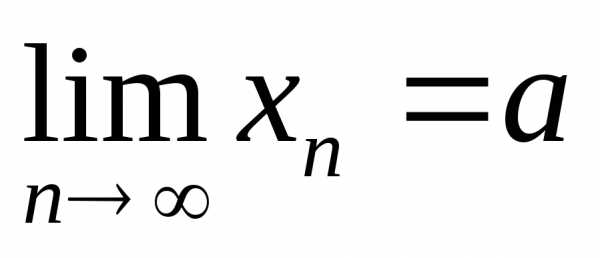 (
(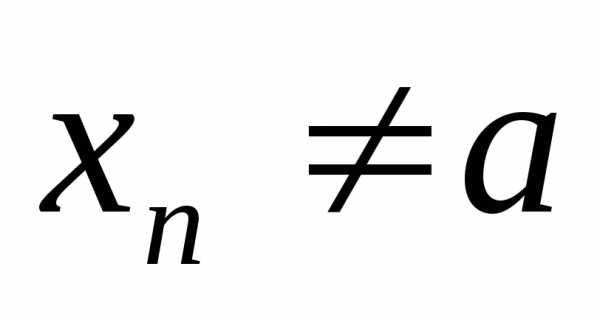 для любогоn). Пусть
подпоследовательность
для любогоn). Пусть
подпоследовательность 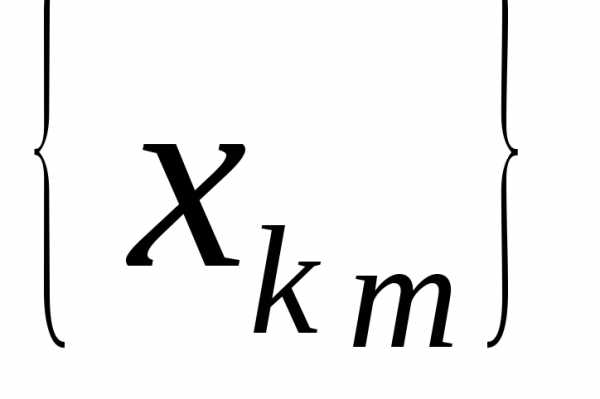 состоит из всех
состоит из всех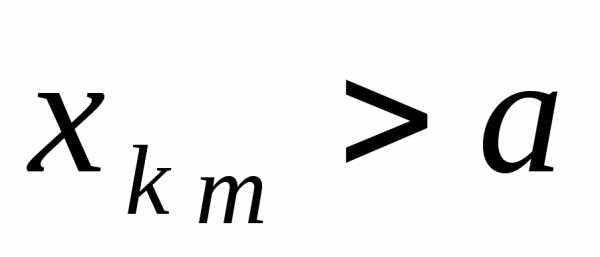 ,
а подпоследовательность
,
а подпоследовательность  из всех
из всех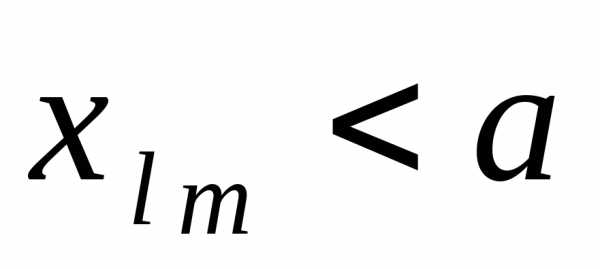 . По условию:
:
. По условию:
: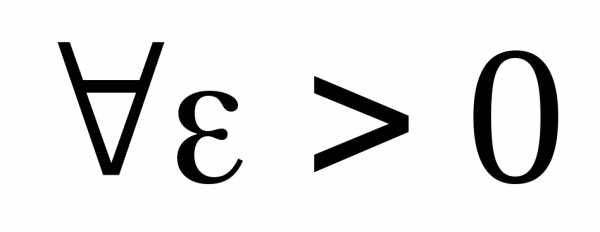 ; ,
; ,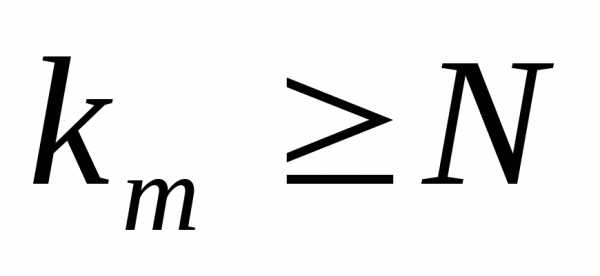 ;,
;,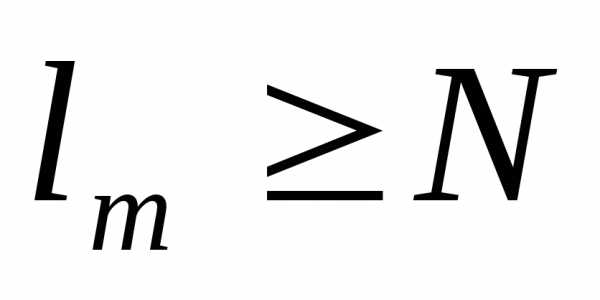 . Так как
и
. Так как
и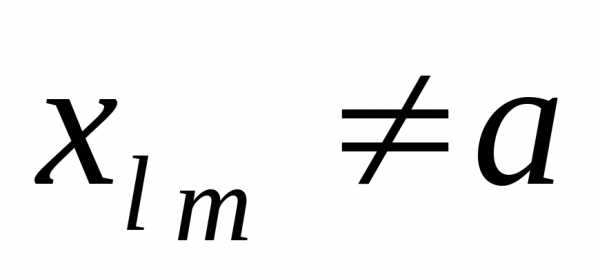 ,
то есть неравенствами охвачены все
элементы
,
то есть неравенствами охвачены все
элементы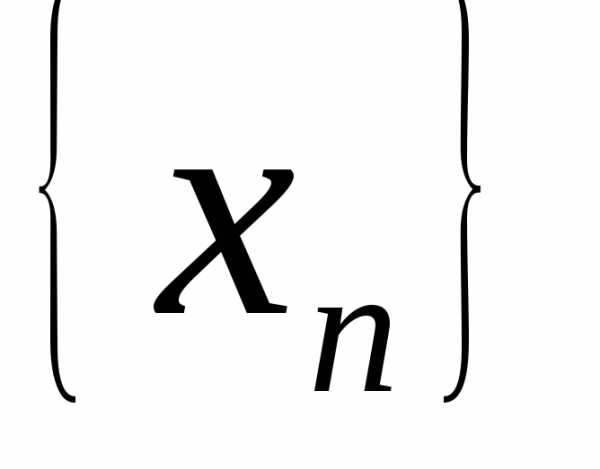
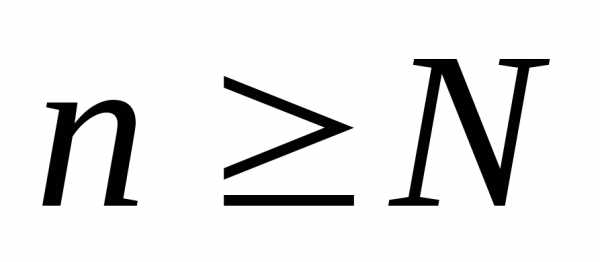 выполняется неравенство .
■
выполняется неравенство .
■Определение 12.4. Число b называется пределом функции при , если для любой бесконечно большой последовательности значений аргумента соответствующая последовательность значений функции сходится к b.
Обозначение: 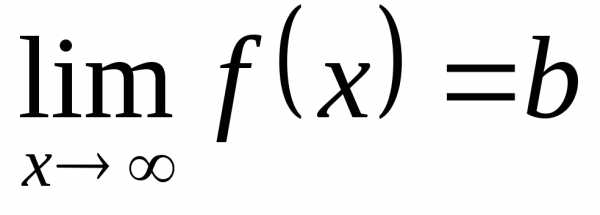 .
.
Определение 12.5. Число b называется предельным
значением функции 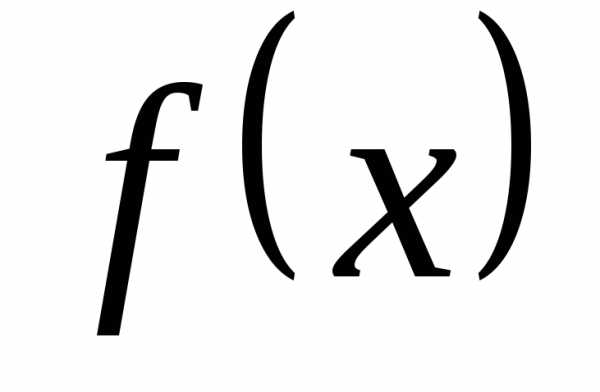 при
стремлении аргумента x к положительной (отрицательной)
бесконечности ,
если для любой бесконечно большой
последовательности значений аргумента,
элементы которой, начиная с некоторого
номера, положительны (отрицательны),
соответствующая последовательность
сходится к b.
при
стремлении аргумента x к положительной (отрицательной)
бесконечности ,
если для любой бесконечно большой
последовательности значений аргумента,
элементы которой, начиная с некоторого
номера, положительны (отрицательны),
соответствующая последовательность
сходится к b.
Обозначение: 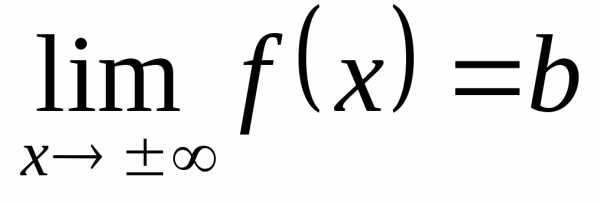 .
.
♦ Теорема 12.1 (критерий
Коши существования предела функции в
точке a). Для того,
чтобы функция 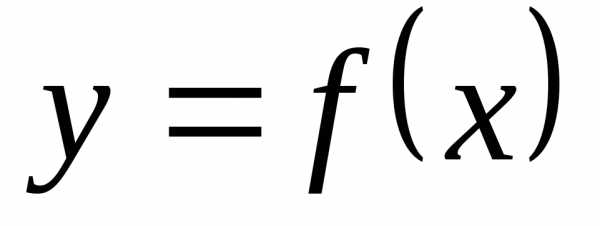 имела в точкеa конечный предел, необходимо и достаточно,
чтобы в точке a функция
имела в точкеa конечный предел, необходимо и достаточно,
чтобы в точке a функция 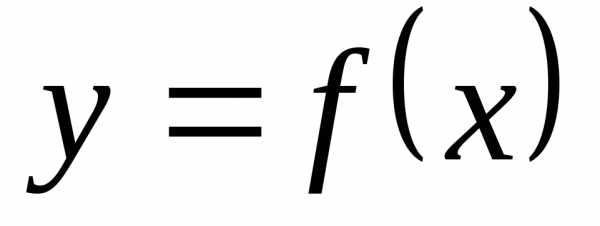 удовлетворяла условию Коши: для любого
сколь угодно малого
удовлетворяла условию Коши: для любого
сколь угодно малого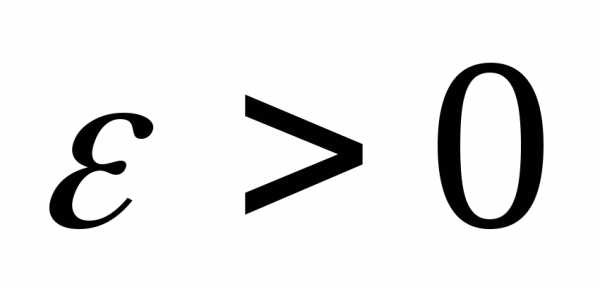 найдется
найдется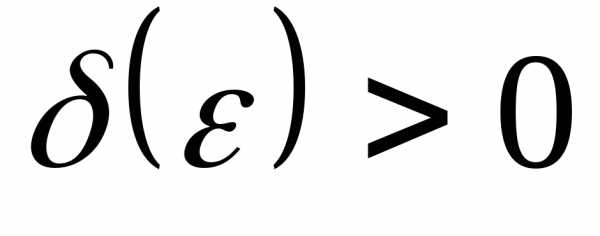 такое, что для любых двух значений
аргумента
такое, что для любых двух значений
аргумента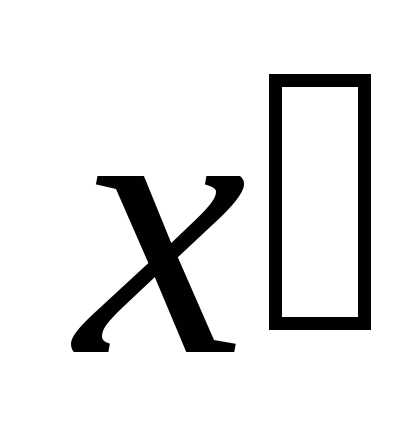
 ,
удовлетворяющих условиям;,
справедливо неравенство.
,
удовлетворяющих условиям;,
справедливо неравенство.12.2. Арифметические операции над функциями, имеющими предельные значения.
Арифметические операции над функциями, имеющими предел в точке a, приводят к функциям, также имеющим предел в точке a.
♦ Теорема 12.2. Пусть две
функции 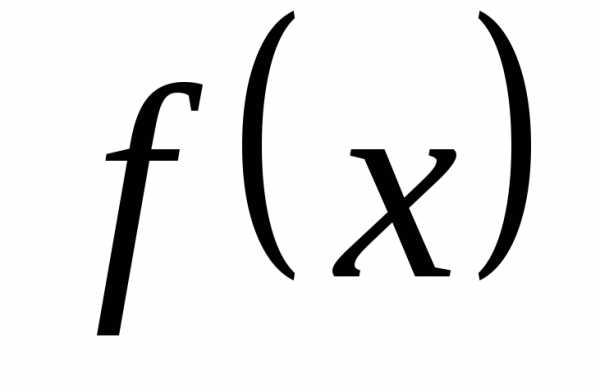 и
и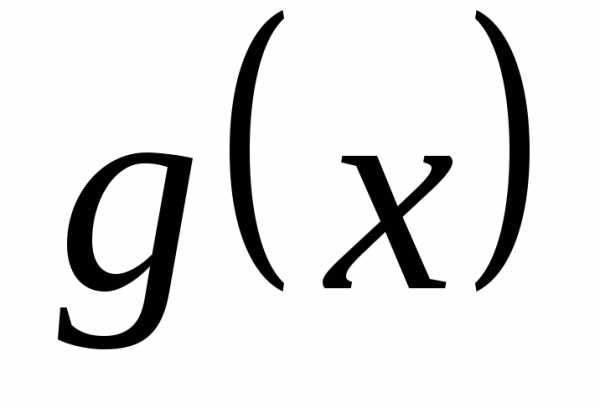 заданы на одном и том же множестве
заданы на одном и том же множестве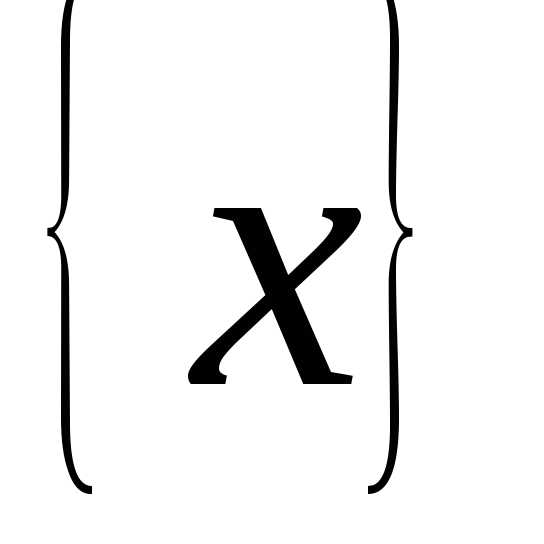 и имеют в точкеa пределы, равные b и c.
Тогда
и имеют в точкеa пределы, равные b и c.
Тогда
,
,
.
Доказательство.
Пусть – произвольная, сходящаяся ка последовательность значений аргумента функций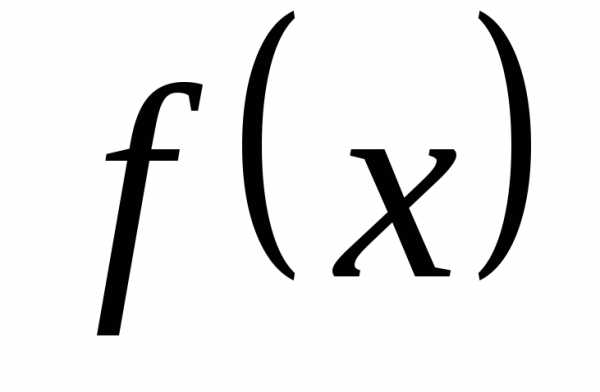 и
и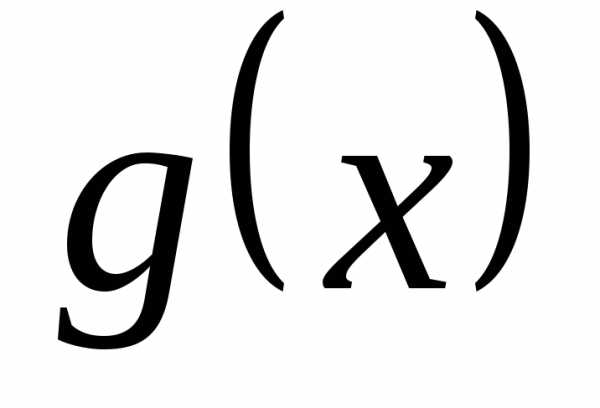 .
Соответствующие последовательности
.
Соответствующие последовательности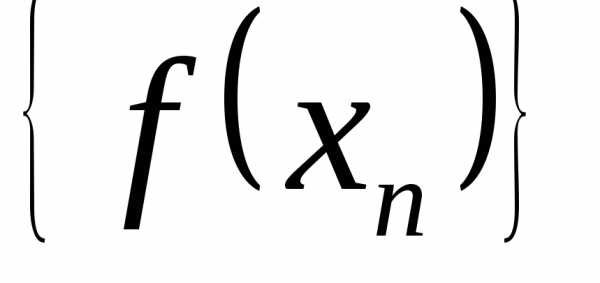 и
и значений этих функций имеют пределыb и c.
Но тогда, в силу теорем 9.3-9.5, последовательности
,и
значений этих функций имеют пределыb и c.
Но тогда, в силу теорем 9.3-9.5, последовательности
,и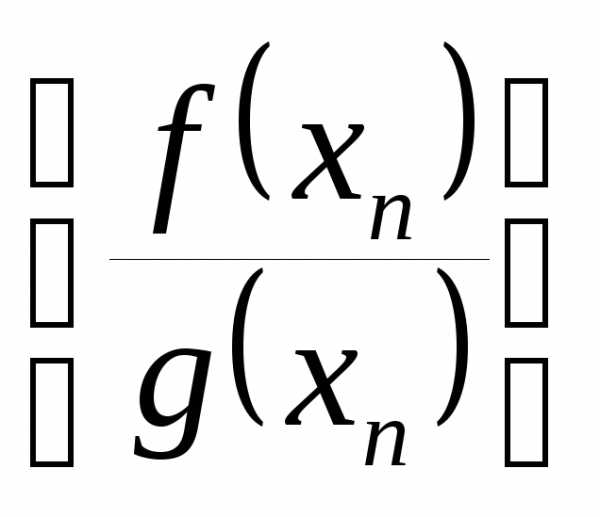 при
при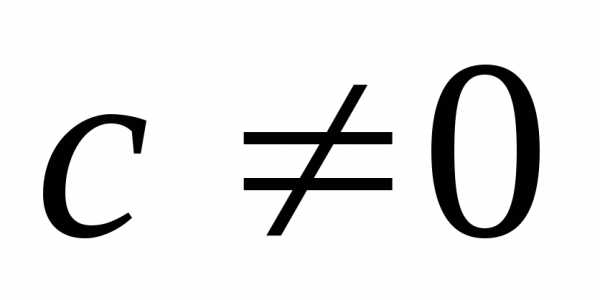 имеют пределы, соответственно равные
имеют пределы, соответственно равные ,
,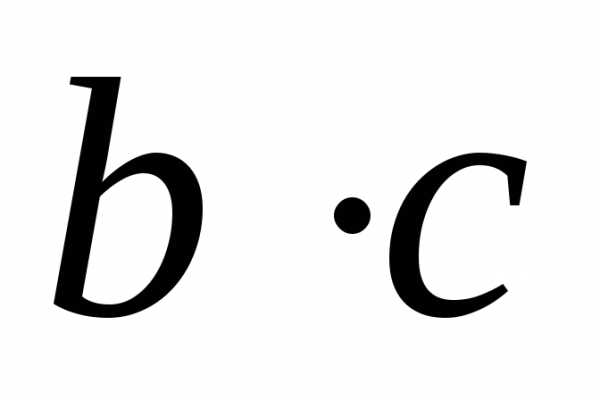 и.
Согласно определению 12.1 предела функции,
это означает, что , , . ■
и.
Согласно определению 12.1 предела функции,
это означает, что , , . ■♦ Утверждение 12.3. Многочлен степени
Доказательство: Так как  ,
, ,
то
,
то и. ■
и. ■
♦ Утверждение 12.4. Рациональная
дробь (частное 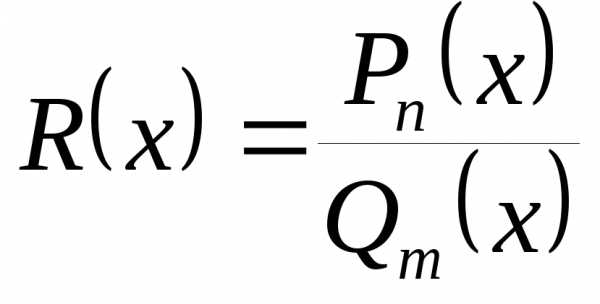 )
имеет предел в любой точке,
не являющейся корнем её знаменателя,
причём
)
имеет предел в любой точке,
не являющейся корнем её знаменателя,
причём
.
12.3. Бесконечно малые и бесконечно большие функции.
Определение 12.6. Функция 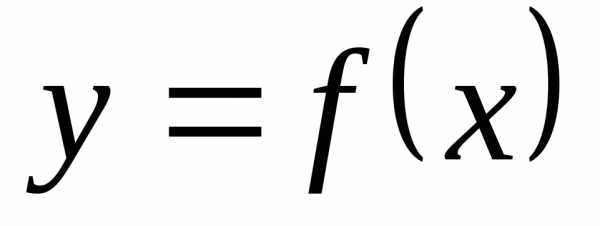 называетсябесконечно
малой в точке
называетсябесконечно
малой в точке 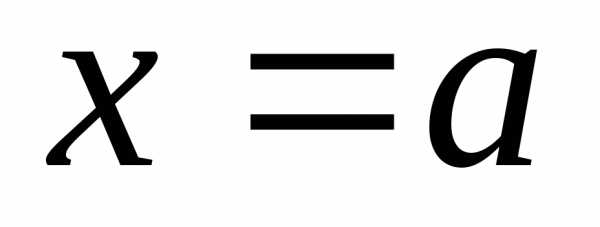 (при),
если
(при),
если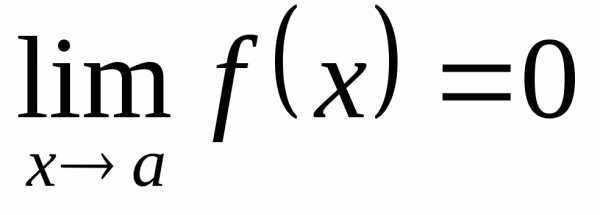 .
.
Например,
,
где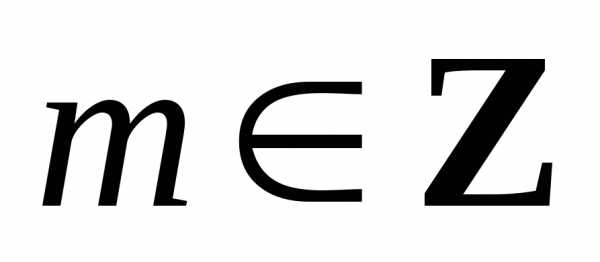 ,
– бесконечно малая функция в любой
точке,
в силу утверждения 12.3:
,
– бесконечно малая функция в любой
точке,
в силу утверждения 12.3:
.
☼ Замечание 12.3. Если 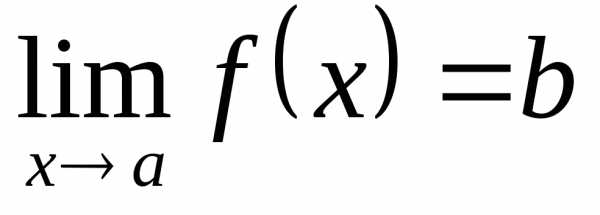 ,
то
– бесконечно малая в точкеa.
Отсюда следует специальное представление
функции
,
где
,
то
– бесконечно малая в точкеa.
Отсюда следует специальное представление
функции
,
где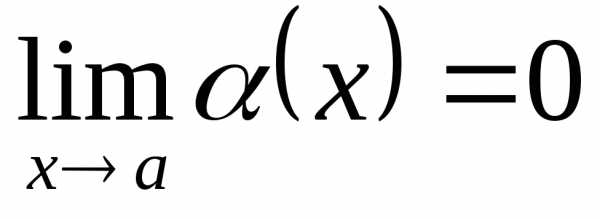 .
Говорят, что функция
.
Говорят, что функция асимптотически равнаb при
.☼
асимптотически равнаb при
.☼
Определение 12.7. Функция 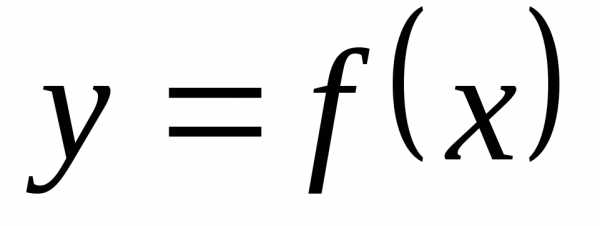 называетсябесконечно
большой в точке
называетсябесконечно
большой в точке 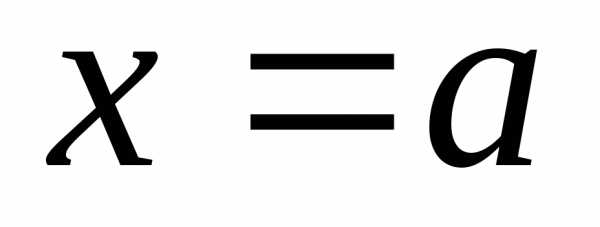 справа
(слева),
если для любой последовательности
справа
(слева),
если для любой последовательности 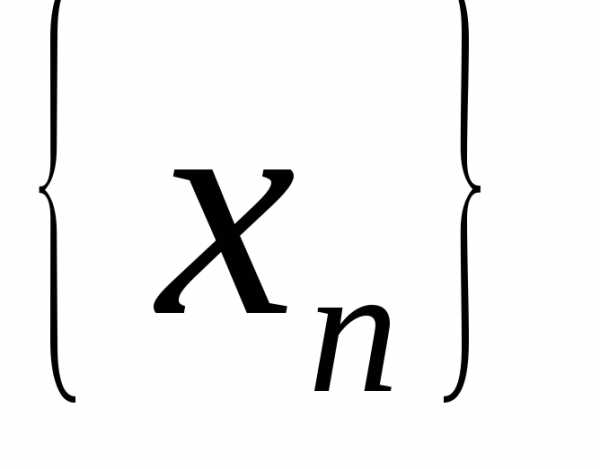 :
: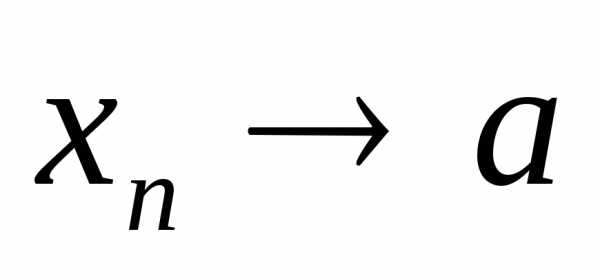 при,
при,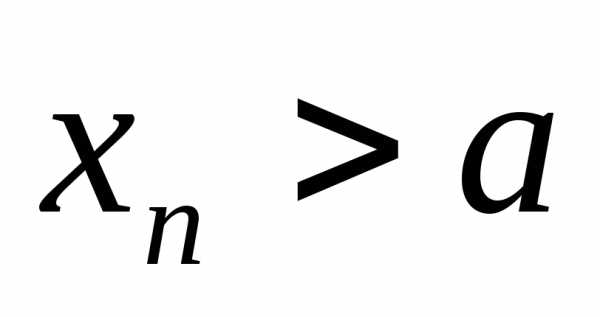 (
(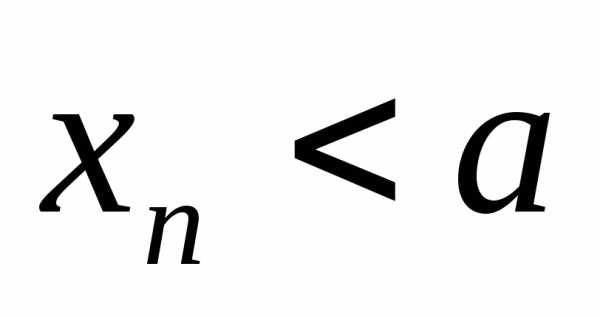 ),
соответствующая последовательность
),
соответствующая последовательность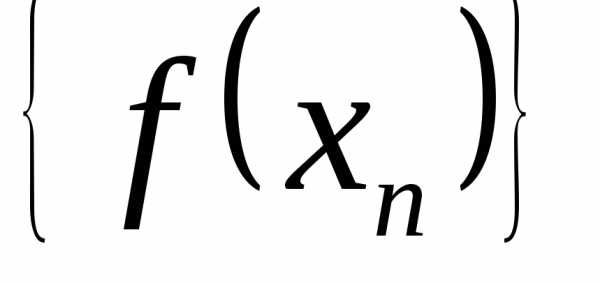 значений функции является бесконечно
большой последовательностью определённого
знака.
значений функции является бесконечно
большой последовательностью определённого
знака.
Например, функция 
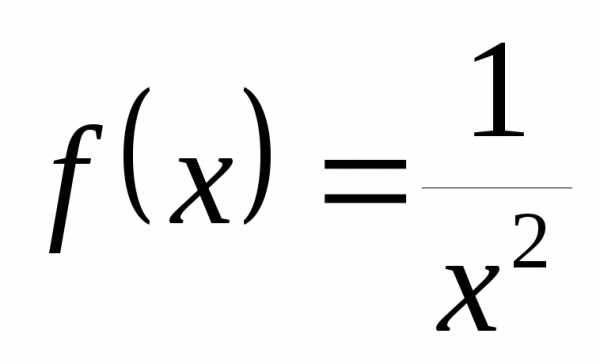 является бесконечно большой при
является бесконечно большой при ,
, .
.
Возможны ситуации и для случая односторонних пределов:
; .
Рассмотрим функцию 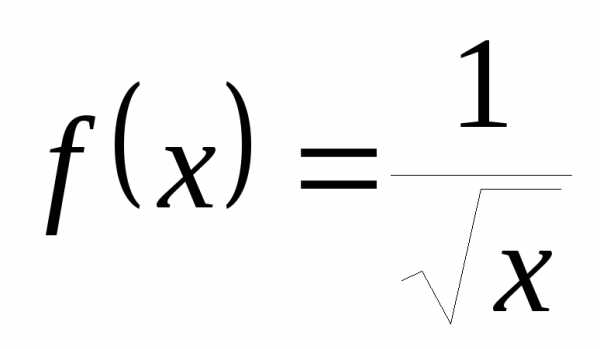 вблизи точки
вблизи точки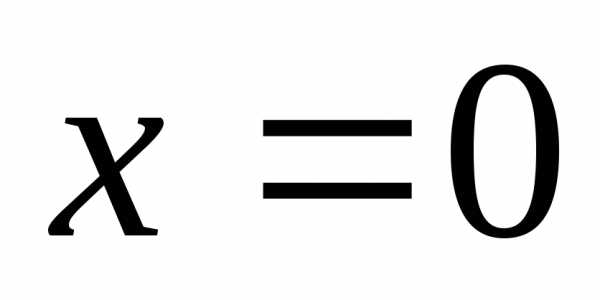 .
Так как она определена лишь при
.
Так как она определена лишь при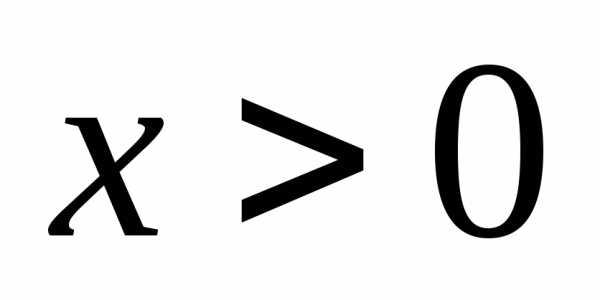 ,
то вблизи
,
то вблизи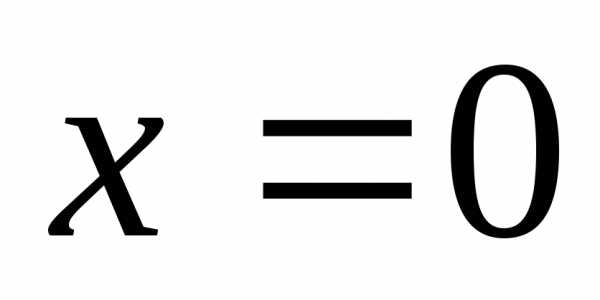 её можно исследовать только при:
её можно исследовать только при: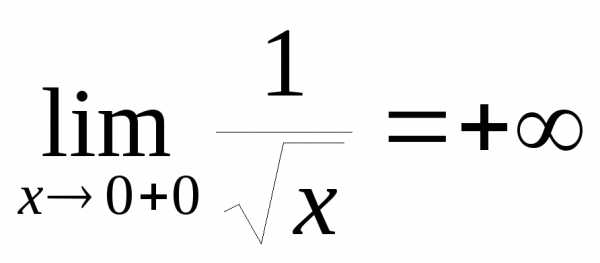 .
То есть функция
.
То есть функция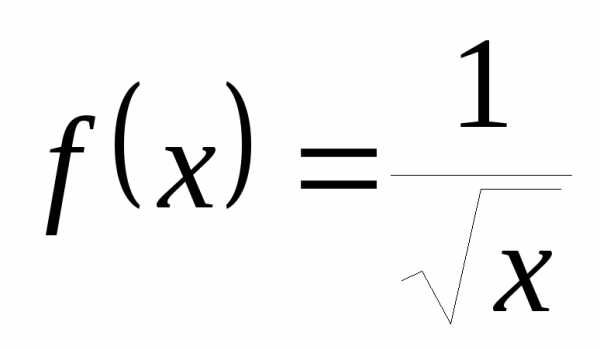 – положительная бесконечно большая
при.
– положительная бесконечно большая
при.
12.4. Сравнение бесконечно малых и бесконечно больших функций.
Определение 12.8. Пусть 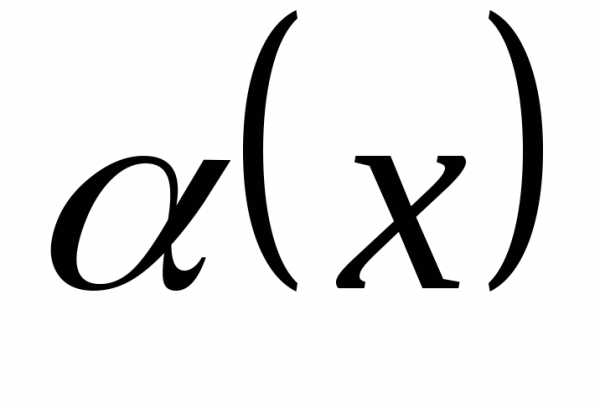 и
и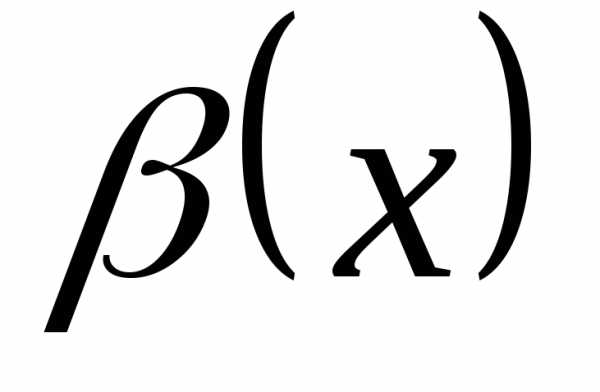 – две бесконечно малые в точке
– две бесконечно малые в точке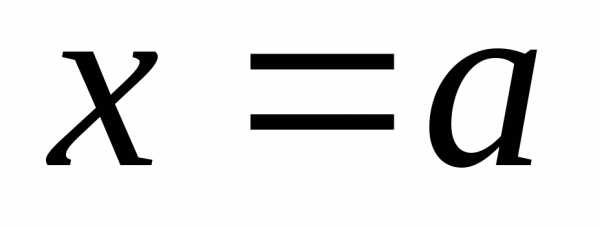 функции и пусть существует
функции и пусть существует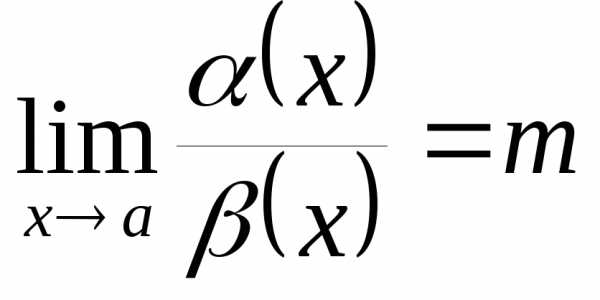 .
Если
.
Если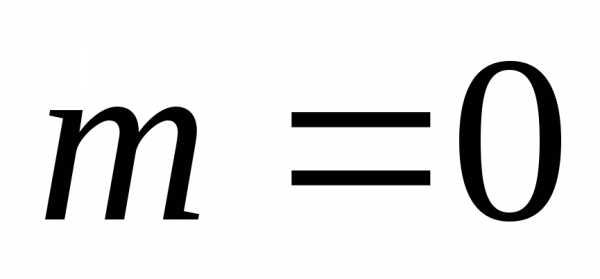 ,
то
,
то –бесконечно
малая более высокого порядка,
чем
–бесконечно
малая более высокого порядка,
чем  . Если
. Если 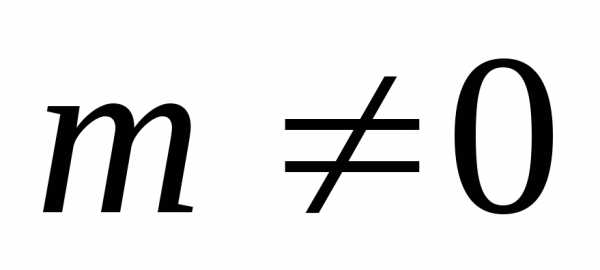 ,
то
,
то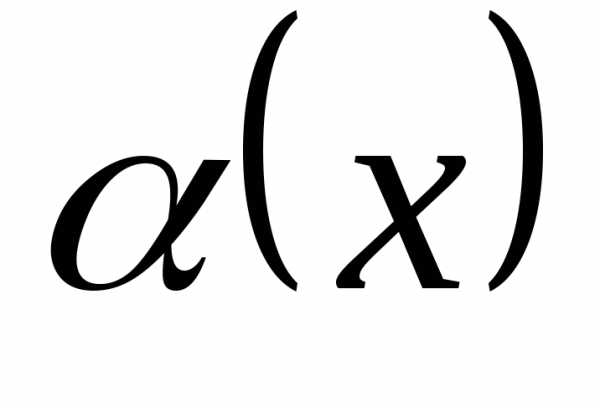 и
и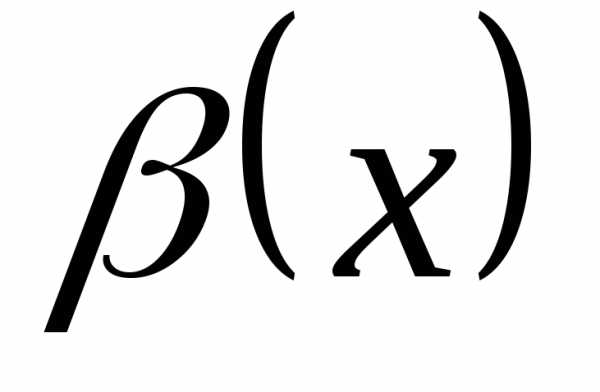 –бесконечно
малые одного порядка. Если
–бесконечно
малые одного порядка. Если 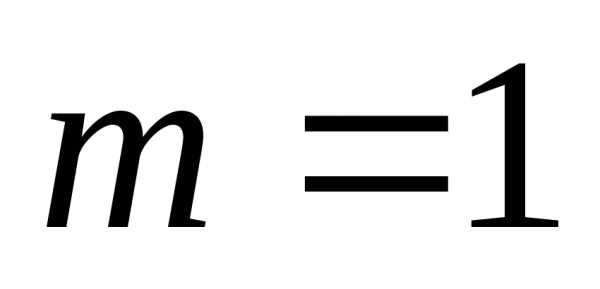 ,
то
,
то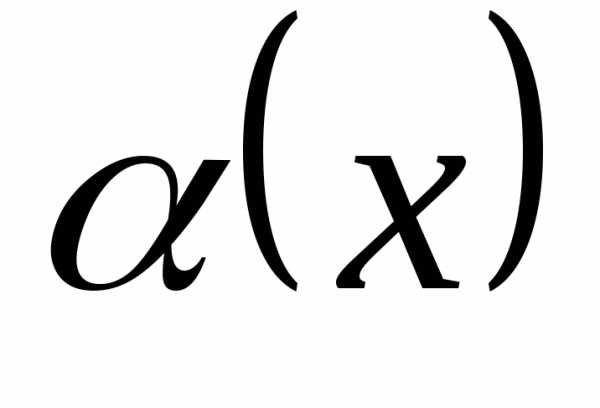 и
и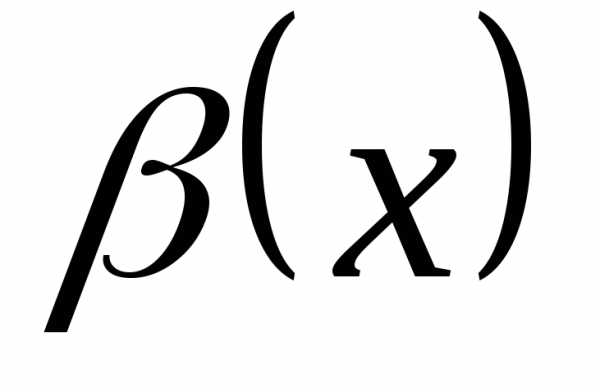 –эквивалентные
бесконечно малые.
–эквивалентные
бесконечно малые.
В качестве стандартной функции сравнения берут функцию .
Говорят, что
бесконечно малая функция 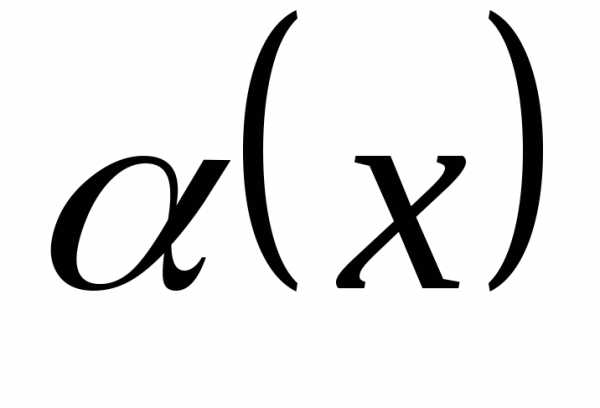 имеет порядок малостиm,
если
имеет порядок малостиm,
если 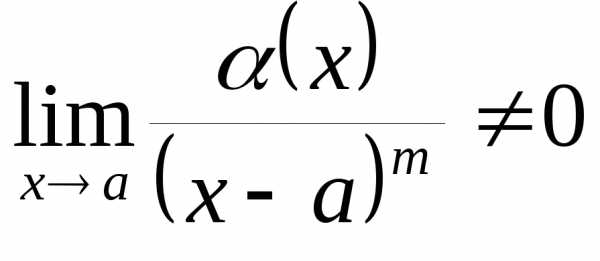 .
.
Используется
следующая символика:  (
( равноo малое от
равноo малое от  ),
если
),
если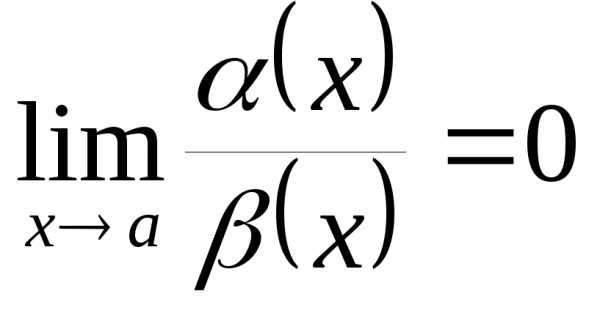 .
.
Пример 12.4. 1) и  – бесконечно малые одного порядка при
– бесконечно малые одного порядка при  ,
так как
,
так как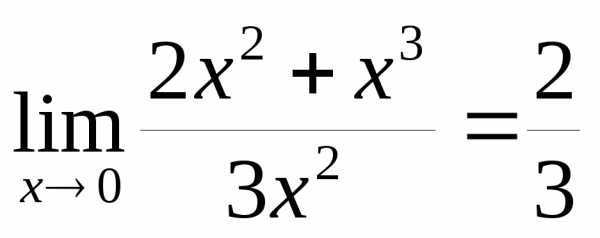 .
.
2) и  – эквивалентные бесконечно малые при
– эквивалентные бесконечно малые при  ,
так как
,
так как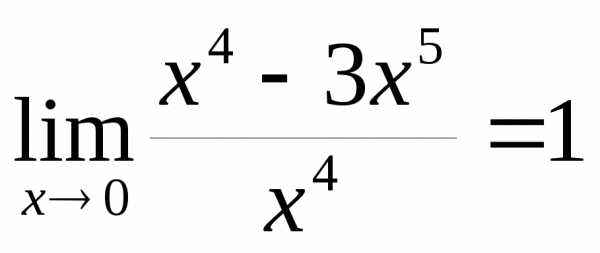 .
.
3) 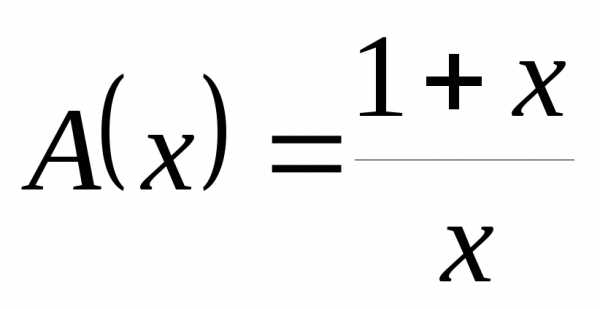 и
и 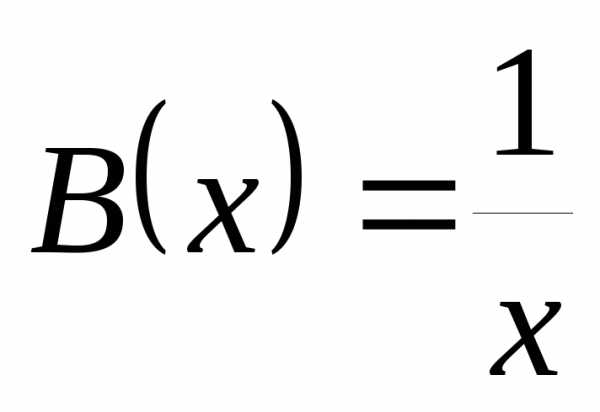 имеют одинаковый порядок роста при
имеют одинаковый порядок роста при  справа и слева, так как
справа и слева, так как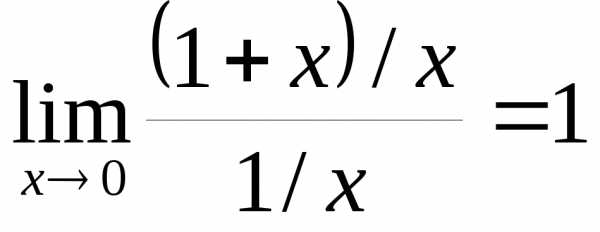 .
.
Аналогично сравниваются бесконечно большие функции.
Определение 12.9. Пусть 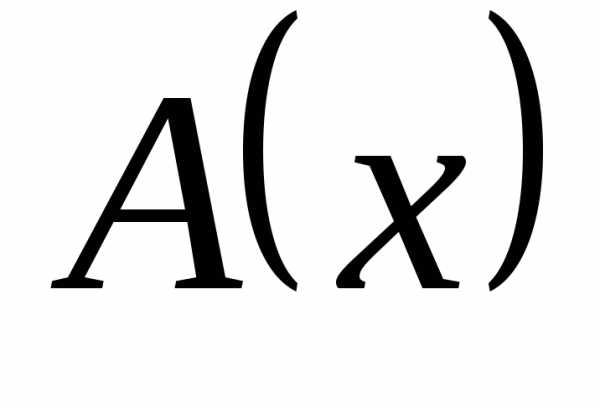 и
и 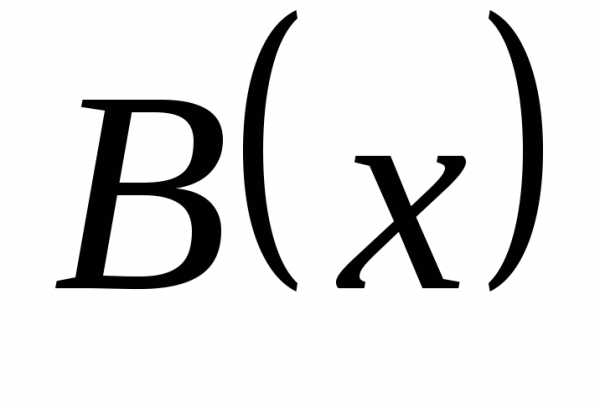 – бесконечно большие в точке
– бесконечно большие в точке 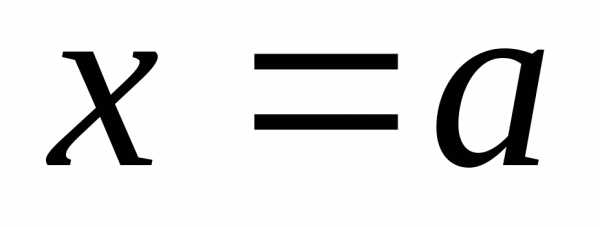 справа функции одного знака: , .
Если
справа функции одного знака: , .
Если  ,
то
,
то 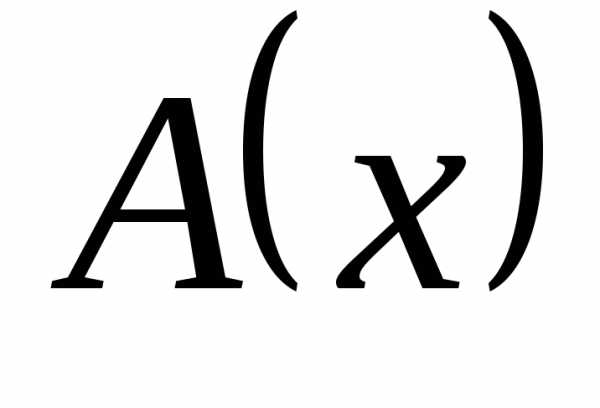 имеет
более высокий порядок роста в точке a справа, чем
имеет
более высокий порядок роста в точке a справа, чем 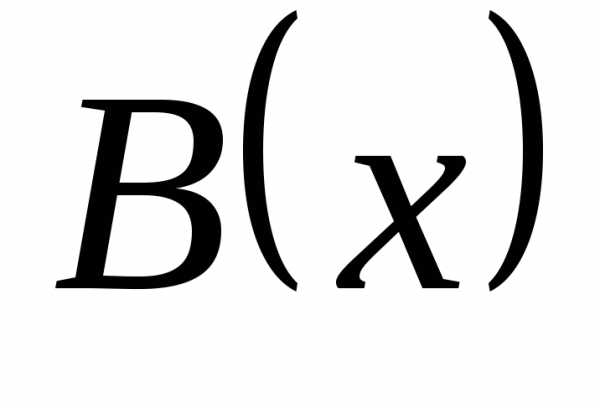 .
Если
.
Если 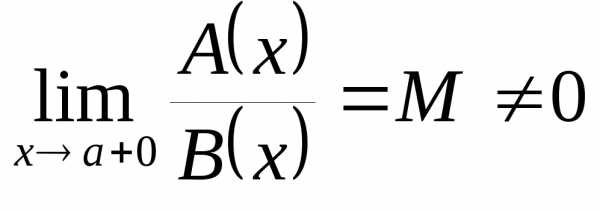 ,
то
,
то 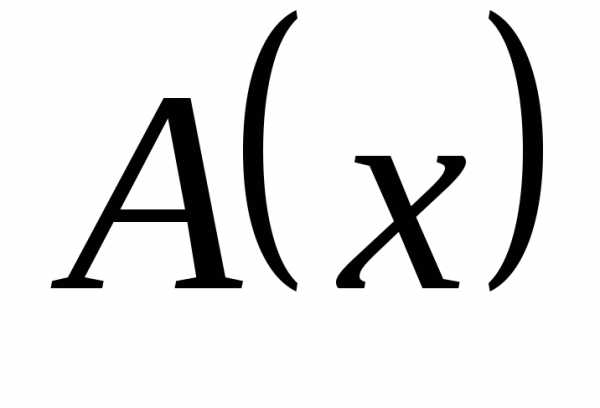 и
и 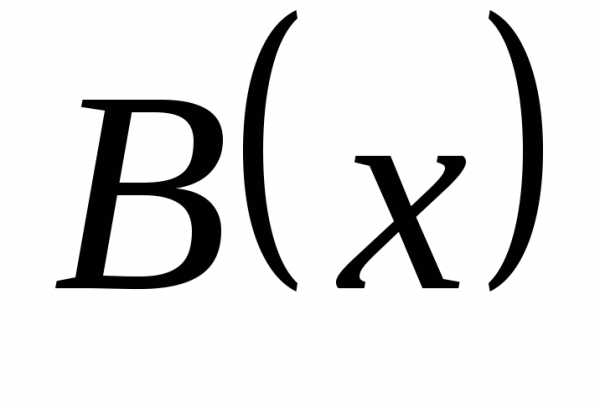 имеют в точке a справа одинаковый порядок роста. Если
имеют в точке a справа одинаковый порядок роста. Если 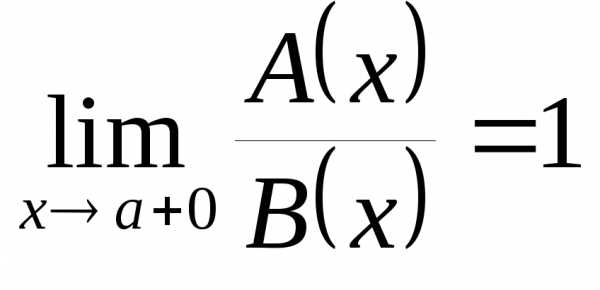 ,
то
,
то  и
и 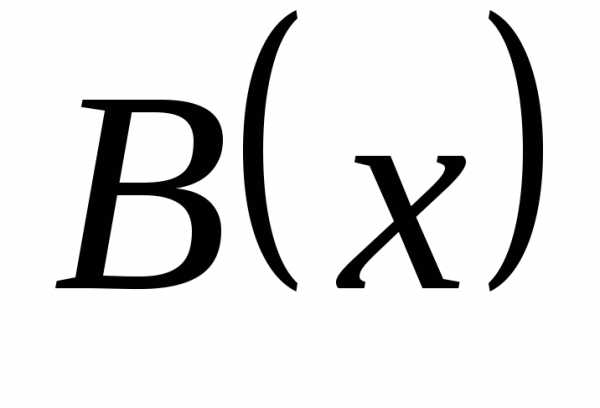 – эквивалентные
бесконечно большие функции.
– эквивалентные
бесконечно большие функции.
Таковы же правила сравнения бесконечно больших функций и при .
Пример 12.5. 1)
, .
Так как  ,
то
,
то 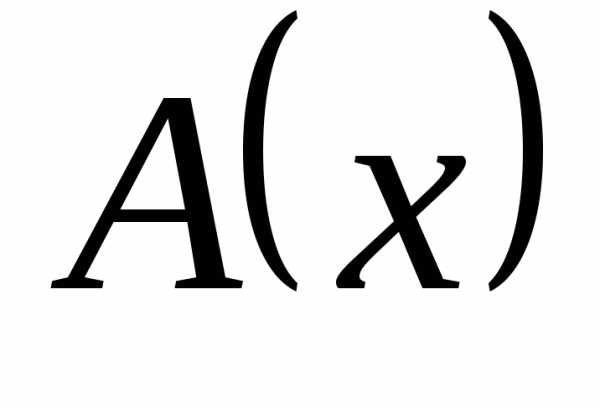 – бесконечно большая более низкого
порядка, чем
– бесконечно большая более низкого
порядка, чем 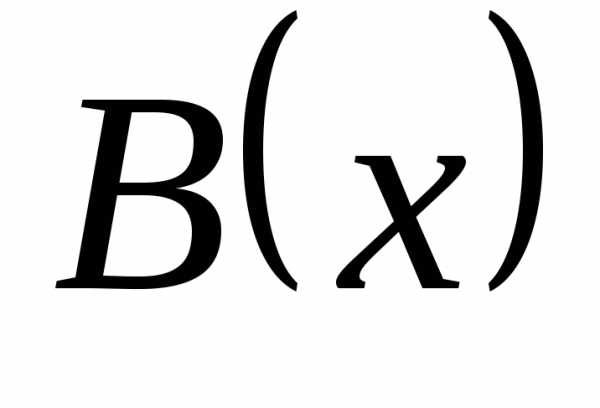 .
А
.
А 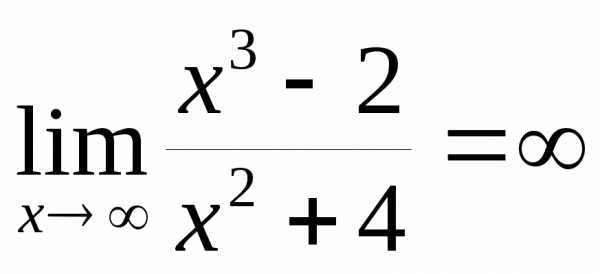 ,
поэтому
,
поэтому 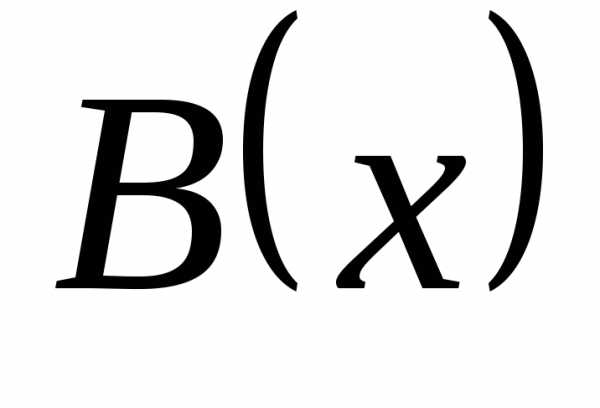 – бесконечно большая более высокого
порядка, чем
– бесконечно большая более высокого
порядка, чем  .
.
2)
, . 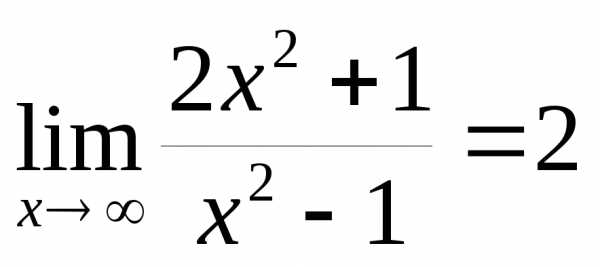 – таким образом,
– таким образом, 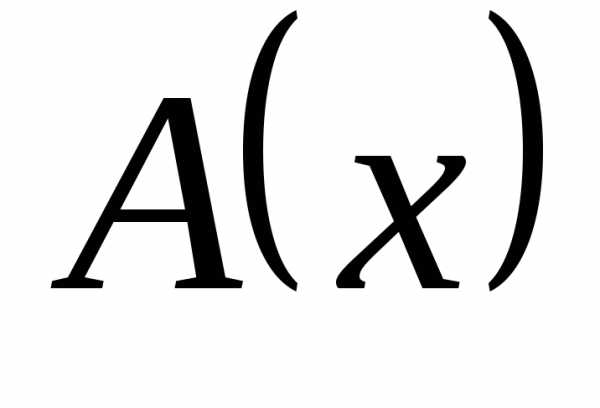 и
и 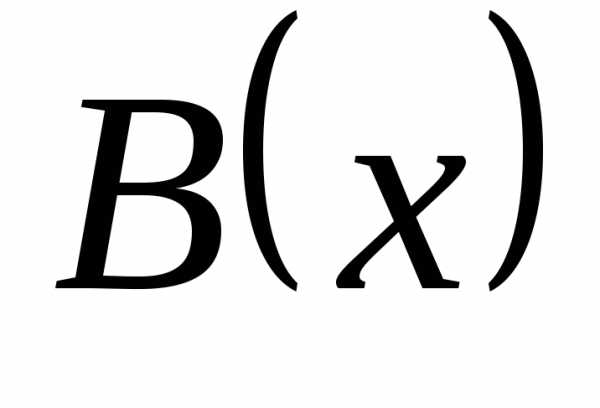 – бесконечно большие одного порядка
(один порядок роста).
– бесконечно большие одного порядка
(один порядок роста).
3)
, .
Здесь 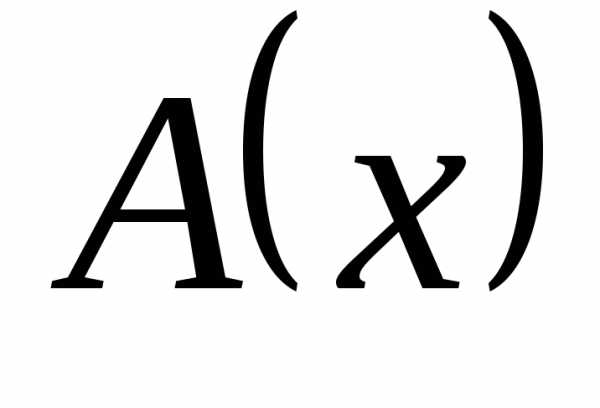 – бесконечно большая второго порядка
по отношению к
– бесконечно большая второго порядка
по отношению к 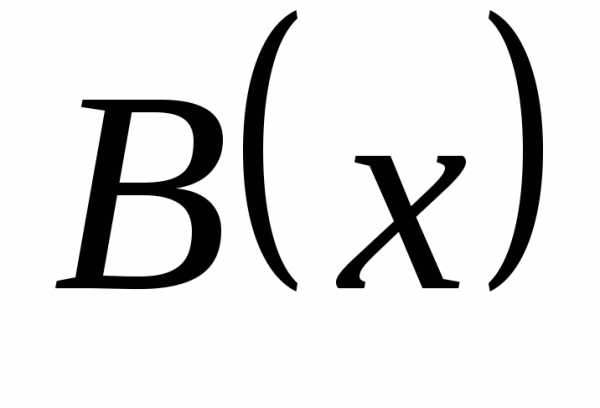 .
.
Таким образом, при вычислении предела отношения члены отношения можно заменять на эквивалентные.
Пример 12.6. 1)  .
.
2) .
3) .
Таким образом,
если  ,
,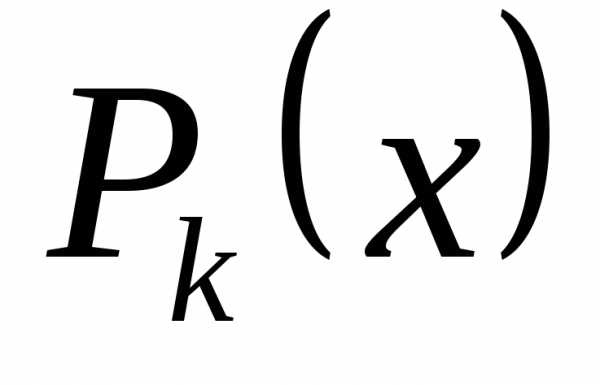 – многочлены степенейm и k соответственно, то
– многочлены степенейm и k соответственно, то 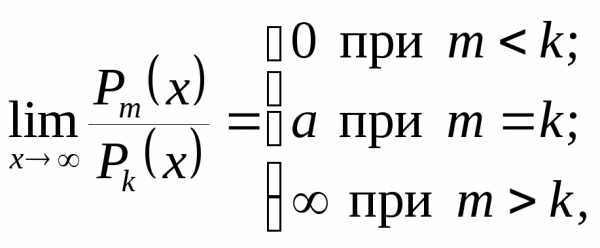 гдеа – отношение коэффициентов при старших
степенях многочленов.
гдеа – отношение коэффициентов при старших
степенях многочленов.
12.5. Связь между бесконечно малыми и бесконечно большими величинами.
♦ Теорема 12.3. 1) Если
функция 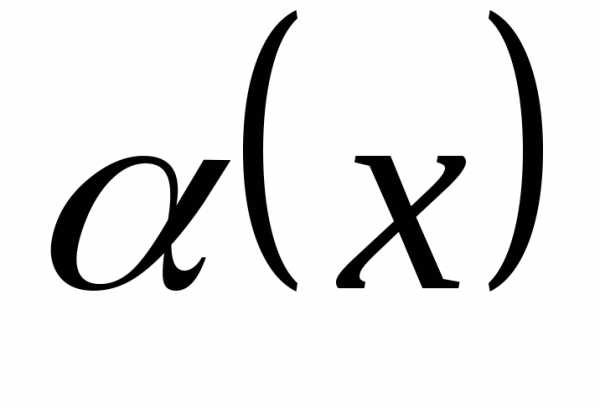 – бесконечно малая при
– бесконечно малая при
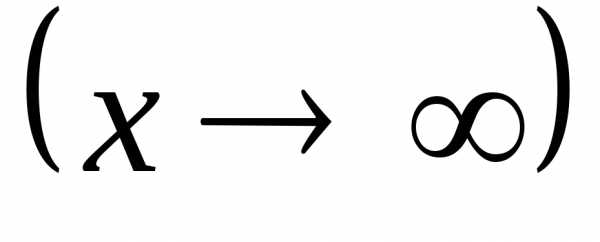 ,
то функция
,
то функция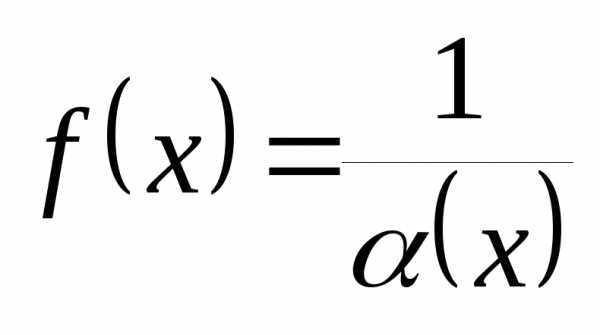 является бесконечно большой при
является бесконечно большой при
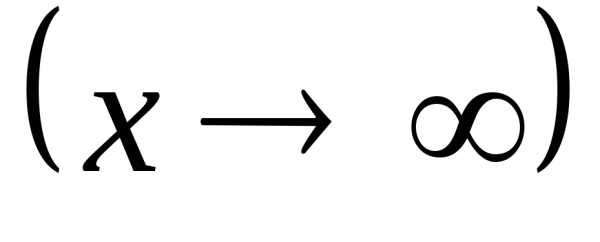 .
.
2) Если функция  – бесконечно большая при
– бесконечно большая при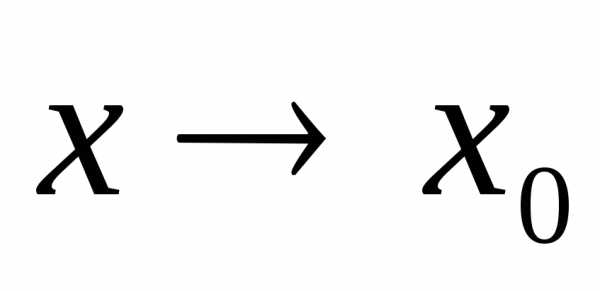
 ,
то функция
,
то функция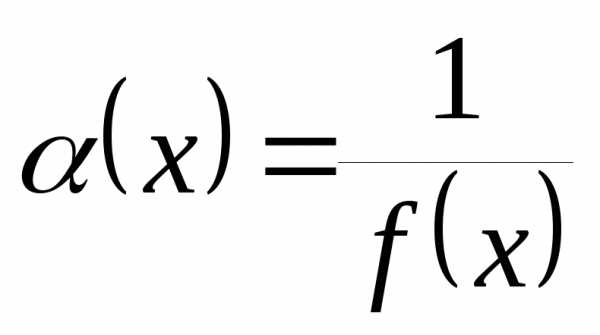 является бесконечно малой при
является бесконечно малой при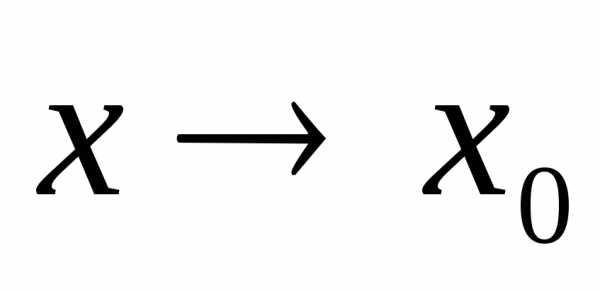
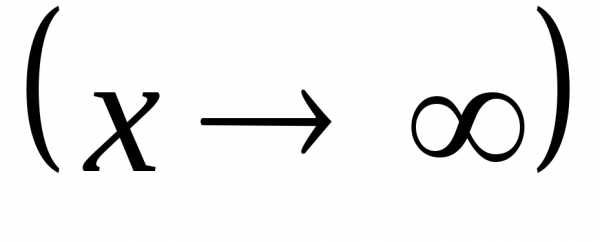 .
.
Доказательство. 1) Пусть при 
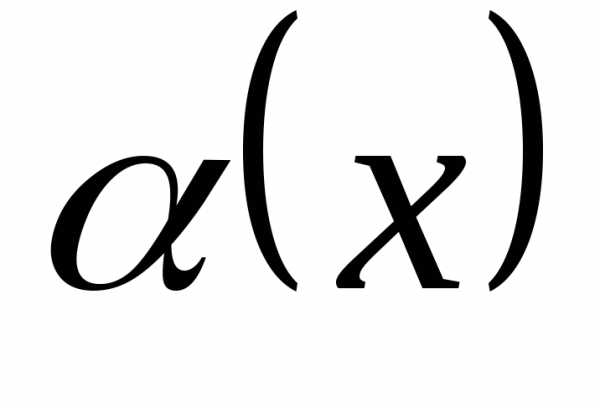 – бесконечно малая, то есть
.
Таким образом,
– бесконечно малая, то есть
.
Таким образом, 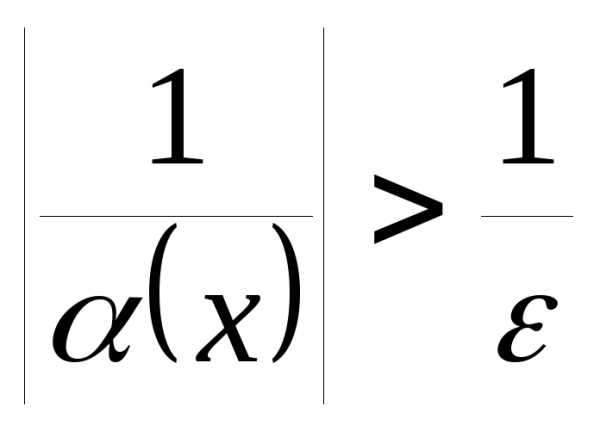 ,
отсюда
,
отсюда 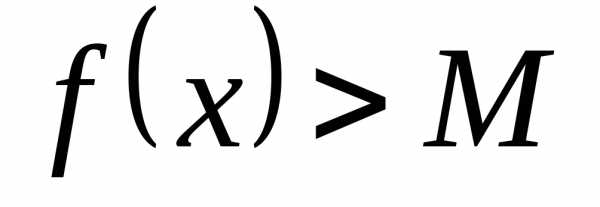 ,
где
,
где 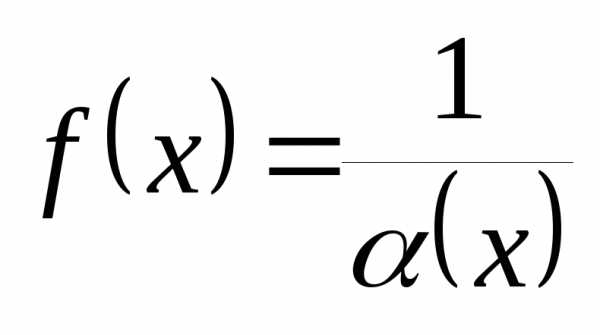 ,
,  .
Получаем, что функция
.
Получаем, что функция 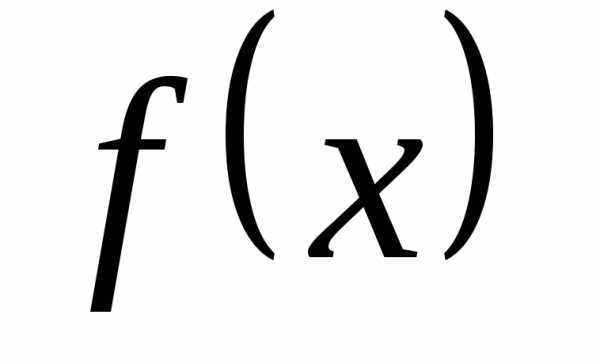 – бесконечно большая.
– бесконечно большая.
2) Доказательство проводится аналогичным образом. ■
Пример 12.7. 1)
при– бесконечно малая, а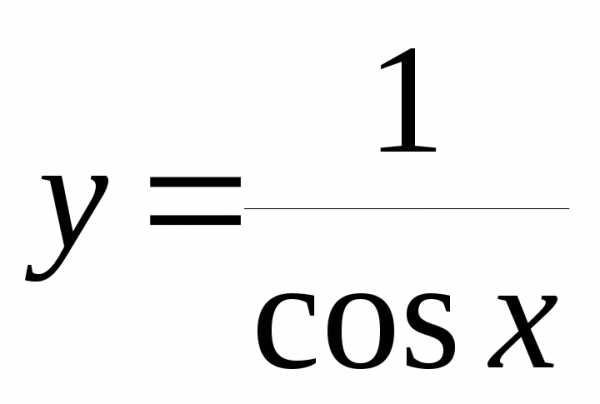 – бесконечно большая величина. При
– бесконечно большая величина. При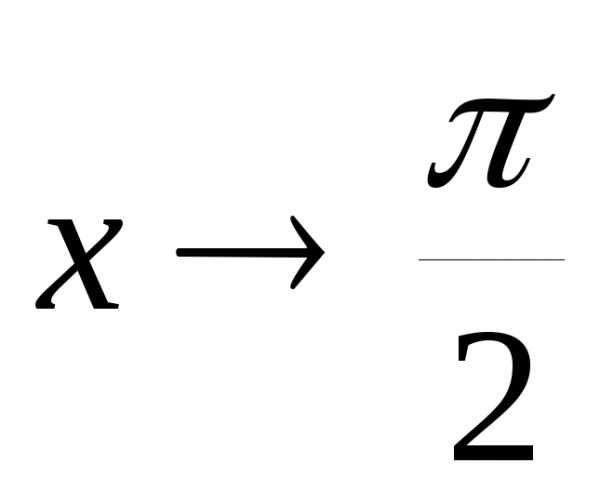 функция
функция – бесконечно большая, а– бесконечно малая.
– бесконечно большая, а– бесконечно малая.
2) 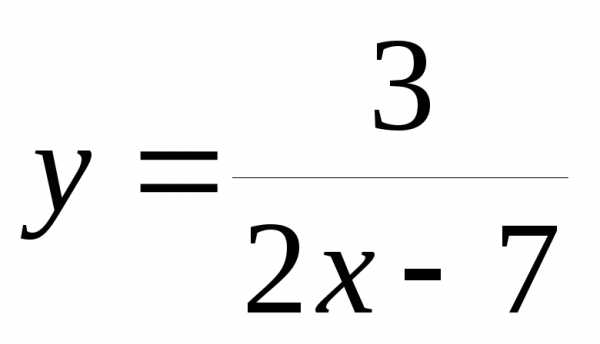 при– бесконечно малая, а
при– бесконечно малая, а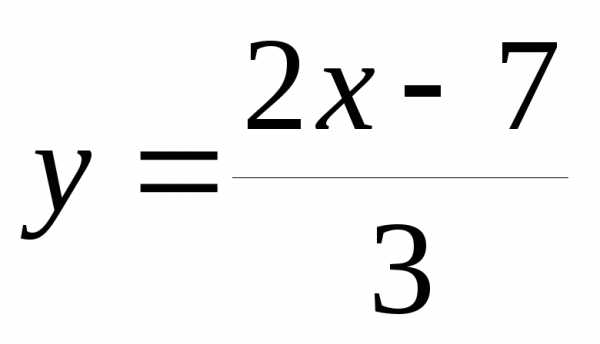 – бесконечно большая.
– бесконечно большая.
3)
при– бесконечно большая, а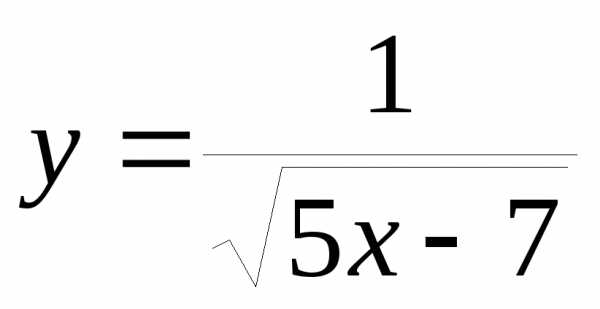 – бесконечно малая.
– бесконечно малая.
57
studfiles.net
Определение предела функции (по Гейне и Коши)
Первое определение предела функции (по Гейне)
Число a называется пределом функции f(x) в точке x0:
,
если
1) существует такая проколотая окрестность точки x0, на которой функция определена;
2) для любой последовательности {xn}, сходящейся к x0:
, элементы которой принадлежат окрестности ,
последовательность {f(xn)} сходится к a:
.
Здесь x0 и a могут быть как конечными числами, так и бесконечно удаленными точками. Окрестность может быть как двусторонней, так и односторонней.
Запишем это определение с помощью логических символов существования и всеобщности:
.
Второе определение предела функции (по Коши)
Число a называется пределом функции f(x) в точке x0:
,
если
1) существует такая проколотая окрестность точки x0, на которой функция определена;
2) для любого положительного числа ε > 0 существует такое число δε> 0, зависящее от ε, что для всех x, принадлежащих проколотой δε — окрестности точки x0:
,
значения функции f(x) принадлежат ε — окрестности точки a:
.
Точки x0 и a могут быть как конечными числами, так и бесконечно удаленными точками. Окрестность также может быть как двусторонней, так и односторонней.
Запишем это определение с помощью логических символов существования и всеобщности:
.
В этом определении используются окрестности с равноудаленными концами. Можно дать и эквивалентное определение, используя произвольные окрестности точек.
Определение с использованием произвольных окрестностей
Число a называется пределом функции f(x) в точке x0:
,
если
1) существует такая проколотая окрестность точки x0, на которой функция определена;
2) для любой окрестности U(a) точки a существует такая проколотая окрестность точки x0, что для всех x, принадлежащих проколотой окрестности точки x0:
,
значения функции f(x) принадлежат окрестности U(a) точки a:
.
С помощью логических символов существования и всеобщности это определение можно записать так:
.
На странице «Окрестность точки» мы показали, что определение предела функции с использованием более простой окрестности с равноудаленными концами эквивалентно определению, в котором используется произвольная окрестность. Формулировка второго определения по Коши имеет более общий вид, и оно часто используется при доказательстве теорем. Первое определение, в математическом смысле, проще. Его удобно применять в вычислениях.
Более подробно определение Коши для конечных точек рассматривается на странице «Определение предела функции в конечной точке»; для бесконечно удаленных точек – на странице «Определение предела функции на бесконечности».
Односторонние и двусторонние пределы
Приведенные выше определения универсальны в том смысле, что их можно использовать для любых типов окрестностей. Если, в качестве мы используем левостороннюю проколотую окрестность конечной точки, то получим определение левостороннего предела . Если в качестве окрестности использовать окрестность бесконечно удаленной точки, то получим определение предела на бесконечности.
Для определения предела по Гейне это сводится к тому, что на произвольную, сходящуюся к , последовательность накладывается дополнительное ограничение – ее элементы должны принадлежать соответствующей проколотой окрестности точки .
Для определения предела по Коши нужно в каждом случае преобразовать выражения и в неравенства, используя соответствующие определения окрестности точки.
См. «Окрестность точки».
Определение, что точка a не является пределом функции
Часто возникает необходимость использовать условие, что точка a не является пределом функции при . Построим отрицания к изложенным выше определениям. В них мы предполагаем, что функция f(x) определена на некоторой проколотой окрестности точки x0. Точки a и x0 могут быть как конечными числами, так и бесконечно удаленными. Все сформулированное ниже относится как к двусторонним, так и к односторонним пределам.
По Гейне.
Число a не является пределом функции f(x) в точке x0: ,
если существует такая последовательность {xn}, сходящаяся к x0:
,
элементы которой принадлежат окрестности ,
что последовательность {f(xn)} не сходится к a:
.
.
По Коши.
Число a не является пределом функции f(x) в точке x0:
,
если существует такое положительное число ε > 0, так что для любого положительного числа δ > 0, существует такое x, принадлежащее проколотой δ — окрестности точки x0:
,
что значение функции f(x) не принадлежит ε — окрестности точки a:
.
.
Разумеется, если точка a не является пределом функции при , то это не означает, что у нее не может быть предела. Возможно, существует предел , но он не равен a. Также возможен случай, когда функция определена в проколотой окрестности точки , но не имеет предела при .

Функция f(x) = sin(1/x) не имеет предела при x → 0.
Например, функция определена при , но предела не существует. Для доказательства возьмем последовательность . Она сходится к точке 0: . Поскольку , то .
Возьмем последовательность . Она также сходится к точке 0: . Но поскольку , то .
Тогда предел не может равняться никакому числу a. Действительно, при , существует последовательность , с которой . Поэтому любое отличное от нуля число не является пределом. Но также не является пределом, поскольку существует последовательность , с которой .
Эквивалентность определений предела по Гейне и по Коши
Теорема
Определения предела функции по Гейне и по Коши эквивалентны.
Доказательство
При доказательстве мы предполагаем, что функция определена в некоторой проколотой окрестности точки (конечной или бесконечно удаленной). Точка a также может быть конечной или бесконечно удаленной.
Доказательство Гейне ⇒ Коши
Пусть функция имеет в точке предел a согласно первому определению (по Гейне). То есть для любой последовательности , принадлежащей окрестности точки и имеющей предел
(1) ,
предел последовательности равен a:
(2) .
Покажем, что функция имеет предел в точке по Коши. То есть для любого существует , что для всех .
Допустим противное. Пусть условия (1) и (2) выполнены, но функция не имеет предела по Коши. То есть существует такое , что для любого существует , так что
.
Возьмем , где n – натуральное число. Тогда существует , причем
.
Таким образом мы построили последовательность , сходящуюся к , но предел последовательности не равен a. Это противоречит условию теоремы.
Первая часть доказана.
Доказательство Коши ⇒ Гейне
Пусть функция имеет в точке предел a согласно второму определению (по Коши). То есть для любого существует , что
(3) для всех .
Покажем, что функция имеет предел a в точке по Гейне.
Возьмем произвольное число . Согласно определению Коши, существует число , так что выполняется (3).
Возьмем произвольную последовательность , принадлежащую проколотой окрестности и сходящуюся к . По определению сходящейся последовательности, для любого существует , что
при .
Тогда из (3) следует, что
при .
Поскольку это выполняется для любого , то
.
Теорема доказана.
Использованная литература:
Л.Д. Кудрявцев. Курс математического анализа. Том 1. Москва, 2003.
Автор: Олег Одинцов. Опубликовано: Изменено:
1cov-edu.ru
Определение предела функции в точке
Определение предела функции по Коши
Конечный предел функции в конечной точке

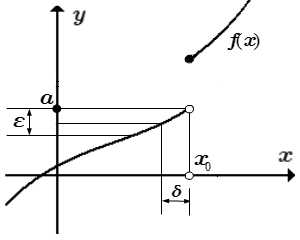
Предел функции в точке:
|f(x) – a| < ε при 0 < |x – x0| < δ
Определение конечного предела функции по Коши
Пусть функция f(x) определена в некоторой проколотой окрестности конечной точки x0. Число a называется пределом функции f(x) в точке x0, если для любого сколь угодно малого положительного числа ε > 0 существует такое число δε> 0, зависящее от ε, что для всех x, принадлежащих проколотой δε — окрестности точки x0: 0 < |x – x0| < δε, значения функции принадлежат ε — окрестности точки a:
|f(x) – a| < ε.
Предел функции обозначается так:
.
Или при .
С помощью логических символов существования и всеобщности определение предела функции можно записать следующим образом:
.
Односторонние пределы
Левый предел функции в точке:
|f(x) – a| < ε при 0 < x0 – x < δ
Функция может быть определена не с двух сторон от точки , а в некоторой левой окрестности точки , при или в некоторой правой окрестности, при . Также функция может иметь разрыв в точке . Тогда используют односторонние пределы.
Левый предел в точке (левосторонний предел):
.
Правый предел в точке (правосторонний предел):
.
Пределы слева и справа часто обозначают так:
; .
Бесконечный предел функции в конечной точке
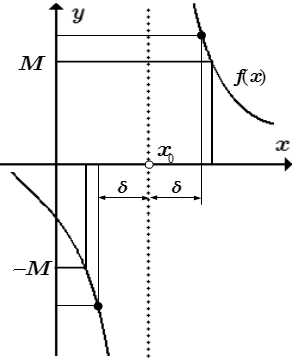
Бесконечный предел функции в точке:
|f(x)| > M при 0 < |x – x0| < δ
Определение бесконечного предела функции по Коши
Пусть функция f(x) определена в некоторой проколотой окрестности конечной точки x0. Предел функции f(x) при x → x0 равен бесконечности, если для любого, сколь угодно большого числа M > 0, существует такое число δM > 0, зависящее от M, что для всех x, принадлежащих проколотой δM — окрестности точки x0: 0 < |x – x0| < δM, значения функции принадлежат окрестности бесконечно удаленной точки:
|f(x)| > M.
Бесконечный предел обозначают так:
.
Или при .
С помощью логических символов существования и всеобщности определение бесконечного предела функции можно записать так:
.
Также можно ввести определения бесконечных пределов определенных знаков, равных и :
.
.
Аналогичным образом вводятся определения односторонних пределов.
Левые пределы.
.
.
.
Правые пределы.
.
.
.
Определение предела функции по Гейне
Пусть функция f(x) определена на некоторой проколотой окрестности точки x0.
Число a (конечное или бесконечно удаленное) называется пределом функции f(x) в точке x0:
,
если для любой последовательности {xn}, сходящейся к x0: ,
элементы которой принадлежат окрестности , последовательность {f(xn)} сходится к a:
.
Если в качестве окрестности взять левостороннюю окрестность точки x0, то получим определение левого предела. Если правостороннюю – то получим определение правого предела.
Определения предела по Гейне и Коши эквивалентны.
Примеры
Пример 1
Используя эпсилон и дельта — рассуждения показать, что
.
Решение
Введем обозначения:
.
Выпишем определение конечного предела функции в точке по Коши:
.
Преобразуем разность:
.
Пусть
.
Тогда
;
;
.
Итак, мы нашли, что при ,
.
Вводим положительные числа и :
.
Отсюда следует, что
при , и .
Поскольку всегда можно уменьшить, то возьмем . Тогда для любого ,
при .
Это означает, что .
Пример 2
Используя определение предела по Коши показать, что
.
Решение
Введем обозначение:
.
Выпишем определение предела функции в точке , равного бесконечности, по Коши:
.
Выразим многочлены в числителе и знаменатели через многочлены от .
;
.
Пусть
.
Тогда
;
;
.
Итак, мы нашли, что при ,
.
Вводим положительные числа и :
.
Отсюда следует, что
при , и .
Поскольку всегда можно уменьшить, то возьмем . Тогда для любого ,
при .
Это означает, что .
Пример 3
Используя определение предела по Коши показать, что
.
Решение
Введем обозначение:
.
Выпишем определение левого предела в точке , равного , по Коши:
.
В нашем случае .
Выразим многочлены в числителе и знаменатели через многочлены от .
;
.
Пусть
.
Тогда
; );
;
;
.
Итак, мы нашли, что при ,
.
Вводим положительные числа и :
.
Отсюда следует, что
при , и .
Поскольку всегда можно уменьшить, то возьмем . Тогда для любого ,
при .
Это означает, что .
Использованная литература:
С.М. Никольский. Курс математического анализа. Том 1. Москва, 1983.
Автор: Олег Одинцов. Опубликовано:
1cov-edu.ru
Определение предела по Коши и по Гейне, их эквивалентность — ПриМат
Определение 1.1. (определение по Коши или на языке ):
— предел функции в точке (и пишут \(\lim\limits_{x\rightarrow a } f(x) = A\)), если:
В определении допускается, что , то есть может не принадлежать области определения функции.
Определение 1.2. (определение по Гейне):
называется пределом функции в точке , если , то есть , соответствующая последовательность значений , то есть .
Замечание 1.1.
Из определения предела функции по Гейне следует, что функция не может иметь в точке два разные предела.
Замечание 1.2.
Понятие предела функции в точке есть локальное понятие: существование и значение предела полностью определяется значениями функции в как угодно малой окрестности этой точки.
Замечание 1.3.
Данную запись в определении можно сформулировать иначе: точка принадлежит проколотой -окрестности точки ()
2. Эквивалентность определений
Пусть число является пределом функции в точке по Коши. Выберем произвольную подходящую последовательность , , то есть такую, для которой . Покажем, что является пределом по Гейне.
Зададим произвольное и укажем для него такое , что для всех из условия следует неравенство . В силу того, что , для найдётся такой номер , что будет выполняться неравенство , то есть .
Докажем теперь обратное утверждение: предположим, что по Гейне, и покажем, что число является пределом функции в точке по Коши. Предположим, что это неверно, то есть: . В качестве рассмотрим , а соответствующие значения будем обозначать . Тогда при любом выполняются условия и . Отсюда следует, что последовательность является подходящей, но число не является пределом функции в точке . Получили противоречие.
Пример 3.1.
а)
, например
б)
Пример 3.2.
Доказать, что не имеет предела в точке 0.
Вывод: последовательность по Гейне не имеет предела.
Лимит времени: 0
Информация
Тест по теме Определение предела по Коши и по Гейне, их эквивалентность.
Желаем удачи!
Вы уже проходили тест ранее. Вы не можете запустить его снова.
Тест загружается…
Вы должны войти или зарегистрироваться для того, чтобы начать тест.
Вы должны закончить следующие тесты, чтобы начать этот:
Правильных ответов: 0 из 5
Ваше время:
Время вышло
Вы набрали 0 из 0 баллов (0)
| Средний результат |
|
| Ваш результат |
|
Рубрики
- Математический анализ 0%
Спасибо Вам за прохождение данного теста, надеюсь вы узнали для себя что-нибудь новое!
| Место | Имя | Записано | Баллы | Результат |
|---|---|---|---|---|
| Таблица загружается | ||||
| Нет данных | ||||
- С ответом
- С отметкой о просмотре
Навигация по записям
ib.mazurok.com
Предел функции
Как видно из примеров, предельная точка множества может как принадлежать, так и не принадлежать ему.
Теорема 2.29. Для того чтобы точкаa R была предельной точкой множестваX R, необходимо и достаточно, чтобы существовала последовательность{xn} элементов множестваX, отличных отa, сходящаяся кa.
Необходимость. Пусть a – предельная точка множества X. Будем считать, что a R. Тогда в окрестности Ua(1/n), n N найдется элемент множества X\{a}, который обозначим через xn. Последователь-
ность {xn} обладает свойствами: xn X\{a}, a −n1 < xn < a +n1 ,n N. Из последнего получаем,что xn → a.
Достаточность. Пусть последовательность {xn} такова, что xn X, xn 6= a, xn → a. Зафиксируем произвольную окрестность Ua точки a. По определению2.3 предела последовательности найдётся номер N = N(Ua) такой, что xn Ua, n > N. Учитывая, что xn X\{a}, получим, что
◦
в Ua содержится бесконечное подмножество множества X, а значит, a – предельная точка множества X.
Теорема 2.30. Всякое бесконечное множество действительных чисел имеет по крайней мере одну предельную точку.
Пусть X – бесконечное подмножество множества R. Ясно, что существует последовательность {xn} попарно различных элементов множества X. Согласно теореме2.20 последовательность {xn} имеет по крайней мере один частичный предел. Пусть a P ({xn}). Тогда най-
дется такая подпоследовательность {xnk }, что a = lim xnk . Поскольку
k→∞
xnk X, k N, и все они, кроме быть может одного, отличны от a, то a – предельная точка множества X.
Замечание. Любое конечное множество X R не имеет предельных точек.
2.2.2Определение предела функции
Вэтой главе будем считать, что X — некоторое непустое подмножество множества R действительных чисел, a – предельная точка множества X и вещественнозначная функция f определена на X. Поэтому всякий раз, когда в последующем будем говорить о функции f, будем подразумевать, если не оговорено нечто другое, что f : X → R.
Определение 2.22. ТочкаA R называется пределом функцииf : X → R в точке a (или ещё говорят, что A — предел функцииf
studfiles.net
Предел функции — ПриМат
Определение. Пусть функция $f$ определена на интервале $(a, b)$ и точка $x_0 \in (a, b)$. Говорят, что функция $f$ непрерывна в точке $x_0$, если
$$\lim_{x \to x_0} f(x) = f (x_0).$$
Используя определение предела функции в смысле Коши, определение непрерывности функции $f$ в точке $x_0$ в кванторах можно записать следующим образом:
$$\forall \varepsilon > 0 \space \exists \delta = \delta (\varepsilon) > 0 : \forall x \in (a, b) : |x−x_0| < \delta \Rightarrow \\ \Rightarrow |f(x)−f(x_0)| < \varepsilon.$$
В этом определении можно не требовать выполнения условия $|x−x_0| > 0$, т. к. при $|x−x_0| = 0$ неравенство $|f(x)−f(x_0)| < \varepsilon$, очевидно, выполнено.
Так как величина $\displaystyle \lim_{x \to x_0} f(x)$ зависит лишь от тех значений, которые функция $f$ принимает в сколь угодно малой окрестности точки $x_0$, то непрерывность — это локальное свойство функции.
В терминах окрестностей определение непрерывности выглядит следующим образом.
Определение. Функция $f$ называется непрерывной в точке $x_0$, если для любой окрестности $V$ точки $f(x_0)$ найдется такая окрестность $U$ точки $x_0$, что для всех $x \in U$ значение $f(x) \in V$ , т. е. $f(U \cap (a, b)) \subset V$.
Применяя определение предела функции в смысле Гейне, определение непрерывности можно сформулировать так.
Определение. Функция $f$, определенная на интервале $(a, b)$, называется непрерывной в точке $x_0 \in (a, b)$, если любая последовательность аргументов $\{x_n\} \space (x_n \in (a, b), x_n \to x_0)$ порождает последовательность значений функции $\{f(x_n)\}$, стремящуюся к $f(x_0)$.
Применяя понятие одностороннего предела (т. е. предела слева и справа) в точке $x_0$, можно дать определения непрерывности слева (справа) в точке $x_0$. Именно, функция $f$ называется непрерывной слева (справа) в точке $x_0$, если $\displaystyle \lim_{x \to x_0−0} f(x) = f(x_0) (\lim_{x \to x_0+0} f(x) = f(x_0))$. При этом в определении непрерывности слева достаточно считать, что функция $f$ определена лишь в левой полуокрестности точки $x_0$, т. е. на $(a, x_0]$, а для непрерывности справа — на $[x_0, b)$.
Легко видеть, что справедливо следующее
Утверждение. Для того, чтобы функция $f$ была непрерывной в точке $x_0$, необходимо и достаточно, чтобы $f$ была непрерывной слева и справа в точке $x_0$.
Определение. Функция $f$, определенная на интервале $(a, b)$, называется разрывной в точке $x_0 \in (a, b)$, если $f$ не является непрерывной в этой точке.
Итак, функция $f$ является разрывной в точке $x_0$, если выполнено одно из двух следующих условий.
1. Либо не существует $\displaystyle \lim_{x \to x_0} f(x)$.
2. Либо предел $\displaystyle \lim_{x \to x_0} f(x)$ существует, но он не равен $f(x_0)$.
Пример 1. $f(x) \equiv C = Const$. Эта функция непрерывна в каждой точке $x_0 \in \mathbb{R}$, т. к. для любого $x \in \mathbb{R} \space |f(x)−f(x_0)| = 0$.
Пример 2. $f(x) = x^2, −\infty < x < +\infty, x_0 \in \mathbb{R}$. Зададим $\varepsilon > 0$. Тогда из неравенства
$$|x^2-x_0^2| \leq (|x|+|x_0|)|x-x_0|$$
следует, что при $|x−x_0| < \delta = \min{\Bigr(1, \frac{\varepsilon}{2|x_0|+1}\Bigl)}$ справедливо неравенство $|x^2-x_0^2| < \varepsilon$, т. е. $\displaystyle \lim_{x \to x_0} x^2 = x_0^2$, а значит, функция $f(x) = x^2$ непрерывна в любой точке $x_0 \in \mathbb{R}$.
Пример 3. $f(x) = \sqrt{x}, \space 0 \leq x < +\infty$. Если $x_0 \in (0, +\infty)$, то
$$|\sqrt{x}-\sqrt{x_0}| = \frac{|x-x_0|}{\sqrt{x}+\sqrt{x_0}} \leq \frac{1}{\sqrt{x_0}} |x-x_0| < \varepsilon,$$
если только $|x-x_0| < \delta \equiv \sqrt{x_0} \cdot \varepsilon$. Таким образом, функция $f(x) = \sqrt{x}$ непрерывна в каждой точке $x_0 > 0$. В точке $x_0 = 0$ можно ставить вопрос о непрерывности справа. Имеем $|\sqrt{x}-\sqrt{0}| = \sqrt{x} < \varepsilon \space$, если только $0 \leq x < \delta \equiv \varepsilon^2$. Итак, $\displaystyle \lim_{x \to 0+} \sqrt{x} = 0 = \sqrt{0}$, т. е. функция $f(x) = \sqrt{x}$ непрерывна справа в точке $0$.
Пример 4. $f(x)=\sin{x}, -\infty < x < +\infty$. Пусть $x_0 \in \mathbb{R}$. Тогда
$$|\sin{x}−\sin{x_0}| = \Bigg|2\cos{\frac{x+x_0}{2}}\sin{\frac{x-x_0}{2}}\Bigg| \leq \\ \leq 2\Bigg|\sin{\frac{x-x_0}{2}}\Bigg| \leq |x−x_0|,$$
где последнее неравенство в этой цепочке следует из доказанного выше неравенства $|\sin{t}| \leq |t| \space (0 < |t| < \pi/2)$. Можем считать, что $|x−x_0| < \pi$. Тогда при $|x−x_0| < \delta \equiv \min{(\pi, \varepsilon)}$ справедливо $|\sin{x}−\sin{x_0}| < \varepsilon$, т. е. функция $f(x) = \sin{x}$ непрерывна в каждой точке $x_0 \in \mathbb{R}$.
Аналогично доказываем, что функция $f(x) = \cos{x}$ непрерывна в каждой точке $x_0 \in \mathbb{R}$.
Пример 5. $f(x) = x \cdot \sin{\frac{1}{x}}$ при $x \neq 0$ и $f(0) = 0$. Покажем, что функция $f$ непрерывна в точке $x_0= 0$. Имеем $f(0) = 0$ и
$$\lim_{x \to 0} f(x) = \lim_{x \to 0} x \sin{\frac{1}{x}} = 0$$
(т. к. $|f(x)−0| = |x \sin{\frac{1}{x}}| \leq |x| < \varepsilon$, если только $|x−0| = |x| < \delta \equiv \varepsilon$). Итак, $\displaystyle \lim_{x \to 0} f(x) = f(0)$, так что $f$ непрерывна в точке $0$.
Пример 6. $f(x) = \operatorname{sign} x, x \in R$. Если $x_0 \neq 0$, то функция $f$ постоянна в некоторой окрестности точки $x_0$ и, следовательно, непрерывна в этой точке. Если же $x_0 = 0$, то не существует предела функции $f$ при $x \to 0$. Значит, функция $f$ разрывна в точке $0$. Более того, $\displaystyle \lim_{x \to 0+} \operatorname{sign} x = 1, \lim_{x \to 0−} \operatorname{sign} x = −1, \operatorname{sign} 0 = 0$, так что функция $\operatorname{sign} x$ разрывна в точке $0$ как слева, так и справа.
Пример 7. Рассмотрим функцию Дирихле
$$\begin{equation*}D(x) = \begin{cases} 1, \quad x \in \mathbb{Q}, \\ 0, \quad x \in \mathbb{R \setminus Q}. \end{cases} \end{equation*}$$
Пусть $x_0 \in \mathbb{R}$. Покажем, что не существует предела функции $D$ при $x \to x_0$. Для этого выберем последовательность $\{x^\prime_n\}$ отличных от $x_0$ рациональных чисел, стремящуюся к $x_0$. Тогда $D(x^\prime_n) = 1$ и, значит, $\displaystyle \lim_{n \to \infty} D(x^\prime_n) = 1$. Если же взять последовательность $\{x^{\prime\prime}_n\}$, отличных от $x_0$ иррациональных чисел, стремящуюся к $x_0$, то получим, что $D(x^{\prime\prime}_n) = 0$ и $\displaystyle \lim_{n \to \infty} D(x^{\prime\prime}_n) = 0$. В силу определения предела функции по Гейне получаем, что функция $D$ не имеет предела в точке $x_0$. Так как $x_0 \in \mathbb{R}$ — произвольная точка, то это означает, что функция Дирихле разрывна в каждой точке.
Пример 8. $f(x) = x \cdot D(x), \space x \in \mathbb{R}$. Функция $f$ разрывна в каждой точке $x_0 \neq 0$. В самом деле, если $\{x^\prime_n\}$ и $\{x^{\prime\prime}_n\}$ соответственно последовательности рациональных и иррациональных отличных от $x_0$ чисел, стремящиеся к $x_0$, то $\displaystyle \lim_{n \to \infty} f(x^\prime_n) = 0$ и $\displaystyle \lim_{n \to \infty} f(x^{\prime\prime}_n) = 0$, так что, в силу определения предела функции по Гейне, функция $f$ не имеет предела в точке $x_0$. Если же $x_0 = 0$, то $\displaystyle \lim_{x \to 0} f(x) = 0 = f(0)$. Действительно, $|f(x)| = |x \cdot D(x)| \leq |x| < \varepsilon$, если только $|x−0| = |x| < \delta \equiv \varepsilon$. Это означает, что данная функция непрерывна в единственной точке $x_0 = 0$.
Примеры решения задач
Пусть функция $f$ определена в окрестности точки $x_0$, кроме самой точки $x_0$. Доопределить функцию $f$, задав $f(x_0)$ так, чтобы получившаяся функция была непрерывна в точке $x_0$, если:
- $\displaystyle f(x) = \frac{x^2-1}{x+1}, \space x_0 = -1$.
Решение
$$\lim_{x \to x_0} f(x) = \lim_{x \to x_0} \frac{(x-1)(x+1)}{x+1} = \lim_{x \to -1} (x-1) = -2$$
Таким образом, положим $\displaystyle f(-1) = \lim_{x \to -1} f(x) = -2$. Значит, функция непрерывна в точке $x_0 = -1$. - $\displaystyle f(x) = \frac{\sqrt{1+x}-1}{x}, \space x_0 = 0$.
Решение
Воспользовавшись таблицей эквивалентных, получим:
$$\lim_{x \to x_0} f(x) = \lim_{x \to x_0} \frac{(1+x)^{\frac{1}{2}}-1}{x} \backsim \lim_{x \to 0} \frac{\frac{1}{2}x}{x} = \frac{1}{2}$$
Таким образом, положим $\displaystyle f(0) = \lim_{x \to 0} f(x) = \frac{1}{2}$. Значит, функция непрерывна в точке $x_0 = 0$. - $\displaystyle f(x) = x\cot{x}, \space x_0 = 0$.
Решение
Воспользовавшись таблицей эквивалентных, получим:
$$\lim_{x \to x_0} f(x) = \lim_{x \to x_0} x\frac{\cos{x}}{\sin{x}} \backsim \lim_{x \to 0} x\frac{\cos{x}}{x} = 1$$
Таким образом, положим $\displaystyle f(0) = \lim_{x \to 0} f(x) = 1$. Значит, функция непрерывна в точке $x_0 = 0$.
Непрерывные функции
Лимит времени: 0
Информация
Проверьте, насколько хорошо вы усвоили эту тему и закрепите свои знания по ней, пройдя тест.
Вы уже проходили тест ранее. Вы не можете запустить его снова.
Тест загружается…
Вы должны войти или зарегистрироваться для того, чтобы начать тест.
Вы должны закончить следующие тесты, чтобы начать этот:
| Место | Имя | Записано | Баллы | Результат |
|---|---|---|---|---|
| Таблица загружается | ||||
| Нет данных | ||||
- С ответом
- С отметкой о просмотре
Поделиться ссылкой:
ib.mazurok.com
2 Предел функции
2.1 Понятие предела функции
Во многих практических задачах требуется определить скорость изменения функции при изменении аргумента. В этом случае используется понятие производной функции. Это понятие в свою очередь вводится с помощью понятия предела функции. Поясним смысл понятия предела на примере.
Функция 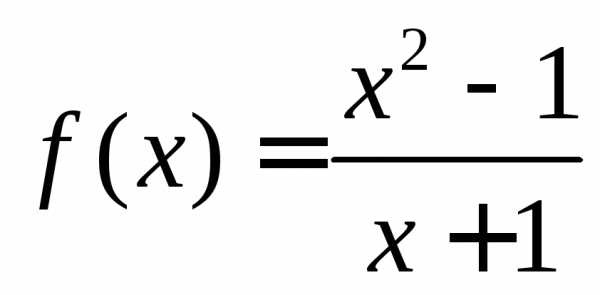 не определена при значении
не определена при значении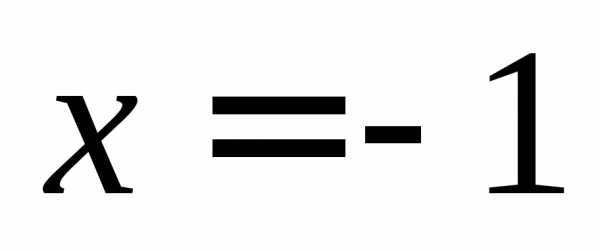 ,
так как при нем знаменатель обращается
в нуль. Таким образом, при
,
так как при нем знаменатель обращается
в нуль. Таким образом, при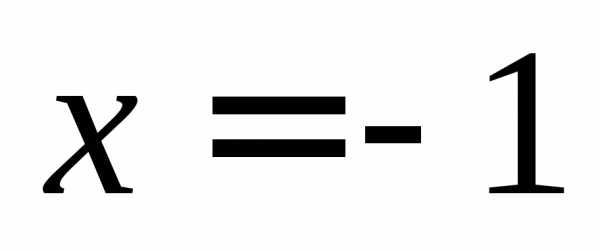 функция имеет разрыв (рисунок 2.1).
функция имеет разрыв (рисунок 2.1).
Рисунок
2.1 – Функция |
Однако
если положить значение функции в точке 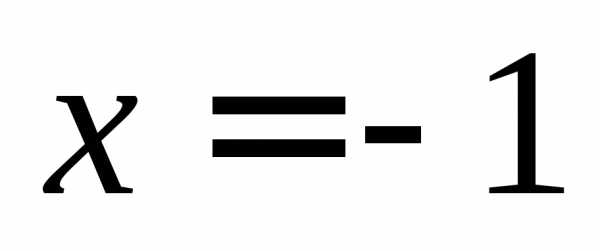 равным,
то получим функцию непрерывную на всей
числовой оси. Математически это
записывается как
равным,
то получим функцию непрерывную на всей
числовой оси. Математически это
записывается как
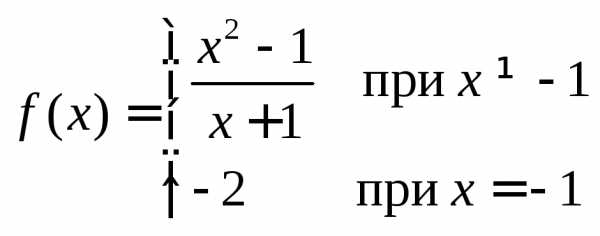
В
общем случае, если  —
точка разрыва функции
—
точка разрыва функции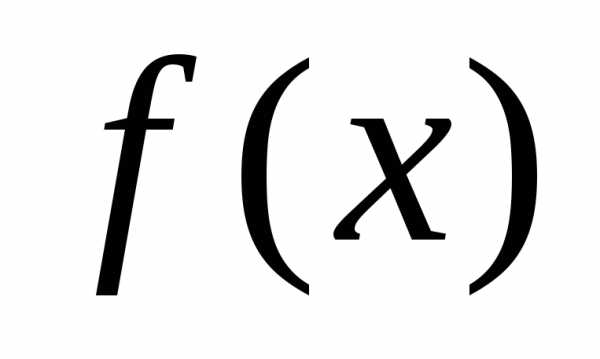 ,
но возможно найти для нее в точке
,
но возможно найти для нее в точке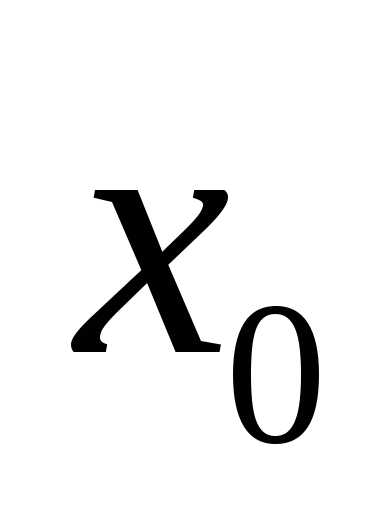 такое значение А, при котором измененная
функция
такое значение А, при котором измененная
функция станет
непрерывной, то это число А называетсяпределом
функции
станет
непрерывной, то это число А называетсяпределом
функции 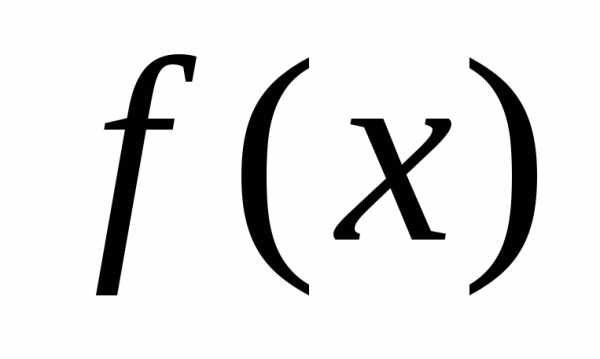 в точке
в точке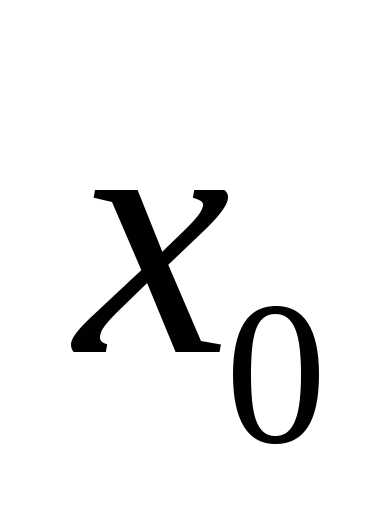 ,
а точка
,
а точка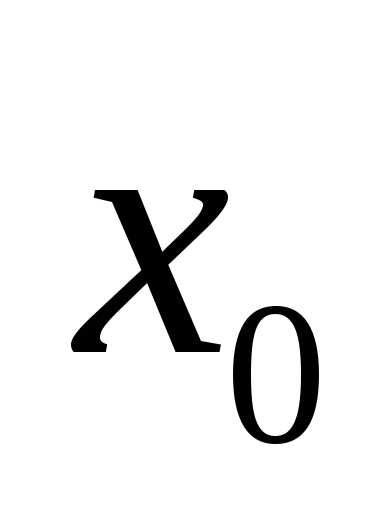 — точкой устранимого разрыва.
— точкой устранимого разрыва.
Математически это записывается формулой:
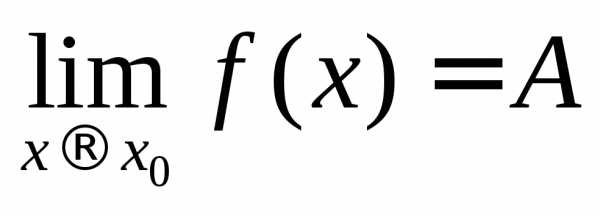
Существование
предела функции  в точке
в точке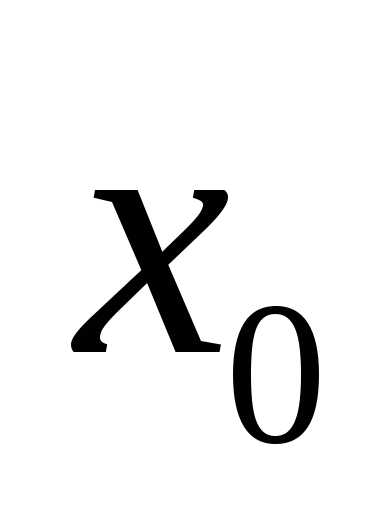 означает, что функция
означает, что функция приближенно равна
приближенно равна для всех значений
для всех значений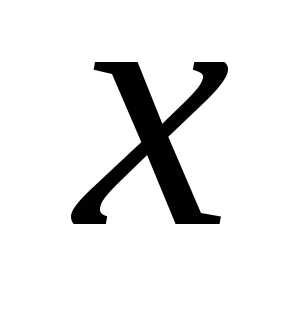 ,
близких к
,
близких к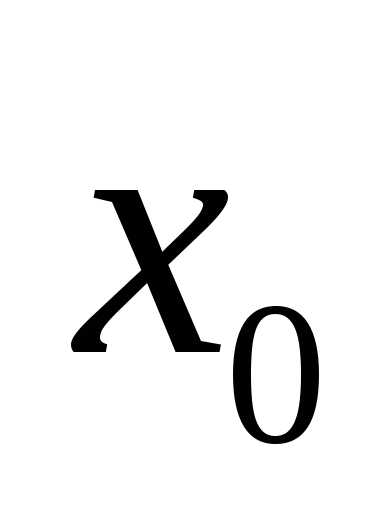 .
.
Определение.
Постоянное число А называется пределом функции f(x) при  ,
если, задав произвольное как угодно
малое положительное число,
можно найти такое
>0 (зависящее от ),
что для всех x,
лежащих в
— окрестности числа
,
если, задав произвольное как угодно
малое положительное число,
можно найти такое
>0 (зависящее от ),
что для всех x,
лежащих в
— окрестности числа 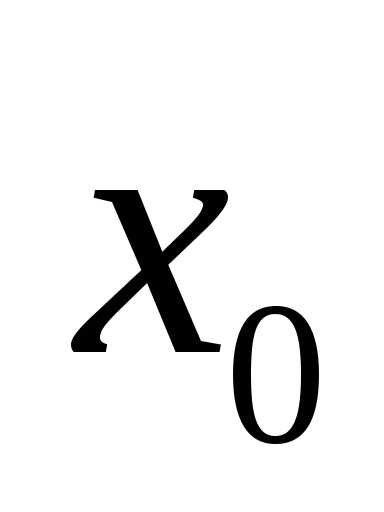 ,
т.е. дляx,
удовлетворяющих неравенству
,
значения функцииf(x) будут лежать в
— окрестности числа А, т.е.
.
,
т.е. дляx,
удовлетворяющих неравенству
,
значения функцииf(x) будут лежать в
— окрестности числа А, т.е.
.
Это определение называют определением предела функции по Коши, или “на языке — “.
На
рисунке 2.2. проиллюстрировано определение
предела функции 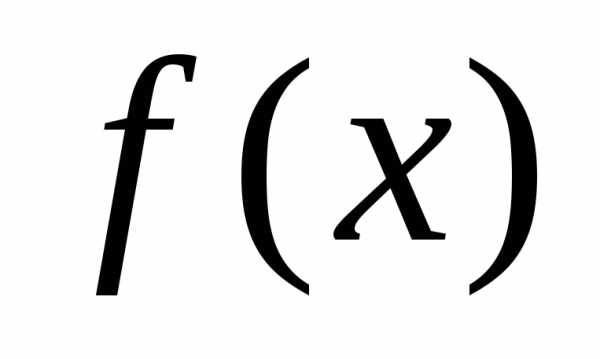 при
при .
Для построения этого рисунка необходимо
выполнить следующие действия:
.
Для построения этого рисунка необходимо
выполнить следующие действия:
построить график функции
 и отметить точки
и отметить точки иА;
иА;построить окрестность точки А, выбрав произвольное число
 ;
;по точкам
 ,
, и графику функции построить
и графику функции построить окрестность
точки
окрестность
точки .
Расстояния от точки
.
Расстояния от точки до точек
до точек и
и должны быть равными, поэтому из двух
полученных отрезков следует взять
меньший и отложить его в обе стороны
от точки
должны быть равными, поэтому из двух
полученных отрезков следует взять
меньший и отложить его в обе стороны
от точки ;
;взять произвольную точку
 ,
принадлежащую окрестности точки
,
принадлежащую окрестности точки ,
и по графику функции найти значение
,
и по графику функции найти значение ,
которое должно попасть в построенную
окрестность точкиА.
,
которое должно попасть в построенную
окрестность точкиА.
Рисунок 2.2 – Определение предела функции |
Если  и при этом
и при этом 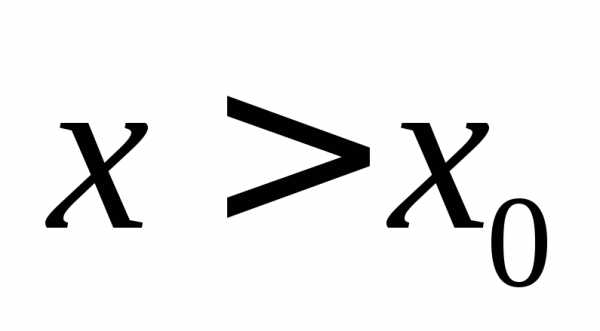 ,
то пишут .
Если, в частности,
,
то пишут .
Если, в частности,  ,
то вместо символа 0+0 пишут +0.
,
то вместо символа 0+0 пишут +0.
Аналогично
если  и при этом
и при этом 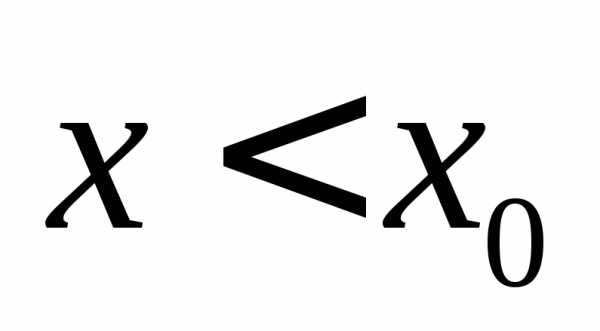 ,
то пишут .
,
то пишут .
Числа  и
и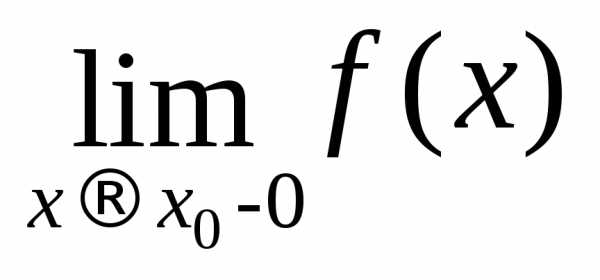 называются соответственнопределом
справа и пределом слева функции f(x) в точке
называются соответственнопределом
справа и пределом слева функции f(x) в точке 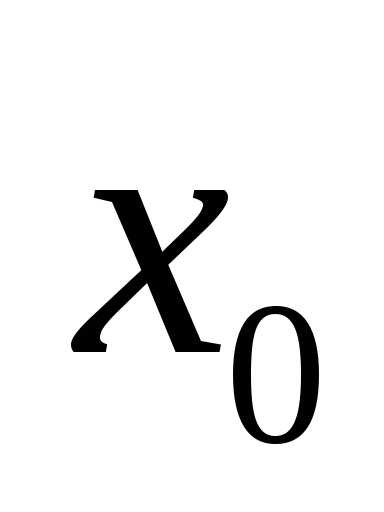 .
.
Для
существования предела функции f(x) при  необходимо и достаточно, чтобы
необходимо и достаточно, чтобы 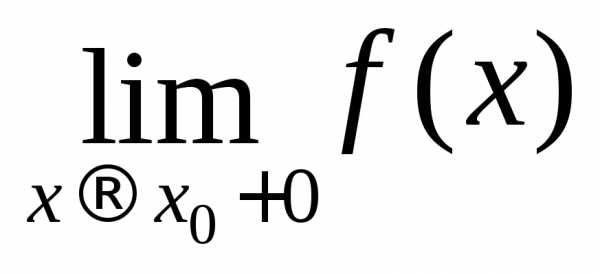 =
=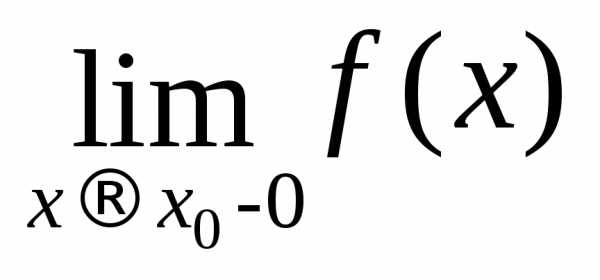 .
.
Определение. Переменная величина (т.е. последовательность или функция), имеющая своим пределом ноль, называется бесконечно малой величиной.
Определение. Переменная величина, имеющая бесконечный предел, называется бесконечно большой величиной.
2.2 Правила вычисления пределов
При вычислении пределов следует учитывать следующие основные правила:
1. Предел суммы (разности) функций равен сумме (разности) пределов слагаемых:
.
2. Предел произведения функций равен произведению пределов сомножителей:
.
3. Предел отношения двух функций равен отношению пределов этих функций:
.
4. Постоянный множитель можно выносить за знак предела:
.
5. Предел постоянной равен самой постоянной:
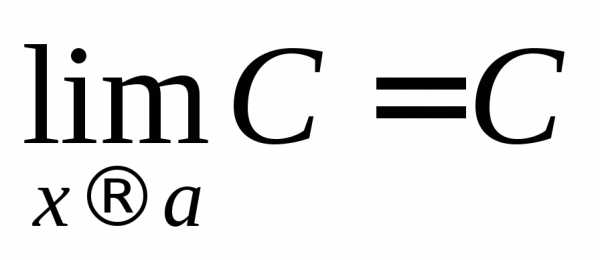 .
.
6. Для непрерывных функций символы предела и функции можно поменять местами:
.
Нахождение
предела функции 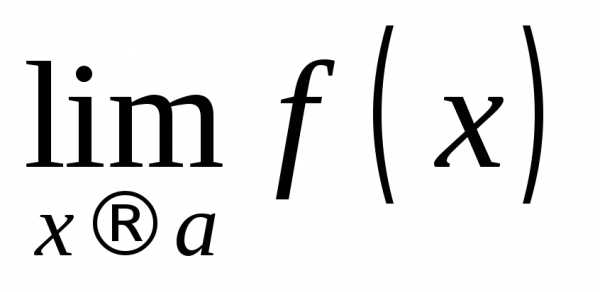 следует начинать с подстановки значения
следует начинать с подстановки значения в выражение для функции. При этом если
получается числовое значение 0 или,
то искомый предел найден.
в выражение для функции. При этом если
получается числовое значение 0 или,
то искомый предел найден.
Пример
2.1. Вычислить предел .
.
Решение.
.
Выражения
вида 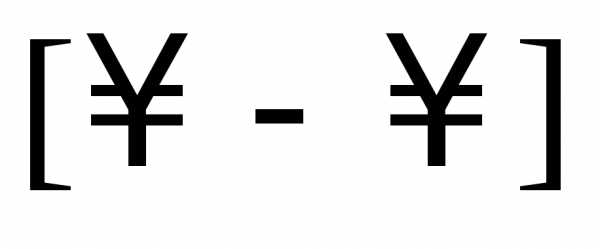 ,
,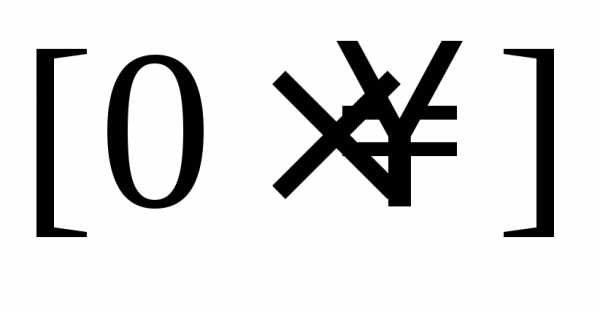 ,
, ,
, ,
, ,
,
 называютсянеопределённостями.
называютсянеопределённостями.
Если
получается неопределенность вида  ,
то для нахождения предела нужно
преобразовать функцию так, чтобы раскрыть
эту неопределенность.
,
то для нахождения предела нужно
преобразовать функцию так, чтобы раскрыть
эту неопределенность.
Неопределенность
вида  обычно получается, когда задан предел
отношения двух многочленов. В этом
случае, для вычисления предела
рекомендуется разложить многочлены на
множители и сократить на общий множитель.
Этот множитель равен нулю при предельном
значениих.
обычно получается, когда задан предел
отношения двух многочленов. В этом
случае, для вычисления предела
рекомендуется разложить многочлены на
множители и сократить на общий множитель.
Этот множитель равен нулю при предельном
значениих.
Пример
2.2. Вычислить предел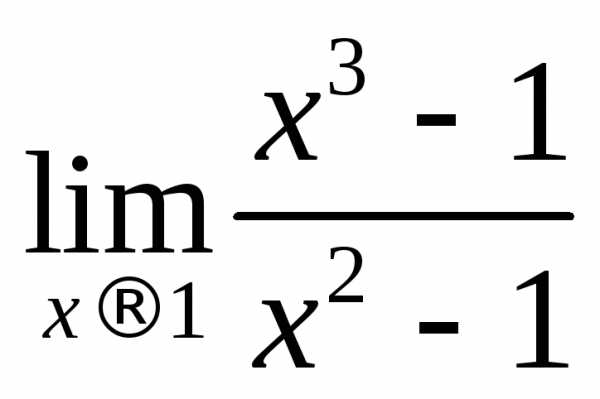 .
.
Решение.
Подставляя 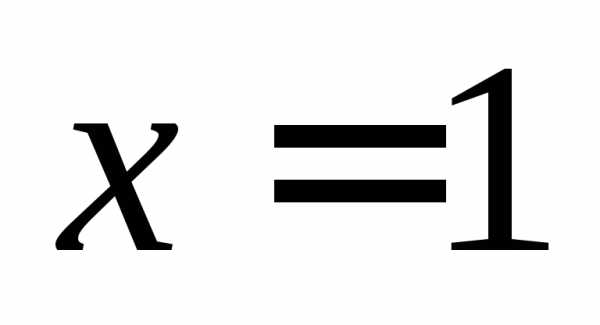 ,
получим неопределенность:
,
получим неопределенность:
.
Разложим числитель и знаменатель на множители:
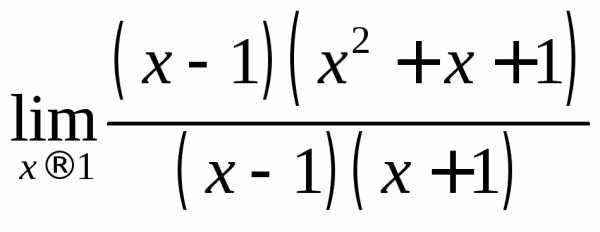 ;
;
Сократим
на общий множитель 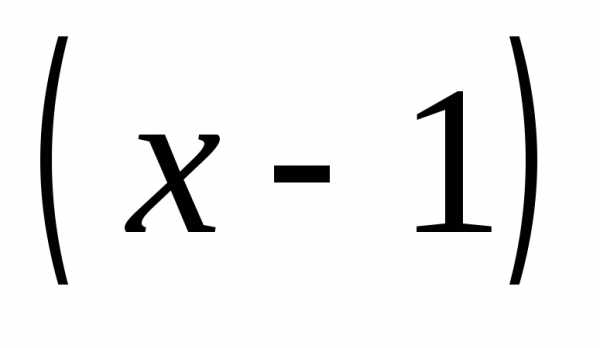 и получим
и получим
.
Неопределенность
вида  получается, когда задан предел отношения
двух многочленов при.
В этом случае для вычисления рекомендуется
разделить оба многочлена нахв старшей степени.
получается, когда задан предел отношения
двух многочленов при.
В этом случае для вычисления рекомендуется
разделить оба многочлена нахв старшей степени.
Пример
2.3.Вычислить предел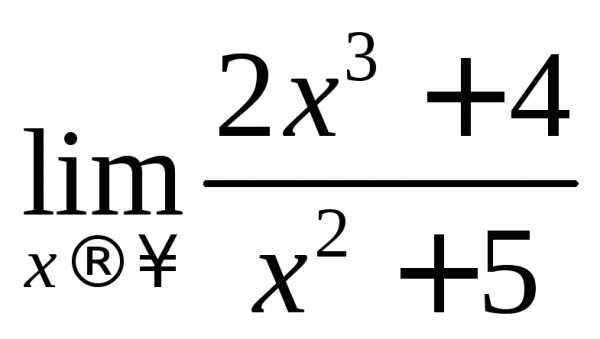 .
.
Решение. При подстановке ∞ получается
неопределенность вида ,
поэтому разделим все члены выражения
наx3.
,
поэтому разделим все члены выражения
наx3.
 .
.
Здесь
учитывается, что  .
.
При вычислении пределов функции, содержащей корни, рекомендуется умножить и разделить функцию на сопряженное выражение.
Пример
2.4. Вычислить предел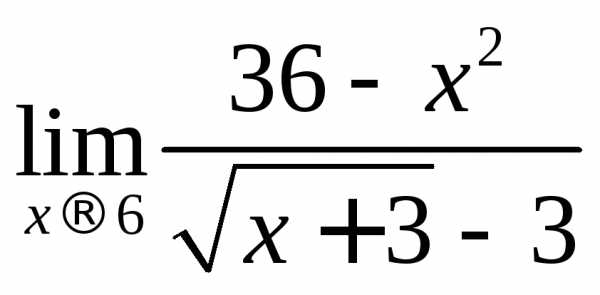
Решение.
При
вычислении пределов для раскрытия
неопределенности вида  или (1)∞часто используются первый
и второй замечательные пределы:
или (1)∞часто используются первый
и второй замечательные пределы:
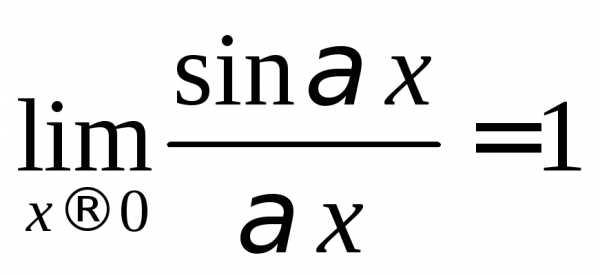
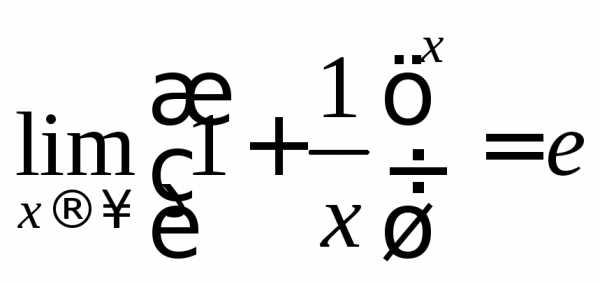 и
и 
Ко второму замечательному пределу приводят многие задачи, связанные с непрерывным ростом какой-либо величины.
Рассмотрим пример Я. И. Перельмана, дающий интерпретацию числа e в задаче о сложных процентах. В сбербанках процентные деньги присоединяются к основному капиталу ежегодно. Если присоединение совершается чаще, то капитал растет быстрее, так как в образовании процентов участвует большая сумма. Возьмем чисто теоретический, весьма упрощенный пример.
Пусть в банк положено 100 ден. ед. из расчета 100 % годовых. Если процентные деньги будут присоединены к основному капиталу лишь по истечении года, то к этому сроку 100 ден. ед. превратятся в 200 ден.ед.
Посмотрим теперь, во что превратятся 100 ден. ед., если процентные деньги присоединять к основному капиталу каждые полгода. По истечении полугодия 100 ден. ед. вырастут в 100 1,5 = 150, а еще через полгода — в 150 1,5 = 225 (ден. ед.). Если присоединение делать каждые 1/3 года, то по истечении года 100 ден. ед. превратятся в 100 (1 +1/3) 237 (ден. ед.).
Будем учащать сроки присоединения процентных денег до 0,1 года, до 0,01 года, до 0,001 года и т.д. Тогда из 100 ден. ед. спустя год получится:
100 (1 +1/10)10 259 (ден. ед.),
100 (1+1/100)100 270 (ден. ед.),
100 (1+1/1000)1000 271 (ден. ед.).
При безграничном сокращении сроков присоединения процентов наращенный капитал не растет беспредельно, а приближается к некоторому пределу, равному приблизительно 271. Более чем в 2,71 раз капитал, положенный под 100% годовых, увеличиться не может, даже если бы наросшие проценты присоединялись к капиталу каждую секунду, потому что
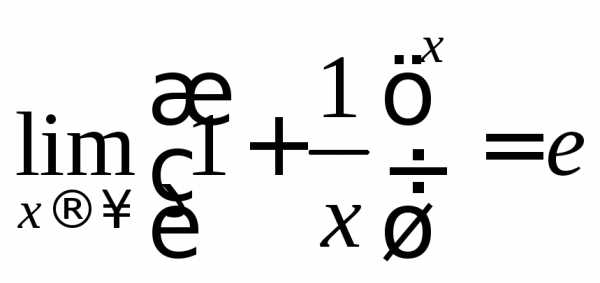
Пример
2.5. Вычислить предел функции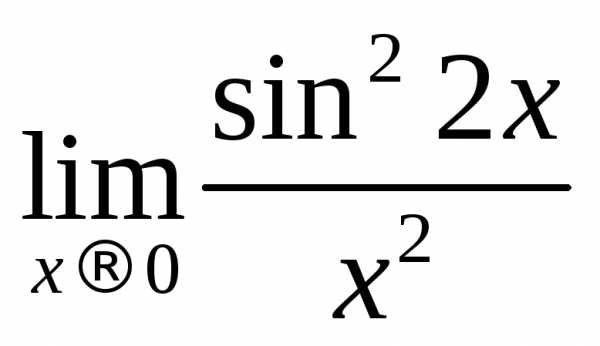
Решение.
Пример
2.6. Вычислить
предел функции 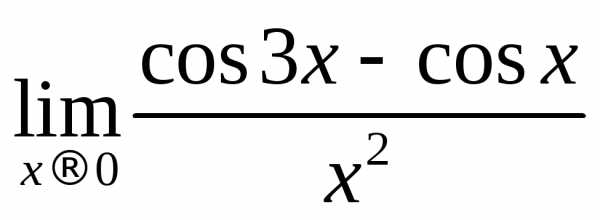 .
.
Решение. Подставляя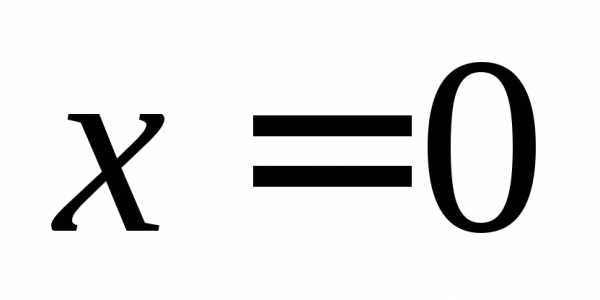 получим неопределенность:
получим неопределенность:
.
Используя тригонометрическую формулу, преобразуем числитель в произведение:
В результате получаем
Здесь
учитывается второй замечательный предел 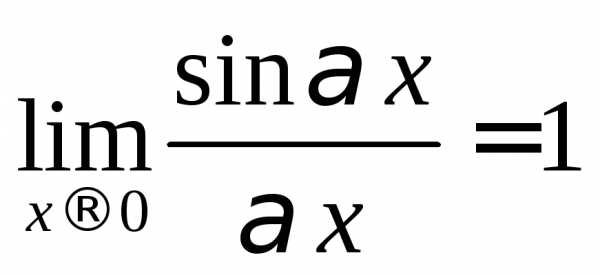 .
.
Пример
2.7. Вычислить предел функции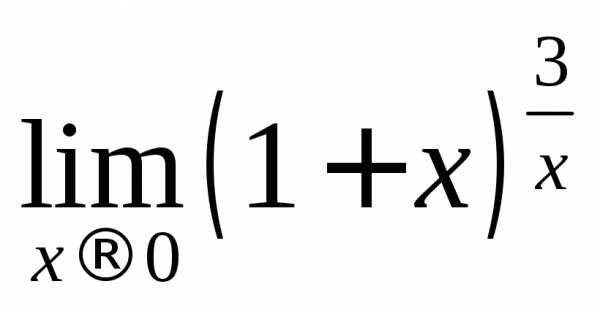
Решение.
.
Для
раскрытия неопределенности вида  или
или можно использовать правило Лопиталя,
которое основано на следующей теореме.
можно использовать правило Лопиталя,
которое основано на следующей теореме.
Теорема. Предел отношения двух бесконечно малых или бесконечно больших функций равен пределу отношения их производных
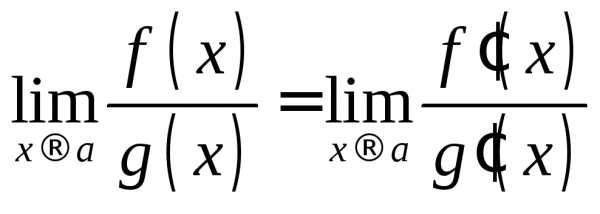
Заметим, что это правило можно применять несколько раз подряд.
Пример
2.8.Найти
Решение. При подстановке ,
имеем неопределенность вида
,
имеем неопределенность вида .
Применяя правило Лопиталя, получим
.
Применяя правило Лопиталя, получим
studfiles.net



 и отметить точки
и отметить точки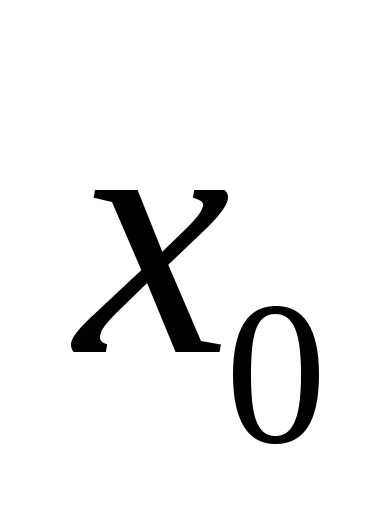 иА;
иА;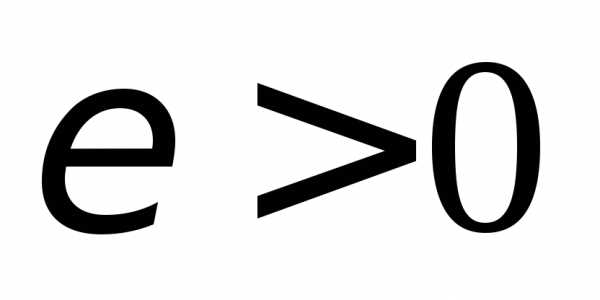 ;
;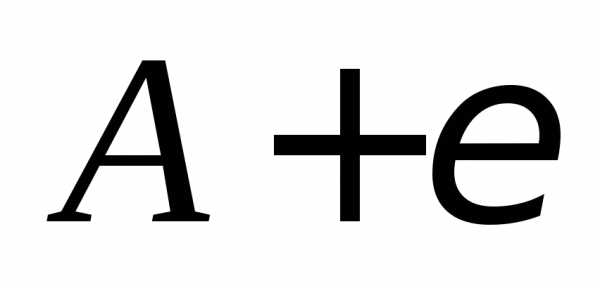 ,
,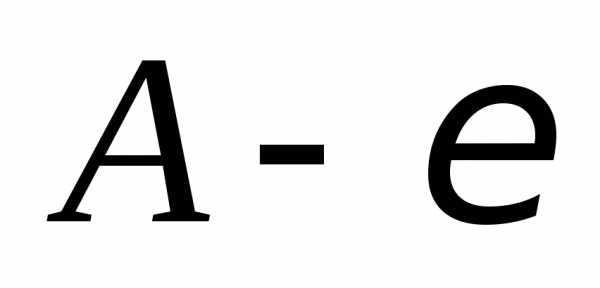 и графику функции построить
и графику функции построить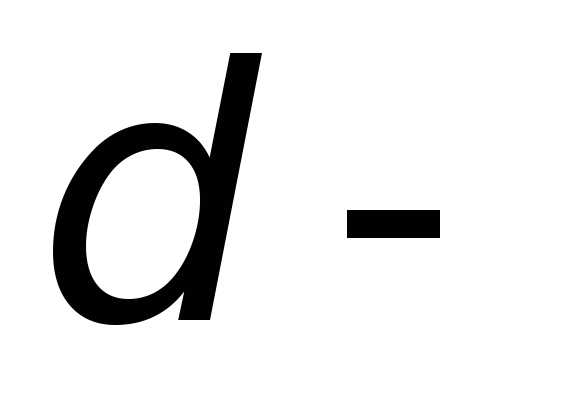 окрестность
точки
окрестность
точки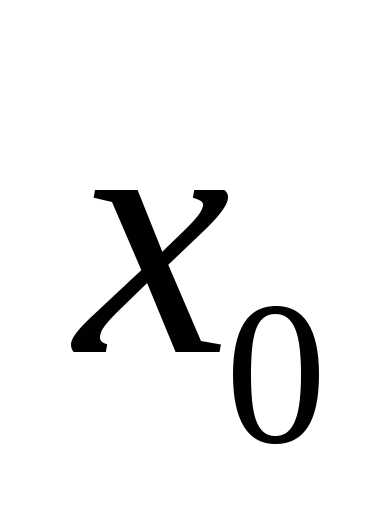 .
Расстояния от точки
.
Расстояния от точки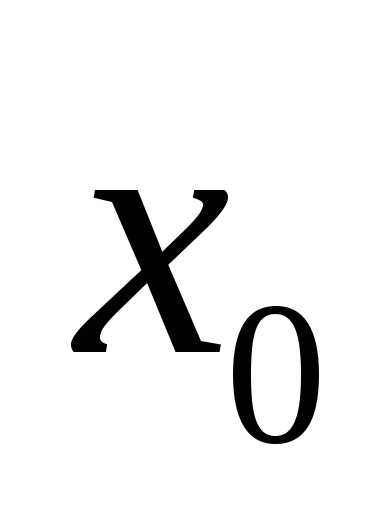 до точек
до точек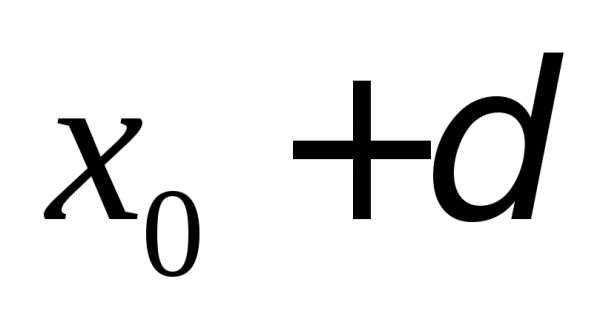 и
и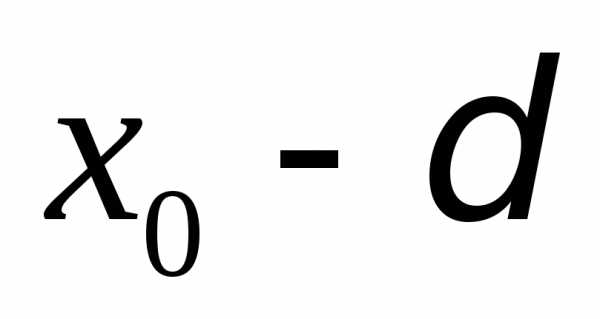 должны быть равными, поэтому из двух
полученных отрезков следует взять
меньший и отложить его в обе стороны
от точки
должны быть равными, поэтому из двух
полученных отрезков следует взять
меньший и отложить его в обе стороны
от точки ;
;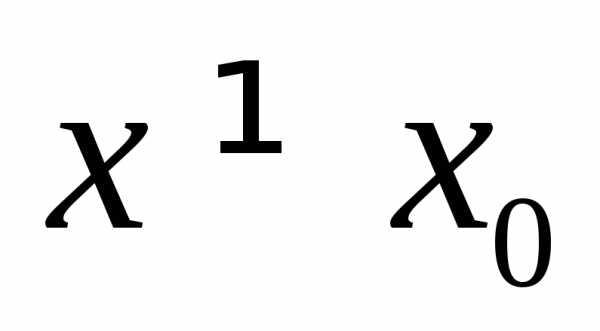 ,
принадлежащую окрестности точки
,
принадлежащую окрестности точки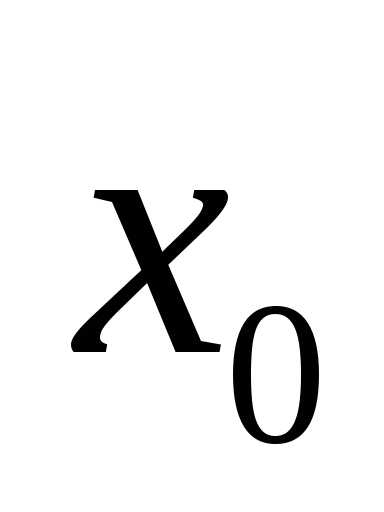 ,
и по графику функции найти значение
,
и по графику функции найти значение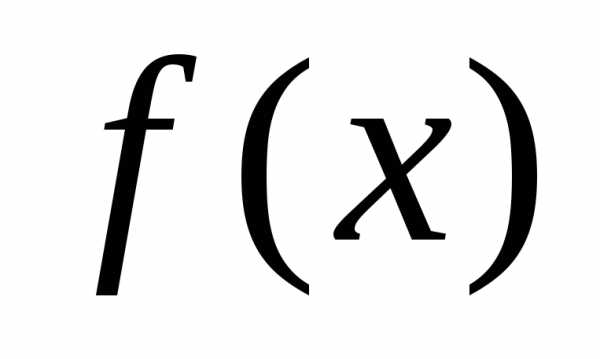 ,
которое должно попасть в построенную
окрестность точкиА.
,
которое должно попасть в построенную
окрестность точкиА.