Определение что такое график функции – Функции. Основные виды, графики, способы задания

alexxlab / / Школьная жизнь

график — это… Что такое график?

  • график — 1. ГРАФИК, а; м. [от греч. graphikos начерченный] 1. Чертёж, диаграмма и т.п., изображающие с помощью линий количественные показатели развития, состояния и т.п. чего л. Г. изменения атмосферного давления. Г. заболеваемости гриппом. Г. проведённых …   Энциклопедический словарь

  • ГРАФИК — (от греч. graphikos начертанный) 1) чертеж, применяемый для наглядного изображения зависимости какой либо величины (напр., пути) от другой (напр., времени), т. е. линия, дающая наглядное представление о характере изменения функции. График функции …   Большой Энциклопедический словарь

  • ГРАФИК — (греч.). 1) чертеж для схематического изображения движение железно дор. поездов. 2) вообще изображение особым чертежом каких либо изменяющихся величин. Словарь иностранных слов, вошедших в состав русского языка. Чудинов А.Н., 1910. ГРАФИК 1)… …   Словарь иностранных слов русского языка

  • график — а, м. graphique, dessin graphique. 1. Чертеж хода поездов. Брокг. 18. Чертеж, употребляемый на в железнодорожной службе для наглядного изображения хода поездов, их взаимного расположения при движении и выяснения пропускной способности… …   Исторический словарь галлицизмов русского языка

  • ГРАФИК — 1) расписание, определяющее последовательность выполнения действий, протекания событий во времени. Например, график движения поездов, график дежурств, график работы; 2) графическое изображение математической зависимости; математическая… …   Экономический словарь

  • ГРАФИК — ГРАФИК, графика, муж. (от греч. graphikos письменный) (спец.). Диаграмма, чертеж, изображающий посредством кривых количественные зависимости различных процессов. График движения поездов. График изменения температуры воздуха. Толковый словарь… …   Толковый словарь Ушакова

  • график — диаграмма, набросок, схема, кривая, чертёж, таблица; расписание, программа, план; табель, табуляграмма, гидрограф, годограф, синусоида, номограмма, эхограмма, ковер, рисовальщик, художник Словарь русских синонимов. график см. расписание Словарь… …   Словарь синонимов

  • ГРАФИК — ГРАФИК, в математике наглядное представление зависимости между числами или величинами. Во многих графиках используется ДЕКАРТОВА СИСТЕМА КООРДИНАТ. Обычно оси чертят под прямым углом друг к другу и наносят на них шкалу переменных величин. На… …   Научно-технический энциклопедический словарь

  • график — Чертеж, наглядно изображающий количественное соотношение и развитие взаимосвязанных процессов или явлений в виде кривой, прямой, ломаной линии, построенной в той или иной системе координат. [ГОСТ Р 7.0.3 2006] график [Лугинский Я. Н. и др. Англо… …   Справочник технического переводчика

  • График — А. Изображение в виде кривой изменения функции при изменении аргумента для математической, физической или другой зависимости. Б. Таблица, расписание последовательности выполнения событий, действий. Словарь бизнес терминов. Академик.ру. 2001 …   Словарь бизнес-терминов

  • ГРАФИК 1 — ГРАФИК 1, а, м. Толковый словарь Ожегова. С.И. Ожегов, Н.Ю. Шведова. 1949 1992 …   Толковый словарь Ожегова

    • dic.academic.ru

    График функции — Википедия. Что такое График функции

    Материал из Википедии — свободной энциклопедии

    График функции — понятие в математике, которое даёт представление о геометрическом образе функции.

    Наиболее наглядны графики вещественнозначных функций вещественного переменного.

    В этом случае, график функции — это геометрическое место точек плоскости, абсциссы (x) и ординаты (y) которых связаны указанной функцией:

    точка (x,y){\displaystyle (x,y)} располагается (или находится) на графике функции f{\displaystyle f} тогда и только тогда, когда y=f(x){\displaystyle y=f(x)}.

    Таким образом, функция может быть адекватно описана своим графиком.

    Из определения графика функции следует, что далеко не всякое множество точек плоскости может быть графиком некоторой функции: никакая прямая, параллельная оси ординат, не может пересекать график функции более чем в одной точке. Если функция обратима, то график обратной функции (как подмножество плоскости) будет совпадать с графиком самой функции (это, попросту, одно и тоже подмножество плоскости).

    График гладкой (требуемое количество раз дифференцируемой функции) является плоской кривой той же степени гладкости.

    При рассмотрении отображения произвольного вида f:X→Y{\displaystyle f:X\to Y}, действующего из множества X{\displaystyle X} в множество Y{\displaystyle Y}, графиком функции называется следующее множество упорядоченных пар:

    Γf={(x,f(x))∈X×Y∣x∈X}.{\displaystyle \Gamma _{f}=\{\,(x,f(x))\in X\times Y\mid x\in X\,\}.}

    В частности, при рассмотрении динамических систем, изображающая точка

    (t,f(t)){\displaystyle (t,f(t))},

    представляет собою график решения соответствующего дифференциального уравнения.

    Примеры

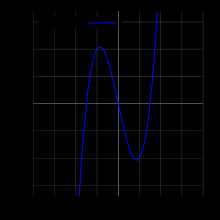    График f(x)=x3−9x{\displaystyle f(x)=x^{3}-9x}
    • График кубического многочлена вещественной переменной
      f(x)=x3−9x{\displaystyle f(x)={{x^{3}}-9x}}
    это множество
    {(x,x3−9x)∈R2 |x∈R}{\displaystyle \{(x,x^{3}-9x)\in \mathbb {R} ^{2}\ |x\in \mathbb {R} \}}.
    • График функции
      f(x)={a,x=1d,x=2c,x=3.{\displaystyle f(x)=\left\{{\begin{matrix}a,&x=1\\d,&x=2\\c,&x=3.\end{matrix}}\right.}
    это множество из трёх точек {(1,a), (2,d), (3,c)}.

    См. также

    Литература

    Ссылки

    wiki.sc

    Понятия функции и ее графика

    § Функцией, определенной на множестве X, называют закон f, который каждой точке x Î X ставит в соответствие некоторую единственную точку y Î Y. При этом множество X называют областью определения функции f (обозначают D(f) или D(y)), точку x Î X – аргументом функции, точку y Î Y, соответствующую x, – значением функции в точке x и обозначают y = f(x). Множество Y называют областью значений функции f (обозначают E(y)).

     
     

     

     

    Если элементами X и Y являются действительные числа, то функцию f называют числовой функцией.

    § Множество точек плоскости с координатами (x,f(x)), x Î X называют графиком функции f.

    Не для всякой функции график будет линией в обычном представлении, например определяет лишь одну точку (0,0) на координатной плоскости.

    9.2. Способы задания функций

    Для изучения функции ее необходимо задать, т.е. указать правило, позволяющее по значению аргумента функции находить соответствующее ему значение функции. Это правило можно указать различными способами. К таким способам можно отнести аналитический, параметрический, графический, табличный, алгоритмический и описательный.

    Мы будем, в основном, изучать числовые функции, т.е. функции, у которых область определения и множество значений являются числовыми множествами. Числовые функции чаще всего задаются аналитическим способом, т.е. при помощи формул. Например, , , . Если уравнение, с помощью которого задается функция не разрешено относительно y, то функция называется неявной. Так, известное со школы уравнение окружности с центром в точке не разрешено относительно и является уравнением неявной функции.

    Иногда числовые функции на различных числовых промежутках задаются различными формулами. Такова, например, функция

    Когда зависимость y от x не задана непосредственно, а вместо этого даны зависимости обоих переменных x и y от некоторого третьего вспомогательного переменного t в виде

    , где ,

    то это – параметрический способ задания функции; тогда вспомогательное переменное t называют параметром.

    При графическом способе задания функции зависимость y от x задают при помощи линии на плоскости x0y.

    Табличный способ задания функции, это способ, когда некоторые значения аргумента и соответствующие им значения функции в определенном порядке размещаются в таблице. Например, тригонометрические функции представлены таблицами Брадиса. В виде таблицы обычно представляют экспериментальные зависимости. Недостаток этого способа состоит в невозможности непосредственного определения значений функции, не входящих в таблицу.

    Алгоритмический способ задания функции широко используют при вычислениях на ЭВМ.

    Описательный (или словесный) способ задания функции – это способ, при котором правило соответствия значений функции значениям аргумента выражено словами. Например, функцию, которая каждому числу ставит в соответствие целую часть этого числа , можно задать следующим образом: «значением функции является наибольшее целое число, не превосходящее х».

    Некоторые свойства функций

    ü Функция , определяемая на множестве D является четной, если выполняются условия и ; нечетной, если выполняются условия и . График четной функции симметричен относительно оси ординат, а график нечетной функции симметричен относительно начала координат.

    ü Функция определена на множестве D и пусть . Если для любых значений : , то функция называется возрастающей на множестве ; , то функция называется убывающей на множестве ; , то функция называется неубывающей на множестве ; , то функция называется невозрастающей на множестве . Возрастающие, убывающие, неубывающие, невозрастающие функции на называются монотонными на этом множестве, а возрастающие и убывающие – строго монотонными. Интервалы, в которых функция монотонна называются интервалами монотонности.

    ü Функцию , определенную на множестве D, называют ограниченной на этом множестве, если существует такое число , что для всех выполняется неравенство . График ограниченной функции лежит между прямыми и .

    ü Функцию , определенную на множестве D, называют периодической на этом множестве, если существует такое число , что при каждом значение и . Число называется периодом функции.

    Обратная функция

    Пусть задана функция с областью определения D и множеством значений E. Если каждому значению соответствует единственное значение , то определена функция с областью определения E и множеством значений D. Такая функция называется обратной к функции .

    Из определения обратной функции вытекает, что функция имеет обратную тогда и только тогда, когда каждому соответствует единственное и наоборот, то есть когда функция задает взаимнооднозначное соответствие между множествами и . Тогда всякая строго монотонная функция имеет обратную, при этом если функция возрастает (убывает), то обратная функция также возрастает (убывает).

    Графики взаимно обратных функций симметричны относительно биссектрисы первого и третьего координатных углов.


    

    infopedia.su

    Что называют графиком функции?

    Графиком функции называется множество всех точек координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты — соответствующим значениям функции.

    В следующей таблице указаны средние месячные температуры в столице нашей страны городе Минске.

    п

    I

    II

    III

    IV

    V

    VI

    vn

    VIII

    IX

    X

    XI

    хп

    t,V

    -6,9

    -6,4

    -2,2

    5,3

    12,6

    16,0

    17,8

    16,2

    U,6

    5,6

    0,0

    -4,5

    Здесь аргументом является порядковый номер месяца, а значением функции — температура воздуха в градусах Цельсия. Например, из этой таблицы мы узнаем, что в апреле среднемесячная температура составляет 5,3 °С.

    Функциональная зависимость может быть задана графиком.

    На рисунке рис 1 представлен график движения тела, брошенного под углом 6СГ к горизонту с начальной скоростью 20 м/с.

    С помощью графика функции можно по значению аргумента найти соответствующее значение функции. По графику на рисунке 1 определяем, что, например, через 2 с от начала движения тело находилось на высоте 15 м, а через 3 с на высоте 7,8 м (рис. 2).

    Можно также решить и обратную задачу, именно по данному значению а функции найти те значения аргумента, при которых функция принимает это значение а. Например, по графику на рисунке 1 находим, что на высоте 10 м тело находилось через 0,7 с и через 2,8 с от начала движения (рис. 3),

    Есть приборы, которые вырисовывают графики зависимостей между величинами. Это барографы — приборы для фиксации зависимости атмосферного давления от времени, термографы — приборы для фиксации зависимости температуры от времени, кардиографы — приборы для графической регистрации деятельности сердца и др. На рисунке 102 схематически изображен термограф. Его барабан равномерно вращается. Бумаги, намотанной на барабан, касается самописец, который в зависимости от температуры поднимается и опускается и вырисовывает на бумаге определенную линию.

    От представления функции формулой можно перейти к ее представлению таблицей и графиком.

    belmathematics.by

    График функции Википедия

    График функции — понятие в математике, которое даёт представление о геометрическом образе функции.

    Наиболее наглядны графики вещественнозначных функций вещественного переменного.

    В этом случае, график функции — это геометрическое место точек плоскости, абсциссы (x) и ординаты (y) которых связаны указанной функцией:

    точка (x,y){\displaystyle (x,y)} располагается (или находится) на графике функции f{\displaystyle f} тогда и только тогда, когда y=f(x){\displaystyle y=f(x)}.

    Таким образом, функция может быть адекватно описана своим графиком.

    Из определения графика функции следует, что далеко не всякое множество точек плоскости может быть графиком некоторой функции: никакая прямая, параллельная оси ординат, не может пересекать график функции более чем в одной точке. Если функция обратима, то график обратной функции (как подмножество плоскости) будет совпадать с графиком самой функции (это, попросту, одно и то же подмножество плоскости).

    График гладкой (требуемое количество раз дифференцируемой функции) является плоской кривой той же степени гладкости.

    При рассмотрении отображения произвольного вида f:X→Y{\displaystyle f:X\to Y}, действующего из множества X{\displaystyle X} в множество Y{\displaystyle Y}, графиком функции называется следующее множество упорядоченных пар:

    Γf={(x,f(x))∈X×Y∣x∈X}.{\displaystyle \Gamma _{f}=\{\,(x,f(x))\in X\times Y\mid x\in X\,\}.}

    В частности, при рассмотрении динамических систем, изображающая точка

    (t,f(t)){\displaystyle (t,f(t))},

    представляет собою график решения соответствующего дифференциального уравнения.

    Примеры

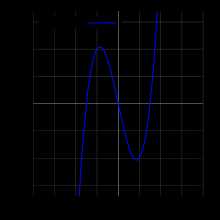    График f(x)=x3−9x{\displaystyle f(x)=x^{3}-9x}
    • График кубического многочлена вещественной переменной
      f(x)=x3−9x{\displaystyle f(x)={{x^{3}}-9x}}
    это множество
    {(x,x3−9x)∈R2 |x∈R}{\displaystyle \{(x,x^{3}-9x)\in \mathbb {R} ^{2}\ |x\in \mathbb {R} \}}.
    • График функции
      f(x)={a,x=1d,x=2c,x=3.{\displaystyle f(x)=\left\{{\begin{matrix}a,&x=1\\d,&x=2\\c,&x=3.\end{matrix}}\right.}
    это множество из трёх точек {(1,a), (2,d), (3,c)}.

    См. также

    Литература

    Ссылки

    wikiredia.ru

    Что такое ФУНКЦИЯ?? ? (Геометрия, график функции)

    В помощь <a href=»/» rel=»nofollow» title=»20521730:##:»>[ссылка заблокирована по решению администрации проекта]</a>

    Аргумент — независимая переменная (х) , функция — зависимая от аргумента переменная (y).

    Ф? УНКЦИЯ, в математике — 1) зависимая переменная величина. 2) Соответствие y = f ( x) между переменными величинами, в силу которого каждому рассматриваемому значению некоторой величины x (аргумента, или независимого переменного) соответствует определенное значение другой величины y (зависимой переменной, или функции) . Такое соответствие может быть задано различным образом, напр. формулой, графически или таблицей (типа таблицы логарифмов) . С помощью функции математически выражаются многообразные количественные закономерности в природе.

    <a rel=»nofollow» href=»http://ru.wikipedia.org/wiki/Функция_(математика)» target=»_blank» >Ссылка на википедию</a> здесь правильно дается определение Функция f (отображение, операция, оператор) — это закон или правило, согласно которому каждому [3] элементу x из множества X ставится в соответствие единственный элемент y из множества Y.[4] При этом говорят, что функция f задана на множестве X, или что f отображает X в Y. внизу ссылкка на график функции <a rel=»nofollow» href=»http://ru.wikipedia.org/wiki/График_функции» target=»_blank» >ссылка</a>

    Проще говоря- это зависимость одной величины от другой. Например: у = 3х если х = -1, то у = -3 усли х = 0, то у = 0, если х=+1, то у = 3 то есть величина у зависит от х, поэтому и говорят «у есть функция от х»

    touch.otvet.mail.ru

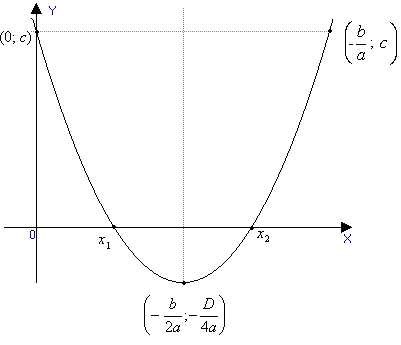
    Функции и Графики — сайт по математике и не только!!! Всё о Математических функциях и их графиках…

    КВАДРАТИЧНАЯ ФУНКЦИЯ

    y = ax2 + bx + c, где a 0. График квадратичной функции — парабола.

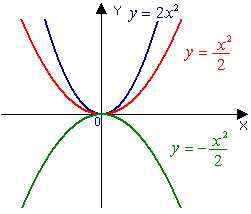
    Свойства функции и вид её графика определяются, в основном, значениями коэффициента a
    и дискриминанта D = b2 — 4ac.

    a > 0, D > 0a > 0, D = 0a > 0, D
    a D > 0a D = 0a D

    РАЗЛИЧНЫЕ ПРЕДСТАВЛЕНИЯ КВАДРАТИЧНОЙ ФУНКЦИИ

    1. ВЫДЕЛЕНИЕ ПОЛНОГО КВАДРАТА:
    2. РАЗЛОЖЕНИЕ НА ЛИНЕЙНЫЕ МНОЖИТЕЛИ при D > 0 y = ax2 + bx + c = a(x — x1)(x — x2) при D = 0 y = ax2 + bx + c = a(x — x1)2 при D
    СВОЙСТВА КВАДРАТИЧНОЙ ФУНКЦИИ НАПРАВЛЕНИЕ ВЕТВЕЙ, ХАРАКТЕРНЫЕ ТОЧКИ И ОСЬ СИММЕТРИИ ПАРАБОЛЫ,
    являющейся графиком функции у = ax2 + bx + c
    • Направление ветвей параболы: при a > 0 ветви направлены вверх при a
    • Координаты вершины параболы: (-b/2a; —D/4a)
    • Ось симметрии параболы — прямая
    • Точки пересечения (касания) графика с осью х: D > 0: (точки пересечения) D = 0: x1 = — b/(2a) (точка касания) D х нет
    • Точка пересечения графика с осью у:(0,c), симметричная ей точка относительно параболы (-b/a;c)
    Для построения графика квадратичной функции можно использовать некоторые из указанных характеристик. Например, если уравнение ax2 + bx + c = 0 имеет два корня, удобно использовать координаты вершины параболы и координаты двух точек пересечения параболы с осью х. ПОСТРОЕНИЕ ГРАФИКА КВАДРАТИЧНОЙ ФУНКЦИИ ПО НАПРАВЛЕНИЮ ВЕТВЕЙ, ХАРАКТЕРНЫМ ТОЧКАМ И ОСИ СИММЕТРИИ ПАРАБОЛЫ Примеры:
    ПОСТРОЕНИЕ ГРАФИКА КВАДРАТИЧНОЙ ФУНКЦИИ С ПОМОЩЬЮ ЭЛЕМЕНТАРНЫХ ПРЕОБРАЗОВАНИЙ ГРАФИКА ФУНКЦИИ y = x2 С помощью выделения полного квадрата любую квадратичную функцию можно представить в виде:
    Это свойство позволяет построить график квадратичной функции с помощью элементарных преобразований графика функции y = x2. Построение графика y = a(x — m)2 + n можно произвести в три этапа: Результат преобразования: график функции y = a(x — m)2+n

    Примеры:

    1. Растяжение графика функции y = x 2 вдоль оси y в 2 раза2. Параллельный перенос графика функции y = 2x 2 вдоль оси x на 3 вправоПараллельный перенос графика функции
    y = 2(x — 3)2 вдоль оси y на 1 вверх.
    1. Сжатие графика функции y = x 2 вдоль оси y в 2 раза и преобразование симметрии относительно оси x2. Параллельный перенос графика функции y = — x 2 вдоль оси x на 2 влевоПараллельный перенос графика функции
    y = — (x + 2)2/ 2
    Используются технологии uCoz

    fgraphiks.narod.ru

    No related posts.

    Добавить комментарий

    Ваш адрес email не будет опубликован. Обязательные поля помечены *