Лекция по высшей математике «Мнимая единица. Алгебраическая форма комплексного числа»
Тема: Мнимая единица, ее степени. Комплексные числа.
Алгебраическая форма комплексного числа.
Цели: расширить понятие числа, ввести понятие мнимой единицы и ее степеней, понятие комплексного числа; рассмотреть алгебраическую форму комплексного числа; развивать умения обобщать полученные знания, способствовать развитию логического мышления;
воспитывать у обучающихся сознательное отношение к процессу обучения.
План (изучаемые вопросы)
Мнимые числа. Определение мнимой единицы. Степени мнимой единицы.
Определение комплексного числа.
Алгебраическая форма комплексного числа.
1.Мнимые числа
обозначается і; і 2= -1
Определение. Числа, которые имеют вид bі, где b — действительное число, называются
мнимыми числами.
Например: 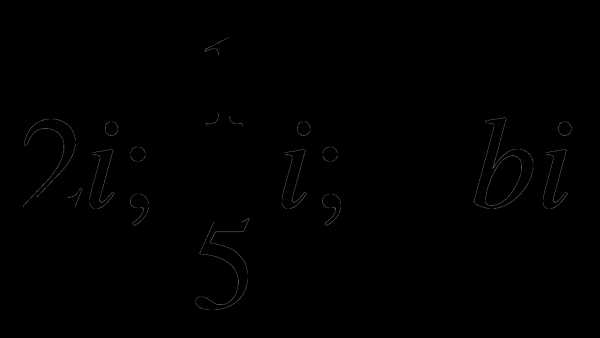
Известно, что действительные числа изображаются точками на оси ОХ. Мнимые числа изображаются точками на оси ОУ, в связи с чем ось ОХ называется действительной осью, а ось ОУ — мнимой осью. Множество мнимых чисел находится во взаимно однозначном соответствии с множеством действительных чисел.
Определение. Два мнимых числа b1i и b2i называются равными, если b1=b2
Определение. Мнимое число (-bi) называется противоположным мнимому числу bі.
Например: 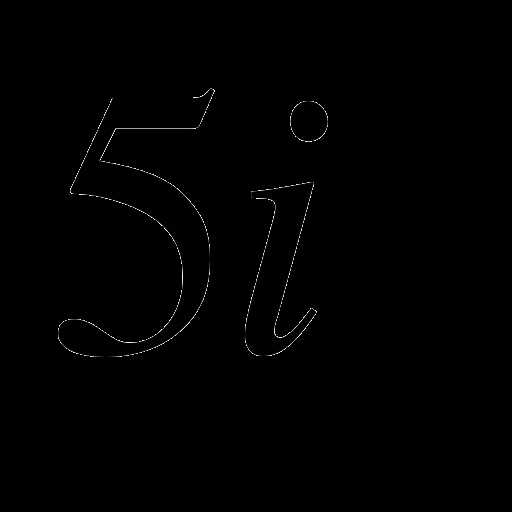 и
и 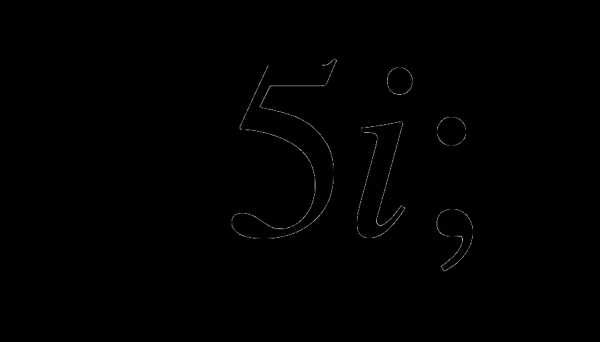
 и
и 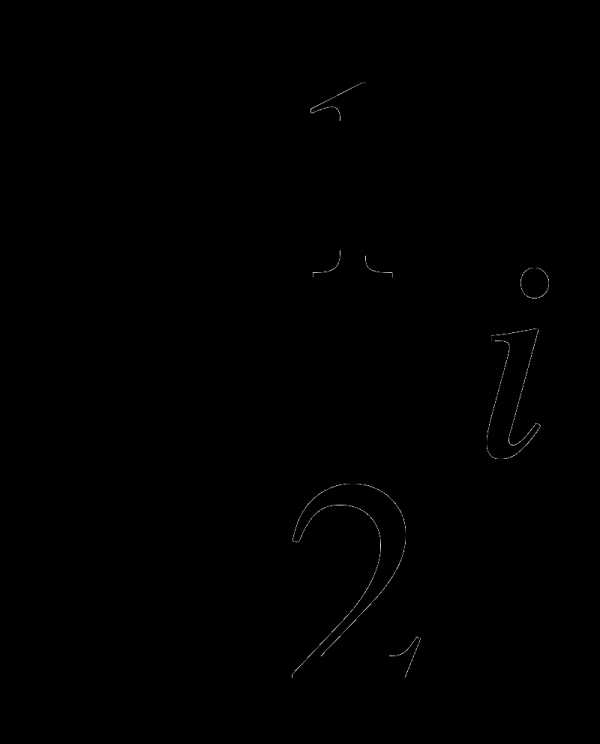 .
.
Теорема. Любая натуральная степень числа і может быть преобразована к
одной из четырех видов 1; і; -1; -і.
Доказательство.
Рассмотрим выражение іm, где m — натуральное число. Понятно, что возможны четыре случая:
1) m = 4k, k=1,2,…
3) m 4k +2, k = 0,1,2,…
4) m=4k+3, k=0,1,2,….
Пусть m = 4k, тогда ім=іАк=(іА) к=1к =1
Пусть m=4k +1, тогда ім = іАк+1 = іАк і=1і=і
Пусть m= 4k +2, тогда ім=іАк+2 = іАк і 2 =1(-1)=-1
Пусть m=4k+3, тогда ім
Пример. Вычислить значение выражения
Решение:
.
Замечание. Для того, чтобы вычислить степень мнимой единицы, удобно пользоваться таким правилом:
1) разделить показатель степени на 4;
2) заменить ім на ір, где р — остаток, полученный при делении т на 4, то есть число р находится из равенства т = 4к + р.
2.Комплексные числа
Определение. Комплексным числом называется число, которое имеет вид а+bi, где а, b –
действительные числа, i — мнимая единица. При этом число «а» называется
действительной частью комплексного числа, «b» — мнимой частью
комплексного числа.
Символически действительную и мнимую части комплексного числа обозначают так: (ре зет), (им зет).
В основе этих обозначений использованы первые буквы латинских слов , что означает «действительный» и «Imaginaries», что означает «мнимый».
Замечание. Иногда мнимой частью комплексного числа z= а+ bі называют bi.
Определение. Два комплексных числа Z1 = a1 + b1i и z2 = а2 + b1i называются равными, если
Re z1 = Re z2, Im z1 = Im z2.
Для комплексных чисел не существует понятий больше и меньше, то есть комплексные числа не сравнимы.
Определение. Комплексное число (-а-bi) называется противоположным комплексному числу
а + bі.
Определение. Два комплексных числа, у которых действительные части равны, а мнимые
части противоположные, называются комплексно сопряженными числами и
обозначаются соответственно и .
3.Алгебраическая форма комплексного числа. Действия над комплексными числами, заданными в алгебраической форме.
Комплексное число, представленное в виде называется комплексным числом в алгебраической форме.
Сложение комплексных чисел
Определение. Суммой двух комплексных чисел и называется
комплексное число .
Итак, (1)
Таким образом, чтобы сложить два комплексных числа нужно сложить их действительные части, и это дает действительную часть суммы, и сложить мнимые части, что дает мнимую часть суммы.
Сумма сопряженных чисел всегда является действительным числом
то есть, . (2)
Вычитание комплексных чисел
Определение. Разностью двух комплексных чисел и называется такое
комплексное число , которое в сумме с числом 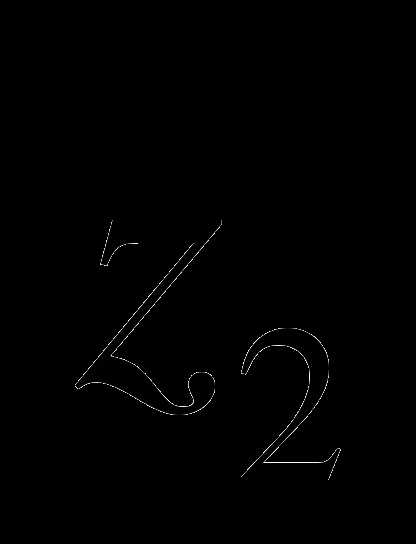 дает число
дает число  .
.
Вычитание комплексных чисел всегда возможно.
Теорема. Для любых комплексных чисел и всегда существует разница , которая определена однозначно.
Таким образом, для того, чтобы вычесть комплексные числа, достаточно вычесть их действительные части и их разницу взять за действительную часть разности, а также вычесть мнимую часть разности
Получается, (3)
Разность двух сопряженных чисел всегда является мнимым числом. ,
то есть, (4)
Умножение комплексных чисел
Определение. Произведением двух комплексных чисел и называется такое комплексное число, которое определяется формулой: (5)
Чтобы умножить комплексные числа следует умножить их по правилу умножения многочленов, заменив при этом 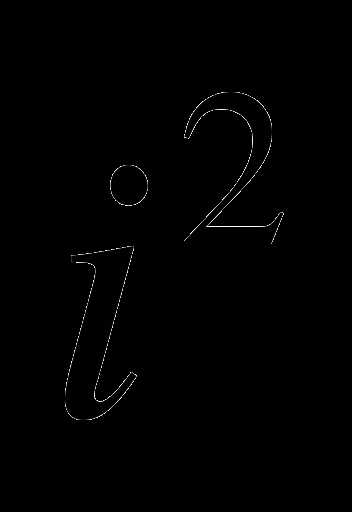 на -1 и привести подобные члены.
на -1 и привести подобные члены.
В процессе умножения комплексных чисел лучше выполнять непосредственное умножение. Произведение сопряженных чисел всегда является действительным числом
. 
Пример. Найти значение выражения .
Решение: .
.
Деление комплексных чисел
Определение. Частным двух комплексных чисел и называется такое
комплексное число z, которое в произведении с 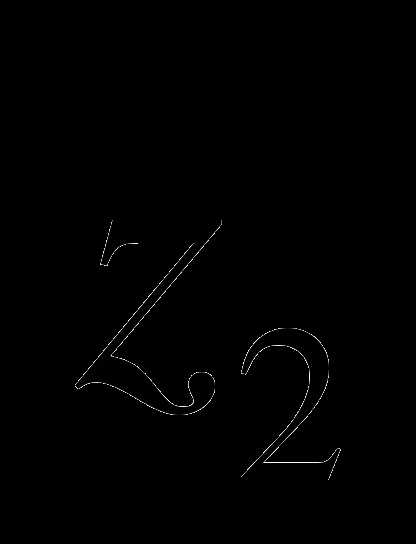 дает
дает  .
.
Всегда существует частное от деления двух комплексных чисел, если знаменатель отличается от нуля.
Теорема. Частное 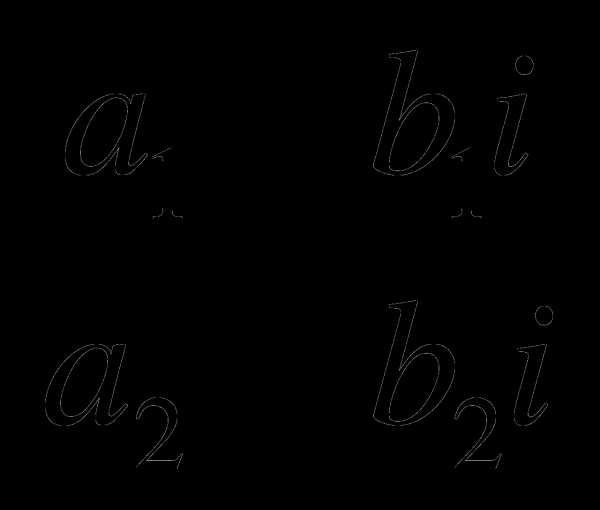 определено и к тому же однозначно для всех комплексных чисел
определено и к тому же однозначно для всех комплексных чисел  и
и  , если только , то есть .
, если только , то есть .
(7)
Пример. Вычислить значение выражения 
Решение:
Над комплексными числами в алгебраической форме возможно выполнять и такие действия, как возведение в степень, извлечения корня. Но выполнение этих действий в алгебраической форме довольно трудоемкое.
Закрепление изученного материала.
1. Вычислить:
2. Среди приведенных примеров укажите :
а) чисто мнимые комплексные числа;
б) чисто действительные комплексные числа;
в) сопряженные комплексные числа;
г) равные комплексные числа:
3. Выполнить действия:  Ответ.
Ответ. 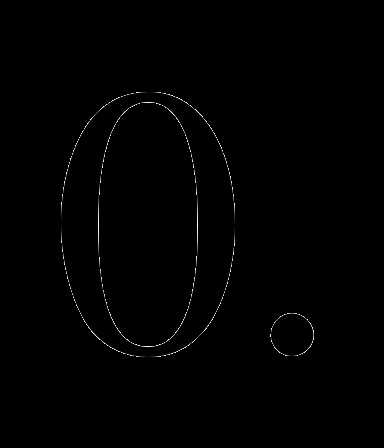
4. На основании равенства комплексных чисел найти действительные числа
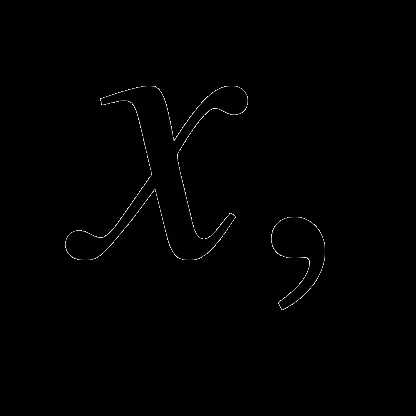 и
и если Ответ.
если Ответ. 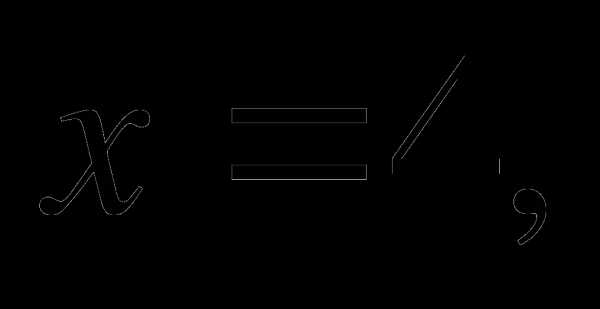

5. Решить квадратные уравнения и проверить выполнение теоремы Виета:
а) б) Ответ. а)  б)
б)
Контрольные вопросы:
1.Дать определение комплексного числа.
2.Сформулировать определение мнимой единицы.
3.Как найти степень мнимой единицы.
4.Какие комплексные числа называют равными, сопряженными?
5.Записать формулу для нахождения произвольного степени мнимой единицы.
6. Приведите примеры чисто мнимых чисел.
7. Дать определение суммы, произведения и частного двух комплексных чисел.
Литература
Письменный, Д. Т. Конспект лекций по высшей математике: полный курс Д. Т. Письменный. – 9-е изд. – М.: Айрис-пресс, 2009. 608 с.: ил. – (Высшее образование).
Лунгу, К. Н. Сборник задач по высшей математике. 1 курс / К. Н. Лунгу, Д. Т. Письменный, С. Н. Федин, Ю. А. Шевченко. – 7-е изд. – М.: Айрис-пресс, 2008. 576 с.: – (Высшее образование).
Григорьев В. П. Элементы высшей математики: учебник для студ. учреждений сред. проф. образования / В. П. Григорьев, Ю. А. Дубинский. – 10-е изд., стер. – М. Издательский центр «Академия», 2014. – 320 с.
infourok.ru
Мнимая единица — WiKi

Мни́мая едини́ца — комплексное число, квадрат которого равен −1 (минус единице). Термин может употребляется также в обобщённом смысле не только для комплексных чисел[⇨].
В математике, физике мнимая единица обозначается как латинская i{\displaystyle i} или j{\displaystyle j}. Она позволяет расширить поле вещественных чисел до поля комплексных чисел. Точное определение зависит от способа расширения.
Причиной введения мнимой единицы является то, что не каждое полиномиальное уравнение f(x)=0{\displaystyle f(x)=0} с вещественными коэффициентами имеет решения в поле вещественных чисел. Так, уравнение x2+1=0{\displaystyle x^{2}+1=0} не имеет вещественных корней. Однако оказывается, что любое полиномиальное уравнение с комплексными коэффициентами имеет комплексное решение — «Основная теорема алгебры».
Исторически мнимая единица сначала была введена для решения вещественного кубического уравнения: нередко, при наличии трёх вещественных корней, для получения двух из них формула Кардано требовала брать кубический корень в комплексных числах.
Утверждение, что мнимая единица — это «квадратный корень из −1», не совсем точно: ведь «−1» имеет два квадратных корня, один из которых можно обозначить как «i», а другой как «−i». Какой именно корень принять за мнимую единицу — неважно: все равенства сохранят силу при одновременной замене всех «i» на «-i» и «-i» на «i». Однако из-за этой двусмысленности, чтобы избежать ошибочных выкладок, не следует применять обозначение для i{\displaystyle i} через радикал (как −1{\displaystyle {\sqrt {-1}}}).
Определение
Мнимая единица — это число, квадрат которого равен −1. Т.е. i{\displaystyle i} — это одно из решений уравнения
- x2+1=0,{\displaystyle x^{2}+1=0,} или x2=−1.{\displaystyle x^{2}=-1.}
И тогда его вторым решением уравнения будет −i{\displaystyle -i} , что проверяется подстановкой.
Степени мнимой единицы
Факториал
Факториал мнимой единицы i можно определить как значение гамма-функции от аргумента 1 + i:
- i!=Γ(1+i)≈0.4980−0.1549i.{\displaystyle i!=\Gamma (1+i)\approx 0.4980-0.1549i.}
Также
- |i!|=πsinh(π)≈0.521564….{\displaystyle |i!|={\sqrt {\pi \over \sinh(\pi )}}\approx 0.521564….} [1]
Корни из мнимой единицы
 Корни квадратные из мнимой единицы
Корни кубические из мнимой единицы (вершины треугольника)
Корни квадратные из мнимой единицы
Корни кубические из мнимой единицы (вершины треугольника)В поле комплексных чисел корень n-й степени имеет n решений. На комплексной плоскости корни из мнимой единицы находятся в вершинах правильного n-угольника, вписанного в окружность с единичным радиусом.
- uk=cosπ2+2πkn+i sinπ2+2πkn,k=0,1,…,n−1{\displaystyle u_{k}=\cos {\frac {{\frac {\pi }{2}}+2\pi k}{n}}+i\ \sin {\frac {{\frac {\pi }{2}}+2\pi k}{n}},\quad k=0,1,…,n-1}
В частности, i={1+i2; −1−i2}{\displaystyle {\sqrt {i}}=\left\{{\frac {1+i}{\sqrt {2}}};\ {\frac {-1-i}{\sqrt {2}}}\right\}} и i3={−i; i+32; i−32}{\displaystyle {\sqrt[{3}]{i}}=\left\{-i;\ {\frac {i+{\sqrt {3}}}{2}};\ {\frac {i-{\sqrt {3}}}{2}}\right\}}
Также корни из мнимой единицы могут быть представлены в показательном виде:
- uk=e(π2+2πk)in,k=0,1,…,n−1{\displaystyle u_{k}=e^{\frac {({\frac {\pi }{2}}+2\pi k)i}{n}},\quad k=0,1,…,n-1}
Иные мнимые единицы
К вопросу об интерпретации и названии
| Гаусс утверждал также, что если бы величины 1, −1 и √−1 назывались соответственно не положительной, отрицательной и мнимой единицей, а прямой, обратной и побочной, то у людей не создавалось бы впечатления, что с этими числами связана какая-то мрачная тайна. По словам Гаусса, геометрическое представление дает истинную метафизику мнимых чисел в новом свете. Именно Гаусс ввел термин «комплексные числа» (в противоположность «мнимым числам» Декарта) и использовал для обозначения √−1 символ i. Морис Клайн, «Математика. Утрата определённости». Глава VII. Нелогичное развитие: серьёзные трудности на пороге XIX в. |
Обозначения
Обычное обозначение i{\displaystyle i} , но в электро- и радиотехнике мнимую единицу принято обозначать j{\displaystyle j} , чтобы не путать с обозначением мгновенной силы тока: i=i(t){\displaystyle i=i(t)} .
В языке программирования Python мнимая единица записывается как 1j.
В языке программирования Wolfram Language мнимая единица записывается как I.
См.также
Примечания
Ссылки
www.ru-wiki.org
Откуда есть пошло комплексное число / Habr
В современной математике комплексное число является одним из фундаментальнейших понятий, находящее применение и в «чистой науке», и в прикладных областях. Понятно, что так было далеко не всегда. В далекие времена, когда даже обычные отрицательные числа казались странным и сомнительным нововведением, необходимость расширения на них операции извлечения квадратного корня была вовсе неочевидной. Тем не менее, в середине XVI века математик Рафаэль Бомбелли вводит комплексные (в данном случае точнее сказать, мнимые) числа в оборот. Собственно, предлагаю посмотреть, в чем была суть затруднений, доведших в итоге солидного итальянца до подобных крайностей.Существует распространенное заблуждение, что комплексные числа потребовались для того, чтобы решать квадратные уравнения. На самом деле, это совершенно не так: задача поиска корней квадратного уравнения никоим образом введение комплексных чисел не мотивирует. Вот совершенно.
Давайте убедимся сами. Всякое квадратное уравнение можно представить в виде:
.
Геометрически, это означает, что мы хотим найти точки пресечения некоторой прямой и параболы
Я тут даже картинку сделал, для иллюстрации.
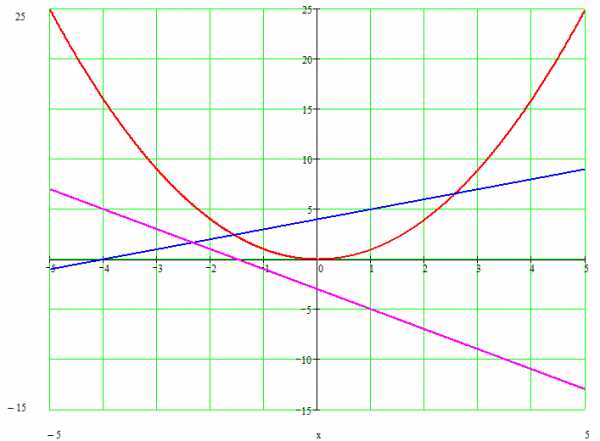
Как нам всем хорошо известно из школы, корни квадратного уравнения (в указанных выше обозначениях) находятся по следующей формуле:
Оказываются возможными 3 варианта:
1. Подкоренное выражение положительно.
2. Подкоренное выражение равно нулю.
3. Подкоренное выражение отрицательно.
В первом случае имеются 2 различных корня, во втором два совпадающих, в третьем уравнение «не решается». Все эти случаи имеют вполне наглядную геометрическую интерпретацию:
1. Прямая пересекает параболу (синяя прямая на рисунке).
2. Прямая касается параболы.
3. Прямая не имеет с параболой общих точек (сиреневая прямая на рисунке).
Ситуация проста, логична, непротиворечива. Пытаться извлекать квадратный корень из отрицательного числа нет совершенно никаких оснований. Никто и не пытался.
Обстановка существенно изменилась, когда пытливая математическая мысль добралась до кубических уравнений. Чуть менее очевидно, используя некоторую несложную подстановку, всякое кубическое уравнение можно свести к виду: . С геометрической точки зрения ситуация похожа на предыдущую: мы ищем точку пересечения прямой и кубической параболы.
Взгляните на картинку: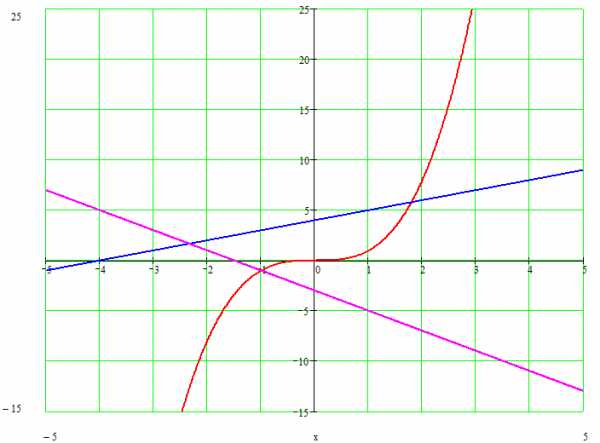
Существенное отличие от случая квадратного уравнения в том, что какую бы прямую мы не взяли, она всегда пересечет параболу. Т.е., уже из чисто геометрических соображений, кубическое уравнение всегда имеет хотя бы одно решение.
Найти его можно воспользовавшись формулой Кардано:
где
.
Немного громоздко, но пока, вроде бы, все в порядке. Или нет?
Вообще, формула Кардано — это яркий пример «принципа Арнольда» в действии. И что характерно, Кардано никогда на авторство формулы не претендовал.
Вернемся, однако, к нашим баранам. Формула замечательная, без преувеличение великое достижение математики начала-середины XVI века. Но есть у нее один нюанс.
Возьмем классический пример, который рассматривал еще Бомбелли:
.
Внезапно,
,
и, соответственно,
.
Приплыли. А формулу жалко, а формула-то хорошая. Тупик. При том, что решение у уравнения, безусловно, есть.
Идея Рафаэля Бомбелли заключалась в следующем: давайте прикинемся шлангом и сделаем вид, что корень из отрицательного — это какое-то число. Мы, конечно, знаем, что таких чисел нет, но тем не менее, давайте представим, что оно существует и его, как обычные числа, можно складывать с другими, умножать, возводить в степень и т.п.
Используя подобный подход, Бомбелли установил, в частности, что
,
и
.
Давайте проверим:
.
Заметьте, в выкладках никаких предположений о свойствах квадратных корней из отрицательных чисел не предполагалось, кроме упомянутого выше допущения, что они ведут себя как «обычные» числа.
В сумме получаем . Что вполне себе правильный ответ, который элементарно проверяется прямой подстановкой. Это был настоящий прорыв. Прорыв в комплексную плоскость.
Тем не менее, подобные выкладки выглядят как некоторая магия, математический фокус. Отношение к ним, как к некоему трюку, сохранялось среди математиков еще очень долго. Собственно, придуманное Рене Декартом для корней из отрицательных название «мнимые числа» вполне отражает отношение математиков тех времен к таким развлечениям.
Однако, время шло, «трюк» применялся с неизменным успехом, авторитет «мнимых чисел» в глазах математического общества рос, сдерживаемый, однако, неудобством их использования. Лишь получение Леонардом Эйлером (кстати, это именно он ввел ныне общеупотребительное обозначение для мнимой единицы) знаменитой формулы
открыло комплексным числам дорогу в самые различные области математики и ее приложений. Но это уже совсем другая история.
habr.com
Мнимая единица — Википедия (с комментариями)
В поле комплексных чисел корень n-й степени имеет n решений. На комплексной плоскости корни из мнимой единицы находятся в вершинах правильного n-угольника, вписанного в окружность с единичным радиусом.
- Невозможно разобрать выражение (Выполняемый файл <code>texvc</code> не найден; См. math/README — справку по настройке.): u_k=\cos {\frac{{\frac{\pi}{2}} + 2\pi k}{n}} +i\ \sin {\frac{{\frac{\pi}{2}} + 2\pi k}{n}}, \quad k=0,1,…,n-1
Это следует из формулы Муавра и того, что мнимая единица может быть представлена в тригонометрическом виде:
- Невозможно разобрать выражение (Выполняемый файл <code>texvc</code> не найден; См. math/README — справку по настройке.): i=\cos\ {\frac{\pi}{2}} + i\ \sin\ {\frac{\pi}{2}}
В частности, Невозможно разобрать выражение (Выполняемый файл <code>texvc</code> не найден; См. math/README — справку по настройке.): \sqrt{i } = \left\{\frac{1 + i}{\sqrt{2}};\ \frac{-1 — i}{\sqrt{2}} \right\} и Невозможно разобрать выражение (Выполняемый файл <code>texvc</code> не найден; См. math/README — справку по настройке.): \sqrt[3]{i } = \left\{-i;\ \frac{i + {\sqrt{3}}}{2};\ \frac{i — {\sqrt{3}}}{2} \right\}
Также корни из мнимой единицы могут быть представлены в показательном виде:
- Невозможно разобрать выражение (Выполняемый файл <code>texvc</code> не найден; См. math/README — справку по настройке.): u_k=e^{\frac{(\frac{\pi}{2} + 2\pi k) i}{n} }, \quad k=0,1,…,n-1
Иные мнимые единицы
В конструкции Кэли — Диксона (или в алгебрах Клиффорда) «мнимых единиц расширения» может быть несколько, и/или их квадрат может быть =»+1″ или даже =»0″. Но в этом случае могут возникать делители нуля, имеются и иные свойства, отличные от свойств комплексного «i». Например, в теле кватернионов три антикоммутативных мнимых единицы, а также имеется бесконечно много решений уравнения «Невозможно разобрать выражение (Выполняемый файл <code>texvc</code> не найден; См. math/README — справку по настройке.): x^2 = -1 ».
К вопросу об интерпретации и названии
| « | Гаусс утверждал также, что если бы величины 1, −1 и √−1 назывались соответственно не положительной, отрицательной и мнимой единицей, а прямой, обратной и побочной, то у людей не создавалось бы впечатления, что с этими числами связана какая-то мрачная тайна. По словам Гаусса, геометрическое представление дает истинную метафизику мнимых чисел в новом свете. Именно Гаусс ввел термин «комплексные числа» (в противоположность «мнимым числам» Декарта) и использовал для обозначения √−1 символ i. Морис Клайн, «Математика. Утрата определённости». Глава VII. Нелогичное развитие: серьёзные трудности на пороге XIX в. | » |
Обозначения
Обычное обозначение Невозможно разобрать выражение (Выполняемый файл <code>texvc</code> не найден; См. math/README — справку по настройке.): i , но в радиотехнике мнимую единицу принято обозначать Невозможно разобрать выражение (Выполняемый файл <code>texvc</code> не найден; См. math/README — справку по настройке.): j , чтобы не путать с обозначением мгновенной силы тока: Невозможно разобрать выражение (Выполняемый файл <code>texvc</code> не найден; См. math/README — справку по настройке.): i = i (t) .
См.также
Напишите отзыв о статье «Мнимая единица»
Примечания
Ссылки
Отрывок, характеризующий Мнимая единица
– Этому нельзя научить, Изидора. У людей должна появиться потребность к Свету, потребность к Добру. Они должны сами желать изменения. Ибо то, что даётся насильно, человек инстинктивно старается побыстрее отвергнуть, даже не пытаясь что-либо понять. Но мы отвлеклись, Изидора. Желаешь ли, чтобы я продолжил историю Радомира и Магдалины?Я утвердительно кивнула, в душе сильно сожалея, что не могу вот так просто и спокойно вести с ним беседу, не волнуясь об отпущенных мне судьбой последних минутах моей искалеченной жизни и не думая с ужасом о нависшей над Анной беде…
– В библии очень много пишется об Иоанне Крестителе. Был ли он по-настоящему с Радомиром и рыцарями Храма? Его образ так удивительно хорош, что иногда заставлял сомневаться, являлся ли Иоанн настоящей фигурой? Можешь ли ты ответить, Север?
Север тепло улыбнулся, видимо вспоминая что-то, очень для него приятное и дорогое…
– Иоанн был мудрым и добрым, как большое тёплое солнце… Он был отцом для всех идущих с ним, их учителем и другом… Его ценили, слушались и любили. Но он никогда не был тем молодым и удивительно красивым юношей, каким его обычно рисовали художники. Иоанн в то время был уже пожилым волхвом, но всё ещё очень сильным и стойким. Седой и высокий, он был скорее похож на могучего былинного воина, чем на удивительно красивого и нежного юношу. Он носил очень длинные волосы, как впрочем, и все остальные, находящиеся с Радомиром.
Это был Радан, он был и правда необычайно красивым. Он, как и Радомир, с малых лет жил в Мэтэоре, рядом со своей матерью, Ведуньей Марией. Вспомни, Изидора, как много картин существует, в которых Мария написана с двумя, почти одного возраста, младенцами. Их почему-то рисовали все знаменитые художники, возможно, даже не понимая, КОГО по-настоящему изображала их кисть… И что самое интересное – это то, что именно на Радана Мария смотрит на всех этих картинах. Видимо уже тогда, будучи ещё младенцем, Радан уже был таким же весёлым и притягивающим, каким он оставался всю свою короткую жизнь…
И ещё… если бы и рисовали художники именно Иоанна на этих картинах, то как же тогда тот же самый Иоанн сумел бы так чудовищно постареть ко времени своей казни, свершённой по желанию капризницы Саломеи?.. Ведь по Библии это случилось ещё до распятия Христа, значит, Иоанну должно было быть в то время никак не более тридцати четырёх лет! Каким же образом из по-девичьи красивого, златокудрого юноши он превратился в старого и совсем уж несимпатичного еврея?!
– Значит Волхв Иоанн не погиб, Север? – обрадовано спросила я. – Или он погиб по-другому?..
– К сожалению, настоящему Иоанну и правда отрубили голову, Изидора, но это не произошло по злой воле капризной избалованной женщины. Причиной его гибели было предательство иудейского «друга», которому он доверял, и у которого в доме жил несколько лет…
– Но как же он не почувствовал? Как не увидел, что это за «друг»?! – возмутилась я.
– Наверное, невозможно подозревать каждого человека, Изидора… Думаю, им и так было достаточно сложно кому-то довериться, ведь им всем приходилось как-то приспосабливаться и жить в той чужой, незнакомой стране, не забывай этого. Потому, из большого и меньшего зла они, видимо, старались выбрать меньшее. Но предугадать всё невозможно, ты ведь сама прекрасно знаешь это, Изидора… Смерть Волхва Иоанна произошла уже после распятия Радомира. Его отравил иудей, в доме у которого Иоанн в то время жил вместе с семьёй погибшего Иисуса. В один из вечеров, когда весь дом уже почивал, хозяин, беседуя с Иоанном, преподнёс ему его любимый чай с примесью сильнейшего травяного яда… На следующее утро никто даже не сумел понять, что же такое случилось. По словам хозяина, Иоанн просто мгновенно уснул, и уже никогда не проснулся более… Его тело нашли утром в его окровавленном ложе с… отрубленной головой… По словам того же хозяина, иудеи очень боялись Иоанна, так как считали его непревзойдённым магом. И чтобы быть уверенными, что он никогда уже не воскреснет – они обезглавили его. Голову же Иоанна позже выкупили (!!!) у них и забрали с собою рыцари Храма, сумев сохранить её и привезти в Долину Магов, чтобы таким образом дать Иоанну хотя бы такое малое, но достойное и заслуженное почтение, не разрешая иудеям просто глумиться над ним, выполняя какие-нибудь свои магические ритуалы. С тех пор голова Иоанна была с ними всегда, где бы они ни находились. И за эту же голову через две сотни лет рыцарей Храма обвинили в преступном поклонении Дьяволу… Ты ведь помнишь последнее «дело Тамплиеров» (Рыцарей Храма), не так ли, Изидора? Именно там их обвинили в поклонении «говорящей голове», которая бесила всё церковное духовенство.
– Прости меня, Север, но почему Рыцари Храма не привезли голову Иоанна сюда, в Мэтэору? Ведь, насколько я понимаю, вы все очень любили его! И откуда тебе известны все эти подробности? Тебя ведь не было вместе с ними? Кто рассказал тебе всё это?
– Рассказала нам всю эту печальную историю Ведунья Мария, мать Радана и Радомира…
– А разве Мария вернулась к вам после казни Иисуса?!.. Ведь, насколько известно мне, она была с её сыном во время распятия. Когда же она вернулась к вам? Возможно ли, что она всё ещё жива?.. – затаив дыхание, спросила я.
o-ili-v.ru
Реферат Мнимая единица
скачатьРеферат на тему:
План:
- Введение
- 1 Определение
- 2 Степени мнимой единицы
- 3 Корни из мнимой единицы Примечания
Введение
Мнимая единица — комплексное число, квадрат которого равен отрицательной единице.
В математике, физике мнимая единица обозначается как латинская i или j. Она позволяет расширить поле вещественных чисел до поля комплексных чисел. Точное определение зависит от способа этого расширения.
Основной причиной введения мнимой единицы является то, что не каждое полиномиальное уравнение f(x) = 0 с вещественными коэффициентами имеет решения в поле вещественных чисел. Например, уравнение x2 + 1 = 0 не имеет вещественных корней. Однако если предположить, что корнями являются комплексные числа, тогда это уравнение, как и любое другое полиномиальное уравнение, имеет решение.
Исторически мнимая единица была введена для решения кубического уравнения, так как если такое уравнение имеет три вещественных корня, для получения двух из них по формуле Кардано требуется брать комплексные значения используемых кубических корней.
Утверждение о том, что мнимая единица — это «квадратный корень из −1», не совсем корректно, т.к. −1 имеет два арифметических квадратных корня, один из которых можно обозначить как i, а другой как − i. Какой именно корень принимать за мнимую единицу — неважно, все математические равенства сохраняют свою силу при одновременной замене всех i на − i и − i на i.
1. Определение
Мнимая единица — число, квадрат которого равен −1. Таким образом i — это решение уравнения
или
Если мы определим i таким образом и будем считать ее неизвестной («воображаемой», «мнимой») переменной, тогда вторым решением уравнения будет − i, что можно проверить подстановкой.
2. Степени мнимой единицы
Степени i повторяются в цикле:
Что может быть записано для любой степени в виде:
где n — любое целое число.
Отсюда:
где mod 4 представляет остаток от деления на 4.
Число ii является вещественным :
- [1]
3. Корни из мнимой единицы
В поле комплексных чисел корень n-ой степени имеет n решений. На комплексной плоскости эти корни находятся в вершинах правильного n-угольника, вписанного в окружность с единичным радиусом.
Это следует из формулы Муавра и того, что мнимая единица может быть представлена в тригонометрическом виде:
В частности, и
Также корни мнимой единицы могут быть представлены в показательном виде:
wreferat.baza-referat.ru
Мнимая единица — Википедия РУ

Мни́мая едини́ца — комплексное число, квадрат которого равен −1 (минус единице). Термин может употребляется также в обобщённом смысле не только для комплексных чисел[⇨].
В математике, физике мнимая единица обозначается как латинская i{\displaystyle i} или j{\displaystyle j}. Она позволяет расширить поле вещественных чисел до поля комплексных чисел. Точное определение зависит от способа расширения.
Причиной введения мнимой единицы является то, что не каждое полиномиальное уравнение f(x)=0{\displaystyle f(x)=0} с вещественными коэффициентами имеет решения в поле вещественных чисел. Так, уравнение x2+1=0{\displaystyle x^{2}+1=0} не имеет вещественных корней. Однако оказывается, что любое полиномиальное уравнение с комплексными коэффициентами имеет комплексное решение — «Основная теорема алгебры».
Исторически мнимая единица сначала была введена для решения вещественного кубического уравнения: нередко, при наличии трёх вещественных корней, для получения двух из них формула Кардано требовала брать кубический корень в комплексных числах.
Утверждение, что мнимая единица — это «квадратный корень из −1», не совсем точно: ведь «−1» имеет два квадратных корня, один из которых можно обозначить как «i», а другой как «−i». Какой именно корень принять за мнимую единицу — неважно: все равенства сохранят силу при одновременной замене всех «i» на «-i» и «-i» на «i». Однако из-за этой двусмысленности, чтобы избежать ошибочных выкладок, не следует применять обозначение для i{\displaystyle i} через радикал (как −1{\displaystyle {\sqrt {-1}}}).
Определение
Мнимая единица — это число, квадрат которого равен −1. Т.е. i{\displaystyle i} — это одно из решений уравнения
- x2+1=0,{\displaystyle x^{2}+1=0,} или x2=−1.{\displaystyle x^{2}=-1.}
И тогда его вторым решением уравнения будет −i{\displaystyle -i} , что проверяется подстановкой.
Степени мнимой единицы
Факториал
Факториал мнимой единицы i можно определить как значение гамма-функции от аргумента 1 + i:
- i!=Γ(1+i)≈0.4980−0.1549i.{\displaystyle i!=\Gamma (1+i)\approx 0.4980-0.1549i.}
Также
- |i!|=πsinh(π)≈0.521564….{\displaystyle |i!|={\sqrt {\pi \over \sinh(\pi )}}\approx 0.521564….} [1]
Корни из мнимой единицы
 Корни квадратные из мнимой единицы
Корни кубические из мнимой единицы (вершины треугольника)
Корни квадратные из мнимой единицы
Корни кубические из мнимой единицы (вершины треугольника)В поле комплексных чисел корень n-й степени имеет n решений. На комплексной плоскости корни из мнимой единицы находятся в вершинах правильного n-угольника, вписанного в окружность с единичным радиусом.
- uk=cosπ2+2πkn+i sinπ2+2πkn,k=0,1,…,n−1{\displaystyle u_{k}=\cos {\frac {{\frac {\pi }{2}}+2\pi k}{n}}+i\ \sin {\frac {{\frac {\pi }{2}}+2\pi k}{n}},\quad k=0,1,…,n-1}
В частности, i={1+i2; −1−i2}{\displaystyle {\sqrt {i}}=\left\{{\frac {1+i}{\sqrt {2}}};\ {\frac {-1-i}{\sqrt {2}}}\right\}} и i3={−i; i+32; i−32}{\displaystyle {\sqrt[{3}]{i}}=\left\{-i;\ {\frac {i+{\sqrt {3}}}{2}};\ {\frac {i-{\sqrt {3}}}{2}}\right\}}
Также корни из мнимой единицы могут быть представлены в показательном виде:
- uk=e(π2+2πk)in,k=0,1,…,n−1{\displaystyle u_{k}=e^{\frac {({\frac {\pi }{2}}+2\pi k)i}{n}},\quad k=0,1,…,n-1}
Иные мнимые единицы
К вопросу об интерпретации и названии
| Гаусс утверждал также, что если бы величины 1, −1 и √−1 назывались соответственно не положительной, отрицательной и мнимой единицей, а прямой, обратной и побочной, то у людей не создавалось бы впечатления, что с этими числами связана какая-то мрачная тайна. По словам Гаусса, геометрическое представление дает истинную метафизику мнимых чисел в новом свете. Именно Гаусс ввел термин «комплексные числа» (в противоположность «мнимым числам» Декарта) и использовал для обозначения √−1 символ i. Морис Клайн, «Математика. Утрата определённости». Глава VII. Нелогичное развитие: серьёзные трудности на пороге XIX в. |
Обозначения
Обычное обозначение i{\displaystyle i} , но в электро- и радиотехнике мнимую единицу принято обозначать j{\displaystyle j} , чтобы не путать с обозначением мгновенной силы тока: i=i(t){\displaystyle i=i(t)} .
В языке программирования Python мнимая единица записывается как 1j.
В языке программирования Wolfram Language мнимая единица записывается как I.
См.также
Примечания
Ссылки
www.http-wikipediya.ru
мнимая единица — определение — русский
Пример предложения с «мнимая единица», памяти переводов
ProjectSyndicateОна включала в себя сложные синтетические ценные бумаги, которые происходили из ценных бумаг, обеспеченных закладными на недвижимость, путем клонирования их в мнимые единицы, которые имитировали оригиналы.springerКак вспомогательный результат, мы можем физически интерпретировать мнимые единицы, входящие, как известно, в попереченые координаты в суперлюминальных преобразованиях Лоренца.springerМы зкстраполируем пп амплитуды с изоспином единица и двойка вt-канале на мнимуюv≡(s−u)/4mπ ось в комплекснойv-плоскости с помощью «оптимальных» пуассоновых взвешенных дисперсионных соотношений.UN-2О мнимой приверженности Израиля мирному процессу и двугосударственному урегулированию можно реально судить по его недавним объявлениям о строительстве тысяч новых единиц жилья для поселенцев, особенно в оккупированном Восточном Иерусалиме и вокруг него, по непрекращающемуся уничтожению Израилем палестинских жилых домов и имущества и по изощренным попыткам израильского правительства легализовать его противозаконные поселенческие замыслы.MultiUnКроме того, Уголовный кодекс карает незаконное владение огнестрельным оружием (статьи # и # ), а также «хранение, импорт, экспорт, торговлю или транзит, подлинный или мнимый, через Княжество, а также изготовление запрещенных видов оружия или муляжей этого оружия согласно разделу # статьи # указа от # июля # года, за исключением указанных в пункте # случаев, когда в виде санкций применяется лишение свободы на срок до # лет», и «нелегальное ношение одной или нескольких единиц оружия…, наказуемое лишением свободы на срок до пяти лет» (статьи # иUN-2Кроме того, Уголовный кодекс карает незаконное владение огнестрельным оружием (статьи 289 и 290), а также «хранение, импорт, экспорт, торговлю или транзит, подлинный или мнимый, через Княжество, а также изготовление запрещенных видов оружия или муляжей этого оружия согласно разделу 2 статьи 2 указа от 3 июля 1989 года, за исключением указанных в пункте 8 случаев, когда в виде санкций применяется лишение свободы на срок до 10 лет», и «нелегальное ношение одной или нескольких единиц оружия…, наказуемое лишением свободы на срок до пяти лет» (статьи 89 и 90).Показаны страницы 1. Найдено 7 предложения с фразой мнимая единица.Найдено за 4 мс.Накопители переводов создаются человеком, но выравниваются с помощью компьютера, что может вызвать ошибки. Они приходят из многих источников и не проверяются. Будьте осторожны.
ru.glosbe.com
