Определение подобных треугольников
Рассмотрим два прямоугольных треугольника с острыми углами в 60° и 30° (рис. 364).
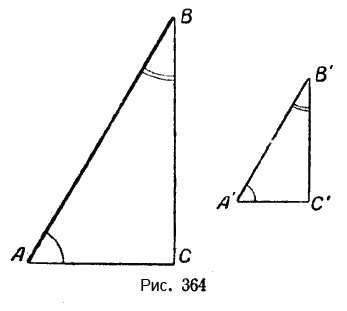
Стороны второго треугольника по сравнению с первым уменьшены в два раза:
\(\frac{AB}{A’B’}\) = 2; \(\frac{AC}{A’C’}\) = 2; \(\frac{BC}{B’C’}\) = 2.
У этих треугольников углы попарно равны. Стороны, лежащие против равных углов, пропорциональны:
\(\frac{AB}{A’B’}\) = \(\frac{AC}{A’C’} = \frac{BC}{B’C’}\) = 2.
Такие треугольники называют подобными. Стороны, лежащие против равных углов, называются сходственными.
Таким образом, подобными называются треугольники, у которых yглы попарно равны, а сходственные стороны пропорциональны.
Подобие треугольников записывается так: \(\Delta\)ABС \(\sim\) \(\Delta\)А’В’С’.
Отношение сходственных сторон подобных фигур называется коэффициентом подобия. В данном случае коэффициентом подобия треугольников АBС и А’В’С’ будет число 2.
Если же взять отношения A’B’/AB = A’C’/AC = B’C’/BC , то коэффициент подобия будет равен 1/2.
Свойство прямой, параллельной какой-либо стороне треугольника.
Проведём в треугольнике АBС прямую DЕ параллельно стороне АС (рис. 365).
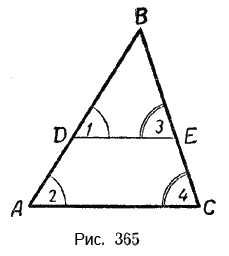
Получим треугольник DВЕ. Докажем, что \(\Delta\)ABС \(\sim\) \(\Delta\)DВЕ.
Вследствие параллельности сторон DЕ и АС ∠1 = ∠2 и ∠3 = ∠4.
Угол В является общим для этих треугольников. Следовательно, углы этих треугольников попарно равны.
Так как DЕ || АС, то \(\frac{AB}{DB} = \frac{BC}{BE}\).
Проведём через точку Е прямую, параллельную стороне AB (рис. 366).
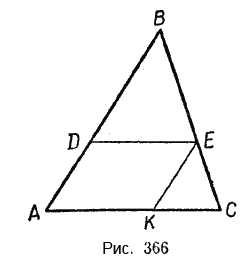
Получим: \(\frac{BC}{BE} = \frac{AC}{AK}\), но АК = DЕ.
Поэтому
\(\frac{BC}{BE} = \frac{AC}{DE}\)
Сопоставляя полученную пропорцию с пропорцией \(\frac{AB}{DB} = \frac{BC}{BE}\) получим:
\(\frac{AB}{DB} = \frac{BC}{BE} = \frac{AC}{DE}\), т.е.
сходственные стороны треугольников AВС и DВЕ пропорциональны.
Раньше было доказано, что углы этих треугольников попарно равны.
Значит, \(\Delta\)ABС \(\sim\) \(\Delta\)DВЕ.
Следовательно, прямая, проведённая параллельно какой-либо стороне треугольника, отсекает от него треугольник, подобный данному.
Отношение площадей двух подобных треугольников
Пусть \(\triangle AВС \sim \triangle AВС\)(черт. 380). Из подобия треугольников следует, что
∠A = ∠A, ∠B = ∠B и ∠С = ∠С. Кроме того, AB/AB = BC/BC = AC/AC.
В этих треугольниках из вершин В и В проведём высоты и обозначим их через h и h. Площадь первого треугольника будет равна AC•h/2, а площадь второго треугольника AC•h/2.
Обозначив площадь первого треугольника через S, а площадь второго — через S получим: S/S = AC•h/AC•h или S/S = AC/AC • h/h
Из подобия треугольников АВО и АВО (они подобны, потому что прямоугольные, и, кроме того, имеют по равному острому углу, а именно ∠A = ∠A) следует:
h/h = AB/AB . Но AB/AB= AC/AC . Следовательно, h/h = AC/AC. Заменив в формуле S/S = AC/AC • h/h отношение h/h равным ему отношением AC/AC , получим:
S/S = AC/AC • AC/AC , или
$$ \frac{S}{S} = \frac{(AC)^2}{(AC)^2} $$
Итак, площади подобных треугольников относятся как квадраты сходственных сторон.
Полученную формулу можно преобразовать так: S/S = (AC/AC)2.
Значит, можно сказать, что отношение площадей двух подобных треугольников равно квадрату отношения их сходственных сторон.
Построение подобных треугольников
Мы уже знаем, что для построения треугольника, подобного данному, достаточно из какой-нибудь точки, взятой на стороне треугольника, провести прямую, параллельную стороне треугольника. Получим треугольник, подобный данному (черт. 382):
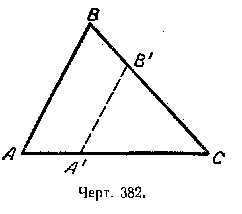
razdupli.ru
| 1. | Отношение сторон подобных треугольников | 1 вид — рецептивный | лёгкое | 1 Б. | Написание отношения сторон подобных треугольников. |
| 2. | Отношение отрезков | 2 вид — интерпретация | лёгкое | 1 Б. | Вычисление длины отрезка, если известна длина другого отрезка и их отношение. |
| 3. | Отношение отрезков, длина отрезка | лёгкое | 1 Б. | Вычисление длины отрезка по данному отношению и длине другого отрезка. | |
| 4. | Пропорциональные отрезки | 2 вид — интерпретация | лёгкое | 2 Б. | Пропорциональные отрезки. Вычисление неизвестного члена пропорции, который находится в числителе. |
| 5. | Подобные треугольники, отношение площадей | 2 вид — интерпретация | среднее | 1 Б. | Нахождение отношений периметров или площадей подобных треугольников. |
| 6. | Длины частей отрезка | 2 вид — интерпретация | среднее | 3 Б. | Вычисление длин частей отрезка, если известна длина всего отрезка и отношение его частей. |
| 7. | Периметры и площади подобных треугольников | 2 вид — интерпретация | среднее | 3 Б. | Вычисление периметра и площади одного из данных подобных треугольников. |
| 8. | Площади подобных треугольников | 2 вид — интерпретация | среднее | 4 Б. | Вычисление площадей подобных треугольников. |
| 9. | Периметр равнобедренной трапеции | 2 вид — интерпретация | среднее | 3 Б. | Вычисление периметра равнобедренной трапеции, подобные треугольники. |
| 10. | Подобные прямоугольные треугольники | 2 вид — интерпретация | среднее | 3 Б. | Вычисление стороны одного из подобных прямоугольных треугольников. |
| 11. | Подобные треугольники | 2 вид — интерпретация | среднее | 3 Б. | Вычисление стороны одного из данных подобных треугольников. |
| 12. | Подобные треугольники, коэффициент подобия (1) | 2 вид — интерпретация | среднее | 4 Б. | Вычисление стороны одного из данных подобных треугольников, коэффициент подобия k < 1. |
| 13. | Подобные треугольники, коэффициент подобия (2) | 2 вид — интерпретация | среднее | 4 Б. | Вычисление стороны одного из данных подобных треугольников, коэффициент подобия k > 1. |
| 14. | Площади подобных треугольников | 3 вид — анализ | сложное | 4 Б. | Использование соотношения площадей подобных треугольников для определения сторон. |
www.yaklass.ru
Урок «Определение подобных треугольников»
Урок геометрии в 8 классе
Тема. Определение подобных треугольников.
Учитель математики МБОУ СОШ №49 г.Шахты
Гладкая Н.В.
Цель:
Ввести новые понятия: отношение отрезков, пропорциональные отрезки, сходственные стороны, подобные треугольники, коэффициент подобия.
Учить использовать новые понятия, а также известные определения и теоремы для решения задач.
Развивать логическое мышление.
Ход урока.
①Повторение ранее изученных понятий.
Что называют отношением чисел? (Это частное от деления двух чисел, которое показывает, во сколько раз одно число больше другого, или, какую часть одно число составляет от другого)
Что называют пропорцией? (Равенство двух отношений)
В чем заключается основное свойство пропорции? (Произведение крайних членов пропорции равно произведению ее средних членов)
② Проверка решения задач, подготавливающих введение новых понятий. (Домашнее задание)
Задача №1.
Длина прямой тропинки на дачном участке, ведущей от дома к сараю, составляет 12 м, а тропинки, ведущей к колодцу, составляет 15 м.
Найти отношение первой длины ко второй. . Что показывает данная величина? ( Показывает, какую часть составляет первая величина от второй).
Найти отношение второй длины к первой.. Что показывает данная величина? ( Показывает, во сколько раз вторая величина больше первой).
Выразить величины в сантиметрах и снова найти отношения. (.
Выразить величины в километрах и найти отношения. .
Сделать вывод о том, зависит ли отношение длин отрезков от того, в каких единицах они выражены. (Не зависит).
Задача №2.
Найти отношение отрезков:
Выбрать равные отношения и записать их равенство.
Решение:
③ Самостоятельная работа с текстом и закрепление новых знаний.
Работа с текстом пункта 56 «Пропорциональные отрезки» из §1 ( учебник Л. С. Атанасяна). Прочесть текст, выбрать, сформулировать и записать определения следующих понятий.
Отношение отрезков. (Отношением отрезков АВ и СD называется отношение их длин, то есть.
Пропорциональные отрезки. (Отрезки АВ и СD пропорциональны отрезкам , если . Отрезки , если справедливо равенство .
Закрепление новых знаний.
№533 (устно). Найти отношение отрезков ABи CD, если их длины равны соответственно 15 см и 20 см. Изменится ли это отношение, если длины отрезков выразить в миллиметрах? (Отношение равно ; при изменении единиц длины оно не меняется)
№534 (устно, использовать результаты решения домашней задачи №2). Пропорциональны ли изображенные на рисунке отрезки: а); б); в)? (рисунок к домашней задаче №2, раздел ②) – в случаях (а) и (б) пропорциональны, в случае (в) – нет.
④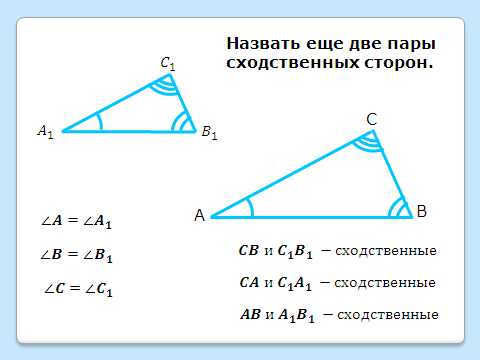 Определение подобных треугольников.
Определение подобных треугольников.
Демонстрация двух треугольников, у которых углы соответственно равны.
Первоначально на рисунке изображены два треугольника.
Выделить цветным мелом пару равных углов: , а за тем пару сторон, лежащих против этих углов: ; вводится их название – сходственные стороны.
Для закрепления понимания предлагается назвать еще две пары сходственных сторон, после чего появляется соответствующая запись: .
Демонстрация двух треугольников: , у которых о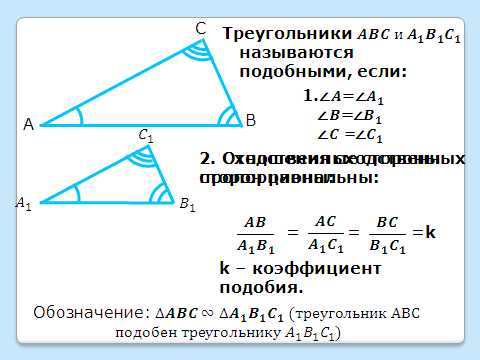 тмечены соответственно равные углы, а рядом – запись «Треугольники называются подобными, если…»
тмечены соответственно равные углы, а рядом – запись «Треугольники называются подобными, если…»
«.»
«Отношения сходственных сторон…»
Задание ученикам: Назвать отношения сходственных сторон.
Сделать запись на доске, выражающая отношения сходственных сторон: .
-Какой знак можно поставить между этими отношениями?
-Что означает равенство отношений для отрезков ?
Вывод: «Сходственные стороны пропорциональны»
Затем вводится число k для обозначения равных отношений, его название – коэффициент подобия, появляются соответствующие записи на слайде.
Последним шагом вводится обозначение подобных треугольников: .
⑤Решение задач.
№541.Подобны ли треугольники , если ?
Дано:ΔABC
ΔDEF
∠A=106ᵒ
∠B=34ᵒ
∠E=106ᵒ
∠F=40ᵒ
AC=4,4 см
AB=5,2 см
BC=7,6 см
DE=15,6 см
DF=22,8 см
EF=13,2 см
Найти
ΔABC∾ΔDEF?
Решение:
ΔABC: ∠A=106ᵒ; ∠B=34ᵒ; ∠C=180ᵒ — (106ᵒ+34ᵒ)=40ᵒ (из теоремы Пифагора)
ΔDEF: ∠E=106ᵒ; ∠F=40ᵒ; ∠D=180ᵒ — (106ᵒ+40ᵒ)=34ᵒ (из теоремы Пифагора)
П
олучили: ∠A=∠E; ∠B=∠D; ∠C=∠FСходственные стороны (лежат против равных углов): ABи ED; ACи EF; BCи DF.
Так как ∠A=∠E; ∠B=∠D; ∠C=∠F;
, то ΔABC∾ΔEDF (по определению)
Вывод: ΔABC∾ΔEDF.
⑥Домашнее задание.
§1(п. 56, п. 57) – знать смысл понятий
Отношение отрезков.
Пропорциональные отрезки.
Сходственные стороны у треугольников.
Подобные треугольники.
Коэффициент подобия.
№542 (решить)
№535 (разобрать и записать доказательство, разбив его на пункты)
Решение задач.
№542.
Дано:ΔABC∾ΔKMN;
ABи KM– сходственные;
BCи MN – сходственные;
АВ=4 см;
ВС=5 см;
СА=7 см;
Найти:
KM; MN; KN.
Решение:
Сходственные стороны в подобных треугольниках лежат против равных углов.
АВ и КМ – сходственные, значит ∠С=∠N.
ВС и МN – сходственные, значит∠А=∠К.
2)Получаем следующий чертеж
3
) (так как ΔMNK∾ΔBCA) и . Тогда
.
Ответ:KN=14,7 см; KM=8,4 см; MN=10,5 см.
№535.
Дано:ΔАВС;
AD – биссектриса
Доказать:
Ч
ертеж:
Доказательство:
; .
Так как∠BAD=∠DAC, то по теореме об отношении площадей треугольников, имеющих соответственно равные углы .
Учитывая пункты 1 и 2, получаем
Вывод. Биссектриса треугольника делит противоположную сторону на отрезки, пропорциональные прилежащим сторонам.
infourok.ru
| 1. |
Отношение сторон подобных треугольников
Сложность: лёгкое |
1 |
| 2. |
Отношение отрезков
Сложность: лёгкое |
1 |
| 3. |
Отношение отрезков, длина отрезка
Сложность: лёгкое |
1 |
| 4. |
Пропорциональные отрезки
Сложность: лёгкое |
2 |
| 5. |
Подобные треугольники, отношение площадей
Сложность: среднее |
1 |
| 6. |
Длины частей отрезка
Сложность: среднее |
3 |
| 7. |
Периметры и площади подобных треугольников
Сложность: среднее |
3 |
| 8. |
Площади подобных треугольников
Сложность: среднее |
4 |
| 9. |
Периметр равнобедренной трапеции
Сложность: среднее |
3 |
| 10. |
Подобные прямоугольные треугольники
Сложность: среднее |
3 |
| 11. |
Подобные треугольники
Сложность: среднее |
3 |
| 12. |
Подобные треугольники, коэффициент подобия (1)
Сложность: среднее |
4 |
| 13. |
Подобные треугольники, коэффициент подобия (2)
Сложность: среднее |
4 |
| 14. |
Площади подобных треугольников
Сложность: сложное |
4 |
www.yaklass.ru
Определение подобных треугольников
Поиск ЛекцийОтношение показывает, во сколько раз первое число больше второго, или какую часть первое число составляет от второго.
Отношением отрезков и называется отношение их длин, т. е. .
Отрезки и пропорциональны отрезкам и , если .
Фигуры одинаковой формы называют подобными.
Стороны и , и , и называются сходственными.
Подобными называются треугольники, у которых углы соответственно равны, а сходственные стороны пропорциональны.

Число , равное отношению сходственных сторон подобных треугольников, называется коэффициентом подобия.
Теорема.Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия.
Отношение периметров двух подобных треугольников равно коэффициенту подобия.
Признаки подобия треугольников
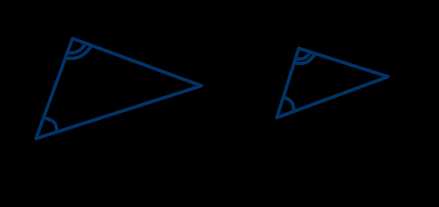 Первый признак подобия треугольников:
Первый признак подобия треугольников:
Если два угла одного треугольника соответственно равны двум углам другого треугольника, то такие треугольники подобны.
Прямая, параллельная одной из сторон треугольника, отсекает от него треугольник, подобный данному.
Прямоугольные треугольники подобны по острому углу.
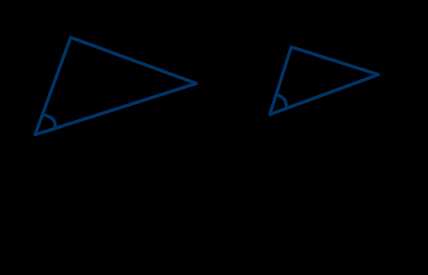
Второй признак подобия треугольников:
Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы между ними равны, то такие треугольники подобны.
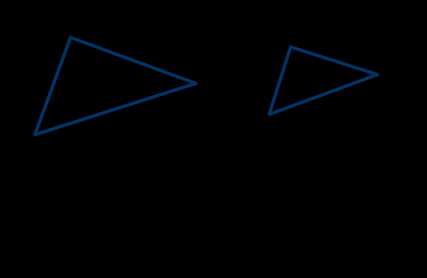
Третий признак подобия треугольников:
Если три стороны одного треугольника соответственно пропорциональны трём сторонам другого треугольника, то такие треугольники подобны.
Применение подобия к доказательству теорем и решению задач
Средней линией треугольника называют отрезок, соединяющий середины двух его сторон.
Теорема.
Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны.
Медианы треугольника пересекаются в одной точке, которая делит каждую медиану в отношении , считая от вершины.
Отрезок называется средним пропорциональным(или средним геометрическим) для отрезков и , если .
Высота прямоугольного треугольника, проведенная из вершины прямого угла, есть среднее пропорциональное для отрезков, на которые делится гипотенуза этой высотой.
Катет прямоугольного треугольника есть среднее пропорциональное для гипотенузы и отрезка гипотенузы, заключенного между катетом и высотой, проведенной из вершины прямого угла.
Соотношения между сторонами и углами прямоугольного треугольника
Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.
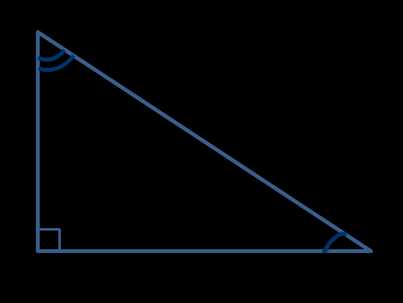
Косинусом острого угла прямоугольного
треугольника называется отношение прилежащего катета к гипотенузе.
Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему.
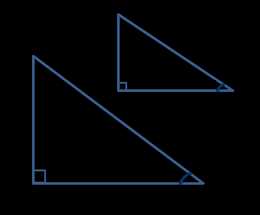
Если острый угол одного прямоугольного треугольника равен острому углу другого прямоугольного треугольника, то синусы этих углов равны, косинусы этих углов равны и тангенсы этих углов равны.
Рекомендуемые страницы:
Поиск по сайту
poisk-ru.ru
