Квадратичная функция, ее свойства, примеры и график
Функция y = ax² + bx + c, где a, b и c — заданные числа, a ≠ 0, x — переменная, называется квадратичной функцией. Другими словами, квадратичная функция – это зависимость, содержащая аргумент в квадрате. Отсюда и ее название.
При этом многочлен ax² + bx + c называют квадратным трехчленом. Числа a, b и c называются коэффициентами квадратного трехчлена: a — первым коэффициентом, b — вторым, c — свободным членом. Значения x, при которых квадратный трехчлен обращается в нуль, называются корнями квадратного трехчлена.
Для нахождения корней квадратного трехчлена нужно решить квадратное уравнение ax² + bx + c = 0. Рассмотрим пример, найдем корни квадратного трехчлена x² — x — 2. Решая уравнение x² — x — 2 = 0, получаем: x1 = -1, x2 = 2.
Число корней квадратного уравнения ax² + bx + c = 0 зависит от знака его дискриминанта D = b² — 4ac, а значит и квадратный трехчлен:
- имеет два различных корня, если D > 0;
- имеет один корень (два равных корня), если D = 0;
- не имеет действительных корней, если D < 0.
Рассмотрим пример, квадратный трехчлен 3x² — 8x + 5 имеет два различных корня, так как D = 8² — 4* 3*5 = 4 > 0, корни этого трехчлена: x1 = 5/3, x2 = 1.
Квадратный трехчлен 4x² — 4x + 1 имеет один корень, так как D = 4² — 4*4*1 = 0, корень этого трехчлена х = 1/2.
Квадратный трехчлен 2x² — 5x + 6 не имеет действительных корней, так как D = 5² — 4*2*6 = — 23 < 0.
График квадратичной функции
Рассмотрим самую простую квадратичную функцию y = x², т. е. функцию y = ax² + bx + c, при a = 1, b = c = 0. Для построения графика этой функции составим таблицу ее значений.
| х | -2 | -1 | 0 | 1 | 2 |
| у | 4 | 1 | 0 | 1 | 4 |
Отметим точки на координатной плоскости и соединим их плавной линией.
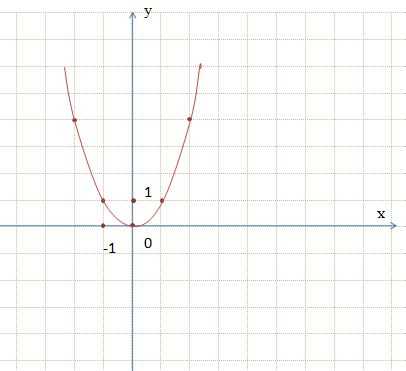
Кривая, являющаяся графиком функции y = x², называется параболой. Ось ординат является осью симметрии параболы. Точку пересечения параболы с ее осью симметрии называют вершиной параболы. Вершиной параболы y = x² является начало координат.
Рассмотрим функцию вида y = 2x², чтобы построить график составим таблицу значений.
| x | -2 | 0 | 1 | 2 | |
| y | 8 | 2 | 0 | 2 | 8 |
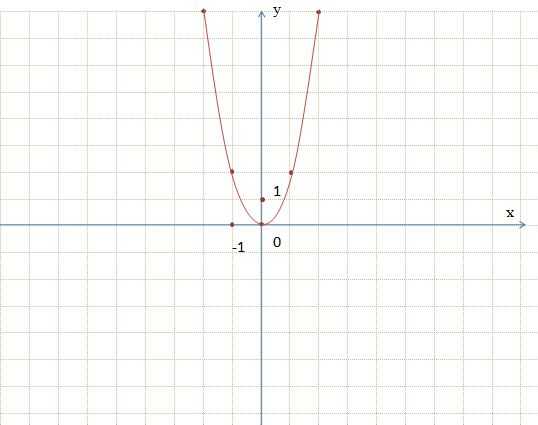
Сравним графики функций y = 2х² и y = х². При одном и том же х значение функции y = 2х² в 2 раза больше значения функции y = х². Это значит, что каждую точку графика y = 2х² можно получить из точки графика функции y = х² с той же абсциссой увеличением ее ординаты в 2 раза. Говорят, что график функции y = 2х² получается растяжением графика функции y = х² в 2 раза вдоль оси ординат.
Рассмотрим функцию вида y = 1/2x², чтобы построить график составим таблицу значений.
| х | -2 | -1 | 0 | 1 | 2 |
| y | 2 | 0.5 | 0 | 0.5 | 2 |
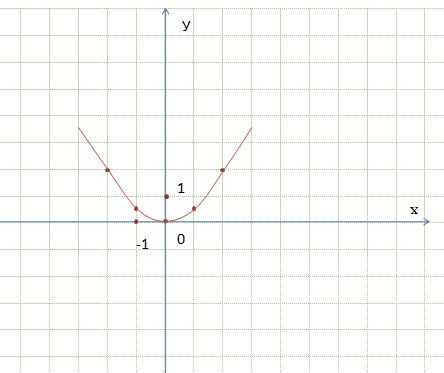
Сравним графики функций y = 1/2x² и y = х². Каждую точку графика y = 1/2x² можно получить из точки графика функции y = х² с той же абсциссой уменьшением ее ординаты в 2 раза. Говорят, что график функции y = 1/2x² получается сжатием графика функции y = х² в 2 раза вдоль оси ординат.
Рассмотрим функцию вида y = —x², и сравним с функцией y = х². При одном и том же значении х значения этих функций равны по модулю и противоположны по знаку. Следовательно, график функции y = —x² можно получить симметрией относительно оси абсцисс графика функции y = х². Составим таблицу значений.
| х | -2 | -1 | 0 | 1 | 2 |
| у | -4 | -1 | 0 | -1 | -4 |
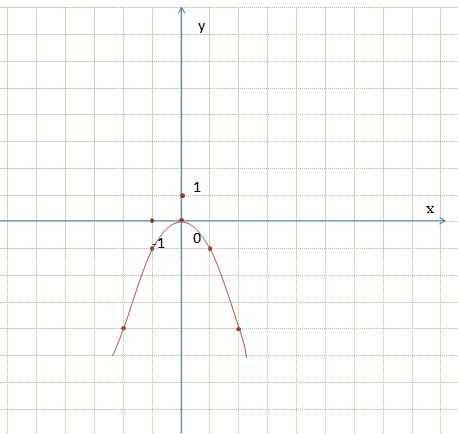
Говорят, что ветви параболы y = х² направлены вверх, а ветви параболы y = —x² направлены вниз. Аналогично график функции y = -2х² симметричен графику функции y = 2х² относительно оси абсцисс. График функции y = -1/2х² симметричен графику функции y = 1/2х² относительно оси абсцисс. График функции y = ах² при любом а ≠ 0 также называют параболой. При а > 0 ветви параболы направлены вверх, а при а < 0 вниз.
Рассмотрим функцию вида y = x² — 2х — 3, чтобы построить график составим таблицу значений.
| х | -2 | -1 | 0 | 1 | 2 | 3 | 4 |
| у | 5 | 0 | -3 | -4 | -3 | 0 | 5 |
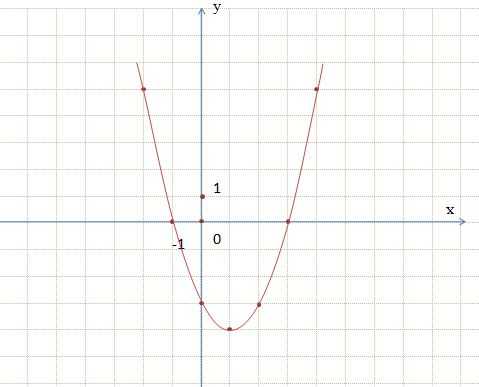
Вообще, графиком функции y = ax² + bx + c является парабола, получаемая сдвигом параболы y = ax² вдоль координатных осей. Равенство y = ax² + bx + c называют уравнением параболы.
Автор публикации
0 Комментарии: 3Публикации: 81Регистрация: 04-09-2015prostoi-sovet.ru
График квадратичной функции | Формулы с примерами
Графики квадратичной функции 9 класс
ПравилоЛюбую квадратичную функцию можно представить в виде , где
Примеры, свойства, правила
Правила1) y = 2x2 — 4x + 3.
I способ — выделение полного квадрата:
y = 2x2 — 4x + 3 = 2(x2 — 2x) + 3 =
= 2(x2 — 2 • x • 1 + 12) — 2 • 12 + 3 = 2(x — 1)2 + 1;
II способ — по формулам:
x0 = -4 2 • 2 = 1, y0 = y(1) = 2 • 12 — 4 • 1 + 3 = 1, значит y = 2(x — 1)2 + 1.
2) y = 2 — 3x2 + x = 2 — 3(x2 — 13x) =
= 2 — 3(x2 — 2 • 16 • x + (16)2 + 3 • (16)2) = -3 (x — 16)2 + 2 1 12.
График квадратичной функции, рисунок
ПравилоГрафик функции — y = a(x — x0)2 + y0 — парабола, которую можно получить из параболы y = ax 2 с помощью двух параллельных переносов (сдвигов:
1) вдоль оси OX на X0 вправо, если x0 > 0,
или на |x0| влево, если x0
2) вдоль оси OY на y0 вверх, если y0 > 0,
или на |y0| вниз, если y0
Порядок выполнения сдвигов — любой.
ПравилоВершина параболы y = a(x — x0)2 + y0— точка O1(x0,y0).
Ось симметрии — прямая x = x0.
Область значений — интервал [y0, +?), если a > 0, или (-?, y0], если a
Пример 11) y = 2x2 — 4x + 3 y = 2(x -1)2 + 1

2) y = 1 — 12x2 — 2x y = -(x + 2)

Формулы по алфавиту:
© 2019 Все права защищеныПри использовании материалов данного сайта обязательно указывать ссылку на источник
formula-xyz.ru
Квадратичная функция — урок. Алгебра, 8 класс.
Функция y=kx2 и её график
В \(7\)-м классе мы изучали функции \(у = m\), \(у = kx\), \(у = kx + m\), y=x2 и пришли в итоге к выводу, что уравнение с двумя переменными вида \(у = f(x)\) (функция) есть математическая модель, удобная для того, чтобы, задав конкретное значение независимой переменной \(x\) (аргумента), вычислить соответствующее значение зависимой переменной \(y\).
На самом деле функция y=kx2 в одном случае нам немного знакома. Смотри: если \(k = 1\), то получаем y=x2; эту функцию мы изучили в \(7\)-м классе, и ты, наверное, помнишь, что её графиком является парабола.
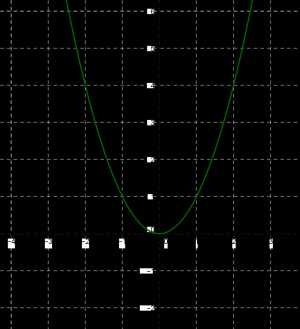
Обсудим, что происходит при других значениях коэффициента \(k\).
Рассмотрим две функции: y=2×2 и y=0.5×2. Составим таблицу значений для первой функции y=2×2:
| \(x\) | \(0\) | \(1\) | \(-1\) | \(2\) | \(-2\) | \(1.5\) | \(-1.5\) |
| \(y\) | \(0\) | \(2\) | \(2\) | \(8\) | \(8\) | \(4.5\) | \(4.5\) |
Построим точки \((0; 0), (1; 2), (-1; 2), (2; 8), (-2; 8), (1,5; 4,5), (-1,5; 4,5)\) на координатной плоскости; они намечают некоторую линию. Проведём её.
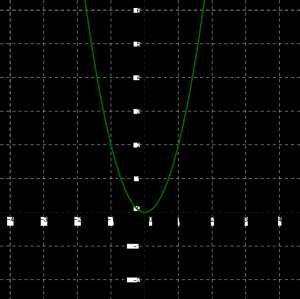
Составим таблицу значений для второй функции y=0.5×2:
| \(x\) | \(0\) | \(1\) | \(-1\) | \(2\) | \(-2\) | \(3\) | \(-3\) |
| \(y\) | \(0\) | \(0.5\) | \(0.5\) | \(2\) | \(2\) | \(4.5\) | \(4.5\) |
Построим точки \((0; 0), (1; 0,5), (-1; 0,5), (2; 2), (-2; 2), (3; 4,5), (-3; 4,5)\) на координатной плоскости; они намечают некоторую линию. Проведём её.
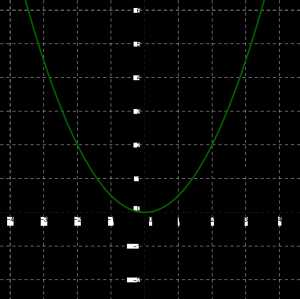
Сравни полученные рисунки. Не правда ли, проведённые линии похожи? Каждую из них называют параболой.
Точку \((0; 0)\) называют вершиной параболы, а ось \(y\) — осью симметрии параболы.
Обрати внимание!
От величины коэффициента \(k\) зависит «скорость устремления» ветвей параболы вверх или, как ещё говорят, «степень крутизны» параболы.
Точно так же обстоит дело с любой другой функцией вида y=kx2, где \(k > 0\).
Графиком её является парабола с вершиной в начале координат, ветви параболы направлены вверх, причём тем круче, чем больше коэффициент \(k\).
Ось \(y\) является осью симметрии параболы.
Кстати, ради краткости речи математики часто вместо длинной фразы «парабола, служащая графиком функции y=kx2» говорят «парабола y=kx2», а вместо термина «ось симметрии параболы» используют термин «ось параболы».
Ты замечаешь, что имеется аналогия с функцией \(у = kx\)?
Если \(k > 0\), то графиком функции \(у = kx\) является прямая, проходящая через начало координат (помнишь, мы говорили коротко: прямая \(у = kx\)), причём и здесь от величины коэффициента \(k\) зависит «степень крутизны» прямой. Это хорошо видно на рисунке, где в одной системе координат изображены графики линейных функций \(у = kx\) при трёх значениях коэффициента \(k\).
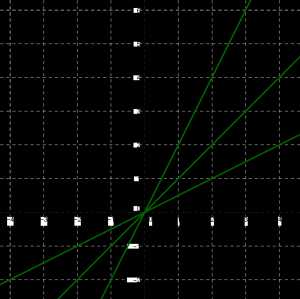
Вернёмся к функции y=kx2. Выясним, как обстоит дело в случае отрицательного коэффициента \(k\). Построим, например, график функции y=−x2 (здесь \(k = — 1\)). Составим таблицу значений:
| \(x\) | \(0\) | \(1\) | \(-1\) | \(2\) | \(-2\) | \(3\) | \(-3\) |
| \(y\) | \(0\) | \(-1\) | \(-1\) | \(-4\) | \(-4\) | \(-9\) | \(-9\) |
Отметим точки \((0; 0), (1; -1), (-1; -1), (2; -4), (-2; -4), (3; -9), (- 3; — 9)\) на координатной плоскости; они намечают некоторую линию. Проведём её.
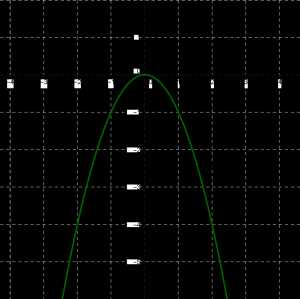
Это парабола с вершиной в точке \((0; 0)\), ось \(y\) — ось симметрии, но в отличие от случая, когда \(k > 0\), на этот раз ветви параболы направлены вниз. Аналогично обстоит дело и для других отрицательных значений коэффициента \(k\).
Обрати внимание!
Итак, графиком функции y=kx2 (k≠0) является парабола с вершиной в начале координат; ось \(y\) является осью параболы; ветви параболы направлены вверх при \(k>0\) и вниз — при \(k<0\).
Отметим ещё, что парабола y=kx2 касается оси \(x\) в точке \((0; 0)\), т. е. одна ветвь параболы плавно переходит в другую, как бы прижимаясь к оси \(x\).
Если построить в одной системе координат графики функций y=x2 и y=−x2, то нетрудно заметить, что эти параболы симметричны друг другу относительно оси \(x\), что хорошо видно на рисунке.
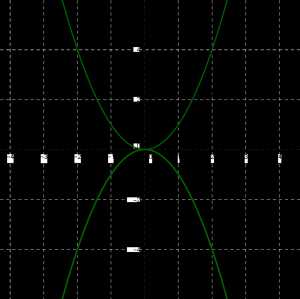
Точно так же симметричны друг другу относительно оси \(x\) параболы y=2×2 и y=−2×2.
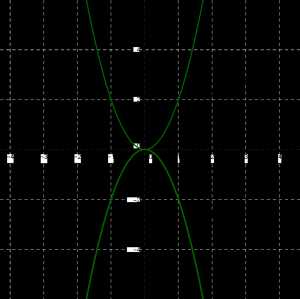
Обрати внимание!
Вообще график функции \(у = — f(x)\) симметричен графику функции \(у = f(x)\) относительно оси абсцисс.
www.yaklass.ru
Пошаговое руководство построение графика квадратичной функции
Для того, чтобы начертить график функции в Прямоугольной системе координат, нам необходимы две перпендикулярные прямые xOy (где O это точка пресечения x и y), которые называются «координатными осями», и нужна единица измерения.
У точки в этой системе есть две координаты.
M(x, y): M это название точки, x это абсцисса и она измеряется по Ox, а y это ордината и мерится по Oy.
Если мы рассмотрим функцию f: A -> B (где A — область определения, B — область значений функции), тогда точку на графике данной функции можно представить в форме P(x, f(x)).
Пример
f:A -> B, f(x) = 3x — 1
If x = 2 => f(2) = 3×2 — 1 = 5 => P(2, 5) ∈ Gf (где Gf это график данной функции).
Квадратичная функция
Стандартная форма: f(x) = ax2 + bx + c
Вершинная форма: $f(x)=(a+\frac{b}{2a})^2-\frac{\Delta}{4a}$
где Δ = b2 — 4ac
Если a > 0, то минимальным значением f(x) будет $-\frac{\Delta}{4a}$ , которое получается, если $x=-\frac{b}{2a}$. Графиком будет выпуклая парабола, вершина которой (точка, в которой она меняет направление) это $V(-\frac{b}{2a};-\frac{\Delta}{4a})$.
Если a < 0, то минимальное значение f(x) будет $-\frac{\Delta}{4a}$ , которое получается, если $x=-\frac{b}{2a}$. Графиком будет вогнутая парабола, вершина которой это$V(-\frac{b}{2a};-\frac{\Delta}{4a})$.
Парабола симметрична относительно прямой, которую она пересекает $x=-\frac{b}{2a}$ и которая называется «осью симметрии».
Именно поэтому, ког
www.math10.com
[Билет 24] Квадратичная функция. Выделение полного квадрата. Вывод формулы корней квадратного уравнения, условия их существования и числа. Прямая и обратная теоремы Виета. Разложение квадратного трёхчлена на линейные множители.
Квадратичная функция.Функция, заданная формулой y = ax2 + bx + c , где x и y — переменные, а a, b, c — заданные числа, причем a не равно 0 ,
называется квадратичной функцией
Выделение полного квадрата.
Вывод формулы корней квадратного уравнения, условия их существования и числа.
 – дискриминант квадратного уравнения.
– дискриминант квадратного уравнения.Прямая и обратная теоремы Виета.
3. Теорема ВиетаТеорема. Сумма корней приведённого квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену.Доказательство. Рассмотрим приведённое квадратное уравнение. Обозначим второй коэффициент буквой p, а свободный член — буквой q.Пусть D>0 .Тогда это уравнение имеет два корня: и найдём сумму и произведение корней: |
3.1 Теорема, обратная теореме ВиетаТеорема. Если числа m и n таковы, что их сумма равна –p, а произведение равно q, то эти числа являются корнями уравненияДоказательство. По условию m+n=-p,а mn=q. Значит, уравнениеможно записать в виде: Подставив вместо x число m, получим: Значит, число m является корнем уравнения. Аналогично можно показать, что число n так же является корнем уравнения: |
Разложение квадратного трёхчлена на линейные множители.
Теорема. Пусть
x1 и x2 — корни квадратного трехчлена x2 + px + q. Тогда этот трехчлен раскладывается на линейные множители следующим образом: x2 + px + q = (x — x1) (x — x2).Доказательство. Подставим вместо
p и q их выражения через x1 и x2 и воспользуемся способом группировки:x2 + px + q = x2 — (x1 + x2) x + x1 x2 = x2 — x1 x — x2 x + x1 x2 = x (x — x1) — x2 (x — x1) = = (x — x1) (x — x2). Теорема доказана.
Квадратное уравнение. График квадратного трехчлена
• Уравнение вида
называется квадратным уравнением. Число D = b2 — 4ac — дискриминант
этого уравнения.
Если
то числа
являются корнями (или решениями) квадратного уравнения. Если D = 0, то корни совпадают:
Если D < 0, то квадратное уравнение корней не имеет.
Справедливы формулы:
— формулы Виета; а
ах2 + bх + с = а(х — х1)(х — х2) —
формула разложения на множители.
Графиком квадратичной функции (квадратного трехчлена) у = ах2 + bх + с является парабола. Расположение параболы в зависимости от знаков коэффициента а и дискриминанта D приведено на рис.
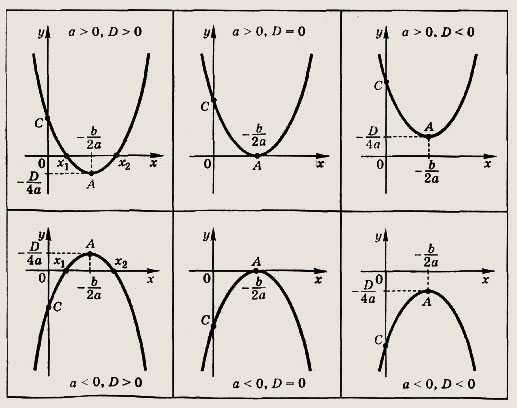
Числа х1 и х2 на оси абсцисс — корни квадратного уравнения ах2 + bх + + с = 0; координаты вершины параболы (точки А) во всех случаях
точка пересечения параболы с осью ординат имеет координаты (0; с).
Подобно прямой и окружности парабола разбивает плоскость на две части. В одной из этих частей координаты всех точек удовлетворяют неравенству у > ах2 + bх + с, а в другой — противоположному. Знак неравенства в выбранной части плоскости определяем, найдя его в какой-либо точке этой части плоскости.
Рассмотрим понятие касательной к параболе (или окружности). Прямую у — kx + 1 назовем касательной к параболе (или окружности), если она имеет с этой кривой одну общую точку.
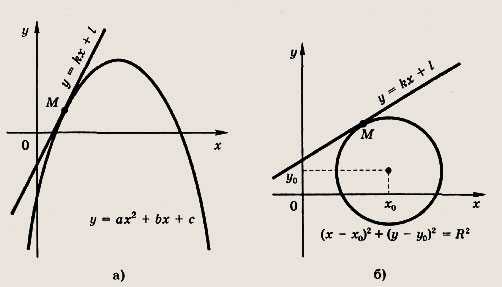
В точке касания М(х; у) для параболы выполняется равенство kx +1 = ах2 + bх + с (для окружности — равенство (х — х0)2 + (kx + 1 — у0)2 — R2). Приравнивая дискриминант полученного квадратного уравнения нулю (так как уравнение должно иметь единственное решение), приходим к условиям для вычисления коэффициентов касательной.
fizmatinf.blogspot.com
Как построить график квадратичной функции
Автор Сергей Валерьевич
Четверг, Декабрь 10, 2015
Построение графика квадратичной функции всегда было проблемой для многих школьников. Проблема в том, что на уроках в школе этому важнейшему материалу зачастую уделяют не достаточно внимания. В результате, когда появляется необходимость, ученику очень трудно отыскать в школьном учебнике или интернете чёткий алгоритм построения графика квадратичной функции (параболы), а вместо этого приходится по крупицам выискивать необходимую информацию из множества различных источников. Решим эту проблему раз и навсегда! В данной статье репетитором по математике и физике представлен алгоритм построения параболы.
Алгоритм построения графика функции y=ax²+bx+c
Данный алгоритм продемонстрируем на примере построения графика квадратичной функции . В этом случае: , и .
1. Определим, куда направлены ветви соответствующей параболы. Если , то ветви параболы направлены вверх, если , то ветви параболы направлены вниз.
В нашем примере . Следовательно, ветви параболы направлены вниз.
2. Найдем координаты вершины параболы. Абсцисса вершины параболы определяется по формуле:
Ордината вершины параболы определяется путем подстановки в уравнение квадратичной функции и вычисления соответствующего значения.
В нашем случае абсцисса вершины параболы равна:
yourtutor.info
Квадратичная функция — это… Что такое Квадратичная функция?
квадратичная функция — — [[http://www.rfcmd.ru/glossword/1.8/index.php?a=index d=23]] квадратичная функция Функция вида y= ax2 + bx + c (a ? 0). График К.ф. — парабола, вершина которой имеет координаты [ b/ 2a, (b2 4ac) /4a], при а>0 ветви параболы… … Справочник технического переводчика
КВАДРАТИЧНАЯ ФУНКЦИЯ — КВАДРАТИЧНАЯ ФУНКЦИЯ, математическая ФУНКЦИЯ, значение которой зависит от квадрата независимой переменной, х, и задается, соответственно, квадратичным МНОГОЧЛЕНОМ, например: f(x) = 4х2 + 17 или f(x) = х2 + 3х + 2. см. также КВАДРАТНОЕ УРАВНЕНИЕ … Научно-технический энциклопедический словарь
Квадратичная функция — Квадратичная функция [quadratic function] — функция вида y= ax2 + bx + c (a ≠ 0). График К.ф. — парабола, вершина которой имеет координаты [ b/ 2a, (b2 4ac) /4a], при а> 0 ветви параболы направлены вверх, при a< 0 –вниз… … Экономико-математический словарь
КВАДРАТИЧНАЯ ФУНКЦИЯ, КВАДРАТНЫЙ, КВАДРАТИЧНЫЙ — (quadratic) Функция, имеющая следующий вид: у=ах2+bх+с, где a≠0 и высшая степень х – квадрат. Квадратное уравнение у=ах2 +bх+с=0 может быть также решено с использованием следующей формулы: х= –b+ √ (b2–4ac) /2а. Эти корни являются действительными … Экономический словарь
Аффинно-квадратичная функция — Аффинно квадратичной функцией на аффинном пространстве S называется всякая функция Q: S→K, имеющая в векторизованной форме вид Q(x)=q(x)+l(x)+c, где q квадратичная функция, l линейная функция, с константа. Содержание 1 Перенос начала отсчета 2… … Википедия
Афинно-квадратичная функция — Аффинно квадратичной функцией на аффинном пространстве называется всякая функция , имеющая в векторизованной форме вид , где симметричная матрица, линейная функция, константа. Содержание … Википедия
Квадратичная форма — функция на векторном пространстве, задаваемая однородным многочленом второй степени от координат вектора. Содержание 1 Определение 2 Связанные определения … Википедия
Функция потерь — – функция, которая в теории статистических решений характеризует потери при неправильном принятии решений на основе наблюдаемых данных. Если решается задача оценки параметра сигнала на фоне помех, то функция потерь является мерой расхождения… … Википедия
целевая функция — — [Я.Н.Лугинский, М.С.Фези Жилинская, Ю.С.Кабиров. Англо русский словарь по электротехнике и электроэнергетике, Москва, 1999 г.] целевая функция В экстремальных задачах — функция, минимум или максимум которой требуется найти. Это… … Справочник технического переводчика
Целевая функция — [target function] в экстремальных задачах функция, минимум или максимум которой требуется найти. Это ключевое понятие оптимального программирования. Найдя экстремум Ц.ф. и, следовательно, определив значения управляемых переменных, которые к нему… … Экономико-математический словарь
dic.academic.ru
