Соотношения между сторонами и углами прямоугольного треугольника
На данном уроке мы вспомним основные теоретические факты о прямоугольном треугольнике, рассмотрим связи между его сторонами и углами, вспомним формулы, связывающие тригонометрические функции острого угла.
Если у вас возникнет сложность в понимании темы, рекомендуем посмотреть урок «Основы геометрии»
Тема: Повторение курса геометрии 8 класса
Урок: Соотношения между сторонами и углами прямоугольного треугольника
Нарисуем прямоугольный треугольник , угол прямой. , катет , , катет . Гипотенуза (см. Рис. 1).
Соотношения между углами и сторонами в прямоугольном треугольнике задаются тригонометрическими функциями – синусом, косинусом, тангенсом, котангенсом.
Рис. 1
Определение
Синусом острого угла прямоугольного треугольника называется отношение противолежащего ему катета к гипотенузе.
Определение
Косинусом острого угла прямоугольного треугольника называется отношение прилежащего ему катета к гипотенузе.
Определение
Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего ему катета к прилежащему.
Определение:
Котангенсом острого угла прямоугольного треугольника называется отношение прилежащего ему катета к противолежащему.
Кроме того, важный факт касается углов прямоугольного треугольника: сумма острых углов прямоугольного треугольника составляет .
Для удобства выпишем выражения для всех сторон треугольника через тригонометрические соотношения.
Правило нахождения катета через гипотенузу:
Катет прямоугольного треугольника равен произведению гипотенузы на синус противолежащего ему угла или на косинус прилежащего ему угла.
Правило нахождения катета через второй катет:
Катет прямоугольного треугольника равен произведению второго катета на тангенс противолежащего искомому катету угла или на котангенс прилежащего искомому катету угла.
Напомним другие важные тригонометрические соотношения:
1. – основное тригонометрическое тождество;
Доказательство:
Вспомним теорему Пифагора, согласно которой сумма квадратов катетов равна квадрату гипотенузы:
α=b
Согласно правилу нахождения гипотенузы:
АВ=аsinα=c
Рис. 2
Итак, мы рассмотрели основные соотношения, связывающие углы и стороны в прямоугольном треугольнике. Вспомнили основные формулы, которые связывают тригонометрические функции острого угла. Кроме того, мы решили несколько типовых задач.
Список литературы
- Александров А.Д. и др. Геометрия, 8 класс. – М.: Просвещение, 2006.
- Бутузов В.Ф., Кадомцев С.Б., Прасолов В.В. Геометрия, 8 класс. – М.: Просвещение, 2011.
- Мерзляк А.Г., Полонский В.Б., Якир С.М. Геометрия, 8 класс. – М.: ВЕНТАНА-ГРАФ, 2009.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Uztest.ru (Источник).
- Terver.ru (Источник).
- Bymath.net (Источник).
Домашнее задание
- Задание 1: в равнобедренном треугольнике ∆КРО с основанием РО проведена высота КН. Найдите угол ∠ОKН, если угол ∠Р=54°.
- Задание 2: один из углов прямоугольного треугольника 60°, а сумма гипотенузы и меньшего из катетов равна 26,4с м. Найдите гипотенузу треугольника.
- Задание 3: в прямоугольном треугольнике ∆АВС с прямым углом ∠С внешний угол при вершине А равен 120°. АС+АВ = 18 см, найдите длины АС и АВ.
interneturok.ru
Соотношение между углами и сторонами треугольника — урок. Геометрия, 7 класс.
В треугольнике против большей стороны лежит больший угол.
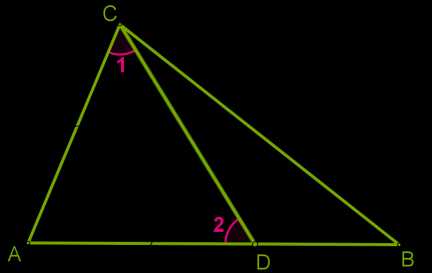
Доказательство
Пусть в треугольнике \(ABC\) сторона \(AB\) больше стороны \(AC\).
Докажем, что ∡ \(C >\) ∡ \(B\).
Отложим на стороне \(AB\) отрезок, равный стороне \(AC\).
Так как \(AD < AB\), то точка \(D\) лежит между точками \(A\) и \(B\).
Следовательно, угол \(1\) является частью угла \(C\) и, значит, ∡ \(C >\) ∡ \(1\).
Угол \(2\) — внешний угол треугольника \(BDC\), поэтому ∡ \(2 >\) ∡ \(B\).
∡ \(1 =\) ∡ \(2\) как углы при основании равнобедренного треугольника \(ADC\).
Таким образом, ∡ \(C >\) ∡ \(1 =\) ∡ \(2 >\) ∡ \(B\).
Отсюда следует, что ∡ \(C >\) ∡ \(B\).
Справедлива и обратная теорема.
В треугольнике против большего угла лежит большая сторона.
Следствия
Следствие 1. Если два угла треугольника равны, то треугольник равнобедренный (признак равнобедренного треугольника).
Следствие 2. Если три угла треугольника равны, то треугольник равносторонний.
Следствие 3. В прямоугольном треугольнике гипотенуза больше катета.
Неравенство треугольника
Каждая сторона треугольника меньше суммы двух других сторон.
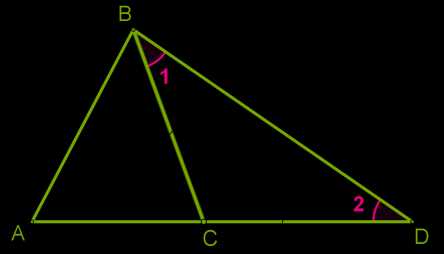
Доказательство
Рассмотрим треугольник \(ABC\) и докажем, что \(AB < AC + BC\).
Продолжим сторону \(AC\) и отложим отрезок \(CD = BC\).
Треугольник \(BCD\) — равнобедренный, следовательно, ∡ \(1 = \) ∡ \(2\).
В треугольнике \(ABD\) очевидно, что ∡ \(ABD >\) ∡ \(1\), а это значит, что ∡ \(ABD >\) ∡ \(2\).
Так как против большего угла лежит большая сторона, \(AB
Следствие 4. Для любых трёх точек \(A\), \(B\) и \(C\), не лежащих на одной прямой, справедливы неравенства:
\(AB < AC + CB, AC < AB + BC, BC < AB + AC\).
www.yaklass.ru
Соотношения между сторонами и углами треугольника. Неравенство треугольника [wiki.eduVdom.com]
Теорема 1. В треугольнике против большей стороны лежит больший угол.
Доказательство. Пусть в треугольнике ABC сторона АВ больше стороны АС (рис.1, а).
Рис.1
Докажем, что ∠ С > ∠ В. Отложим на стороне АВ отрезок AD, равный стороне АС (рис.1, б). Так как AD < АВ, то точка D лежит между точками А и В. Следовательно, угол 1 является частью угла С и, значит, ∠ C > ∠ 1. Угол 2 — внешний угол треугольника BDC, поэтому Z 2 > Z В. Углы 1 и 2 равны как углы при основании равнобедренного треугольника ADC. Таким образом, ∠ С > ∠ 1, ∠ 1 = ∠ 2, ∠ 2 > ∠ B. Отсюда следует, что ∠ С > ∠ В.
Справедлива и обратная теорема (ее доказательство проводится методом от противного).
Теорема 2. В треугольнике против большего угла лежит большая сторона.Из теоремы 1 вытекает
Следствие 1. Если два угла треугольника равны, то треугольник равнобедренный (признак равнобедренного треугольника).
Доказательство следствия проводится методом от противного.
Из следствия 1 следует, что если три угла треугольника равны, то треугольник равносторонний.
Из теоремы 2 получаем
Следствие 3. В прямоугольном треугольнике гипотенуза больше катета.
С использованием теоремы 2 устанавливается следующая теорема.
Теорема 3. Каждая сторона треугольника меньше суммы двух других сторон.
Следствие 4. Для любых трех точек А, В и С, не лежащих на одной прямой, справедливы неравенства:
АВ < АС + СВ, АС < АВ + ВС, ВС < ВА + АС.
Каждое из этих неравенств называется неравенством треугольника.
Пример 1. Сравнить углы треугольника ABC и выяснить, может ли быть угол А тупым, если АВ > ВС > АС.
Решение. Согласно теореме 1 имеем: ∠ C> ∠ A > ∠ B. Угол А тупым быть не может, так как тогда ∠ С тоже тупой и, значит, ∠ A + ∠ B + ∠ C > 180°, что невозможно (Теорема о сумме углов треугольника).
Пример 2. Сравнить стороны треугольника ABC, если ∠ A > ∠ B > ∠ C.
Решение. Согласно теореме 1 имеем: ВС > АС > АВ.
Пример 3. Две стороны равнобедренного треугольника равны 6 и 2. Чему равна третья сторона?
Решение. Так как каждая сторона треугольника меньше суммы двух других сторон (теорема 3), то третья сторона может быть равной только 6.
Решение. Обозначим третью сторону треугольника через х. Тогда х < 1,5 + 0,7 = 2,2 (теорема 3). Отсюда, учитывая, что эта сторона выражается натуральным числом, следует, что х = 2 или х = 1.
www.wiki.eduvdom.com
Соотношения между сторонами и углами треугольника
Соотношения между сторонами и углами треугольника помогают сравнивать углы треугольника, зная соотношение его сторон, и наоборот.
Теорема
(соотношения между сторонами и углами треугольника).
В треугольнике:
1) против большей стороны лежит больший угол;
2) против большего угла лежит большая сторона.
1) Дано: ∆ ABC, AC>AB.
Доказать: ∠B>∠C.
Доказательство:
Отложим на стороне AC отрезок AK: AK=AB.
Так как AC>AB, то точка K лежит между точками A и C. Следовательно, ∠ABC=∠ABK+∠KBC, то есть ∠ABC>∠ABK.
Так как AK=AB, то треугольник ABK — равнобедренный с основанием BK.
Значит, у него углы при основании равны: ∠ABK=∠AKB.
Для треугольника BCK ∠AKB — внешний.
Поэтому ∠AKB=∠KBC+∠C, а значит, ∠AKB>∠C.
Имеем:
2) Дано: ∆ ABC,
∠B>∠C.
Доказать: AC>AB.
Доказательство:
(методом от противного).
Предположим, что неравенство AC>AB — неверное. Тогда либо AC=AB, либо AC<AB.
Если AC=AB, то треугольник ABC — равнобедренный с основанием BC и у него углы при основании равны: ∠B=∠C, что противоречит условию.
По доказанному в пункте 1), против большей стороны лежит больший угол. Поэтому, если AC<AB, то ∠B<∠C. Снова пришли к противоречию.
Значит, выдвинутое нами предположение неверно. Следовательно, AC>AB.
Что и требовалось доказать.
www.treugolniki.ru
Задача по геометрии за 7 класс по Анатасяну
тут нужно рисунок рисовать.. . сумма углов треугольника =180 градусов, следовательно 3х+7х+8х=180, х=10, отсюда углы в треугольнике равны 30, 70 и 80 градусов соответственно. рассмотрим внешний угол треуг, при угле 30 градусов, он =180-30-150. рассмотрим внешн. угол треугольника при угле =70 градусов он равен 180-70=110. рассмотрим внешн. угол треугольника при угле 80 градусов, он равен 180-80=100. следовательно внешние углы треугольника относятся как 15:11:10
учись лутше тогда узнаеш ответ
допустим X- 1/(3+7+8)=1/18 3Х+7Х+8Х=180 (т. к. сумма углов треугольника=180) 18Х=180 Х=10 длины сторон: 3*10=30, 7*10=70, 8*Х=80
Внутренние углы треугольника относятся как 3:7:8, тогда углы равны: 1-ый=(180/10)*3=30, 2-ой=(180/10)*7=70, 3-ий=(180/10)*8=80 Внешние равны: 150, 110, 100. Найти отношение углов.
1)К (коэф. пр. ) (3+7+8)=180(сумма углов треугольника равна 180 градусов) 18К=180 К=10 2)180-3*К=180-30=150 3)180-7К=180-70=110 4)180-8К=180-80=100 5)150/К=150/10=15 6)110/К=110/10=11 7)100/К=100/10=1 Ответ: 15/11/1 (но если хотите улучшить оценку тогда придется каждый ваш ход объяснить.).
touch.otvet.mail.ru
