Как найти площадь треугольника
Треугольники.
Как вы можете помнить из школьной программы по геометрии, треугольник – это фигура, образованная из трех отрезков, соединяющихся тремя точками, не лежащими на одной прямой. Треугольник образует три угла, отсюда и название фигуры. Определение может быть и иным. Треугольник можно так же назвать многоугольником с тремя углами, ответ будет так же верным. Треугольники делятся по числу равных сторон и по величине углов в фигурах. Так выделяют такие треугольники, как равнобедренный, равносторонний и разносторонний, а так же прямоугольный, остроугольный и тупоугольный, соответственно.
Формул вычисления площади треугольника очень много. Выбирать, как найти площадь треугольника, т.е. какой формулой воспользоваться, только вам. Но стоит отметить лишь некоторые обозначения, которые используются во многих формулах вычисления площади треугольника. Итак, запоминайте:
S – это площадь треугольника,
a, b, c – это стороны треугольника,
h – это высота треугольника,
R – это радиус описанной окружности,
p – это полупериметр.
Вот основные обозначения, которые могут вам пригодиться, если вы совершенно забыли курс геометрии. Ниже будут приведены наиболее понятные и не сложные варианты вычисления неизвестной и загадочной площади треугольника. Это не сложно и пригодится как вам в домашних нуждах, так и для помощи своим детям в домашнем задании. Давайте вспомним, как вычислить площадь треугольника проще простого:
В нашем случае площадь треугольника равна: S = ½ * 2,2 см. * 2,5 см. = 2,75 кв.см. Помните, что площадь измеряется в квадратных сантиметрах (кв.см.).
Прямоугольный треугольник и его площадь.
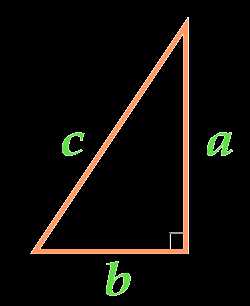
Прямоугольный треугольник – это треугольник, у которого один угол равен 90 градусам (потому называется прямым). Прямой угол образуют две перпендикулярные линии (в случае с треугольником – два перпендикулярных отрезка). В прямоугольном треугольнике прямой угол может быть только один, т.к. сумма всех углов одного любого треугольника равна 180 градусам. Получается, что 2 других угла должны делить между собой оставшиеся 90 градусов, например 70 и 20, 45 и 45 и т.д. Итак, основное вы вспомнили, осталось узнать, как найти площадь прямоугольного треугольника. Представим, что перед нами вот такой прямоугольный треугольник, и нам необходимо найти его площадь S.
1. Самый простой способ определения площади прямоугольного треугольника высчитывается по следующей формуле:
В нашем случае, площадь прямоугольного треугольника равна: S = 2,5 см. * 3 см. / 2 = 3,75 кв.см.
В принципе, больше нет необходимости выверения площади треугольника иными способами, т.к. в быту пригодится и поможет только этот. Но существуют и варианты измерения площади треугольника через острые углы.
2. Для других способов вычисления необходимо иметь таблицу косинусов, синусов и тангенсов. Посудите сами, вот какие варианты вычисления площадей прямоугольного треугольника еще можно использовать:
Мы решили воспользоваться первой формулой и с небольшими помарками (чертили в блокноте и использовали старую линейку и транспортир), но у нас вышел верный расчет:
S = (2,5*2,5)/(2*0,9)=(3*3)/(2*1,2). У нас вышли такие результаты 3,6=3,7, но с учетом сдвига клеток, этот нюанс нам можно простить.
Равнобедренный треугольник и его площадь.
Если перед вами стоит задача вычислить формулу равнобедренного треугольника, то проще всего воспользоваться главной и как считается классической формулой площади треугольника.
Но для начала, перед тем, как найти площадь равнобедренного треугольника, узнаем, что это за фигура такая. Равнобедренным треугольником называется треугольник, у которого две стороны имеют одинаковую длину. Эти две стороны называются боковыми, третья сторона называется основанием. Не путайте равнобедренный треугольник с равносторонним, т.е. правильным треугольником, у которого все три стороны равны. В таком треугольнике нет особых тенденций к углам, точнее к их величине. Однако углы у основания в равнобедренном треугольнике равны, но отличаются от угла между равными сторонами. Итак, первую и главную формулу вы уже знаете, осталось узнать, какие еще формулы определения площади равнобедренного треугольника известны:
Как вы можете заметить, в этих формулах активно используются углы, их величины, косинусы, синусы и тангенсы. По этой причине, без специальной книжки вам не обойтись, хотя всю информацию вы сможете найти в Интернете. Отметим только, что в формулах угол альфа – тот, что находится между боковой стороной и основанием, а угол гамма (y) – тот, что находится между равными боковыми сторонами треугольника.
kakznatok.ru
Площадь треугольника
Площадь треугольника, формулы для вычисления площади различных видов треугольников и калькулятор для решения онлайн. Площадь треугольника — это численная характеристика, характеризующая размер плоскости, ограниченной геометрической фигурой, образованной тремя отрезками (сторонами), которые соединяют три точки (вершины), не лежащие на одной прямой.
Для вычисления площади треугольника применяются различные формулы, в зависимости от известных исходных данных. Ниже приведены формулы и калькулятор, который поможет вычислить площадь треугольника или проверить уже выполненные вычисления. Приведены общие формулы для всех типов треугольников, частные случаи для равносторонних, равнобедренных и прямоугольных треугольников.
Наш калькулятор для вычисления площади поможет вам вычислить площадь разных видов треугольников или проверить уже выполненные вычисления.
Для всех треугольников
1
Площадь треугольника по основанию и высоте
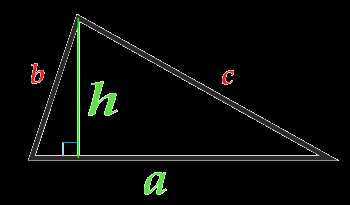
Площадь треугольника равна половине произведения основания треугольника на высоту, опущенную на это основание: . Основанием треугольника может быть выбрана любая из сторон треугольника.
Сторона a
Высота h
2
Площадь треугольника по двум сторонам и углу между ними

Площадь треугольника равна половине произведения двух любых его сторон на синус угла между этими сторонами: . Угол α между сторонами может быть любым: тупым, острым, прямым.
Сторона a
Сторона b
Угол α° между сторонами a и b
3
Площадь треугольника по радиусу вписанной окружности и трем сторонам
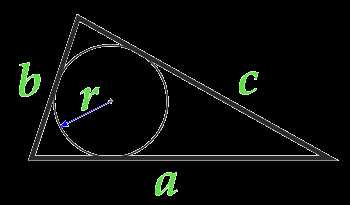
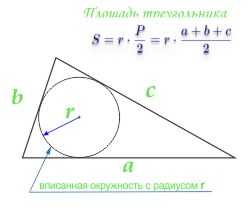
Площадь треугольника равна половине суммы всех трех сторон треугольника умноженной на радиус вписанной окружности. или по-другому можно сказать: «Площадь треугольника равна половине периметра треугольника, умноженного на радиус вписанной окружности.»
Сторона a
Сторона b
Сторона c
Радиус r вписанной окружности
4
Площадь треугольника по радиусу описанной окружности и трем сторонам
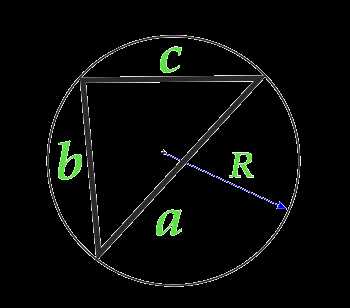
Площадь треугольника равна произведению трех сторон треугольника, деленных на четыре радиуса описанной окружности:
Сторона a
Сторона b
Сторона c
Радиус R описанной окружности5
Площадь треугольника по формуле Герона
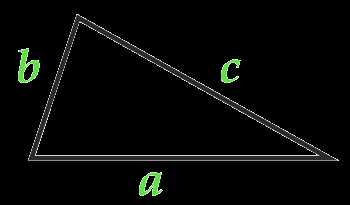
Если известны все три стороны треугольника, можно вычислить его площадь используя формулу Герона: , где p – это полупериметр треугольника, вычисляемый по формуле
Сторона a
Сторона b
Сторона c
Полупериметр:
Для равнобедренных треугольников
6
Площадь равнобедренного треугольника по боковым сторонам и углу между ними
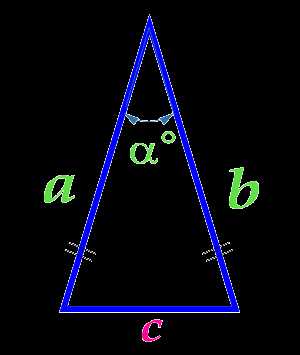
Вычислить площадь:
Боковая сторона a (a = b)
Угол α° между боковыми сторонами
7
Площадь равнобедренного треугольника по боковым сторонам и углу между ними
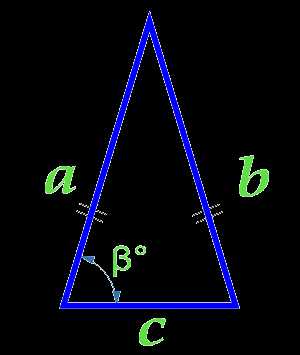
Вычислить площадь:
Боковая сторона a (a = b)
Основание треугольника c
Угол β° между основанием и стороной
8
Площадь равнобедренного треугольника по основанию и углу между боковыми сторонами
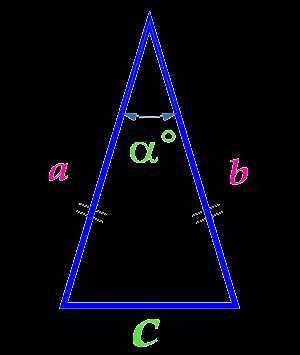
Вычислить площадь:
Основание треугольника c
Угол α° между боковыми сторонами
Для равносторонних треугольников
9
Площадь равностороннего треугольника по стороне

Вычислить площадь:
Сторона a (a = b = c)
10
Площадь равностороннего треугольника по высоте
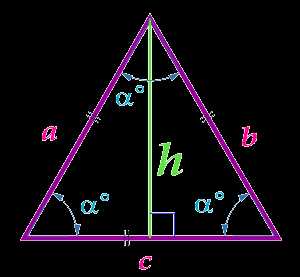
Вычислить площадь:
Высота h
11
Площадь равностороннего треугольника по радиусу вписанной окружности
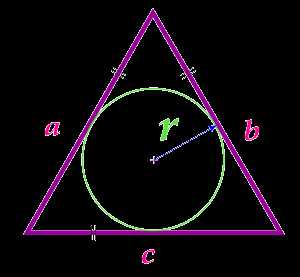
Вычислить площадь:
Радиус r вписанной окружности
12
Площадь равностороннего треугольника по радиусу описанной окружности
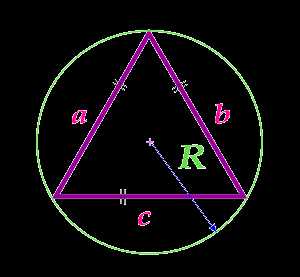
Вычислить площадь:
Радиус R описанной окружности
Для прямоугольных треугольников
13
Площадь прямоугольного треугольника по двум катетам
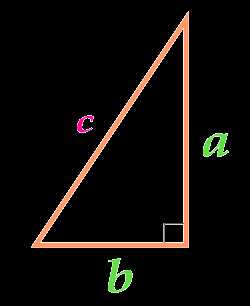
Вычислить площадь:
Катет a
Катет b
14
Площадь прямоугольного треугольника по отрезкам, на которые делит гипотенузу вписанная окружность
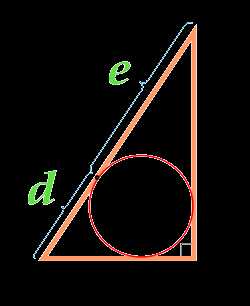
Вычислить площадь:
Отрезок d
Отрезок e
15
Площадь прямоугольного треугольника по формуле Герона
Формула Герона для прямоугольного треугольника , где p – это полупериметр треугольника, вычисляемый по формуле
Вычислить площадь:
Сторона a
Сторона b
Сторона c
Полупериметр:
Определения
Треугольник – это геометрическая фигура, образованная тремя отрезками, которые соединяют три точки, не лежащие на одной прямой. Отрезки называют сторонами треугольника, а точки – вершинами треугольника.
Площадь – это численная характеристика, характеризующая размер плоскости, ограниченной замкнутой геометрической фигурой.
Площадь измеряется в единицах измерения в квадрате: км2, м2, см2, мм2 и т.д.
В зависимости от вида треугольника и его известных исходных данных, площадь треугольника можно вычислить:
Для всех треугольников
- по основанию и высоте
-
по двум сторонам и углу между ними

-
по радиусу вписанной окружности и трем сторонам
-
по радиусу описанной окружности и трем сторонам

- по формуле Герона
Для равнобедренных треугольников
- по боковым сторонам и углу между ними
- по боковой стороне, основанию и углу между боковыми сторонами и основанием
- по основанию и углу между боковыми сторонами
Для равносторонних треугольников
- по стороне
- по высоте
- по радиусу вписанной окружности
- по радиусу описанной окружности
Для прямоугольных треугольников
- по двум катетам
- по отрезкам, на которые делит гипотенузу вписанная окружность
- по формуле Герона
doza.pro
Формулы площади треугольника
Формулы площади треугольника
Подождите пару секунд пока подгрузятся формулы
Внимание! Десятичную дробь надо писать с точкой(.), а не с запятой!
Через основание и высоту
$$S= \frac{1}{2} ah $$ \(S\) — площадь треугольника\(a\) — основание
\(h\) — высота
\(a =\) \(h =\)
Через две стороны и угол
$$S= \frac{1}{2} ab sin \alpha $$ \(S\) — площадь треугольника\(a\) — сторона
\(b\) — сторона
\( \alpha \) — угол между сторонами \(a\) и \(b\)
\(a =\) \(b =\) \( \alpha =\)
Формула Герона
$$S= \sqrt{p(p-a)(p-b)(p-c)} $$ \(S\) — площадь треугольника\(a\) — сторона
\(b\) — сторона
\(c\) — сторона
\(p\) — полупериметр, \(p= \frac{a+b+c}{2}\)
\(a =\) \(b =\) \(c =\)
Через радиус вписанной окружности
$$S= rp $$ \(S\) — площадь треугольника\(r\) — радиус вписанной окружности
\(a\) — сторона
\(b\) — сторона
\(c\) — сторона
\(p\) — полупериметр, \(p= \frac{a+b+c}{2}\)
\(r =\) \(p =\)
Через радиус описанной окружности
\(S= \frac{abc}{4R} \)\(S\) — площадь треугольника
\(R\) — радиус описанной окружности
\(a\) — сторона
\(b\) — сторона
\(c\) — сторона
\(a =\) \(b =\)
\(c =\) \(R =\)
Площадь прямоугольного треугольника
$$S= \frac{1}{2} ab $$ \(S\) — площадь треугольника\(a\) — сторона
\(b\) — сторона
\(a =\) \(b =\)
Площадь прямоугольного треугольника
$$S= de $$ \(S\) — площадь треугольника\(d =\) \(e =\)
Формула Герона для прямоугольного треугольника
$$ S= (p-a)(p-b) $$ \(S\) — площадь треугольника\(a\) — сторона
\(b\) — сторона
\(p\) — полупериметр, \(p= \frac{a+b+c}{2}\)
\(a =\) \(b =\) \(p =\)
Площадь равнобедренного треугольника
$$S= \frac{1}{2} a^2 sin \alpha$$ \(S\) — площадь треугольника\(a\) — сторона
\(\alpha\) — угол между боковыми сторонами
\(a =\) \( \alpha =\)
Площадь равнобедренного треугольника
\(a\) — сторона
\(b\) — сторона
\(\alpha\) — угол между боковыми сторонами и основанием
\(a =\) \(b =\) \( \alpha =\)
Площадь равнобедренного треугольника
$$S= \frac{b^2}{4tg \frac{ \alpha }{2}} $$ \(S\) — площадь треугольника\(b\) — сторона
\(\alpha\) — угол между боковыми сторонами и основанием
\(b =\) \(\alpha =\)
Формула Герона для равнобедренного треугольника
a = b =Площадь равностороннего треугольника
$$S= \frac{ \sqrt{3}a^2}{4} $$ \(S\) — площадь треугольника\(a\) — сторона
\(a =\)
Площадь равностороннего треугольника
$$S= \frac{3 \sqrt{3}R^2}{4}$$ \(S\) — площадь треугольника\(R\) — радиус описанной окружности
\(R =\)
Площадь равностороннего треугольника
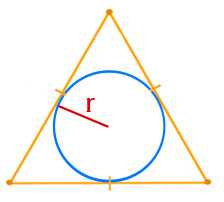 $$S= 3 \sqrt{3}r^2 $$
\(S\) — площадь треугольника
$$S= 3 \sqrt{3}r^2 $$
\(S\) — площадь треугольника\(r\) — радиус вписанной окружности
\(r =\)
Площадь равностороннего треугольника
$$S= \frac{h^2}{\sqrt{3}}$$ \(S\) — площадь треугольника\(h\) — высота
\(h =\)
www.100formul.ru
Как найти площадь прямоугольного треугольника 3 класс формула пример
Решебник к сборнику задач «Ершова А.П., Голобородько В.В., Ершова А.С. Самостоятельные и контрольные работы по алгебре и геометрии для 8 класса. Применение подобия к решению задач. СА-12. Соотношения между сторонами и углами прямоугольного треугольника. КА-4. Применение подобия к.
Площадь прямоугольного треугольника. 3-й класс
Цели:
- Образовательные:
- закреплять материал, изученный на предыдущих уроках:
- нахождение части от числа и числа от части, нахождение площади прямоугольника, нахождение процентов.
обработать понятие катеты, гипотенуза, площадь прямоугольного треугольника; вычислительные навыки, знание P и S; закреплять умение решать задачи на повторение (нахождение части от числа, % в этом числе и нахождение площади).
Развивающие:
- развивать логическое мышление, наблюдательность, речь, умение анализировать, сравнивать, делать обобщения. развивать познавательные интересы и творческие способности учащихся.
Воспитательные:
- совершенствовать умение работать в небольших группах, прислушиваться к мнению одноклассников, отстаивать свою точку зрения. прививать умение использовать знания, полученные на уроке из повседневной жизни и жизненного опыта на уроке и наоборот.
– Работу начинаем в группах постоянного состава. Зашифрованы слова. Вспомните порядок действий, формулы вычисления и расшифруйте слова (устные вычисления прилагаются).
На доске плакат. Исключим каждую третью фигуру. Осталось две фигуры назовите их (прямоугольный треугольник, прямоугольник).
Сегодня на уроке мы узнаем много нового о прямоугольном треугольнике и научимся находить его площадь.
III. Объяснение нового материала
1) Работа в парах со сменным составом.
Дан прямоугольник ABCD со сторонами 4 см и 5 см, разрежьте его по диагонали AC. Что получили?
Обменяйтесь треугольниками и докажите, что полученные треугольники равны.
Измерьте с помощью палетки площади треугольников ABC и ACD. Сравните S своего треугольника с S треугольника своего соседа. Что заметили?
Встаньте пары, у которых S треугольников получились одинаковыми.
3) Смена пар (ручеек).
Сравните площади двух треугольников ABC и ADC с площадью прямоугольника ABCD. Сделайте вывод.
Из каких двух треугольников мы составили прямоугольник?
1) В треугольнике MNK угол М прямой, поэтому его называют прямоугольным треугольником. Достройте треугольник MNK до прямоугольника. Измерьте стороны прямоугольника и найдите площадь. Можно ли с помощью полученного результата найти площадь треугольника MNK?
Дети находят S треугольника, зная S прямоугольника (= 10 см 2 ).
2) Знакомство с катетами и гипотенузой. Читают учебник с. 93, №3, закрепляют. На доске и в учебнике:
– Какие стороны образуют прямой угол?
– Как называется третья сторона треугольника? (Обведи красным карандашом).
3) Обобщим, что мы делали?
1 – Дан прямоугольник.
2 – Разделили по диагонали на два треугольника.
3 – Нашли площадь треугольника. Она равна S площадей двух треугольников.
4 – Узнали, что стороны, образующие прямой угол, называют катетами, сторона, лежащая напротив прямого угла, называется гипотенузой.
4) – Молодцы! Перед нами стоит новая задача. Как вычислить S прямоугольного треугольника, если известны его катеты а и b?
5) – Обсудите в парах (или четверках).
Подумайте о зависимости между величинами S, a, b.
Выведите формулу, устанавливающую эту зависимость.
(Дети делают вывод, если затрудняются в формулировке — помогаю.)
6) – Закрепляем теорию по учебнику: с. 94, правило №5 (1 фигура).
V. Закрепление нового материала по учебнику с. 94, №5 (2, 3 фигуры)
Работа в группах постоянного состава.
1 и 3 группа фигура №2
2 и 4 группа фигура №3
Взаимопроверка. Представители от групп рассказывают о проделанной работе.
Вывод: чтобы найти площадь прямоугольного треугольника, нужно катеты перемножить и произведение разделить на 2.
VI. – Молодцы! Немного отдохнём.
1. Нарисуй недостающую картинку(c. 95).
2. Найди нарушенную закономерность:
VII. Решим более сложную задачу ( в тетрадях)
Дети решают уравнения по вариантам с.95, №10
Два ученика у доски. Проверка в парах.
1. с.94 разминка.
2. Решение задач с. 95 ,№7, схема на доске, решают цепочкой на доске и в учебнике.
Учащиеся повторяют алгоритм решения текстовых задач. (Класс разделяется на 5 малых групп с помощью геометрических фигур разного цвета, формы и размера).
1) Каждая группа фиксирует алгоритм решения текстовой задачи в виде блок-схемы.
2) Состав группы меняется (геометрические фигуры меняются по размеру). Группа в новом составе выполняет 1 действие и поясняет его.
3) Состав группы меняется (геометрические фигуры меняются по цвету). Группа выполняет 2 действие и поясняет его.
4) Состав группы меняется (геомет
poiskvstavropole.ru
Площадь треугольника. Площадь треугольника формулы. 6 формул площади треугольника.
В этой статье собраны наиболее популярные формулы для нахождения площади треугольника.
Если известно основание и высота, проведенная к основанию треугольника, можно вычислить площадь треугольника.
\(S=\frac{1}{2}a*h\)
Формула Герона помогает вычислить площадь треугольника по трем сторонам треугольника:
\(S=\sqrt{p(p-a)(p-b)(p-c)}\)
где \(a,b,c\) – стороны треугольника, \(p=\frac{a+b+c}{2}\) – его полупериметр.
Известная формула площади для физиков по двум сторонам и углу между ними :
\(P=\frac{1}{2}ab*sinα \)
Площадь треугольника можно вычислить, если известно три стороны и описанная окружность:
\(S=\frac{a*b*c}{4R}\)
Площадь треугольника, когда мы знаем полупериметр и радиус вписанной окружности:
\(S=pr\)
где r — радиус вписанной окружности, \(p=\frac{a+b+c}{2}\)– его полупериметр.
Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!
Запишитесь на бесплатное тестирование знаний!
myalfaschool.ru
Площадь треугольника по трем сторонам
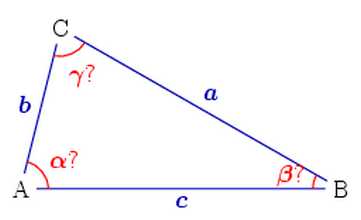 Найти площадь треугольника можно различными способами. Конечно же, в зависимости от данных переменных и подбирается необходимая формула. В основном, для нахождения площади треугольника применяется формула Герона.
Найти площадь треугольника можно различными способами. Конечно же, в зависимости от данных переменных и подбирается необходимая формула. В основном, для нахождения площади треугольника применяется формула Герона.
Если известны все три стороны треугольника ABC, то формула площади треугольника по трем сторонам легко применится на практике:
где:
- p – полупериметр треугольника,
- a, b, c – длины сторон треугольника.
Периметр – это сумма длин всех сторон треугольника. Соответственно полупериметр – это сумма длин всех сторон разделенная на 2.
Дан треугольник. Стороны a = 3 см., b = 4 см., c = 5 см. Для начала найдем полупериметр
=6 см.
Далее рассчитаем площадь
Площадь треугольника равна 6 кв. см
Также можно найти площадь треугольника и по другим формулам – через синус и косинус.
2mb.ru
как найти площадь треугольника 3 класса, если стороны 2 см, 3см, 3,5 см.
длину умнож на ширину и раздели на два
Вообще существует формула через полупериметр, но там корень квадратный присутствует. вряд ли такое в 3 классе проходят. площадь= корень из р (р-а) (р-в) (р-с) , т. е. корень из 4,25(4,25-3)(4,25-3,5)(4,25-2)= корень из 4,25*1,25*0,75*2,25= корень из 8,96484375
Вообще существует формула через полупериметр, но там корень квадратный присутствует. вряд ли такое в 3 классе проходят. площадь= корень из р (р-а) (р-в) (р-с) , т. е. корень из 4,25(4,25-3)(4,25-3,5)(4,25-2)= корень из 4,25*1,25*0,75*2,25= корень из 8,96484375
надо найти периметр воображаемого треугольника и разделить на 2
touch.otvet.mail.ru
