Построение параболы, с примерами
Алгоритм построения графика параболы
Если парабола задана уравнением , то чтобы построить ее график, понадобится:
- Выяснить направление ветвей параболы: если коэффициент , то ветви направлены вверх, а если – вниз.
- Определить координаты вершины параболы. Чтобы определить абсциссу вершины параболы пользуются формулой
Для определения ординаты вершины параболы нужно подставить в уравнение параболы вместо найденное в предыдущем шаге значение :
- Нанести полученную точку на график и провести через неё ось симметрии, параллельно координатной оси .
- Найти точки пересечения с осями координат:
- Найти координаты произвольной точки , которая принадлежит параболе. Для этого возьмем произвольное значение и подставим его в уравнение параболы.
- Соединить полученные точки на графике плавной линией и продолжить график за крайние точки, до конца координатной оси.
– с осью – найти корни уравнения , если уравнение не имеет действительных корней, то график не пересекает ось абсцисс,
– с осью – подставить в уравнение значение и вычислить значение .
Примеры решения задач
| Понравился сайт? Расскажи друзьям! | |||
ru.solverbook.com
Как построить параболу | Алгебра
Как построить параболу? Существует несколько способов построения графика квадратичной функции. Каждый из них имеет свои плюсы и минусы. Рассмотрим два способа.
Начнём с построения графика квадратичной функции вида y=x²+bx+c и y= -x²+bx+c.
График квадратичной функции y=x²+bx+c — парабола, ветви которой направлены вверх. Для построения графика достаточно найти координаты вершины параболы. Абсцисса вершины параболы находится по формуле
для нахождения ординаты можно подставить в формулу y=x²+bx+c вместо каждого x найденное значение хₒ: yₒ=xₒ²+bxₒ+c. От вершины (хₒ; yₒ ) строим параболу y=x².
Пример.
Построить график функции y=x²+2x-3.
Решение:
y=x²+2x-3 — квадратичная функция. График — парабола ветвями вверх. Координаты вершины параболы
От вершины (-1;-4) строим график параболы y=x²(как от начала координат. Вместо (0;0) — вершина (-1;-4). От (-1;-4) идём вправо на 1 единицу и вверх на 1 единицу, затем влево на 1 и вверх на 1; далее: 2 — вправо, 4 — вверх, 2- влево, 4 — вверх; 3 — вправо, 9 — вверх, 3 — влево, 9 — вверх. Если этих 7 точек недостаточно, далее — 4 вправо, 16 — вверх и т. д.).
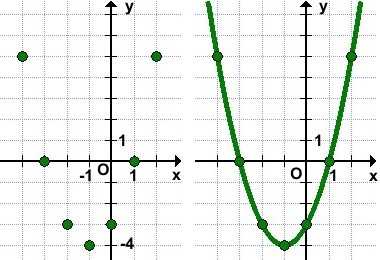
y=x²+2x-3
График квадратичной функции y= -x²+bx+c — парабола, ветви которой направлены вниз. Для построения графика ищем координаты вершины и от неё строим параболу y= -x².
Пример.
Построить график функции y= -x²+2x+8.
Решение:
y= -x²+2x+8 — квадратичная функция. График — парабола ветвями вниз. Координаты вершины параболы
От вершины строим параболу y= -x² (1 — вправо, 1- вниз; 1 — влево, 1 — вниз; 2 — вправо, 4 — вниз; 2 — влево, 4 — вниз и т. д.):

y= -x²+2x+8
Этот способ позволяет построить параболу быстро и не вызывает затруднений, если вы умеете строить графики функций y=x² и y= -x². Недостаток: если координаты вершины — дробные числа, строить график не очень удобно. Если требуется знать точные значения точек пересечения графика с осью Ох, придется дополнительно решить уравнение x²+bx+c=0 (или —x²+bx+c=0), даже если эти точки непосредственно можно определить по рисунку.
Другой способ построения параболы — по точкам, то есть можно найти несколько точек графика и через них провести параболу (с учетом того, что прямая x=хₒ является её осью симметрии). Обычно для этого берут вершину параболы, точки пересечения графика с осями координат и 1-2 дополнительные точки.
Примеры.
Построить график функции y=x²+5x+4.
Решение:
y=x²+5x+4 — квадратичная функция. График — парабола ветвями вверх. Координаты вершины параболы
то есть вершина параболы — точка (-2,5; -2,25).
Ищем точки пересечения графика с осями координат. В точке пересечения с осью Ох y=0: x²+5x+4=0. Корни квадратного уравнения х1=-1, х2=-4, то есть получили две точки графике (-1; 0) и (-4; 0).
В точке пересечения графика с осью Оy х=0: y=0²+5∙0+4=4. Получили точку (0; 4).
Для уточнения графика можно найти дополнительную точку. Возьмем х=1, тогда y=1²+5∙1+4=10, то есть еще одна точка графика — (1; 10). Отмечаем эти точки на координатной плоскости. С учетом симметрии параболы относительно прямой, проходящей через её вершину, отметим еще две точки: (-5; 6) и (-6; 10) и проведем через них параболу:
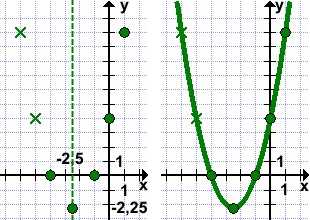
y=x²+5x+4
Построить график функции y= -x²-3x.
Решение:
y= -x²-3x — квадратичная функция. График — парабола ветвями вниз. Координаты вершины параболы
Вершина (-1,5; 2,25) — первая точка параболы.
В точках пересечения графика с осью абсцисс y=0, то есть решаем уравнение -x²-3x=0. Его корни — х=0 и х=-3, то есть (0;0) и (-3; 0) — еще две точки графика. Точка (о; 0) является также точкой пересечения параболы с осью ординат.
При х=1 y=-1²-3∙1=-4, то есть (1; -4) — дополнительная точка для построения графика.
y= -x²-3x
Построение параболы по точкам — более трудоёмкий, по сравнению с первым, способ. Если парабола не пересекает ось Oх, дополнительных точек потребуется больше.
Прежде чем продолжить построение графиков квадратичных функций вида y=ax²+bx+c, рассмотрим построение графиков функций с помощью геометрических преобразований. Графики функций вида y=x²+c также удобнее всего строить, используя одно из таких преобразований — параллельный перенос.
www.algebraclass.ru
Квадратичная функция и ее график
В этой статье мы поговорим о том, что такое квадратичная функция, научимся строить ее график
Итак.
Функция вида , где называется квадратичной функцией.
В уравнении квадратичной функции:
a — старший коэффициент
b — второй коэффициент
с — свободный член.
Графиком квадратичной функции является квадратичная парабола, которая для функции имеет вид:
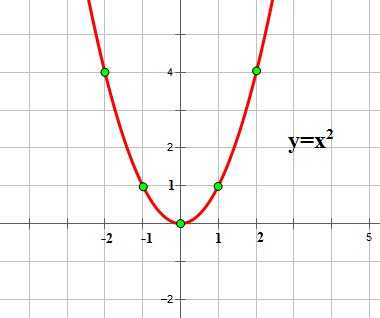
Обратите внимание на точки, обозначенные зелеными кружками — это, так называемые «базовые точки». Чтобы найти координаты этих точек для функции , составим таблицу:
Внимание! Если в уравнении квадратичной функции старший коэффициент , то график квадратичной функции имеет ровно такую же форму, как график функции при любых значениях остальных коэффициентов.
График функции имеет вид:

Для нахождения координат базовых точек составим таблицу:
Обратите внимание, что график функции симметричен графику функции относительно оси ОХ.
Итак, мы заметили:
Если старший коэффициент a>0, то ветви параболы напрaвлены вверх.
Если старший коэффициент a<0, то ветви параболы напрaвлены вниз.
Второй параметр для построения графика функции — значения х, в которых функция равна нулю, или нули функции. На графике нули функции — это точки пересечения графика функции с осью ОХ.
Поскольку ордината (у) любой точки, лежащей на оси ОХ равна нулю, чтобы найти координаты точек пересечения графика функции с осью ОХ, нужно решить уравнение .
В случае квадратичной функции нужно решить квадратное уравнение .
Теперь внимание!
В процессе решения квадратного уравнения мы находим дискриминант: , который определяет число корней квадратного уравнения.
И здесь возможны три случая:
1. Если ,то уравнение не имеет решений, и, следовательно, квадратичная парабола не имеет точек пересечения с осью ОХ. Если ,то график функции выглядит как-то так:
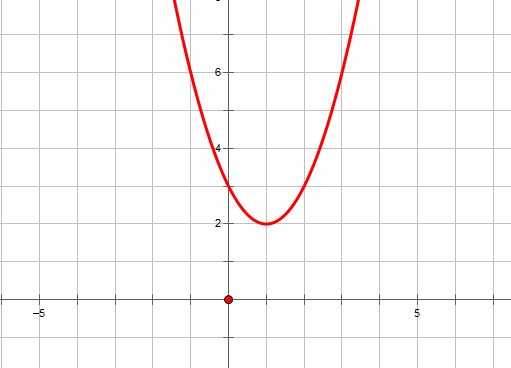
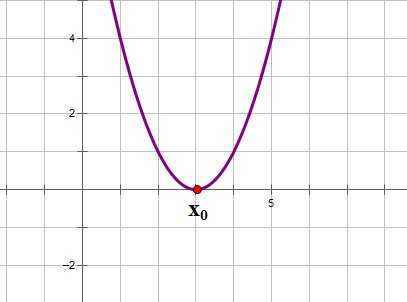
2. Если ,то уравнение имеет одно решение, и, следовательно, квадратичная парабола имеет одну точку пересечения с осью ОХ. Если ,то график функции выглядит примерно так:
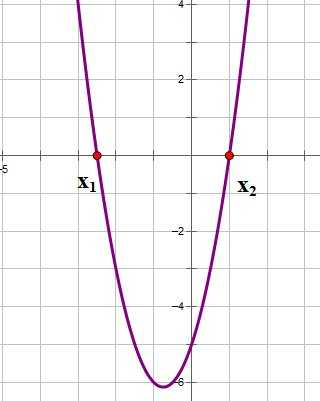
3. Если ,то уравнение имеет два решения, и, следовательно, квадратичная парабола имеет две точки пересечения с осью ОХ:
,
Если ,то график функции выглядит примерно так:
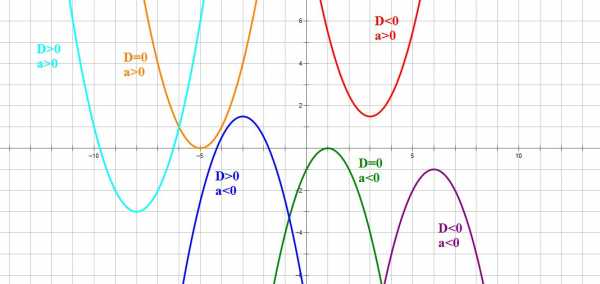
Следовательно, зная направление ветвей параболы и знак дискриминанта, мы уже можем в общих чертах определить, как выглядит график нашей функции.
Следующий важный параметр графика квадратичной функции — координаты вершины параболы:
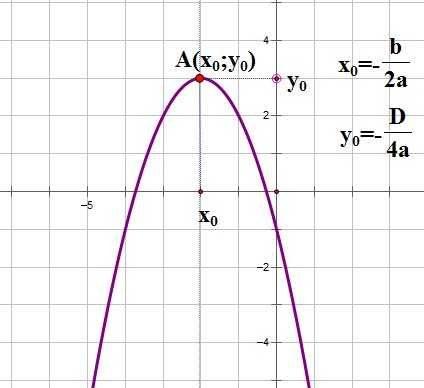
Прямая, проходящая через вершину параболы параллельно оси OY является осью симметрии параболы.
И еще один параметр, полезный при построении графика функции — точка пересечения параболы с осью OY.
Поскольку абсцисса любой точки, лежащей на оси OY равна нулю, чтобы найти точку пересечения параболы с осью OY, нужно в уравнение параболы вместо х подставить ноль: .
То есть точка пересечения параболы с осью OY имеет координаты (0;c).
Итак, основные параметры графика квадратичной функции показаны на рисунке:
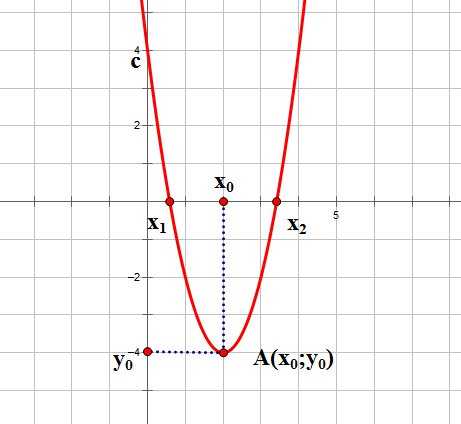
Рассмотрим несколько способов построения квадратичной параболы. В зависимости от того, каким образом задана квадратичная функция, можно выбрать наиболее удобный.
1. Функция задана формулой .
Рассмотрим общий алгоритм построения графика квадратичной параболы на примере построения графика функции
1. Направление ветвей параболы.
Так как ,ветви параболы направлены вверх.
2. Найдем дискриминант квадратного трехчлена
Дискриминант квадратного трехчлена больше нуля, поэтому парабола имеет две точки пересечения с осью ОХ.
Для того, чтобы найти их координаты, решим уравнение:
,
3. Координаты вершины параболы:
4. Точка пересечения параболы с осью OY: (0;-5),и ей симметричная относительно оси симметрии параболы.
Нанесем эти точки на координатную плоскость, и соединим их плавной кривой:
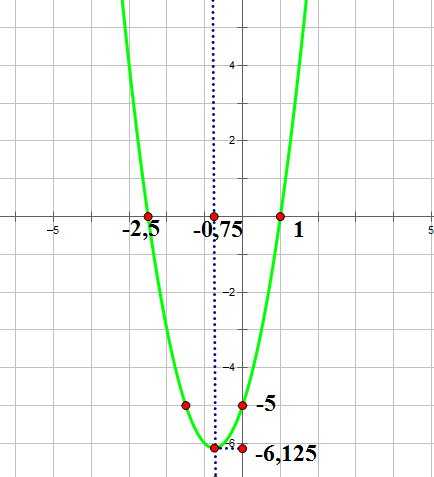
Этот способ можно несколько упростить.
1. Найдем координаты вершины параболы.
2. Найдем координаты точек, стоящих справа и слева от вершины.
Воспользуемся результатами построения графика функции
Кррдинаты вершины параболы
Ближайшие к вершине точки, расположенные слева от вершины имеют абсциссы соответственно -1;-2;-3
Ближайшие к вершине точки, расположенные справа имеют абсциссы соответственно 0;1;2
Подставим значения х в уравнение функции, найдем ординаты этих точек и занесем их в таблицу:
Нанесем эти точки на координатную плоскость и соединим плавной линией:
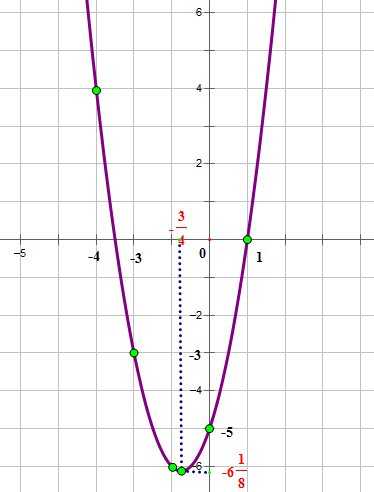
2. Уравнение квадратичной функции имеет вид — в этом уравнении — координаты вершины параболы
или в уравнении квадратичной функции , и второй коэффициент — четное число.
Построим для примера график функции .
Вспомним линейные преобразования графиков функций. Чтобы построить график функции , нужно
- сначала построить график функции ,
- затем одинаты всех точек графика умножить на 2,
- затем сдвинуть его вдоль оси ОХ на 1 единицу вправо,
- а затем вдоль оси OY на 4 единицы вверх:
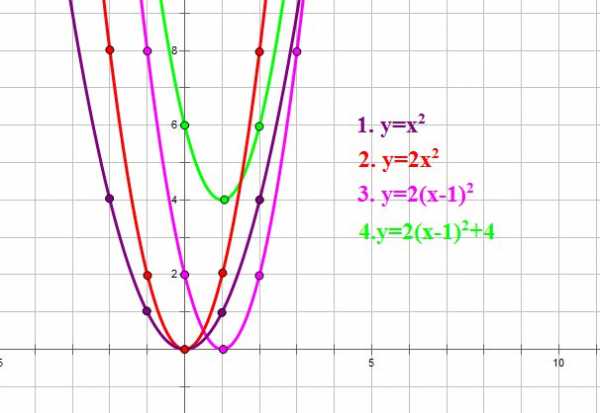
Теперь рассмотрим построение графика функции . В уравнении этой функции , и второй коэффициент — четное число.
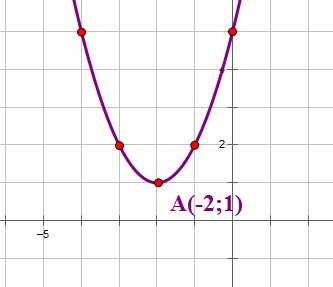
Выделим в уравнении функции полный квадрат:
Следовательно, координаты вершины параболы: . Старший коэффициент равен 1, поэтому построим по шаблону параболу с вершиной в точке (-2;1):
3. Уравнение квадратичной функции имеет вид y=(x+a)(x+b)
Построим для примера график функции y=(x-2)(x+1)
1. Вид уравнения функции позволяет легко найти нули функции — точки пересечения графика функции с осью ОХ:
(х-2)(х+1)=0, отсюда
2. Координаты вершины параболы:
3. Точка пересечения с осью OY: с=ab=(-2)(1)=-2 и ей симметричная.
Нанесем эти точки на координатную плоскость и построим график:
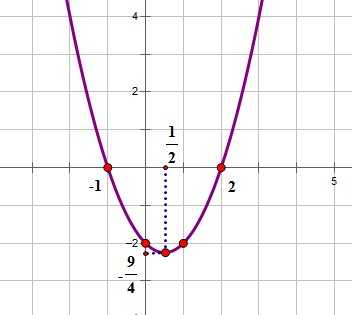
График квадратичной функции.
Перед вами график квадратичной функции вида .
Кликните по чертежу.
Подвигайте движки.
Исследуйте зависимость
— ширины графика функции от значения коэффициента ,
— сдвига графика функции вдоль оси от значения ,
— сдвига графика функции вдоль оси от значения
— направления ветвей параболы от знака коэффициента
— координат вершины параболы от значений и :
Скачать таблицу квадратичная функция
И.В. Фельдман, репетитор по математике.
ege-ok.ru
Как построить параболу |
 С понятием “парабола” учащиеся знакомятся в 7 классе, а более подробно изучают в теме “Квадратичная функция” (9 класс). И один из главных вопросов этой теме, как построить параболу как график квадратичной функции.
С понятием “парабола” учащиеся знакомятся в 7 классе, а более подробно изучают в теме “Квадратичная функция” (9 класс). И один из главных вопросов этой теме, как построить параболу как график квадратичной функции.
Конспект урока “Квадратичная функция y=ax2+bx+c , ее график и свойства” был уже представлен на сайте “Математический Тандем” , причем на двух языках: украинском и русском.
Но в данной статье приведем только алгоритм построения параболы, чтобы не нагружать учащихся излишней методической информацией, предназначенной для учителя, содержащейся в упомянутом конспекте.
Как построить параболу – график функции y=ax2+bx+c.
[pwal description=»Чтобы увидеть остальную часть статьи и обучающий видео-ролик, пожалуйста, нажмите одну из кнопок социальных сетей.»]
1 шаг.
Найдем координаты вершины параболы.
Для этого используем формулы, подставляя коэффициенты a, b, с из заданной функции в формулы:
Можно поступить иначе : найти только абсциссу вершины хв , а ординату ув получить, подставляя в заданную функцию найденное значение хв .
Итак, координаты вершины (хв; ув)
2 шаг.
Найдем точки пересечения параболы с осью ОХ (нули функции).
Для этого приравняем заданную функцию к нулю : ax2+bx+c= 0 и решим квадратное уравнение .
Напомним, что сначала нужно найти дискриминант: D = b2 – 4ac, а затем корни :
Т.о. на оси ОХ есть точки с координатами :
(х1; 0) и (х2; 0), если D>0;
(х1; 0) (одна точка, и она совпадает с вершиной параболы), если D=0;
парабола не пересекает ось ОХ, если D<0.
3 шаг.
Найдем точку пересечения параболы с осью ОY.
Для этого нужно подставить х=0 в уравнение параболы y=ax2+bx+c и получить, что y=с.
Имеем на оси ОY точку с координатами (0; c).
Кроме этого, можно построить еще одну точку параболы, учитывая, что парабола симметрична относительно прямой, проходящей через ее вершину и параллельную оси OY .
Результат применения алгоритма “Как построить параболу” на картинке:

Пример того, как построить параболу смотрите в этом видео-ролике.
[/pwal]
P.S.
Этот материал будет также полезен учащимся 10-11 классов, особенно при подготовке к ЕГЭ (Россия) и ВНО (Украина).
repetitor-problem.net
Как построить параболу? Как построить график?
Урок: как построить параболу или квадратичную функцию?
Строить параболу очень легко самое главное запомнить последовательность несложных действий.
1 действие: запомнить общую формулу параболы y=ax^2+bx+c и что график симметричен относительно оси OY
2 действие: вытекает из первого рассмотрим свободный член c в этой точке пересекается парабола с осью OY. Если а>0 то ветви параболы смотрят вверх, а 3 действие: найти вершину по формуле x=(-b)/2a, а чтоб у просчитать то нужно x подставить в формулу y=ax^2+bx+c
4 действие: найти точки пересечения параболы с осью OX или по-другому они называются корни уравнения. Чтобы найти корни мы уравнение приравниваем к 0 ax^2+bx+c=0
Здесь могут быть подпункты, так как уравнения параболы могут быть разными.
a)Полное квадратное уравнение имеет вид ax^2+bx+c=0 и решается по дискриминанту
b)Неполное квадратное уравнение вида ax^2+bx=0. Чтобы его решить нужно вынести х за скобки и потом каждый множитель прировнять к 0. х(ax+b)=0, х=0 и ax+b=0.
c)Неполное квадратное уравнение вида ax^2 +c=0. Чтобы его решить нужно неизвестные перенести в одну сторону, а известные в другую. x =±√(c/a)
5 действие: делать не обязательно, но оно поможет вам построить более точный график параболы. Это взять несколько дополнительных точек для построения функции.
И так теперь на примере разберем все по действиям
1)y=x^2+4x+3
2) c=3 значит парабола пересекает OY в точке х=0 у=3. Ветви параболы смотрят вверх так как а=1 1>0.
3) a=1 b=4 c=3 x=(-b)/2a=(-4)/(2*1)=-2 y= (-2)^2+4*(-2)+3=4-8+3=-1 вершина находится в точке (-2;-1)
4) Найдем корни уравнения x^2+4x+3=0
По дискриминанту находим корни
a=1 b=4 c=3
D=b^2-4ac=16-12=4
x=(-b±√(b^2-4ac))/2a
x1=(-4+2)/2=-1
x2=(-4-2)/2=-3
5) Возьмем несколько произвольных точек, так как у нас вершина лежит в точке (-2;-1) нам выгодно брать точки возле х=-2
х -4 -3 -1 0
у 3 0 0 3
Подставляем вместо х в уравнение y=x^2+4x+3 значения
y=(-4)^2+4*(-4)+3=16-16+3=3
y=(-3)^2+4*(-3)+3=9-12+3=0
y=(-1)^2+4*(-1)+3=1-4+3=0
y=(0)^2+4*(0)+3=0-0+3=3
Видно по значениям что значения у симметричны
1)y=-x^2+4x
2)c=0 значит парабола пересекает OY в точке х=0 у=0. Ветви параболы смотрят вниз так как а=-1 -1
3)a=-1 b=4 c=0 x=(-b)/2a=(-4)/(2*(-1))=2 y=-(2)^2+4*2=-4+8=4 вершина находится в точке (2;4)
4)Найдем корни уравнения -x^2+4x=0
Неполное квадратное уравнение вида ax^2+bx=0. Чтобы его решить нужно вынести х за скобки и потом каждый множитель прировнять к 0.
х(-x+4)=0, х=0 и x=4.
5)Возьмем несколько произвольных точек, так как у нас вершина лежит в точке (2;4) нам выгодно брать точки возле х=2
х 0 1 3 4
у 0 3 3 0
Подставляем вместо х в уравнение y=-x^2+4x значения
y=0^2+4*0=0
y=-(1)^2+4*1=-1+4=3
y=-(3)^2+4*3=-9+13=3
y=-(4)^2+4*4=-16+16=0
Видно по значениям что значения у симметричны
1)y=x^2+4
2)c=4 значит парабола пересекает OY в точке х=0 у=4. Ветви параболы смотрят вверх так как а=1 1>0.
3)a=1 b=0 c=4 x=(-b)/2a=0/(2*(1))=0 y=(0)^2+4=4 вершина находится в точке (0;4)
4)Найдем корни уравнения x^2+4=0
Неполное квадратное уравнение вида ax^2 +c=0. Чтобы его решить нужно неизвестные перенести в одну сторону, а известные в другую. x =±√(c/a)
x2=4
x1=2
x2=-2
5)Возьмем несколько произвольных точек, так как у нас вершина лежит в точке (0;4) нам выгодно брать точки возле х=0
х -2 -1 1 2
у 0 3 3 0
Подставляем вместо х в уравнение y=x^2+4 значения
y=(-2)^2+4=4+4=8
y=(-1)^2+4=1+4=5
y=1^2+4=1+4=5
y=2^2+4=4+4=8
Видно по значениям что значения у симметричны
ege-gia.blogspot.com
Как определить вершину параболы 🚩 формула для вершины параболы 🚩 Математика
Парабола — это бесконечная кривая, которая состоит из точек, равноудаленых от заданной прямой, называемой директрисой параболы, и заданной точки — фокуса параболы. Парабола является коническим сечением, то есть представляет собой пересечение плоскости и кругового конуса.
В общем виде математическое уравнение параболы имеет вид: y=ax^2+bx+c, где a не равно нулю, b отражает смещение графика функции по горизонтали относительно начала координат, а c — вертикальное смещение графика функции относительно начала координат. При этом, если a>0, то ветви параболы при построении графика будут направленны вверх, а в случае, если aСвойства параболы
Парабола — это кривая второго порядка, которая имеет ось симметрии, проходящую через фокус параболы и перпендикулярную директрисе параболы.
Парабола обладает особым оптическим свойством, заключающемся в фокусировки параллельных относительно оси ее симметрии световых лучей, направленных в параболу, в вершине параболы и расфокусировки пучка света, направленного в вершину параболы, в параллельные световые лучи относительной той же оси.
Если произвести отражение параболы относительно любой касательной, то образ параболы окажется на ее директрисе. Все параболы подобны между собой, то есть для каждых двух точек A и B одной параболы, найдутся точки A1 и B1, для которых верно утверждение |A1,B1| = |A,B|*k, где k – коэффициент подобия, который в численном значении всегда больше нуля.
Некоторые космические тела, такие как кометы или астероиды, проходящие вблизи крупных космических объектов на высокой скорости имеют траекторию движения в форме параболы. Это свойство малых космических тел используется при гравитационных маневрах космических кораблей.
Для тренировок будущих космонавтов, на земле проводятся специальные полеты самолетов по траектории параболы, чем достигается эффект невесомости в гравитационном поле земли.
В быту параболы можно встретить в различных осветительных приборах. Это связано с оптическим свойством параболы. Одним из последних способов применения параболы, основанных на ее свойствах фокусировки и расфокусировки световых лучей, стали солнечные батареи, которые все больше входят в сферу энергоснабжения в южных регионах России.
www.kakprosto.ru
Построение графика квадратичной функций: алгоритм и примеры
Квадратичной функцией называется функция вида:
y=a*(x^2)+b*x+c,
где а – коэффициент при старшей степени неизвестной х,
b – коэффициент при неизвестной х,
а с — свободный член.
Графиком квадратичной функции является кривая, называемая параболой. Общий вид параболы представлен на рисунке ниже.

Рис.1 Общий вид параболы.
Есть несколько различных способов построения графика квадратичной функции. Мы рассмотрим основной и самый общий из них.
Алгоритм построения графика квадратичной функции y=a*(x^2)+b*x+c
1. Построить систему координат, отметить единичный отрезок и подписать координатные оси.
2. Определить направление ветвей параболы (вверх или вниз).
Для этого надо посмотреть на знак коэффициента a. Если плюс — то ветви направлены вверх, если минус — то ветви направлены вниз.
3. Определить координату х вершины параболы.
Для этого нужно использовать формулу Хвершины = -b/2*a.
4. Определить координату у вершины параболы.
Для этого подставить в уравнение Увершины = a*(x^2)+b*x+c вместо х, найденное в предыдущем шаге значение Хвершины.
5. Нанести полученную точку на график и провести через неё ось симметрии, параллельно координатной оси Оу.
6. Найти точки пересечения графика с осью Ох.
Для этого требуется решить квадратное уравнение a*(x^2)+b*x+c = 0 одним из известных способов. Если в уравнение не имеет вещественных корней, то график функции не пересекает ось Ох.
7. Найти координаты точки пересечения графика с осью Оу.
Для этого подставляем в уравнение значение х=0 и вычисляем значение у. Отмечаем эту и симметричную ей точку на графике.
8. Находим координаты произвольной точки А(х,у)
Для этого выбираем произвольное значение координаты х, и подставляем его в наше уравнение. Получаем значение у в этой точке. Нанести точку на график. А также отметить на графике точку, симметричную точке А(х,у).
9. Соединить полученные точки на графике плавной линией и продолжить график за крайние точки, до конца координатной оси. Подписать график либо на выноске, либо, если позволяет место, вдоль самого графика.
Пример построения графика
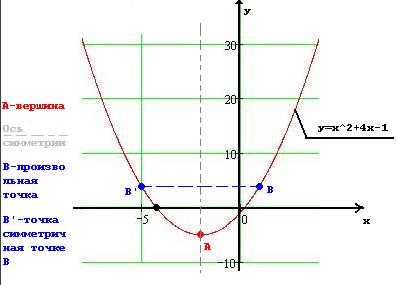
В качестве примера, построим график квадратичной функции заданной уравнением y=x^2+4*x-1
1. Рисуем координатные оси, подписываем их и отмечаем единичный отрезок.
2. Значения коэффициентов а=1, b=4, c= -1. Так как а=1, что больше нуля ветви параболы направлены вверх.
3. Определяем координату Х вершины параболы Хвершины = -b/2*a = -4/2*1 = -2.
4. Определяем координату У вершины параболы
Увершины = a*(x^2)+b*x+c = 1*((-2)^2) + 4*(-2) – 1 = -5.
5. Отмечаем вершину и проводим ось симметрии.
6. Находим точки пересечения графика квадратичной функции с осью Ох. Решаем квадратное уравнение x^2+4*x-1=0.
х1=-2-√3 х2 = -2+√3. Отмечаем полученные значения на графике.
7. Находим точки пересечения графика с осью Оу.
х=0; у=-1
8. Выбираем произвольную точку B. Пусть она имеет координату х=1.
Тогда у=(1)^2 + 4*(1)-1= 4.
9. Соединяем полученные точки и подписываем график.
В результате получится такой график.
Нужна помощь в учебе?
Предыдущая тема: Графики функции: от чего зависит вид графика функции
Следующая тема:   Решение неравенств второй степени с одной переменной: приводим примеры
Все неприличные комментарии будут удаляться.
www.nado5.ru
