Показатели степеней при сложении – Что делать со степенями при сложении и вычитании числа? — Любопытная Варвара

Степень — свойства, правила, действия и формулы

Одной из главных характеристик в алгебре, да и во всей математике является степень. Конечно, в 21 веке все расчеты можно проводить на онлайн-калькуляторе, но лучше для развития мозгов научиться делать это самому.

В данной статье рассмотрим самые важные вопросы, касающиеся этого определения. А именно, поймем что это вообще такое и каковы основные его функции, какие имеются свойства в математике.

Рассмотрим на примерах то, как выглядит расчет, каковы основные формулы. Разберем основные виды величины и то, чем они отличаются от других функций.

Поймем, как решать с помощью этой величины различные задачи. Покажем на примерах, как возводить в нулевую степень, иррациональную, отрицательную и др.

Онлайн-калькулятор возведения в степень

Что такое степень числа

Что же подразумевают под выражением «возвести число в степень»?

Степенью n числа а является произведение множителей величиной а n-раз подряд.

Математически это выглядит следующим образом:

aⁿ = a * a * a * …a_n.

Причем, левая часть уравнения будет читаться, как a в степ. n.

Например:

• 2³ = 2 в третьей степ. = 2 * 2 * 2 = 8;
• 4² = 4 в степ. два = 4 * 4 = 16;
• 5⁴ = 5 в степ. четыре = 5 * 5 * 5 * 5 = 625;
• 10⁵ = 10 в 5 степ. = 10 * 10 * 10 * 10 * 10 = 100000;
• 10⁴ = 10 в 4 степ. = 10 * 10 * 10 * 10 = 10000.

Ниже будет представлена таблица квадратов и кубов от 1 до 10.

Таблица степеней от 1 до 10

Ниже будут приведены результаты возведения натуральных чисел в положительные степени – «от 1 до 100».

Ч-ло	2-ая ст-нь	3-я ст-нь
1	1	1
2	4	8
3	9	27
4	16	64
5	25	125
6	36	216
7	49	343
8	64	512
9	81	279
10	100	1000

Свойства степеней

Что же характерно для такой математической функции? Рассмотрим базовые свойства.

Учеными установлено следующие признаки, характерные для всех степеней:

• aⁿ * a^m = (a)^(n+m);
• aⁿ : a^m = (a)^(n-m);
• (a^b ) ^m=(a)^(b*m).

Проверим на примерах:

2³ * 2² = 8 * 4 = 32. С другой стороны 2⁵ = 2 * 2 * 2 * 2 * 2 =32.

Аналогично: 2³ : 2² = 8 / 4 =2. Иначе 2^3-2 = 2¹ =2.

(2³)² = 8² = 64. А если по-другому? 2⁶ = 2 * 2 * 2 * 2 * 2 * 2 = 32 * 2 = 64.

Как видим, правила работают.

А как же быть со сложением и вычитанием? Всё просто. Выполняется сначала возведение в степень, а уж потом сложение и вычитание.

Посмотрим на примерах:

• 3³ + 2⁴ = 27 + 16 = 43;
• 5² – 3² = 25 – 9 = 16. Обратите внимание: правило не будет выполняться, если сначала произвести вычитание: (5 — 3)² = 2² = 4.

А вот в этом случае надо вычислять сначала сложение, поскольку присутствуют действия в скобках: (5 + 3)³ = 8³ = 512.

Как производить вычисления в более сложных случаях? Порядок тот же:

• при наличии скобок – начинать нужно с них;
• затем возведение в степень;
• потом выполнять действия умножения, деления;
• после сложение, вычитание.

Есть специфические свойства, характерные не для всех степеней:

1. Корень n-ой степени из числа a в степени m запишется в виде: a^m/n.
2. При возведении дроби в степень: этой процедуре подвержены как числитель, так и ее знаменатель.
3. При возведении произведения разных чисел в степень, выражение будет соответствовать произведению этих чисел в заданной степени. То есть: (a * b)ⁿ = aⁿ * bⁿ.
4. При возведении числа в отрицательную степ., нужно разделить 1 на число в той же ст-ни, но со знаком «+».
5. Если знаменатель дроби находится в отрицательной степени, то это выражение будет равно произведению числителя на знаменатель в положительной степени.
6. Любое число в степени 0 = 1, а в степ. 1 = самому себе.

Эти правила важны в отдельных случаях, их рассмотрим подробней ниже.

Степень с отрицательным показателем

Что делать при минусовой степени, т. е. когда показатель отрицательный?

Исходя из свойств 4 и 5 (смотри пункт выше), получается:

A^(-n) = 1 / Aⁿ, 5^(-2) = 1 / 5² = 1 / 25.

И наоборот:

1 / A

(-ⁿ⁾ = Aⁿ, 1 / 2^(-3) = 2³ = 8.

А если дробь?

(A / B)^(-n) = (B / A)ⁿ, (3 / 5)^(-2) = (5 / 3)² = 25 / 9.

Степень с натуральным показателем

Под ней понимают степень с показателями, равными целым числам.

Что нужно запомнить:

A⁰ = 1, 1⁰ = 1; 2⁰ = 1; 3.15⁰ = 1; (-4)⁰ = 1…и т. д.

A¹ = A, 1¹ = 1; 2¹ = 2; 3¹ = 3…и т. д.

Кроме того, если (-a)²ⁿ⁺², n=0, 1, 2…то результат будет со знаком «+». Если отрицательное число возводится в нечетную степень, то наоборот.

Общие свойства, да и все специфические признаки, описанные выше, также характерны для них.

Дробная степень

Этот вид можно записать схемой: A^m/n. Читается как: корень n-ой степени из числа A в степени m.

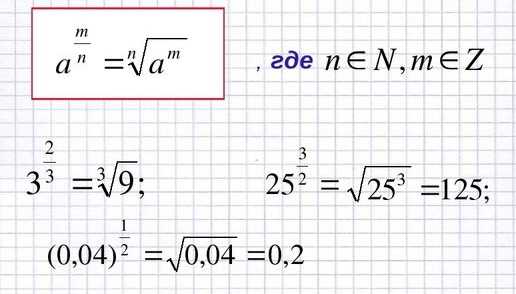
С дробным показателем можно делать, что угодно: сокращать, раскладывать на части, возводить в другую степень и т. д.

Степень с иррациональным показателем

Пусть α – иррациональное число, а А ˃ 0.

Чтобы понять суть степени с таким показателем, рассмотрим разные возможные случаи:

• А = 1. Результат будет равен 1. Поскольку существует аксиома – 1 во всех степенях равна единице;
• А˃1.

А^r1 ˂ А^α ˂ А^r2, r₁ ˂ r₂ – рациональные числа;

В этом случае наоборот: А^r2 ˂ А^α ˂ А^r1 при тех же условиях, что и во втором пункте.

Например, показатель степени число π. Оно рациональное.

r₁ – в этом случае равно 3;

r₂ – будет равно 4.

Тогда, при А = 1, 1

π = 1.

А = 2, то 2³ ˂ 2^π ˂ 2⁴, 8 ˂ 2^π ˂ 16.

А = 1/2, то (½)⁴ ˂ (½)^π ˂ (½)³, 1/16 ˂ (½)^π ˂ 1/8.

Для таких степеней характерны все математические операции и специфические свойства, описанные выше.

Заключение

Подведём итоги — для чего же нужны эти величины, в чем преимущество таких функций? Конечно, в первую очередь они упрощают жизнь математиков и программистов при решении примеров, поскольку позволяют минимизировать расчеты, сократить алгоритмы, систематизировать данные и многое другое.

Где еще могут пригодиться эти знания? В любой рабочей специальности: медицине, фармакологии, стоматологии, строительстве, технике, инженерии, конструировании и т. д.

1001student.ru

Степень с натуральным показателем и её свойства

Степень с натуральным показателем и ее свойства.

Степенью числа a с натуральным показателем n, большим 1, называется произведение n множителей, каждый из которых равен a:

aⁿ = 

В выражении aⁿ :

—  число а (повторяющийся множитель) называют основанием степени

—  число n (показывающее сколько раз повторяется множитель) – показателем степени

Например: 2⁵ = 2·2·2·2·2 = 32, здесь: 2   – основание степени, 5   – показатель степени, 32 – значение степени

Отметим, что основание степени может быть любым числом.

Вычисление значения степени называют действием возведения в степень. Это действие третьей ступени. То есть при вычислении значения выражения, не содержащего скобки, сначала выполняют действие третьей ступени, затем второй (умножение и деление) и, наконец, первой (сложение и вычитание).

Для записи больших чисел часто применяются степени числа 10. Так, расстояние от земли до солнца примерно равное 150 млн. км, записывают в виде 1,5 · 10⁸

Каждое число большее 10 можно записать в виде: а · 10ⁿ , где 1

Например:  4578 = 4,578 · 10³ ;

103000 = 1,03 · 10⁵.

Свойства степени с натуральным показателем:

1. При умножении степеней с одинаковыми основаниями основание остается прежним, а показатели степеней складываются

a^m · aⁿ = a^{m + n}

например:  7^1.7 · 7 ^{— 0.9} = 7^{1.7+( — 0.9)}

= 7^{1.7 — 0.9} =  7^0.8

2. При делении степеней с одинаковыми основаниями основание остается прежним, а показатели степеней вычитаются

a^m / aⁿ = a^{m — n} ,

где,  m > n,

a ? 0

например: 13^3.8 / 13 ^-0.2 = 13^{(3.8 -0.2)} = 13^3.6

3. При возведении степени в степень основание остается прежним, а показатели степеней перемножаются.

(a^m )ⁿ = a ^{m ·  n}

например: (2³)² = 2 ^3·2 = 2⁶

4. При возведении в степень произведения в эту степень возводится каждый множитель

(a · b)ⁿ = aⁿ · b ^m ,

например:(2·3)³ = 2ⁿ · 3 ^m ,

5. При возведении в степень дроби в эту степень возводятся числитель и знаменатель

(a / b)ⁿ = aⁿ / bⁿ

например: (2 / 5)³ = (2 / 5) · (2 / 5) · (2 / 5) = 2³ / 5³

mirurokov.ru

Смысл степени с натуральным,отрицательным,дробным показателем,Правила действия над степенями: — МегаЛекции

1)Степени с натуральным показателем:

В стране чисел возникли проблемы. Астрономы собрались посчитать размеры видимой части Вселенной. Они утверждали, что для этого необходимо умножить 25 раз число 10 само на себя. Поскольку для этого требовалось очень много места, они требовали снести Дворец алгоритма Евкида, выставку чисел-близнецов и многие другие объекты. Хотя всем хотелось узнать, какая же наша Вселенная, но никому не хотелось жертвовать столь прекласными и ценными сооружениями. Была создана комиссия, которая занялась поисками требуемой свободной площади, но вскоре зашла в тупик.

Неожиданно положение Таблица умножения. Она рассказла свою историю: — Меня придумали для того, чтобы не складывать большое количество одинаковых слагаемых. Ведь теперь никто не пишет 3 + 3 + 3 + 3 + 3 + 3 + 3, теперь записывают 3 х 7. Это очень экономит место. Давайте придумаем что-нибудь похожее для умножения.

И сразу придумали. Число множителей стали записываь маленькой цифрой сзади числа:

Все выражение стали на зывать степенью, количество множителей (маленькую цифру сверху) – показателем степени, а сам множитель – основание степени.

Не прошло и получаса, как торжественно ввели новое действие – возведение в степень, как по стране чисел стали бегать 5⁶, 17⁴ и многие другие. Но только бегать неинтересно, хочется выполнять сложение, умножение, вычитание, то есть вести себя как все порядочные числа. и ту возникли следующие проблемы. После введения действий надо установить правила действий, так, чтобы никому не мешать и никакие законы не нарушать.

Сначала попробовали выполнять сложение, открыли свод законов и ничего не нашли. О вычитании даже думать не стали, а умножение пошло очень легко, ведь всякая степень получается из множителей, значит, если взять одинаковые основания степени, то

Сразу записали в свод законов новое правило:

При умножении степеней с одинаковым основание основание остается неизменным, а показатели складывают





С делением возникли проблемы. Всем казалось, что если деление действие обратное уиножению, то приделении надо показатели вычитать, но если , а если .Тогда постановили (под влиянием консервативного меньшинства), что

При делении степеней с одинаковыми основаниями , если m>n, и , если n>m.

Провести проверку нового правил предложили 6⁵ и 6³: , а

При делении степеней с одинаковыми основаниями показатели вычитаются. а полностью правило сформулировать трудно.

 

Разобралися также со степенями с разными основаниями и одинаковыми показателями. На помощь пришли переместительный и сочетательный законы: , потому, что ;

Чтобы умножить степени с одинаковыми показателями надо перемножить основания, а показатель оставить без изменения.

Чтобы разделить степени содинаковыми основаниями надо разделит основания, а показатель оставить без изменения.

;

Оказалось, что можно даже возводить степени в степень.

Наступил всеобщий праздник. Особенно понравилось сокращать дроби, раскладывая их на множители:

Подарок преподнес распределительный закон. Он предложил как складывать одинаковые степени, например, , ,т.е. можно складывать коэффициенты.

А если степени с одинаковыми основаниями, но с разными коэффициентами, то можно общий множитель вынести за скобку:

2)степени с отрицательным показателем:

Все уже привыкли к действиям со степенями с натуральными показателями (их так называют, потомучто показатели – натуральные числа).

И нашлись недовольные, те кто не принял участие в создании новых чисел.Революционно настроенные представители отрицательных чисел выступили с заявлением, что их притесняют, не дают развиваться науке,

— Всем известно, что при вычитании может получаться 0, а также отрицательные числа, — говорили они и организовали движение в поддержку степеней с отрицательным показателе.

— Как же может быть отрицательное количество сомножителей?- удивились натуральные числа.

— Надо определить , это как раз подходит под ваше правило:.

-А степени с отрицательным показателем определить, как ( Z_— — отрицательнын целые числа).

Например,

Тогда формула для деления степеней станет просто

— Хорошо, — сказали хранители Свода законов, — тогда докажите, что все правила действий со степенями сохранятся и при введении степеней с отрицательным показателями.

Больше того, отрицательные числа предложили план доказательства всех теорем, о действиях со степенями.

1.В выражении по определению заменить степень с отрицательным показателем на степень с натуральным показателем.

2.Выполнить действия по правилам действий со степенями с натуральными показателями

3.По определению перейти от степеней с натуральными показателя к степеням с отрицательными показателями.

А также привели поясняющие примеры: , записывать можно короче:

Итак, оказалось, что все правила действий сохранились для степеней с отрицательными показателями.

3)степени с дробным показателем:

при извлечении корня из степени делят показатель степени на показатель корня, если такое деление выполнется нацело; например: √a⁴ = a², ³√x⁹ = x³ и т. п. Условимся теперь распространить это правило и на те случаи, когда показатель степени не делится нацело на показатель корня. Например, мы условимся принимать, что

Вообще мы условимся, что выражение означает корень, показатель которого есть знаменатель, а показатель подкоренного числа — числитель дробного показателя (т. е.ⁿ√a^m).

Условимся еще допускать и отрицательные дробные показатели в том же смысле, в каком мы допустили отрицательные целые показатели; например, условимся, что

Замечание. Дробные показатели были введены в алгебру главным образом голландским инженером Симоном Стевином в начале XVII столетия Позднее, в конце XVII столетия, Оксфордский профессор Джон Валлис ввел в употребление отрицательные показатели.

259. Основное свойство дробного показателя. Величина степени с дробным показателем не изменится, если мы умножим или разделим на одно и то же число (отличное от нуля) числитель и знаменатель дробного показателя. Так:

Действительно, знаменатель дробного показателя означает показатель корня, а числитель его означает показатель подкоренного выражения, а такие показатели, как мы видели можно умножать и делить на одно и то же число.

Основываясь на этом свойстве, мы можем преобразовывать дробный показатель совершенно так же, как и обыкновенную дробь: например, мы можем сокращать дробный показатель, или приводить несколько дробных показателей к одному знаменателю.

 

---

Рекомендуемые страницы:




Воспользуйтесь поиском по сайту:

megalektsii.ru

No related posts.