Показательные неравенства
Решение простейших показательных неравенств основано на свойствах монотонности показательной функции при и . Вы знаете, что эта функция возрастает при а и убывает при .
Если а , то есть функция является возрастающей, тогда справедливо следующее утверждение: для возрастающей функции большему значению функции соответствует большее значение аргумента.
Если , то есть функция является убывающей, тогда справедливо следующее утверждение: для убывающей функции большему значению функции соответствует меньшее значение аргумента.
Рассмотрим некоторые виды показательных неравенств и методы их решения.
Первый метод: приведение обеих частей неравенства к одному основанию.
Решим неравенство 1: .
Решение.
Поскольку , а , то исходное неравенство равносильно неравенству .
Основание степени , следовательно, функция возрастающая.
Значит, можем записать, что
Отсюда .
Ответ: решением исходного неравенства является .
Решим неравенство 2: .
Решение.
Поскольку , то функция убывающая. Значит, данное неравенство равносильно следующему .
Возведём обе части уравнения в квадрат. Получим неравенство . Область определения этого неравенства .
Перенесём слагаемые из левой части неравенства в правую .
Приведём подобные. Имеем .
Решениями последнего неравенства будут и .
Мы с вами уже говорили, что область определения предыдущего неравенства
. Тогда решением исходного неравенства является объединение промежутков
Не забудем записать ответ .
Второй метод: вынесение общего множителя за скобки.
Решим неравенство 1: .
Решение.
,
Тогда исходное неравенство мы можем переписать в следующем виде .
Теперь в левой части последнего неравенства вынесем общий множитель .
Вычислим выражение в скобках. Получим .
Разделим обе части получившегося неравенства на 13.
Получим , или .
, то есть имеем возрастающую функцию.
Значит, можем записать . Отсюда .
Запишем ответ: .
Решим неравенство 2: .
Решение.
В левой части неравенства вынесем за скобки, в правой части за скобки. Получим равносильное неравенство .
Посчитаем выражения в скобках. Получим
Теперь разделим обе части неравенства на , при этом не забудем поменять знак неравенства на противоположный.
Сократим. Получим . Или.
Заметим, что в получившемся неравенстве равны не основания степени, а показатели. Разделим обе части этого неравенства на . Тогда имеем неравенство или .
.
, то есть наша функция убывающая.
Значит .
Не забудем записать ответ: .
Метод 3: решение неравенства при помощи замены , где .
Решим неравенство: .
Решение. Преобразуем исходное неравенство. Первое слагаемое .
Тогда наше неравенство примет следующий вид: .
Введём замену , где, . Тогда получившееся неравенство примет следующий вид: .
Найдём корни уравнения .
Его корнями будут и .
Тогда наше неравенство можем разложить на следующие множители . Решим это неравенство методом интервалов.
Видим, решением данного неравенства является промежуток от минус одной второй и до четырёх.
Когда мы вводили замену, то говорили, что .
Значит, решением последнего неравенства будет промежуток .
Вернёмся к замене. Тогда получаем, что , или .
, имеем возрастающую функцию.
Значит, , или .
Запишем ответ: .
Неравенство 2: .
Решение. Обратите внимание, первое слагаемое мы можем записать, как , а последнее представить, как .
Тогда наше исходное неравенство мы можем привести к следующему виду: .
Разделим обе части неравенства на . Получим .
Введём замену , где и поменяем местами второе и третье слагаемые.
Тогда наше неравенство примет вид .
Решим уравнение .
Применяя теорему Виета, получаем, что это уравнение имеет два корня и .
Первый корень не подходит, так как при вводе замены, мы говорили, что
Значит, решением неравенства будет .
Вернёмся к замене. Получим неравенство , или .
. Значит, функция убывающая.
Тогда имеем неравенство .
Не забудем записать ответ .
videouroki.net
Показательные неравенства. Видеоурок. Алгебра 11 Класс
Напомним определение и основные свойства показательной функции. Именно на свойствах базируется решение всех показательных уравнений и неравенств.
Показательная функция – это функция вида , где основание степени и Здесь х – независимая переменная, аргумент; у – зависимая переменная, функция.
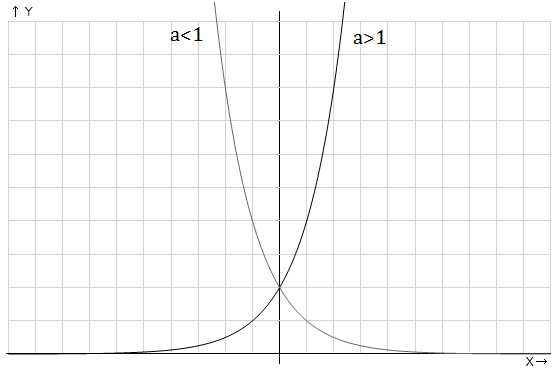
Рис. 1. График показательной функции
На графике показаны возрастающая и убывающая экспоненты, иллюстрирующие показательную функцию при основании большем единицы и меньшем единицы, но большим нуля соответственно.
Обе кривые проходят через точку (0;1)
Свойства показательной функции:
Область определения: ;
Область значений: ;
Функция монотонна, при возрастает, при убывает.
Монотонная функция принимает каждое свое значение при единственном значении аргумента.
При , когда аргумент возрастает от минус до плюс бесконечности, функция возрастает от нуля не включительно до плюс бесконечности, т. е. при данных значениях аргумента мы имеем монотонно возрастающую функцию (). При наоборот, когда аргумент возрастает от минус до плюс бесконечности, функция убывает от бесконечности до нуля не включительно, т. е. при данных значениях аргумента мы имеем монотонно убывающую функцию ().
На основании вышесказанного приведем методику решения простейших показательных неравенств:
Методика решения неравенств:
Уравнять основания степеней;
Сравнить показатели, сохранив или изменив на противоположный знак неравенства.
Решение сложных показательных неравенств заключается, как правило, в их сведении к простейшим показательным неравенствам.
Пример 1:
Преобразуем правую часть согласно свойствам степени:
Основание степени больше единицы, значит, знак неравенства сохраняется:
Пример 2:
Преобразуем правую часть согласно свойствам степени:
Основание степени меньше единицы, знак неравенства необходимо поменять на противоположный:
Для решения квадратного неравенства решим соответствующее квадратное уравнение:
По теореме Виета находим корни:
Ветви параболы направлены вверх.
Таким образом, имеем решение неравенства:
Пример 3:
Несложно догадаться, что правую часть можно представить как степень с нулевым показателем:
Основание степени больше единицы, знак неравенства не меняется, получаем:
Напомним методику решения таких неравенств.
Рассматриваем дробно-рациональную функцию:
Находим область определения:
Находим корни функции:
Функция имеет единственный корень,
Выделяем интервалы знакопостоянства и определяем знаки функции на каждом интервале:
Рис. 2. Интервалы знакопостоянства
Таким образом, получили ответ.
Ответ:
Рассмотрим неравенства с одинаковыми показателями, но различными основаниями.
Пример 4:
Одно из свойств показательной функции – она при любых значениях аргумента принимает строго положительные значения, значит, на показательную функцию можно разделить. Выполним деление заданного неравенства на правую его часть:
Основание степени больше единицы, знак неравенства сохраняется.
Ответ:
Проиллюстрируем решение:
На рисунке 6.3 изображены графики функций и . Очевидно, что когда аргумент больше нуля, график функции расположен выше, эта функция больше. Когда же значения аргумента отрицательны, функция проходит ниже, она меньше. При значении аргумента функции равны, значит, данная точка также является решением заданного неравенства.
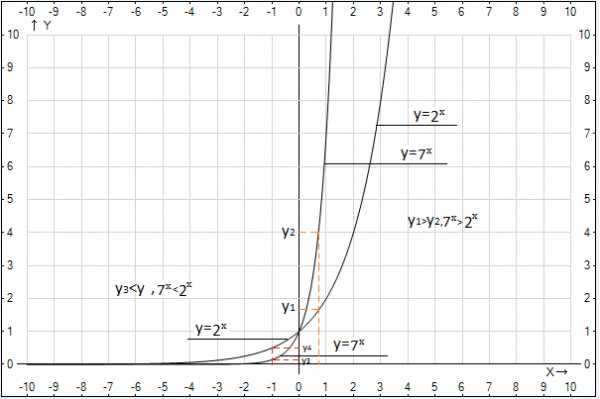
Рис. 3. Иллюстрация к примеру 4
Пример 5:
Преобразуем заданное неравенство согласно свойствам степени:
Приведем подобные члены:
Разделим обе части на :
Теперь продолжаем решать аналогично примеру 4, разделим обе части на :
Основание степени больше единицы, знак неравенства сохраняется:
Ответ:
Пример 6 – решить неравенство графически:
Рассмотрим функции, стоящие в левой и правой части и построим график каждой из них.
Функция – экспонента, возрастает на всей своей области определения, т. е. при всех действительных значениях аргумента.
Функция – линейная, убывает на всей своей области определения, т. е. при всех действительных значениях аргумента.
Если данные функции пересекаются, то есть система имеет решение, то такое решение единственное и его легко можно угадать. Для этого перебираем целые числа ()
Несложно заметить, что корнем данной системы является :
Таким образом, графики функций пересекаются в точке с аргументом, равным единице.
Теперь нужно получить ответ. Смысл заданного неравенства в том, что экспонента должна быть больше или равна линейной функции, то есть быть выше или совпадать с ней. Очевиден ответ: (рисунок 6.4)
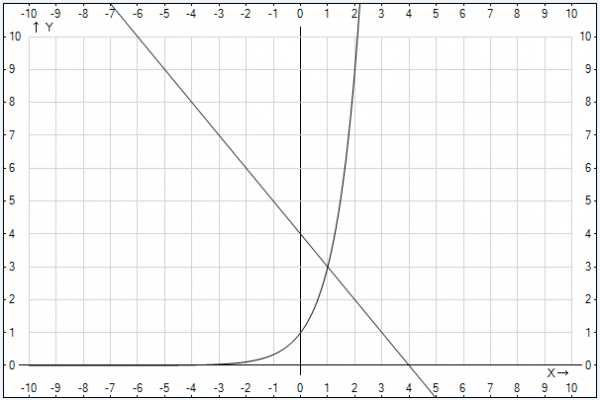
Рис. 4. Иллюстрация к примеру 6
Итак, мы рассмотрели решение различных типовых показательных неравенств. Далее перейдем к рассмотрению более сложных показательных неравенств.
Список литературы
- Мордкович А.Г. Алгебра и начала математического анализа. – М.: Мнемозина.
- Муравин Г.К., Муравина О.В. Алгебра и начала математического анализа. – М.: Дрофа.
- Колмогоров А.Н., Абрамов А.М., Дудницын Ю.П. и др. Алгебра и начала математического анализа. – М.: Просве
interneturok.ru
Показательные неравенства. Как решать показательные неравенства?
Примеры:
\(4^{x}\geq32\)
\(5^{2x-1}-5^{2x-3}≤4,8\)
\((\sqrt{7})^{2x+2}-50(\sqrt{7})^{x}+7>0\)
Как решать показательные неравенства?
Нужно стремиться свести неравенство к виду: \(a^{f(x)}\) \(˅\) \(a^{g(x)}\) (\(˅\) означает любой из знаков сравнения) – это позволяет избавиться от оснований и сделать переход к виду \(f(x) ˅ g(x)\).
Примеры:
| \(4^{x}≥32\) | \((0,5)^{2x}>0,125\) |
| \(2^{2x}≥2^5\) | \((0,5)^{2x}>(0,5)^3\) |
| \(2x≥5\) | \(2x<3\) |
| \(x≥2,5\) | \(x<1,5\) |
Но есть одна важная тонкость в переходе в показательных неравенствах:
\(-\) если основание степени больше \(1\), то знак неравенства должен оставаться прежним,
\(-\) если же основание — число большее \(0\), но меньшее \(1\) (лежит между нулем и единицей), то знак неравенства должен меняться на противоположный, т.е.
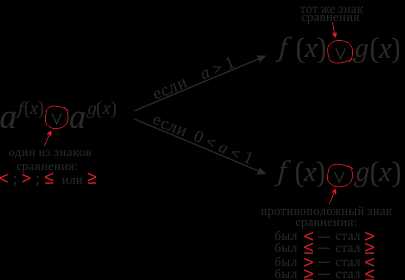
\(2^{x+1}\) \(≥\) \(2^3 ⇒ x+1\) \(≥\) \(3\)
\(0,5^{4x+3}\) \(≤\) \(0,5^{6x-1} ⇒ 4x+3\) \(≥\) \(6x-1\)
Важно! Есть два требования для перехода в показательных неравенствах:
\(-\) число в основании степени слева и справа должно быть одинаковым;
\(-\) степени слева и справа должны быть «чистыми», то есть не должно быть никаких коэффициентов, умножений, делений и т.д.
Например:
|
1) \(3^{x+2}>5^{8-x}\) |
Переход к \(x+2> 8-x \) невозможен, так как в основаниях разные числа |
|
2) \(7^{x}+7^{3x}<7^{2x}\) |
Переход к \(x+3x<2x\) невозможен, так как степени не «чистые» (слева есть сумма) |
|
3) \(2^{5-x}≥-2^{7x}\) |
Переход к \(5-x≥7x\) невозможен, так как степени не «чистые» (перед степенью справа стоит минус) |
Пример. Решить показательное неравенство: \(2^{x}+2^{x+2}\leq 20\)
Решение:
|
\(2^{x}+2^{x+2}\leq 20\) |
Сразу переход делать нельзя, сумма в левой части не дает. Поэтому используем свойства степеней и преобразуем \(2^{x+2}=2^{x} \cdot 2^2=4 \cdot 2^x\) |
|
|
\(2^{x}+4 \cdot 2^{x}\leq 20\) |
Теперь \(2^x\) и \(4 \cdot 2^{x}\) – подобные слагаемые, можно их сложить |
|
|
\(5 \cdot 2^x≤20\) \(| ∶5\) |
Делим обе части неравенства на \(5\) |
|
|
\(2^x≤4\) |
Представляем четверку как \(2^2\) |
|
|
\(2^x≤2^2\) |
|
Вот теперь делаем переход: избавляемся от оснований, не меняя знак сравнения, т.к. основание \(2>1\) |
|
\(x≤2\) |
|
Пример. Решить показательное неравенство: \(4^{2x}-5 \cdot 4^{x}+4< 0\)
Решение:
|
\(4^{2x}-5 \cdot 4^{x}+4< 0\) |
Перед нами типичное показательно-квадратное неравенство. Преобразуем по свойству степеней \(4^{2x}=(4^x)^2\), чтобы на следующем шаге сделать замену. |
|
|
\((4^{x})^2-5 \cdot 4^{x}+4< 0\) |
Делаем замену переменных |
|
|
\(t=4^x\) |
Записываем неравенство в новом виде |
|
|
\(t^2-5t+4<0\) |
Раскладываем на множители правую часть |
|
|
\((t-1)(t-4)<0\) |
|
Решаем неравенство с помощью метода интервалов |
|
|
|
Записываем промежуточное решение в виде системы и делаем обратную замену |
|
\(\begin{cases}t>1\\t<4\end{cases} \Leftrightarrow \begin{cases}4^x>1\\4^x<4\end{cases}\) |
|
Решаем показательные неравенства |
|
\(\begin{cases}4^x>4^0\\4^x<4^1\end{cases} \Leftrightarrow \begin{cases}x>0\\x<1\end{cases}\) |
|
Записываем ответ |
Решение показательных неравенств с разными основаниями
А что делать, если невозможно привести левую и правую часть неравенства к степеням с одинаковыми основаниями (т.е. к виду \(a^{f(x)} ˅ a^{g(x)})\) ? Тогда на сцену выходит его величество логарифм. По основному логарифмическому тождеству — \(c=a^{\log_{a}{c}}\) , а значит любое положительное число можно представить в виде степени с любым основанием: \(5=2^{\log_{2}{5}}\) ; \(0,1=200^{\log_{200}{0,1}}\) и т.д.
Пример: Решить показательное неравенство:
|
\(0,2^{-7x+4}≥4\) |
Заменим \(4\) на \(0,2^{\log_{0,2}{4}}\) |
|
|
\(0,2^{-7x+4}≥0,2^{\log_{0,2}{4}}\) |
Избавимся от оснований с переменой знака т.к. \(0,2<1\) |
|
|
\(-7x+4≤\log_{0,2}{4}\) |
\(\log_{0,2}{4}\) – число некрасивое, но все-таки число, т.е. перед нами обычное линейное неравенство. |
|
|
\(-7x≤\log_{0,2}{4}-4\) |
Поделим обе части на \(-7\) |
|
|
\(x≥\) \(\frac{4-\log_{0,2}{4}}{7}\) |
Ответ: \(x∈\)\([\frac{4-\log_{0,2}{4}}{7}\)\(;∞)\)
Знаю, выглядит не очень, но ответ не выбирают.
Особые виды показательных неравенств
Решим неравенство \(5^x<-5\). Подумайте, каким должен быть икс, чтобы \(5^x\) превратилось в \(-5\)? Наверно, вы подумали о минус единице? Давайте проверим эту гипотезу: \(5^{-1}=\frac{1}{5}\) – не подходит.
На самом деле, никакая степень не превратит положительное число в отрицательное. Почему? Потому что показателе степени говорит лишь о том сколько раз умножается само на себя основание. А основание – положительно, и произведение положительных чисел – всегда положительно.
Таким образом, никакой \(x\) не сделает \(5^x\) отрицательным. То же самое можно сказать про \(2^x\), \(3^x\), \(4^x\), \(6^x\) и т.д.
Если \(a\) – положительно, то \(a^x>0\) при любых \(x\)
Поэтому у показательного неравенства \(5^x<-5\) нет решений.
Рассмотрим обратное неравенство: \(5^x>-5\).
\(5^x\) – всегда больше нуля, и, уж тем более, оно будет больше \(-5\). Значит, решением неравенства \(5^x>-5\) будет любое число: \(x∈(-∞;∞)\).
Смотрите также:
Показательные уравнения
Логарифмические уравнения
Равносильные преобразования неравенств
Логарифмические неравенства
cos-cos.ru
Показательные неравенства
\(\blacktriangleright\) На ОДЗ верны следующие формулы:
\[\large{\begin{array}{|ll|} \hline a^0=1 &a^1=a\\ a^{nm}=(a^n)^m &a^n\cdot a^m=a^{n+m}\\ \dfrac{a^n}{a^m}=a^{n-m}&a^{-n}=\dfrac{1}{a^n}\\ a^n\cdot b^n=(a\cdot b)^n &\\ a^{\frac{k}{r}}=\sqrt[r]{a^k} \qquad \qquad \qquad \qquad& \dfrac{a^n}{b^n}=\left(\dfrac{a}{b}\right)^n\\&\\ a,b>0, \ \ a,b\ne 1, \ k\in \mathbb{Z},& r\in\mathbb{N}, \ m,n\in\mathbb{R}\\ \hline \end{array}}\]
\(\blacktriangleright\) Стандартное показательное неравенство: \[{\Large{a^{h(x)}\geqslant a^{g(x)} \ (*)}}\] где \(a>0,\ a\ne 1\)
(на месте знака \(\geqslant\) может стоять любой из знаков \(\leqslant,\
>,\ <\))
Показательная функция \(f(x)=a^x\) является возрастающей, если число \(a>1\), и убывающей, если \(0<a<1\), и определена при всех \(x\) (то есть ее область определения \(x\in\mathbb{R}\)).
На графике приведен пример возрастающей показательной функции \(f_1(x)=2^x\) и убывающей показательной функции \(f_2(x)=(0,5)^x\).
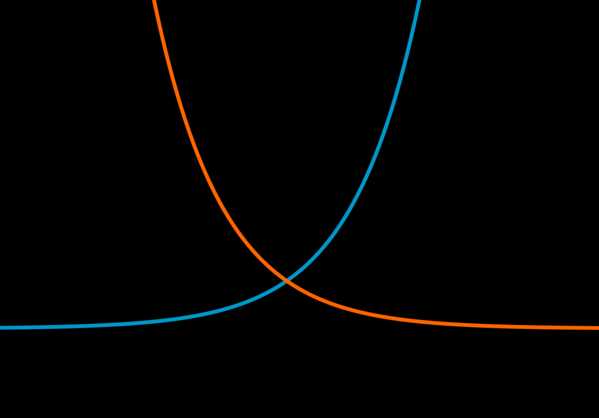
Напомним, что функция возрастает, если при увеличении \(x\) увеличивается и \(f(x)\). Функция убывает, если при увеличении \(x\) уменьшается \(f(x)\).
Действительно, для функции \(f_1(x)=2^x\), например, \(f_1(2)>f_1(3)
\Leftrightarrow 4>8\), а для функции \(f_2(x)=0,5^x\), например, \(f_2(2)<f_2(3) \Leftrightarrow 0,25<0,125\).
Таким образом, неравенство \((*)\) есть не что иное, как сравнение \(f(h)\) и \(f(g)\). Если функция \(f\) — возрастает, то неравенство \(f(h)\geqslant f(g)\) равносильно неравенству \(h\geqslant g\), а если убывает — то неравенству \(h\leqslant g\).
Поэтому для того, чтобы решить неравенство \((*)\), нужно сравнить основание \(a\) с единицей:
если \({\large{a>1}}\), то данное неравенство равносильно \[{\Large{h(x)\geqslant g(x)}}\]
если \({\large{0<a<1}}\), то данное неравенство равносильно \[{\Large{h(x)\leqslant g(x)}}\]
\(\blacktriangleright\) Напомним, что область значений показательной функции — все положительные числа, т.е. \(a^x>0\) при всех возможных \(a\) и \(x\).
\(\blacktriangleright\) С помощью формулы \({\Large{b=a^{\log_ab}}}\) можно любое число \(b>0\) представить в виде степени необходимого нам числа \(a>0,\ a\ne 1\).
Пример 1. Решить неравенство \(2^x>3^{x-1}\).
Нужно представить левую и правую части неравенства как степени с одинаковым основанием. Воспользовавшись формулой, можно записать \(3=2^{\log_23}\). Тогда неравенство примет вид:
\(2^x>2^{\log_23\cdot (x-1)}\). Т.к. основания \(2>1\), то знак неравенства не будет меняться и данное неравенство равносильно неравенству
\(x>\log_23\cdot (x-1)\). Отсюда \((1-\log_23)x>-\log_23\). Т.к. \(\log_23>1\), то \((1-\log_23)<0\), значит, при делении правой и левой частей неравенства на \((1-\log_23)\) нужно изменить знак неравенства на противоположный, то есть \[x<-\dfrac{\log_23}{1-\log_23}
\Leftrightarrow x<\dfrac{\log_23}{\log_23-1}\].
\(\blacktriangleright\) Рассмотрим неравенства вида \[{\Large{(f(x))^{h(x)}\lor(f(x))^{g(x)}}}\] то есть когда в основании находится не конкретное число, а функция, также зависящая от \(x\).
В таких неравенствах \(f(x)\) может быть равно единице, если знак неравенства нестрогий (т.е. \(\geqslant, \ \leqslant\)) и если это не противоречит ОДЗ неравенства. Действительно, тогда мы получаем, например, \(1^{h(x)}\geqslant 1^{g(x)}\), что верно, т.к. единица в любой степени дает единицу.
Таким образом, имеем: \[\textbf{I. }{\Large{(f(x))^{h(x)}> (f(x))^{g(x)} \quad \Leftrightarrow\quad \left[\begin{gathered}
\begin{aligned}
&\begin{cases} f(x)>1\\ h(x)>
g(x) \end{cases}\\[2pt]
&\begin{cases} 0<f(x)<1\\ h(x)< g(x) \end{cases}
\end{aligned}
\end{gathered}
\right.}}\]
\[\textbf{II. }{\Large{(f(x))^{h(x)}\geqslant (f(x))^{g(x)} \quad\Leftrightarrow\quad \left[\begin{gathered} \begin{aligned} &\begin{cases} f(x)>1\\ h(x)\geqslant g(x) \end{cases}\\[2pt] &\begin{cases} 0<f(x)<1\\ h(x)\leqslant g(x) \end{cases}\\[2pt] &f(x)=1 \end{aligned} \end{gathered} \right.}}\]
Пример 2. Решить неравенство \(x^{\sqrt{x-0,5}}\geqslant x^2\)
Запишем ОДЗ: выражение под корнем должно быть неотрицательным, т.е. \(x-0,5\geqslant 0 \Leftrightarrow x\geqslant
0,5\). Тогда на ОДЗ данное неравенство равносильно:
\(\left[\begin{gathered}
\begin{aligned}
&\begin{cases} x>1\\ \sqrt{x-0,5}\geqslant
2 \end{cases}\\[2pt]
&\begin{cases} 0<x<1\\ \sqrt{x-0,5}\leqslant 2 \end{cases}\\[2pt]
&x=1
\end{aligned}
\end{gathered}
\right. \Rightarrow \left[\begin{gathered}
\begin{aligned}
&\begin{cases} x>1\\ x\geqslant
4,5 \end{cases}\\[2pt]
&\begin{cases} 0<x<1\\ x\leqslant 4,5 \end{cases}\\[2pt]
&x=1
\end{aligned}
\end{gathered}
\right. \Rightarrow x\in (0;1]\cup [4,5;+\infty)\)
Пересекая полученный ответ с ОДЗ, получим \[x\in [0,5;1]\cup [4,5;+\infty)\]
shkolkovo.net
Решение показательных неравенств
 Решение показательных неравенств.
Решение показательных неравенств.
В этой статье, как вы догадались, речь пойдет о решении показательных неравенств. Простейшее показательное неравенство имеет вид:
V , где V — один из знаков: <,>,≤, или ≥.
Чтобы решить показательное неравенство, нам нужно от сравнения степеней перейти к сравнению показателей.
Как мы помним, показательная функция возрастает при всех действительных значениях , если . Это значит, что большему значению аргумента соответствует большее значение функции. То есть из неравенства
следует неравенство
Аналогично, так как показательная функция убывает, если , и большему значению аргумента соответствует меньшее значение функции, из неравенства
следует неравенство
То есть при решении простейших показательных неравенств прежде чем сравнивать выражения, стоящие в показателе степени, нужно сравнить с единицей основание степеней.
Ещё раз, это важно:
если основание степени больше единицы, то при переходе к выражениям, стоящим в показателе, знак неравенства сохраняется
если основание степени больше нуля, но меньше единицы, то при переходе к выражениям, стоящим в показателе, знак неравенства меняется на противоположный.
Все показательные неравенства любого уровня сложности, в конечном итоге, сводятся к решению простейших показательных неравенств.
Рассмотрим несколько примеров.
1. Решим неравенство:
Так как основание степеней , при переходе к выражениям, стоящим в показателе, знак неравенства меняется на противоположный:
Перенесем все влево, и приведем к общему знаменателю:
Корни числителя:
,
Решим неравенство методом интервалов: нанесем корни числителя и знаменателя на числовую ось и расставим знаки:
Ответ: , ,
2. Решим неравенство:
Перенесем все слагаемые влево и разложим основания степеней на простые множители:
Если бы это было уравнение, мы решали бы его с помощью замены переменной. Поступим также.
Вообще, показательные неравенства делятся на те же типы, что и показательные уравнения, и решаются теми же способами.
Внимание! Если мы решаем неравенство с помошью замены переменных, то нужно решать относительно замены до получения простейшего неравенства. Поясню на этом примере.
Введем замену: ,
Получим систему неравенств:
Отсюда:
То есть
Запишем двойное неравенство в виде системы:
Вот теперь мы можем вернуться к исходной переменной:
Отсюда: ,
Ответ:
И.В. Фельдман, репетитор по математике.
ege-ok.ru
Показательные неравенства
Учитель математики МБОУ «Гимназия №1 им. Р.Фахреддина» г.Альметьевск РТ Закирова М.А.
11б класс. Тема: Показательные неравенства
Тип урока: Урок формирования новых знаний
Цели урока:
— познакомить обучающихся с показательными неравенствами, формирование знаний об основных методах решения показательных неравенств.
– развитие умений сравнивать, выявлять закономерность, обобщать, развитие логики, памяти.
– воспитание ответственного отношения к учебному труду, внимательности.
Оборудование: проектор, презентация «Показательные неравенства», карточки
Этапы урока и их содержание
1. Организационный этап. На уроке будут рассмотрены показательные неравенства, решение которых требует хорошего знания теоретического материала. Данные неравенства ежегодно присутствуют в вариантах ЕГЭ по математике.
2.Проверка домашнего задания. №12.18; 12.23; 12.25
3. Актуализация знаний. А)Теоретический опрос: слайд 1
1) функцию какого вида называют показательной;
2) какова область определения показательной функции;
3) каково множество значений показательной функции;
4) что можно сказать о монотонности показательной функции в зависимости от основания а;
5) уравнение какого вида называется показательным;
Б) Среди заданных функций укажите те, которые являются показательными: слайд 2
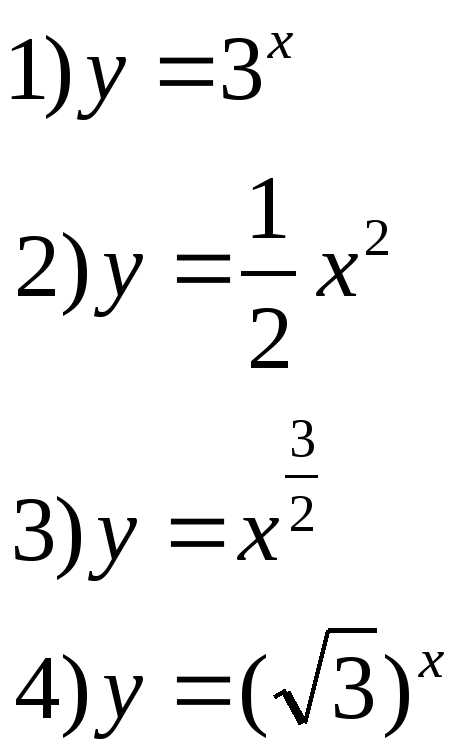
В) Какие из заданных функций являются возрастающими, какие убывающими?
г).Решите уравнения: слайд 4
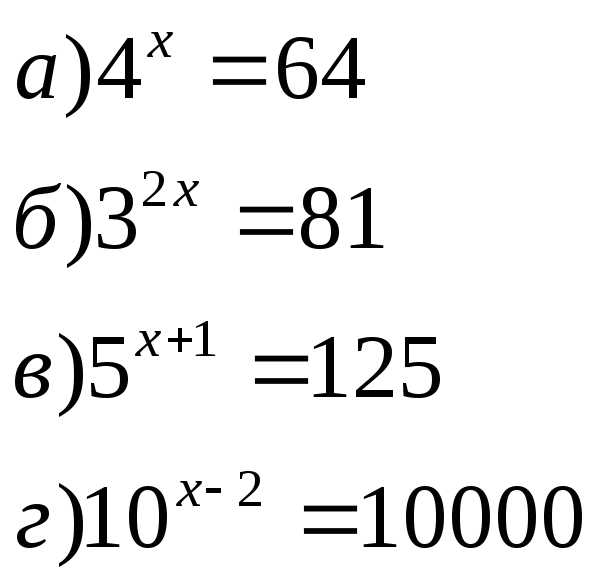
Ответ: а) 3; б) 2; в)2; г)6.
4.Изучение новой темы
Определение: Показательными неравенствами называются неравенства вида , где а>0 и а≠1. Слайд 5
Используя свойство монотонности показательной функции делаем вывод, что неравенство при равносильно неравенству а при равносильно неравенству
Простейшие показательные неравенства имеют вид (слайды 9,10,11)
решений не имеет, а неравенство выполняется при всех значениях аргумента, поскольку
Способы решения показательных уравнений и неравенств: слайд 8
Уравнивание оснований
Введение новой переменной (замена переменной)
Вынесение общего множителя за скобку
Деление на показательную функцию
Графический способ
Рассмотрим 1 способ – способ уравнивания оснований
1. слайд 12
2) Рассмотрим решение ещё нескольких показательных неравенств:( слайды 14,15)
а
 )
)
б)

в)
3.) А теперь рассмотрим решение двойных неравенств: слайд 16
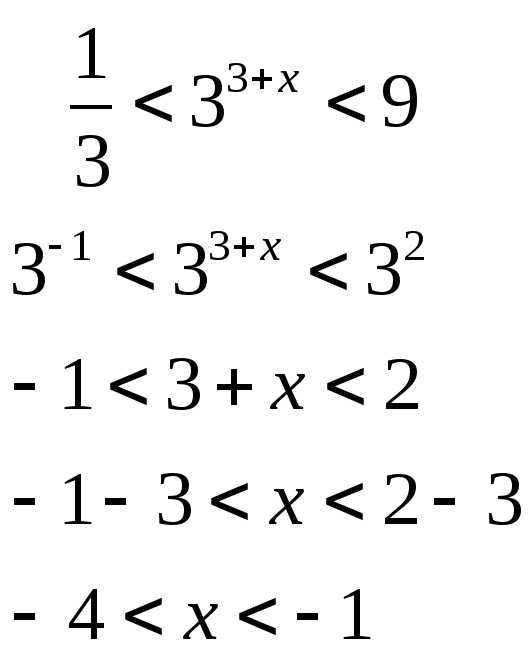
Ответ: (- 4; -1).
Рассмотрим 2 способ — метод замены переменной.
А теперь рассмотрим решение показательных неравенств методом введения новой переменной или замены переменной: слайды 17,18
Пример 1: Сведение к квадратному неравенству.


Примеры некоторых заданий профильного уровня ЕГЭ- 2015 из сайта «Алексарин Ларин», которые решаются методом замены переменной. (разобрать образцы 17 задания ЕГЭ-2015 профильного уровня)
Пример 2: Сведение к рациональному неравенству, которое решаем применяя метод интервалов для непрерывных функций.
Ответ:
4.Закрепление изученной темы:
Решить устно №13.1; №13.2
Решить письменно №13.3; №13.5; 13.8
5.Самостоятельная работа по карточкам (слайд 22)
6. Домашнее задание. Прочитать п 13; решить № 13.4; 13.6; 13.8
7.Итоги урока.
xn--j1ahfl.xn--p1ai
Решение показательного неравенства с разными основаниями
В этой статье я покажу как решать показательное неравенство вида
Решим неравенство:
Запишем неравенство в таком виде:
Разделим обе части неравенства на 3:
Теперь возьмем от обеих частей неравенства логарифм по основанию 3. Мы имеем право это сделать, так как обе части неравенства больше нуля. Основание логарифма больше единицы, поэтому знак неравенства не изменится.
Получим:
Перенесем слагаемые, содержащие неизвестное влево, а не содержащие — вправо:
Разделим обе части неравенства на , предварительно исследовав знак этого выражения.
Т.к. ,
Получим:
Ответ:
И.В. Фельдман, репетитор по математике.
ege-ok.ru
