Формулы приведения
Определение. Формулами приведения называют формулы, которые позволяют перейти от тригонометрических функций вида к функциям аргумента . С их помощью синус, косинус, тангенс и котангенс произвольного угла можно привести к синусу, косинусу, тангенсу и котангенсу угла из интервала от 0 до 90 градусов (от 0 до радиан). Таким образом, формулы приведения позволяют нам переходить к работе с углами в пределах 90 градусов, что, несомненно, очень удобно.
Формулы приведения:
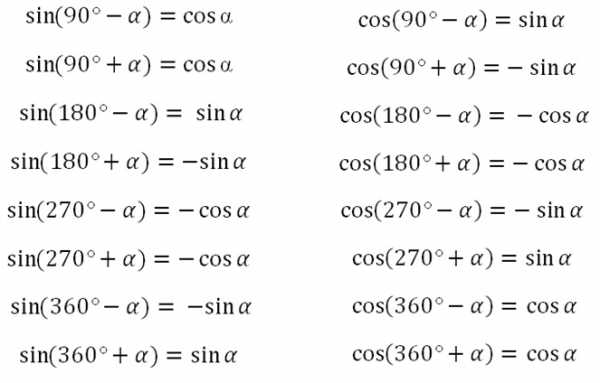
Для использования формул приведения существует два правила.
1. Если угол можно представить в виде (π/2 ±a) или (3*π/2 ±a), то название функции меняется sin на cos, cos на sin, tg на ctg, ctg на tg. Если же угол можно представить в виде (π ±a) или (2*π ±a), то название функции остается без изменений.
Посмотрите на рисунок ниже, там схематично изображено, когда следует менять знак, а когда нет
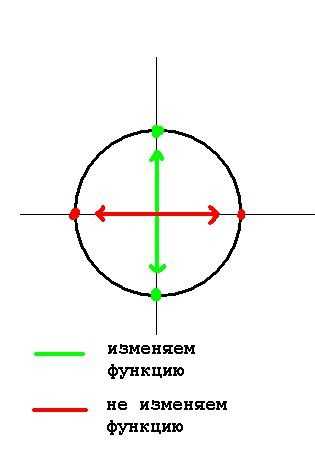
2. Знак приведенной функции остается прежним. Если исходная функция имела знак «плюс», то и приведенная функция имеет знак «плюс». Если исходная функция имела знак «минус», то и приведенная функция имеет знак «минус».
На рисунке ниже представлены знаки основных тригонометрических функций в зависимости от четверти.
Пример:
Вычислить
Воспользуемся формулами приведения:
Sin(150˚) находится во второй четверти, по рисунку видим что знак sin в этой четверти равен «+». Значит у приведенной функции тоже будет знак «+». Это мы применили второе правило.
Теперь 150˚ = 90˚ +60˚. 90˚ это π/2. То есть имеем дело со случаем π/2+60, следовательно по первому правилу меняем функцию с sin на cos. В итоге получаем Sin(150˚) = cos(60˚) = ½.
ya-znau.ru
Формулы приведения и решение типовых задач. Видеоурок. Алгебра 10 Класс
Тема: Тригонометрические функции
Урок: Формулы приведения и решение типовых задач
Формулы приведения подчиняются двум правилам, которые мы рассмотрели на прошлом уроке. Они позволяют привести значения тригонометрических функций к более удобным углам. Особенно важны углы, кратные
Рассмотрим таблицу значений тригонометрических функций для таких углов.
|
α |
0 |
|
π |
||||||||||||||
|
sinα |
0 |
1 |
0 |
-1 |
0 |
||||||||||||
|
cosα |
1 |
0 |
|
0 |
1 |
||||||||||||
|
tgα |
0 |
1 |
0 |
1 |
— |
0 |
|||||||||||
|
ctgα |
— |
1 |
0 |
— |
1 |
|
— |
По вертикали отложены функции, по горизонтали – углы, кратные на отрезке
Держать такую таблицу в голове довольно сложно. Надо иметь способ быстрого получения значений тригонометрических функций для этих углов. Применение формул приведения и есть такой способ. Для этого достаточно запомнить значения тригонометрических функций для углов
Рассмотрим расположение углов на числовой оси и числовой окружности.
Углы из отрезка кратные на координатной оси (рис. 1).
Углы из отрезка кратные на единичной окружности (рис. 2).
a) Значения кратные
b) Значения кратные
На рисунке показан не только каждый угол, но и значения синуса угла
и косинуса угла. Таким образом, знания значений тригонометрических функций угловinterneturok.ru
Формулы приведения. Лошадиное правило. Примеры
Стоит ли учить формулы приведения?
Вы в состоянии выучить вот такую таблицу? 🙁
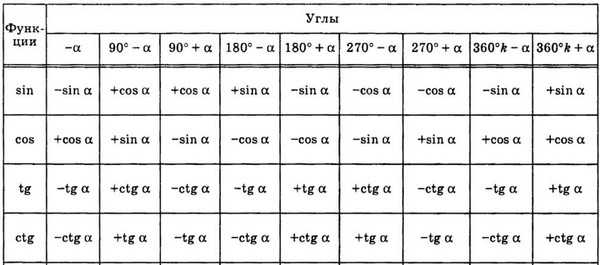
А без приведения сложных аргументов тригонометрических функций к аргументам первой четверти на ЕГЭ по математике никуда.
Но нет необходимости учить эту таблицу!
Нужно просто потратить немного времени и понять алгоритм применения формул приведения.
Не будем терять время! Поехали!
Зачем вообще формулы приведения?
Формулы приведения позволяют упростить вычисления, привести сложные аргументы тригонометрических функций к аргументам I четверти.
Вот, например, типичное задание из ЕГЭ по математике:
Вычислите или
Давайте разбираться. А к примерам вернемся чуть позже.
Если хотите докапаться до самой сути, то –> + показать
Можно и пропустить 🙁
Медленно, но верно
Преобразование 1.
Упростим .
Считаем – углом первой четверти!
Отмечаем углы , :
Отмечаем значения и :
Очевидно, длина «зеленого» катета равна длине «красного» в силу равенства «серых» треугольников:
Но только – отрицательная величина, а – положительная.
Поэтому
Преобразование 2.
Упростим .
Вот и :
Вот :
И вот :
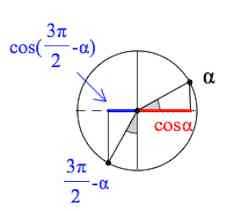
Из следующей картинки хорошо видно, что длина отрезка, помеченного синим цветом, равна длине отрезка, помеченного зеленым цветом.
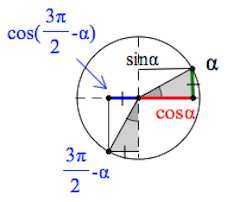
При этом – отрицательная величина, – положительная.
Поэтому
Преобразование 3.
Упростим .
Вот :
Значение же , как хорошо видно на картинке, то же, что и
Поэтому .
Можно разбирать примеры и дальше для более четкого выявления закономерностей, но давайте уже сформулируем правило, на которое будем опираться при работе с формулами приведения.
Вы всегда сможете проверить «правильность» формулы способом, который мы только что применяли.
Мнемоническое правило для формул приведения
1. Задаем себе вопрос: «Меняется ли название функции на кофункцию?» (то есть синнус на косинус, косинус на синус, тангенс на котангенс и котангенс на тангенс).
Чтобы ответить на этот вопрос нужно, не смейтесь, – подвигать головой вдоль оси, на которой располагается ключевая точка. Ключевые точки всегда располагаются здесь (см. рис.):
Например, в формулах – ключевые точки – это .
Так вот если вы мотаете головой вдоль горизонтальной прямой, потому что ключевая точка располагается на ней, то вы, как бы, отвечаете «нет» на вопрос «Меняется ли название функции на кофункцию?»
Если вы киваете головой вдоль вертикальной прямой, потому что ключевая точка располагается на ней, то вы отвечаете «да» на вопрос «Меняется ли название функции на кофункцию?».
2. Ставим справа, на выходе, тот знак, какой несет в себе левая, исходная, часть.
Данное правило еще называется «лошадиным».
Примеры
При выполнении заданий нам понадобятся основные значения тригонометрических функций.
Задача 1.
Вычислить .
Решение:
1.
Ключевая точка располагается на горизонтальной оси:
Название функции меняться не будет.
2. Исходное значение – отрицательно, так как располагается в IV четверти:
Итак,
Ответ: -0,5.
Задача 2.
Вычислить
Решение:
1.
Ключевая точка располагается на горизонтальной оси:
Название функции меняться не будет.
2. Исходное значение – отрицательно, так как располагается в III четверти:
Итак,
Ответ: -1.
Задача 3.
Упростить
Решение:
(название не меняем, знаки и различаются, как видим из картинки, – ставим справа знак «-»)
(название меняем, знаки и , как видно из картинки, одинаковы, – ставим справа знак «+»)
(название меняем, проверять знак нет необходимости, так как все равно у нас функция – в квадрате)
(название не меняем, знаки и , как видно из картинки, одинаковы, ставим справа знак «+»)
(название меняем, знаки и , как видно из картинки, одинаковы, ставим справа знак «+» )
Итак,
Ответ:
egemaximum.ru
Формулы приведения / Блог :: Бингоскул
- Блог
- →
- Формулы приведения
Таблица формул приведения
Два правила формул приведения
- при 900 и при 2700 (в виде (π/2 ±a) или (3*π/2 ±a)) — функция меняется на кофункцию (sin на cos либо в обратную сторону, tg на ctg либо в обратную).
- при 1800 и при 3600 (в виде (π ±a) или (2*π ±a)) — функция НЕ изменяется.
2 способа запоминания формул приведения
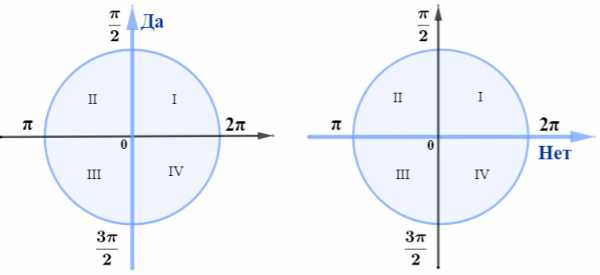
1. «Правило лошади»:
Если мы откладываем угол от вертикальной оси, лошадь говорит «да» (киваем головой вдоль оси OY) и приводимая функция меняет свое название: синус на косинус, косинус на синус, тангенс на котангенс, котангенс на тангенс.
Если мы откладываем угол от горизонтальной оси, лошадь говорит «нет» (киваем головой вдоль оси OХ) и приводимая функция не меняет свое название.
Знак правой части равенства совпадает со знаком приводимой функции, стоящей в левой части равенства.
2. Использование четности и периодичности.
нечетная функция
- sin (-α) = -sin α
- tg (-α) = -tg α
- сtg (-α) = -сtg α
четная функция
Тригонометрические функции (синус, косинус, тангенс, котангенс) являются периодическими:
- sin α, cos α — периодические функции с наименьшим положительным периодом 2π: sin(α+2kπ) = sin α,cos(α+2kπ) = cos α, k ∈ Z.
- tg α, ctg α — периодические функции с наименьшим положительным периодом π: tg(α+kπ) = tgα, ctg(α+kπ) = ctg α, k ∈ Z.
Формулы приведения в виде списка
sin
- sin(900 — α) = cos α
- sin (900 + α) = cos α
- sin (1800 — α) = sin α
- sin (1800 + α) = -sin α
- sin (2700 — α) = -cos α
- sin (2700 + α) = -cos α
- sin (3600 — α) = -sin α
- sin (3600 + α) = sin α
cos
- cos (900 — α) = sin α
- cos (900 + α) = -sin α
- cos (1800 — α) = -cos α
- cos (1800 + α) = -cos α
- cos (2700 — α) = -sin α
- cos (2700 + α) = sin α
- cos (3600 — α) = cos α
- cos (3600 + α) = cos α
tg
- tg(900 — α) = ctg α
- tg (900 + α) = -ctg α
- tg (1800 — α) = -tg α
- tg (1800 + α) = tg α
- tg (2700 — α) = ctg α
- tg (2700 + α) = -ctg α
- tg (3600 — α) = -tg α
- tg (3600 + α) = tg α
ctg
- ctg (900 — α) = tg α
- ctg (900 + α) = -tg α
- ctg (1800 — α) = -ctg α
- ctg (1800 + α) = ctg α
- ctg (2700 — α) = tg α
- ctg (2700 + α) = -tg α
- ctg (3600 — α) = -ctg α
- ctg (3600 + α) = ctg α
Угол альфа α находится в интервале 0 — 90°.
Знаки основных тригонометрических функций в зависимости от четверти
Дополнительный материал: Формулы тригонометрии
Смотри также: Основные формулы по математике
bingoschool.ru
Формулы приведение | tutomath
Тригонометрия.Формулы приведения.
Формулы приведения не нужно учить их нужно понять. Понять алгоритм их вывода. Это очень легко!
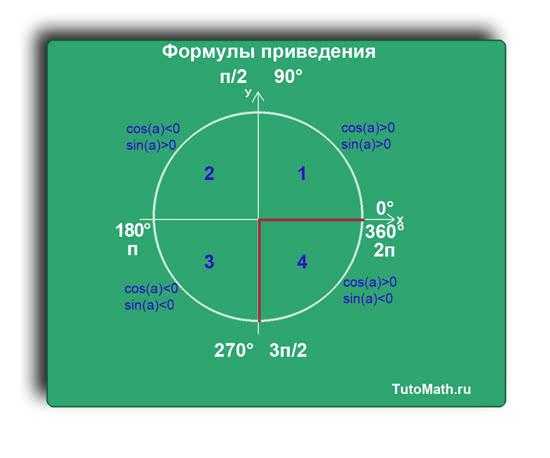
Возьмем единичную окружность и расставим все градусные меры (0°; 90°; 180°; 270°; 360°) на ней.

Разберем в каждой четверти функции sin(a) и cos(a).
Запомним, что функцию sin(a) смотрим по оси Y, а функцию cos(a) по оси X.
В первой четверти видно, что функция sin(a)>0, потому что ось Y положительна в этой четверти.
И функция cos(a)>0, потому что ось X положительна в этой четверти.
Первую четверть можно описать через градусную меру, как (90-α) или (360+α).

Во второй четверти видно, что функция sin(a)>0, потому что ось Y положительна в этой четверти.
А функция cos(a), потому что ось X отрицательна в этой четверти.
Вторую четверть можно описать через градусную меру, как (90+α) или (180-α).
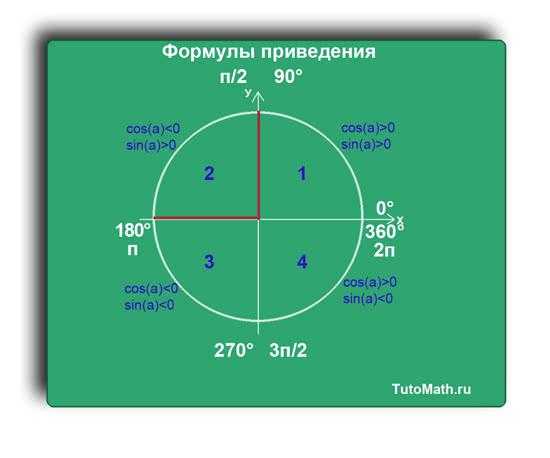
В третьей четверти видно, что функции sin(a), потому что ось Y и X отрицательны в этой четверти.
Третья четверть можно описать через градусную меру, как (180+α) или (270-α).
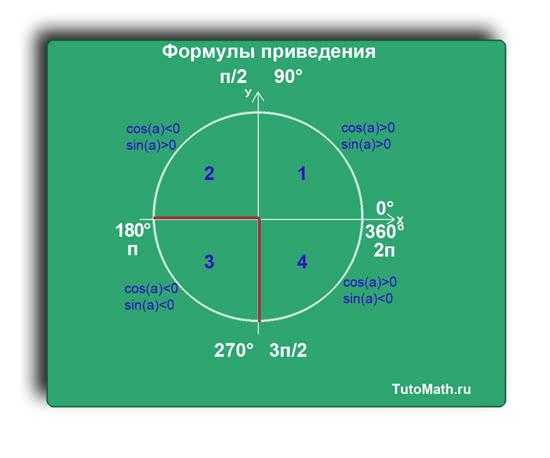
В четвертой четверти видно, что функция sin(a), потому что ось Y отрицательна в этой четверти.
А функция cos(a)>0, потому что ось X положительна в этой четверти.
Четвертую четверть можно описать через градусную меру, как (270+α) или (360-α).
Теперь рассмотрим сами формулы приведения.
Запомним простой алгоритм:
1. Четверть. (Всегда смотрите в какой вы четверти находитесь).
2. Знак. (Относительно четверти смотрите положительны или отрицательный функции косинуса или синуса).
3. Если у вас есть в скобочках (90° или π/2) и (270° или 3π/2), то функция меняется.
И так начнем разбирать по четвертям данный алгоритм.
Выясни чему будет равно выражение cos(90-α)
Рассуждаем по алгоритму:
1. Четверть первая.
2. В первой четверти знак у функции косинуса положительный.
3. В скобочках есть (90° или π/2), то функция меняется с косинуса на синус.
Будет cos(90-α) = sin(α)
Выясни чему будет равно выражение sin(90-α)
Рассуждаем по алгоритму:
1. Четверть первая.
2. В первой четверти знак у функции синуса положительный.
3. В скобочках есть (90° или π/2), то функция меняется с синуса на косинус.
Будет sin(90-α) = cos(α)
Выясни чему будет равно выражение cos(360+α)
Рассуждаем по алгоритму:
1. Четверть первая.
2. В первой четверти знак у функции косинуса положительный.
3. В скобочках нет (90° или π/2) и (270° или 3π/2), то функция не меняется.
Будет cos(360+α) = cos(α)
Выясни чему будет равно выражение sin(360+α)
Рассуждаем по алгоритму:
1. Четверть первая.
2. В первой четверти знак у функции синуса положительный.
3. В скобочках нет (90° или π/2) и (270° или 3π/2), то функция не меняется.
Будет sin(360+α) = sin(α)
Выясни чему будет равно выражение cos(90+α)
Рассуждаем по алгоритму:
1. Четверть вторая.
2. Во второй четверти знак у функции косинуса отрицательный.
3. В скобочках есть (90° или π/2), то функция меняется с косинуса на синус.
Будет cos(90+α) = -sin(α)
Выясни чему будет равно выражение sin(90+α)
Рассуждаем по алгоритму:
1. Четверть вторая.
2. Во второй четверти знак у функции синуса положительный.
3. В скобочках есть (90° или π/2), то функция меняется с синуса на косинус.
Будет sin(90+α) = cos(α)
Выясни чему будет равно выражение cos(180-α)
Рассуждаем по алгоритму:
1. Четверть вторая.
2. Во второй четверти знак у функции косинуса отрицательный.
3. В скобочках нет (90° или π/2) и (270° или 3π/2), то функция не меняется.
Будет cos(180-α) = cos(α)
Выясни чему будет равно выражение sin(180-α)
Рассуждаем по алгоритму:
1. Четверть вторая.
2. Во второй четверти знак у функции синуса положительный.
3. В скобочках нет (90° или π/2) и (270° или 3π/2), то функция не меняется.
Будет sin(180-α) = sin(α)
Рассуждаю про третью и четвертую четверть подобным образом составим таблицу:
Подписывайтесь на канал на YOUTUBE и смотрите видео, подготавливайтесь к экзаменам по математике и геометрии с нами.
tutomath.ru
Формулы приведения. Как быстро получить любую формулу приведения
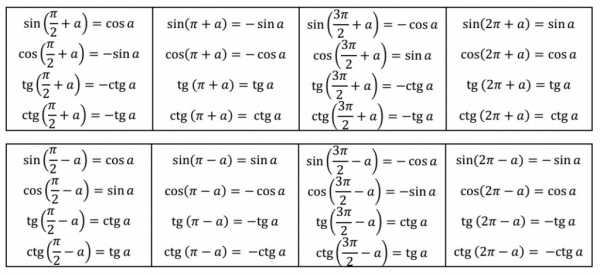
Формулы приведения разработаны для углов, представленных в одном из следующих видов: \(\frac{\pi}{2}+a\), \(\frac{\pi}{2}-a\), \(π+a\), \(π-a\), \(\frac{3\pi}{2}+a\), \(\frac{3\pi}{2}-a\), \(2π+a\) и \(2π-a\). Аналогично их можно использовать для углов представленных в градусах: \(90^°+a\), \(90^°-a\), \(180^°+a\), \(180^°-a\), \(270^°+a\), \(270^°-a\), \(180^°+a\), \(180^°-a\). К счастью, учить наизусть формулы привидения вам не придется, потому что есть легкий и надежный способ вывести нужную за пару секунд.
Как быстро получить любую формулу приведения
Для начала обратите внимание, что все формулы имеют похожий вид:

Здесь нужно пояснить термин «кофункция» — это та же самая функция с добавлением или убиранием приставки «ко-». То есть, для синуса кофункцией будет косинус, а для косинуса – синус. С тангенсом и котангенсом – аналогично.
Функция: Кофункция:
\(sin\) \(a\) \(→\) \(cos\) \(a\)
\(cos\) \(a\) \(→\) \(sin\) \(a\)
\(tg\) \(a\) \(→\) \(ctg\) \(a\)
\(ctg\) \(a\) \(→\) \(tg\) \(a\)
Таким образом, например, синус при применении этих формул никогда не поменяется на тангенс или котангенс, он либо останется синусом, либо превратиться в косинус. А котангенс никогда не станет синусом или косинусом, он либо останется котангенсом, либо станет тангенсом. И так далее.
Едем дальше. Так как исходная функция и ее аргумент нам обычно даны, то весь вывод нужной формулы сводится к двум вопросам:
— как определить знак перед конечной функцией (плюс или минус)?
— как определить меняется ли функция на кофункцию или нет?
Как определить знак перед конечной функцией (плюс или минус)?
Какой знак был у исходной функции в исходной четверти, такой знак и нужно ставить перед конечной функцией.
Например, выводим формулу приведения для \(cos(\frac{3\pi}{2}-a) =….\) С исходной функцией понятно – косинус, а исходная четверть?
Для того, чтобы ответить на этот вопрос, представим, что \(a\) – угол от \(0\) до \(\frac{\pi}{2}\), т.е. лежит в пределах \(0°…90^°\) (хотя это может быть не так, но для определения знака данная условность необходима). В какой четверти тригонометрической окружности при таком условии будет находиться точка, обозначающая угол \(\frac{3\pi}{2}-a\)?
Чтобы ответить на вопрос, надо от точки, обозначающей \(\frac{3\pi}{2}\), повернуть в отрицательную сторону на угол \(a\).
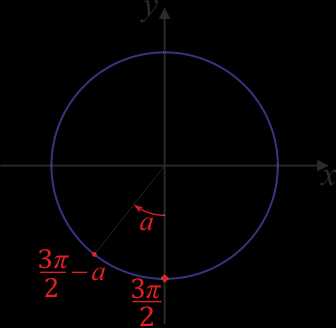
В какой четверти мы окажемся? В третьей. А какой же знак имеет косинус в третьей четверти? Минус. Поэтому перед итоговой функцией будет стоят минус: \(cos(\frac{3\pi}{2}-a)=-…\)
Менять ли функцию на кофункцию или оставить прежней?
Здесь правило еще проще:
— если «точка привязки» \(\frac{\pi}{2}\) (\(90^°\)) или \(\frac{3\pi}{2}\) (\(270^°\))– функция меняется на кофункцию;
— если «точка привязки» \(π\) (\(180^°\)) или \(2π\) (\(360^°\)) – функция остается той же.
То есть, при аргументах исходной функции \(\frac{\pi}{2}+a\), \(\frac{\pi}{2}-a\), \(\frac{3\pi}{2}+a\) или \(\frac{\pi}{2}-a\), мы должны поменять функцию, а при аргументах \(π+a\), \(π-a\), \(2π+a\) или \(2π-a\) — нет. Для того, чтоб это легче запомнить, вы можете воспользоваться мнемоническим правилом, которое в школе называют «лошадиным правилом»:
Точки, обозначающие \(\frac{\pi}{2}\) \((90^°)\) и \(\frac{3\pi}{2}\) \((270^°)\), расположены вертикально, и если вы переводите взгляд с одной на другую и назад, вы киваете головой, как бы говоря «да».
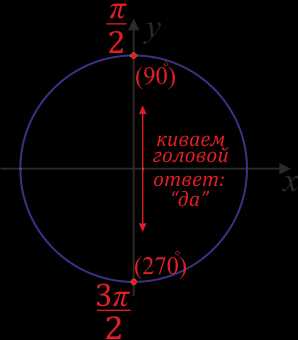
Точки же, обозначающие \(π\) (\(180^°\)) и \(2π\) (\(360^°\)), расположены горизонтально, и если вы переводите взгляд между ними, вы мотаете головой, как бы говоря «нет».

Эти «да» и «нет» — и есть ответ на вопрос: «меняется ли функция?».
Таким образом, согласно правилу, в нашем примере выше \(cos(\frac{3π}{2}-a)=…\) косинус будет меняться на синус. В конечном итоге получаем, \(cos(\frac{3π}{2}-a)=-sin\) \(a\). Это и есть верная формула приведения.
Примеры с формулами приведения:
Зачем нужны формулы привидения? Ну, например, они позволяют упрощать выражения или находить значения некоторых тригонометрических выражений без использования калькулятора.
Пример. (Задание из ЕГЭ) Найдите значение выражения \(\frac{18 \cos {{41}^°} }{\sin {{49}^°}}\)
Решение:|
\(\frac{18 \cos {{41}^°} }{\sin{{49}^°}}=\) |
Углы \({41}^°\) и \({49}^°\) нестандартные, поэтому «в лоб» без калькулятора вычислить непросто. Однако использовав формулы привидения, мы легко найдем правильный ответ. |
|
|
\(=\frac{18 \cos {41^° }}{\sin {({90}^°-{41}^°)}}=\) |
Теперь применим к синусу формулу приведения:
\(\sin{(90^°-41^°)}=\cos 41^° \) |
|
|
\(=\frac{18 \cos {41^° }}{\cos {{41}^°}}=\) |
В числителе и знаменателе получились одинаковые косинусы. Сокращаем их. |
|
|
\(= 18\) |
Записываем ответ |
Ответ: \(18\)
Пример. Найдите значение выражения \(\frac{3 \sin{(\pi-a)}-\cos(\frac{\pi}{2}+a) }{\cos {(\frac{3\pi}{2}-a)}}\)
Решение:|
\(\frac{3 \sin{(\pi-a)}-\cos(\frac{\pi}{2}+a) }{\cos {(\frac{3\pi}{2}-a)}}=\) |
Рассмотрим первое слагаемое числителя: \(\sin(π-a)\). Воспользуемся формулами приведения, выведя ее самостоятельно:
Таким образом, \(\sin(π-a)=\sina\) |
|
|
\(=\frac{3 \sin{a}-\cos(\frac{\pi}{2}+a) }{\cos {(\frac{3\pi}{2}-a)}}=\) |
Второе слагаемое числителя: \(\cos{(\frac{π}{2} + a)}\):
Таким образом, \(\cos{(\frac{π}{2} + a)}=-\sina\) |
|
|
\(=\frac{3 \sin{a}-(-\sin{a}) }{\cos {(\frac{3\pi}{2}-a)}}=\) |
Теперь знаменатель: \(\cos(\frac{3π}{2} — a)\). Его мы разобрали выше, он равен минус синусу. \(\cos(\frac{3π}{2} — a)=-\sin{a}\) |
|
|
\(=\frac{3 \sin{a}-(-\sin{a}) }{-\sin {a}}=\) |
Раскрываем скобки и приводим подобные слагаемые. |
|
|
\(=\frac{3 \sin{a}+\sin{a}}{-\sin {a}}=\frac{4\sin{a}}{-\sin{a}}\) |
Сократив на \(\sin{a}\), получаем ответ. |
|
|
\(=\frac{4 }{-1}=\)\(-4\) |
Ответ: \(-4\)
Пример. Вычислить чему равен \(ctg(-a-\frac{7π}{2})\), если \(tg\) \(a=2\)
Решение:
|
\(ctg(-a-\frac{7π}{2}) =\) |
Здесь сразу формулу приведения применять нельзя, так как аргумент нестандартный. Что не так? Прежде всего, \(a\) стоит первой, хотя должна быть после «точки привязки». Поменяем местами слагаемые аргумента, сохраняя знаки. |
|
|
\(= ctg(-\frac{7π}{2}-a) =\) |
Уже лучше, но все еще есть проблемы – «точка привязки» с минусом, а такого аргумента у нас нет. Избавимся от минуса, вынеся его за скобку внутри аргумента. |
|
|
\(= ctg(-(\frac{7π}{2}+a)) =\) |
Теперь вспомним о том, что котангенс – функция нечетная, то есть |
|
|
\(= — ctg(\frac{7π}{2}+a) =\) |
Несмотря на то, что точка привязки \(\frac{7π}{2}\) мы все равно можем использовать формулы приведения, потому что \(\frac{7π}{2}\) лежит на пересечении одной из осей и числовой окружности (смотри пояснение ниже). \((\frac{7π}{2}+a)\) это четвертая четверть, и котангенс там отрицателен. «Точка привязки» — вертикальная, то есть функцию меняем. Окончательно имеем \(ctg(\frac{7π}{2}+a)=-tg a\) . |
|
|
\(= — (- tg\) \(a) = tg\) \(a = 2\) |
Готов ответ. |
Ответ: \(2\)
Еще раз проговорим этот важный момент: с точки зрения формулы приведения \(\frac{7π}{2}\) — это тоже самое, что и \(\frac{3π}{2}\). Почему? Потому что \(\frac{7π}{2}=\frac{3π+4π}{2}=\frac{3π}{2}+\frac{4π}{2}=\frac{3π}{2}+2π\). Иными словами, они отличаются ровно на один оборот \(2π\). А на значения тригонометрических функций количество оборотов никак не влияет:
\(cos\) \(t=cos (t+2π)=cos (t+4π)=cos (t+6π)= …=cos (t-2π)=cos (t-4π)=cos (t-6π)…\)
\(sin\) \(t=sin (t+2π)=sin (t+4π)=sin (t+6π)= …=sin (t-2π)=sin (t-4π)=sin (t-6π)…\)
Аналогично с тангенсом и котангенсом (только у них «оборот» равен \(π\)).
\(tg\) \(t=tg(t+π)=tg(t+2π)=tg(t+3π)= …=tg(t-π)=tg(t-2π)=tg(t-3π)…\)
\(ctg\) \(t=ctg(t+π)=ctg(t+2π)=ctg(t+3π)= …=ctg(t-π)=ctg(t-2π)=ctg(t-3π)…\)
Таким образом, \(-ctg(\frac{7π}{2}+a)=- ctg(\frac{3π}{2}+2π+a)=- ctg(\frac{3π}{2}+a)\).
То есть, для определения знака и необходимости смены функции важно лишь местоположение «точки привязки», а не её значение, поэтому так расписывать не обязательно (но можно если вы хотите впечатлить своими знаниями учительницу).
Ответы на часто задаваемые вопросы
Вопрос: Есть ли формулы приведения с аргументами \((\frac{π}{3}-a)\),\((\frac{π}{4}+a)\),\((\frac{7π}{6}+a)\) или тому подобное?
Ответ: К сожалению, нет. В таких ситуациях выгодно использовать формулы разности и суммы аргументов. Например, \(cos(\frac{π}{3}-a)=cos\frac{π}{3} cosa+sin\frac{π}{3} sina=\frac{1}{2}cosa+\frac{\sqrt{3}}{2} sina\).
Смотрите также Как доказать тригонометрическое тождество?
Скачать статьюcos-cos.ru
Внеклассный урок — Формулы приведения для тригонометрических функций
Формулы приведения для тригонометрических функций
Формулы приведения – это формулы, позволяющие упростить сложные выражения тригонометрической функции.
Выражения типа π + t, 3π/2 – t, π/2 + t и т.п. можно упростить настолько, что они будут состоять лишь из одного аргумента t. В предыдущих разделах мы имели дело с несколькими такими упрощениями – например, sin (π + t) = –sin t.
Формул приведения очень много. Запомнить их трудно – но самое главное, в этом нет необходимости. Достаточно запомнить одно-единственное правило – и вы легко сможете самостоятельно выводить формулы и упрощать выражения.
Правило приведения:
Для выражений | Для выражений |
1) В приведенном выражении следует сохранить тригонометрическую функцию преобразуемого выражения. 2) Перед полученной функцией следует поставить тот знак, который имела бы преобразуемая функция при условии, что 0 < t < π/2. | 1) В приведенном выражении следует изменить тригонометрическую функцию преобразуемого выражения на противоположную. 2) Перед полученной функцией следует поставить тот знак, который имела бы преобразуемая функция при условии, что 0 < t < π/2. |
Обратите внимание: в левом и правом столбцах различаются только первые пункты правила. Вторые пункты абсолютно идентичны.
Пример 1: Надо преобразовать выражение cos (π + t).
Решение.
Следуем правилу:
1) Выражение не имеет дроби – значит, применяем левое правило. То есть функция после приведения остается прежней:
cos (π + t) = cos t.
2) Осталось определиться со знаком полученной функции.
Если предположить, что аргумент t больше нуля и меньше π/2, то π + t – это аргумент третьей четверти (то есть отмерили полукруг от точки А, а потом еще прошли дугу t длиной меньше π/2 и оказались в третьей четверти). А в третьей четверти косинус имеет знак минус. Значит, после преобразования наша функция обрела следующий тождественный вид:
cos (π + t) = –cos t.
Пример решен.
Пример 2: Надо преобразовать выражение sin (3π/2 – t).
Решение.
Следуем правилу:
1) Выражение имеет дробь – поэтому применяем правое правило. То есть функция меняется на обратную:
sin (3π/2 – t) = cos t
2) Теперь выясним, с каким знаком должно быть наше приведенное выражение. Снова предположим, что 0 < t < π/2. Тогда аргумент 3π/2 – t находится в третьей четверти. А в третьей четверти преобразуемая функция синус имеет знак минус. Значит, наше новое тождественное выражение тоже со знаком минус:
sin (3π/2 – t) = –cos t.
Пример решен.
Следуя этому правилу, можно составить другие формулы приведения.
Формулы приведения.
cos (π + t) = –cos t | sin (π + t) = –sin t | tg (π + t) = tg t | ctg (π + t) = ctg t |
cos (π – t) = –cos t | sin (π – t) = sin t | tg (π – t) = –tg t | ctg (π – t) = –ctg t |
cos (2π + t) = cos t | sin (2π + t) = sin t | tg (2π + t) = tg t | ctg (2π + t) = ctg t |
cos (2π – t) = cos t | sin (2π – t) = –sin t | tg (2π – t) = –tg t | ctg (2π – t) = –ctg t |
cos (π/2 + t) = –sin t | sin (π/2 + t) = cos t | tg (π/2 + t) = –ctg t | ctg (π/2 + t) = –tg t |
cos (π/2 – t) = sin t | sin (π/2 – t) = cos t | tg (π/2 – t) = ctg t | ctg (π/2 – t) = tg t |
cos (3π/2 + t) = sin t | sin (3π/2 + t) = –cos t | tg (3π/2 + t) = –ctg t | ctg (3π/2 + t) = –tg t |
cos (3π/2 – t) = –sin t | sin (3π/2 – t) = –cos t | tg (3π/2 – t) = ctg t | ctg (3π/2 – t) = tg t |
Примечание:
Часто встречаются более сложные выражения, но они не меняют правила.
Например, если cos (2π + t) = cos t, то cos (2π + 3t) = cos 3t.
raal100.narod.ru
