Порядок выполнения действий / Справочник по математике для начальной школы
- Главная
- Справочники
- Справочник по математике для начальной школы
- Порядок выполнения действий
В данном разделе мы познакомимся с порядком действий, с выражениями со скобками и без них.
1) Если тебе нужно выполнить только сложение и вычитание или только умножение и деление, то все действия выполняют по порядку слева направо.
Например,
В числовом выражении 3 арифметических действия: сложение, вычитание и вычитание.
Определим порядок действий и запишем их над арифметическими знаками: так как нет ни умножения ни деления, действия выполняют по порядку слева направо:
Вычисляем:
1) 10 + 15 = 25
2) 25 — 6 = 19
3) 19 — 8 = 11
Полностью пример записываем так:
10 + 15 — 6 — 8 = 25 — 6 — 8 = 19 — 8 = 11
Например,
В числовом выражении 3 арифметических действия: деление, умножение и деление.
Определим порядок действий и запишем их над арифметическими знаками: так как нет ни сложения ни вычитания, действия выполняют по порядку слева направо:
Вычисляем:
1) 15 : 5 = 3
2) 3 • 4 = 12
3) 12 : 6 = 2
Полностью пример записываем так:
15 : 5 • 4 : 6 = 3 • 4 : 6 = 12 : 6 = 2
2) Если тебе нужно выполнить несколько арифметических действий (сложение, вычитание, умножение и деление), то сначала выполняют умножение и деление по порядку слева направо, а затем сложение и вычитание по порядку слева направо.
Например,
В числовом выражении 4 арифметических действия: вычитание, деление, сложение и умножение.
Определим порядок действий и запишем их над арифметическими знаками: сначала производим деление, потом умножение, затем вычитание и сложение.
1)15 : 3 = 5
2) 6 • 8 = 48
3) 10 — 5 = 5
4) 5 + 48 = 53
Полностью пример записываем так:
10 — 15 : 3 + 6 • 8 = 10 — 5 + 6 • 8 = 10 — 5 + 48 = 5 + 48 = 53
3) Если в выражении есть скобки, то сначала выполняют действия в скобках, но обязательно учитывать первое и второе правила.
Например,
В числовом выражении 4 арифметических действия: вычитание, деление, сложение и умножение.
Определим порядок действий и запишем их над арифметическими знаками: сначала производим вычитание в скобках, затем деление, потом умножение и сложение.
1) 25 — 10 = 15
2) 15 : 3 = 5
3) 6 • 8 = 48
4) 5 + 48 = 53
Полностью пример записываем так:
(25 — 10) : 3 + 6 • 8 = 15 : 3 + 6 • 8 = 5 + 6 • 8 = 5 + 48 = 53
Например,
В числовом выражении 4 арифметических действия: сложение, деление, сложение и деление.
Определим порядок действий и запишем их над арифметическими знаками: сначала производим действия в скобках (деление, затем сложение), затем деление, потом сложение.
1) 12 : 4 = 3
2) 6 + 3 = 9
3) 18 : 9 = 2
4) 42 + 2 = 44
Полностью пример записываем так:
42 + 18 : (6 + 12 : 4) = 42 + 18 : (6 + 3) = 42 + 18 : 9 = 42 + 2 = 44
Вывод:

Поделись с друзьями в социальных сетях:
Советуем посмотреть:
Скобки
Правило встречается в следующих упражнениях:
2 класс
Страница 12, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть
Страница 48, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть
Страница 49, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть
Страница 52, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть
Страница 57, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть
Страница 61, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть
Страница 62, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть
Страница 89, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть
Страница 98, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть
Страница 110, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть
3 класс
Страница 21, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть
Страница 109, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть
Страница 49, Моро, Волкова, Рабочая тетрадь, 1 часть
Страница 66, Моро, Волкова, Рабочая тетрадь, 1 часть
Страница 35. Вариант 2. № 3, Моро, Волкова, Проверочные работы
Страница 4, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть
Страница 24, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть
Страница 27, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть
Страница 25, Моро, Волкова, Рабочая тетрадь, 2 часть
Страница 27, Моро, Волкова, Рабочая тетрадь, 2 часть
5 класс
Задание 22, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 30, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 64, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 74, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 98, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 167, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 180, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 191, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Упражнение 13, Мерзляк, Полонский, Якир, Учебник
Упражнение 37, Мерзляк, Полонский, Якир, Учебник
6 класс
Задание 18, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 85, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 92, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 400, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 411, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 413, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 417, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 422, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 445, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 454, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
© 2019 — budu5.com, Буду отличником!
budu5.com
Умножение и деление целых чисел
При умножении и делении целых чисел применяется несколько правил. В данном уроке мы рассмотрим каждое из них.При умножении и делении целых чисел следует обращать внимание на знаки чисел. От них будет зависеть какое правило применять. Также, необходимо изучить несколько законов умножения и деления. Изучение этих правил позволяет избежать некоторые досадные ошибки в будущем.
Законы умножения
Некоторые из законов математики мы рассматривали в уроке законы математики. Но мы рассмотрели не все законы. В математике немало законов, и разумнее будет изучать их последовательно по мере необходимости.
Для начала вспомним из чего состоит умножение. Умножение состоит из трёх параметров: множимого, множителя и произведения. Например, в выражении 3 × 2 = 6, число 3 — это множимое, число 2 — множитель, число 6 — произведение.
Множимое показывает, что именно мы увеличиваем. В нашем примере мы увеличиваем число 3.
Множитель показывает во сколько раз нужно увеличить множимое. В нашем примере множитель это число 2. Этот множитель показывает во сколько раз нужно увеличить множимое 3. То есть в ходе операции умножения число 3 будет увеличено в два раза.
Произведение это собственно результат операции умножения. В нашем примере произведение это число 6. Это произведение является результатом умножения 3 на 2.
Выражение 3 × 2 также можно понимать, как сумму двух троек. Множитель 2 в таком случае будет показывать сколько раз нужно повторить число 3:
Таким образом, если число 3 повторить два раза подряд, получится число 6.
Переместительный закон умножения
Множимое и множитель называют одним общим словом – сомножители. Переместительный закон умножения выглядит следующим образом:
От перестановки мест сомножителей произведение не меняется.
Проверим так ли это. Умножим к примеру 3 на 5. Здесь 3 и 5 это сомножители.
3 × 5 = 15
Теперь поменяем местами сомножители:
5 × 3 = 15
В обоих случаях, мы получаем ответ 15, значит между выражениями 3 × 5 и 5 × 3 можно поставить знак равенства, поскольку они равны одному тому же значению:
3 × 5 = 5 × 3
15 = 15
А с помощью переменных переместительный закон умножения можно записать так:
a × b = b × a
где a и b — сомножители
Сочетательный закон умножения
Этот закон говорит о том, что если выражение состоит из нескольких сомножителей, то произведение не будет зависеть от порядка действий.
К примеру выражение 3 × 2 × 4 состоит из нескольких сомножителей. Чтобы его вычислить, можно перемножить 3 и 2, затем полученное произведение умножить на оставшееся число 4. Выглядеть это будет так:
3 × 2 × 4 = (3 × 2) × 4 = 6 × 4 = 24
Это был первый вариант решения. Второй вариант состоит в том, чтобы перемножить 2 и 4, затем полученное произведение умножить на оставшееся число 3. Выглядеть это будет так:
3 × 2 × 4 = 3 × (2 × 4) = 3 × 8 = 24
В обоих случаях мы получаем ответ 24. Поэтому между выражениями (3 × 2) × 4 и 3 × (2 × 4) можно поставить знак равенства, поскольку они равны одному и тому же значению:
(3 × 2) × 4 = 3 × (2 × 4)
24 = 24
а с помощью переменных сочетательный закон умножения можно записать так:
a × b × c = (a × b) × c = a × (b × c)
где вместо a, b, c могут стоять любые числа.
Распределительный закон умножения
Распределительный закон умножения позволяет умножить сумму на число. Для этого каждое слагаемое этой суммы умножается на это число, затем полученные результаты складывают.
Например, найдём значение выражения (2 + 3) × 5
Выражение находящееся в скобках является суммой. Эту сумму нужно умножить на число 5. Для этого каждое слагаемое этой суммы, то есть числа 2 и 3 нужно умножить на число 5, затем полученные результаты сложить:
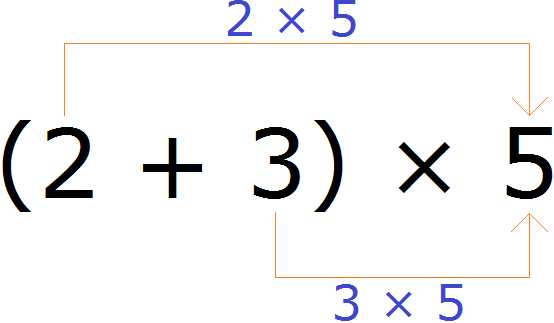
(2 + 3) × 5 = 2 × 5 + 3 × 5 = 10 + 15 = 25
Значит значение выражения (2 + 3) × 5 равно 25.
С помощью переменных распределительный закон умножения записывается так:
(a + b) × c = a × c + b × c
где вместо a, b, c могут стоять любые числа.
Закон умножения на ноль
Этот закон говорит о том, что если в любом умножении имеется хотя бы один ноль, то в ответе получится ноль.
Произведение равно нулю, если хотя бы один из сомножителей равен нулю.
Например, выражение 0 × 2 равно нулю
0 × 2 = 0
В данном случае число 2 является множителем и показывает во сколько раз нужно увеличить множимое. То есть во сколько раз увеличить ноль. Буквально это выражение читается так: «увеличить ноль в два раза». Но как можно увеличить ноль в два раза, если это ноль? Ответ — никак.
Иными словами, если «ничего» увеличить в два раза или даже в миллион раз, всё равно получится «ничего».
И если в выражении 0 × 2 поменять местами сомножители, опять же получится ноль. Это мы знаем из предыдущего переместительного закона:
0 × 2 = 2 × 0
0 = 0
Примеры применения закона умножения на ноль:
5 × 0 = 0
5 × 5 × 5 × 0 = 0
2 × 5 × 0 × 9 × 1 = 0
В последних двух примерах имеется несколько сомножителей. Увидев в них ноль, мы сразу в ответе поставили ноль, применив закон умножения на ноль.
Мы рассмотрели основные законы умножения. Далее рассмотрим умножение целых чисел.
Умножение целых чисел
Пример 1. Найти значение выражения −5 × 2
Это умножение чисел с разными знаками. −5 является отрицательным числом, а 2 – положительным. Для таких случаев нужно применять следующее правило:
Чтобы перемножить числа с разными знаками, нужно перемножить их модули, и перед полученным ответом поставить минус.
−5 × 2 = − (|−5| × |2|) = − (5 × 2) = − (10) = −10
Обычно записывают короче: −5 × 2 = −10
Любое умножение может быть представлено в виде суммы чисел. Например, рассмотрим выражение 2 × 3. Оно равно 6.
2 × 3 = 6
Множителем в данном выражение является число 3. Этот множитель показывает во сколько раз нужно увеличить двойку. Но выражение 2 × 3 также можно понимать как сумму трёх двоек:
То же самое происходит и с выражением −5 × 2. Это выражение может быть представлено в виде суммы
А выражение (−5) + (−5) равно −10. Мы это знаем из прошлого урока. Это сложение отрицательных чисел. Напомним, что результат сложения отрицательных чисел есть отрицательное число.
Пример 2. Найти значение выражения 12 × (−5)
Это умножение чисел с разными знаками. 12 – положительное число, (−5) – отрицательное. Опять же применяем предыдущее правило. Перемножаем модули чисел и перед полученным ответом ставим минус:
12 × (−5) = − (|12| × |−5|) = − (12 × 5) = − (60) = −60
Обычно решение записывают покороче:
12 × (−5) = −60
Пример 3. Найти значение выражения 10 × (−4) × 2
Это выражение состоит из нескольких сомножителей. Сначала перемножим 10 и (−4), затем полученное число умножим на 2. Попутно применим ранее изученные правила:
Первое действие:
10 × (−4) = −(|10| × |−4|) = −(10 × 4) = (−40) = −40
Второе действие:
−40 × 2 = −(|−40 | × | 2|) = −(40 × 2) = −(80) = −80
Значит значение выражения 10 × (−4) × 2 равно −80
Запишем решение покороче:
10 × (−4) × 2 = −40 × 2 = −80
Пример 4. Найти значение выражения (−4) × (−2)
Это умножение отрицательных чисел. В таких случаях нужно применять следующее правило:
Чтобы перемножить отрицательные числа, нужно перемножить их модули и перед полученным ответом поставить плюс
(−4) × (−2) = |−4| × |−2| = 4 × 2 = 8
Плюс по традиции не записываем, поэтому просто записываем ответ 8.
Запишем решение покороче (−4) × (−2) = 8
Возникает вопрос почему при умножении отрицательных чисел вдруг получается положительное число. Давайте попробуем доказать, что (−4) × (−2) равно 8 и ни чему другому.
Сначала запишем следующее выражение:
4 × (−2)
Заключим его в скобки:
( 4 × (−2) )
Прибавим к этому выражению наше выражение (−4) × (−2). Его тоже заключим в скобки:
( 4 × (−2) ) + ( (−4) × (−2) )
Всё это приравняем к нулю:
(4 × (−2)) + ((−4) × (−2)) = 0
Теперь начинается самое интересное. Суть в том, что мы должны вычислить левую часть этого выражения, и в результате получить 0.
Итак, первое произведение (4 × (−2)) равно −8. Запишем в нашем выражении число −8 вместо произведения (4 × (−2))
−8 + ((−4) × (−2)) = 0
Теперь вместо второго произведения временно поставим многоточие
−8 + … = 0
Теперь внимательно посмотрим на выражение −8 + … = 0. Какое число должно стоять вместо многоточия, чтобы соблюдалось равенство? Ответ напрашивается сам. Вместо многоточия должно стоять положительное число 8 и никакое другое. Только так будет соблюдаться равенство. Ведь −8 + 8 равно 0.
Возвращаемся к выражению −8 + ((−4) × (−2)) = 0 и вместо произведения ((−4) × (−2)) записываем число 8
−8 + 8 = 0
Пример 5. Найти значение выражения −2 × (6 + 4)
Применим распределительный закон умножения, то есть умножим число −2 на каждое слагаемое суммы (6 + 4)
−2 × (6 + 4) = −2 × 6 + (−2) × 4
Теперь выполним умножение, и сложим полученные результаты. Попутно применим ранее изученные правила. Запись с модулями можно пропустить, чтобы не загромождать выражение
Первое действие:
−2 × 6 = −12
Второе действие:
−2 × 4 = −8
Третье действие:
−12 + (−8) = −20
Значит значение выражения −2 × (6 + 4) равно −20
Запишем решение покороче:
−2 × (6 + 4) = (−12) + (−8) = −20
Пример 6. Найти значение выражения (−2) × (−3) × (−4)
Выражение состоит из нескольких сомножителей. Сначала перемножим числа −2 и −3, и полученное произведение умножим на оставшееся число −4. Запись с модулями пропустим, чтобы не загромождать выражение
Первое действие:
(−2) × (−3) = 6
Второе действие:
6 × (−4) = −(6 × 4) = −24
Значит значение выражения (−2) × (−3) × (−4) равно −24
Запишем решение покороче:
(−2) × (−3) × (−4) = 6 × (−4) = −24
Законы деления
Прежде чем делить целые числа, необходимо изучить два закона деления.
В первую очередь, вспомним из чего состоит деление. Деление состоит из трёх параметров: делимого, делителя и частного. Например, в выражении 8 : 2 = 4, 8 – это делимое, 2 – делитель, 4 – частное.
Делимое показывает, что именно мы делим. В нашем примере мы делим число 8.
Делитель показывает на сколько частей нужно разделить делимое. В нашем примере делитель это число 2. Этот делитель показывает на сколько частей нужно разделить делимое 8. То есть в ходе операции деления, число 8 будет разделено на две части.
Частное – это собственно результат операции деления. В нашем примере частное это число 4. Это частное является результатом деления 8 на 2.
Далее рассмотрим законы деления.
На ноль делить нельзя
Любое число запрещено делить на ноль.
Дело в том, что деление это действие, обратное умножению. Данную фразу можно понимать в прямом смысле. Например, если 2 × 5 = 10, то 10 : 5 = 2.
Видно, что второе выражение записано в обратном порядке. Если к примеру, у нас имеется два яблока и мы захотим увеличить их в пять раз, то мы запишем 2 × 5 = 10. Получится десять яблок. Затем, если мы захотим обратно уменьшить эти десять яблок до двух, то мы запишем 10 : 5 = 2
Точно так же можно поступать и с другими выражениями. Если к примеру, 2 × 6 = 12, то мы можем обратно вернуться к изначальному числу 2. Для этого достаточно записать выражение 2 × 6 = 12 в обратном порядке, разделяя 12 на 6
12 : 6 = 2
Теперь рассмотрим выражение 5 × 0. Мы знаем из законов умножения, что произведение равно нулю, если хотя бы один из сомножителей равен нулю. Значит и выражение 5 × 0 равно нулю
5 × 0 = 0
Если записать это выражение в обратном порядке, то получим:
0 : 0 = 5
Сразу в глаза бросается ответ 5, который получается в результате деления ноль на ноль. Это невозможно.
В обратном порядке можно записать и другое похожее выражение, например 2 × 0 = 0
0 : 0 = 2
В первом случае, разделив ноль на ноль мы получили 5, а во втором случае 2. То есть каждый раз деля ноль на ноль, мы можем получить разные значения, а это недопустимо.
Второе объяснение заключается в том, что разделить делимое на делитель означает найти такое число, которое при умножении на делитель даст делимое.
Например выражение 8 : 2 означает найти такое число, которое при умножении на 2 даст 8
… × 2 = 8
Здесь вместо многоточия должно стоять число, которое при умножении на 2 даст ответ 8. Чтобы найти это число, достаточно записать это выражение в обратном порядке:
8 : 2 = 4
Получили число 4. Запишем его вместо многоточия:
4 × 2 = 8
Теперь представим, что нужно найти значение выражения 5 : 0. В данном случае 5 – это делимое, 0 – делитель. Разделить 5 на 0 означает найти такое число, которое при умножении на 0 даст 5
… × 0 = 5
Здесь вместо многоточия должно стоять число, которое при умножении на 0 даст ответ 5. Но не существует числа, которое при умножении на ноль даёт 5.
Выражение … × 0 = 5 противоречит закону умножения на ноль, который утверждает, что произведение равно нулю, когда хотя бы один из сомножителей равен нулю.
А значит записывать выражение … × 0 = 5 в обратном порядке, деля 5 на 0 нет никакого смысла. Поэтому и говорят, что на ноль делить нельзя.
С помощью переменных данный закон записывается следующим образом:
, при b ≠ 0
Это выражение можно прочитать так:
Число a можно разделить на число b, при условии, что b не равно нулю.
Свойство частного
Этот закон говорит о том, что если делимое и делитель умножить или разделить на одно и то же число, то частное не изменится.
Например, рассмотрим выражение 12 : 4. Значение этого выражения равно 3
12 : 4 = 3
Попробуем умножить делимое и делитель на одно и то же число, например на число 4. Если верить свойству частного, мы опять должны получить в ответе число 3
(12 × 4) : (4 × 4)
(12 × 4) : (4 × 4) = 48 : 16 = 3
Получили ответ 3.
Теперь попробуем не умножить, а разделить делимое и делитель на число 4
(12 : 4) : (4 : 4)
(12 : 4) : (4 : 4) = 3 : 1 = 3
Получили ответ 3.
Видим, что если делимое и делитель умножить или разделить на одно и то же число, то частное не меняется.
Мы рассмотрели два закона деления. Далее рассмотрим деление целых чисел.
Деление целых чисел
Пример 1. Найти значение выражения 12 : (−2)
Это деление чисел с разными знаками. 12 — положительное число, (−2) – отрицательное. Чтобы решить этот пример, нужно модуль делимого разделить на модуль делителя, и перед полученным ответом поставить минус.
12 : (−2) = −(|12| : |−2|) = −(12 : 2) = −(6) = −6
Обычно записывают покороче:
12 : (−2) = −6
Пример 2. Найти значение выражения −24 : 6
Это деление чисел с разными знаками. −24 – это отрицательное число, 6 – положительное. Опять же модуль делимого делим на модуль делителя, и перед полученным ответом ставим минус.
−24 : 6 = −(|−24| : |6|) = −(24 : 6) = −(4) = −4
Запишем решение покороче:
−24 : 6 = −4
Пример 3. Найти значение выражения −45 : (−5)
Это деление отрицательных чисел. Чтобы решить этот пример, нужно модуль делимого разделить на модуль делителя, и перед полученным ответом поставить знак плюс.
−45 : (−5) = |−45| : |−5| = 45 : 5 = 9
Запишем решение покороче:
−45 : (−5) = 9
Пример 4. Найти значение выражения −36 : (−4) : (−3)
Согласно порядку действий, если в выражении присутствует только умножение или деление, то все действия нужно выполнять слева направо в порядке их следования.
Разделим −36 на (−4), и полученное число разделим на −3
Первое действие:
−36 : (−4) = |−36| : |−4| = 36 : 4 = 9
Второе действие:
9 : (−3) = −(|9| : |−3|) = −(9 : 3) = −(3) = −3
Запишем решение покороче:
−36 : (−4) : (−3) = 9 : (−3) = −3
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Навигация по записям
spacemath.xyz
Примеры со скобками, урок с тренажерами. — Kid-mama
Мы рассмотрим в этой статье три варианта примеров:
1. Примеры со скобками (действия сложения и вычитания)
2. Примеры со скобками (сложение, вычитание, умножение, деление)
3. Примеры, в которых много действий
1 Примеры со скобками (действия сложения и вычитания)
Рассмотрим три примера. В каждом из них порядок действий обозначен цифрами красного цвета:
Мы видим, что порядок действий в каждом примере будет разный, хотя числа и знаки одинаковые. Это происходит потому, что во втором и третьем примере есть скобки.
Запомните правило:
|
*Это правило для примеров без умножения и деления. Правила для примеров со скобками, включающих действия умножения и деления мы рассмотрим во второй части этой статьи.
Чтобы не запутаться в примере со скобками, можно превратить его в обычный пример, без скобок. Для этого результат, полученный в скобках, записываем над скобками, далее переписываем весь пример, записывая вместо скобок этот результат, и далее выполняем все действия по порядку, слева направо:
В несложных примерах можно все эти операции производить в уме. Главное — сначала выполнить действие в скобках и запомнить результат, а затем считать по порядку, слева направо.
А теперь — тренажеры!
1) Примеры со скобками в пределах до 20. Онлайн тренажер.

Перейти на страницу с тренажером
2) Примеры со скобками в пределах до 100. Онлайн тренажер.

Перейти на страницу с тренажером
3) Примеры со скобками. Тренажер №2

Перейти на страницу с тренажером
4) Вставь пропущенное число — примеры со скобками. Тренажер

Перейти на страницу с тренажером
2 Примеры со скобками (сложение, вычитание, умножение, деление)
Теперь рассмотрим примеры, в которых кроме сложения и вычитания есть умножение и деление.
Сначала рассмотрим примеры без скобок:
Запомните правило:
|
Есть одна хитрость, как не запутаться при решении примеров на порядок действий. Если нет скобок, то выполняем действия умножения и деления, далее переписываем пример, записывая вместо этих действий полученные результаты. Затем выполняем сложение и вычитание по порядку:
Если в примере есть скобки, то сначала нужно избавиться от скобок: переписать пример, записывая вместо скобок полученный в них результат. Затем нужно выделить мысленно части примера, разделенные знаками «+» и «-«, и посчитать каждую часть отдельно. Затем выполнить сложение и вычитание по порядку:
3 Примеры, в которых много действий
Если в примере много действий, то удобнее будет не расставлять порядок действий во всем примере, а выделить блоки, и решить каждый блок отдельно. Для этого находим свободные знаки «+» и «–» (свободные — значит не в скобках, на рисунке показаны стрелочками).
Эти знаки и будут делить наш пример на блоки:
Выполняя действия в каждом блоке не забываем про порядок действий, приведенный выше в статье. Решив каждый блок, выполняем действия сложения и вычитания по порядку.
А теперь закрепляем решение примеров на порядок действий на тренажерах!
1. Примеры со скобками в пределах чисел до 100, действия сложения, вычитания, умножения и деления. Онлайн тренажер.

Перейти на страницу с тренажером

Перейти на страницу с тренажером
3. Порядок действий (расставляем порядок и решаем примеры)

Перейти на страницу с тренажером
kid-mama.ru
что сначала делается умножения или деление
1). В школе дается следующее правило, определяющее порядок выполнения действий в выражениях без скобок: ▪ действия выполняются по порядку слева направо, ▪ причем сначала выполняется умножение и деление, а затем – сложение и вычитание. ☆ пример: Вычислим значение выражения 17−5·6:3−2+4:2. ▪ Сначала определим, в каком порядке следует выполнять действия в исходном выражении. Оно содержит и умножение с делением, и сложение с вычитанием. Сначала слева направо нужно выполнить умножение и деление. Так 5 умножаем на 6, получаем 30, это число делим на 3, получаем 10. Теперь 4 делим на 2, получаем 2. Подставляем в исходное выражение вместо 5·6:3 найденное значение 10, а вместо 4:2 — значение 2, имеем 17−5·6:3−2+4:2=17−10−2+2. * В полученном выражении уже нет умножения и деления, поэтому остается по порядку слева направо выполнить оставшиеся действия: 17−10−2+2=7−2+2=5+2=7. Ответ: 17−5·6:3−2+4:2=7. ———————————————————- 2). Выражения часто содержат скобки, указывающие порядок выполнения действий. В этом случае правило, задающее порядок выполнения действий в выражениях со скобками, формулируется так: сначала выполняются действия в скобках, при этом также по порядку слева направо выполняется умножение и деление, затем – сложение и вычитание. ☆ Пример: Выполним указанные действия 5+(7−2·3)·(6−4):2. * Решение : Выражение содержит скобки, поэтому сначала выполним действия в выражениях, заключенных в эти скобки. Начнем с выражения 7−2·3. В нем нужно сначала выполнить умножение, и только потом вычитание, имеем 7−2·3=7−6=1. Переходим ко второму выражению в скобках 6−4. Здесь лишь одно действие – вычитание, выполняем его 6−4=2. * Подставляем полученные значения в исходное выражение: 5+(7−2·3)·(6−4):2=5+1·2:2. В полученном выражении сначала выполняем слева направо умножение и деление, затем – вычитание, получаем 5+1·2:2=5+2:2=5+1=6. На этом все действия выполнены, мы придерживались такого порядка их выполнения: 5+(7−2·3)·(6−4):2. *Запишем краткое решение: 5+(7−2·3)·(6−4):2=5+1·2:2=5+1=6. Ответ: 5+(7−2·3)·(6−4):2=6.
Сначала умножение или деление, а потом сложение или вычитание)
они равноправны
В зависимости от уравнения. Обычно первое из этого делается то, что левее.
По порядку слева направо. Умножение и деление имеют равный приоритет.
Без разницы. Как удобней.
touch.otvet.mail.ru
Свойства сложения, вычитания, умножения и деления — Памятки по математике — Памятки ученикам
Свойства (или законы) арифметических действий на числовых примерах мы рассматривали в теме «Законы арифметики» для начальной школы.
В 5 классе законы арифметики записываются с помощью буквенных выражений. Поэтому теперь мы рассмотрим эти и другие свойства в виде буквенных выражений.
Свойства сложения
Переместительное свойство сложения
От перестановки слагаемых сумма не меняется.
В буквенном виде свойство записывается так:
a + b = b + aВ этом равенстве буквы a и b могут принимать любые натуральные значения и значение 0.
Сочетательное свойство сложения
Чтобы к сумме двух чисел прибавить третье число можно к первому числу прибавить сумму второго и третьего числа.
В буквенном виде:
(a + b) + c = a + (b + c)Так как результат сложения трёх чисел не зависит от того как поставлены скобки, то скобки можно не ставить и писать просто a + b + с.
(a + b) + c = a + (b + c) = a + b + cПереместительное и сочетательное свойство сложения позволяют сформулировать правило преображения сумм.
При сложении нескольких чисел их можно как угодно объединять в группы и переставлять.
Свойство нуля при сложении
Сумма двух натуральных чисел всегда больше каждого из слагаемых. Но это не так, если хотя бы одно из слагаемых равно нулю.
Если к числу прибавить нуль, получится само число.
a + 0 = 0 + a = a
Свойства вычитания
Свойство вычитания суммы из числа
Чтобы вычесть сумму из числа, можно из него вычесть одно слагаемое и затем из результата вычесть другое слагаемое.
a — (b + c) = (a — b) — c
или
a — (b + c) = (a — с) — b
Скобки в выражении (a — b) — c не имеют значения и их можно опустить.
(a — b) — c = a — b — c
Свойство вычитания числа из суммы
Чтобы вычесть число из суммы, можно вычесть его из одного слагаемого, а к результату прибавить оставшееся слагаемое.
(a + b) — c = (a — c) + b (если a > c или а = с)
или
(a + b) — c = (b — c) + a (если b > c или b = с)
Свойство нуля при вычитании
Если из числа вычесть нуль, получится само число.
a — 0 = a
Если из числа вычесть само число, то получится нуль.
a — a = 0www.mamapapa-arh.ru
