| Построим графики функций y=x и y=sin x. | .|
| Далее при каждом x перемножим ординаты двух графиков.
Сначала рассмотрим точки, в которых функция y=sin x
принимает нулевые значения.
В этих точках значения функции произведения тоже будут равны 0 . Отметим эти точки красным цветом. | |
| Теперь рассмотрим точки, в которых функция y=sin x принимает значения равные единице
(они обозначены голубым цветом). В этих же точках определяем значения функции y=x (
при нажатии на кнопку «следующая» — ординаты синего цвета). | |
| Значения функции произведения в этих точках будут равны значениям функции y=x. | |
| Далее рассмотрим точки, в которых функция y=sin x
принимает значения равные
минус единице (они обозначены голубым цветом).В этих же точках определяем значения функции y=x (
при нажатии на кнопку «следующая» — ординаты синего цвета). | |
| Значения функции произведения в этих точках будут противоположны по знаку и равны по абсолютной величине значениям функции y=x. Поэтому, чтобы получить значение функции произведения в этих точках, нужно отложить ординаты функции y=x в этих точках с противоположным знаком. | |
| Итак, мы получили значения функции произведения в рассматриваемых точках.
Мы видим, что эти значения принадлежат прямой y= -x . Для наглядности проведем ее голубым цветом. | |
| Теперь мы знаем, что искомая кривая будет ограничена прямыми y=x и y= -x , эта кривая будет периодичной функцией (так как получается в результате умножения на периодичную функцию y=sin x ). Через полученные точки, соответствующие значениям функции произведения, проводим кривую красным цветом. | |
| Заметим, что функция y=x·sin x четная, то есть её график симметричен относительнo оси OY. Поэтому построение графика можно было производить только при положительных аргументах, а затем симметрично отразить полученную кривую относительно оси OY. |
or-gr2005.narod.ru
Практика_6._ Графики_функций
Пример 5. ( 342) Применяя правило умножения графиков, построить график функции
y= x cos x.
Область определения функции множество всех x 2 R. Функция нечетная, поэтому построим ее график при x 0, а затем совершим симметрию относительно начала
координат. При построении графика будем руководствоваться тем, что ординаты его точек
получаются перемножением ординат точек графиков функций y = x и y = cos x (ðèñ. 5). График проходит через начало координат, пересекает ось Ox при x =2 + n, n 2 Z
(где cos x = 0). Поскольку 1 cos x 1 при x 0 имеем
x x cos x x;
т. е. график лежит между прямыми y = x и y = x. При x = 2 n, n 2 Z (где cos x = 1), график имеет общие точки с прямой y = x, а при x = + 2 n, n 2 Z (где cos x = 1), общие точки с прямой y = x.
Если 0 < x < 1, то 0 < x cos x < cos x и x cos x < x, т. е. график лежит ниже графиков y = cos x и y = x. При x = 1 графики y = x cos x и y = cos x пересекаются, при этом y = cos 1 0; 54. Если x > 1, то jx cos xj > j cos xj, если cos x 6= 0, т. е. точки графика y = x cos x лежат дальше от оси Ox, чем соответствующие точки графика y = x cos x
(ðèñ. 5à).
В соответствии с этим, рассчитав и отметив несколько промежуточных точек, изображаем график (ðèñ. 5á ).
Рис. 5: Правило умножения графиков: y = x cos x. Пример 6. ( 353) Построить график функции y =f(1x), åñëè f(x) = sin2 x.
Областью определения функции является множество всех x 2 R, таких, что f(x) 6= 0,
ò.е. x 6= n, n 2 Z. Функция четная, периодическая с периодом . Построим график на интервале (0; =2], затем отобразим его на интервал [ =2; 0) симметрично относительно
оси Oy, а далее продолжим периодически с периодом . Если x 2 (0; =2], то 0 < sin2 x sin x 1; и поэтому
|
| 1 | 1; |
| |
| sin2 x |
| |||
причем |
|
| 1 | x==2 |
|
1 |
|
| = 1: | ||
min sin2 x | = sin2 x | ||||
|
|
|
|
|
|
studfiles.net
Урок 13. Построение и преобразование графиков функций. Обзор графиков основных функций. Теория
Эксперимент
Урок 13. Построение и преобразование графиков функций. Обзор графиков основных функций
Теория
Конспект урока
Начнем с построения графиков основных функций.
1) Линейная функция. Ее графиком является прямая.
Общий вид линейной функции:
где под и понимают следующие параметры:
угловой коэффициент;
свободный член или смещение по оси ординат.
Рассмотрим основные формы таких графиков в зависимости от значений параметров и поймем их названия.
показывает координату пересечения прямой с осью ординат;
прямая проходит через начало координат;
угол наклона прямой к положительному направлению оси абсцисс острый;
угол наклона прямой к положительному направлению оси абсцисс тупой;
прямая параллельна оси абсцисс.
Как видим, параметр «» определяет наклон прямой к оси абсцисс.
Метод построения графика линейной функции самый стандартный, и называется «построение по точкам». Поскольку любая прямая может быть однозначно восстановлена по двум точкам, то нам будет достаточно определить координаты двух точек, удовлетворяющих функции, и затем провести через них прямую линию, которая и будет необходимым графиком.
Обычно для этого используется небольшая табличка, в которую записывают произвольно выбранные координаты точек по оси абсцисс, а затем для них вычисляют координаты точек по оси ординат.
Пример. Проделаем эти действия для функции .
Решение.
Для вычисления необходимых игреков подставляем значения иксов в формулу, которая задает функцию. При этом удобно выбирать минимальные по модулю целые значения иксов для простоты расчетов:
После этого точки наносятся на координатную плоскость, и через них проводится прямая линия, которая и будет графиком.
Обратите внимание, что форма графика соответствует знакам коэффициентов функции.
2) Теперь рассмотрим квадратичную функцию и ее график, который принято называть параболой.
Общий вид квадратичной функции:
Где под параметрами понимают:
старший коэффициент;
второй коэффициент;
свободный член.
От знаков этих параметров зависит расположение параболы:
ветки параболы направлены вверх;
ветки параболы направлены вниз;
Знаки коэффициента явно и наглядно ничего не определяют;
показывает координату пересечения параболы с осью ординат.
Уже можно было обратить внимание, что в графиках функций, которые представлены в виде многочленов, свободный коэффициент показывает точку пересечения с осью ординат. А в общем случае такой точкой является значение функции при подстановке аргумента, равного нулю.
Для ознакомления с изображением параболы построение следует начать с простейшего частного случая рассматриваемой функции .
Для построения параболы по общему виду функции есть несколько стандартных приемов, укажем один наиболее простой и удобный из них.
Метод построения «по вершине».
В этом способе сначала находят координаты вершины, а затем в зависимости от знака старшего коэффициента строят эскиз графика.
Координаты вершины находят по следующим формулам:
Как видим, для вычисления значения игрековой координаты вершины выполняется подстановка в функцию найденного значения иксовой координаты вершины.
После этого вершина обозначается в системе координат и с учетом известного нам направления веток параболы в зависимости от знака старшего коэффициента функции изображается эскиз графика.
Пример. Построить график функции .
Решение. Воспользуемся указанными формулами для .
, .
Учтем, что , т.е. ветки параболы направлены вверх. Для точности нанесем точку пересечения с осью : .
Чтобы увеличить точность построения графика, можно найти и точки его пересечения с осью . Решим для этого уравнение , как мы уже знаем, приравняв функцию к нулю. Но мы не будем делать этого в примере, если вам интересно, то можете проделать это действие самостоятельно и решить квадратное уравнение.
3) Перейдем к простейшему виду дробно-рациональной функции, графиком которой является гипербола.
Общий вид такой функции , т.е. в числителе и знаменателе дроби находятся линейные двучлены.
У указанных параметров нет общепринятых названий.
Начнем знакомство с графиком, который называют гиперболой, с изображения простейшего частного случая дробно-рациональной функции, когда , т.е. . Он имеет вид:
Как видим, у графика есть вспомогательные элементы, которые называются «асимптоты». Их две: горизонтальная и вертикальная.Вспомним, что вертикальная асимптота строится в координате по оси абсцисс, при которой знаменатель дроби превращается в ноль.
Горизонтальная асимптота проводится в том значении координаты по оси ординат, к которому стремится функция при аргументе, стремящемся к бесконечности. Для функций указанного типа горизонтальную асимптоту можно найти и проще, значением ее игрековой координаты будет отношение коэффициента при иксе в числителе и в знаменателе. Разобраться почему так вы можете изучив тему «Предел функции».
Пример. Построим график дробно-рациональной функции общего положения .
Способ построения мы назовем «по асимптотам» и он будет состоять из трех шагов:
1. Находим уравнение вертикальной асимптоты: ;
2. Находим уравнение горизонтальной асимптоты: . Можно так же воспользоваться способом приведения числителя к константе, который мы показали в предыдущем уроке.
3. Расположение веток гиперболы неоднозначно: или справа вверху и слева внизу, например, в простейшем случае
или слева вверху и справа внизу, например,
Поэтому необходимо точно определить, как они будут изображаться. Для этого просто подставим любое целое значение икса в функцию из области определения и найдем одну точку, которая принадлежит графику.
Подставим, например, и построим ее в системе координат с найденными асимптотами.
Ветки гиперболы должны прижиматься к асимптотам и по расположению построенной точки мы определяем положение одной из веток гиперболы, а соответственно и другой, т.к. ветки всегда лежат наискось относительно друг друга, если к графику не применялись специальные преобразования.
Теперь менее подробно перечислим графики основных функций, для которых не выделяют отдельных методов построения. Также вспомним графики тех функций, которые мы недавно изучали.
4) График неизвестной в четной степени, где вы
interneturok.ru
Методы графического сложения, вычитания.
Чтобы построить график функции y = f(x) + g(x) , надо построить на одном чертеже графики y = f(x) и y = g(x) , потом при каждом x сложить ординаты двух графиков.
Если необходимо построить график разности двух функций y = f(x) — g(x) , то этот случай сводится к построению суммы: y = f(x) + ( — g(x)) . Причем, график функции y = — g(x) получается из графика функции y = g(x) симметричным отражением относительно оси OX .
В случае, когда вторая функция — константа, то графическое сложение означает сдвиг графика первой функции по вертикали на эту константу, причем, если константа положительная, то сдвиг осуществляется вверх, а если отрицательная, то вниз.
Чтобы построить график функции y=f(x)·g(x) , надо построить на одном чертеже графики y=f(x) и y=g(x) , потом при каждом x перемножить ординаты двух графиков.
Графическое деление выполняется аналогично произведению.
В частном случае при построении графика функции y=A·f(x) , где A — константа надо график функции y=f(x) растянуть в |A| раз по вертикали, при условии |A|≥1 , или сжать в раз по вертикали, если |A|<1 , и затем полученный график отобразить симметрично относительно оси OX, если A<0 .
В данном параграфе рассмотрены следующие примеры:
| Умножение двух функций: | Делениее двух функций: |
| Умножение функции на константу A > 0: | Умножение функции на константу A < 0: |
or-gr2005.narod.ru
Преобразование графиков функций
Преобразование графиков функций
В этой статье я познакомлю вас с линейными преобразованиями графиков функций и покажу, как с помощью этих преобразований из графика функции получить график функции
Линейным преобразованием функции называется преобразование самой функции и/или ее аргумента к виду , а также преобразование, содержащее модуль аргумента и/или функции.
Наибольшие затруднения при построении графиков с помощью линейных преобразований вызывают следующие действия:
- Вычленение базовой функции, собственно, график которой мы и преобразовываем.
- Определения порядка преобразований.
Именно на этих моментах мы и остановимся подробнее.
Рассмотрим внимательно функцию
В ее основе лежит функция . Назовем ее базовой функцией.
При построении графика функции мы совершаем преобразования графика базовой функции .
Если бы мы совершали преобразования функции в том же порядке , в каком находили ее значение при определенном значении аргумента, то
Рассмотрим какие виды линейных преобразований аргумента и функции существуют, и как их выполнять.
Преобразования аргумента.
1. f(x) f(x+b)
1. Строим график фунции
2. Сдвигаем график фунции вдоль оси ОХ на |b| единиц
- влево, если b>0
- вправо, если b<0
Построим график функции
1. Строим график функции
2. Сдвигаем его на 2 единицы вправо:
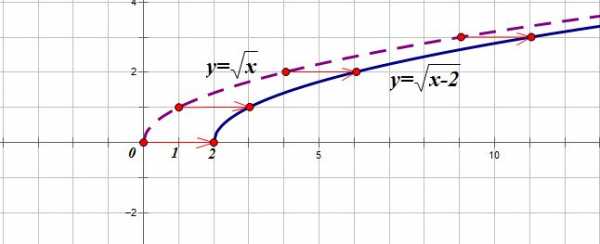
2. f(x) f(kx)
1. Строим график фунции
2. Абсциссы точек графика делим на к, ординаты точек оставляем без изменений.
Построим график функции .
1. Строим график функции
2. Все абсциссы точек графика делим на 2, ординаты оставляем без изменений:
3. f(x) f(-x)
1. Строим график фунции
2. Отображаем его симметрично относительно оси OY.
Построим график функции .
1. Строим график функции
2. Отображаем его симметрично относительно оси OY:
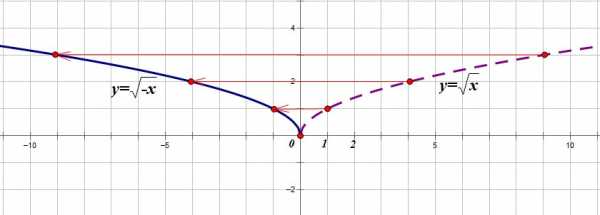
4. f(x) f(|x|)
1. Строим график функции
2. Часть графика, расположенную левее оси ОY стираем, часть графика, расположенную правее оси ОY Достраиваем симметрично относительно оси OY:
График функции выглядит так:
Построим график функции
1. Строим график функции (это график функции , смещенный вдоль оси ОХ на 2 единицы влево):
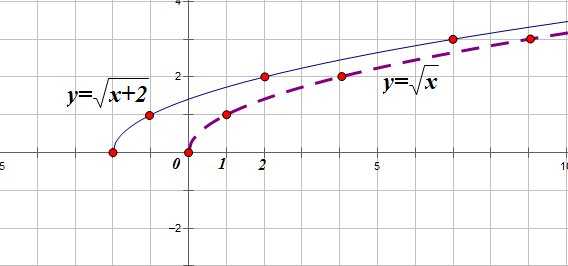
2. Часть графика, расположенную левее оси OY (x<0) стираем:
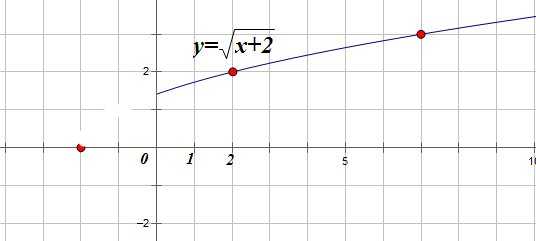
3. Часть графика, расположенную правее оси OY (x>0) достраиваем симметрично относительно оси OY:
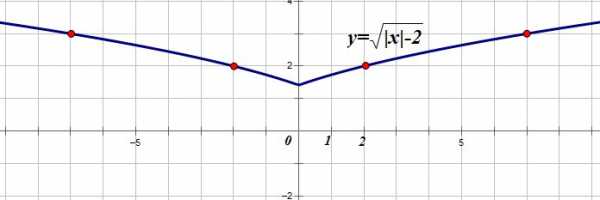
Важно! Два главных правила преобразования аргумента.
1. Все преобразования аргумента совершаются вдоль оси ОХ
2. Все преобразования аргумента совершаются «наоборот» и «в обратном порядке».
Например, в функции последовательность преобразований аргумента такая:
1. Берем модуль от х.
2. К модулю х прибавляем число 2.
Но построение графика мы совершали в обратном порядке:
Сначала выполнили преобразование 2. — сместили график на 2 единицы влево (то есть абсциссы точек уменьшили на 2, как бы «наоборот»)
Затем выполнили преобразование f(x) f(|x|).
Коротко последовательность преобразований записывается так:
Теперь поговорим о преобразовании функции. Преобразования совершаются
1. Вдоль оси OY.
2. В той же последовательности, в какой выполняются действия.
Вот эти преобразования:
1. f(x)f(x)+D
1. Строим график функции y=f(x)
2. Смещаем его вдоль оси OY на |D| единиц
- вверх, если D>0
- вниз, если D<0
Построим график функции
1. Строим график функции
2. Смещаем его вдоль оси OY на 2 единицы вверх:
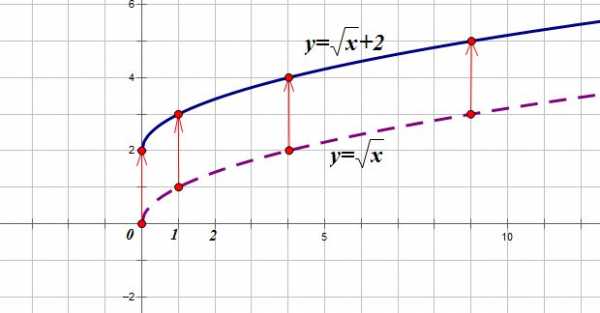
2. f(x)Af(x)
1. Строим график функции y=f(x)
2. Ординаты всех точек графика умножаем на А, абсциссы оставляем без изменений.
Построим график функции
1. Построим график функции
2. Ординаты всех точек графика умножим на 2:
3. f(x)-f(x)
1. Строим график функции y=f(x)
2. Отображаем его симметрично относительно оси ОХ.
Построим график функции .
1. Строим график функции .
2. Отображаем его симметрично относительно оси ОХ.
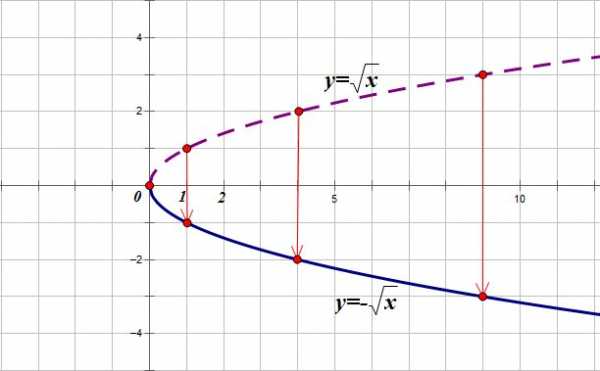
4. f(x)|f(x)|
1. Строим график функции y=f(x)
2. Часть графика, расположенную выше оси ОХ оставляем без изменений, часть графика, расположенную ниже оси OX, отображаем симметрично относительно этой оси.
Построим график функции
1. Строим график функции . Он получается смещением графика функции вдоль оси OY на 2 единицы вниз:
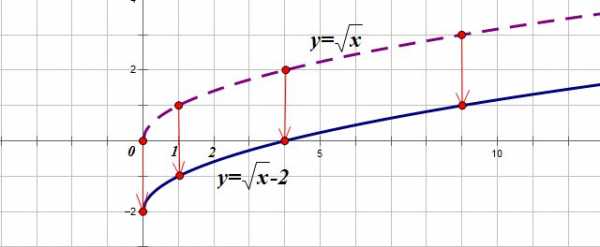
2. Теперь часть графика, расположенную ниже оси ОХ, отобразим симметрично относительно этой оси:
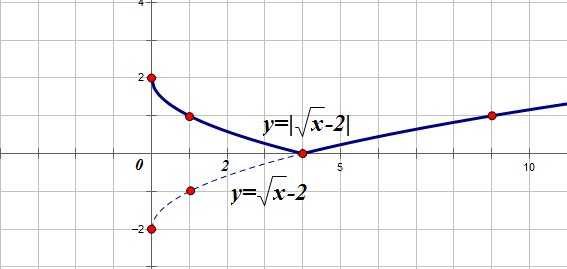
И последнее преобразование, которое, строго говоря, нельзя назвать преобразованием функции, поскольку результат этого преобразования функцией уже не является:
y=f(x) |y|=f(x)
1. Строим график функции y=f(x)
2. Часть графика, расположенную ниже оси ОХ стираем, затем часть графика, расположенную выше оси ОХ достраиваем симметрично относительно этой оси.
Построим график уравнения
1. Строим график функции :
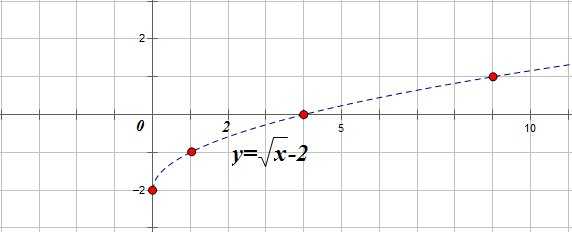
2. Часть графика, расположенную ниже оси ОХ стираем:
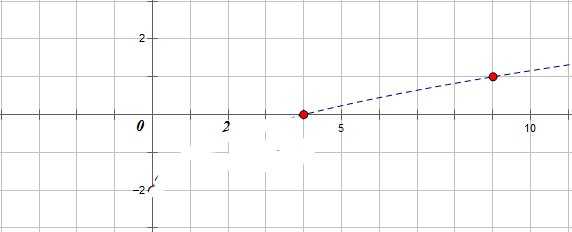
3. Часть графика, расположенную выше оси ОХ достраиваем симметрично относительно этой оси.
И, наконец, предлагаю вам посмотреть ВИДЕОУРОК в котором я показываю пошаговый алгоритм построения графика функции
График этой функции выглядит так:
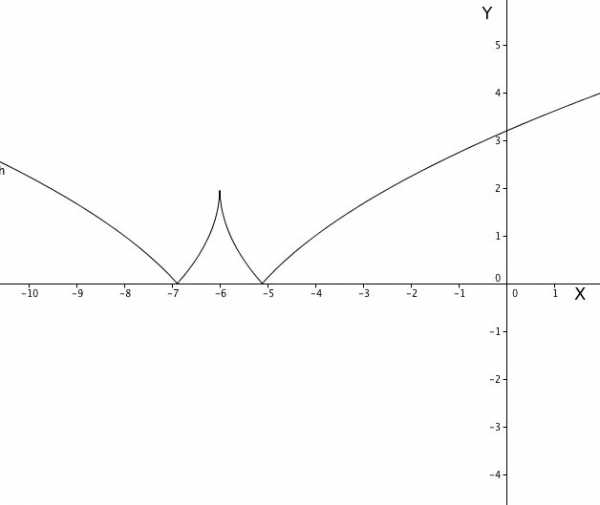
И.В. Фельдман, репетитор по математике.
ege-ok.ru
Конспект урока по алгебре «Элементы комбинаторики. Правило умножения.»
УРОК №1
Тема: Элементы комбинаторики. Правило умножения.
Тип урока: урок – объяснения нового материала (лекция)
Цель: Ввести новые понятия по теме «Элементы комбинаторики»
Задачи:
Образовательные:
ввести понятие случайного явления, определение комбинаторики;
познакомить учащихся с правилом умножения для подсчета всех возможных исходов независимого проведения двух испытаний.
начать формирование умений по применению знаний в решении заданий;
Развивающие:
Создать условия для развития логического мышления, долговременной память, внимательности;
развивать умение рассуждать, обобщать и делать выводы;
развивать правильную математическую речь, вычислительный навык;
Воспитательные:
воспитывать усидчивость, дисциплинированность, инициативность;
воспитывать уважение к преподавателю, одноклассникам.
(слайды 1-4)
Оборудование: презентация к уроку №1
Ход урока.
Орг. момент.
Вступительное слово учителя (актуальность темы)
Математику многие любят за ее вечные истины: дважды два всегда – четыре, сумма четных чисел четна, а площадь прямоугольника равна произведению его смежных сторон. В любой задаче, которую мы решаем на уроках математики, у всех получается один и тот же ответ — нужно только не делать ошибок в решении. Реальная жизнь не так проста и однозначна. Исходы многих явлений заранее предсказать невозможно, какой бы полной информацией о них мы не располагали. Нельзя, например, сказать наверняка, какой стороной упадет подброшенная вверх монета, когда в следующем году выпадет первый снег или сколько человек в городе захотят в течение ближайшего часа позвонить по телефону. Такие непредсказуемые явления называются случайными. (слайд 5)
Все мы довольно часто говорим «это невероятно», «более вероятно, что…», «это мало вероятно», «можно утверждать со стопроцентной вероятностью, что…» и т.д., когда пытаемся спрогнозировать наступление того или иного события. При этом обычно мы опираемся на интуицию, жизненный опыт, здравый смысл. Но часто такие оценки являются недостаточными и бывает важно знать, на сколько или во сколько раз одно случайное событие вероятнее другого. Иными словами, нужны точные количественные оценки, нужно уметь численно характеризовать возможность наступления того или иного события. Раздел математики, посвященный исследованию количественных оценок случайных событий, называют теорией вероятностей.(слайд 5)
Вероятности различных событий в ряде азартных игр (карты, кости…) вычислили французские математики XVII века Пьер Ферма и Блез Паскаль. Они использовали метод, который позже был назван комбинаторным анализом или проще комбинаторикой.
Комбинаторика – это искусство подсчета числа различных комбинаций, соединений, сочетаний, перестановок тех или иных элементов некоторых множеств. Именно с комбинаторики начнется наше знакомство с элементами теории вероятностей.(слайд 6)
Объяснение нового материала
Решим задачу.
Задача 1. Сколько четных двузначных чисел можно составить из цифр 0, 1, 2, 3, 4, 5, 9?( слайд 7)
Решение. (слайды 8-9)
Первый способ. Выпишем по порядку все числа от 10 до 99 и выберем те, что нам нужны: 10, 12,14, 20,22, 24, 40, 42, 44, 50, 52, 54, 90, 92, 94. Всего 15 чисел.
Второй способ. Первой цифрой не может быть 0. Если первая цифра 1, то вторая (четная!) цифра – 0,2 или 4. Всего 3 варианта. Если первая цифра 2, то для второй цифры возможны те же 3 варианта. В случаях, когда первая цифра равна 4,5 или 9, рассуждение повторяется, и в каждом из случаев будет по 3 варианта. Всего получается 5 раз по 3, т.е. 15 четных двузначных чисел, составленных из цифр 0, 1, 2, 3, 4, 5, 9.
Третий способ. Для выбора первой цифры есть 5 вариантов: 1, 2, 4, 5 или 9. Для второй цифры есть 3 варианта: 0,2 или 4. Значит, всего есть 5·3 вариантов составления нужных нам чисел.
Обсудим предложенные решения. Первый способ неплох, но тут можно сбиться со счета или что-то пропустить. Кроме того, перспективы поступать таким же образом в более сложных ситуациях (например, с четырехзначными числами) довольно безрадостны.
Второй способ, по существу, просто упорядочивает подсчет вариантов в первом способе и в сложных ситуациях также вряд ли применим. Третий способ наиболее ясен с формальной точки зрения. Непонятно только обоснование:
« …Значит, имеются 5·3 …». На чем основано это «значит»? Почему 5 и 3 следует именно перемножить, а, например, не сложить? Ответ на эти вопросы фактически дает второй способ решения. В нем как раз и приведено объяснение: 5·3 – это 5 раз по 3. Чтобы не приводить к каждой задаче два решения – краткое и подробное, поступим так. Сформулируем правило умножения и в дальнейшем будем использовать именно его в качестве подсчета вариантов. ( слайд 10)
Правило умножения
Для того чтобы найти число всех возможных исходов независимого проведения двух испытаний А и В, следует перемножить число всех исходов испытания А и число всех исходов испытания В.
В примере 1 испытание А состоит в выборе первой цифры числа, и у него имеется 5 возможных исходов, а испытание В состоит в выборе второй цифры, и у него имеется 3 возможных исхода. Так как выбор первой цифры независим от выбора второй цифры, то, по правилу умножения, всего получается 5•3=15 исходов. Вот как выглядят рассуждения в примере 1:
0
2
4
1
10
12
14
2
20
22
24
4
40
42
44
5
50
52
54
9
90
92
94
Всего 5•3=15 чисел.
Правило умножения для двух независимых испытаний удобно объяснять, используя прямоугольные таблицы. Но если проводятся три испытания, то для иллюстрации придется использовать и длину, и высоту, и ширину. На картинке получится прямоугольный параллелепипед, разбитый на кубики. Здесь уже и рисунок, и объяснения выглядят сложнее, поскольку, например, будут невидимые кубики. Еще хуже дело обстоит с четырьмя испытаниями. Окружающее нас пространство всего лишь трехмерно, и для рисунка в этом случае не хватит измерений. Необходимо правило умножения для произвольного числа независимых испытаний.
Обобщенное правило умножения. Если элемент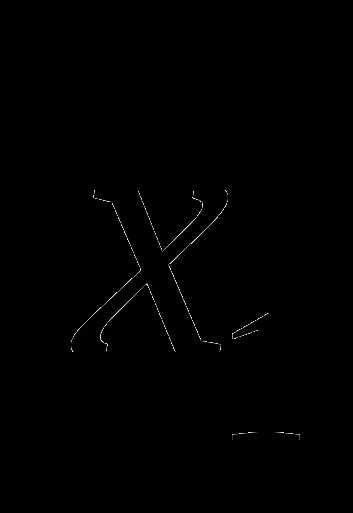 
может быть выбран 
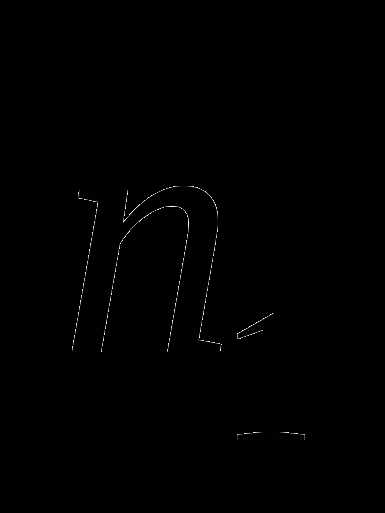способами, после этого элемент 
может быть выбран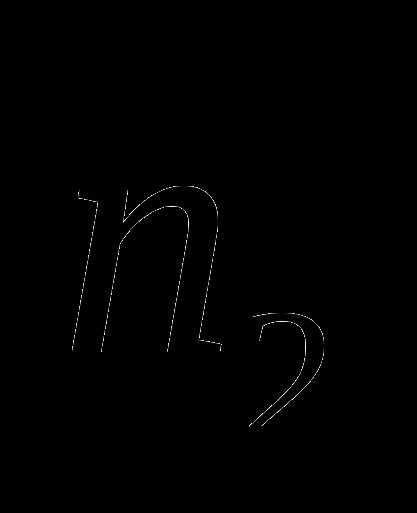 
способами, а для любого после выбора элементов элемент 
может быть выбран 
способами, то выбор упорядоченной последовательности из m элементов может быть осуществлён способами.
(Слайд 11)
Задача 2. В коридоре 3 лампочки. Сколько имеется различных способов освещения коридора (включая случай, когда все лампочки не горят)? (Слайд 12)
Решение. Пронумеруем лампочки. Первая лампочка может или гореть, или не гореть, т.е. имеются два возможных исхода. Но то же самое относится и ко второй, и к третьей лампочкам. Мы предполагаем, что лампочки горят или нет независимо друг от друга. По правилу умножения получаем, что число всех способов освещения равно 2•2•2=8. (Слайд 13)
Приведем так называемое дерево вариантов для примера 2. На этом дереве наглядно представлен способ получения всех восьми вариантов освещения.
Первая лампочка
+(горит) -(не горит)
Вторая лампочка Вторая лампочка
+ —
Третья лампочка Третья лампочка Третья лампочка Третья лампочка
+ — + — + — + —
+++ ++- +-+ +- — -++ -+- — -+ — — —
В рассмотренном примере речь шла фактически о выборе того или иного подмножества данного трехэлементного множества { }. Выбор подмножества { } означает, что горят первая и третья лампочки; выбор пустого подмножества Ø означает, что не горит ни одна лампочка; выбор всего множества означает, что горят все лампочки. Оказалось, что у трехэлементного множества =8 подмножеств.
Задача 3. В трёх 8-х классах 23, 24 и 25 учащихся. Сколькими способами можно выбрать трёх представителей по одному из каждого класса? (Слайд 14)
Решение: (Слайд 15)
Выбор представителя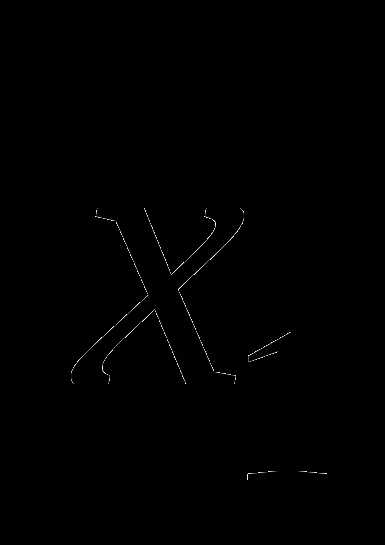 
от первого класса можно сделать 23 способами. Для каждого представителя существует 24 способа выбора представителя 
второго класса. По правилу произведения число таких пар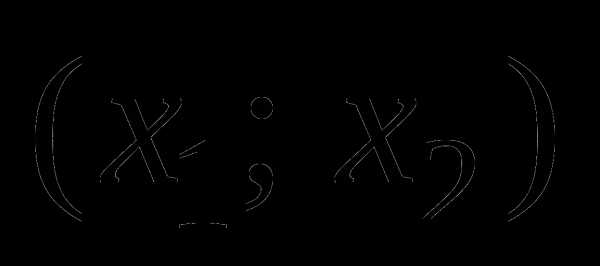 
представителей равно 
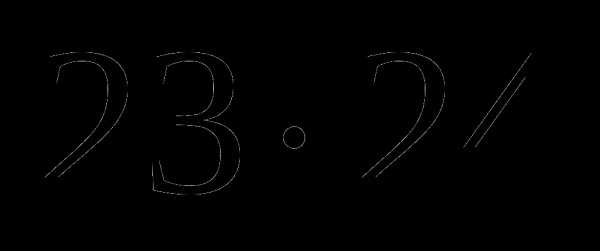. Наконец, после выбора двух представителей из первых двух классов представителя 
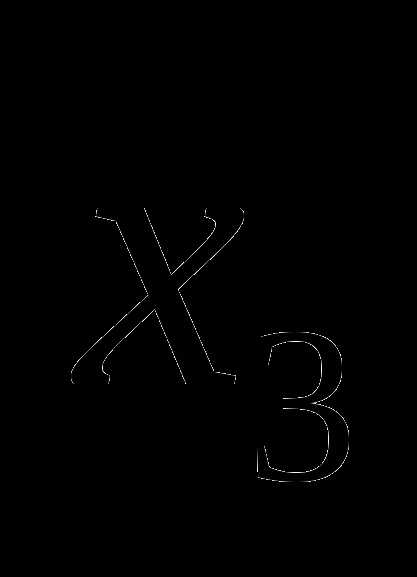из третьего класса можно выбрать 25 способом. Поэтому по правилу произведения тройку представителей 8-х классов можно выбрать способами.
Задача 4. Сколько четырёхзначных чисел можно записать с помощью цифр 1, 2, 3? (Слайд 16)
Решение: (Слайд 17)
В качестве первой цифры четырехзначного числа можно взять любую из цифр 1, 2, 3, т.е. первая цифра числа может быть выбрана тремя способами. После этого вторая цифра также выбирается из заданных трех цифр, т.е. опять тремя способами. По правилу произведения существует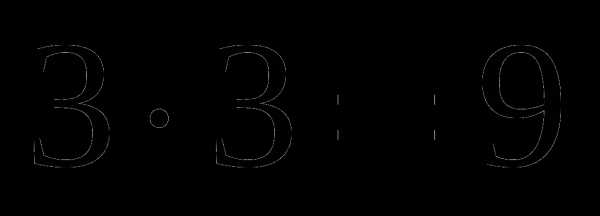 
способов выбрать первые две цифры четырехзначного числа. После выбора первой и второй цифры числа его третья и четвертая цифры опять выбираются тремя способами каждая. Поэтому число способов, которыми из трех заданных цифр можно составить четырехзначное число, равно .
Задача 5. Имеется девять карточек, на которых написаны цифры от 1 до 9. Сколько четырёхзначных чисел можно составить с помощью этих карточек? (Слайд 18)
Решение: (Слайд 19)
В качестве первой цифры числа можно взять любую из цифр 1, …, 9, т.е. она может быть выбрана 9 способами. После этого для выбора второй цифры остается 8 возможностей (одна цифра уже использована). Значит, теперь первые две цифры числа можно выбрать способами. Третья цифра числа может быть выбрана 7 способами, а после этого последняя, четвертая, – 6 способами. Следовательно, число способов, которыми с помощью имеющихся карточек можно составить четырехзначное число, равно .
В третьей из рассмотренных задач комбинаторная конфигурация составляется из элементов трех множеств, в четвёртой и пятой – из элементов одного множества. При этом в четвёртой задаче выбор элементов может осуществляться с повторением, в пятой же задаче – выбор однократный. Тем не менее, все три задачи решаются единообразно. С помощью обобщенного правила умножения.
А сейчас решите самостоятельно задачу.
Задача 6. В компьютере каждый символ (буква, цифра, специальный знак) кодируется последовательностью из восьми 0 и 1, например:
01000110 — код буквы «F»;
00110010 — код цифры «2» и т.д.
Сколько различных символов можно закодировать таким образом?
Другими словами, сколько существует различных двоичных кодов длины 8? (Слайд 20)
Решение задачи затем разбирается совместно с учителем.
Выстраивая комбинацию из восьми нулей и единиц, мы можем выбрать первую цифру двумя способами, после чего вторую цифру — тоже двумя способами и т.д. Всего получаем 2 • 2 • … •2 = 28 = 256 комбинаций. Именно столько символов содержит так называемая таблица ASCII, давно ставшая стандартом для представления символов в памяти компьютера (сейчас ей на смену пришли более длинные 16-разрядные коды, позволяющие кодировать уже 216 = 65536 различных символов).
Выписывать все 256 комбинаций у нас нет возможностей, напишем только начало и конец этой последовательности: 00000000; 00000001; 00000010; …11111110; 11111111.(можно попросить записать в тетрадях и на доске начало и конец последовательности).
Бывают задачи, в которых после выбора одного из а объектов в качестве первого элемента комбинации нельзя однозначно сказать, сколькими способами можно выбрать второй элемент – это зависит от того, какой именно объект был выбран первым. Рассмотрим такую ситуацию на примере.
(Слайд 20)
Задача7.(дополнительная задача)
Сколько двузначных чисел, которые можно составить из цифр 1,2,3 так, чтобы первая цифра была меньше второй. Решение:
На первое место цифру можно выбрать тремя способами, а вот на второе место после этого:
— двумя способами, если первой цифрой была выбрана 1;
— одним способом, если 2;
— нулем способов, если 3.
4. А сейчас проверим , как вы усвоили правило умножения, выполним тест ( тест с самопроверкой, ответы высвечиваются на слайде, после выполнения теста) (Слайд 21)
ТЕСТ
Сколькими способами можно составить расписание одного учебного дня из 5 различных уроков?
1) 30 2) 100 3) 120 4) 5
2 . Сколько способами могут рассесться участники Квартета?
24 2) 16 3) 6 4) 12
3. Сколько различных пятизначных чисел можно составить из цифр 1, 2, 3, 4, 5?
1) 100 2) 30 3) 5 4) 120
4. Сколькими способами могут быть расставлены 8 участниц финального забега на восьми беговых дорожках?
1) 40320 2) 64 3) 128 4) 16
5. Курьер должен разнести пакеты в 7 различных учреждений. Сколько маршрутов он может выбрать?
1) 49 2) 5040 3)14 4) 96
№ задания
1
2
3
4
5
№ ответа
3
1
4
1
2
5. Итоги урока. После самопроверки , (Слайд 22)
узнать кто решил всё правильно, а кто допустил по 1,2 ошибки. Похвалить детей за хорошую работу. Можно активным поставить оценки.
5.Задание на дом: выучить лекцию и решить задачи. (Слайд 23)
Задача №1. (Слайд 24)
Наряд студентки состоит из блузки, юбки и туфель. Девушка имеет в своем гардеробе четыре блузки, пять юбок и трое туфель. Сколько нарядов может иметь студентка?
Решение. Пусть сначала студентка выбирает блузку. Этот выбор может быть совершен четырьмя способами, так как студентка имеет четыре блузки, затем пятью способами произойдет выбор юбки и тремя способами
выбор туфель. По принципу умножения получается 4*5*3=60 нарядов (комбинаций).
Задача№2 (Слайд 24)
В кафе имеются три первых блюда, пять вторых блюд и два третьих. Сколькими способами посетитель кафе может выбрать обед, состоящий из первого, второго и третьего блюд?
Решение. Первое блюдо можно выбрать 3 способами. Для каждого выбора первого блюда существует 5 возможностей выбора второго блюда. Значит, первые два блюда можно выбрать 3·5 способами. Наконец, для каждого выбора третьего блюда, т.е. существует 3·5·2 способов составления обеда из трех букв. Итак, обед из трех букв может быть составлен 30 способами.
Задача №3. (Слайд 25)
Сколько трехзначных чисел можно составить из цифр 1, 3, 5, 7, используя в записи числа каждую из них не более одного раза?
Решение: Первую цифру трехзначного числа можно выбрать четырьмя способами. Так после выбора первой цифры останутся три, то вторую цифру можно выбрать из оставшихся цифр уже тремя способами. Наконец, третью цифру можно выбрать (из оставшихся двух) двумя способами. Следовательно, общее число искомых трехзначных чисел равно произведению 4·3·2 = 24.
Задача №4. (Слайд 25)
Сколько имеется трехзначных чисел, которые не меняются при перемене местами первой и последней цифр?
Решение: Первой цифрой может быть любая цифра, кроме 0, всего 9 вариантов. Второй может быть любая цифра, всего 10 вариантов.
Третья цифра по условию – такая же, как и первая, т.е. тут вариант единственный. По правилу умножения получаем ответ: 9 ·10· 1 = 90.
Литература (сдайд 26)
Дорофеев Г.В., Суворова С.Б., Шарыгин И.Ф. и др. Математика. 8-й класс: Учеб. для общеобразоват. учеб.заведений — М.: Дрофа, 1997.
Дорофеев Г.В.Математика. 8-й класс: Рабочая тетрадь: К учебнику под редакцией Г.В.Дорофеева, И.Ф.Шарыгина «Математика 6». — М.: Дрофа, 1998.
Макарычев Ю.Н., Миндюк Н.Г. Алгебра. Элементы статистики и теории вероятностей. Учебное пособие для учащихся 7-9 классов общеобразовательных учреждений/ под редакцией Теляковского С.А. – М., «Просвещение», 2003.
Лекции дистанционного курса «Стандарты второго поколения: стохастическая линия элементы комбинаторики, теории вероятностей и статистики в школьном курсе»
Интернет – ресурсы (http//combinatorika.narod.ru/,
http//bankzadach.ru/, http//schol-collection.edu.ru/, и т.д.
infourok.ru
Правило умножения для комбинаторных задач
Разделы: Математика, Конкурс «Презентация к уроку»
Презентация к уроку
Загрузить презентацию (1,4 МБ)
Внимание! Предварительный просмотр слайдов используется исключительно в ознакомительных целях и может не давать представления о всех возможностях презентации. Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.
Тип урока: Усвоение новых знаний
Образовательные цели / задачи педагога на уроке:
- создать условия для формирования представлений о комбинаторных задачах, переборе всех возможных вариантов, о дереве возможных вариантов, как о геометрической модели рассматриваемой ситуации, о записи произведения первых п натуральных чисел в виде факториала, о решении комбинаторных задач, применяя способы перебора возможных вариантов; с помощью графа, называемого деревом вариантов; правила умножения.
Образовательные цели / задачи учащегося на уроке:
Иметь представление о переборе всех возможных вариантов, о комбинаторных задачах, о дереве возможных вариантов, понятии записи произведения первых п натуральных чисел в виде факториала, о правиле умножения; овладеть умением решать комбинаторные задачи, применяя различные способы.
Планируемые результаты изучения темы:
Личностные: проявляют познавательный интерес к изучению темы; осознают важность и необходимость знаний для человека.
Предметные: знают о переборе всех возможных вариантов, о комбинаторных задачах, о дереве возможных вариантов, о правиле умножения.
Метапредметные результаты изучения темы (универсальные учебные действия):
- познавательные: ориентируются на разнообразие способов решения задач;
- регулятивные: учитывают правило в планировании и контроле способа решения; умеют участвовать в диалоге, осмысливать точку зрения собеседника, признавать право на свое мнение, развернуто обосновывать суждение;
- коммуникативные: считаются с разными мнениями и стремятся к координации различных позиций в сотрудничестве.
Оборудование:
Учебник, мультимедиа проектор, компьютер, карточки с набором задач для групповой работы, карточки для рефлексии.
Этапы урока:
1) Организационный момент.
2) Мотивация учебной деятельности учащихся. Постановка цели урока.
3) Актуализация опорных знаний.
4) Изучение нового материала.
5) Первичное закрепление новых знаний.
6) Исторический экскурс.
7) Обобщение нового знания. Включение нового знания в систему ранее изученного.
8) Итог урока. Рефлексия содержания учебного материала.
9) Информация о домашнем задании.
Ход урока
1. Организационный момент.
Приветствие учащихся. Проверка готовности класса к уроку. Организация внимания.
2. Мотивация учебной деятельности. Постановка цели урока.
Учитель формулирует цели и задачи урока, предлагает провести урок под девизом:
“Кто хочет ограничиться настоящим, без знания прошлого, тот никогда его не поймет”. (Г.В.Лейбниц)
3. Актуализация знаний
Учитель напоминает учащимся, что знакомство с темой этого урока началось еще в 5 классе и предлагает учащимся решить задачу №1 различными способами:
Задача №1 (Слайд №3)
Запишите все трехзначные числа, для записи которых употребляются только цифры 0 и 7.
Проверка решения задачи осуществляется на доске, с обсуждением всех предложенных способов решения (Слайд № 4)
4. Изучение нового материала.
Учитель вводит понятие комбинаторика, комбинаторные задачи:
В математике есть задачи, подобные решенной нами, в которых требуется составить различные наборы, подсчитать количество всевозможных расположений (комбинаций) элементов некоторого множества, составленных по определённому правилу, такие задачи называют комбинаторными.
Раздел математики, именуемый комбинаторикой, изучает комбинации и перестановки предметов, расположение элементов, обладающее заданными свойствами.
Учитель подчеркивает важную роль комбинаторики как одной из ветвей математики. (Слайды № 5 — 6)
К комбинаторным задачам относятся также задачи построения магических квадратов, задачи расшифровки и кодирования, с которыми мы с вами познакомимся подробнее на факультативных занятиях.
Учащимся предлагается решить задачу №2.
Задача №2. ( Слайд №7)
Сколько пальцев на лапах у 20 обезьян?
Решение.
20 обезьян, у каждой 4 лапы, на каждой лапе – 5 пальцев.
Получаем 20 х 4 х 5 = 400
Можно рассуждать и так:
Одну обезьяну можно выбрать 20 способами.
1 лапа – 4 выбора.
1 палец – 5 выборов.
Итого 20 х 4 х 5 = 400 пальцев.
Вернемся к задаче №1 и обратим внимание на третий способ решения: 2 х 2 = 4.
Учитель предлагает учащимся сформулировать общее правило для решения данных задач.
Учащиеся приводят свои варианты формулировок. После обсуждения учитель формулирует правило умножения для комбинаторных задач:
Если элемент А можно выбрать m способами, а элемент В можно выбрать n способами, то пару А и В можно выбрать m х n способами. (Слайд 8)
5. Первичное применение нового знания.
Задача № 3. (Слайд №9)
В четверг в шестом классе должно быть 5 уроков: русский язык, литература, математика, история и физкультура. Сколько различных вариантов расписания можно составить на этот день?
Проверка решения на доске. 5 х 4 х 3 х 2 х 1 = 120 (вариантов)
Сколько различных вариантов расписания можно составить на этот день, если:
а) последний урок-физкультура;
б) последний урок физкультура, а первый –математика?
Проверка решения на доске 4 х 3 х 2 х 1 = 24 (варианта)
Проверка решения на доске 3 х 2 х 1 = 6 (вариантов).
Учитель обращает внимание учащихся на то, что решение задачи можно записать в виде:
1 х 2 х 3 = 3!
1 х 2 х 3 х 4 = 4!
1 х 2 х 3 х 4 х 5 = 5! и знакомит учащихся с понятием “факториал”. (Слайд №10)
Учащиеся вычисляют значение выражения: 6! – 5!
Решение: 720 – 120 = 600
6. Исторический экскурс
Трое учащихся получили индивидуальное домашнее задание подготовить к данному уроку сообщения по теме “Из истории развития комбинаторики”.
При подготовке сообщений детям предложен поиск информации с использованием:
а) библиотечного фонда (“ История математики в школе” Г.И. Глейзер, М., Просвещение; 1983г.)
б) интернет-ресурсов (сайт:http://nsportal.ru/shkola/algebra/library/2014/02/02/kombinatorika-i-kombinatornye-zadachi)
Ребята слушают сообщения одноклассников и задают вопросы. Выступающие отвечают на вопросы сами или с помощью учителя. Приложение 1.
7. Обобщение нового знания. Включение нового знания в систему ранее изученного.
Учитель формулирует проблемный вопрос:
Вспомните героев литературного произведения, которые в споре решают комбинаторную задачу? (Герои басни И.А. Крылова “Квартет” осел, козел, мартышка и косолапый мишка)
Может ли комбинаторика помочь нам в реальной жизни?
Учащиеся обсуждают вопрос и высказывают свое мнение.
Учитель обобщает высказанные мнения. Многие жизненные проблемы требуют для своего решения комбинаторного подхода, умения просчитать все возможные варианты и с учетом дополнительных условий выбрать наилучший. Ведь в повседневной жизни нередко перед нами возникают ситуации, которые имеют не одно, а несколько решений, которые нужно сравнить, чтобы выбрать наиболее подходящее для конкретного случая. Для этого надо осуществить перебор всех возможных вариантов или хотя бы подсчитать их число.
Люди, которые владеют техникой решения комбинаторных задач, а, следовательно, обладают хорошей логикой, умением рассуждать, перебирать различные варианты решений, очень часто находят выходы, казалось бы, из самых трудных безвыходных ситуаций.
Для того чтобы увидеть связь комбинаторики и повседневной жизни мы проведем конкурс на звание лучшего экскурсовода, который познакомит ребят с достопримечательностями города Тихвина. (Слайд № 11)
Класс учащихся разбивается на пять групп. Каждой группе предлагается решить задачи (Приложение 2) и представить решение одной из них по выбору учителя на доске. В решениях задач должны быть показаны три различных способа. Для каждой задачи выбирается один наиболее рациональный способ.
Во время групповой работы учитель контролирует ход работы в группах, в случае крайней необходимости оказывает помощь отдельным учащимся или группе.
При проверке задач при необходимости используются (слайды №12 – 17).
По окончанию работы, членами групп дается оценка деятельности каждого учащегося в соответствии с его вкладом в решение поставленной задачи.
Подводятся итоги конкурса. Объявляются оценки.
8. Итог урока. Рефлексия.
Рефлексия содержания учебного материала. 1. Сегодня я узнал… 2. Теперь я могу… 3. Для меня было открытием, что… 4. Мне показалось важным…
9. Домашнее задание.
Придумать комбинаторную задачу для представления на конкурс задач.
Критерии оценивания задач:
1. Самостоятельность при составлении условия задачи (5 баллов)
2. Практическая направленность задачи (4 балла)
3. Представление трех способов решения (6 баллов).
Приложение 3.
Использованная литература:
1. Математика. 6 класс. И.И. Зубарева А.Г.Мордкович. М.: Мнемозина, 2012.
2. “История математики в школе” Г.И. Глейзер, книга 3. М., Просвещение; 1983г.
24.03.2015
xn--i1abbnckbmcl9fb.xn--p1ai