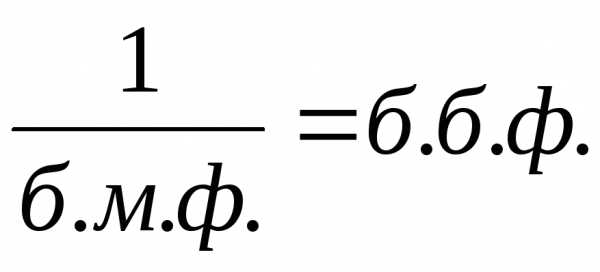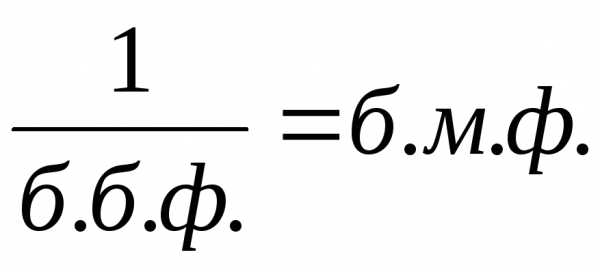2. Основные свойства пределов
1. Если предел
функции в точке  существует, то он единственный.
существует, то он единственный.
2. Предел постоянной величины равен самой постоянной:
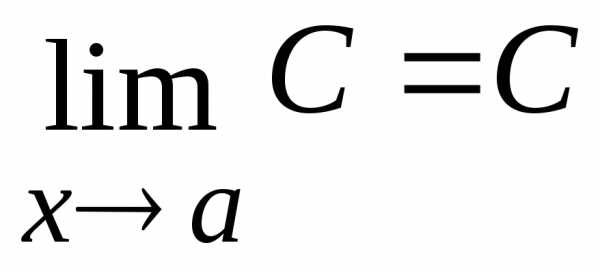 .
.
3. Предел суммы (разности) конечного числа функций равен соответственно сумме (разности) пределов этих функций:
.
4. Предел произведения конечного числа функций равен произведению пределов этих функций:
.
Следствие. Постоянный множитель можно выносить за знак предела:
.
4. Предел частного двух функций равен частному пределов этих функций, если предел знаменателя не равен нулю:
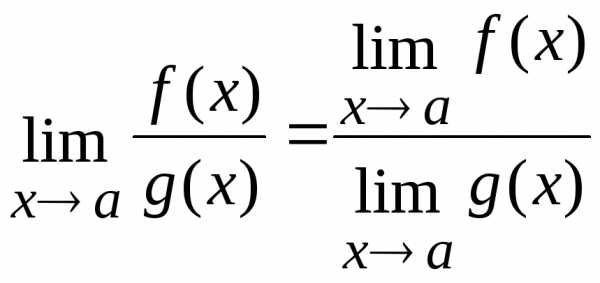 (при ).
(при ).Все свойства имеют смысл, если пределы функций существуют.
Для вычисления
пределов используется свойство элементарных
функций: если 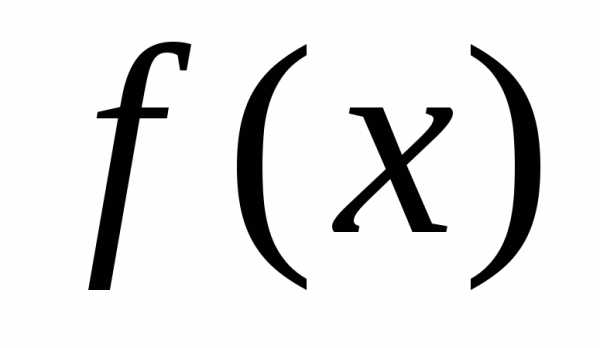 — элементарная функция,
то
.
Это означает, что если предельная точка
— элементарная функция,
то
.
Это означает, что если предельная точка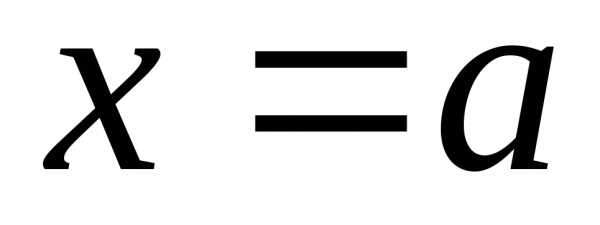 принадлежит области определения функции
принадлежит области определения функции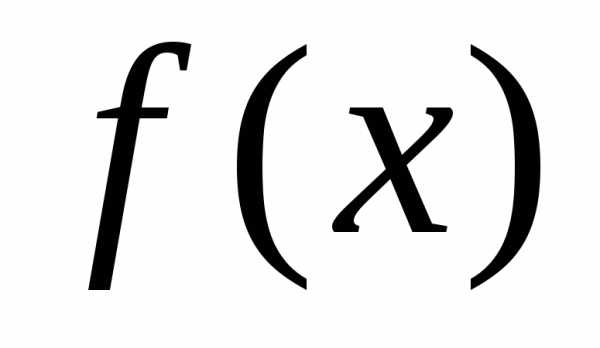 ,
то вычисление предела
,
то вычисление предела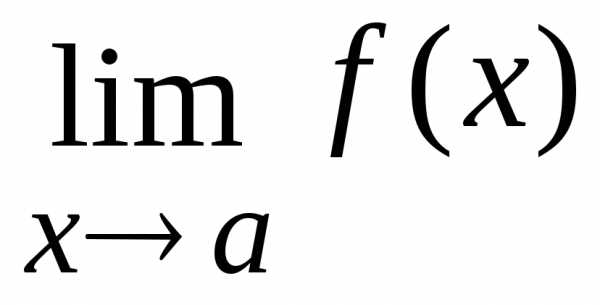 сводитсяк
подстановке в функцию
сводитсяк
подстановке в функцию 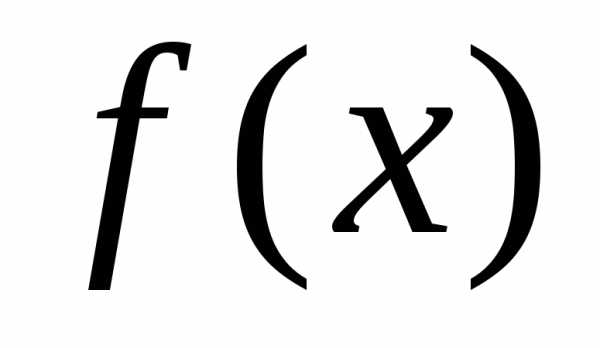 вместо
вместо 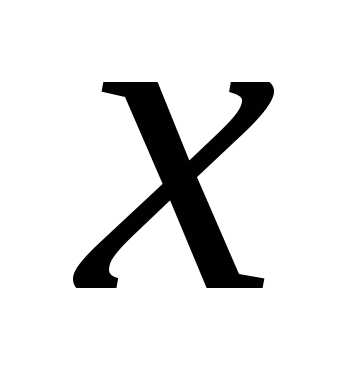 числа
числа  .
.
Пример.
Вычислить предел 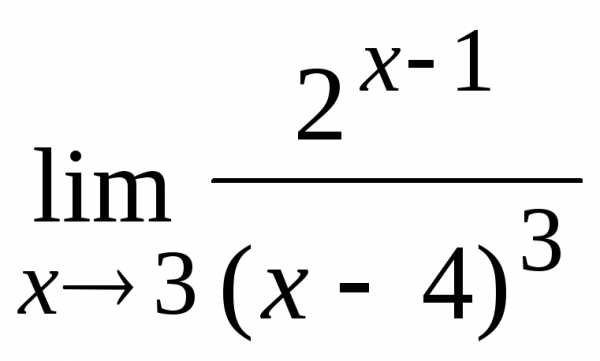
Точка 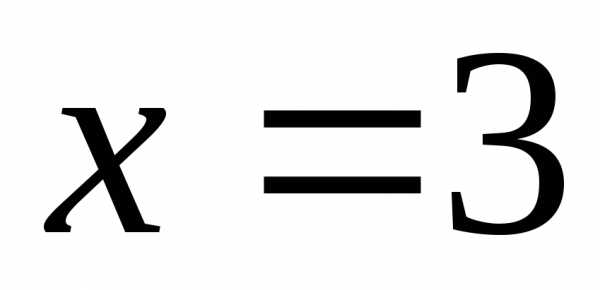 принадлежит области определения функции
принадлежит области определения функции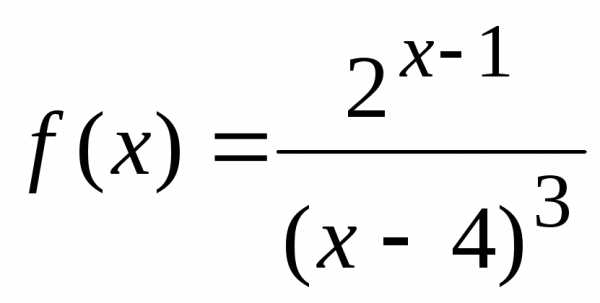 ,
значит,.
,
значит,.
3. Бесконечно малые и бесконечно большие функции
При вычислении пределов большую роль играют бесконечно малые и бесконечно большие функции и их свойства.
Примеры.
Функция — б.м.ф. в точках
 ,
т.к..
,
т.к..Функция
 — б.м.ф. при,
т.к.
— б.м.ф. при,
т.к. .
.
Примеры.
Функция — б.б.ф. при, т.к.
 .
.Функция

 ,
т.к.
,
т.к. .
.
Отметим важные свойства бесконечно малых и бесконечно больших функций.
Теорема (Свойства б.м.ф.)
Алгебраическая сумма конечного числа б.м.ф. и произведение конечного числа б.м.ф. есть бесконечно малая функция.
Произведение б.м.ф. на ограниченную функцию есть бесконечно малая функция.
Частное от деления б.м.ф. на функцию, имеющую в точке
 ненулевой предел, есть б.м.ф.
ненулевой предел, есть б.м.ф.Функция, обратная к бесконечно малой, есть бесконечно большая функция:

Теорема (Свойства б.б.ф.)
Произведение конечного числа б.б.ф. есть бесконечно большая функция.
Произведение б.б.ф. на функцию, имеющую предел, не равный нулю, есть бесконечно большая функция.
Функция, обратная к бесконечно большой, есть бесконечно малая функция:

Примеры. Вычислить пределы.
1. .
2.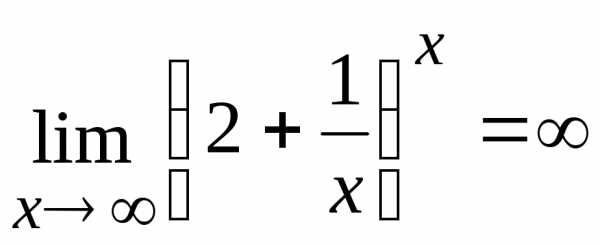 .
.
3. 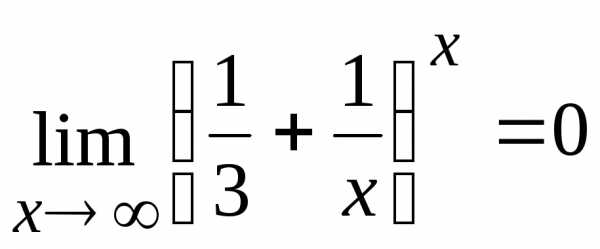 .
.
4. Раскрытие неопределенностей ,
Часто подстановка
предельного значения аргумента в функцию
приводит к неопределенным выражениям
вида  ,
, ,
,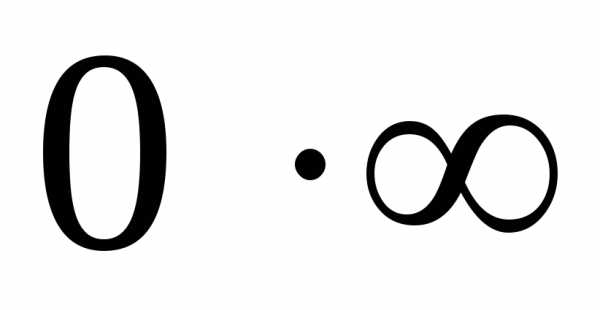
Для раскрытия
неопределенностей в пределе  используют различные приемы.
используют различные приемы.
Неопределенность
вида  .
Если функция
.
Если функция 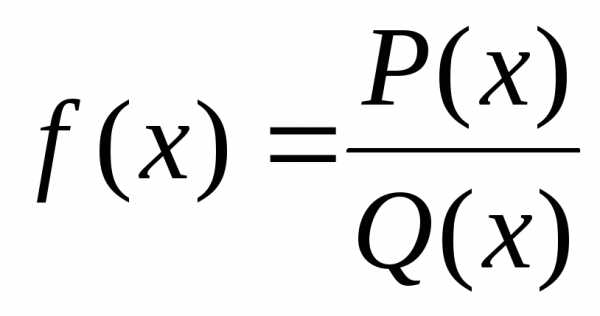 есть отношение многочленов, то для
раскрытия неопределенности
есть отношение многочленов, то для
раскрытия неопределенности  нужно числитель и знаменатель разделить
почленно на
нужно числитель и знаменатель разделить
почленно на 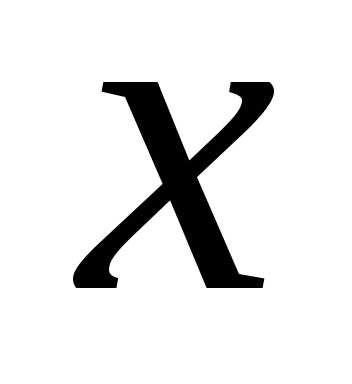 в наибольшей степени.
в наибольшей степени.
Пример.
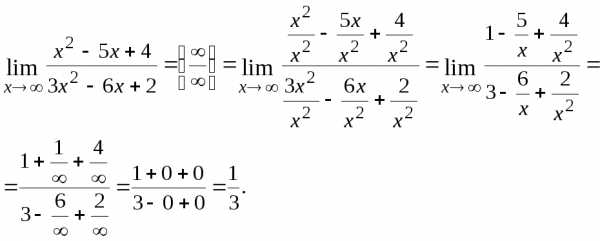
Запишем правило
вычисления предела отношения двух
многочленов при раскрытии неопределенности
типа 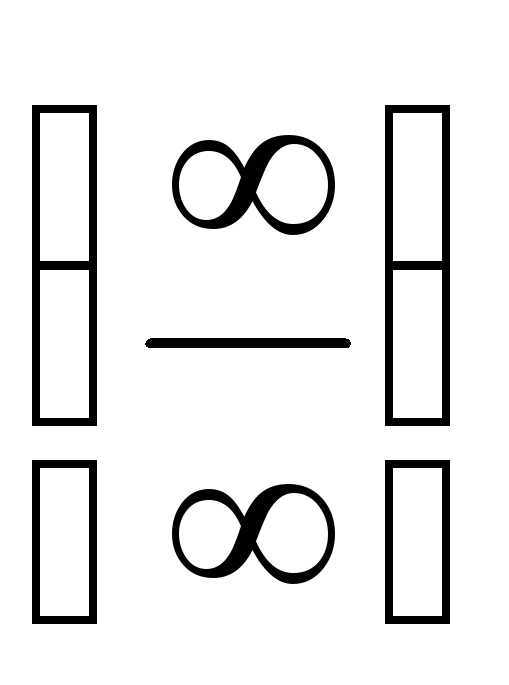 .
.

Неопределенность
вида 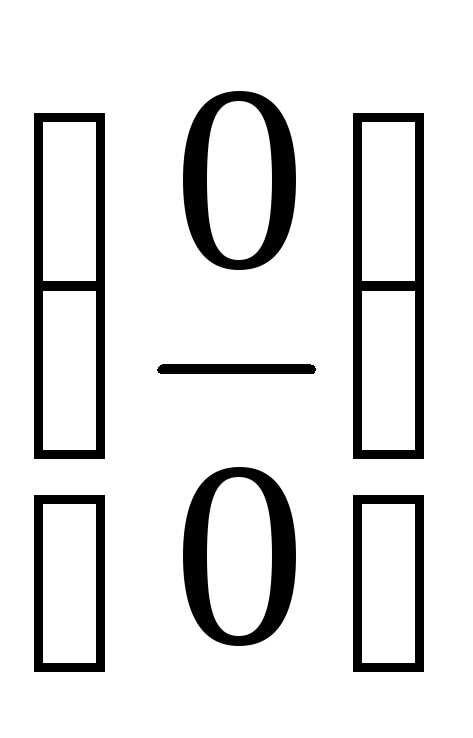 .
.
А) Если функция 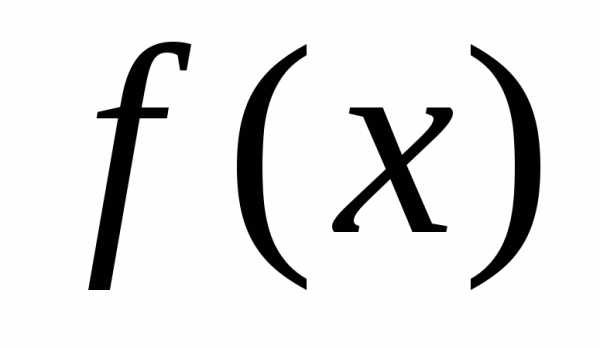 естьотношение
многочленов
естьотношение
многочленов 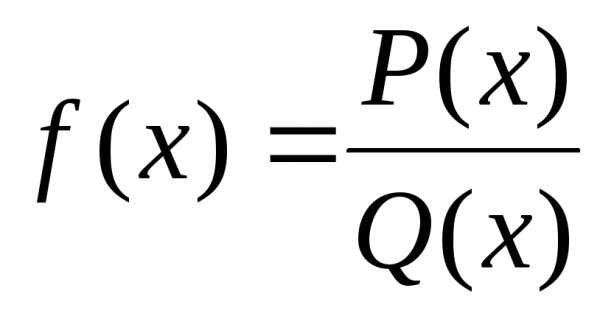 ,
то для раскрытия неопределенности
,
то для раскрытия неопределенности  нужно разложить многочлены
нужно разложить многочлены 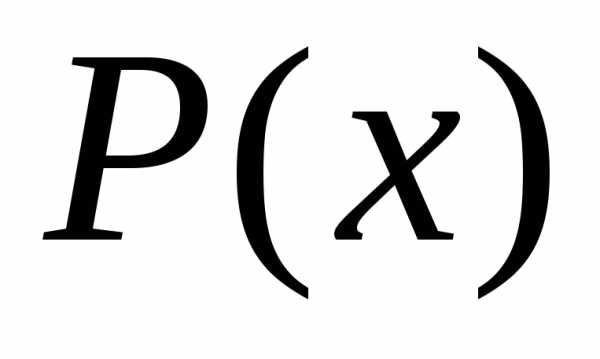 ина множители и сократить на множитель
ина множители и сократить на множитель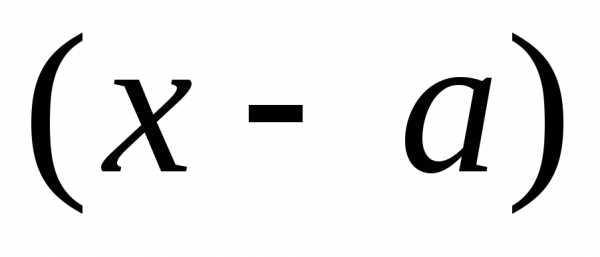 ,
стремящийся к нулю.
,
стремящийся к нулю.
Б) Если 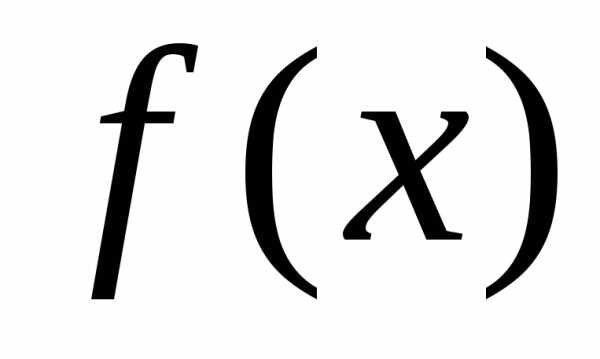 содержит
иррациональность,
то для раскрытия неопределенности
содержит
иррациональность,
то для раскрытия неопределенности  нужно избавиться от иррациональности
с помощью формул сокращенного умножения
и др.
нужно избавиться от иррациональности
с помощью формул сокращенного умножения
и др.
studfiles.net
Свойства пределов функции
Предел функции является в математическом анализе одним из основных понятий. Функция f(x) в точке х0 предел имеет L. Если все значения х достаточно близки к х0, то близко к L и значение f(x).
На бесконечности предел функции описывает поведение значения самой функции, когда аргумент ее становится бесконечно большим.
Предел функции обозначается в виде f(x) → L в случае, если х→а
К основным свойствам пределов функции относят:
- предел постоянной величины, который равен самой постоянной величины;
- предел суммы, который равен сумме пределов самих функций. Также по аналогии и предел разности функций равен разности пределов данных функций;
- предел суммы множества функций равен также сумме пределов таких функций. По аналогии рассчитывает и предел нескольких функций, который равен разности пределов данных функций;
- повышение предела произведения функции (постоянного коэффициента) на знак предела;
- произведению пределов функций равен предел произведения двух функций;
- расширенное свойство предела произведения, которое в том заключается, что предел произведения функций равен и произведению пределов данных функций;
- предел частного функций равен отношению пределов данных функций, но только в том случае, если предел знаменателя нулю не равен;
- предел функции степенной, где действительным числом является степень р;
- предел функции показательной, при которой основание b больше 0;
- предел функции логарифмической, в которой основание b больше 0;
- теорема «двух милиционеров», при которой «зажатой» остается функция f(x)между другими двумя функции, которые также стремятся к пределу А.
Все перечисленные свойства пределов позволяют исходный предел функции свести к уже известному, чтобы получить ответ.
Определение и свойства пределов | ||||||||||
| Число b называется пределом функции f(x) при x → a, если для любого ε > 0 сущестувует δ > 0 такое, что для любого x из δ-окрестности a (|x — a| | ||||||||||
| Запись: ∀ ε > 0 ∃ δ > 0 : |x — a| |f(x) — f(a)| | ||||||||||
Обозначение | ||||||||||
Свойства пределов | ||||||||||
| ||||||||||
| ||||||||||
| ||||||||||
| ||||||||||
Замечательные пределы | ||||||||||
| ||||||||||
| e = 2,718281828459045235360287471352662497757… | ||||||||||
Связь между десятичными и натуральными логарифмами | ||||||||||
| lg(x) = M ln(x), | ||||||||||
| где M = lg(e) = 0,43429448190325182765112891891666… |
mateshka.ru
4. Основные свойства пределов
Пусть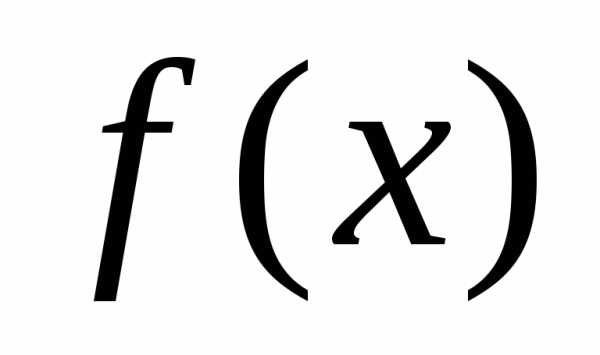 и
и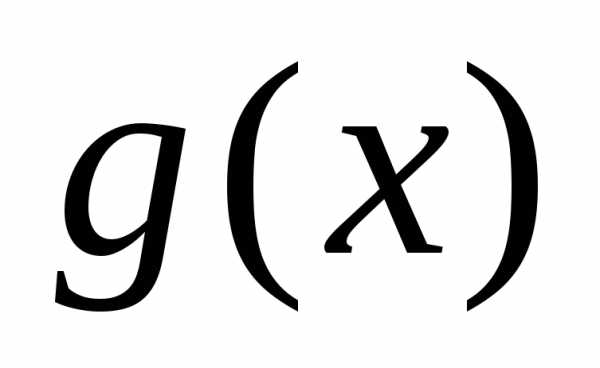 – функции, для которых существуют
пределы при
– функции, для которых существуют
пределы при (или при):,.
(или при):,.
Сформулируем основные свойства пределов.
1. Предел суммы функций равен сумме пределов этих функций, т.е.:
(4.13)
2. Предел произведения функций равен произведению пределов этих функций, т.е.:
(4.14)
3. Предел частного двух функций равен частному пределов этих функций (при условии, что предел делителя не равен нулю), т.е.:
(4.15)
4. Предел от константы равен данной константе:
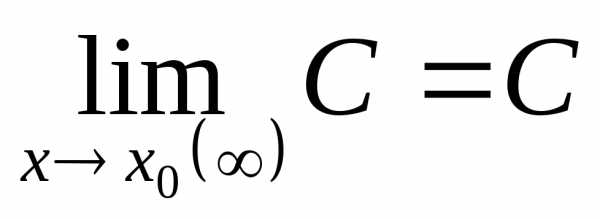 (4.16)
(4.16)
5. Если в некоторой окрестности точки x0 (или при достаточно больших x) , то:
(4.17)
6. Если , то:
(4.18)
5. Замечательные пределы
Первый замечательный предел:
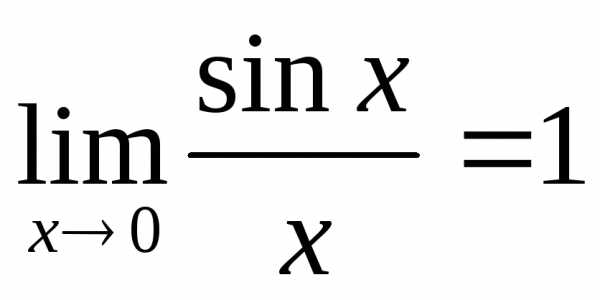 (4.19)
(4.19)
Второй замечательный предел:
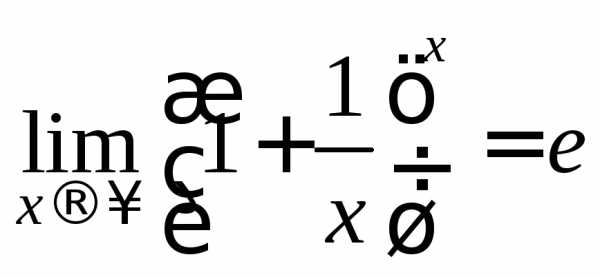 (4.20)
(4.20)
где e=2,718281… – трансцендентное число.
6. Способы вычисления пределов
Неопределенность
типа 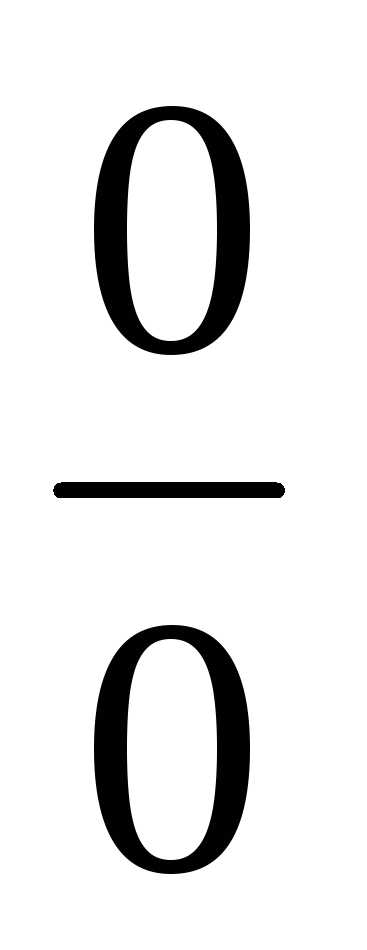 .
.
Пример 4.8. Вычислить 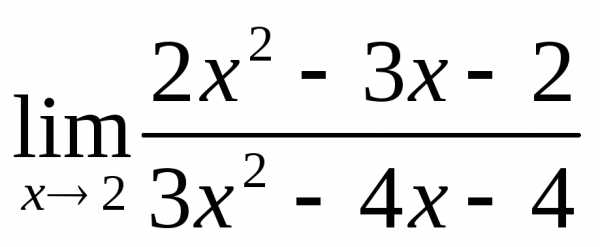 .
.
Решение:
Если подставить
в функцию вместо 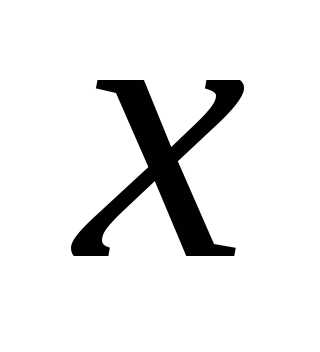 число 2, то и в числителе и в знаменателе
получатся нулю, т.е. появится неопределенность
вида
число 2, то и в числителе и в знаменателе
получатся нулю, т.е. появится неопределенность
вида 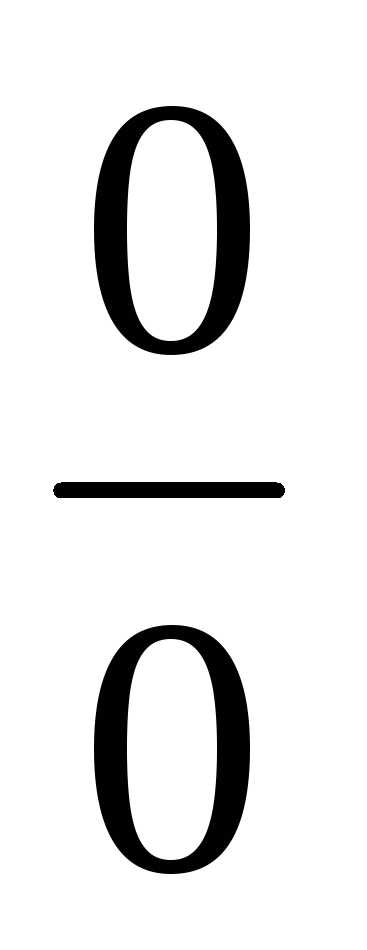 .
Чтобы вычислить предел необходимо
избавиться от данной неопределенности. Для этого надо представить числитель
и знаменатель в виде сомножителей:
.
Чтобы вычислить предел необходимо
избавиться от данной неопределенности. Для этого надо представить числитель
и знаменатель в виде сомножителей:
Здесь предварительно имеем: ,
где 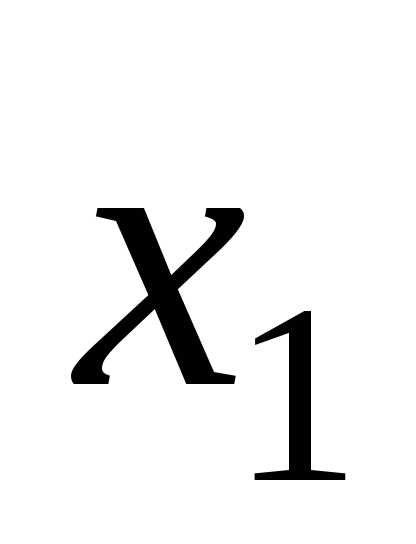 и
и 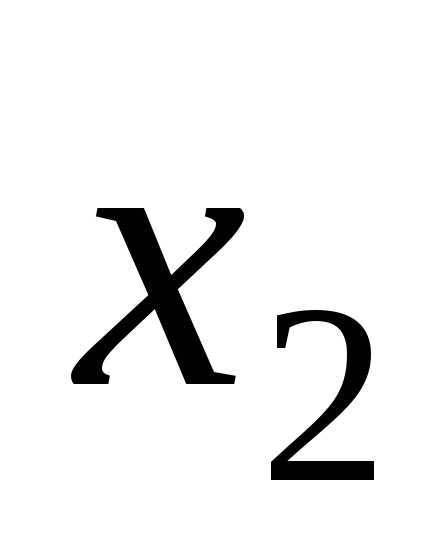 – корни квадратного трехчлена.
– корни квадратного трехчлена.
1) Числитель ; 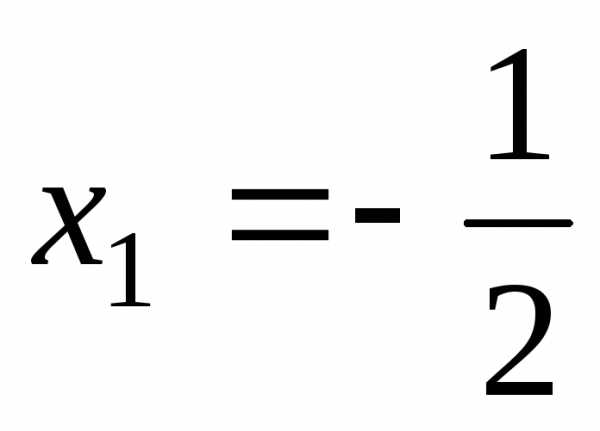 ;
;  ; .
; .
2) Знаменатель ; 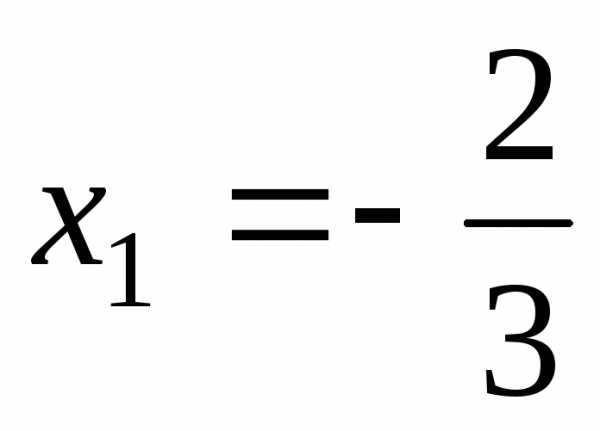 ;
; 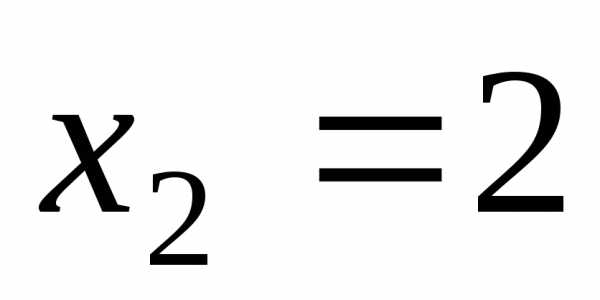 ; .
; .
Неопределенность
вида  .
.
Пример 4.9. Вычислить 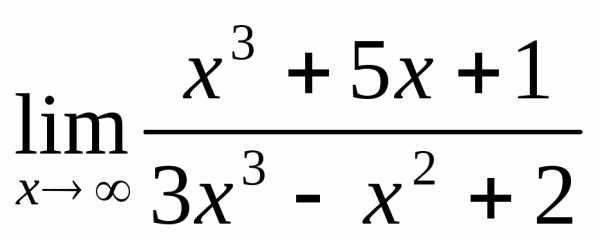 .
.
Решение:
При подстановке
в числитель и знаменатель  ,
появляется неопределенность вида
,
появляется неопределенность вида .
Избавиться от нее можно следующим
образом:
.
Избавиться от нее можно следующим
образом:
,
так как 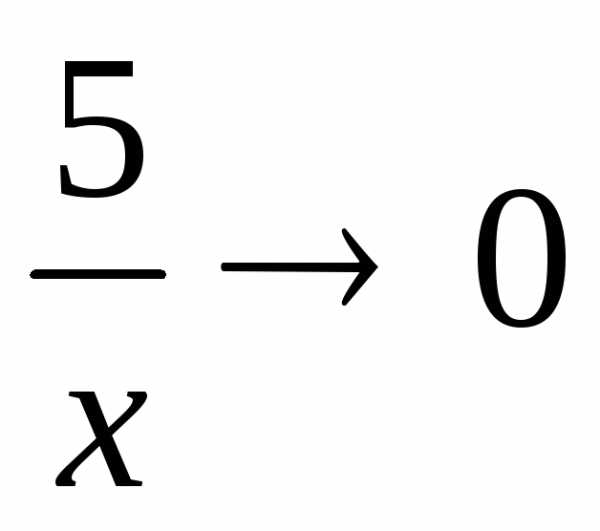 ;
; 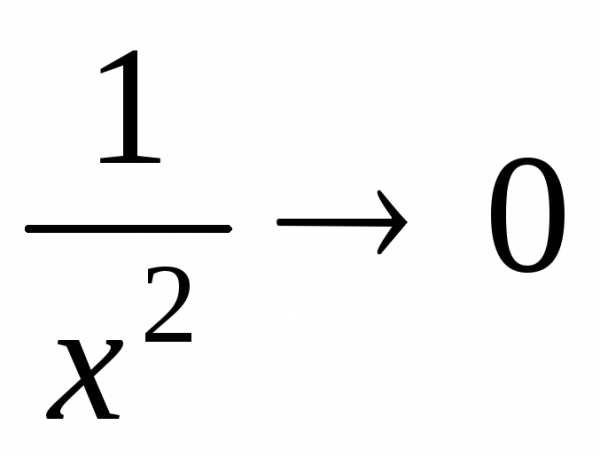 ;
; 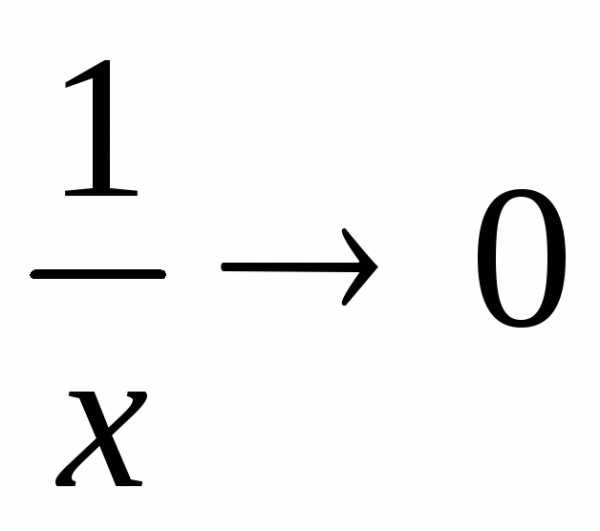 и
и 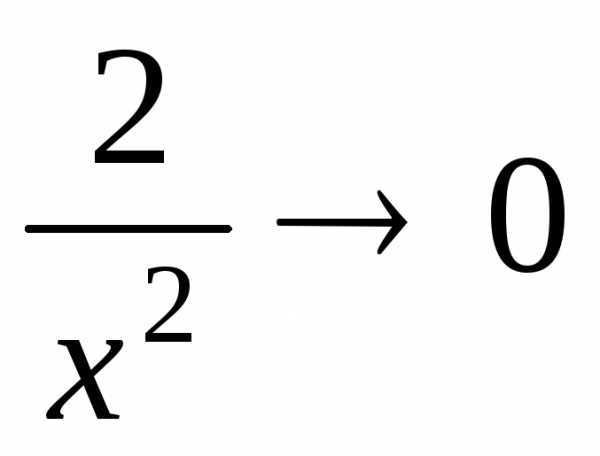 при .
при .
Контрольные вопросы
1. Сформулируйте понятие числовой последовательности. 2. Какая числовая последовательность называется ограниченной? 3. Приведите пример монотонной ограниченной числовой последовательности. 4. Приведите пример монотонной неограниченной числовой последовательности. 5. Какая точка называется предельной для данной числовой последовательности. 6. Сформулируйте теорему Больцано-Вейерштрасса. 7. Сформулируйте понятие предела числовой последовательности. 8. В чем заключается геометрический смысл предела числовой последовательности? 9. Сформулируйте понятие функции. Способы задания функции. 10. Сформулируйте понятие предела функции. 11. Запишите основные свойства пределов. 12. Запишите первый и второй замечательные пределы.
6
studfiles.net
Арифметические свойства предела функции (доказательства)
Пусть функции и определены на некоторой проколотой окрестности конечной или бесконечно удаленной точки . И пусть существуют конечные пределы:
и .
Тогда существует предел суммы (или разности) двух функций, и он равен сумме (или разности) их пределов:
; доказательство ⇓
существует предел произведения функций и он равен произведению их пределов:
; доказательство ⇓
если b ≠ 0, то существует предел частного функций и он равен частному их пределов:
. доказательство ⇓
В частности, если C – постоянная, то есть заданное число, то постоянную можно выносить за знак предела:
; доказательство ⇓
Предел абсолютного значения функции равен абсолютному значению ее предела:
если , то . Доказательство ⇓
Мы привели арифметические свойства пределов для двух функций. Методом математической индукции легко показать, что они выполняются и для конечного числа функций.
Так, если n функций имеют конечные пределы в точке , то предел их суммы или разности равен сумме или разности их пределов; предел произведения равен произведению пределов.
В частности, если существует конечный предел , то предел от функции , возведенной в натуральную степень n, равен пределу этой функции в степени n:
.
Такое равенство справедливо не только для натуральных показателей степени n, но здесь мы рассматриваем только следствия арифметических свойств.
Доказательство арифметических свойств
Теорема о пределе суммы (или разности) двух функций
Все формулировки ⇑ Пусть существуют конечные пределы функций:
и .
Тогда существует предел суммы (или разности) двух функций, и он равен сумме (или разности) их пределов:
.
Доказательство
Поскольку существуют пределы и , то существует такая проколотая окрестность точки , на которой функции и определены. Используем определение предела функции по Гейне. Пусть есть произвольная последовательность, сходящаяся к точке , элементы которой принадлежат проколотой окрестности . Тогда определены последовательности и . Поскольку и , то эти последовательности имеют пределы и .
Рассмотрим функцию , которая является суммой (или разностью) функций и . Используя свойство предела суммы и разности числовых последовательностей, имеем:
.
Поскольку есть произвольная последовательность, сходящаяся к и элементы которой принадлежат проколотой окрестности , то, согласно определению предела функции по Гейне,
, или
.
Теорема о пределе произведения двух функций
Все формулировки ⇑ Пусть существуют конечные пределы функций:
и .
Тогда существует предел произведения функций и он равен произведению их пределов:
.
Доказательство
Поскольку существуют пределы и , то существует такая проколотая окрестность точки , на которой функции и определены. Используем определение предела функции по Гейне. Пусть есть произвольная последовательность, сходящаяся к точке , элементы которой принадлежат проколотой окрестности . Тогда определены последовательности и . Поскольку и , то эти последовательности имеют пределы и .
Рассмотрим функцию . Используя свойство предела произведения числовых последовательностей, имеем:
.
Поскольку есть произвольная последовательность, сходящаяся к , элементы которой принадлежат проколотой окрестности , то, согласно определению предела функции по Гейне,
, или
.
Теорема о пределе частного двух функций
Все формулировки ⇑ Пусть существуют конечные пределы функций:
и .
Тогда, если b ≠ 0, то существует предел частного функций и он равен частному их пределов:
.
Доказательство
Поскольку существуют пределы и , то существует такая проколотая окрестность точки , на которой функции и определены. Используем определение предела функции по Гейне. Пусть есть произвольная последовательность, сходящаяся к точке , элементы которой принадлежат проколотой окрестности, на которой определены функции и . Тогда определены последовательности и . Поскольку и , то эти последовательности имеют пределы и .
Рассмотрим функцию . По условию, . Воспользуемся теоремой об ограниченности снизу функции, имеющей конечный ненулевой предел. Согласно этой теореме, существует такая проколотая окрестность точки , на которой . Отсюда следует, что существует такая проколотая окрестность этой точки, на которой .
Пусть есть проколотая окрестность точки , на которой определены функции и , и на которой . Используя свойство предела частного числовых последовательностей, имеем:
.
Поскольку есть произвольная последовательность, сходящаяся к , элементы которой принадлежат проколотой окрестности , то, согласно определению предела функции по Гейне,
, или
.
Теорема о вынесении постоянной за знак предела
Все формулировки ⇑ Пусть существует конечный предел функции:
.
И пусть C – постоянная, то есть заданное число. Тогда постоянную можно выносить за знак предела:
.
Доказательство
Введем постоянную функцию , значения которой для всех x равны некоторому числу C. Согласно свойству о пределе постоянной функции,
.
Используя доказанное только что свойство предела произведения двух функций, имеем:
.
Теорема о пределе абсолютного значения функции
Все формулировки ⇑ Пусть существует конечный предел функции:
.
Тогда существует предел абсолютного значения функции, равный абсолютному значению ее предела:
.
Доказательство
Поскольку существует предел , то существует такая проколотая окрестность точки , на которой функция определена. Используем определение предела функции по Гейне. Пусть есть произвольная последовательность, сходящаяся к точке , элементы которой принадлежат проколотой окрестности . Тогда определена последовательность . Поскольку , то эта последовательность имеет предел .
Используя свойство предела последовательности, состоящей из элементов, взятых по модулю, имеем:
.
Поскольку есть произвольная последовательность, сходящаяся к , элементы которой принадлежат проколотой окрестности , то, согласно определению предела функции по Гейне,
.
Пример
Найти предел функции
.
Решение
Воспользуемся тем, что .
Последовательно применяем арифметические свойства пределов функции.
;
;
;
;
.
Ответ
.
Использованная литература:
С.М. Никольский. Курс математического анализа. Том 1. Москва, 1983.
Автор: Олег Одинцов. Опубликовано: Изменено:
1cov-edu.ru
Свойства пределов функции.
1. Если
и на
некоторой окрестности 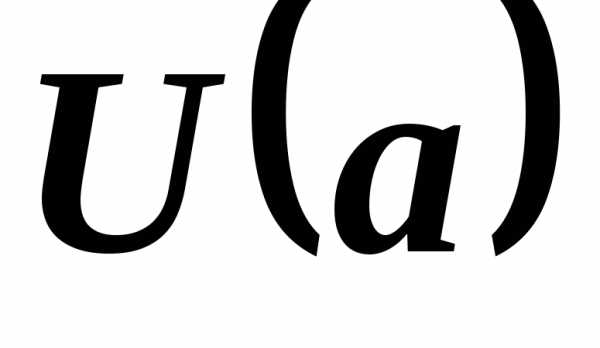 ,
,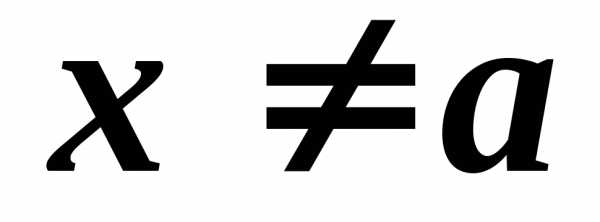 ,,
то
,,
то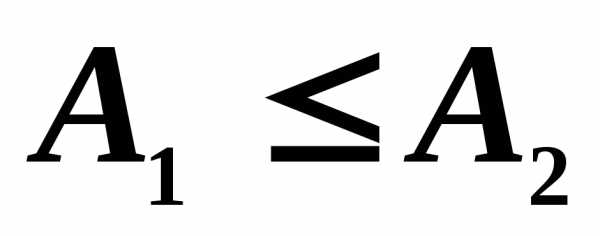 .
.
2. Если
и на
некоторой окрестности 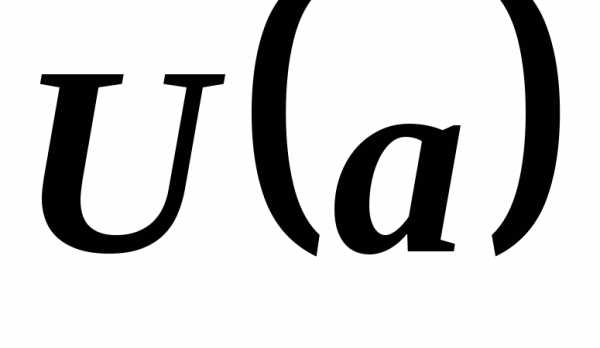 ,
, ,,
то.
,,
то.
3.
Пусть
,
где и
и — конечные числа. Тогда
— конечные числа. Тогда
5. Признаки существования пределов
Теорема
1.
Если
,
где- конечное число, то на некоторой
окрестности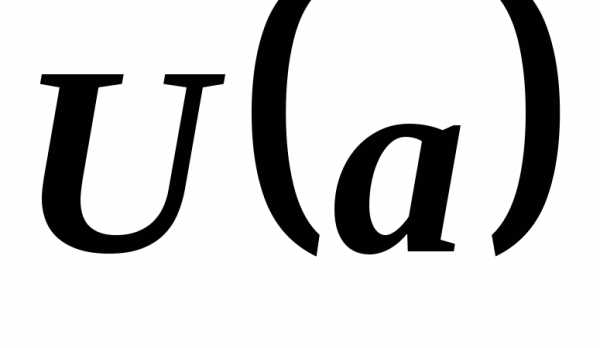 функция
функция ограничена, т.е. существует положительное
числотакое, что
ограничена, т.е. существует положительное
числотакое, что
Теорема
3.
(критерий Коши существования предела).
Для того чтобы существовал предел
(конечный) 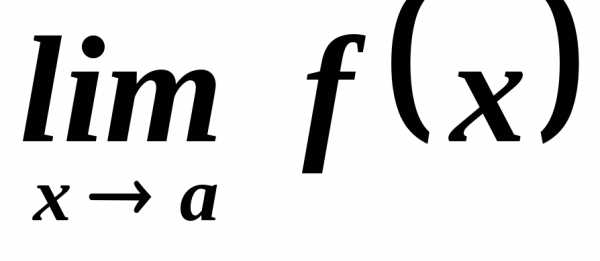 ,
необходимо и достаточно, чтобы функция
,
необходимо и достаточно, чтобы функция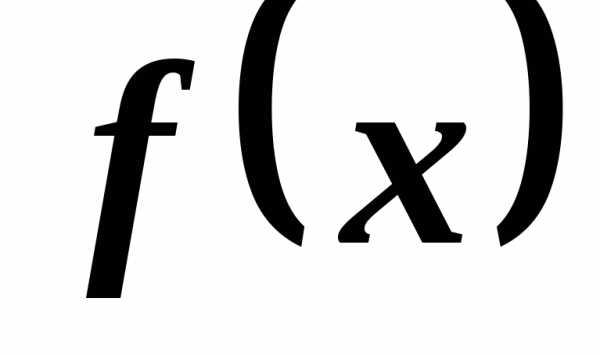 была определена в окрестности
была определена в окрестности ,
за исключением, быть может, самой точки
,
за исключением, быть может, самой точки ,
и для всякого
,
и для всякого существовала такая окрестность
существовала такая окрестность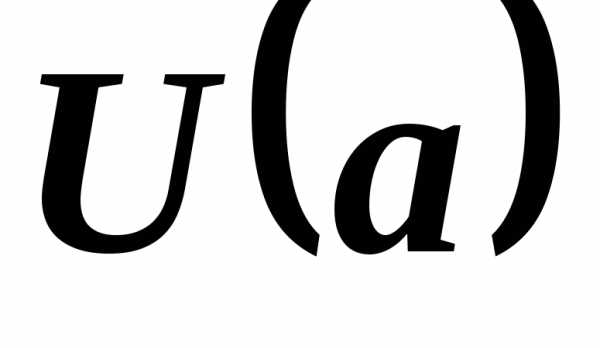 ,
что, каковы бы не были точки
,
что, каковы бы не были точки
Односторонние пределы
По
определению число  называется пределом функции
называется пределом функции в точке
в точке справа (слева), если она определена на
некотором полуинтервале
справа (слева), если она определена на
некотором полуинтервале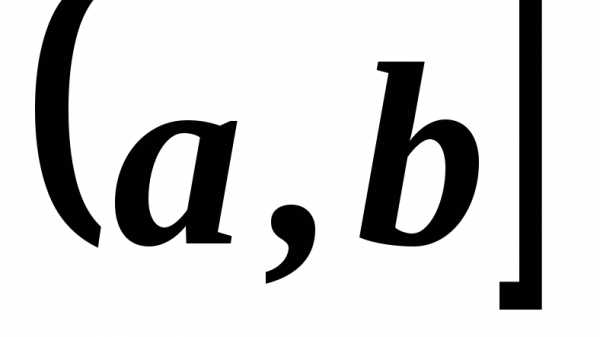 (
(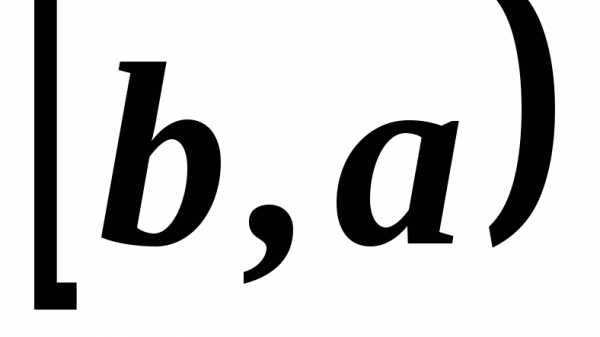 )
и для нее существует
)
и для нее существует
для
любой указанной последовательности 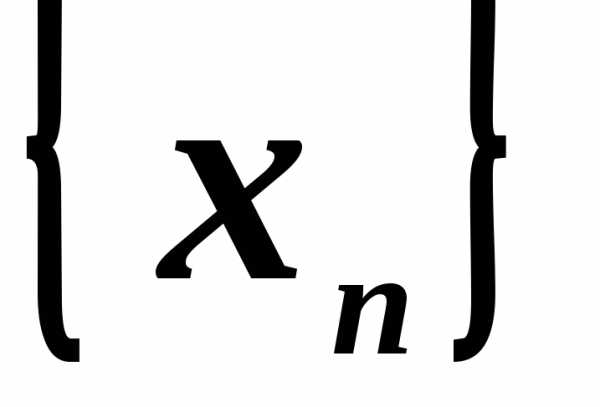 .
.
Предел
справа (слева) функции  в точке
в точке принято обозначать так:
принято обозначать так:
Если  определена на интервале
определена на интервале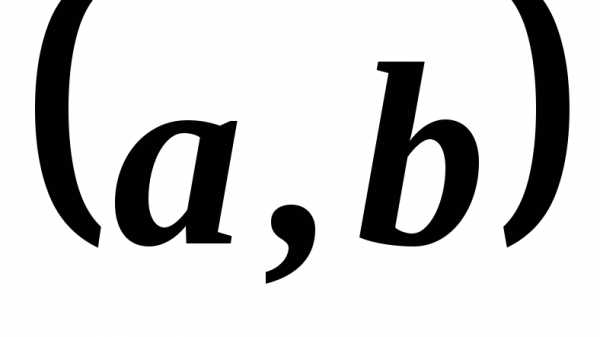 ,
то в точке
,
то в точке может иметь смысл только число
может иметь смысл только число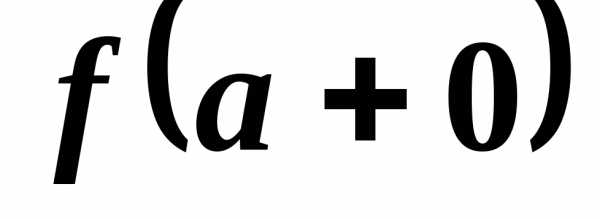 ,
а в точке
,
а в точке — только число
— только число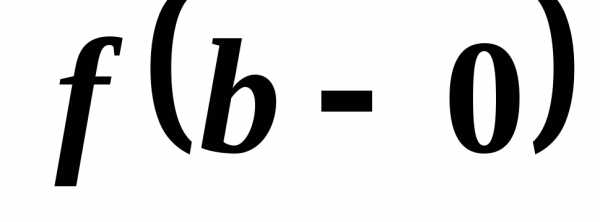 .
.
Равенства эквивалентны существованию предела.
6. Бесконечно большие и бесконечно малые функции
Функцию,
для которой
называется бесконечно большой при .
.
Функцию,
для которой
называется бесконечно малой при .
.
Свойства бесконечно малых величин.
1. Сумма бесконечно малых величин есть бесконечно малая величина.
2. Произведение двух бесконечно малых величин есть бесконечно малая величина.
3. Произведение бесконечно малой величины на константу есть бесконечно малая величина.
Свойство 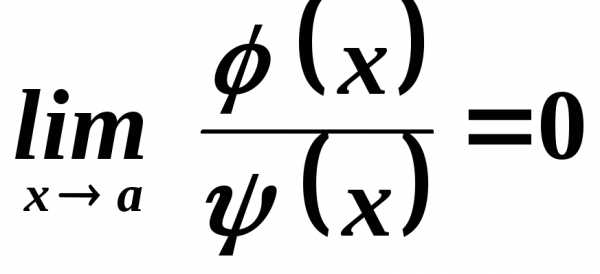 отражает тот факт, что функцию
отражает тот факт, что функцию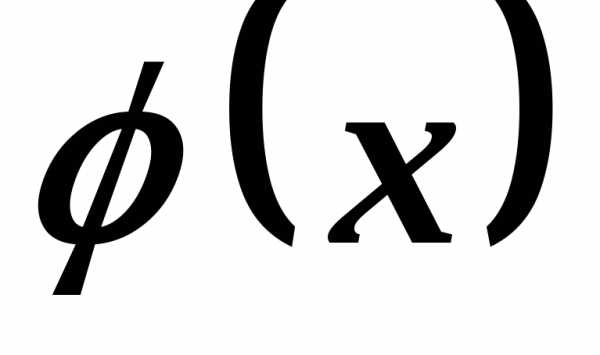 можно записать в виде,
где
можно записать в виде,
где при
при .
.
Если
функции  и
и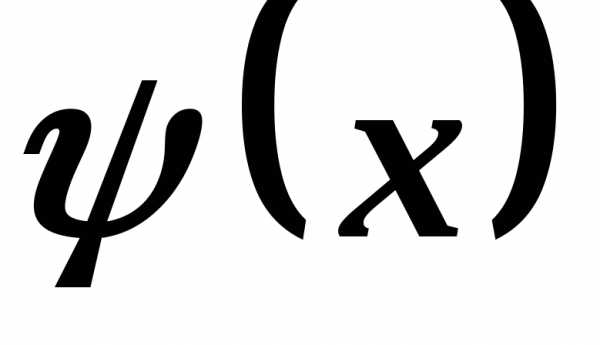 сами бесконечно малые, то символ
сами бесконечно малые, то символ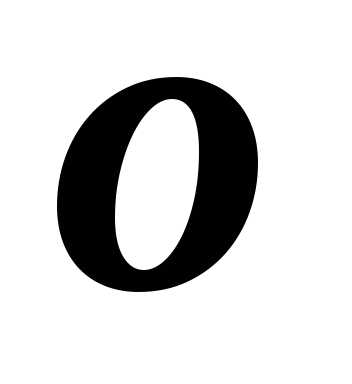 (по старинной терминологии) означает
бесконечно малую, более высокого порядка
.
(по старинной терминологии) означает
бесконечно малую, более высокого порядка
.
Если
функции 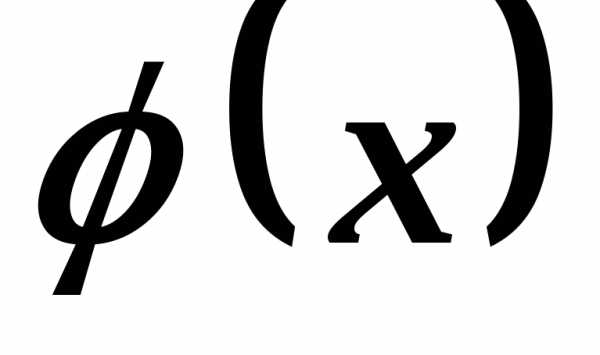 и
и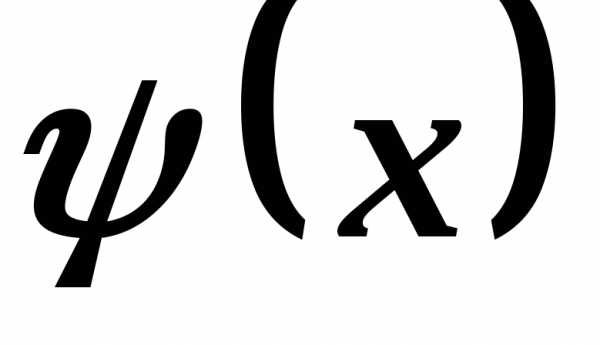 суть бесконечно большие, то символ
суть бесконечно большие, то символ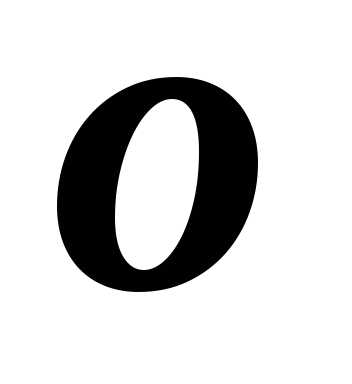 (по старинной терминологии), означает
бесконечно большую более высокого
порядка .
(по старинной терминологии), означает
бесконечно большую более высокого
порядка .
Кроме того, пишут
и
называют функции 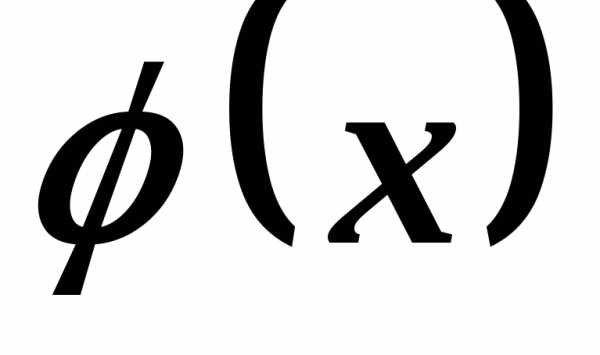 и
и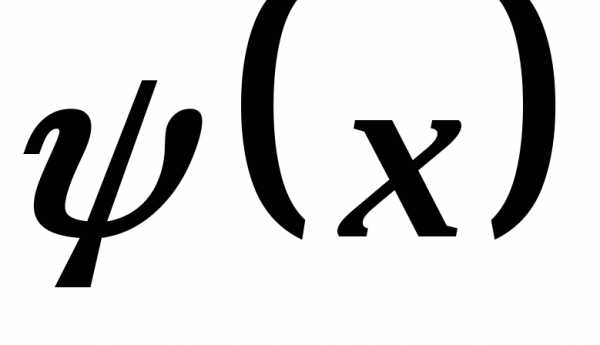 эквивалентными (асимптотически равными)
при
эквивалентными (асимптотически равными)
при ,
если выполняется свойство:
,
если выполняется свойство:
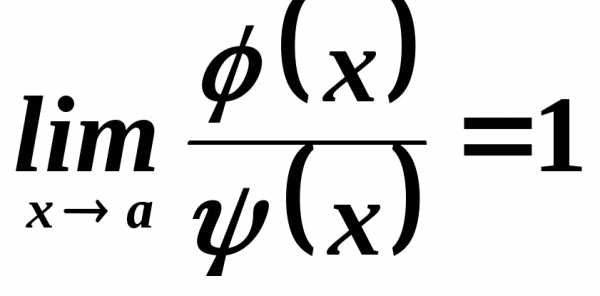
Например.
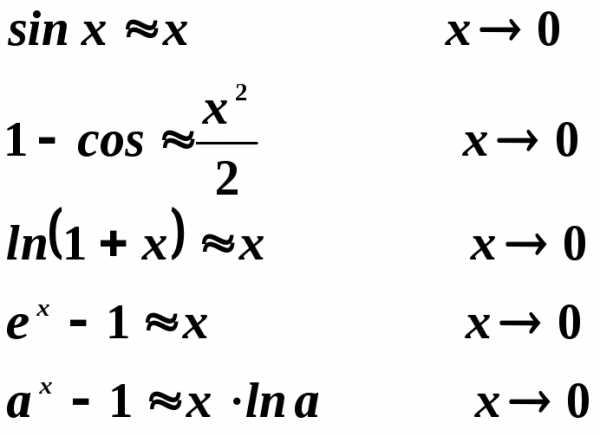
7. Замечательные пределы
1. 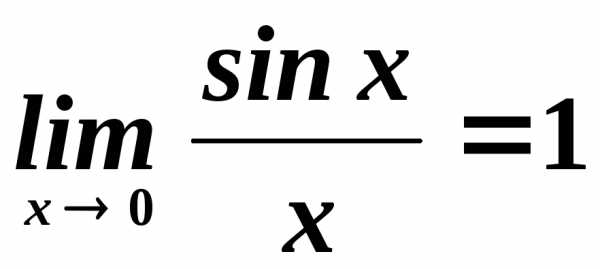
Так
как функция
является непрерывной, топри .
Поэтому выражение
.
Поэтому выражение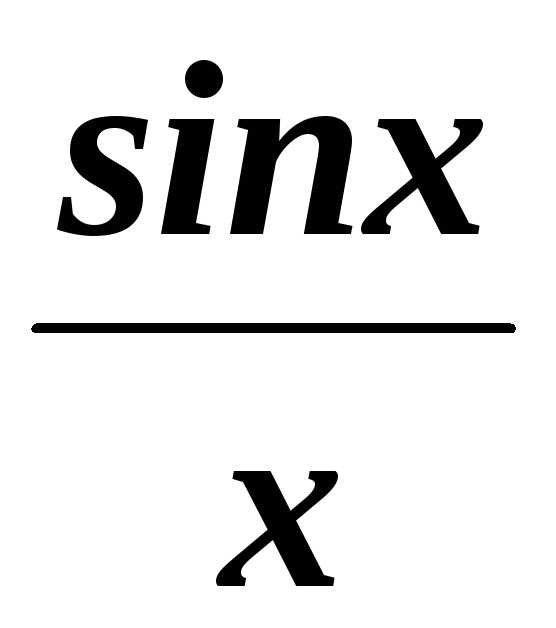 представляет собой неопределенность
типа
представляет собой неопределенность
типа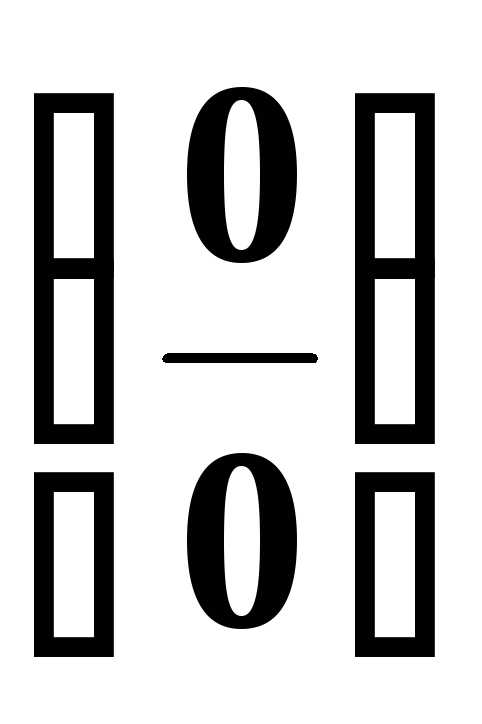 .
Предел раскрывает эту неопределенность.
.
Предел раскрывает эту неопределенность.
2. 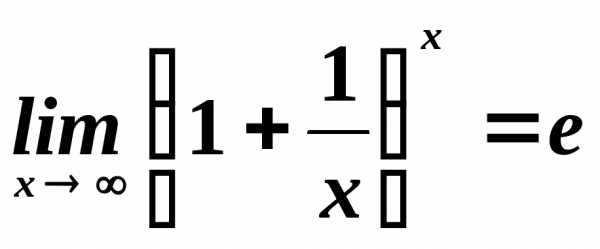
Пример. . Получается из второго замечательного предела заменой.
Пример. 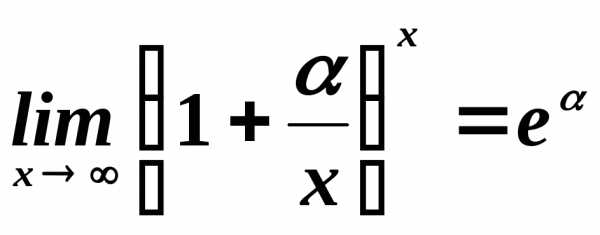
Если
,
то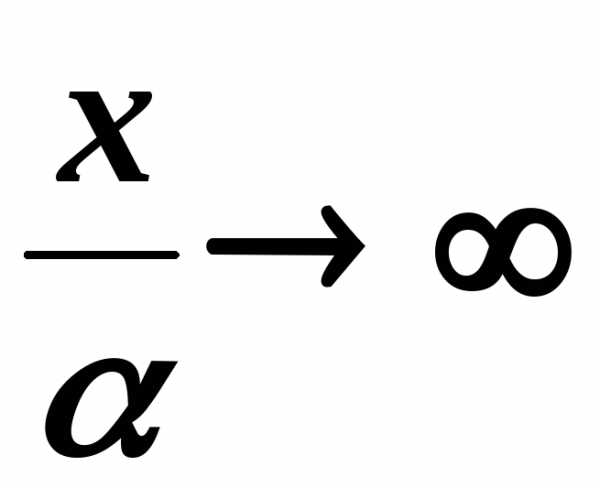 и
и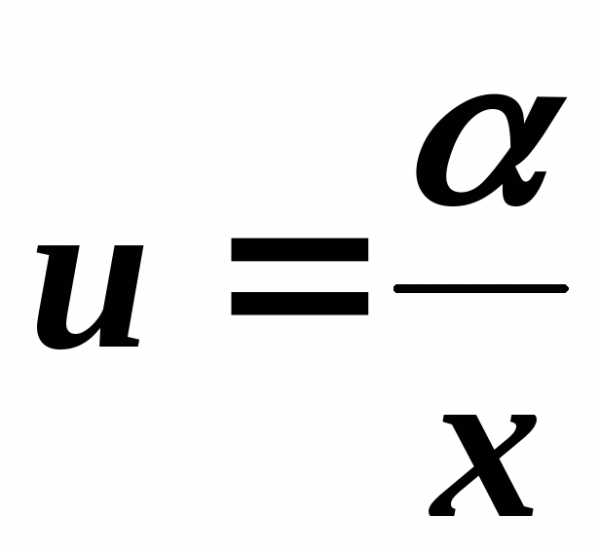
Пример.  ,.
,.
Доказательство.
Пример. ,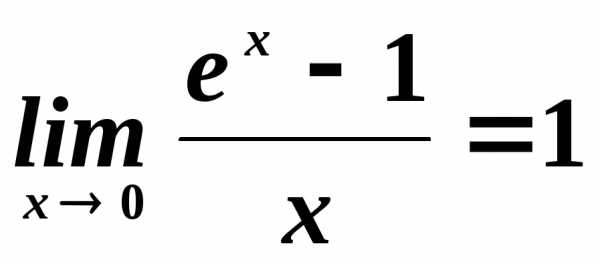 .
.
Доказательство. Положим . Тогда
8. Непрерывные функции. Определение непрерывности с помощью приращений.
На
рисунке изображен график функции .
Зададим точку.
Близкая ей точка,
где
.
Зададим точку.
Близкая ей точка,
где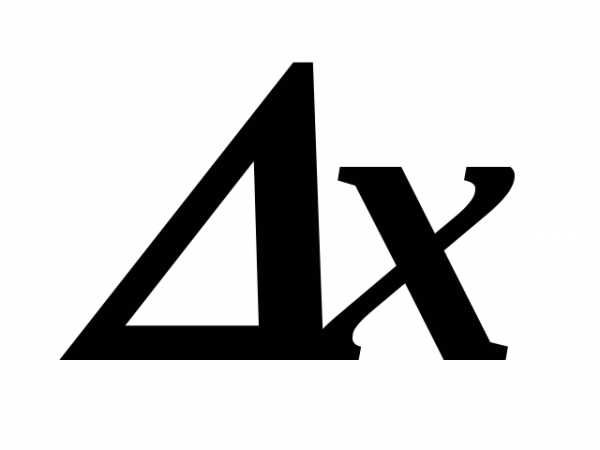 — приращение
— приращение .
Разность
.
Разность
называется
приращением функции  в точке
в точке ,
соответствующим приращению
,
соответствующим приращению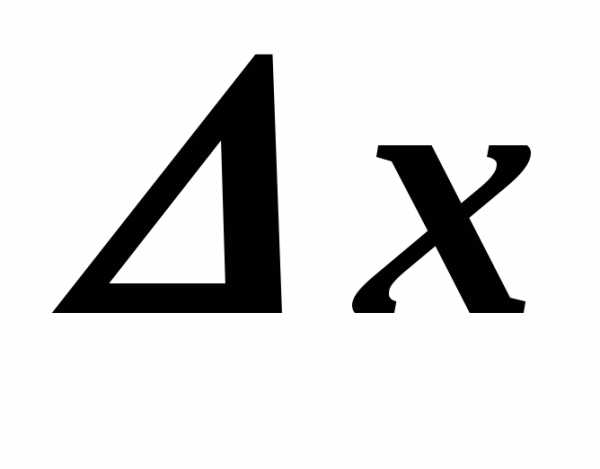 .
На рисунке,.
.
На рисунке,.
Будем
стремить 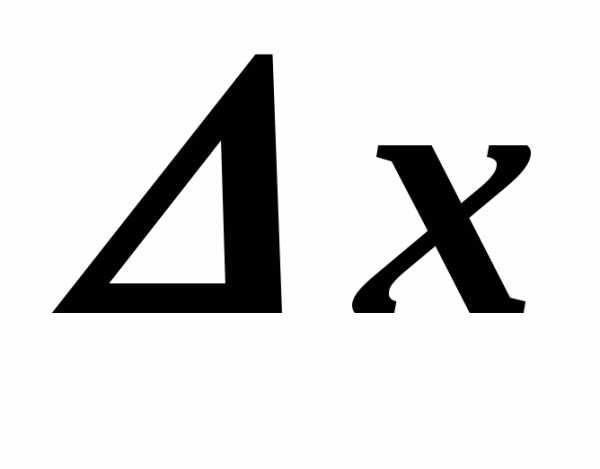 к нулю. Тогда для рассматриваемой функции
и
к нулю. Тогда для рассматриваемой функции
и будет стремиться к нулю
будет стремиться к нулю
Рассмотрим
теперь график другой функции
.
Придадим теперь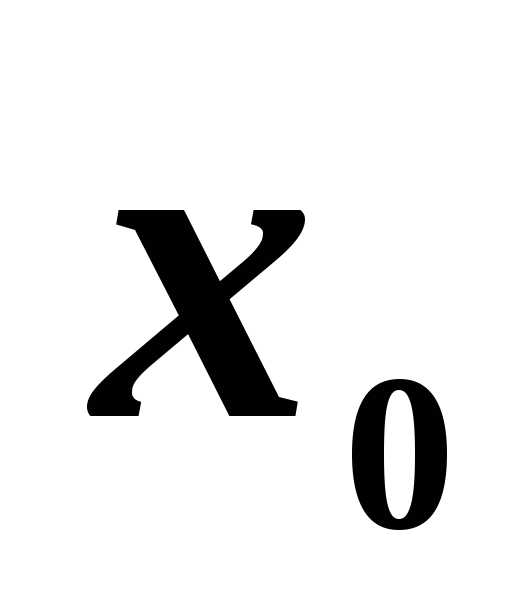 приращение
приращение и определим соответствующее приращение
функции
и определим соответствующее приращение
функции
Если
мы будем  стремить к нулю, то теперь уже нельзя
сказать, что
стремить к нулю, то теперь уже нельзя
сказать, что стремится к нулю.
стремится к нулю.
Теперь можно дать определение.
Функцию  ,
заданную на отрезке
,
заданную на отрезке ,
называютнепрерывной в точке
,
называютнепрерывной в точке  этого отрезка, если приращение ее в этой
точке, соответствующее приращению
этого отрезка, если приращение ее в этой
точке, соответствующее приращению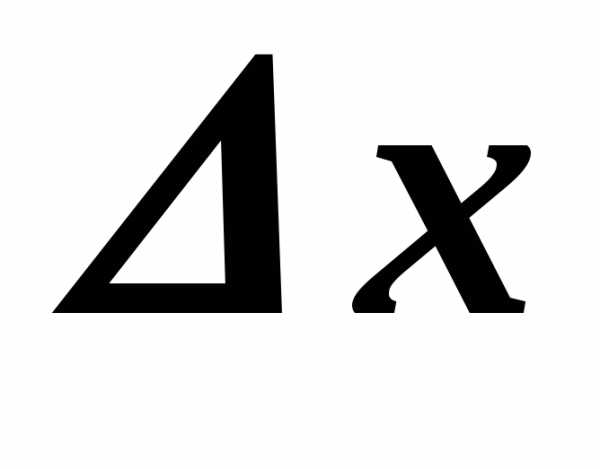 ,
стремится к нулю при любом способе
стремления
,
стремится к нулю при любом способе
стремления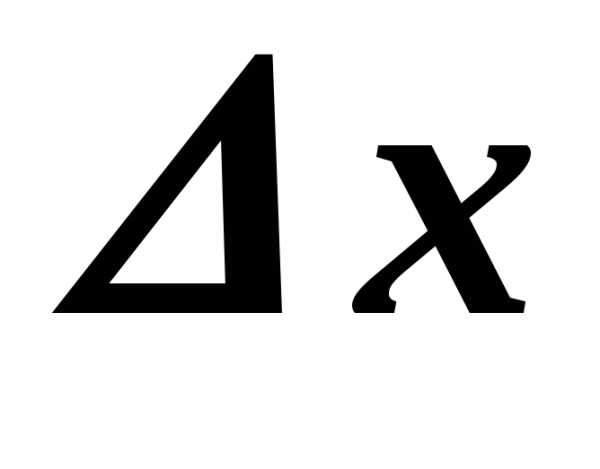 к нулю.
к нулю.
Это
свойство непрерывности  в точке
в точке записывают в виде
записывают в виде
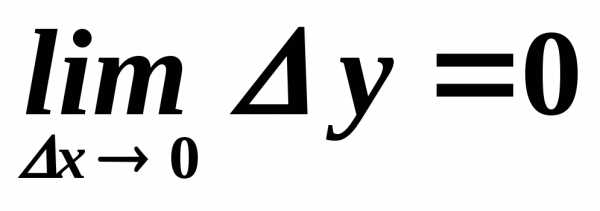
В противном случае функция называется разрывной.
Функция непрерывная в любой точке отрезка (интервала), называется непрерывной на этом отрезке (интервале).
Функция 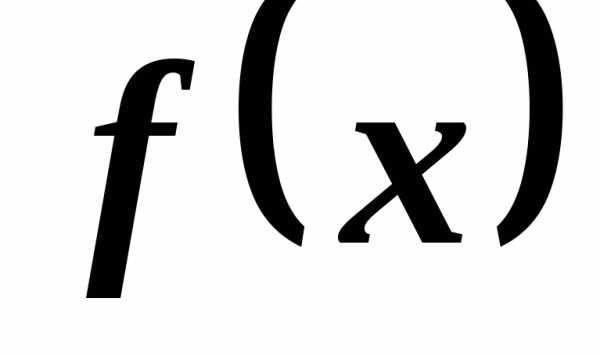 называется непрерывной в точке
называется непрерывной в точке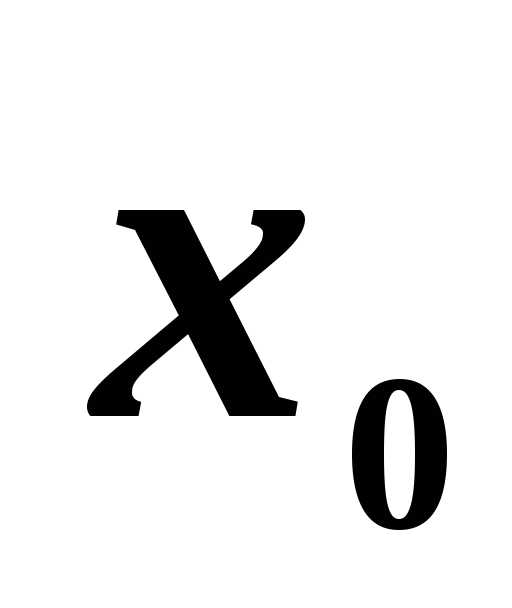 ,
если она определена в некоторой
окрестности этой точки, в том числе и в
самой точке
,
если она определена в некоторой
окрестности этой точки, в том числе и в
самой точке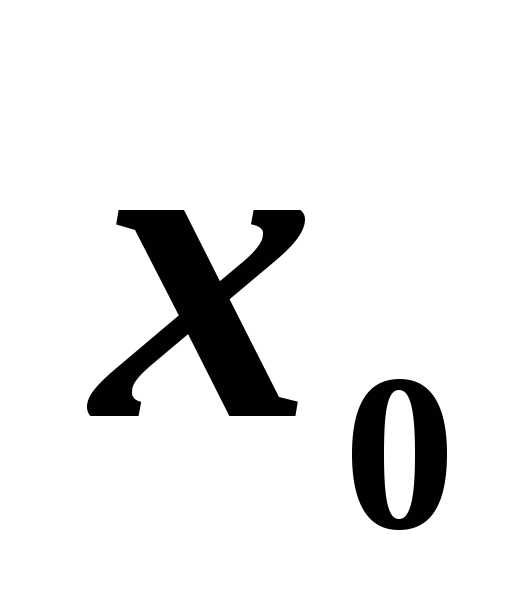 ,
и если ее приращение в этой точке,
соответствующее приращению аргумента
,
и если ее приращение в этой точке,
соответствующее приращению аргумента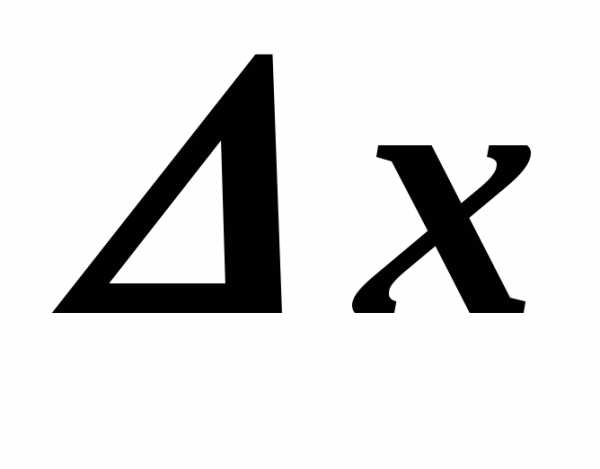 ,
стремится к нулю при
,
стремится к нулю при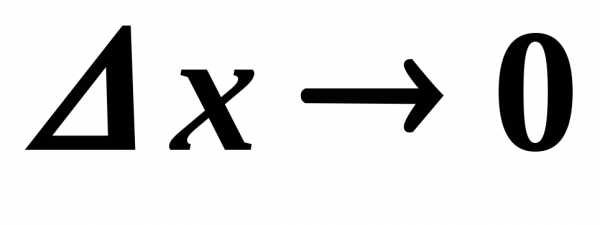
Либо ;;
.
Пример.
Функция
непрерывна для любого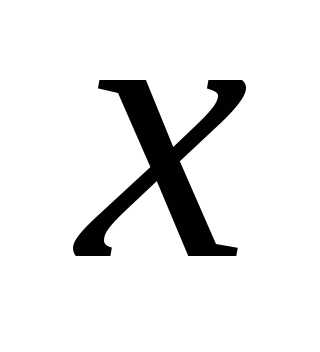 .
В самом деле.
.
В самом деле.
Но для
любого  имеет место неравенство
имеет место неравенство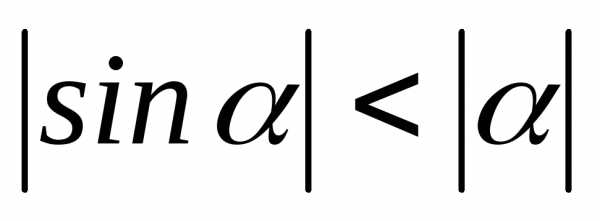 .
Если
.
Если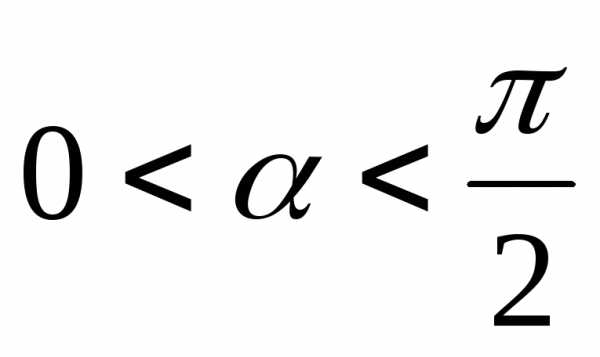 ,
то это следует из рисунка (длина дуги
больше стягивающей ее хорды). Отсюда
следует
,
то это следует из рисунка (длина дуги
больше стягивающей ее хорды). Отсюда
следует
Но
тогда, очевидно, 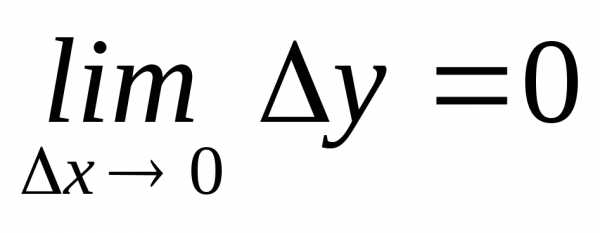 .
Что и требовалось доказать.
.
Что и требовалось доказать.
Т. Если
функции  и
и непрерывны в точке
непрерывны в точке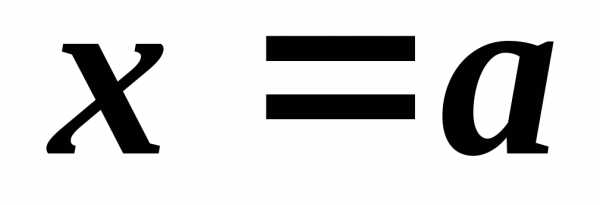 ,
то непрерывны также в этой точке их
сумма, разность, произведение и частное
(при
,
то непрерывны также в этой точке их
сумма, разность, произведение и частное
(при ).
).
Пример. Функция непрерывна. Она является композицией двух непрерывных функций:, и.
studfiles.net
Понятие предела функции, свойства пределов
В экономических, социологических и математических прогнозах, имеющих связь с непрерывными процессами, при вычислении финансовой ренты, банковских процентов, построении асимптот для разнообразных графиков при исследовании их свойств нередко требуются знания о том, что такое предел функции. Понятие это на уровне интуитивного восприятия использовалось, начиная с конца XVII века, многими знаменитыми учеными, математиками, механиками, физиками, астрономами, в их замечательных исследованиях. Новатором в данном вопросе являлся еще Исаак Ньютон. Его примеру последовали вскоре знаменитые Эйлер, Лагранж и другие гениальные научные деятели. Но первые конкретные определения в данной области в XIX веке дали чешский ученый Больцано и математик из Франции Луи Коши (его портрет представлен ниже).

Числовые ряды
Понятия предела последовательности и предела функции тесно связаны между собой. И это вполне естественно. Действительно, ведь если некоторая функция строится из определенного ряда, значения которого находятся при возрастании натуральных чисел от 1 до ∞, это и есть числовая последовательность.
Приведем конкретный пример. Пусть некоторый ряд чисел задан выражением:
an = (n2 + n + 1) / (n + 2).
Выясним первые пять составляющих этой последовательности. Ими оказываются числа: 1; 7/4; 13/5; 21/6; 31/7. Можно продолжить этот ряд. И нетрудно понять, что любое последующее число окажется больше предыдущего, а значение каждого из них будет приближаться к бесконечности. Она-то и станет пределом этой последовательности.
Ниже представлен портрет Бернарда Больцано, внесшего большой вклад в исследование множеств и их пределов, автора научного труда «Парадоксы бесконечного».

Предел числового ряда
Последовательности типа, о которой говорилось выше, принято именовать бесконечно большими. Это и значит, что предел их равен ∞. Но числовой ряд, задаваемый обратной формулой, то есть 1/an, в математике называется бесконечно малым, потому что значения каждого из последующих чисел становятся все меньше, стремясь к нулю.
Существуют и другие типы последовательностей. К примеру, ряд, заданный выражением an = 105 — 7n, приближается по значению членов не к нулю, а к бесконечности, только отрицательной. И начиная с n = 16, составляющие числового ряда обретают минусовые значения, поэтому он не считается возрастающим, как в первом случае, и называется убывающим.
Ряд, определяемый выражением an = 1 / 2n, является бесконечно малым. Но в данном случае последовательность, заданная обратной формулой, будет, напротив, бесконечно большой.
Числовые ряды могут стремиться не только к 0 и ∞, а к какому-то определенному числу. Можно указать сколько угодно таких последовательностей. К примеру, предел an = 5n / (n + 1) равен 5.
Возможно, что последовательность и вовсе не имеет предела, тогда ее именуют расходящейся.
Понятие предела функции

Из приведенного определения несложно понять, что аналогично последовательностям рассматривается вопрос, а также когда дело касается функций. Хотя здесь есть свои особенности. Если аргумент (то есть значение переменной х) стремится к некоему определенному числу или к бесконечности, то значение функции тоже может стремиться к какой-то определенной величине. И в случае, когда таковая существует, она-то и считается пределом. Но лучше и удобнее рассмотреть этот процесс наглядно на графике, тем самым выяснив понятие предела функции и его геометрический смысл.

Вполне допустимы случаи, когда функция и вовсе не определена в той самой точке своего предела или значение ее не является эквивалентным ему. Тем не менее предел все равно считается существующим и равным А.
Фантастический пример для разъяснения
Рассмотрим немаловажный вопрос: а может ли у функции в выбранной точке быть два предела? Нет, это никак невозможно. Если он существует, то обязательно является единственным.
По сути предел является некоей величиной, к которой стремится приблизиться функция. Значения ее подходят к ней сколько угодно невероятно близко, но не в состоянии этой величины достигнуть, и находятся постоянно лишь только в какой-то «окрестности» числа, выражающего ее значение.

Для наглядности пояснения понятия предела функции можно рассмотреть некоторую фантастическую ситуацию. Допустим, бегун, стремясь достигнуть финиша, по велению всемогущего волшебника постоянно уменьшается, поэтому делает все более мелкие шаги (величина их стремится к нулю). По причине такого колдовства, все упорней продвигаясь к заветной цели, этот рекордсмен, тем не менее, не станет победителем, потому что не в состоянии пересечь финишную черту.
Обозначения и свойства
Пределы принято указывать буквами lim. Стрелочка ниже их дает представление о величине, к которой стремится аргумент. Справа от символа предела пишут саму функцию. Далее обычно следует знак равенства и указывается числовое значение предельной величины. Такие обозначения используются во всем мире. Для уяснения понятия предела функции свойства пределов знать просто необходимо. Они приведены ниже.

Такие свойства означают, что при сложении функций, имеющих предел, для нахождения общего lim необходимо сложить пределы каждой из них. То же самое касается произведения и частного двух функций. Последнее же приведенное свойство гласит, что за знак предела можно вынести общий множитель, что не нарушает равенство в выражениях с пределами.
Примеры
Рассмотрим некоторые задачи нахождения предела функции в точке и на бесконечности. Понятия, описанные выше, тогда станут гораздо ясней.
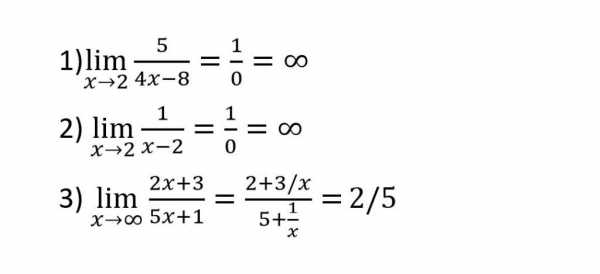
Предел в первых двух примерах считается равным бесконечности ввиду того, что при стремлении аргумента к указанной величине знаменатель в обоих случаях превращается в нечто бесконечно малое. А это значит, что само выражение, напротив, становится бесконечно большим. В этом и заключается секрет решения подобных примеров.
В третьем случае предел равен некоторому определенному числу. Если решать задачу без всяких хитростей, просто подставив вместо х бесконечность, то само выражение под знаком предела примет вид: (∞/∞). А это неопределенность. Ввиду этого для решения подобных примеров прибегают к распространенному приему, разделив обе части дроби на х. Таким образом величины 3/x и 1/x в предельной точке становятся настолько малы, что величины их для получения значения третьего выражения становятся не важными. Поэтому в ответе и выходит 2/5.
Виды неопределенностей
В последнем примере, рассмотренном нами выше, нахождение предела оказалось затруднено из-за выявленной в процессе вычислений неопределенности. Подобные случаи особенно исключительными и редкими не являются. При решении самых разных задач могут возникнуть и другие виды неопределенностей. Понятие предела функции поможет научиться выходить из таких ситуаций, только следует усвоить некоторые приемы, помогающие избавиться от указанных проблем.
А теперь рассмотрим еще ряд аналогичных примеров.

В первом случае никаких сложностей в нахождении результата не возникает. Здесь просто нужно подставить предельное значение переменной х в само выражение и получить ответ.
А вот во втором примере выявляется неопределенность уже рассмотренного нами типа: (∞/∞). Для выхода из сложной ситуации воспользуемся приемом, похожим на уже нами примененный ранее. А именно поделим в выражении числитель и знаменатель на х7. И тогда дробь примет вид, при котором некоторые члены выражения превратятся в величины бесконечно малые, а из значимых чисел останется только 1/3. Оно и будет пределом исходной функции.
Метод преобразования выражений
Продолжим рассматривать понятие предела функции.
В третьем и четвертом примерах, указанных выше, если подставить придельное значение в верхнюю и нижнюю часть дроби, возникает неопределенность другого рода (0/0). Как известно, в математике это недопустимо. В таких ситуациях можно применить метод преобразования выражений.
В задании № 3 для начала числитель раскладывают как разность квадратов. А потом, произведя сокращения, подставляют в выражение х=1. Таким образом и получают ответ. Как видно из примера, предел функции равен 0.
Задание № 4 немного сложней. Здесь дробь тоже необходимо сократить. Но для разложения на множители числителя и знаменателя сначала решают квадратные уравнения. Далее находятся корни, и производится разложение на множители способом, как это обычно делают в квадратных трехчленах. Тогда под знаком предела остается только выражение: (x — 3) / (3x — 2). Теперь следует подставить значение переменной и узнать, что предел равен 4.
Непрерывность
Связывая понятие пределов и непрерывность функции одной переменной, поясним сразу некоторые важные моменты, уточнив, что второе из этих математических представлений обычно определяется через первое.

В случае, если все только что обозначенные условия выполняются, то можно утверждать с полной уверенностью, что функция в некой, заранее заданной точке является непрерывной. Когда же хотя бы один из пунктов нарушается, это значит, что линия графика в указанном месте прерывается, то есть функция терпит разрыв.
Аналогичным образом связываются также понятие предела и непрерывности функции двух переменных.
Идея предела
Рассматриваемое нами понятие, относимое к математическому анализу, по праву считается одним из самых тонких в этой дисциплине. И хотя указанная наука возникла относительно недавно, саму идею предела использовал в своих работах еще великий житель древних Сиракуз – Архимед. Для вычисления площадей и объемов сложных геометрических форм он применял так называемый метод исчерпывания. В отдельных своих работах он изложил некую аксиому непрерывности, которая фактически содержала в себе интуитивную идею о пределах.

Как известно, в познании математических истин Архимед значительно опередил свое время, хотя и до него находились великие умы, которые высказывали подобные соображения. Но этот гениальный философ, инженер и ученый таким образом сумел вычислить площадь круга и самых разных многоугольников, определил объем конуса, пирамиды, цилиндра, призмы, большого количества других фигур. После смерти Архимеда идеи великого грека совершенствовались и развивались более двух тысячелетий, прежде чем превратились в теорию для вычисления дифференциалов и интегралов.
fb.ru
23. Предел функции, свойства Раскрытие неопределённостей вида (бесконечность/бесконечность). Свойства предела функции
1. Для того, чтобы число А было пределомf(x) приx->a, необходимо и достаточно, чтобы эта функция была представима в видеf(x)=A+альфа(х), где альфа(х) – бесконечно малая.
2. Предел постоянной величины равен самой постоянной.LimC,x->a=C.
3. Еслиf(x)>= 0 (f(x)<=0) в некоторой окрестности точки а, кроме самой точки а, и в этой точке имеет предел, то пределlimf(x),x->a>=0 (limf(x)x->a, <=0)
4. Если функцииf1(x),f2(x) имеют пределы в точке а, то и их сумма, произведение и частное имеет пределы, причемlim(f1(x)+f2(x)),x->a=limf1(x),x->a+limf2(x),x->a, так же с произведением и частным
5. Еслиf(x) имеет предел в точке а, тоlim(f(x))^n,x->a= (limf(x),x->a)^n, гдеn– натуральное число
6. Постоянный множитель можно выносить за знак предела.Lim cf(x), x->a = cLim f(x), x->a.
7. Если для функцийf(x),f1(x),f2(x) в некоторой окрестности в точке а выполняется неравенствоf1(x)<=f(x)<=f2(x) и пределlimf1(x),x->a=limf2(x),x->a=A, тоlimf(x),x->a=A.
8. Limc^x,x->б = бесконечности, еслиc>1 и 0, если 0<c<1.
Неопределенность вида бесконечность на бесконечность
Разделить все на х в наивысшей степени, учитывая уменьшение степени в корне.
Lim(x->0) sin 5x/sin3x = [0/0]=lim(x->0) x sin5x/x sin3x = lim(x->0) sin5x/x*lim(x->0) x/sin3x=lim(x->0) 5sin5x/5x*lim 3sin3x/3x)=5/3
Lim(x-unl) (1+1/x)x=e;
1/x=a=>x=1/a, a->0
Lim(a-0) (1+a)1/2=e
Lim(x-0) (loga(1+x))/x = lim(x-0) 1/x*loga(1+x)=lim(x-0) loga(1+x)1/x=logalim(x-0)(1+x)1/x=logae
Lim(x-0) ln(1+x)/x=ln e=1
Lim(x-0) ax-1/x=|ax-1=t;ax=t+1;ln ax=ln(t+1)
Сравнение бесконечно малых функций
Пусть a(x,b(x) – бесконечно малые ф-ции при х->a
Тогда
1. Lim(x->a)a(x)/b(x)=0 =>a(x) – бесконечно малая более высокого порядка, чемb(x)
2. Lim(x->a)a(x)/b(x) =c<>0=>aиb– бесконечно малые функции одного порядка
3. Lim(x->a)a(x)/b(x) = 1 =>aub– эквивалентные бесконечно малые функции
4. Lim(x->a)d(x)/bn(x) =c<>0 =>a– бесконечно малая функция н-ного порядка относительноb(x)
Cos2x=1-2sin2x
Теорема: если б.м. а(х) эквивалентна а1(х) иb(x) ~b1(x) иlim(x->a)a(x)/b(x) =>lim(x->a)a1(x)/b1(x)
1. Sinkx~kx
2. Tgkx~kx
3. Arcsinkx~kx
4. Arctgkx~kx
5. Ekx-1 ~ kx
6. Akx~kx ln a
7. Ln |1+kx|~kx
8. 1-cos kx ~kx2/2
23. Предел функции, теоремы о пределах. Неопределённость вида 0/0. Бесконечно большие и бесконечно малые.
Функция f(x) стремится к бесконечности при x стремящимся к a, если для любого M > 0 можно указать такое значение > 0, что для всех x удовлетворяющих неравенству xa < имеет место неравенство f(x) > M.
limxa=
Функция ограниченная при x a.
Функция ограниченная при x .
Теорема. Если limxaf(x)=b, то функция f(x) ограниченная при x a.
Бесконечно малые и их свойства. limxa (x)=0
Теорема. 1. Если f(x)=b+, где — б.м. при x a, то limxaf(x)=b и обратно, если limxaf(x)=b, то можно записать f(x)=b+(x).
Теорема. 2. Если limxa (x)=0 и (x) 0, то 1/ .
Теорема. 3. Сумма конечного числа б.м. есть б.м.
Теорема. 4. Произведение б.м. на ограниченную функцию есть б.м.
Теоремы о пределах.
Теорема. 1. Предел суммы есть сумма пределов.
Теорема. 2. Предел произведения есть произведение пределов.
Теорема. 3. Предел частного есть частное пределов (если знаменатель не обращается в 0).
Теорема. 4. Если u(x) z(x) v(x), и limxau(x)=limxav(x)=b, то limxaz(x)=b. («Теорема о двух милиционерах»).
Первый замечательный предел.
|
|
Второй замечательный предел.
Переменная величина
|
при nимеет предел, заключенный между 2 и 3. В данной работе мы рассмотрим неопределенность видадля функции. Для нахождения предела функции мы применяем метод преобразования, метод замены и определение бесконечно малых величин.
Пусть требуется найти предел дроби
(1)
где P(x) и Q(x) функции определенные в окрестности предельного аргумента a, но в самом предельном значении обращаются в ноль.
Теорема 1. Пусть число a для многочлена n-й степени P(x) = Pn(x) является k кратным решением, а для многочлена m-й степени Q(x) = Qn(x) является r кратным решением, тогда
(2)
где Pn-k(a) и Qm-r(a) значения соответствующих многочленов Pn-k(x) и Qm-r(x) в точке x = a.
Доказательство. Так как, число a является решением многочленов Pn(x) и Qm(x), то их в любое время можно представить в виде:
Тогда
(3)
Биномы (x — a)kи (x — a)rв окрестности точки x = a бесконечно малы, а их основания эквивалентные бесконечно малые. Отсюда
Полагаясь на последнее равенство, можно из (3) предела получить формулу (2). 25. 1-ый Замечательный предел.
Первый замечательный предел:
studfiles.net

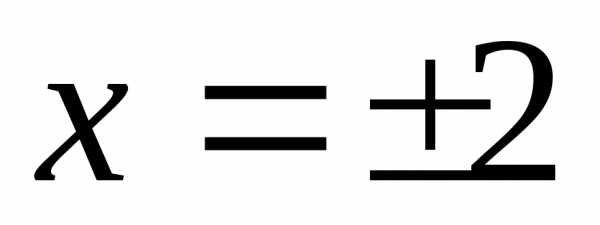 ,
т.к..
,
т.к..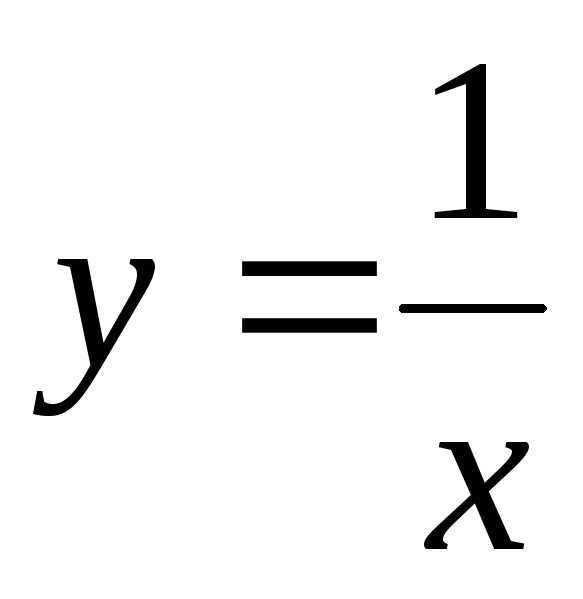 — б.м.ф. при,
т.к.
— б.м.ф. при,
т.к.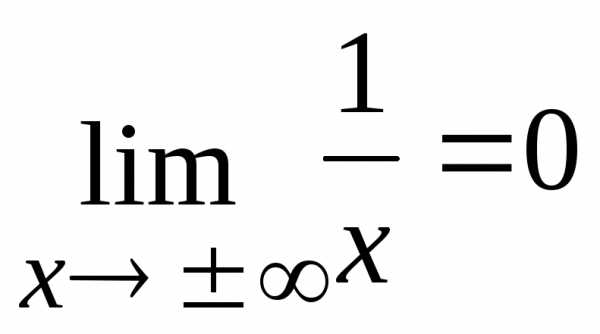 .
.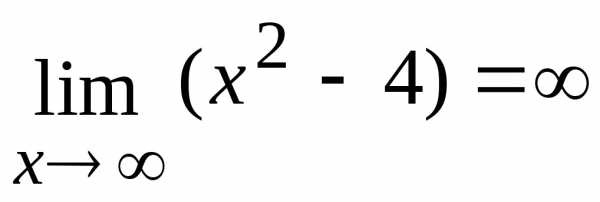 .
.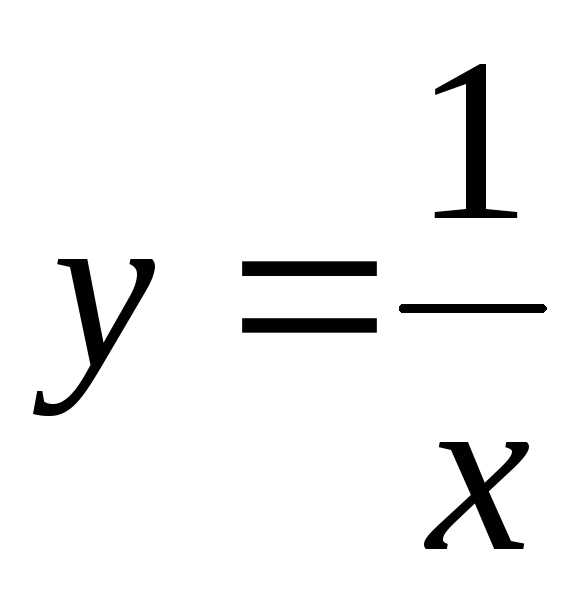
 ,
т.к.
,
т.к. .
. ненулевой предел, есть б.м.ф.
ненулевой предел, есть б.м.ф.