Примеры неравенство – Тема 4. Неравенства и системы неравенств

Неравенства

Отметим множество решений неравенства на числовой прямой и запишем ответ в виде числового промежутка.

 Алгебраические неравенства.

Квадратные неравенства. Рациональные неравенства высших степеней.

Дробно-рациональные неравенства.

 

Методы решения неравенств зависят в основном от того, к какому классу относятся функции, составляющие неравенство.

1. I. Квадратные неравенства, то есть неравенства вида

ax² + bx + c > 0 (< 0), a ≠ 0.

Будем считать, что a>0. Если это не так, то умножив обе части неравенства на -1 и изменив знак неравенства на противоположный, получим желаемое.

Чтобы решить неравенство можно:

1. Квадратный трехчлен разложить на множители, то есть неравенство записать в виде

a (x — x₁) (x — x₂) > 0 (< 0).

2. Корни многочлена нанести на числовую ось. Корни разбивают множество действительных чисел на промежутки, в каждом из которых соответствующая квадратичная функция будет знакопостоянной.
3. Определить знак a (x — x₁) (x — x₂) в каждом промежутке и записать ответ.

Если квадратный трехчлен не имеет корней, то при D<0 и a>0 квадратный трехчлен при любом x положителен.

Примеры:

• Решить неравенство. x² + x — 6 > 0.

Решение.

Разложим квадратный трехчлен на множители (x + 3) (x — 2) > 0

Ответ: x  (-∞; -3)  (2; +∞).

2) (x — 6)² > 0

Решение:

Это неравенство верно при любом х, кроме х = 6.

Ответ: (-∞; 6)  (6; +∞).      

3) x² + 4x + 15 < 0.

Решение:

Здесь D < 0, a = 1 > 0. Квадратный трехчлен положителен при всех х.

Ответ: x Î Ø.

Решить неравенства:

1. 1 + х — 2х² < 0.                              Ответ:
2. 3х² — 12х + 12 ≤ 0. Ответ:
3. 3х² — 7х + 5 ≤ 0. Ответ:
4. 2х² — 12х + 18 > 0.          Ответ:
5. При каких значениях a неравенство

      x² — ax >  выполняется для любых х?               Ответ:

1. II. Рациональные неравенства высших степеней, то есть неравенства вида

a_nxⁿ + a_n-1x^n-1 + … + a₁x + a₀ > 0 (<0), n>2.

Многочлен высшей степени следует разложить на множители, то есть неравенство записать в виде

a_n (x — x₁) (x — x₂) ·…· (x — x_n) > 0 (<0).

Отметить на числовой оси точки, в которых многочлен обращается в нуль.

Определить знаки многочлена на каждом промежутке.

Примеры:

1) Решить неравенство x⁴ — 6x³ + 11x² — 6x < 0.

Решение:

x⁴ — 6x³ + 11x² — 6x = x (x³ — 6x² + 11x -6) = x (x³ — x² — 5x² + 5x +6x — 6) =x (x — 1)( x² -5x + 6) =

x (x — 1) (x — 2) (x — 3). Итак, x (x — 1) (x — 2) (x — 3)<0

Ответ: (0; 1)  (2; 3).

2) Решить неравенство  (x -1)⁵ (x + 2) (x — ½)⁷ (2x + 1)⁴ <0.

Решение:

Отметим на числовой оси точки, в которых многочлен обращается в нуль. Это х = 1, х = -2, х =  ½, х = — ½.

В точке х = — ½ смены знака не происходит, потому что двучлен (2х + 1) возводится в четную степень, то есть выражение (2x + 1)⁴ не меняет знак при переходе через точку х = — ½.

Ответ: (-∞; -2)  (½; 1).

3) Решить неравенство: х² (х + 2) (х — 3) ≥ 0.

Решение:

Данное неравенство равносильно следующей совокупности

 Решением (1) является х  (-∞; -2)  (3; +∞). Решением (2) являются х = 0, х = -2, х = 3. Объединяя полученные решения, получаем х Î (-∞; -2]  {0}  [3; +∞).

Ответ: х  (-∞; -2]  {0}  [3; +∞).

Решить неравенства:

1. (5х — 1) (2 — 3х) (х + 3) > 0. Ответ:
2. x³ + 5x² +3x — 9 ≤ 0. Ответ:
3. (x — 3) (x — 1)² (3x — 6 — x²) < 0. Ответ:
4. (x² -x)² + 3 (x² — x) + 2 ≥ 0. Ответ:

III. Дробно-рациональные неравенства.

При решении таких неравенств можно придерживаться следующей схемы.

1. Перенести все члены неравенства в левую часть.
2. Все члены неравенства в левой части привести к общему знаменателю, то есть неравенство записать в виде

 > 0 (<0).

3. Найти значения х, при которых функция y=может менять свой знак. Это корни уравнений
4. Нанести найденные точки на числовую ось. Эти точки разбивают множество действительных чисел на промежутки, в каждом их которых функция будет знакопостоянной.
5. Определить знак в каждом промежутке, вычисляя, например, значение данного отношения в произвольной точке каждого промежутка.
6. Записать ответ, обращая особое внимание на граничные точки промежутков. При решении строгого неравенства >0 (<0) граничные точки в ответ не включаются. При решении нестрогого неравенства ≥ 0 ( ≤ 0), если точка является корнем знаменателя, то она не включается в ответ (даже если она одновременно является корнем числителя). Если же точка является корнем одного числителя, то она включается в ответ.

Примеры.

1). Решить неравенство .

Решение:  > 0, > 0,  > 0

Найдем нули числителя и знаменателя. Это х = 3, х = 5, х=1. Наносим найденные точки на числовую ось и определяем знаки  в каждом промежутке   

Выбираем любой х(5; +), например х = 10. Тогда  < 0.

               Выбираем х = 4 (3; 5).

Получаем  > 0. При х = 2 (1; 3). Получаем > 0.

Наконец, при х = 0 (-; 1). Вычисляем   < 0.

Ответ: х (1; 3)  (3; 5).

2). Найти сумму целых решений неравенства.

Решение. Найдем нули числителя и знаменателя дроби. Это х = -1, х=8, х = 3, х= 5.

Нанесем найденные точки на числовую ось и определим знак дроби в каждом промежутке, вычисляя значение этой дроби в произвольной точке каждого промежутка.

Решением исходного неравенства является

х [-1, 3)  (3; 5)  {8}. Найдем сумму целых решений: -1 +1+0+ 2 + 4 + 8 = =14.

Ответ: 14.

 

ya-znau.ru

Числовые неравенства и их свойства

С неравенствами мы познакомились  в школе, где применяем числовые неравенства. В данной статье рассмотрим свойства числовых неравенств, не которых строятся принципы работы с ними.

Свойства неравенств аналогичны свойствам числовых неравенств. Будут рассмотрены свойства, его обоснования, приведем примеры.

Yandex.RTB R-A-339285-1

Числовые неравенства: определение, примеры

При введении понятия неравенства имеем, что их определение производится по виду записи.  Имеются алгебраические выражения, которые имеют знаки ≠, <, >, ≤ , ≥. Дадим определение.

Определение 1

Числовым неравенством называют неравенство, в записи которого обе стороны имеют числа и числовые выражения.

Числовые неравенства рассматриваем еще в школе после изучения натуральных чисел. Такие операции сравнения изучаются поэтапно. Первоначальные имею вид 1<5, 5+7>3. После чего правила дополняются, а неравенства усложняются, тогда получаем неравенства вида 523>5,1(2), ln 0.73-172<0.

Свойства числовых неравенств

Чтобы правильно работать с неравенствами, необходимо использовать свойства числовых неравенств. Они идут из понятия неравенства. Такое понятие задается при помощи утверждения, которое обозначается как «больше» или «меньше».

Определение 2

• число a больше b, когда  разность a-b – положительное число;
• число a меньше b, когда разность a-b – отрицательное число;
• число a равно b, когда разность a-bравняется нулю.

Определение используется при решении неравенств с отношениями «меньше или равно», «больше или равно». Получаем, что

Определение 3

• a больше или равно b, когда a-b является неотрицательным числом;
• a меньше или равно b, когда a-b является неположительным числом.

Определения будут использованы при доказательствах свойств числовых неравенств.

Основные свойства

Рассмотрим 3 основные неравенства. Использование знаков < и > характерно при свойствах:

Определение 4

• антирефлексивности, которое говорит о том, что любое число a из неравенств a<a и a>a считается неверным. Известно, что для любого a имеет место быть равенство a−a=0, отсюда получаем, что а=а. Значит, a<a и a>a неверно. Например, 3<3 и -41415>-41415 являются неверными.
• ассиметричности. Когда числа a

zaochnik.com

Рациональные неравенства — теория и формулы, подготовка к ЕГЭ по математике

Рациональное неравенство — это неравенство, которое можно свести к виду \[\Large{\dfrac{P(x)}{Q(x)}\lor 0}\]где \(P(x),\ Q(x)\) — многочлены.
(\(\lor\) — один из знаков \(\geqslant, \ \leqslant, \ >, \ <\))
Например, следующие неравенства являются рациональными: \[\dfrac1{x+1}>0,\qquad x+2+\dfrac{x-1}{x+3}<1,\qquad x^2+x-2\leqslant 0\]

\[{\Large{\text{Линейные неравенства}}}\] Линейные неравенства – это неравенства вида \[ax+b \lor 0, \qquad \lor — \text{ один из знаков } \geqslant, \ \leqslant, \ >, \ <;\quad a,b — \text{ числа,}\]или сводящиеся к такому виду.
Область допустимых значений \(x\) (ОДЗ) таких неравенств — все вещественные числа (\(x\in \mathbb{R}\)).

 

Общее правило решения линейных неравенств:

1) Для того, чтобы решить данное неравенство, необходимо привести его к виду \(ax\lor -b\), то есть перенести число \(b\) в правую часть.

2) Если коэффициент \(a\) перед \(x\) – положительный, то неравенство равносильно \(x\lor -\dfrac ba\), то есть после деления обеих частей неравенства на \(a\) знак неравенства не меняется.

3) Если коэффициент \(a\) перед \(x\) – отрицательный, то неравенство равносильно \(x\land -\dfrac ba\), то есть после деления обеих частей неравенства на \(a\) знак неравенства меняется на противоположный.

4) Если \(a=0\), то неравенство равносильно \(0\lor -b\), что либо верно при всех значениях переменной \(x\) (например, если это \(0>-1\)), либо неверно ни при каких значениях \(x\) (например, если это \(0\leqslant -3\)).
То есть ответом будут либо \(x\in\mathbb{R}\), либо \(x\in \varnothing\).

 

Замечание
Заметим, что знаку \(\leqslant\) противоположен знак \(\geqslant\), а знаку \(<\) – знак \(>\). И наоборот.

 

Пример 1
Решить неравенство \(5-3x>-1\).

 

Решение. I способ
Сделаем цепочку преобразований:

\[5-3x>-1 \ \Rightarrow \ -3x>-1-5 \ \Rightarrow \ -3x>-6 \ \Rightarrow \ x<\dfrac 63 \ \Rightarrow \ x<2\] Таким образом, ответом будет \(x\in(-\infty;2)\).
Заметим, что т.к. мы делили неравенство на \(-3\), то знак неравенства поменялся.

 

Решение. II способ
Можно перенести слагаемое \(-3x\) в правую часть, а \(-1\) – в левую:

\[5-3x>-1 \ \Rightarrow \ 5+1>3x \ \Rightarrow \ 3x<6 \ \Rightarrow \ x<2\]

Пример 2
Решить неравенство \((1-\sqrt2)x+2\leqslant 0\).

 

Решение
Заметим, что перед \(x\) находится отрицательный коэффициент. Поэтому:

\[(1-\sqrt2)x\leqslant -2 \Rightarrow x\geqslant -\dfrac 2{1-\sqrt2}\] Преобразуем число \(-\dfrac 2{1-\sqrt2}\): домножим числитель и знаменатель дроби на сопряженное к \(1-\sqrt2\), то есть на \(1+\sqrt2\), чтобы избавиться от иррациональности в знаменателе:

\[-\dfrac 2{1-\sqrt2}=-\dfrac{2(1+\sqrt2)}{(1-\sqrt2)(1+\sqrt2)}= -\dfrac{2(1+\sqrt2)}{1-2}=2(1+\sqrt2)\]
Таким образом, ответ \(x\in [2+2\sqrt2;+\infty)\).
Перейдем к квадратичным неравенствам, которые являются очень важным инструментом в решении задач.

 

\[{\Large{\text{Метод интервалов}}}\]

Приступим к рассмотрению общего метода для решения любого рационального неравенства, то есть неравенства вида

\[(**)\qquad \dfrac{P(x)}{Q(x)}\geqslant 0 \qquad (\text{на месте }\geqslant \text{может стоять любой из} \leqslant, \ <, \ >)\]

Область допустимых значений \(x\) (ОДЗ) таких неравенств — все вещественные числа, кроме нулей знаменателя.

 

Существует два способа решения таких неравенств:

 

1 способ: Классический. Т.к. дробь положительна (отрицательна) тогда и только тогда, когда числитель и знаменатель дроби одного знака (разных знаков), то неравенство \((*)\) равносильно совокупности: \[{\large{\left[\begin{gathered} \begin{aligned} &\begin{cases} P(x)\geqslant 0\\ Q(x)>0 \end{cases}\\ &\begin{cases} P(x)\leqslant 0\\ Q(x)<0 \end{cases} \end{aligned} \end{gathered} \right.}}\]

 

Такой способ подойдет для решения любого неравенства, где слева стоит дробь, а справа — \(0\).
Но, как правило, для решения большинства рациональных неравенств он неудобен. Почему? Вы сможете убедиться в этом после того, как мы рассмотрим метод интервалов.

 

2 способ: Удобный. Метод интервалов (будем рассматривать этот метод на примере конкретного неравенства, чтобы было понятней).
Заметим, что первые три шага созданы для того, чтобы преобразовать неравенство к более простому виду, что поможет вам не допустить ошибку в решении подобных задач. Метод интервалов – это всего лишь удобный инструмент для решения рациональных неравенств, и если вы будете всегда пользоваться одним и тем же алгоритмом, то вероятность допустить ошибку при решении таких неравенств будет минимальной.
Данный алгоритм специально расписан подробно, чтобы у вас не возникло вопросов; всего после нескольких использований этого алгоритма вы будете решать рациональные неравенства очень быстро и без ошибок!

 

1 ШАГ. Необходимо перенести все слагаемые в одну часть (пусть это будет левая часть) неравенства так, чтобы в другой части неравенства остался \(0\), и привести эти слагаемые к общему знаменателю так, чтобы в левой части неравенства получилась дробь. Затем нужно разложить числитель и знаменатель полученной дроби, то есть многочлены \(P(x), \ Q(x)\), на множители.   Например, неравенство \(\dfrac1{x+1}<1\) нужно переписать в виде \(\dfrac1{x+1}-1<0\), затем привести к общему   знаменателю \(\dfrac1{x+1}-\dfrac{x+1}{x+1}<0\), затем записать в виде одной дроби левую часть: \(\dfrac{1-(x+1)}{x+1}<0\) и   привести подобные слагаемые: \(\dfrac{-x}{x+1}<0\).

 

Итак, пусть после разложения на множители неравенство приняло вид \[\dfrac{x^2(x-1)^3(x+1)(2x^2+3x+5)(2x-x^2-3)}{(x+1)^3(3-x)(2-3x)^2} \geqslant0\]

Заметим, что любой многочлен можно (а в нашем способе НУЖНО) разложить до произведения только линейных скобок (\(ax+b\)) и квадратичных скобок с отрицательным дискриминантом \((ax^2+bx+c), \ D<0\).

 

2 ШАГ. Рассмотрим скобки, в которых остался квадратичный трехчлен с \(D<0\).

 

\(\bullet\) Если при \(x^2\) находится положительный коэффициент \(a>0\), то при всех значениях \(x\) выражение \(ax^2+bx+c\) положительно (не может быть равно нулю!). Т.к. мы имеем право делить неравенство на любое число/выражение, не равное \(0\), то разделим обе части неравенства на такие скобки (в нашем неравенстве такой скобкой является \((2x^2+3x+5)\)). Причем заметим, что т.к. мы делим на положительное выражение, то знак неравенства не меняется!

 

\(\bullet\) Если при \(x^2\) находится отрицательный коэффициент \(a<0\), то при всех значениях \(x\) выражение \(ax^2+bx+c\) отрицательно. Т.к. мы имеем право делить неравенство на любое число/выражение, не равное \(0\), то разделим обе части неравенства на такие скобки (в нашем неравенстве такой скобкой является \((2x-x^2-3)\)). Причем заметим, что т.к. мы делим на отрицательное выражение, то знак неравенства должен измениться на противоположный!  

Итак, обобщим 2 шаг: квадратичные скобки с отрицательным дискриминантом можно просто вычеркнуть, причем при вычеркивании скобок с \(a>0\) знак неравенства остается прежним, а вот при вычеркивании скобок с \(a<0\) знак неравенства меняется на противоположный столько раз, сколько было таких скобок. Лучше вычеркивать их последовательно по одной, каждый раз меняя знак неравенства на противоположный.

 

Таким образом, неравенство примет вид \[\dfrac{x^2(x-1)^3(x+1)}{(x+1)^3(3-x)(2-3x)^2} \leqslant 0\]

 

3 ШАГ. Рассмотрим линейные скобки \((ax+b)\).

 

Назовем скобку хорошей, если при \(x\) находится положительный коэффициент (такие скобки мы трогать не будем), и плохой, если при \(x\) находится отрицательный коэффициент (в таких скобках необходимо поменять все знаки на противоположные, то есть сделать их хорошими).

 

Для того, чтобы в одной плохой скобке поменять все знаки на противоположные, необходимо домножить правую и левую части неравенства на \(-1\). Таким образом, после одного такого действия знак неравенства сменится на противоположный. Значит, если плохих скобок четное количество, то знак неравенства не изменится, если нечетное – то знак неравенства изменится на противоположный.

 

Заметим, что выражение \((ax+b)^n\) — это не что иное, как произведение \(n\) скобок \((ax+b)\).

В нашем неравенстве среди плохих одна скобка \((3-x)\) и две скобки \((2-3x)\) (т.к. \((2-3x)^2=(2-3x)(2-3x)\)), то есть всего три плохих скобки, следовательно, знак неравенства изменится и неравенство примет вид: \[\dfrac{x^2(x-1)^3(x+1)}{(x+1)^3(x-3)(3x-2)^2} \geqslant0\quad (***)\]

Заметим, что множитель \(x^2\) — это скобка \((x-0)^2\), или, что то же самое, \((x-0)(x-0)\) – произведение двух одинаковых линейных скобок.

 

4 ШАГ. Теперь, когда левая часть неравенства состоит из произведения только хороших линейных скобок (в каких-то степенях), можно приступить к самому методу интервалов.

 

Его суть состоит в том, что левая часть неравенства — всюду непрерывная функция, кроме тех точек, где знаменатель дроби равен нулю. Поэтому точки, в которых эта функция равна нулю (то есть ее числитель равен нулю) и точки, в которых эта функция не существует (то есть ее знаменатель равен нулю), разбивают область определения этой функции на промежутки, причем на каждом промежутке функция принимает значения строго одного знака.

 

А нам как раз нужно найти те значения \(x\), при которых функция \(\geqslant 0\). Причем, т.к. наша функция — рациональная, то ее область определения — это все действительные числа (\(\mathbb{R}\)), кроме нулей знаменателя. Поэтому отметим нули каждой скобки на вещественной прямой (а ноль каждой скобки – это как раз ноль числителя или знаменателя), причем нули знаменателя – выколотые, нули числителя – закрашенные (если знак неравенства нестрогий, как в примере, то есть \(\geqslant \) или \(\leqslant \)) или выколотые (если знак неравенства строгий, то есть \(>\) или \(<\)).
Заметим, что если мы отметили \(n\) точек, то числовая прямая разобьется на \(n+1\) промежутков.

 

Расставим знак на каждом промежутке \(\color{red}{{\Large{\text{справа налево}}}}\). Будем ставить “\(+\)”, если функция на этом промежутке принимает положительные значения, и “\(-\)” — если отрицательные. Нулю функция равна в закрашенных точках.
Первые три шага мы делали для того, чтобы не подставлять точки из каждого промежутка и не вычислять, какого знака будет левая часть неравенства (что бывает неудобно, если числа, которые нужно отмечать на прямой, “некрасивые”). Знаки мы будем расставлять, выявив некоторую закономерность. Какую – вы узнаете дальше.
Но в любом случае способ расстановки знаков путем подстановки чисел остается в нашем арсенале.

 

Т.к. все скобки – хорошие, то первый знак всегда будет “\(+\,\)” (именно для этого мы и приводили неравенство к такому виду!). Действительно, если подставить любое число, превышающее самый большой корень (у нас самый большой корень \(x=3\)), то каждая скобка будет положительна, значит, и произведение таких скобок будет всегда положительно.

 

Если какой-то корень входит в четное количество скобок, то при переходе через него (справа налево!) знак меняться не будет. В нашем неравенстве это точки \(-1, \ 0, \ \dfrac23\) (например, точка \(-1\) входит в четное количество скобок: одна в числителе \((x+1)\) и три в знаменателе \((x+1)^3\)).

 

Если точка входит в нечетное количество скобок, то при переходе через эту точку (справа налево!) знак будет меняться (в нашем неравенстве это точки \(3\) и \(1\)).

 

Объясним, почему так происходит. Каждая линейная скобка в нечетной степени \((x-a)^{2n+1}\) имеет ровно один корень \(x=a\), причем, т.к. мы сделали ее хорошей, то для всех \(x>a\) она будет положительной, для всех \(x<a\) она будет отрицательной (а для \(x=a\), естественно, равной нулю). Значит, когда \(x\in (1;3)\), то все скобки, кроме \((x-3)\), будут оставаться положительными, и лишь эта скобка \((x-3)\) станет отрицательной. Значит, их произведение также станет отрицательным. Аналогично при переходе через точку \(x=1\).
Каждая линейная скобка в четной степени \((x-b)^{2n}\) также имеет ровно один корень \(x=b\), но т.к. она в четной степени, то при всех \(x\ne b\) она всегда будет положительной! И только при \(x=b\) она будет равна нулю. Именно поэтому при переходе через точку \(x=\dfrac23\), т.е. на \(x\in(0;\frac23)\), скобка \((3x-2)^2\) не сменит свой знак на отрицательный, поэтому вся левая часть останется по знаку такой же, как и была на \((\frac23;1)\) (т.е. положительной). Аналогично при переходе через точки \(0, -1\).

 

5 ШАГ. Неравенство практически решено и нам остается только записать ответ. В нашем случае, т.к. знак преобразованного \((***)\) неравенства \(\geqslant 0\) (нестрогий), то в ответ пойдут промежутки со знаком “\(+\,\)” (где значение функции больше нуля) и закрашенные точки (где значение функции равно нулю): \[x\in \Big(-\infty;-1\Big)\cup \left(-1;\dfrac23\right)\cup \left(\dfrac23;1\right]\cup\Big(3;+\infty\Big)\]Напоминаем, что если точка не входит в ответ, то она пишется в круглой скобке “\((\)” или “\()\)”, если входит в ответ – то в квадратной скобке “\([\)” или “\(]\)”. Бесконечности всегда пишутся в круглых скобках.  

\[{\Large{\text{Квадратичные неравенства}}}\]

Квадратичным неравенством называется любое неравенство вида \[ax^2+bx+c \lor 0, \quad a\ne 0,\]

или сводящееся к такому виду.

 

Область допустимых значений \(x\) (ОДЗ) таких неравенств — все вещественные числа (\(x\in \mathbb{R}\)).

 

Квадратичные неравенства – это те же самые рациональные неравенства, следовательно, их также можно решать с помощью метода интервалов. Но давайте рассмотрим еще один способ, при помощи которого, как правило, удобнее решать квадратичные неравенства. Для этого нам понадобится вспомнить про параболу.

 

Замечание

Вспомним, как преобразуется квадратичный трехчлен \(ax^2+bx+c\) в зависимости от того, сколько корней он имеет.
Если квадратное уравнение \(ax^2+bx+c=0\)

 

\(\bullet\) имеет два корня \(x_1\) и \(x_2\) (дискриминант \(D>0\)), то \(ax^2+bx+c=a(x-x_1)(x-x_2)\).

 

\(\bullet\) имеет один корень \(x_1\) (\(D=0\)), то \(ax^2+bx+c=a(x-x_1)^2\).

 

\(\bullet\) не имеет корней (\(D<0\)), то квадратный трехчлен \(ax^2+bc+c\) никогда не может быть равен нулю и не разлагается на линейные множители.

 

Шаг 1. Рассмотрим функцию \(f(x)=ax^2+bx+c\). Графиком такой функции является парабола.
Для того, чтобы решить квадратичное неравенство, изобразим схематично параболу: то есть определим, куда направлены ее ветви и в каких точках она пересекает ось \(Ox\).

 

Если \(a>0\), то ветви направлены вверх, если \(a<0\), то ветви направлены вниз. Корни уравнения \(ax^2+bx+c=0 \ (*)\) и есть абсциссы точек, в которых парабола пересекает ось \(Ox\).

 

Шаг 2. Таким образом, наша парабола будет одного из 6 видов: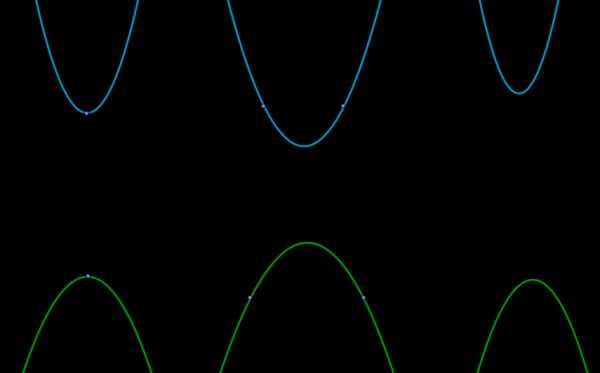
\((1)\) и \((4)\) — когда уравнение \((*)\) имеет один корень;
\((2)\) и \((5)\) — когда уравнение \((*)\) имеет два корня;
\((3)\) и \((6)\) — когда уравнение \((*)\) не имеет корней.

Часть параболы, находящая выше оси \(Ox\), отвечает за \(f(x)>0\);
часть параболы, находящаяся ниже оси \(Ox\), отвечает за \(f(x)<0\);
точки, в которых парабола пересекает ось \(Ox\), отвечают за \(f(x)=0\).

 

Пример 1.
Решить неравенство \(x^2+3x+2\geqslant 0\).

 

Решение
Решим уравнение \(x^2+3x+2=0 \Leftrightarrow x_1=-2, x_2=-1\). Таким образом, неравенство можно переписать в виде: \((x+1)(x+2)\geqslant 0\). Ветви параболы направлены вверх, следовательно, схематично она выглядит как \((2)\). Т.к. знак неравенства \(\geqslant\), то решением неравенства будут те значения \(x\), для которых график находится выше оси \(Ox\), а именно \(x\in (-\infty;-2]\cup[-1;+\infty)\).

 

Заметим, что точки \(-2, -1\) входят в ответ, потому что знак “больше или равно”.

 

Пример 2.
Решить неравенство \(11x-3x^2-6>0\)

 

Решение
Решим уравнение \(11x-3x^2-6=0 \quad\Leftrightarrow\quad x_1=\dfrac23, x_2=3\). Таким образом, неравенство можно переписать в виде: \(-3(x-3)(x-\frac23)>0\).

 

1 способ. Ветви параболы направлены вниз, следовательно, схематично она выглядит как \((5)\). Т.к. знак неравенства \(>\), то решением неравенства будут \(x\in \left(\dfrac23;3\right)\).

 

2 способ. Домножим правую и левую части неравенства на \(-1\), получим \(3(x-3)(x-\frac23)<0\) (заметим, что знак сменился на противоположный). У новой параболы \(\Big(f(x)=3(x-3)(x-\frac23)\Big)\) ветви направлены вверх, следовательно, схематично она выглядит как \((2)\). Но знак неравенства уже \(<\). Решением нового неравенства, естественно, будут те же \(x\in \left(\dfrac23;3\right)\).

 

Таким образом, если в квадратичном неравенстве отрицательный знак при \(x^2\), то можно сначала домножить неравенство на \(-1\) (и не забыть поменять знак неравенства), чтобы ветви параболы всегда были направлены вверх.

 

Пример 3.
Решить неравенство \(x^2+4x+4 \geqslant 0\).

 

Решение
Вспомнив формулу сокращенного умножения, получаем \((x+2)^2\geqslant 0\) (это быстрее, чем находить корни через дискриминант :)). Таким образом, парабола пересекает ось \(Ox\) в единственной точке \(x_1=-2\) и выглядит как \((1)\). А т.к. нам нужны те \(x\), для которых график находится не ниже оси \(Ox\), то решением неравенства будут \(x\in \mathbb{R}\), то есть выражение \((x+2)^2\) всегда больше или равно \(0\).  

shkolkovo.net

Равносильные неравенства. Основные приемы решения неравенств

Два неравенства, содержащие одни и те же неизвестные, называются равносильными, если они верны при одних и тех же значениях этих неизвестных.

Так же определяется равносильность двух систем неравенств.

Пример 1. Неравенства 3х+1 > 2x+4 и 3x > 2x+3 равносильны, так как оба верны при x > 3 и оба неверны, когда x ≤ 3

Пример 2. Неравенства 2x ≤ 6 и x² ≤ 9 не равносильны, так как решение первого есть x ≤ 3, а решение второго -3x ≤ x ≤ 3, так что, например x = -4 первое верно, а второе неверно.

Процесс решения неравенства заключается в основном в замене данного неравенства (или данной системы неравенств) другими равносильными¹. При решении неравенств применяются следующие основные приемы (ср. § 18).

1. Замена одного выражения другим, тождественно ему равным.
2. Перенос слагаемого из одной части неравенства в другую с заменой знака на противоположный (в силу § 50, п.3).
3. Умножение или деление обеих частей неравенства на одну и ту же числовую величину (не равную нулю). При этом если множитель положителен, то знак неравенства остается тем же, если же отрицателен, то знак неравенства меняется на противоположный (§ 50, п.6).

Каждое их этих преобразований дает неравенство, равносильное исходному.

Пример. Дано неравенство (2x-3)² < 4x²+2. Заменяем левую часть тождественно равным выражением 4x²-12x+9. Получаем 4x²-12x+9 < 4x²+2. Переносим из правой части член 4x²в левую, а из левой части член 9 в правую часть. После приведения подобных членов получаем -12x(7/12).

Умножать (а также делить) неравенство на нуль нельзя. Умножая или деля обе части неравенства на буквенные выражения, мы получаем неравенство, которое, как правило, не равносильно исходному.

Пример. Дано неравенство (x-2)x < x-2. Если разделить обе его части на x-2, то получим x < 1. Но это неравенство не равносильно исходному, так как, например, значение x=0 не удовлетворяет неравенству (x-2)x < x-2. Неравенство x < 1 тоже не равносильно исходному, так как, например, значение x=3 неравенству (x-2)x

totangens.ru

Неравенство — Википедия. Что такое Неравенство

Нера́венство в математике — отношение, связывающее два числа или иных математических объекта с помощью одного из перечисленных ниже знаков^[1].

Строгие неравенства

Неравенства a>b{\displaystyle a>b} и b<a{\displaystyle b<a} равносильны. Говорят, что знаки >{\displaystyle >} и <{\displaystyle <} противоположны; например, выражение «знак неравенства сменился на противоположный» означает, что <{\displaystyle <} заменено на >{\displaystyle >} или наоборот.

Нестрогие неравенства

Русскоязычная традиция начертания знаков ⩽{\displaystyle \leqslant } и ⩾{\displaystyle \geqslant } отличается от принятой за рубежом, где обычно используются знаки ≤{\displaystyle \leq } и ≥{\displaystyle \geq }.Про знаки ⩽{\displaystyle \leqslant } и ⩾{\displaystyle \geqslant } также говорят, что они противоположны.

Другие типы неравенств

Далее в данной статье, если не оговорено иное, понятие неравенства относится к первым 4 типам.

В элементарной математике изучают числовые неравенства. В общей алгебре, анализе, геометрии рассматриваются неравенства также и между объектами нечисловой природы.

Связанные определения

Неравенства с одинаковыми знаками называются одноимёнными (иногда используется термин «одного смысла» или «одинакового смысла»).

Допускается двойное или даже многократное неравенство, объединяющее несколько неравенств в одно. Пример:

a<b<c{\displaystyle a<b<c} — это краткая запись пары неравенств: a<b{\displaystyle a<b} и b<c.{\displaystyle b<c.}

Числовые неравенства

Числовые неравенства содержат вещественные числа (для комплексных чисел сравнение на больше-меньше не определено) и могут содержать также символы неизвестных (x,y,…).{\displaystyle (x,y,\dots ).} Числовые неравенства, содержащие неизвестные величины, подразделяются (аналогично уравнениям) на алгебраические и трансцендентные. Алгебраические неравенства, в свою очередь, подразделяются на неравенства первой степени, второй степени и так далее. Например, неравенство 18x<414{\displaystyle 18x<414} — алгебраическое первой степени, неравенство 2×3−7x+6>0{\displaystyle 2x^{3}-7x+6>0} — алгебраическое третьей степени, неравенство 2x>x+4{\displaystyle 2^{x}>x+4} — трансцендентное^[2].

Свойства

Свойства числовых неравенств в некоторых отношениях близки к свойствам уравнений^[1]:

• К обеим частям неравенства можно прибавить одно и то же число.
• От обеих частей неравенства можно отнять одно и то же число. Следствие: как и для уравнений, любой член неравенства можно перенести в другую часть с противоположным знаком. Например, из a+b<c{\displaystyle a+b<c} следует, что a<c−b.{\displaystyle a<c-b.}
• Обе части неравенства можно умножить на одно и то же положительное число.
• Одноимённые неравенства можно складывать: если, например, a<b{\displaystyle a<b} и c<d,{\displaystyle c<d,} то a+c<b+d.{\displaystyle a+c<b+d.} Неравенства с противоположными знаками можно аналогично почленно вычитать.
• Если все четыре части двух неравенств положительны, то неравенства можно перемножить.
• Если обе части неравенства положительны, то их можно возвести в одну и ту же (натуральную) степень, а также логарифмировать с любым основанием (если основание логарифма меньше 1, то знак неравенства надо изменить на противоположный).

Другие свойства

• (Транзитивность) Если a<b{\displaystyle a<b} и b<c,{\displaystyle b<c,} то a<c{\displaystyle a<c} и аналогично для прочих знаков.
• Если обе части неравенства умножить на одно и то же отрицательное число, то знак неравенства изменится на противоположный: больше на меньше, больше или равно на меньше или равно и т. д.

Решение неравенств

Если неравенство содержит символы неизвестных, то решение его означает выяснение вопроса, при каких значениях неизвестных неравенство выполняется. Примеры:

x2<4{\displaystyle x^{2}<4} выполняется при −2<x<2.{\displaystyle -2<x<2.}

x2>4{\displaystyle x^{2}>4} выполняется, если либо x>2,{\displaystyle x>2,} либо x<−2.{\displaystyle x<-2.}

x2<−4{\displaystyle x^{2}<-4} не выполняется никогда (решений нет).

x2>−4{\displaystyle x^{2}>-4} выполняется при всех x{\displaystyle x} (тождество).

Внимание: если возвести в чётную степень неравенство, содержащее неизвестные, могут появиться «лишние» решения. Пример: если неравенство x>3{\displaystyle x>3} возвести в квадрат: x2>9,{\displaystyle x^{2}>9,} то появится ошибочное решение x<−3,{\displaystyle x<-3,} не удовлетворяющее исходному неравенству. Поэтому все полученные таким образом решения следует проверить подстановкой в исходное неравенство.

Неравенства первой степени

Неравенство первой степени имеет общий формат: ax>b{\displaystyle ax>b} или ax<b,{\displaystyle ax<b,} где a≠0{\displaystyle a\neq 0} (работа со знаками ⩾{\displaystyle \geqslant } и ⩽{\displaystyle \leqslant } аналогична). Чтобы его решить, разделите неравенство на a{\displaystyle a} и, если a<0,{\displaystyle a<0,} измените знак неравенства на противоположный^[3]. Пример:

5x−11>8x+1.{\displaystyle 5x-11>8x+1.} Приведём подобные члены: −3x>12,{\displaystyle -3x>12,} или x<−4.{\displaystyle x<-4.}

Системы неравенств первой степени

Если одно и то же неизвестное входит более чем в одно неравенство, надо решить каждое неравенство в отдельности и затем сопоставить эти решения, которые должны выполняться все вместе.

Пример 1. Из системы {4x−3>5x−52x+4<8x{\displaystyle {\begin{cases}4x-3>5x-5\\2x+4<8x\end{cases}}} получаем два решения: для первого неравенства x<2,{\displaystyle x<2,} для второго: x>23.{\displaystyle x>{2 \over 3}.} Соединяя их, получаем ответ: 23<x<2.{\displaystyle {2 \over 3}<x<2.}

Пример 2. {2x−3>3x−52x+4>8x{\displaystyle {\begin{cases}2x-3>3x-5\\2x+4>8x\end{cases}}} Решения: x<2{\displaystyle x<2} и x<23.{\displaystyle x<{2 \over 3}.} Второе решение поглощает первое, так что ответ: x<23.{\displaystyle x<{2 \over 3}.}

Пример 3. {2x−3<3x−52x+4>8x{\displaystyle {\begin{cases}2x-3<3x-5\\2x+4>8x\end{cases}}} Решения: x>2{\displaystyle x>2} и x<23,{\displaystyle x<{2 \over 3},} они несовместимы, поэтому исходная система не имеет решений.

Неравенства второй степени

Общий вид неравенства второй степени (называемого также квадратным неравенством):

x2+px+q>0{\displaystyle x^{2}+px+q>0} или x2+px+q<0.{\displaystyle x^{2}+px+q<0.}

Если квадратное уравнение x2+px+q=0{\displaystyle x^{2}+px+q=0} имеет вещественные корни x1,x2,{\displaystyle x_{1},x_{2},} то неравенство можно привести к виду соответственно:

(x−x1)(x−x2)>0{\displaystyle (x-x_{1})(x-x_{2})>0} или (x−x1)(x−x2)<0.{\displaystyle (x-x_{1})(x-x_{2})<0.}

В первом случае x−x1{\displaystyle x-x_{1}} и x−x2{\displaystyle x-x_{2}} должны иметь одинаковые знаки, во втором — разные. Для окончательного ответа надо применить следующее простое правило^[4].

Квадратный трёхчлен x2+px+q{\displaystyle x^{2}+px+q} с разными вещественными корнями отрицателен в интервале между корнями и положителен вне этого интервала.

Если оказалось, что у уравнения x2+px+q=0{\displaystyle x^{2}+px+q=0} вещественных корней нет, то его левая часть сохраняет один и тот же знак при всех x.{\displaystyle x.} Поэтому исходное неравенство второй степени либо является тождеством, либо не имеет решений (см. ниже примеры^[5]).

Пример 1. −2×2+14x−20>0.{\displaystyle -2x^{2}+14x-20>0.} Разделив на −2,{\displaystyle -2,} приведём неравенство к виду: x2−7x+10<0.{\displaystyle x^{2}-7x+10<0.} Решив квадратное уравнение x2−7x+10=0,{\displaystyle x^{2}-7x+10=0,} получаем корни x1=2;x2=5,{\displaystyle x_{1}=2;x_{2}=5,} поэтому исходное неравенство равносильно такому: (x−2)(x−5)<0.{\displaystyle (x-2)(x-5)<0.} Согласно приведенному выше правилу, 2<x<5,{\displaystyle 2<x<5,} что и является ответом.

Пример 2. −2×2+14x−20<0.{\displaystyle -2x^{2}+14x-20<0.} Аналогично получаем, что x−2{\displaystyle x-2} и x−5{\displaystyle x-5} имеют одинаковые знаки, то есть, согласно правилу, либо x<2,{\displaystyle x<2,} либо x>5.{\displaystyle x>5.}

Пример 3. x2+6x+15>0.{\displaystyle x^{2}+6x+15>0.} Уравнение x2+6x+15=0{\displaystyle x^{2}+6x+15=0} не имеет вещественных корней, поэтому левая часть его сохраняет знак при всех x.{\displaystyle x.} При x=0{\displaystyle x=0} левая часть положительна, поэтому исходное неравенство есть тождество (верно при всех x{\displaystyle x}).

Пример 4. x2+6x+15<0.{\displaystyle x^{2}+6x+15<0.} Как и в предыдущем примере, здесь левая часть всегда положительна, поэтому неравенство не имеет решений.

Аналогично, разложением на множители, можно решать неравенства высших степеней. Другой способ — построить график левой части и определить, какие знаки она имеет в различных интервалах^[6].

Некоторые известные неравенства

Ниже приведены практически полезные неравенства, тождественно выполняющиеся, если неизвестные попадают в указанные границы^[7].

(1+x)n⩾1+nx,{\displaystyle (1+x)^{n}\geqslant 1+nx,} где x⩾−1,n{\displaystyle x\geqslant -1,n} — натуральное число.

|a+b|⩽|a|+|b|{\displaystyle |a+b|\leqslant |a|+|b|}

См. следствия этого неравенства в статье Абсолютная величина.

Знаки неравенства в языках программирования

Символ «не равно» в разных языках программирования изображается по-разному.

Символ	Языки
!=	C, Java, PHP, Python
<>	Basic, Pascal
~=	Lua
/=	Haskell, Fortran, Ada
#	Modula-2, Oberon

Коды знаков неравенств

См. также

Примечания

1. ↑ ^{1 2} Неравенства // Математическая энциклопедия (в 5 томах). — М.: Советская Энциклопедия, 1982. — Т. 3. — С. 999.
2. ↑ Справочник по элементарной математике, 1978, с. 177.
3. ↑ Справочник по элементарной математике, 1978, с. 178.
4. ↑ Элементарная математика, 1976, с. 217—222.
5. ↑ Справочник по элементарной математике, 1978, с. 180—181.
6. ↑ Элементарная математика, 1976, с. 212—213, 219—222.
7. ↑ Справочник по элементарной математике, 1978, с. 174—176.

Литература

• Беккенбах Э. Ф. Неравенства. — М.: Мир, 1965.
• Выгодский М. Я. Справочник по элементарной математике. — М.: Наука, 1978.
• Зайцев В. В., Рыжков В. В., Сканави М. И. Элементарная математика. Повторительный курс. — Издание третье, стереотипное. — М.: Наука, 1976. — 591 с.
• Харди Г. Г., Литлвуд Д. И., Полиа Д. Неравенства. — М.: Иностранная литература, 1948.

wiki.sc

Основные методы решения неравенств

21 января 2014 г. 15:09:55

Неравенством называется запись, в которой функции соединены знаком (или несколькими знаками) отношения «>», «<«, » «, » «.

Неравенства, содержащие два знака отношения, называются двойными, три знака отношения — тройными и т.п. Примеры таких неравенств:

f(x) > g(x),

f(x) < g(x),

f(x)   g(x),

f(x)   g(x).

f(x) < h(x) < g(x) это пример двойного неравенства.

Неравенства f(x) > g(x),   f(x) < g(x),  называются  строгими,   а  неравенства
f(x)   g(x), f(x)   g(x) — нестрогими.

Решением неравенства, называется всякое значение переменой, при котором  данное  неравенство  верно.  Например,   решением  неравенства        f(x) > g(x) является всякое значение переменной x = a, при котором справедливо неравенство 
f(a) > g(a), или функция f(x) при x = a принимает большее значение чем функция g(x).

Задание «решить неравенство» означает, что требуется найти множество всех его решений. Это множество может оказаться пустым — в случае, когда решений нет. Множество всех решений неравенства будем называть его ответом.

Неравенство  В  называется следствием неравенства  А , если всякое решение  А является решением неравенства  В . В этом случае используется запись  А    В.  Два неравенства  А  и  В  называются равносильными (или эквивалентными пишем
А     В  либо  А  ~  В) , если их ответы совпадают. Если А    В  и В   А, то неравенства А и В эквивалентны.

Запись нескольких неравенств под знаком фигурной скобки называется системой (число и вид неравенств, входящих в систему, может быть произвольным). Решение системы неравенств есть пересечение решений всех входящих в нее неравенств. Двойное неравенство f(x) < g(x) < h(x) можно записать в виде системы:

Запись нескольких неравенств, объединенных квадратной скобкой, называется совокупностью данных неравенств. Решение совокупности есть объединение решений входящих в нее неравенств.

 

Пример 1.  Решить неравенство 

Решение.

Частное двух чисел положительно в том случае, когда и делимое, и делитель положительны, или они отрицательны. Опираясь на это утверждение составим совокупность двух систем неравенств.

Сначала решим систему неравенств

Первая система равносильна неравенству х > 1.

Теперь, решаем систему неравенств:

Вторая система равносильна неравенству x < -1.

Решение (множество значений переменной обращающих данное неравенство в истинное числовое неравенство) искомого неравенства можно записать несколькими способами:

1)  x >1 и x < -1.

2) 

3) x  (- ; -1)   (1; + ).

Сформулируем несколько часто используемых при отыскании решений свойств неравенств, все они уже знакомы Вам.

1. К обеим частям неравенства можно прибавить одну и туже функцию определенную в ОДЗ данного неравенства. Если f(x) > g(x) и h(x) — любая функция определенная в ОДЗ данного неравенства, то f(x) + h(x) > g(x) + h(x)

 2. Если обе части неравенства умножить на положительную функцию, определенную в ОДЗ данного неравенства (или на положительное число), то получим неравенство, равносильное исходному неравенству:

 если f(x) > g(x) и h(x) > 0, то f(x)h(x) > g(x)h(x)

3. Если обе части неравенства умножить на отрицательную функцию, определенную в ОДЗ данного неравенства (или на отрицательное число) и знак неравенства изменить на противоположный, то полученное неравенство эквивалентно данному неравенству:

  если  f(x) > g(x) и h(x) < 0, то f(x)h(x) < g(x)h(x)

4. Неравенства одинакового смысла можно почленно складывать. Если f(x) > g(x) и m(x) > h(x), то f(x) + m(x) > g(x) + h(x).

5.Неравенства противоположного смысла можно почленно вычитать  если  f(x) > g(x) и h(x) < m(x), то f(x) — h(x) < g(x) — m(x).

6. Неравенства одного смысла с положительными частями можно почленно умножать.

 Если f(x) > g(x) > 0 и  m(x) > h(x) > 0 , то   f(x) g(x) > m(x) h(x).

7. Неравенства, образованные неотрицательными функциями, можно почленно  возводить  в  положительную  степень:

 если f(x) > g(x) > 0 и m > 0, то (f(x)) ^m  > (g(x)) ^m .

Иногда, решая неравенство, приходится переходить к неравенству — следствию, т.е. выполнять неравносильное преобразование (как правило, связанные с расширением ОДЗ): заменить функцию f(x) — f(x) нулем, сократить неравенство f{x)g{x) > f(x)h{x) на общий положительный множитель f{x) и т.п. Решения, найденные в результате этих действий, могут оказаться посторонними. Перед записью ответа их следует «отсечь»посторонние решения.

Пусть  M  – множество допустимых значений переменной х данного неравенства (ОДЗ).  B  – множество найденных решений неравенства.  A  множество решений данного неравенства. Тогда  A = B   M.

Пример 2  .Решить неравенство  (1). .

Решение.

Вычтем из обеих частей неравенства функцию  получим неравенство 3х > 9.

Разделим обе части полученного неравенства на положительное число 3 в результате получим x > 3 (2). Выполнив это преобразование, мы заменили неравенство (1) неравенством (2). Эти неравенства не равносильны.(1) (2).

M = (- ; 8)  (8; +  )- ОДЗ неравенства (1).

B = (3; + ) — это решение неравенства (2).

Найдем множество решений неравенства (1)

A = B   M (- ; 8) (8; +  )   (3; + ) = (3; 8)   (8; + ),

Ответ: x (3; 8)  (8; + ).

Метод интервалов

Метод интервалов часто используют при решения неравенств. Он позволяет свести решение неравенства f(x) > 0 (<, <, >) к решению уравнения f(x) = 0.

Метод заключается в следующем:

1. Находится ОДЗ неравенства.

2. Неравенство приводится к виду f(x) > 0(<, <, >) (т.е. правая часть переносится влево) и упрощается.

3. Решается уравнение f(x) = 0.

4. На числовой оМетод интервалов часто используют при решения неравенств. Он позволяет свести решение неравенства f(x) > 0 ( , <,  ) к решению уравнения f(x) = 0.

Метод заключается в следующем:венство строгое, и закрашенных, если оно нестрогое.

5. Все точки, отмеченные на ОДЗ и ограничивающие его, разбивают это множество на так называемые интервалы знакопостоянства. На каждом таком интервале определяется знак функции f(х).

6. Ответ записывается в виде объединения  отдельных  множеств, на  которых f{x) имеет соответствующий знак. Точки, отмеченные закрашеными кружками, в ответ входят, отмеченные пустыми — нет. Точки ОДЗ, являющиеся граничными, включаются (или не включаются) в ответ после дополнительной проверки.

Метод интервалов основан на том, что непрерывная функция f(x) может изменить знак либо в граничных точках ОДЗ, где она «разрывается», либо проходя через ноль, т.е. в точках, являющиеся корнях уравнения f(x) = 0. Ни в каких других точках перемены знака не происходит.

 Пример 3.  Решить неравенство. 

Решение.

ОДЗ:  откуда имеем x [-1; 5)  (5; + )

Решим уравнение   Числитель дроби равен 0 при x = -1, это и есть корень уравнения. Отметим найденный корень на чертеже (черным кружком, т.к. неравенство нестрогое), предварительно отметив ОДЗ:

Чтобы определить знак на промежутке (-1; 5) возьмем число 0, 

Чтобы определить знак на втором промежутке возьмем число 8, 

Точки 0 и 8 выбирались произвольно, но так, чтобы упростить процесс вычисления каждого значения функции.

Ответ:   (-5; + ).

Пример 4.  Решить неравенство 

Решение.

Используя свойство частного и определение квадратного корня делаем вывод, что    откуда   ОДЗ: x (0; 1)  (1; 7)  (7; + )

Решим уравнение

x = 1.

На промежутке (0;1) возьмем точку 0,5;

 

На промежутке (1; 7) возьмем точку 4,

На промежутке (7; + ) возьмем точку 9,

Расставим знаки на координатной прямой.

 

Таким образом, решением данного неравенства является множество чисел принадлежащих промежутку (0; 1)  (1; 7)

Эти примеры наглядно демонстрируют, что промежутки знакопостоянства не обязательно чередуются, процесс определения знака на промежутке может оказаться довольно трудной задачей.

Полезно запомнить следующее.

 Если функция представляет собой произведение нескольких не повторяющихся множителей, имеющих вид (ax + b), где a > 0, то знаки функции на промежутках справа на лево чередуются с «плюса» на «минус»… Если какой-то множитель повторяется четное число раз, то при переходе через эту точку смены знака не происходит. В примере №4 Такой точкой была точка 1

Пример №5.  Решить неравенство (2x — 6)(3x + 12)(5x + 1)<0.

Решение.

Нули функции: — 4; — 0,2; 3.

Функция в левой части неравенства представляет собой произведение не повторяющихся множителей, значит знаки  этой функции чередуются cправа на лево с «+» на «-» ….

Решение данного неравенства x  (- ; -4) (-0,2; 3).

 

dz-online.ru

Свойства числовых неравенств, с примерами

Для любых двух действительных чисел имеет место одно из трех соотношений:

Такие соотношения называются числовыми неравенствами. Запись означает, что разность отрицательная, а запись , что разность – положительная.

Неравенства отношений называют строгими, неравенства называют нестрогими.

Свойства числовых неравенств

1. Если , то . Если , то .
2. Если и , то .
3. Если , то для любого числа c имеет место неравенство

      

4. Если , то , если – некоторое положительное число.
5. Если , то , если – отрицательное число.
6. Неравенства одинакового знака можно почленно складывать:

   и , то .

7. Неравенства разных знаков можно почленно вычитать:

   если и , то .

8. Если и , то , где – положительные числа.
9. Обе части неравенства с положительными членами можно возводить в одну и ту же натуральную степень:

   если , то , для положительных чисел .

Примеры решения задач

Понравился сайт? Расскажи друзьям!

ru.solverbook.com