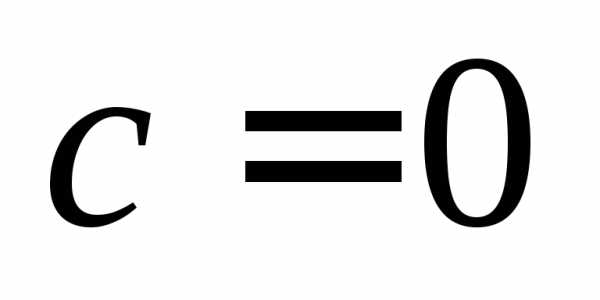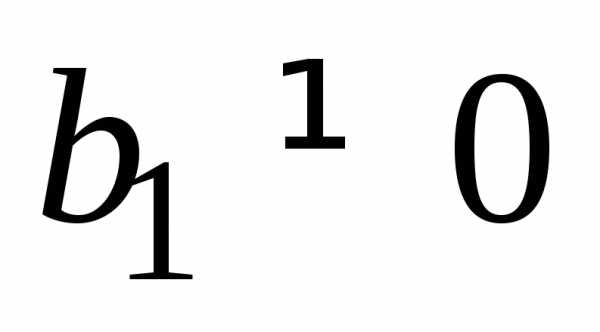4.4. Приведение к каноническому виду уравнения кривой 2-го порядка
Общее уравнение кривой 2-го порядка:
(23)
Уравнение (23) можно представить в виде , где – квадратичная форма уравнения кривой, а – линейная функция.
Приведение уравнения кривой (23) к каноническому виду начинается с приведения к каноническому виду соответствующей квадратичной формы . Её матрица Из характеристического уравнения находятся собственные значения и матрицы , при этом , так как . Затем находят соответствующие собственные векторы, которые после нормировки образуют ОНБ .
В новом базисе квадратичная форма примет канонический вид:
. (24)
Переход от ОНБ к ОНБ описывается матрицей , в столбцах которой находятся координаты векторов ОНБ . Связь между координатами и определяется из уравнения т. е.
. (25)
Подставляя зависимости (25) в линейную функцию получим:
Тогда уравнение (23) примет вид:
(26)
Выделяя в (26) полные квадраты, получим каноническое уравнение одной из кривых 2-го порядка. О какой кривой идет речь, можно определить сразу по матрице квадратичной формы. Если , то линия, задаваемая уравнением (23),
Пример 20. Определить тип кривой 2-го порядка и построить её:
Решение. Уравнение кривой представим в виде Где – квадратичная форма, – линейная функция.
Квадратичная форма, соответствующая заданной кривой, Её матрица .
Так как , то кривая параболического типа. Составим характеристическое уравнение и найдём собственные значения матрицы :
Собственные векторы, соответствующие найденным собственным значениям:
Построим ОНБ из собственных векторов:
Матрица перехода Выполним проверку соответствия ориентации ОНБ ориентации ОНБ : , значит, ориентация совпадает. В этом базисе .
Так как то Подставляя эти разложения в линейную часть кривой, получим:
Тогда уравнение кривой примет вид или т. е. где Заданная кривая изображена на рисунке 1.

Рисунок 1
Пример 21. Привести уравнение кривой 2-го порядка к каноническому виду и определить тип кривой:
Решение. Уравнение кривой представим в виде Где – квадратичная форма, – линейная функция.
В нашем случае , её матрица .
Определим тип кривой. Для этого вычислим Так как То заданная кривая эллиптического типа.
Приведем квадратичную форму к каноническому виду. Для нахождения собственных значений матрицы составим характеристическое уравнение: Т. е. , тогда .
Теперь найдём соответствующие им собственные векторы:
Построим ОНБ: , тогда матрица перехода от ОНБ к ОНБ имеет вид: Так как значит, ориентация ОНБ соответствует ориентации ОНБ .
Матрица заданной квадратичной формы в базисе имеет вид: , а сама квадратичная форма: .
Напомним, что матрица может быть получена в результате преобразования подобия: , где – матрица перехода к новому ОНБ. Координаты и связаны между собой соотношением: т. е. .
Преобразуем линейную часть уравнения кривой:
Теперь можно записать уравнение кривой в координатах :
Таким образом, выполнен первый шаг в преобразовании кривой к каноническому виду, в результате которого в исходном уравнении кривой исчезло слагаемое, содержащее произведение координат и .
Выделим полные квадраты: или . Если то каноническое уравнение заданной кривой 2-го порядка примет вид и задаёт эллипс с полуосями Кривая изображена на рисунке 2.
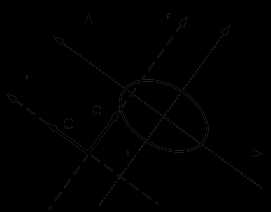
Рисунок 2
Литература: [3, 6, 7, 15].
| < Предыдущая | Следующая > |
|---|
matica.org.ua
АГ. Приведение уравнения алгебраической линии второго порядка к каноническому виду
Теоретический минимумАлгебраические линии второго порядка достаточно часто встречаются в математике и физике, поэтому их исследование представляет собой важную
задачу. К счастью, это исследование несложно провести в наиболее общем виде до конца. В частности можно показать, что общее уравнение
приводится двумя преобразованиями к значительному более простому — каноническому виду. Эти преобразования допускают геометрическую интерпретацию.
Уравнение (1) определяет кривую одного из трёх типов (вырожденные случаи упомянем ниже отдельно): эллипс, гиперболу или параболу. Эти кривые обычно
переходе к системе координат, по отношению к которой кривая будет расположена так, как показано на рис. 1 а, б, в. Обратите внимание: эллипс и гипербола имеют
центр симметрии, и начало координат совмещено с ним. Также следует отметить, что большая ось эллипса расположена вдоль оси абсцисс, а мнимая ось гиперболы —
вдоль оси ординат. У параболы вершина совмещена с началом координат, а ветви направлены вправо. Случаям рис. 1 а, б, в соответствуют уравнения
Именно к такой форме и нужно приводить уравнение кривой второго порядка: в этом случае понятно расположение кривой на координатной плоскости, и легко
определяются её основные характеристики.

Возможны два типа преобразований системы координат : параллельный перенос
(начало координат переносится в точку ) и поворот на угол (против часовой стрелки)
Параллельный перенос может исключить слагаемые, пропорциональные и ; поворот исключает слагаемое, пропорциональное .
Перед тем как начинать преобразовывать уравнение, следует вычислить т.н. малый дискриминант . Он позволяет определить тип кривой:
соответствует эллипсу, соответствует гиперболе, соответствует параболе (опять-таки
возможны случаи вырождения). Если , то первое действие — перенос начала координат в центр симметрии кривой. Выполняем
преобразование (2) и требуем обращения в нуль линейных слагаемых по переменным и . Второе действие — поворот, после которого
исчезнет слагаемое, пропорциональное .
Если , то у кривой нет центра симметрии. Поэтому сначала выполняется поворот, убирающий слагаемое, пропорциональное .
Затем выполняется сдвиг, с помощью которого вершина параболы совмещается с началом координат.
Наконец, упомянем о вырожденных случаях. Эллипс может выродиться в точку или вовсе стать мнимым
. Гипербола может выродиться в две пересекающиеся прямые .
Парабола может выродиться в две параллельные прямые , одну прямую или две мнимые прямые ().
Заметим, что несложно вывести формулы, с помощью которых можно сразу по уравнению (1) указать преобразование координат, приводящее это
уравнение к каноническому виду и сам этот вид. Однако запоминать эти формулы сложно да и не нужно: все преобразования исключительно просты.
Также существуют и другие характерные числа, роль которых подобна роли малого дискриминанта (большой дискриминант, полуинварианты) —
они позволяют, не проводя преобразований, указать не только тип кривой, но и отделить вырожденные случаи. Кроме того, через них выражаются
коэффициенты уравнения кривой в канонической форме. Эти формулы здесь также не обсуждаются.
Рассмотрим несколько примеров. Задание — привести уравнение к каноническому виду.
Примеры.
Пример 1. Случай центральной кривой.
Здесь , т.е. уравнение описывает кривую гиперболического типа. Это значит, что нужно начинать с параллельного
переноса системы координат. Применяя замену (2), получаем
.
Требуем, чтобы коэффициенты при линейных слагаемых обратились в нуль:
Уравнение принимает вид
.
Теперь выполняем поворот (3):
.
Требуем обращения в нуль коэффициента при слагаемом, пропорциональном :
.
Мы выбрали один угол поворота, хотя их существует целое семейство. Уравнение принимает вид
или
.
Уже понятно, что это уравнение гиперболы, но в каноническом виде справа должна быть, строго говоря, единица. Поэтому нужно повернуть
систему координат ещё на угол — переменные поменяются местами и уравнение примет канонический вид.
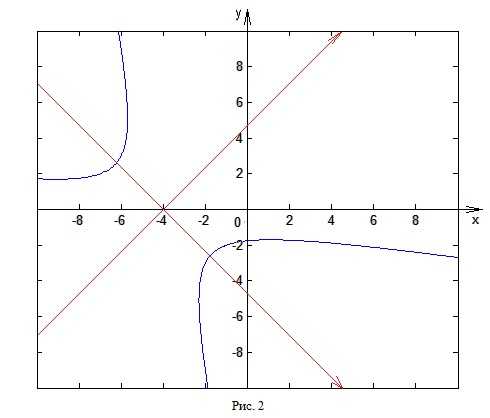
На рис. 2 изображена гипербола в исходной системе координат, и изображены оси координат, в которых уравнение гиперболы имеет
Пример 2. Случай нецентральной кривой: случай преобразования сводящегося к повороту.
Здесь , т.е. уравнение описывает кривую параболического типа. Это значит, что нужно начинать с поворота
системы координат. Применяя замену (3), получаем
.
Требуем обращения в нуль коэффициента при :
.
Опять-таки выбран один из возможных углов поворота. Подстановка этих функций угла поворота в уравнение кривой приводит к уравнению
.
И снова понятно, что получилось уравнение параболы, но оно не каноническое. Для приведения к каноническому виду нужно выполнить ещё один
поворот на угол .
На рис. 3 изображена данная парабола в исходной системе координат, и изображены оси координат, в которых уравнение имеет канонический вид.
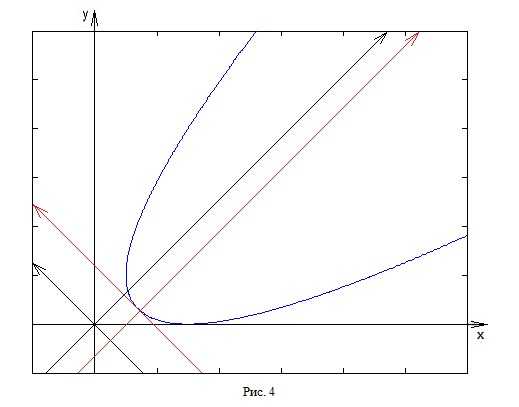
Пример 3. Случай нецентральной кривой.
Здесь , т.е. уравнение описывает кривую параболического типа. Это значит, что нужно начинать с поворота
системы координат. Применяя замену (3), получаем
.
Требуем обращения в нуль коэффициента при :
.
И снова выбран один из возможных углов поворота. Подстановка этих функций угла поворота в уравнение кривой приводит к уравнению
.
Теперь нужно выполнить параллельный перенос системы координат, чтобы совместить вершину параболы с началом координат.
Применять формальную процедуру замены координат нет необходимости (хотя можно сделать и так) — вместо этого перепишем уравнение тождественно
.
Фактически был выделен полный квадрат. Таким образом, второе преобразование очевидно:
.
Приходим к каноническому уравнению параболы:
.
На рис. 4 изображена данная парабола в исходной системе координат, и изображены оси координат, в которых уравнение имеет канонический вид.
Пример 4. Отсутствие геометрического образа.
Здесь , т.е. уравнение описывает кривую эллиптического типа. Это значит, что нужно начинать с параллельного
переноса системы координат. Применяя замену (2), получаем
.
Требуем, чтобы коэффициенты при линейных слагаемых обратились в нуль:
.
Уравнение принимает вид
.
Теперь выполняем поворот (3):
.
Чтобы пропорциональное слагаемое обратилось в нуль, выберем, например, .
Уравнение преобразуется к виду
.
Такое уравнение не задаёт кривой на плоскости (т.н. мнимый эллипс).
corum.mephist.ru
14.3. Приведение общего уравнения кривой второго порядка к каноническому виду
Пусть на плоскости задана декартова
система координат (декартов базис  ,
,  и точкаО– начало координат).
Рассмотрим общее уравнение 2-го порядка:
и точкаО– начало координат).
Рассмотрим общее уравнение 2-го порядка:
. (14.25)
Обозначим через  сумму старших слагаемых:
сумму старших слагаемых:
и рассмотрим квадратичную форму
.
Ее матрица  симметрическая.
симметрическая.
Пусть  — произвольное евклидово пространство,,
— произвольное евклидово пространство,, — линейный оператор в
— линейный оператор в с матрицей
с матрицей в базисе
в базисе ,
, ,
следовательно,
,
следовательно, — самосопряженный оператор в
— самосопряженный оператор в .
Тогда существует ортонормированный
базис, состоящий из собственных векторов
оператора
.
Тогда существует ортонормированный
базис, состоящий из собственных векторов
оператора (см.
лекцию 13, § 13.3, теорема 9), в этом базисе
матрица оператора
(см.
лекцию 13, § 13.3, теорема 9), в этом базисе
матрица оператора диагональная и имеет вид
диагональная и имеет вид ,
где
,
где — собственные значения (см. § 12.3).
— собственные значения (см. § 12.3).
Если матрица перехода от базиса  ,
, к базису
к базису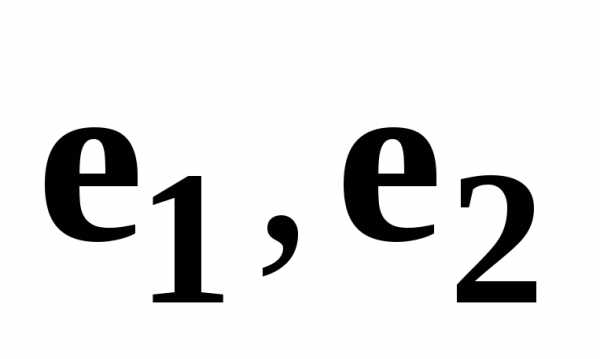 ,
то
,
то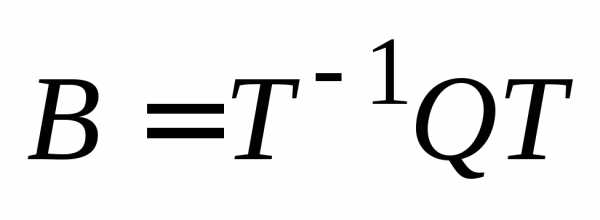 (см.
§ 12.2).
(см.
§ 12.2).
Рассмотрим теперь линейное преобразование
неизвестных с матрицей 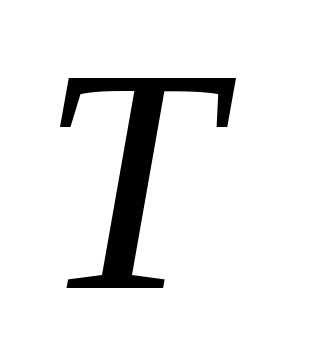 :.
Квадратичная форма от новых неизвестных
:.
Квадратичная форма от новых неизвестных имеет вид,
где
имеет вид,
где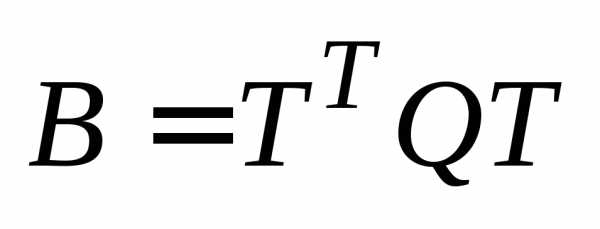 .
.
Итак, если 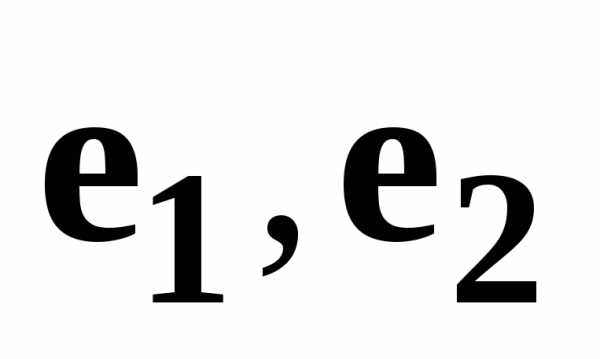 — ортонормированный базис из собственных
векторов оператора
— ортонормированный базис из собственных
векторов оператора ,
матрица
,
матрица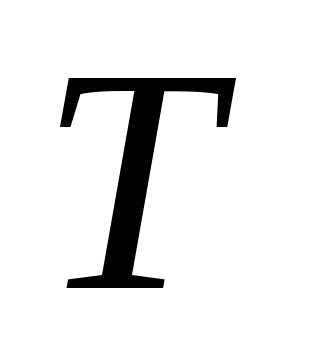 как матрица перехода от ортонормированного
базиса к ортонормированному ортогональна
(
как матрица перехода от ортонормированного
базиса к ортонормированному ортогональна
( )
, следовательно, матрица квадратичной
формы от неизвестных
)
, следовательно, матрица квадратичной
формы от неизвестных диагональная и.
диагональная и.
Такой способ приведения квадратичной формы к каноническому виду называется методом собственных векторов.
Пример 4. Привести квадратичную форму к каноническому виду методом собственных векторов.
Матрица  квадратичной формы имеет вид
квадратичной формы имеет вид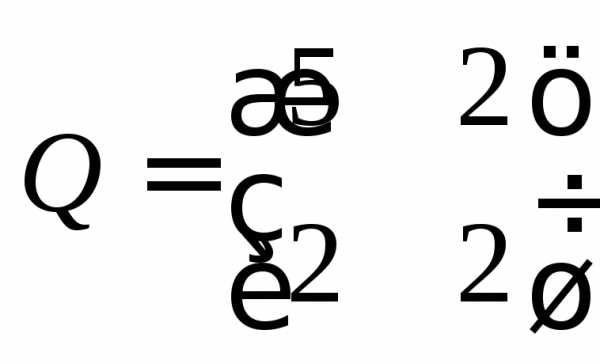 .
Рассмотрим в произвольном евклидовом
пространстве
.
Рассмотрим в произвольном евклидовом
пространстве ,,
линейный оператор
,,
линейный оператор с матрицей
с матрицей в некотором ортонормированном базисе
в некотором ортонормированном базисе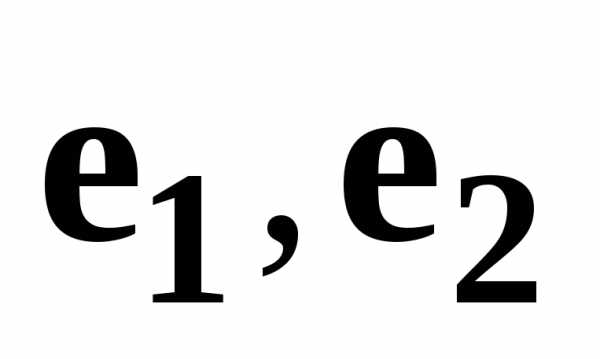 .
Найдем его собственные векторы.
.
Найдем его собственные векторы.
Характеристическое уравнение
,,
его корни ,
, .
.
Имеем для 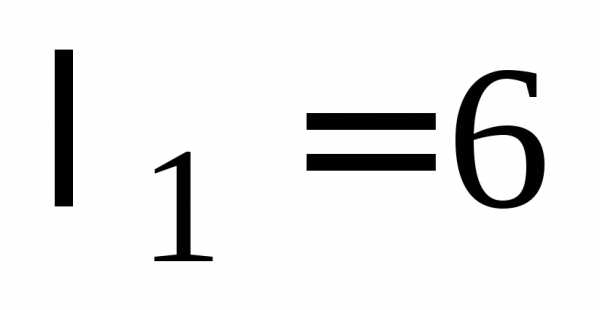 :и
:и ,
, ;
;
для 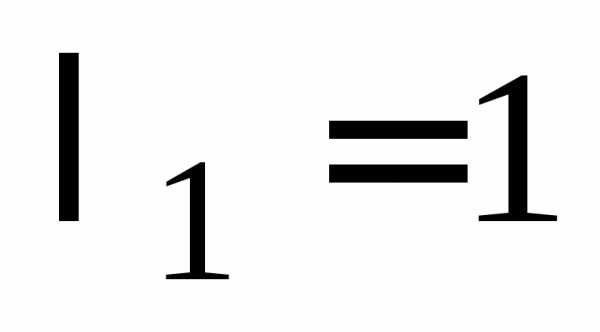 :и
:и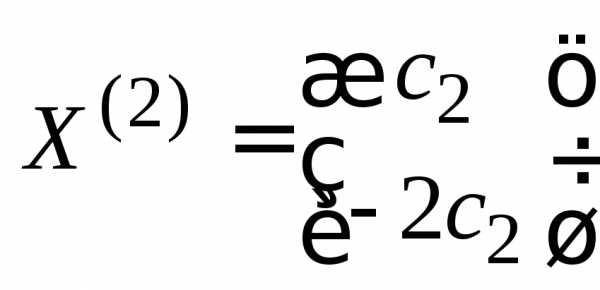 ,
,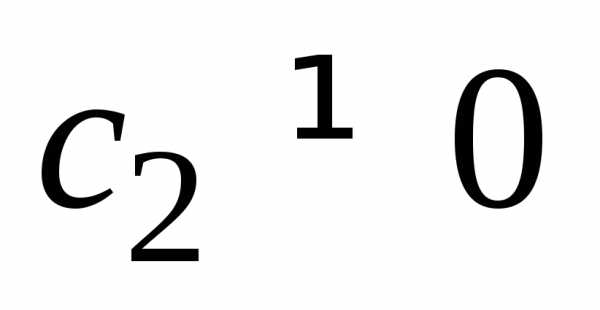 .
.
Положим 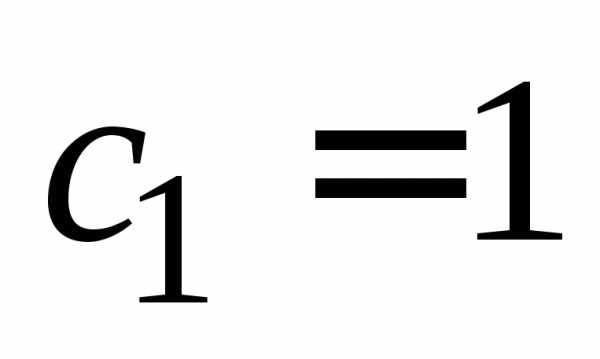 ,
,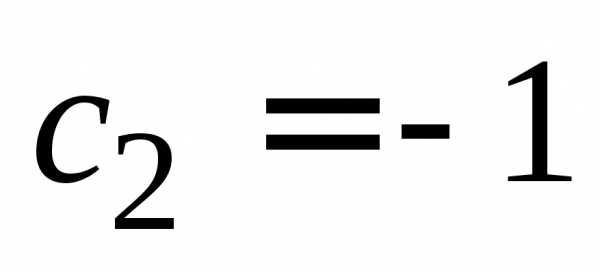 и получим
и получим ,
, .
.
В базисе  ,
, матрица оператора
матрица оператора диагональная:
диагональная: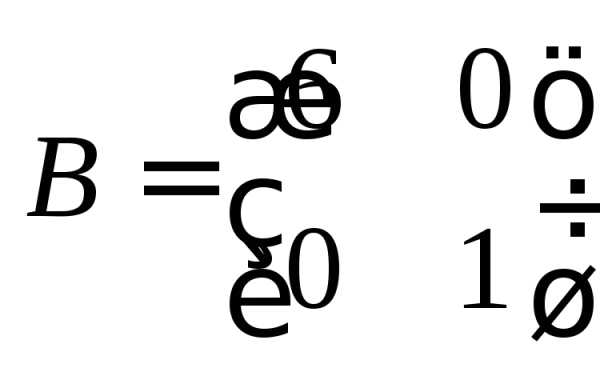 .
Нормируем векторы
.
Нормируем векторы и
и :и
:и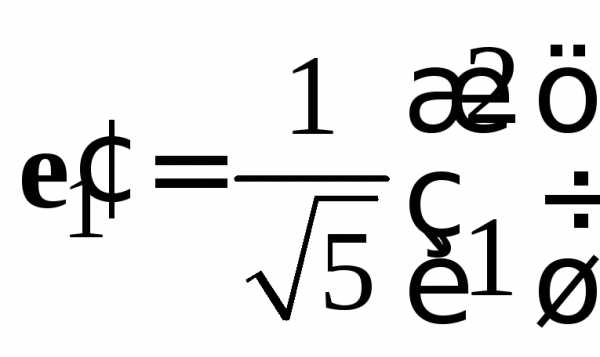 ,
,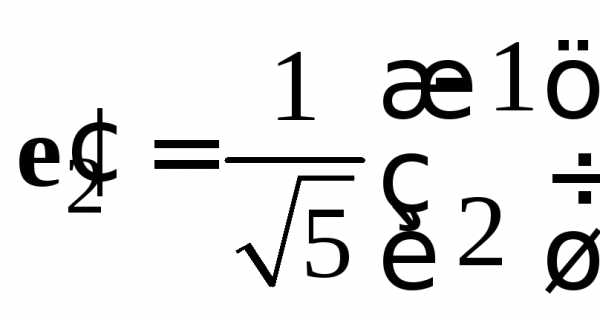 .
.
Матрица перехода от базиса  ,
, к базису
к базису ,
,
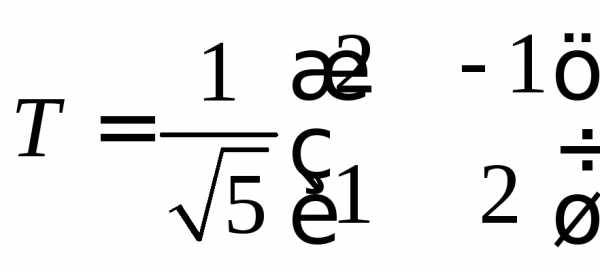 .
Вернемся к квадратичной форме. Положим,
т.е.
.
Вернемся к квадратичной форме. Положим,
т.е.
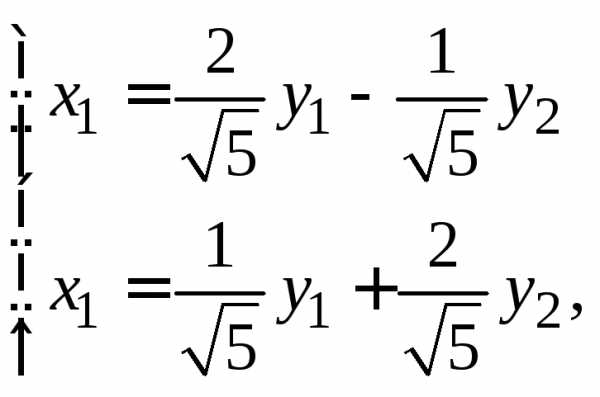 (14.26)
(14.26)
Тогда .
Замечание.Формулы (14.26) – формулы поворота осей
координат на угол против хода часовой стрелки. Угол
против хода часовой стрелки. Угол определяется соотношениями
определяется соотношениями
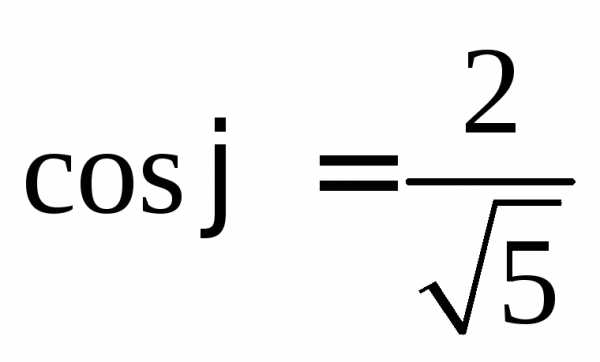 ,
,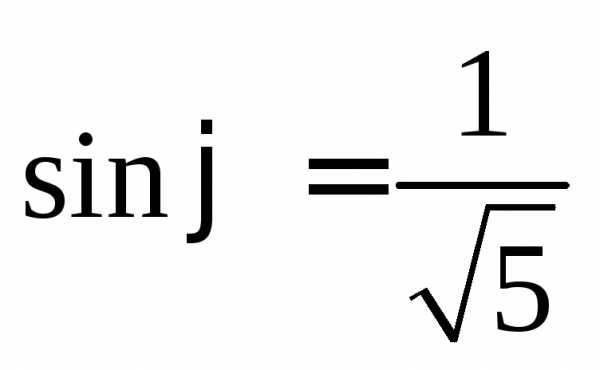 ().
().
В общем случае преобразование поворота
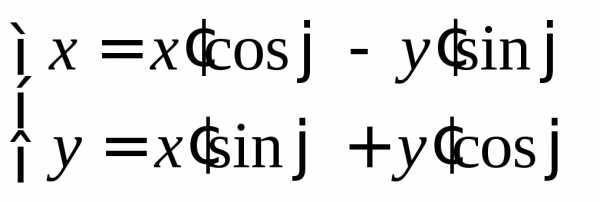 (14.27)
(14.27)
приведет линию (14.25) к виду
. (14.28)
Эта процедура называется приведением
линии 2-го порядка к главным осям (из
дальнейшего изложения будет ясно, что,
если (14.25) – эллипс или гипербола, новые
оси 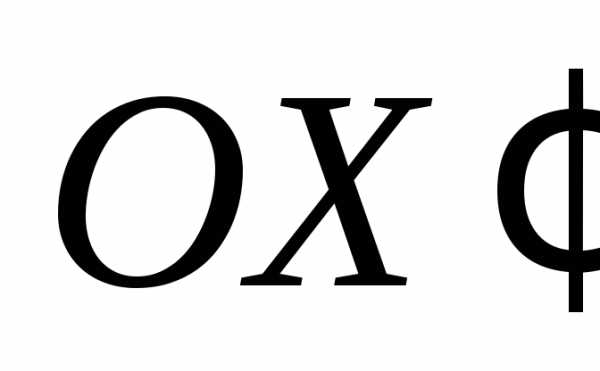 и
и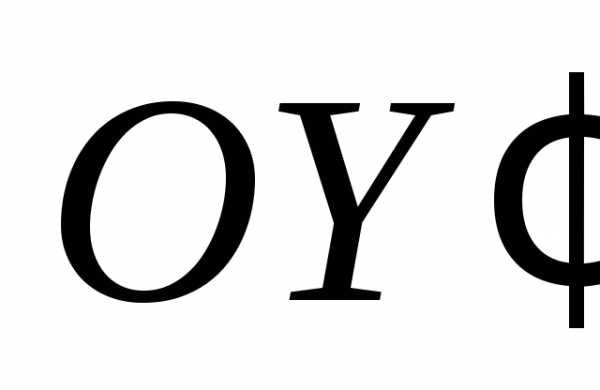 параллельны главным осям кривой).
параллельны главным осям кривой).
Коэффициенты 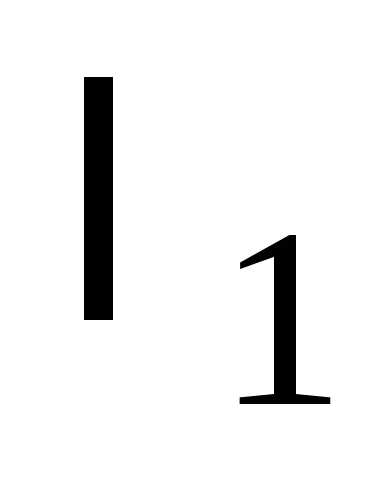 и
и в уравнении (14.28) – характеристические
числа матрицы
в уравнении (14.28) – характеристические
числа матрицы и могут быть найдены как корни уравнения, или
и могут быть найдены как корни уравнения, или
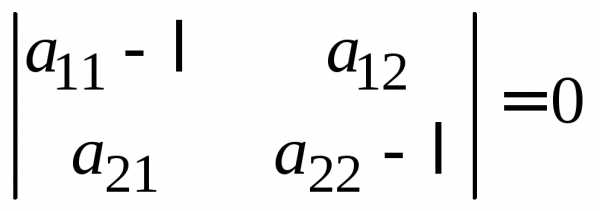 .
(14.29)
.
(14.29)
Обозначим
,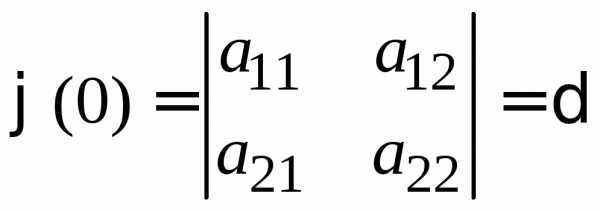 .
.
Имеем  (действительно, из (14.29) находим,
или,
и по теореме Виета).
(действительно, из (14.29) находим,
или,
и по теореме Виета).
Случай 1.(кривая эллиптического типа).
Преобразуем (14.28) следующим образом:
,
или, обозначив  ,
придем к равенству
,
придем к равенству
.
Положим 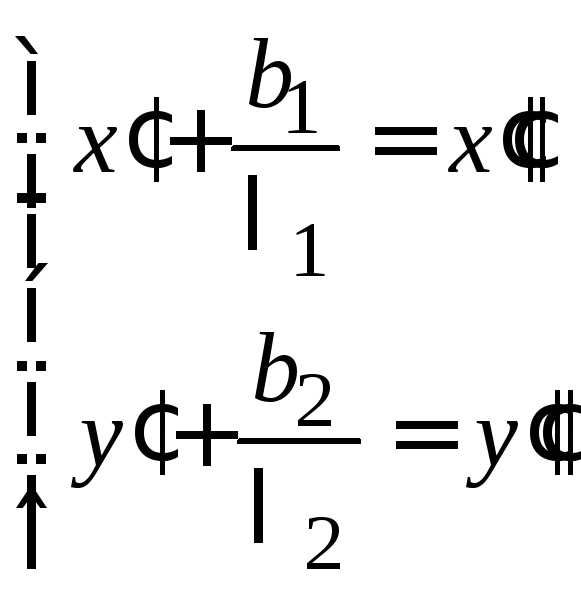 (14.30)
(14.30)
и в новой системе координат  имеем
имеем
. (14.31)
Формулы (14.30) – формулы параллельного
переноса начала координат в точку 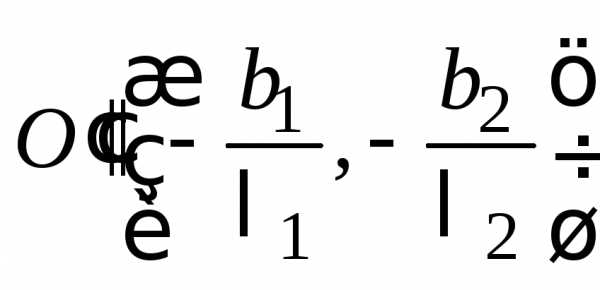 .
.
Случай 1. а) Знак противоположен знаку
противоположен знаку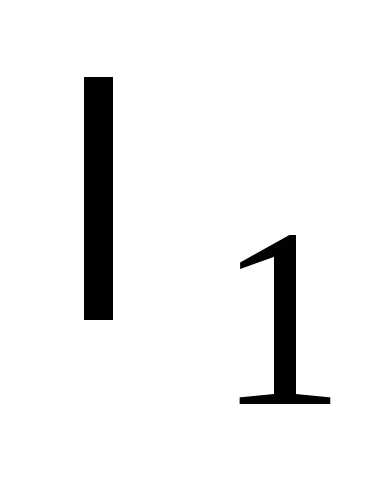 (и, следовательно, знаку
(и, следовательно, знаку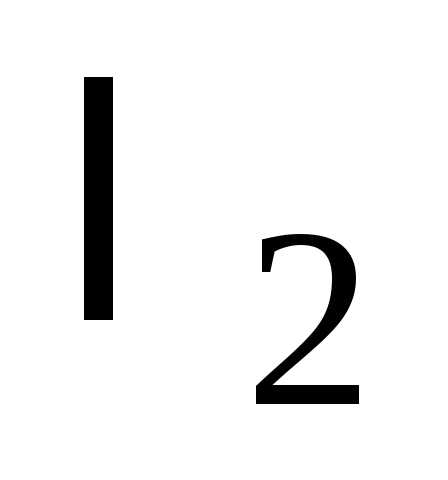 ).
Тогда (14.31) определяет эллипс:
).
Тогда (14.31) определяет эллипс:
 ;
;
б)  ,
уравнение (14.31) определяет одну точку:;
,
уравнение (14.31) определяет одну точку:;
в) Знаки  и
и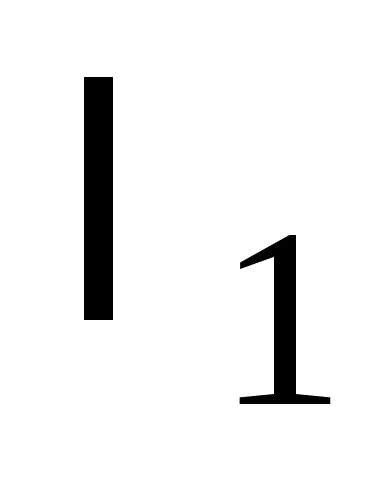 совпадают, нет точек (мнимый эллипс).
совпадают, нет точек (мнимый эллипс).
Случай 2.(кривая гиперболического типа).
В этом случае знаки 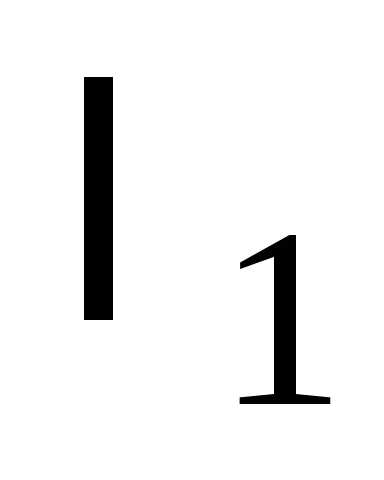 и
и противоположны.
противоположны.
а)  ,
уравнение (14.31) определяет гиперболу:
,
уравнение (14.31) определяет гиперболу:
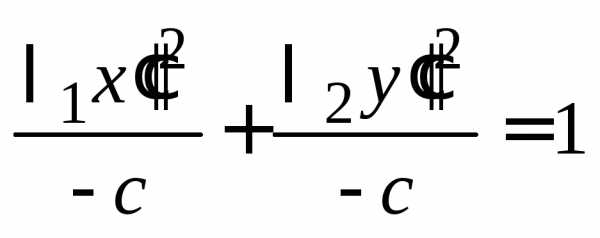 ;
;
б) 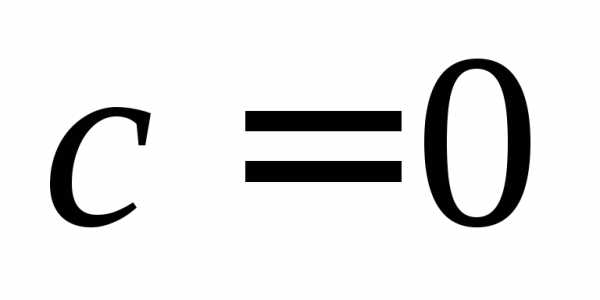 ,
уравнение (14.31) принимает вид:
,
уравнение (14.31) принимает вид:
.
Пусть 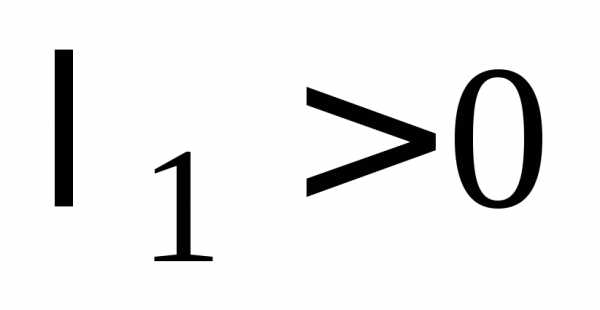 ,
тогда
,
тогда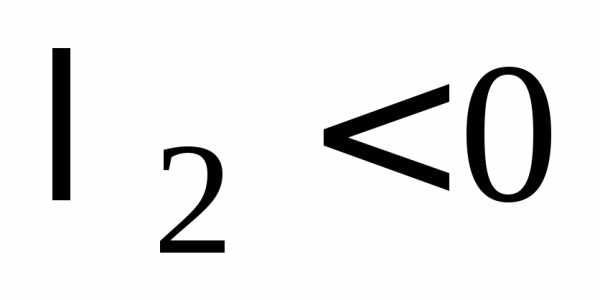 и уравнение (14.31) можно переписать в
следующем виде:
и уравнение (14.31) можно переписать в
следующем виде:
. (14.32)
Уравнение (14.32) определяет пару
пересекающихся прямых: 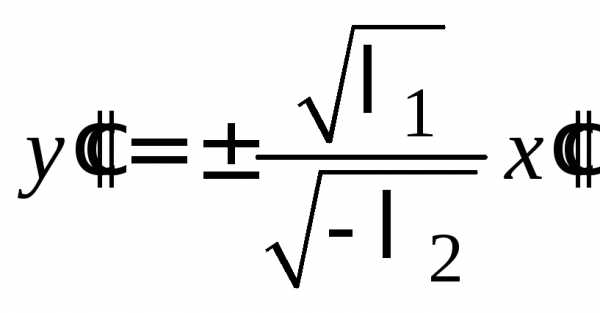 .
.
Случай 3.(кривая параболического типа).
Пусть для определенности 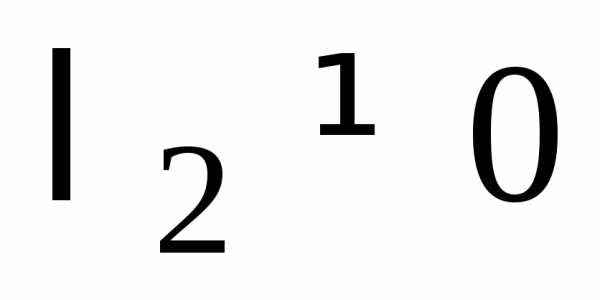 (тогда
(тогда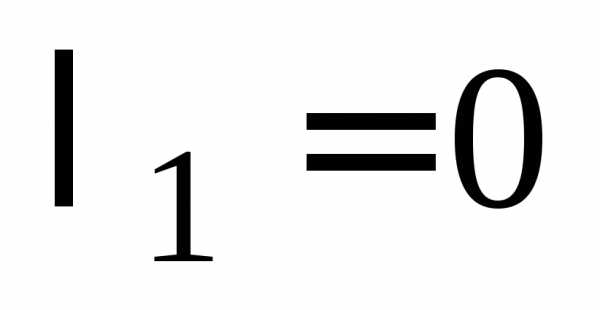 ).
).
Уравнение (14.25) преобразованием (14.27) приводится к виду
. (14.33)
Пусть 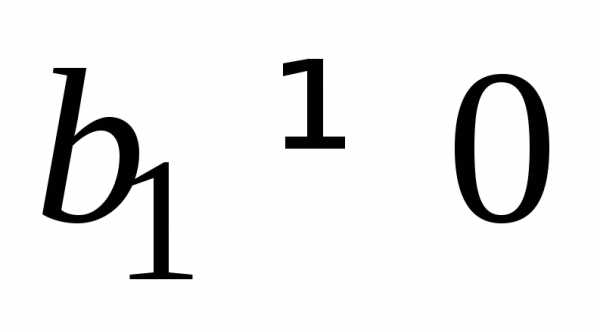 ,
тогда (14.33) можно переписать следующим
образом:
,
тогда (14.33) можно переписать следующим
образом:
.
Получим  и
и
. (14.34)
Уравнение (14.34) определяет параболу.
Если же  ,
то уравнение (14.33) перепишем в виде
,
то уравнение (14.33) перепишем в виде
.
Обозначив 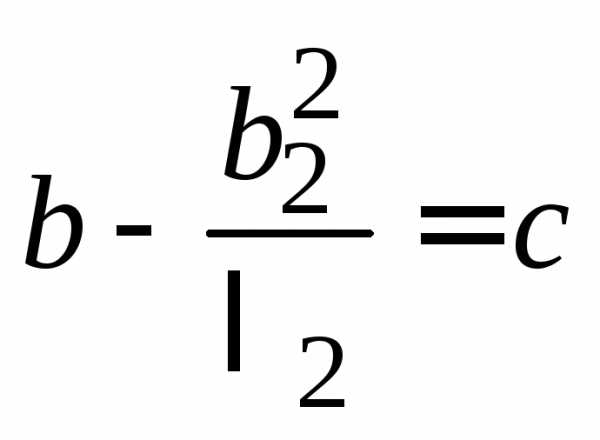 и положив
и положив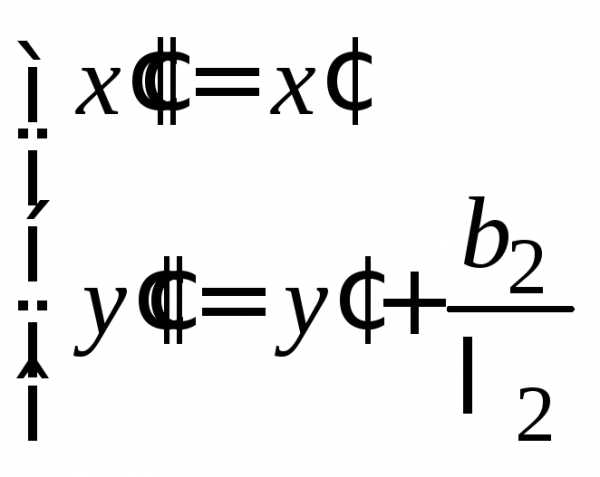 ,
придем к уравнению
,
придем к уравнению
. (14.35)
а) 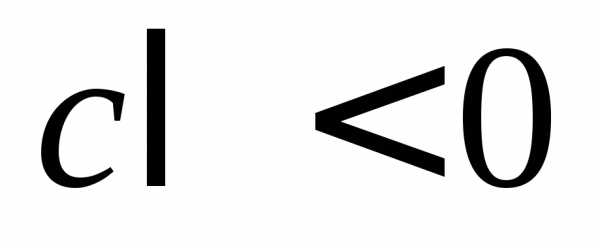 ,
уравнение (14.35) определяет пару параллельных
прямых:
,
уравнение (14.35) определяет пару параллельных
прямых: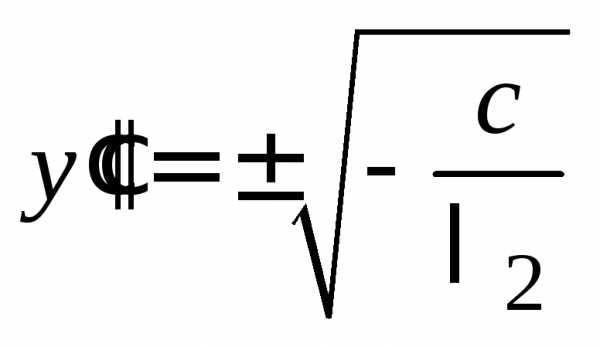 .
.
б)  ,
уравнение (14.35) определяет пару совпадающих
прямых:
,
уравнение (14.35) определяет пару совпадающих
прямых: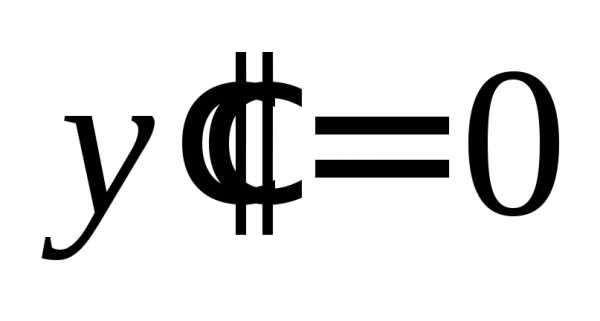 .
.
в) 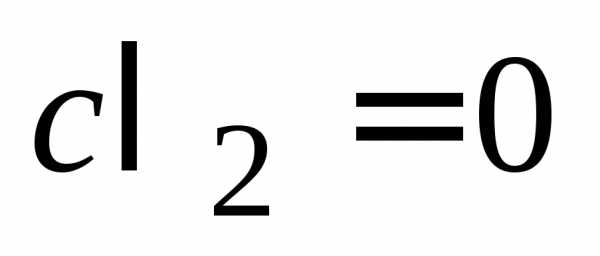 ,
нет точек (пара мнимых прямых).
,
нет точек (пара мнимых прямых).
Сведем полученные результаты в таблицу:
Кривая эллиптического типа |
| Эллипс | |
| Мнимый эллипс | ||
| Точка | ||
Кривая гиперболического типа |
| Гипербола | |
| Пара пересекающихся прямых | ||
Кривая параболического типа |
|
| Пара мнимых параллельных прямых |
| Пара параллельных прямых | ||
| Пара совпадающих прямых | ||
| Парабола | ||
Пример 5. Определить вид и расположение кривой 2-го порядка
. (14.36)
Слагаемые 2-го порядка в (14.36) составляют квадратичную форму
,
которую преобразование неизвестных по формулам
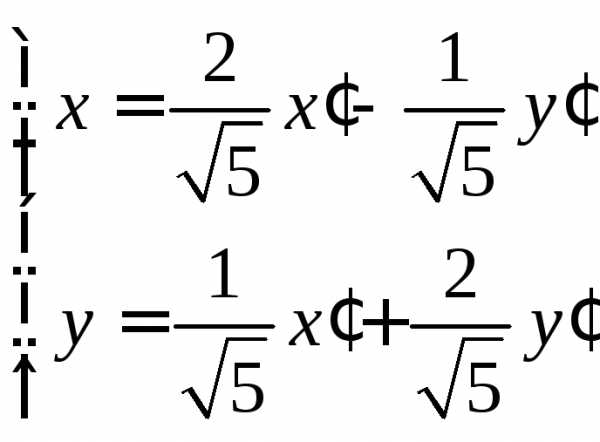 (14.37)
(14.37)
приводит к сумме квадратов (пример 4).
Тогда уравнение кривой (14.36) преобразованием (14.37) приводится к виду
.
Здесь 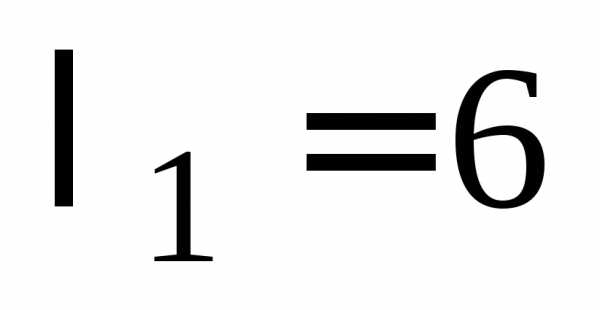 ,
, и, следовательно,,
кривая эллиптического типа.
и, следовательно,,
кривая эллиптического типа.
Как в случае 1, соберем слагаемые,
содержащие неизвестное 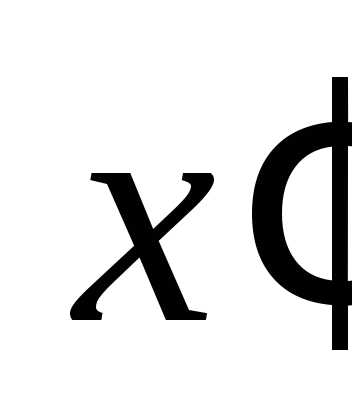 и дополним их до полного квадрата,
аналогично поступим со слагаемыми,
содержащими
и дополним их до полного квадрата,
аналогично поступим со слагаемыми,
содержащими :
:
, или
Положим 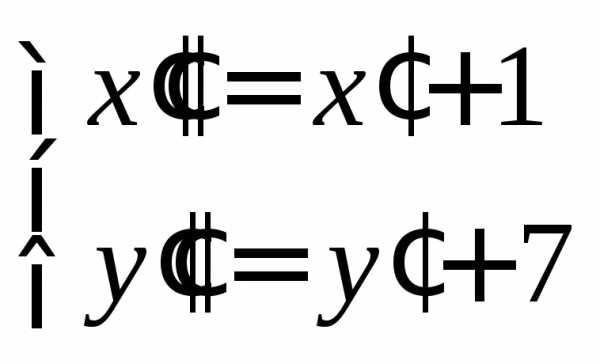 и получим
и получим
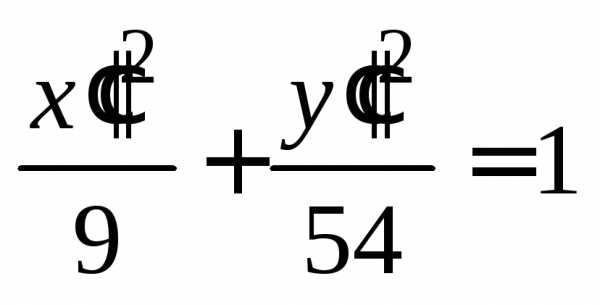
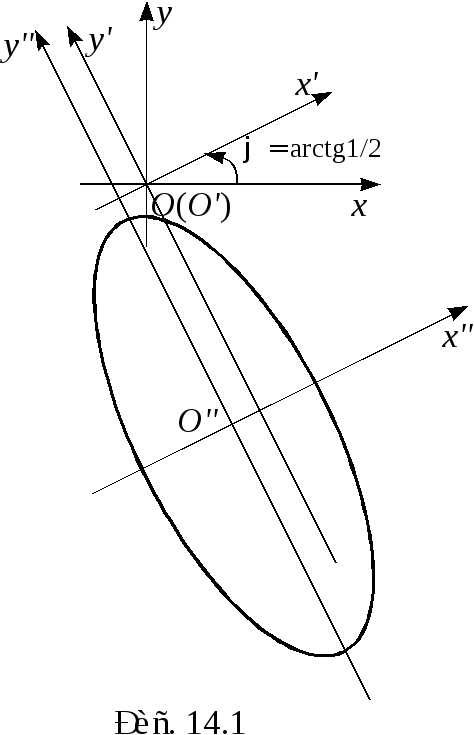 .
(14.38)
.
(14.38)
Уравнение (14.38) – уравнение эллипса с полуосями и центром в точке. Рис. 14.1 — схематический рисунок кривой.
195
studfiles.net
Приведение к каноническому виду общего уравнения кривых второго порядка
Задание 1. Определить тип кривой 2-го порядка, привести к каноническому виду её уравнение
.
Построить кривую.
Решение. Представим уравнение кривой в виде , где и – её квадратичная форма и линейная часть соответственно. Матрица квадратичной формы , , значит, кривая параболического типа.
Составим характеристическое уравнение:
,
Откуда , . Найдём собственные векторы.
При получим, что , откуда или . Пусть – базисная переменная, – свободная, тогда при получим , а соответствующий собственный вектор . Аналогично, при : , откуда , т. е. , тогда .
и ортогональны, так как соответствуют различным собственным значениям. Это можно проверить, вычислив непосредственно их скалярное произведение . Так как , то ОНБ из собственных векторов составят
и .
Проведём проверку соответствия ориентации ОНБ ОНБ . Для этого составим матрицу из векторов построенного ОНБ. Если , то надо менять и местами, если , то ориентации базисов совпадают. В нашем случае ориентации базисов совпадают, так как .
В этом базисе квадратичная форма примет вид: , при этом является матрицей перехода от ОНБ к ОНБ . Связь между координатами в этих базисах выражается соотношениями , . Подставляя эти разложения в линейную часть уравнения кривой, получим
.
Уравнение параболы примет вид: , или , т. е. , где , . Её график изображен на рисунке 11.
Ответ: парабола; .

Рисунок 11
Задание 2. Определить тип кривой 2-го порядка, привести к каноническому виду её уравнение
.
Построить кривую.
Решение. Представим уравнение кривой в виде , где и – её квадратичная форма и линейная часть соответственно. Матрица квадратичной формы , её , значит, кривая эллиптического типа.
Для нахождения собственных значений составим характеристическое уравнение: . Его корни , . Найдём собственные векторы.
При : , откуда получаем, что . Если – базисная переменная, – свободная, то, полагая , получим , тогда . Аналогично, при : , откуда, тогда .
Собственные векторы и ортогональны , а , тогда ОНБ составят , . Проверим соответствие ориентации ОНБ ориентации ОНБ : , т. е. ориентации совпадают. В этом базисе , − матрица перехода от ОНБ к ОНБ . Связь между координатами в разных базисах выражается соотношениями , . Подставляя эти формулы в линейную часть уравнения кривой, получим
,
Тогда уравнение кривой в новой системе координат примет вид: или , т. е. , где , .
График кривой изображен на рисунке 12.
Ответ: эллипс; .

Рисунок 12
| < Предыдущая | Следующая > |
|---|
matica.org.ua

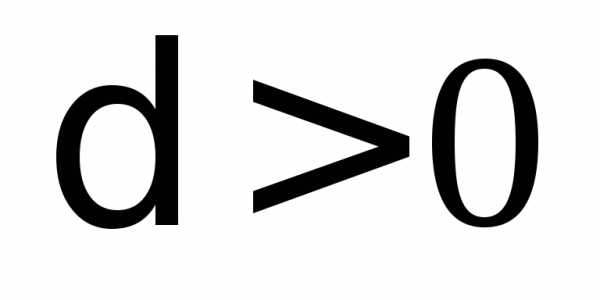
 и
и разных знаков
разных знаков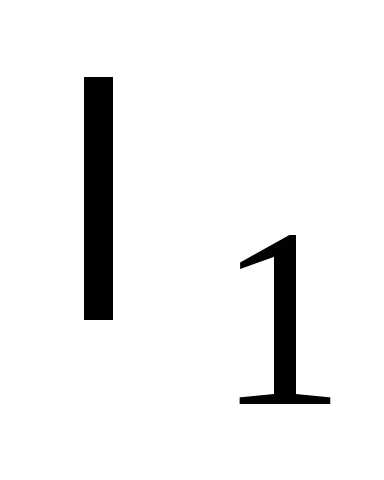 и
и одного знака
одного знака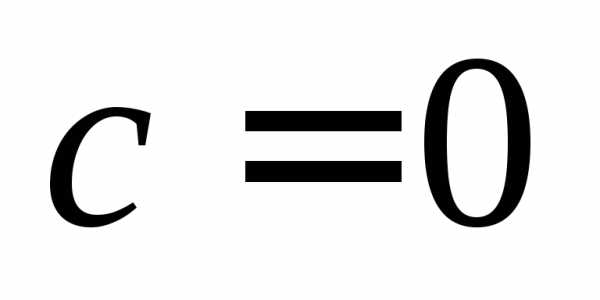
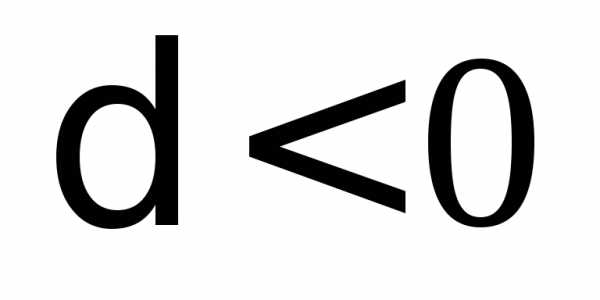

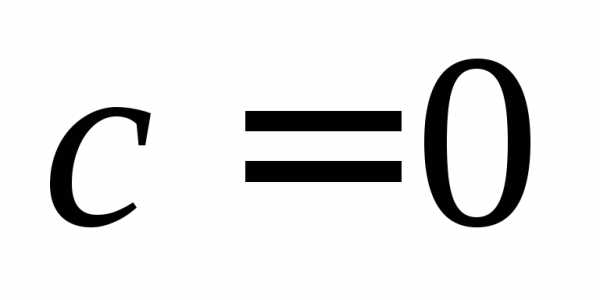


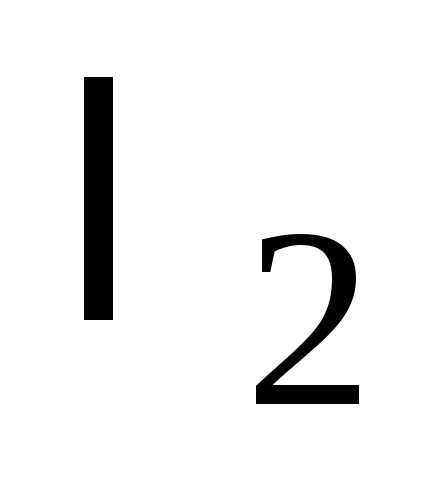 и
и одного знака
одного знака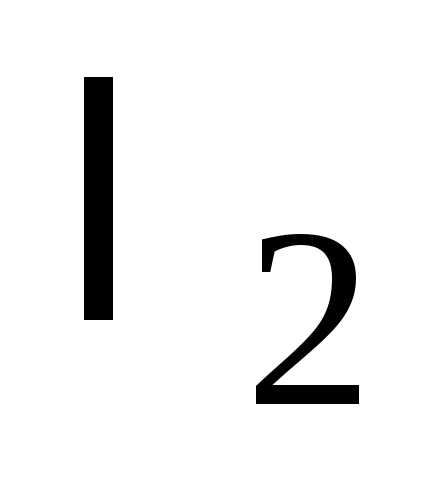 и
и разных знаков
разных знаков