Что такое скаляр и вектор
Физические величины различной природы могут иметь различную математическую структуру описания.
Из элементарного курса известны простейшие определения скаляра (скалярной величины) и вектора (векторной величины):
¾ скаляром называется величина, которая при определенном выборе единицы измерения однозначно характеризуется числом, ее измеряющим;
¾ вектор определяется своей величиной (модулем) и направлением в пространстве и складывается с другим вектором той же физической размерности по правилу треугольника или параллелограмма.
Для описания вектора в трехмерном пространстве (рис. П.1.1) необходимо одновременно задать три параметра (три проекции, или модуль вектора и углы между направлением вектора и какими-либо двумя из трех координатных направлений). Очевидное различие в математических структурах скалярной и векторной величин приводит к различию в свойствах указанных объектов.
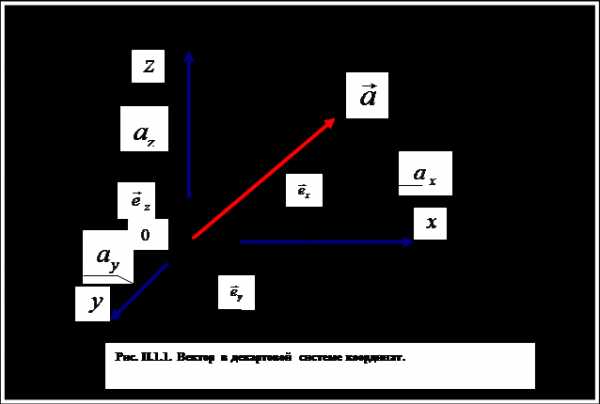
Строгая классификация физических объектов основана на изучении характера изменения их компонент при преобразованиях систем координат (т.е. при переходе от одной координатной системы к другой). В физике чаще всего имеют дело с преобразованиями систем координат в обычном трехмерном пространстве или в четырехмерном пространстве-времени Минковского.
Трансформационные свойства физических величин могут быть различны в этих случаях. К примеру, кинетическая энергия материальной точки — скаляр относительно преобразований системы координат в трехмерном пространстве и одна из компонент 4-вектора относительно преобразований в пространстве Минковского.
Важно отметить, что и вид преобразований системы координат может оказаться существенным. Так “вращения” и “сдвиги” координатных систем отличаются тем, что переводят “правые” координатные системы в “правые”, а «отражение» относительно одной из координатных поверхностей переводит «правую» координатную систему в «левую». Физическая величина может оказаться инвариантной (неизменной) при преобразовании «вращения» и неинвариантной при преобразовании «отражения».
При изучении преобразований систем координат в основной части курса мы ограничимся преобразованиями сдвига и вращения правых декартовых систем координат.
В общем, указание трансформационных свойств физической величины (т.е. ее тензорного характера) имеет смысл только по отношению к определенной группе преобразований координат в данном пространстве. С рассматриваемой точки зрения, скаляр — это величина, инвариантная относительно (разрешенных) преобразований координат, а вектор — совокупность компонент, которые при преобразовании координат трансформируются по определённому правилу, с этим правилом мы познакомимся ниже. Многокомпонентные физические объекты более сложной математической структуры, чем вектор, будут подробно описаны ниже по мере рассмотрения соответствующих физических ситуаций.
Ниже для описания скалярной величины или функции используются общепринятые обозначения. Векторные величины принято описывать или в символической форме (т.е. без указания конкретной системы координат), например, вектор , или в координатной форме , где упорядоченные величины в фигурных скобках представляют собой проекции вектора на соответствующие координатные линии декартовой системы координат.
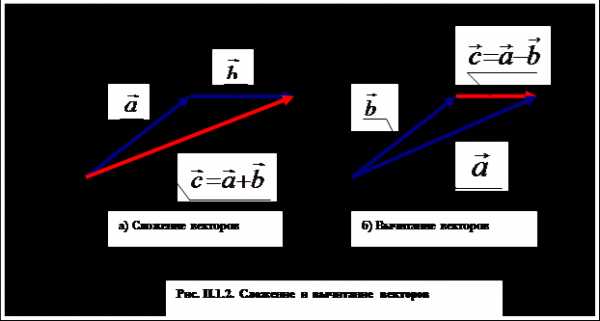
Сложение векторных величин по правилу треугольника или параллелограмма (рис. П.1.2)
эквивалентно покоординатному сложению:
Для векторных величин определено умножение на скалярную величину:
Геометрический образ описанной операции очень нагляден: вектор направлен так же как и вектор , но его величина в «l раз больше» (если l>0 и размерности не имеет). Если l<0, то направление векторов и противоположны. Если l физически размерная величина, сравнить непосредственно величины векторов и не представляется возможным.
Поскольку вектор определен величиной и направлением в пространстве, его можно представить в форме:
,
где – единичный безразмерный вектор (орт), совпадающий по направлению с исходным вектором ; обозначение используется для записи абсолютной величины (модуля) вектора .
Заметим, что в декартовой системе координат имеет место соотношение:
Для декартовой системы координат в трехмерном пространстве удобно ввести орты координатных линий: (используемые иногда обозначения не всегда удобны). В этом случае вектор можно представить в форме:
Определение операций «сложение» и «умножение на скалярную величину» позволяет ввести операцию «вычитания» векторов (рис. П.1.2) по следующему правилу:
.
Для векторных величин известны три различные операции умножения. Первая из них, скалярное произведение двух векторов, определена правилом:
где a— угол между направлениями векторов и , результат операции —скалярная величина (рис. П.1.3).
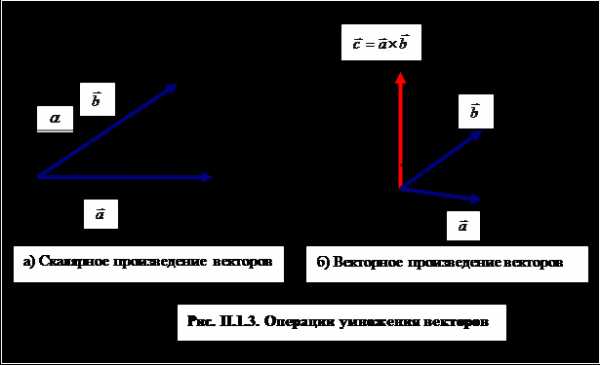
Если для произвольных векторов и , таких, что и , имеет место соотношение , то такие векторы называются ортогональными друг другу. Геометрический смысл скалярного произведения двух векторов становится очевидным, если заметить, что выражение представляет собой либо произведение проекции вектора на направление на модуль вектора , то есть , либо произведение проекции вектора на направление вектора на модуль вектора , то есть . Легко проверить, что .
Векторное произведение векторов и определено правилом:
где – орт, направленный по нормали к плоскости, в которой расположены векторы и , причем система направлений , , является «правой» системой: кратчайшее угловое расстояние между направлениями векторов и (угол a) соответствует движению от к против часовой стрелки, если смотреть с конца орта (или с конца вектора ). Очевидно, что направление орта нормали совпадает с направлением вектора .
Легко видеть, что результатом векторного произведения двух векторов является вектор, причем . В координатной форме записи имеют место соотношения
Если , то векторы и либо параллельны друг другу, т.е. , либо антипараллельны, т.е. .
Геометрический смысл векторного произведения становится наглядным, если векторы и представляют собой направленные отрезки двух прямых, исходящих из одной точки пространства, в этом случае величина представляет собой площадь параллелограмма, построенного на векторах и .
В качестве упражнения рекомендуется проверить соотношения:
Прямое или тензорное произведение двух векторов определено следующим образом. Если имеем вектор , или в координатной форме , и вектор , или в координатной форме {bx,, by, bz}, то можно построить двухиндексный объект – матрицу
=
как результат тензорного произведения = Ä , что в координатной форме имеет вид
Сij = ai bj , i,j=1,2,3.
Объект, построенный таким образом, обладает свойствами тензора второго ранга. Тензоры второго и более высокого ранга используются при описании физических явлений в механике сплошных сред, электродинамике, теории относительности и т.д.
Описание алгебраических операций над векторными величинами заключим напоминанием, что операция деления векторных величин не определена.
Похожие статьи:
poznayka.org
СКАЛЯРЫ И ВЕКТОРЫ
Министерство общего и профессионального образования РФ ВОРОНЕЖСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
Физический факультет Кафедра теоретической физики
ЗАПРЯГАЕВ С. А.
ЭЛЕКТРОДИНАМИКА. Векторный анализ
Методические укзания к практическим занятиям по курсу «ЭЛЕКТРОДИНАМИКА»
для студентов 3-гокурса дневного отделения
Рекомендовано Учебно МетодическимОбъединением университетов РФ в качестве учебного пособия
1
1.1Исходные определения
Скаляром называется величина, определяемая одним численным значением.Вектором называется величина, задаваемая численным значением и направлением в пространстве. Математическое изображение
вектора есть: | ~ | A, или | ~ | (ниже используется обозначение — A). |
A, или | A |
Геометрически, вектор изображается отрезком прямой линии, направление которой совпадает с направлением величины A в данной точке, а длина (или модуль вектора A = |A|) равна численному значению вектора (в определенных единицах измерения). Введено понятиенулевой вектор — это вектор, модуль которого равен нулю. Направление такого вектора не задано. Два вектораравны между собой, если модули их одинаковы и направления совпадают (обозначение A = B). Для векторов введен ряд математических операций (но не все в сравнении с числами).Суммой двух векторовA иB называется векторC, являющийся диагональю параллелограмма, построенного на слагаемых векторах (рис. 1.a). Суммой N векторов является вектор C, замыкающий N + 1 — угольник,
|
|
|
|
|
| 1 | q q | q q |
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
| * |
| |||
HY |
|
|
|
| A2 |
|
| 6 | A |
|
| |||||
|
|
|
| YH |
|
|
| q q |
|
|
|
| ||||
q Hq | Hq q qCq q3q q |
|
|
|
|
|
|
|
| q q q q | q q q q |
| ||||
— |
| HH | C — | AN | B |
|
| C — | −B | |||||||
A | H | Bq |
| A1 | H |
|
|
|
|
|
| ? | ||||
| a) |
| q q q | q | б) |
|
|
|
|
|
|
| в) |
|
|
|
Рис. 1: Сложение векторов
построенный на слагаемых векторах (рис. 1.б). Из определения суммы векторов следует коммутативность A + B = B + A иассоциативность
(A + B) + C = A + (B + C) векторного сложения. Вектор называется противоположным заданному A (обозначается −A), если модуль его равен |A|, а направление прямо противоположно вектору A.Разностью двух векторов A и B называется сумма уменьшаемого вектора с вектором, противоположным вычитаемому A − B = A + (−B) (рис. 1.в).Проекция вектора A на ось e есть число, равное:
где ϕ -уголмежду напрвлением вектора A и положительным направлением оси e.Умножение вектора Aна скаляр a определяет вектор, модуль
P3 k=1
2
которого равен a · A, а направление совпадает с направлением вектора
A, если a > 0 и противоположно направлению вектора A, если a | < | ||
0. Умножение вектора на число удовлетворяет соотношениям: a(b A) | = | ||
(a · b)A, | a(A + B) = | aA + aB. Линейно зависимыми называются | |
векторы, | для которых | выполняется равенство PiN=1 αiAi = 0, где | αi |
-числа,не все равные нулю. Два линейно зависимых вектора параллельны (коллиниарны) друг другу. Три линейно зависимых вектора лежат в одной плоскости (компланарны). Если три вектора линейно независимы, то любой вектор единственным образом разлагается по этим векторам.Базисом трехмерного пространства называется произвольная система трех линейно независимых векторов ei, i 1 ÷ 3. При заданном базисе для любого вектора имеем:
| 3 |
|
| kX | (2) |
A = A1 e1 + A2 e2 + A3 e3 = | Akek | |
| =1 |
|
Откладывая тройку базисных векторов из | одной точки | пространства |
(начало координат) и называя прямые, являющиеся продолжением ek, осями координат, получим косоугольную декартову систему координат. Если базисные векторы взаимно ортогональны и |ek| = 1, то они называютсяортами прямоугольной декартовой системы координат. Часто используются следующие общепринятые обозначения e1 = i-ортоси X, e2 = j-ортоси Y , e3 = k-ортоси Z.Радиусвектор точки (r) — есть вектор, проведенный из начала координат к заданной точке пространства r = x i+y j+z k. Здесь x, y, z — декартовы координаты точки. В дальнейшем будут использованы обозначения x1 ≡ x; x2 ≡ y; x3 ≡ z. В результате
r = xk ek. Модуль радиус вектора обозначается r и равен r =
√
x2 + y2 + z2.Единичный радиусвектор — есть вектор, равный n = r/r.
1.2 Произведения векторов
Для векторов определены два типа произведения — скалярное и векторное. Скалярное произведение двух векторов A и B есть число, равное произведению модулей векторов на косинус угла между ними. Скалярное произведение двух векторов обозначается (A · B) или A · B и по определению(1) равно произведению модуля одного вектора на проекцию
εi j k
| 3 |
второго вектора на направление первого: |
|
A · B = A B cos(Ad· B) = AB · B = A · BA | (3) |
По определению скалярное произведение коммутативно A · B = B · A и дистрибутивно (A + B) · C = A · C + B · C. На основании (3) проекция вектора на ось равна скалярному произведению орта оси на вектор. Из равенства скалярного произведения нулю следует взаимная ортогональность векторов. Орты прямоугольной декартовой системы
координат ортогональны между собой ei · ej | = δij. Используя(2) для | ||
скалярного произведения (3), имеем |
|
| |
| 3 | 3 |
|
A · B = | X | kX | (4) |
Ak Bn (en · ek) = | AkBk | ||
| k,n=1 | =1 |
|
Векторным произведением двух векторов A и B называется вектор, обозначаемый [A × B], равный по величине произведению модулей векторов на синус угла между ними и направленный перпендикулярно плоскости векторов сомножителей в ту сторону, откуда поворот от первого сомножителя A ко второму Bна меньший угол виден против хода часовой стрелки. Векторное произведение некоммутативно, так как [A × B] = −[B × A], но дистрибутивно [A × (B + C)] = [A × B] + [A × C]. Из равенства [A × B] = 0 следует параллельность векторов A и B. Векторное произведение имеет простой геометрический смысл: |[A × B]| равен площади параллелограмма, построенного на этих векторах. Векторное произведение ортов прямоугольной декартовой системы координат равно:
3 |
|
|
kX | i, j 1, 2, 3 | (5) |
[ei × ej] = εi j k ek | ||
=1 |
|
|
— символ Леви-Чевита,равный нулю, если хотя бы два индекса совпадают; равный +1, если i, j, k образуют циклическую; и −1, если i, j, k образуют нециклическую перестановку от последовательности 1, 2, 3. В практических приложениях используются следующие соотношения для εi j k
3 |
|
|
|
|
| 3 |
|
εi k l· εi s t= |
| δks | δkt |
| ; | εi k l· εi k t= 2δlt | (6) |
X |
|
|
|
|
| X |
|
|
|
|
|
|
|
|
|
i=1 |
| ls | lt |
|
| i,k=1 |
|
|
|
|
|
|
|
|
|
Определитель квадратной матрицы 3 × 3 можно представить в следующем виде:
| 3 |
|
det A = ||A|| = | X | (7) |
A1 iA2 jA3 kεi j k. |
i,j,k=1
4
Используя (2), (5), получаем общее выражение для вычисления векторного произведения:
[A B] = | 3 |
|
| 3 |
|
|
| e1 | e2 | e3 |
| (8) | ||
AiBj [ei ej] = | εi j kAiBjek | = | A1 | A2 | A3 |
| ||||||||
|
| X |
|
| X |
|
|
|
|
|
|
|
|
|
× |
|
| × |
|
|
|
|
| B1 | B2 | B3 |
|
| |
|
|
|
|
|
|
|
|
| ||||||
| i,j=1 |
| i,j,k=1 |
|
|
|
|
|
|
|
|
| ||
|
|
|
|
|
|
|
|
|
|
| ||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Смешанное произведение трех векторов |
|
|
|
|
|
|
|
|
| |||||
|
| 3 |
|
| 3 |
|
|
|
|
|
|
|
|
|
|
| X |
|
| X | εi j kAnBiCj (en · ek) = | ||||||||
A · [B × C] = | AnBiCj en · [ei × ej] = | |||||||||||||
|
| i,j,n=1 |
|
| i,j,n,k=1 |
|
|
|
|
|
|
|
|
|
| 3 | εi j k | AkBiCj = | 3 |
| A1 | A2 | A3 |
| (9) | ||||
| = | εk i jAkBiCj= |
| B1 | B2 | B3 |
|
| ||||||
| X |
| X |
|
|
|
|
|
|
|
|
| ||
|
|
|
|
|
|
|
| C1 | C2 | C3 |
|
|
| |
|
|
|
|
|
|
|
|
|
|
| ||||
| i,j,k=1 |
| k,i,j=1 |
|
|
|
|
|
|
|
|
| ||
|
|
|
|
|
|
|
|
|
|
| ||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Из (9) вытекает, что значение смешанного произведения не меняется при циклической перестановке векторов, входящих в него. Численно смешанное произведение равно объему параллелепипеда, построенного на векторах, входящих в произведение. Если любые два вектора в смешанном произведении одинаковы или параллельны, то такое произведение равно нулю. Наконец, если все три вектора лежат в одной плоскости, смешанное произведение также равно нулю. Таким образом, если для трех векторов A · [B × C] 6= 0, то данные векторы образуют базис. При этом, если A · [B × C] > 0, базис называется правым. Если A · [B × C] < 0, базис называется левым. Используя (9), εi j k можно представить в следующем виде
εi j k = [ei × ej] · ek | (10) |
Двойное векторное произведение обозначается [A×[B×C]] и для его вычисления справедлива формула
D ≡ [A × [B × C]] = B (A · C) − C (A · B) | (11) |
Для доказательства равенства (11) перепишем двойное векторное произведение с учетом(2), используя равенство(5), получим:
| 3 |
| 3 |
| X |
| X |
D = | AiBjCk [ei × [ej × ek]] = | AiBjCkεl j kεl n ien | |
| i,j,k=1 |
| i,j,k,l,n=1 |
Выполняя суммирование по l на основании (6) и(4), получим: | |||
| 3 | en = B (A · C) − C (A · B) | |
D = i,n=1 AiBnCi − AiBiCn | |||
| X |
|
|
studfiles.net
Скаляры и векторы. Изображение векторов. Примеры скалярных и векторных величин
В теории электромагнитного поля применяется некоторый традиционный математический аппарат, без которого невозможно построить ясное и обозримое изложение. К числу математических средств, которые нам потребуются, относятся разделы векторной алгебры и векторного анализа. Эти разделы в общем знакомы из курса высшей математики, однако в нашем курсе они тоже будут кратко описаны.
Первым необходимым понятием являются скалярные и векторные величины.
В математике и технике приходится иметь дело с величинами двух родов: одни из величин связаны с понятием о направлении в пространстве, другие имеют чисто числовой характер и не связаны с направлением. Рассмотрим например, температуру, массу, плотность, энергию, перемещение точки, скорость, ускорение, силу. Четыре последние величины резко отличаются от первых тем, что с ними обязательно должно быть связано понятие о направлении: например, точка может перемещаться вверх или вниз, вперед или назад.
Наоборот, температура, например, не имеет направления. и чтобы охарактеризовать ее, мы должны измерить ее например, в градусах Цельсия, полученное число и даст величину температуры. Точно так же можно измерить в соответствующих единицах массу, плотность и т.п. Эти величины принадлежат к классу величин, называемых скалярами.
Скаляром называется величина, характеризующаяся при выбранной единице меры одним числом.
Рассмотрим теперь один из векторов – скорость точки. Указания величины скорости, измеренной, например в м\с недостаточно для характеристики скорости. Нужно еще знать направление движения точки. Точно так же имеют определенное направление и ускорение точки, и сила, действующая на точку. Дадим поэтому следующее определение:
Вектором называется величина, характеризующаяся, помимо измеряющего ее числа, еще своим направлением в пространстве.
Простейшим вектором является прямолинейный
отрезок 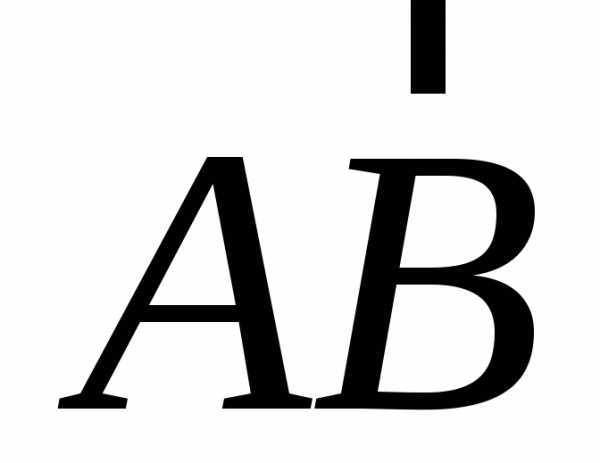 ,
имеющий определенну величину – длинуАВи
определенное направление – от начальной
точкиАк конечной точкеВ.
,
имеющий определенну величину – длинуАВи
определенное направление – от начальной
точкиАк конечной точкеВ.
На чертежах векторы изображаются
стрелками (рисунок Error: Reference source not found).
Направление стрелки указывает на
направление вектора, длина стрелки дает
длину вектора. Обычно векторы обозначаются
жирными латинскими буквами:  ,
но при письме от руки это неудобно,
поэтому мы будем пользоваться буквами
со стрелкой:
,
но при письме от руки это неудобно,
поэтому мы будем пользоваться буквами
со стрелкой: 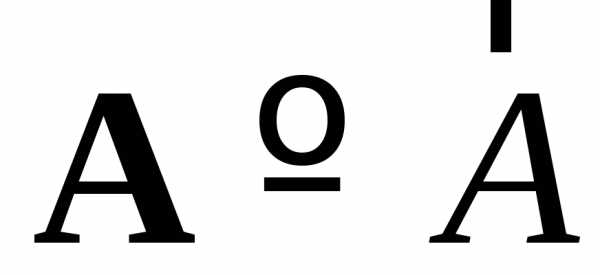 .
.
− Вектор AB
Иногда приходится рассматривать величины тоже направленного характера, но более сложного, чем векторы, строения. Эти величины называются тензорами. Мы рассмотрим их позднее.
Операции над векторами. Скалярное, векторное, смешанное произведение
Векторное исчисление должно ввести ряд операций с векторами и тензорами, как например сложение, умножение, дифференцирование, и изучить эти операции. Эти операции определяются таким образом, чтобы при их помощи легко было интерпретировать те комбинации векторов, которые приходится изучать. В результате как основные элементы векторного исчисления – вектор и тензор, так и операции над ними оказываются хорошо приспособленными для изучения тех физических явлений, в которых большую роль играет направление величин. С одной стороны, это упрощает исследование, с другой, ведет его более естественным и наглядным образом, не требуя введения посторонних элементов.
Рассмотрим, как определяется величина и направление вектора.
Векторы  ,
, 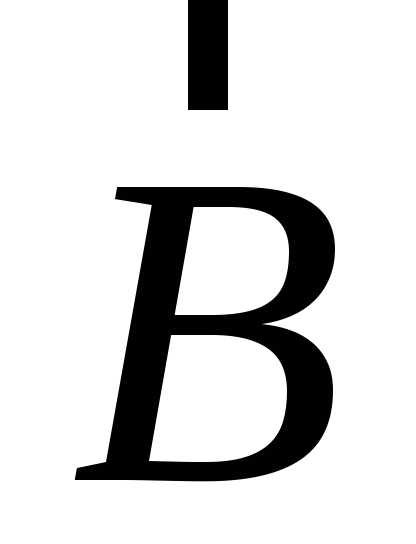 можно представить как
можно представить как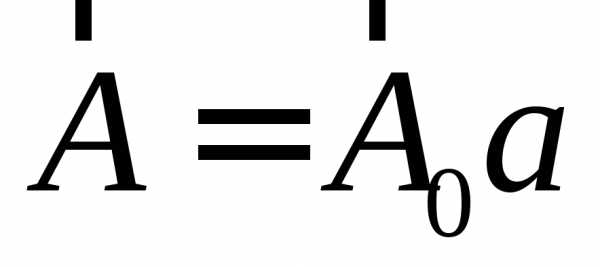 ,
и
,
и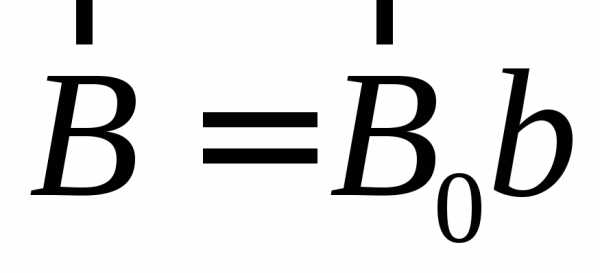 ,
где
,
где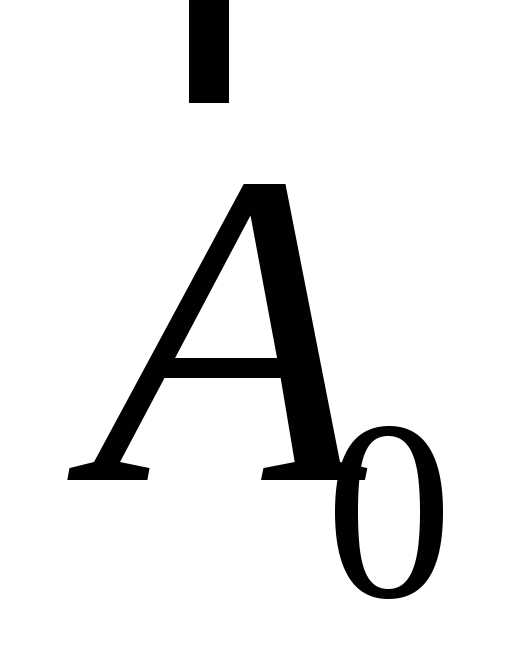 ,
, −
единичные векторы, называемые также
ортами, а числаа,b− абсолютные значения
векторов
−
единичные векторы, называемые также
ортами, а числаа,b− абсолютные значения
векторов ,
, 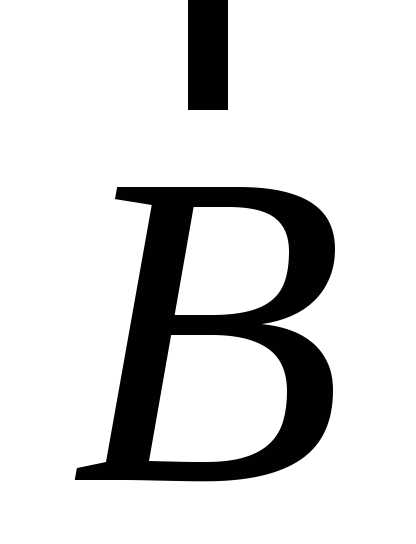 .
.
Орты, соответствующие направлениям
осей x,y,zдекартовой координат,
будут обозначаться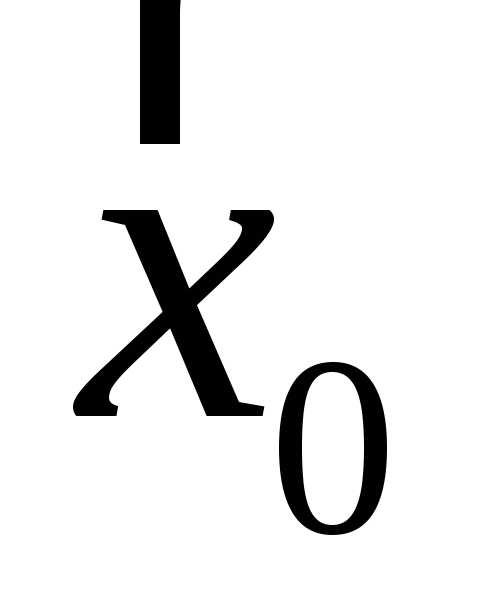 ,
,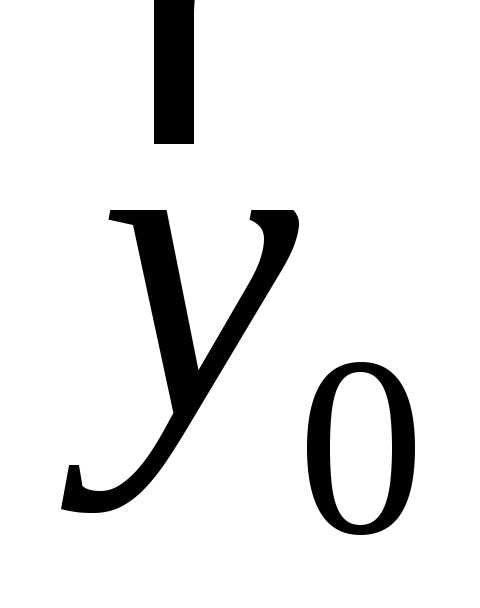 ,
,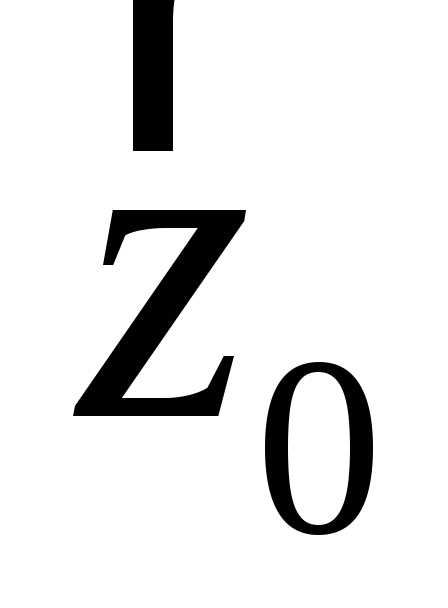 (рисунок Рисунок 2 ). Любой вектор
(рисунок Рисунок 2 ). Любой вектор тогда можно представить в виде разложения,
где
тогда можно представить в виде разложения,
где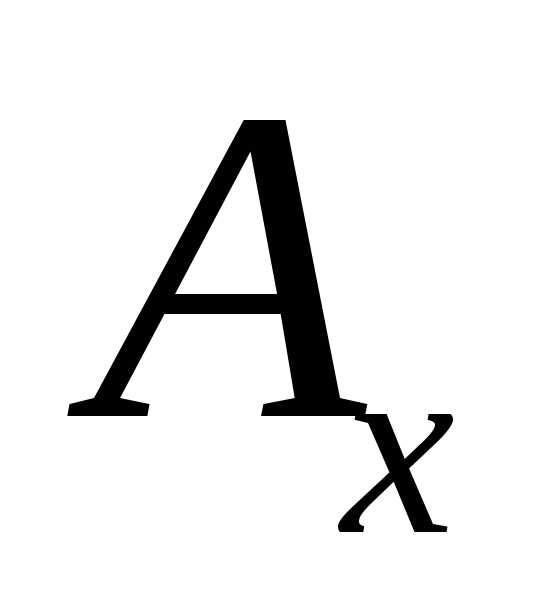 ,
,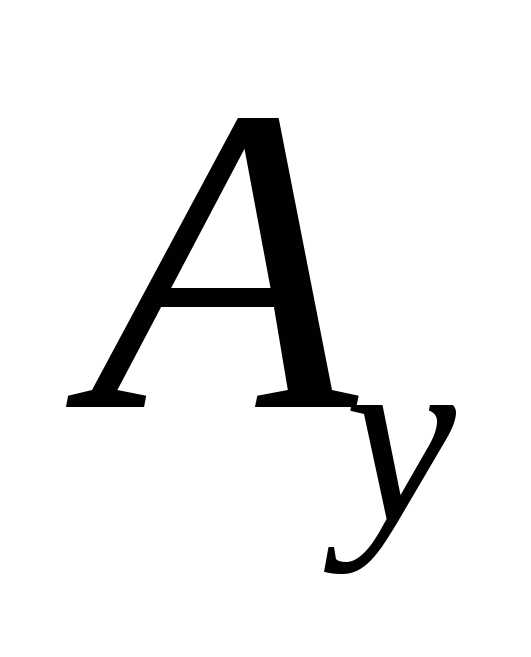 ,
, являются его проекциями на оси декартовой
системы координат. Они также называются
компонентами (составляющими) вектора
являются его проекциями на оси декартовой
системы координат. Они также называются
компонентами (составляющими) вектора .
.
Положение какой-либо точки пространства P может быть определено вектором  ,
начальной точкой которого служит
некоторая, определенным образом выбранная
точкаO, а концом –
точкаP. Вектор
,
начальной точкой которого служит
некоторая, определенным образом выбранная
точкаO, а концом –
точкаP. Вектор 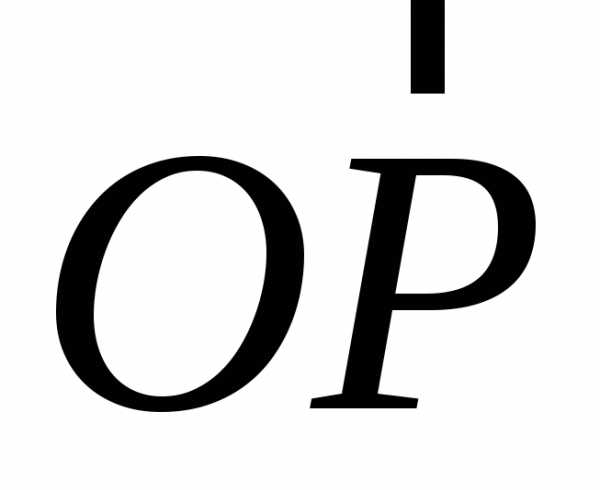 мы будем называть радиусом-вектором
точкиP относительно точкиОи будем обозначать обычно как
мы будем называть радиусом-вектором
точкиP относительно точкиОи будем обозначать обычно как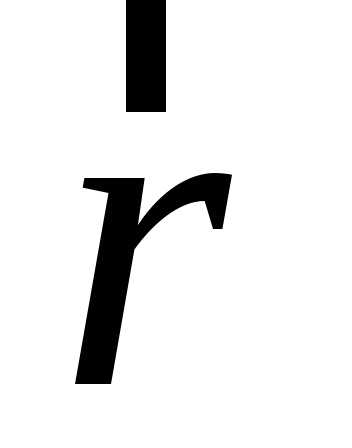 .
Про точкуP, заданную
радиусом-вектором
.
Про точкуP, заданную
радиусом-вектором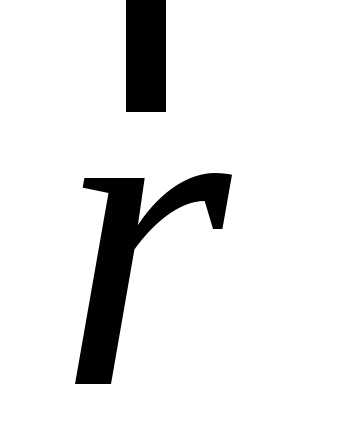 ,
мы будем говорить, для краткости, что
дана точка
,
мы будем говорить, для краткости, что
дана точка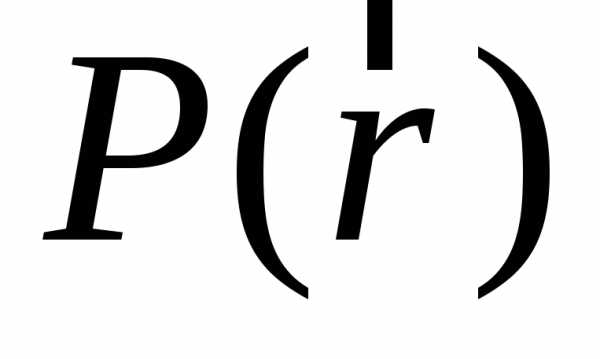 .
.
−Орты декартовой системы координат и радиус-вектор
Сложение векторов векторов сводится к сложению их компонент:
,
эта операция обозначается с помощью обыкновенного знака алгебраического сложения: . Сложение обладает свойством коммутативности: сумма не меняется от перестановки слагаемых:.
Геометрически это выглядит, как показано на рисунке Рисунок 3 .
— Сложение векторов
Скалярное произведение необходимо, например, в механике при вычислении работы, производимой постоянной силой при прямолинейном перемещении и при условии, что сила действует под углом α к перемещению. Работа в этом случае вычисляется как скалярное произведение вектора силы и вектора перемещения. Скалярное произведение двух произвольных векторов определяется как , то есть произведение их длин, умноженное на угол между ними (рисунок Рисунок 4 ). Результатом скалярного произведения является скаляр.
— Скалярное произведение
Векторное произведение. К необходимости рассматривать такую операцию приводят требования геометрического и физического характера.
Векторным произведением векторов  и
и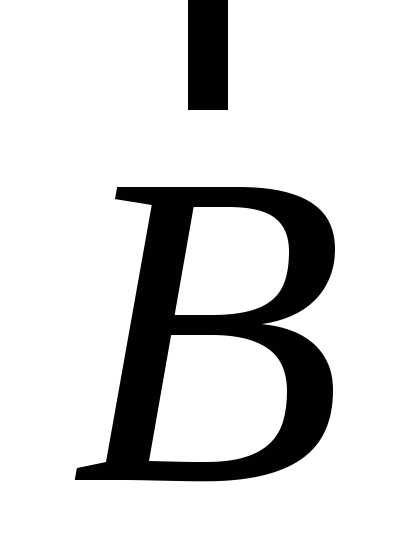 называется
вектор, по величине равный площади
параллелограмма, построенного на
векторах
называется
вектор, по величине равный площади
параллелограмма, построенного на
векторах и
и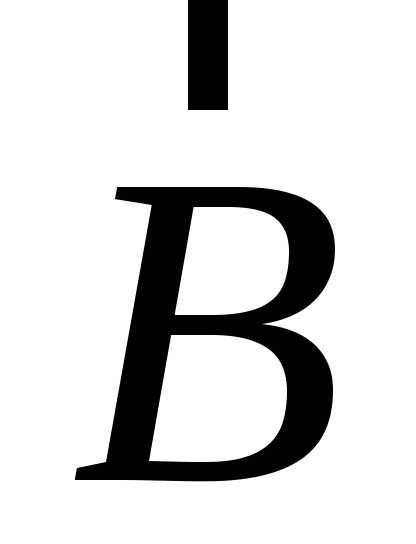 ,
перпендикулярный плоскости этих векторов
и направленный в такую сторону, чтобы
вращение от
,
перпендикулярный плоскости этих векторов
и направленный в такую сторону, чтобы
вращение от к
к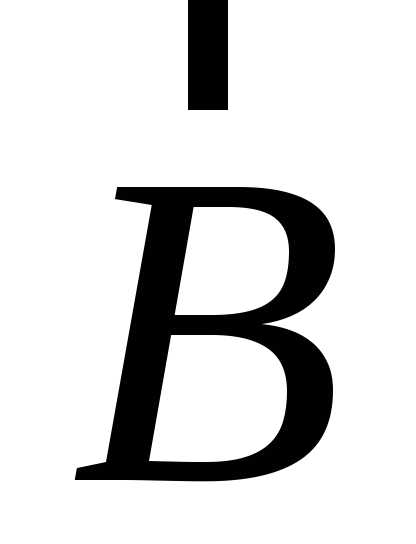 на кратчайшем пути вокруг полученного
вектора происходило в ту же сторону,
как вращение осиxк
осиyвокруг осиz(рисунок Рисунок 5 ).
на кратчайшем пути вокруг полученного
вектора происходило в ту же сторону,
как вращение осиxк
осиyвокруг осиz(рисунок Рисунок 5 ).

−Векторное произведение
Векторное произведение вычисляется как
,
тогда компоненты векторного произведения получаются из раскрытия определителя:
Изменение порядка сомножителей приводит к изменению знака векторного произведения: .
Размерность векторного произведения – единицы измерения площади, т.е. квадратные метры.
Кроме описанных операций сложения, скалярного и векторного произведений, мы будем использовать векторные дифференциальные операторы. Их определение дается позже, непосредственно перед использованием.
studfiles.net
Скаляры и векторы
Физика > Скаляры и векторы
Скаляр и вектор – чем отличаются понятия в физике и какая связь: определения и термины, величина и направление, скаляры без направления, величины и график.
Скаляры – физические величины, отображенные числом, а векторы используют числа и направления.
Задача обучения
- Научиться различать вектор и скаляр.
Основные пункты
- Скаляр – физическая величина, представленная числом.
- Вектор – физическая величина, характеризующаяся величиной и направлением.
- Среди скаляров можно вспомнить высоту, площадь, объем и массу.
- Векторы – смещение, ускорение и скорость.
Термин
Координатная ось – набор перпендикулярных линий, определяющих координаты относительно начала координат. Например, х и у указывают на горизонтальное и вертикальное положения.
Чаще всего, физические величины можно поделить на две категории: вектор и скаляр. Они отличаются необходимой для характеристики информацией. Векторы нуждаются в величине и направлении, а скаляры обходятся лишь первым критерием. Скаляры можно воспринимать как числа, а векторы – стрелки, указывающие на определенное направление.
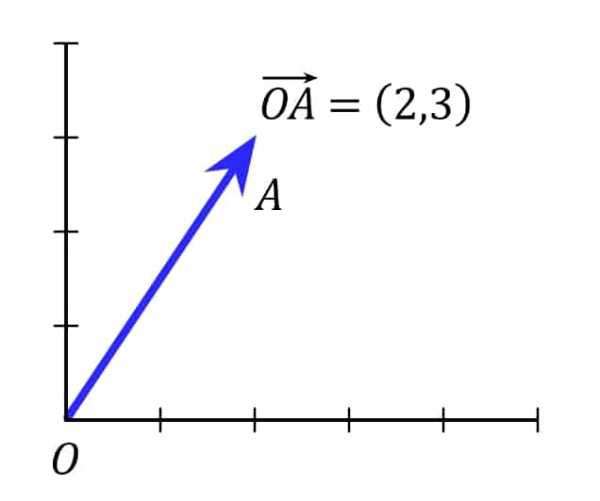
Пример вектора. Обычно они отображаются стрелками с длиной, показывающей величину, а направление указано стрелой
Вектор нуждается в величине и направлении. Величина отображается числом, чтобы можно было сравнить два вектора. Стрелка состоит из двух частей: длина, определяющая величину, и направление на оси координат. Чем больше величина, тем длиннее стрелка. Вектор может отображать скорость, смещение и ускорение. Чтобы указать направление, нужно располагать опорной точкой, которой часто выступают координатные оси.
Скаляры лишены направления. Их используют для отображения величин, которые не нуждаются в направлении (высота, масса, объем).
v-kosmose.com
Введение в скаляры и векторы
Физика > Введение в скаляры и векторы
Скаляр и вектор – описание понятий и определений в физике: координаты, длина, произведение векторов, скалярное произведение векторов, отличие скаляра и вектора.
Вектор – любая величина, обладающая размером и направлением, а скаляр может похвастаться лишь величиной.
Задача обучения
- Отличать скаляры от векторов.
Основные пункты
- Вектор – любое количество с величиной и направлением.
- Скаляр – любое количество с величиной, но лишенное направления.
- Смещение и скорость – векторы, а расстояние и скорость – скаляры.
Термины
- Вектор – количество, обладающее величиной и направлением (между двумя точками).
- Скаляр – количество с величиной, но без направления.
Пример
Скорость человека способна оставаться стабильной при повороте за угол или смене направления. Учитывая этот факт, с чем же мы столкнулись: вектор или скаляр? Скорость – скалярная величина, так как не меняется из-за направления.
В чем отличие между расстоянием и смещением? Первая характеризуется только величиной, в то время как смещение – величиной и направлением. Смещение – пример векторной величины, а расстояние – скалярной.
Вектор отображает геометрический объект, обладающий величиной и направлением. В соответствии с векторной алгеброй, его можно добавить к другим векторам. Направление задается знаками + или -. Вектор отображается отрезком линии с конкретным направлением или стрелой, объединяющей точки А и В — направление вектора.
Вектор часто изображают в виде линейного отрезка с определенным направлением или же как стрелу, соединяющую А и В
Некоторые физические величины, вроде дистанции, не обладают направлением. Здесь и появляется скаляр, который остается стабильным при смене системы координат. Может выражаться числом и обладает величиной, но лишен направления. Например, 45°C, 150 калорий, дистанция в 3 метра – все это скаляры. Если располагаем температурой в -23°C, то отрицательный знак указывает не на направление, а на точку в шкале. Скаляры никогда не отображаются стрелками.
К скалярным величинам относятся длина, площадь, время, температура и т. д.
К векторным величинам относятся: Сила, ускорение, импульс, скорость, индукция, напряжённость…
v-kosmose.com
Скаляры и векторы. Изображение векторов. Примеры скалярных и векторных величин
В теории электромагнитного поля применяется некоторый традиционный математический аппарат, без которого невозможно построить ясное и обозримое изложение. К числу математических средств, которые нам потребуются, относятся разделы векторной алгебры и векторного анализа. Эти разделы в общем знакомы из курса высшей математики, однако в нашем курсе они тоже будут кратко описаны.
Первым необходимым понятием являются скалярные и векторные величины.
В математике и технике приходится иметь дело с величинами двух родов: одни из величин связаны с понятием о направлении в пространстве, другие имеют чисто числовой характер и не связаны с направлением. Рассмотрим например, температуру, массу, плотность, энергию, перемещение точки, скорость, ускорение, силу. Четыре последние величины резко отличаются от первых тем, что с ними обязательно должно быть связано понятие о направлении: например, точка может перемещаться вверх или вниз, вперед или назад.
Наоборот, температура, например, не имеет направления. и чтобы охарактеризовать ее, мы должны измерить ее например, в градусах Цельсия, полученное число и даст величину температуры. Точно так же можно измерить в соответствующих единицах массу, плотность и т.п. Эти величины принадлежат к классу величин, называемых скалярами.
Скаляром называется величина, характеризующаяся при выбранной единице меры одним числом.
Рассмотрим теперь один из векторов – скорость точки. Указания величины скорости, измеренной, например в м\с недостаточно для характеристики скорости. Нужно еще знать направление движения точки. Точно так же имеют определенное направление и ускорение точки, и сила, действующая на точку. Дадим поэтому следующее определение:
Вектором называется величина, характеризующаяся, помимо измеряющего ее числа, еще своим направлением в пространстве.
Простейшим вектором является прямолинейный
отрезок 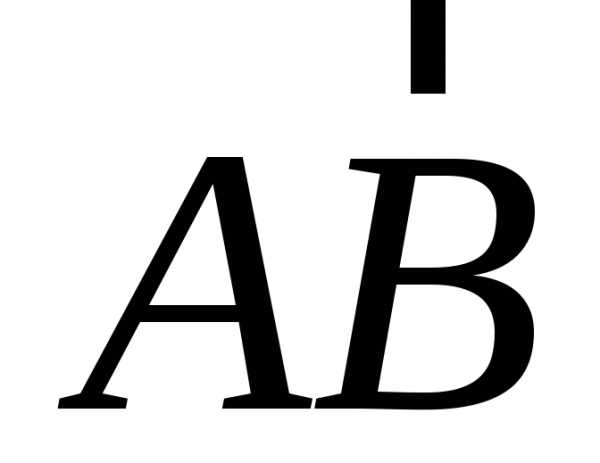 ,
имеющий определенну величину – длинуАВи
определенное направление – от начальной
точкиАк конечной точкеВ.
,
имеющий определенну величину – длинуАВи
определенное направление – от начальной
точкиАк конечной точкеВ.
На чертежах векторы изображаются
стрелками (рисунок Error: Reference source not found).
Направление стрелки указывает на
направление вектора, длина стрелки дает
длину вектора. Обычно векторы обозначаются
жирными латинскими буквами:  ,
но при письме от руки это неудобно,
поэтому мы будем пользоваться буквами
со стрелкой:
,
но при письме от руки это неудобно,
поэтому мы будем пользоваться буквами
со стрелкой: 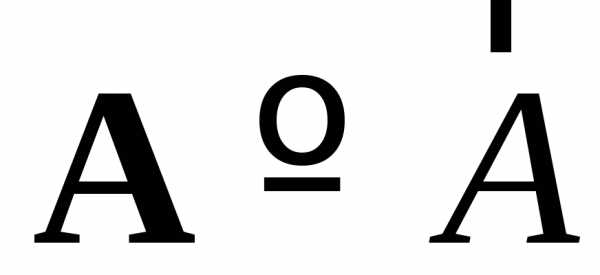 .
.
− Вектор AB
Иногда приходится рассматривать величины тоже направленного характера, но более сложного, чем векторы, строения. Эти величины называются тензорами. Мы рассмотрим их позднее.
Операции над векторами. Скалярное, векторное, смешанное произведение
Векторное исчисление должно ввести ряд операций с векторами и тензорами, как например сложение, умножение, дифференцирование, и изучить эти операции. Эти операции определяются таким образом, чтобы при их помощи легко было интерпретировать те комбинации векторов, которые приходится изучать. В результате как основные элементы векторного исчисления – вектор и тензор, так и операции над ними оказываются хорошо приспособленными для изучения тех физических явлений, в которых большую роль играет направление величин. С одной стороны, это упрощает исследование, с другой, ведет его более естественным и наглядным образом, не требуя введения посторонних элементов.
Рассмотрим, как определяется величина и направление вектора.
Векторы  ,
, 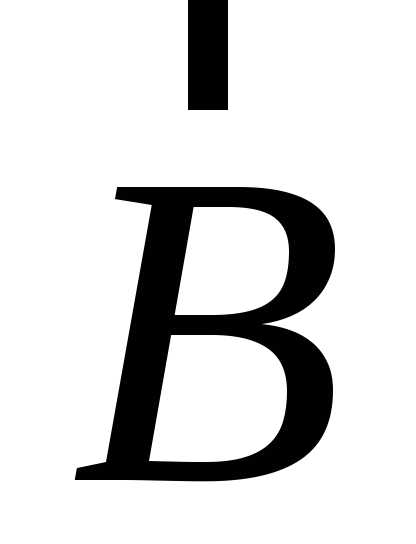 можно представить как
можно представить как ,
и
,
и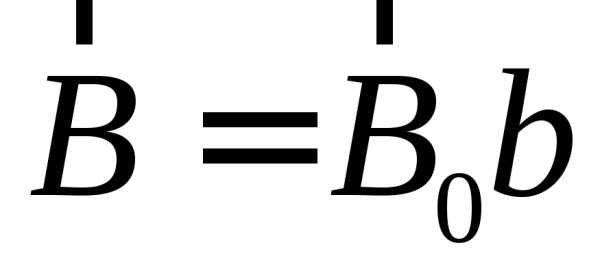 ,
где
,
где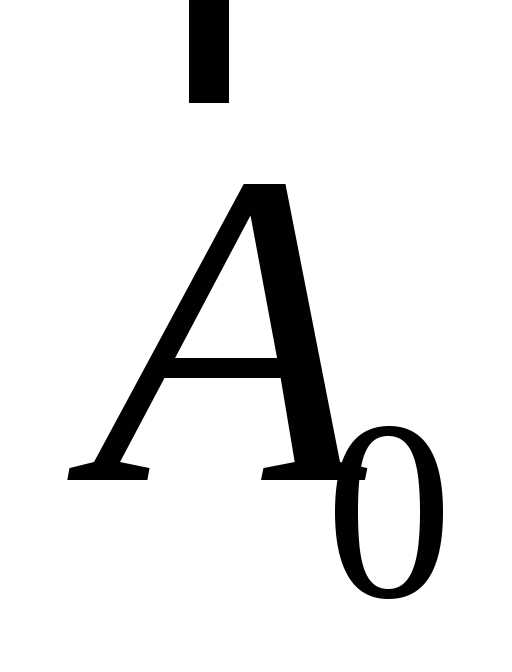 ,
,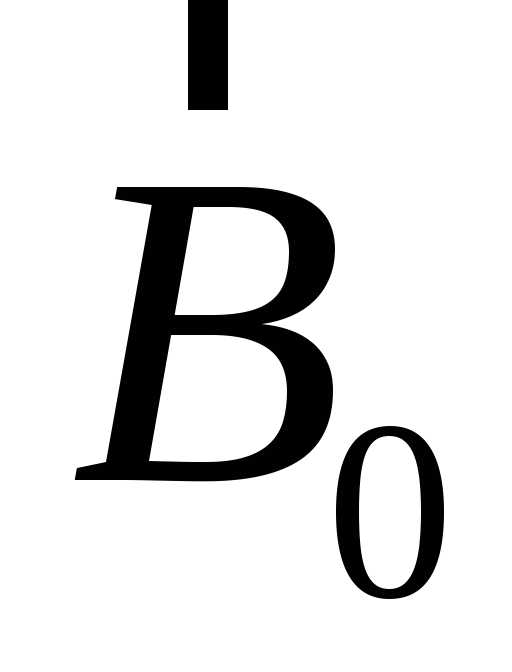 −
единичные векторы, называемые также
ортами, а числаа,b− абсолютные значения
векторов
−
единичные векторы, называемые также
ортами, а числаа,b− абсолютные значения
векторов ,
, 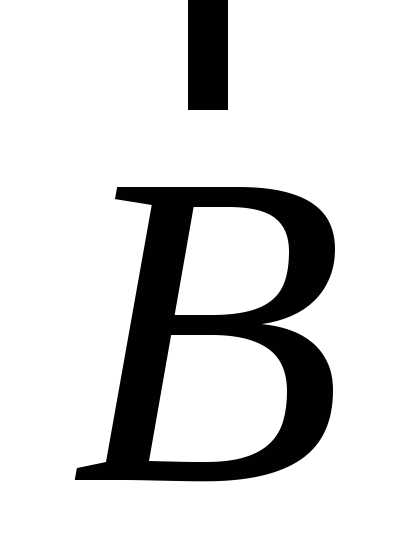 .
.
Орты, соответствующие направлениям
осей x,y,zдекартовой координат,
будут обозначаться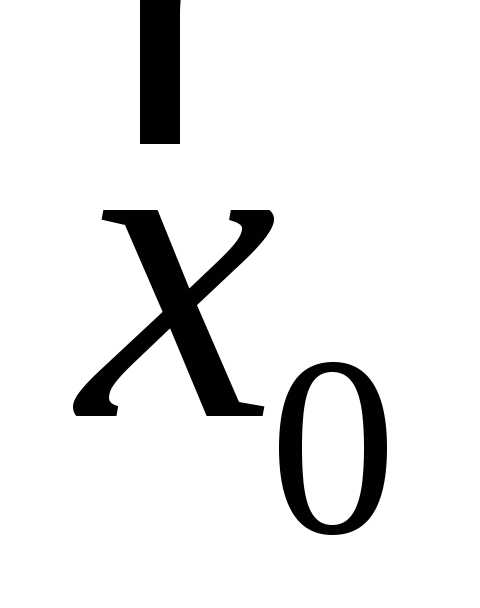 ,
,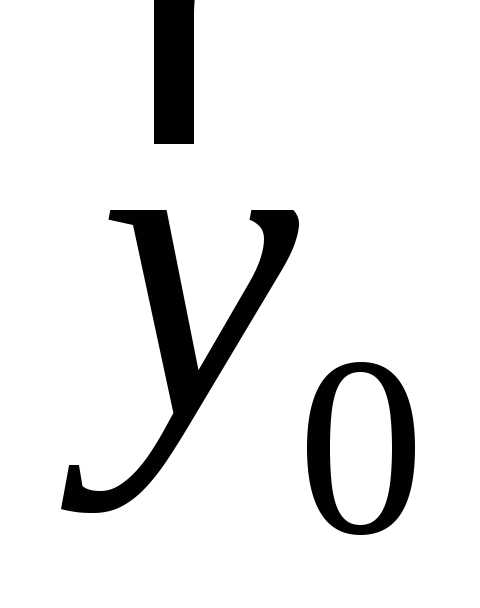 ,
,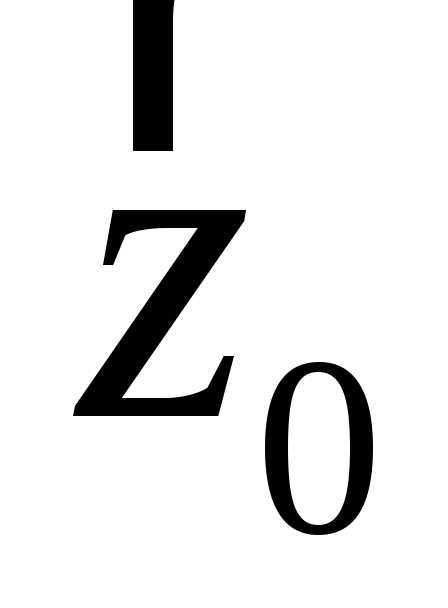 (рисунок Рисунок 2 ). Любой вектор
(рисунок Рисунок 2 ). Любой вектор тогда можно представить в виде разложения,
где
тогда можно представить в виде разложения,
где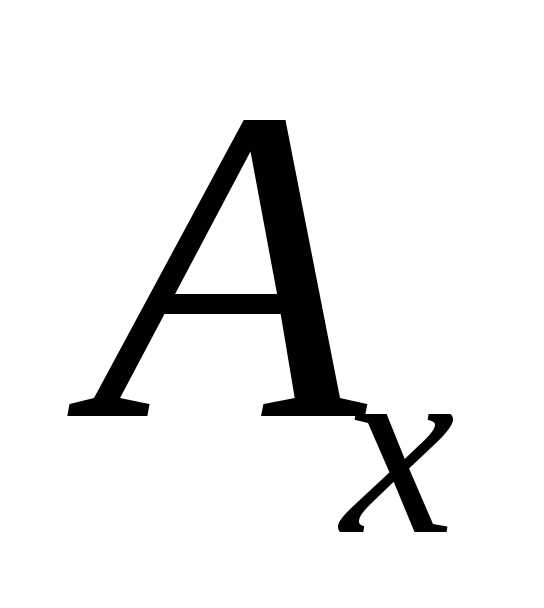 ,
, ,
, являются его проекциями на оси декартовой
системы координат. Они также называются
компонентами (составляющими) вектора
являются его проекциями на оси декартовой
системы координат. Они также называются
компонентами (составляющими) вектора .
.
Положение какой-либо точки пространства P может быть определено вектором 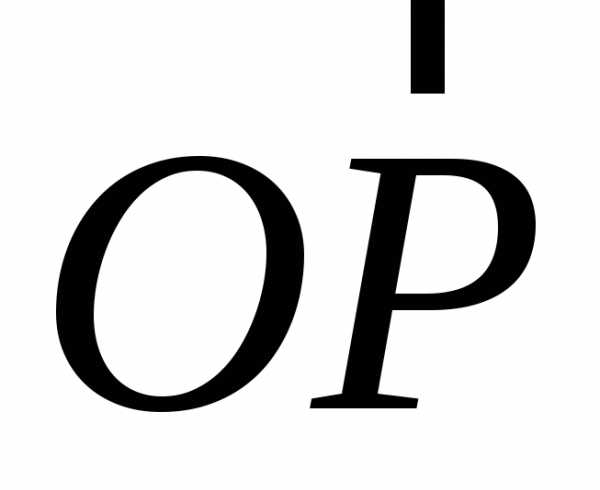 ,
начальной точкой которого служит
некоторая, определенным образом выбранная
точкаO, а концом –
точкаP. Вектор
,
начальной точкой которого служит
некоторая, определенным образом выбранная
точкаO, а концом –
точкаP. Вектор 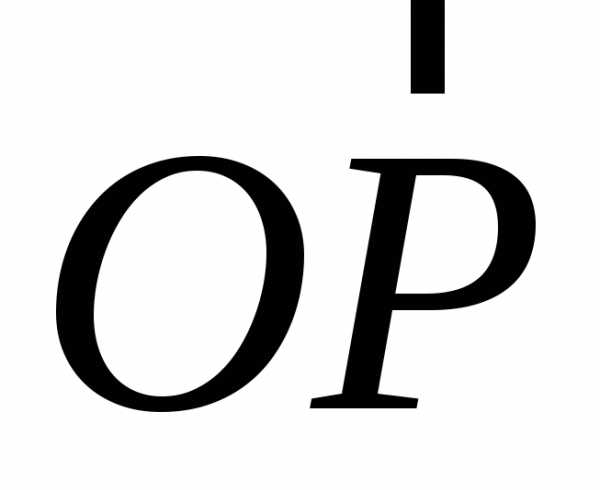 мы будем называть радиусом-вектором
точкиP относительно точкиОи будем обозначать обычно как
мы будем называть радиусом-вектором
точкиP относительно точкиОи будем обозначать обычно как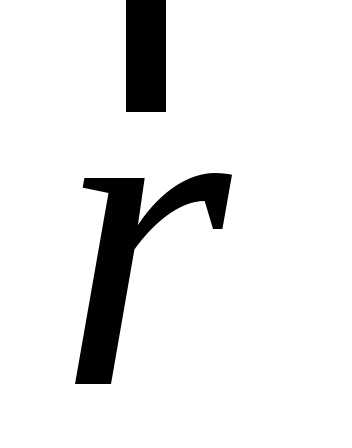 .
Про точкуP, заданную
радиусом-вектором
.
Про точкуP, заданную
радиусом-вектором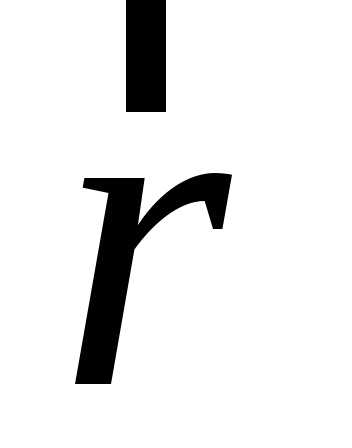 ,
мы будем говорить, для краткости, что
дана точка
,
мы будем говорить, для краткости, что
дана точка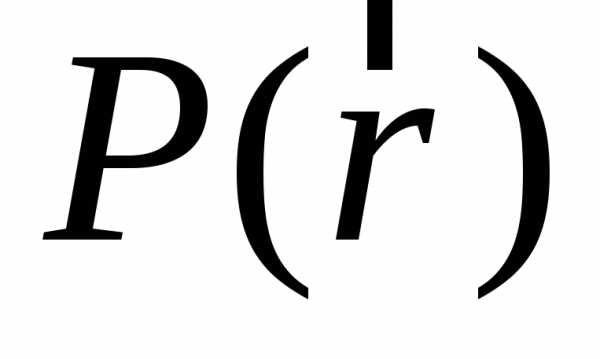 .
.
−Орты декартовой системы координат и радиус-вектор
Сложение векторов векторов сводится к сложению их компонент:
,
эта операция обозначается с помощью обыкновенного знака алгебраического сложения: . Сложение обладает свойством коммутативности: сумма не меняется от перестановки слагаемых:.
Геометрически это выглядит, как показано на рисунке Рисунок 3 .
— Сложение векторов
Скалярное произведение необходимо, например, в механике при вычислении работы, производимой постоянной силой при прямолинейном перемещении и при условии, что сила действует под углом α к перемещению. Работа в этом случае вычисляется как скалярное произведение вектора силы и вектора перемещения. Скалярное произведение двух произвольных векторов определяется как , то есть произведение их длин, умноженное на угол между ними (рисунок Рисунок 4 ). Результатом скалярного произведения является скаляр.
— Скалярное произведение
Векторное произведение. К необходимости рассматривать такую операцию приводят требования геометрического и физического характера.
Векторным произведением векторов  и
и называется
вектор, по величине равный площади
параллелограмма, построенного на
векторах
называется
вектор, по величине равный площади
параллелограмма, построенного на
векторах и
и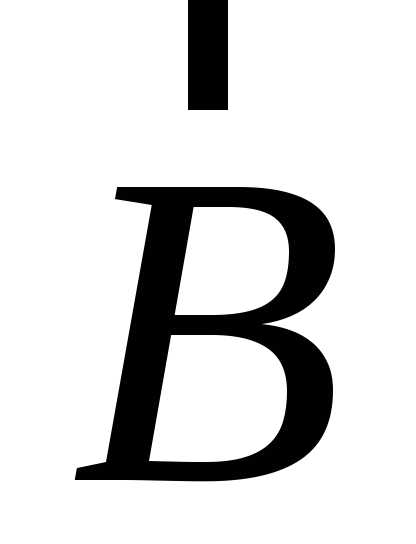 ,
перпендикулярный плоскости этих векторов
и направленный в такую сторону, чтобы
вращение от
,
перпендикулярный плоскости этих векторов
и направленный в такую сторону, чтобы
вращение от к
к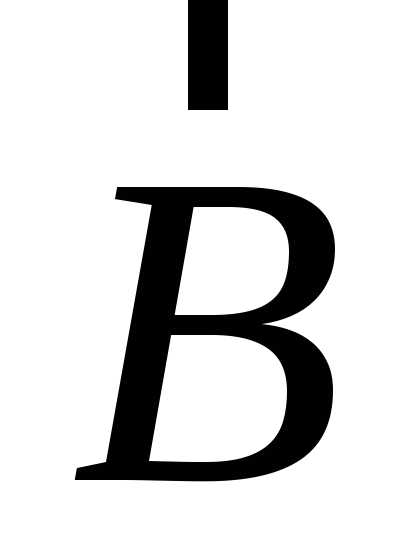 на кратчайшем пути вокруг полученного
вектора происходило в ту же сторону,
как вращение осиxк
осиyвокруг осиz(рисунок Рисунок 5 ).
на кратчайшем пути вокруг полученного
вектора происходило в ту же сторону,
как вращение осиxк
осиyвокруг осиz(рисунок Рисунок 5 ).
−Векторное произведение
Векторное произведение вычисляется как
,
тогда компоненты векторного произведения получаются из раскрытия определителя:
Изменение порядка сомножителей приводит к изменению знака векторного произведения: .
Размерность векторного произведения – единицы измерения площади, т.е. квадратные метры.
Кроме описанных операций сложения, скалярного и векторного произведений, мы будем использовать векторные дифференциальные операторы. Их определение дается позже, непосредственно перед использованием.
studfiles.net
📝векторные и скалярные велечины
Часто многим ученикам или даже студентам сложно понять отличия векторной и скалярной величины. Поэтому я хотел бы объяснить максимально понятным языком суть каждого из этих понятий и на примерах показать главные их отличия. Так как они оба часто используются в математических задачах, для правильного и быстрого решения которых нужно знать это.
Начнём с определений:
Векторной величиной, или вектором (в широком смысле), называется всякая величина, обладающая направлением.
Скалярной величиной, или скаляром, называется величина, не обладающая направлением.
То есть у вас уже должна появиться основная картина, если есть направление у величины, то это вектор, а если нет, то это скаляр. Далее рассмотрим всё на конкретных примерах.
Пример 1. Когда какая-то сила действует на материальную точку, то она будет вектором, так как она обладает направлением. Так же и скорость материальной точки — тоже вектор.
Пример 2. А от уже температура тела будет скаляром, так как с ней не связано никакое направление. Поэтому масса тела и его плотность — тоже будут скалярами.
Если не учитывать направление векторной величины, то ее, как и скалярную, можно измерить, выбрав соответствующую единицу измерения. Но в этом случае полученное число, характеризует скалярную величину полностью, а векторную только частично. Её можно полностью охарактеризовать направленным отрезком, предварительно задав линейный масштаб. И это хорошо показано в следующем примере.
Пример 3. Направленный отрезок АВ при введенном масштабе MN, изображающем единицу силы (1 Н) (более подробно смотрите на рисунке), характеризует силу в 3,5 Н, направление которой совпадает с направлением отрезка АВ (указанным стрелкой).
Думаю, после таких явных данных у вас уже не должно появиться проблем, при различии этих понятий.
Материалы по теме:
Поделиться с друзьями:
Загрузка…matemonline.com
