Угол. Прямой и развернутый угол. Чертежный треугольник
Данная тема рассматривалась ранее.
Повторить эту тему можно, перейдя по ссылке
1. Полный угол (см. Рис. 1)
Рис. 1. Полный угол
Стороны угла совпадают.
Меньший угол не виден. Он называется нулевым углом.
Зато второй угол, больший, захватил плоскость полностью. Такой угол называется полным. Вот он имеет для нас важное значение. Поделив его пополам, а потом еще раз пополам, мы получим еще два типа важных углов.
2. Развернутый угол (см. Рис. 2.)
Рис. 2. Развернутый угол
Если стороны угла будут смотреть в разные стороны, составляя прямую, то два полученных угла будут равны друг другу. При этом вместе они составляют полный угол.
То есть угол, образованный такими лучами, является половиной полного угла.
Сам угол похож на то, как если бы ножки циркуля развернули в разные стороны. Угол так и назвали – развернутым.
3. Прямой угол
Поделим уже развернутый угол пополам. Получим два равных угла (см. Рис. 3).
Рис. 3. Прямой угол
Если столб стоит на земле прямо, то мы видим, что углы с двух сторон равны друг другу. Угол так и называется – прямой. Для него вместо дуги договорились использовать специальную отметку, маленький уголок.
1. Чтобы начертить полный угол, нужно из точки провести луч, подразумевая, что это два совпадающих луча.
2. Чтобы начертить развернутый угол, нужно провести прямую и поставить на ней точку. Получим два луча, идущих в разные стороны, то есть развернутый угол.
3. Чтобы начертить прямой угол, легче всего воспользоваться готовым деревянным или металлическим прямым углом, который называется чертежным треугольником, или угольником (см. Рис. 4).

Рис. 4. Чертежный треугольник
Часто уже есть прямая и точка на ней и нужно провести через эту точку вторую прямую под прямым углом к первой.
Совместим угольник одной стороной с имеющейся прямой так, чтобы его вершина совместилась с точкой на прямой. Теперь проведем вторую прямую. Она расположена под прямым углом к первой прямой. Такие прямые называют перпендикулярными (см. Рис. 5).
Рис. 5. Перпендикулярные прямые и угольник
Дан развернутый угол (см. Рис. 6).
Рис. 6. Развернутый угол AOB
Поделим его пополам.
Угол – прямой (см. Рис. 7).
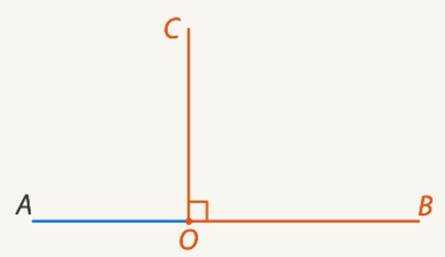
Рис. 7. Прямой угол
Угол меньше прямого угла. Такие углы называются острыми (см. Рис. 8).
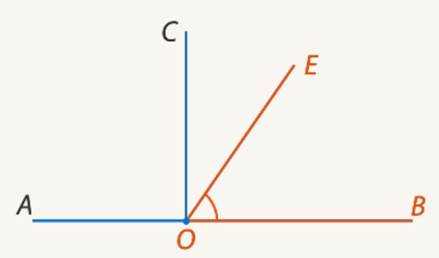
Рис. 8. Острый угол ЕОВ
Угол больше прямого угла. Такие углы называются тупыми (см. Рис. 9).
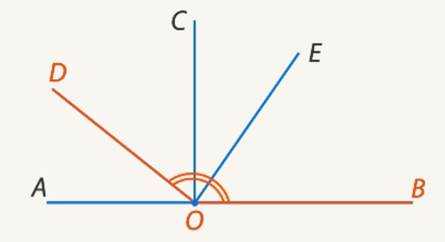
Рис. 9. Тупой угол
Итак, все это можно сформулировать короткими определениями:
1. Прямой угол – это половина развернутого угла.
2. Острый угол – это угол меньше прямого.
3. Тупой угол – это угол больше прямого и меньше развернутого.
Построение прямого угла с помощью циркуля
На листе бумаги можно построить прямой угол, даже если у вас нет угольника.
Помните, что прямой угол – это половина развернутого.
Сначала изобразим развернутый угол (см. Рис. 10).
Рис. 10. Построение прямого угла
Теперь поделим его пополам. Для этого возьмем циркуль и от вершины угла отложим в обе стороны одинаковое расстояние (см. Рис. 11).
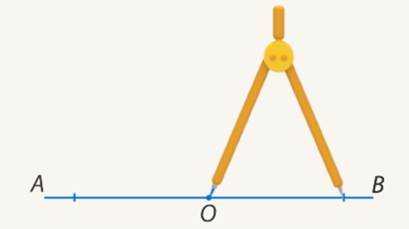
Рис. 11. Построение прямого угла (продолжение)
Увеличим чуть-чуть расстояние между ножками циркуля и отложим две дуги с центрами в полученных точках, чтобы они пересеклись над вершиной угла (см. Рис. 12).
Рис. 12. Построение прямого угла (продолжение)
Мы получим новую точку прямо над вершиной . Соединим точки (см. Рис. 13).
Рис. 13. Построение прямого угла (продолжение)
Мы все делили симметрично, углы получились равными, а значит, прямыми.
Представьте теперь себе землемера в Древнем Египте. Ему нужно разделить поле на прямоугольники, а для этого нужно уметь делать прямые углы. У него нет огромного деревянного угольника. А даже если бы и был, его же тоже нужно уметь сделать.
Египтяне использовали треугольник со сторонами в соотношении 3:4:5. Один угол этого треугольника прямой. Его потом так и назвали – «египетский треугольник».
Чтобы на земле начертить такой треугольник, можно взять веревку 12 метров, отметить на ней три части – 3, 4 и 5 метров. Концы веревки соединить. В отметках привязать колышки. Натянуть за колышки все части веревки и вбить колышки в землю. Получится египетский треугольник, а значит, один прямой угол (см. Рис. 14).
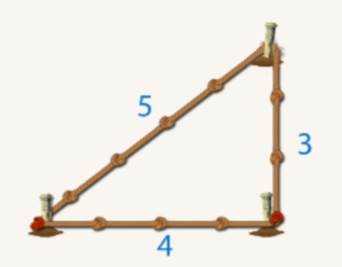
Рис. 14. «Египетский треугольник»
Если у нас ровный пол, то веревка с грузом на конце будет составлять с линией пола прямой угол. Такой инструмент используют строители. Он называется отвес (см. Рис. 15).
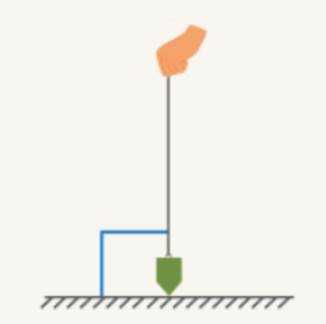
Рис. 15. Отвес
Список литературы
- Зубарева И.И., Мордкович А.Г. Математика. 5 класс. – М.: Мнемозина, 2013.
- Виленкин Н.Я. и др. Математика. 5 кл. – М.: Мнемозина, 2013.
- Ерина Т.М. Математика 5кл. Раб. тетрадь к уч. Виленкина, 2013. – М.: Мнемозина, 2013.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Shkolo.ru (Источник).
- Cleverstudents.ru (Источник).
- Festival.1september.ru (Источник).
Домашнее задание
- Постройте полный, прямой и развернутый углы.
- Назовите все углы на рисунке, а также укажите их вид:
interneturok.ru
План-конспект урока по математике (2 класс) по теме: Угол. Прямой угол.
- Угол. Прямой угол.
- 2-й класс
Данный урок разработан и проведён в рамках деятельности творческой группы «Современные педагогические технологии» с целью демонстрации опыта работы по применению деятельностной технологии в начальной школе
Цель:
- Сформировать представление об угле и его элементах, способность к распознаванию и обозначению углов;
- Познакомить с понятием «прямой угол»;
- Учить находить прямой угол с помощью чертёжного угольника;
- Отрабатывать навыки анализа и решения задач;
- Пополнять активный запас детей; учить работать в паре;
- Развивать математическую речь, мыслительные операции;
- Формировать познавательный интерес;
- Способствовать здоровьесбережению детей;
- Соблюдать гигиенические требования к уроку;
Тип урока: ОНЗ.
Мыслительные операции, необходимые на этапе проектирования: анализ, синтез, обобщение.
- Ход урока
- I. Мотивация к учебной деятельности.
Цель: создать условия для возникновения внутренней потребности включения в учебную деятельность.
– В начале урока мне хочется напомнить известное вам высказывание А. Нивена.
(слайд 2)
Математику нельзя изучать наблюдая, как это делает сосед.
А. Нивен
– Прочитайте его хором.
– Как вы понимаете смысл этих слов? (Если смотреть, как другие анализируют, сравнивают, преодолевают какие-то трудности, а сам ты этого ничего не делаешь. То математику знать не будешь).
– Верно, я думаю, что вы успешно преодолеете все трудности, которые преподносит нам математика.
– Посмотрите, это … (Ёлочка.)
– Что необычного в изображении ёлочки? (Она составлена из геометрических фигур.)
– Назовите их. (Треугольники и прямоугольник.)
– А ведь ёлочка вам подсказывает, какому разделу математики будет посвящён урок. (Геометрии.)
– Да, и сегодня вам предстоит узнать новое из области геометрии.
– Молодцы! С чего начнём? (С повторения необходимого.)
- II. Актуализация знаний и фиксация затруднения в деятельности.
Цель:
- активизировать представление о плоскости и луче;
- тренировать умения чертить, обозначать и называть лучи;
- активизировать мыслительные операции: анализ, синтез, обобщение;
- организовать самостоятельное выполнение учащимися индивидуального задания на применение нового знания, запланированного для изучения на данном уроке;
- организовать фиксацию учащимися возникшего затруднения в обосновании правильности полученного результата.
(Слайд 3)
– Посмотрите, нас встречают жители этой страны
– Назовите эти фигуры одним словом. (Геометрические фигуры)
– Назовите многоугольники ( треугольник, квадрат, прямоугольник)
(По щелчку мыши многоугольники исчезают)
– Назовите геометрическую фигуру, которая состоит из 4-х звеньев ( незамкнутая ломаная линия)
(По щелчку мыши ломаная исчезает)
– Какая геометрическая фигура не имеет ни начала на конца? (прямая линия)
(По щелчку мыши прямая исчезает)
– Назовите лишнюю фигуру среди данных фигур. (отрезок)
(По щелчку мыши отрезок исчезает)
– Какие геометрические фигуры остались? (Лучи)
– Что вы знаете о геометрической фигуре луч? (Луч – это часть прямой, ограниченная с одной стороны)
– Чем отличается луч от прямой? (Луч– это часть прямой, ограниченная с одной стороны, а прямая не имеет ни начала на конца).
– У вас на партах лежат модели лучей.
– Покажите точку, начало луча, покажите весь луч.
(Слайд 7)
– Сравните лучи АВ и АС.
– Что у них общего? (У них общее начало точка А)
– Возьмите модели лучей и наложите их друг на друга так, чтобы точки совпали, а части прямой расходились в разные стороны.
– На сколько частей лучи разделили плоскость? (На 2 части)
– Как бы вы назвали меньшую из этих частей) (Углом) (Слайд 8)
– Как докажете, что данная фигура является углом?
Дети обосновывают своё мнение и приходят к выводу, что не могут доказать, что данная фигура является углом.
– Почему же возникло затруднение при доказательстве того, что выбранная вами фигура угол? (Нам неизвестно, что такое угол, каковы признаки этой геометрической фигуры.)
– Молодцы! Поняв причину, дальше надо … (Поставить цель, выяснить, что такое угол, выявить его признаки.)
– Назовите тему урока. (Угол.)
Открыть часть темы на доске.
- III. «Открытие» нового знания.
Цель:
- организовать построение нового знания об угле;
- организовать фиксацию нового знания в речи;
- организовать выполнение задания, вызвавшего ранее затруднение;
- зафиксировать преодоление возникшего ранее затруднения
– Покажите точку, общее начало лучей.
– Посмотрите, как называется общее начало лучей. (Это вершина угла) (слайд 9)
– Покажите лучи, которые образуют угол.
– Как их называют? (Стороны угла.) (слайд 10)
– Сколько вершин у угла? (1)
– Сколько сторон у угла? (2)
– Так из чего состоит угол? (Из точки – вершины и двух лучей – сторон, которые выходят из этой точки — вершины)
– Кто может сказать, что же такое угол? (Угол – это геометрическая фигура, которая состоит из точки — вершины и двух лучей — сторон, которые выходят из этой точки)
– Продолжаем заполнять геометрический словарь.
– Какие новые слова в него добавили? (Угол, вершина угла, сторона угла).
– Вы конечно знаете, что у каждой геометрической фигуры есть имя, и у углов тоже есть имя.
– Аня, как тебя называет мама? А тебя Саша?
– Вас дома называют разными именами.
– И угол тоже можно назвать по-разному.
– Прочитайте его имя в учебнике на стр. 38.
– Что интересного заметили при чтении имён угла? (Буква, которая называет вершину читается в середине)
– Записывают это так: слово «угол» заменяют специальным знаком:
– Запишем этот знак в тетради.
– Начинаем писать с верхнего правого угла клетки, ведём наклонную в нижний левый угол клетки и вправо по нижней стороне клетки в нижний правый угол. (Дети записывают знак в тетради)
– Как пишется ваше имя?
– А теперь обратите внимание на то, как пишется имя угла. (Все буквы заглавные)
– Как вы думаете, почему так записывают угол? (По названию вершины угла.)
– Правильно. Запишите имя угла в тетради.
- IV. Первичное закрепление с проговариванием во внешней речи
Цель: создать условия для выполнения учащимися нескольких типовых заданий на применение изученного знания с проговариванием во внешней речи.
– А теперь потренируемся в записи углов.
– Выполним задание №2 с.38
– Прочитайте задание.
– Работать будем в парах.
– Один из вас назовёт имена углов. А другой вершины и стороны угла.
– А теперь запишите различные обозначения углов.
(слайд 11)
– Проверяем первый угол, если вы записали так, поставьте «+».
– Катя. Прочитай названия второго угла, если вы записали так, поставьте «+».
– Самостоятельно проверьте, так ли вы записали названия третьего угла, если вы записали так, поставьте «+».
– У кого получилось три «+», у кого два, у кого один.
– Молодцы. А теперь отдохнём и посчитаем.
Физминутка «Счёт через 4»
– Продолжаем работу.
- V. «Открытие» нового знания (продолжение)
Цели:
- организовать построение нового знания о прямом угле;
- организовать фиксацию нового знания в речи.
– Скажите, а можно ли угол сделать больше или меньше по размеру?
(слайд 12-13)
– Смоделируйте полученный угол так, чтобы он стал меньше, а теперь, чтобы он стал больше.
– Какой вывод можем сделать о размере углах? (Углы бывают разные по размеру)
– Верно, углы бывают разные, и наша задача узнать, какой угол самый главный
– Сложите лист бумаги пополам, а потом ещё раз пополам.
– Возьмите линейку и красный карандаш, проведите линии сгиба.
– На сколько частей прямые разделили плоскость? (на 4 части)
– Что можете сказать о прямых? (Они пересекаются)
– Сколько углов образовали пересекающиеся прямые? (4)
– Эти пересекающиеся прямые образовали особенные углы.
– Может кто-нибудь знает названия этих углов?
– Это прямые углы (слайд 14)
– Покажите пальчиком каждый прямой угол.
– Раскрасьте прямые углы разными цветами.
– Поставьте точку на пересечении прямых.
– Чем будет являться эта точка для каждого из углов? (Вершиной угла)
(слайд 15)
– Покажите, где в жизни встречается прямой угол?
– А вот, если две пересекающиеся прямые образуют прямой угол, то их называют перпендикулярными прямыми)
( Повесить на доску карточку)
– Какими новыми понятиями пополнился наш словарь? (Прямой угол, перпендикулярные прямые).
– Ребята, а вы обратили внимание, что у вас на партах лежит ещё один чертёжный инструмент.
– Кто знает, как он называется?
– Правильное его название чертёжный угольник.
– Прямые углы удобно находить и строить с помощью угольника.
– Рассмотрите его внимательно и подумайте, почему?
– Итак, какова наша задача? (Научиться с помощью угольника определять прямые углы.)
(слайд 16)
– Составим алгоритм.
- Совместить вершину прямого угла чертёжного угольника и вершину угла.
- Совместить одну из сторон чертёжного угольника и сторону угла.
- Если вторая сторона угла совпала со второй стороной угольника, то это прямой угол.
– Найдите прямые углы с помощью чертёжного угольника в окружающей нас обстановке.
- VI. Самостоятельная работа c самопроверкой.
Цель: организовать самостоятельное выполнение учащимися типовых заданий на применение новых знаний.
Работа по учебнику с. 39 №4.
– А теперь самостоятельно найдите прямые углы с помощью чертёжного угольника.
Проверка работы с помощью доски.
– Самостоятельно проверьте, так ли вы нашли прямые углы, если так, поставьте «+».
– Каким новым понятием пополнился наш словарь? (чертёжной угольник).
– Какие новые жители поселились в стране Геометрия? (угол, прямой угол) (слайд 12-13)
– Посмотрите на все фигуры (слайд 17) и скажите, какие фигуры имеют углы?
– А какие имеют прямые углы?
– Что мы знали о прямоугольнике? А о квадрате?
– А что нового узнали?
- VII. Повторение изученного.
– Решим задачу, в которой говорится о прямоугольнике и квадрате.
Работа по учебнику с.40 №9.
Задача: Начерти прямоугольник со сторонами 6см и 2см и вычисли его периметр. А теперь начерти квадрат с таким же периметром.
– Прочитайте задачу про себя.
– А теперь прочитайте задачу вслух, чтобы узнать, что известно в задаче, а что надо найти.
– Что же нам известно в задаче?
– Что надо узнать?
– Прежде чем вычислить Р, что надо сделать? (Начертить прямоугольник)
– А потом? (Найти Р).
– Как найти Р прямоугольника? (Надо длину всех сторон сложить).
– Начертите прямоугольник и найдите его Р самостоятельно.
(Проверка: решение дети записывают на доске)
– Прочитайте, что ещё нужно сделать в этой задаче.
– Любой ли квадрат надо начертить? (Нет).
– А какой? (С таким же Р).
– Сможем начертить? Почему? (Не знаем сторону квадрата)
– Что мы знаем о квадрате?
– Как узнать сторону квадрата)
– Как представить 16 четырьмя одинаковыми слагаемыми?
– Значит чему равна сторона квадрата?
– Начертите квадрат.
- VIII. Рефлексия учебной деятельности на уроке.
Цели:
- организовать фиксацию учащимися степени соответствия поставленной цели и полученного результата учебной деятельности;
- создать условия для фиксации учащимися в речи нового знания, изученного на уроке: что такое угол, как определить прямой угол;
- организовать фиксацию затруднений, которые остались, и способов их преодоления;
- организовать самооценку учениками собственной учебной деятельности на уроке;
– Какую цель вы ставили перед собой на уроке? (Узнать, что такое угол, его признаки.)
– Достигли цели? Докажите.
– Что такое угол? (Это меньшая часть плоскости, ограниченная двумя лучами, имеющими общее начало.)
– Углы бывают разные. С каким видом угла вы познакомились сегодня? (С прямым углом.)
– Как называются прямые, образующие прямой угол? (Перпендикулярные.)
– Как вы находили прямой угол среди углов? (С помощью угольника: совмещали угол и одну из сторон угольника. Потом смотрели, совпадает ли другая сторона угла со стороной угольника.)
– Каким значком обозначают прямой угол?
– Как записывают название углов? (Пишут значок угла и букву, обозначающую вершину угла, или три буквы, причём букву, обозначающую вершину, пишут в середине.)
– Оцените свою работу на уроке.
– Выберите круги:
Зелёный – доволен собой, всё понял:
Жёлтый – допускал неточность, неуверен в знаниях;
Красный – надо постараться и успех придёт.
nsportal.ru
Что такое прямой угол?
Здравствуйте! Сейчас мы Вам быстро напомним, что этот угол из себя представляет.
Прямой угол — это угол, градусная мера которого равняется .
Есть фигуры, в образовании которых часто принимаю роль прямые углы, это:
- Прямоугольный треугольник — это такой треугольник, у которого прямой один угол.
- Прямоугольник — геометрическая фигура, у которой все углы прямые.
- Квадрат — геометрическая фигура с прямыми углами.
- Прямоугольная трапеция — вид трапеции, у которой хотя бы один из углов — прямой.
Так же существует другое большое количество иных обозначения для этого угла:
- радиан
- 1/4 оборота или полного угла
- 5400 угловых минут
- 324000 угловых секунд
Решим задачку. Нам нужно найти угол смежный к прямому углу. Давайте вспомним немного теории, сумма смежных углов равняется . А так как прямой угол равняется , то смежный с ним угол будет равняться:
.
Таким образом получается, что угол смежный к прямому углу также будет прямым, что мы и доказали.
Ответ:
Надеюсь теперь Вам стало понятней, что такое прямой угол. Обращайтесь!
ru.solverbook.com
