Радианы и градусы – Перевод градусов в радианы и обратно: формулы, примеры

Перевод градусов в радианы и обратно: формулы, примеры

Углы измеряются в градусах или в радианах. Важно понимать связь между этими единицами измерения. Понимание этой связи позволяет оперировать углами и осуществлять переход от градусов к радианам и обратно. В данной статье выведем формулу для перевода градусов в радианы и радианов в градусы, а также разберем несколько примеров из практики.

Связь между градусами и радианами

Чтобы установить связь между градусами и радианами, необходимо узнать градусную и радианную меру какого-либо угла. Например, возьмем центральный угол, который опирается на диаметр окружности радиуса r. Чтобы вычислить радианную меру этого угла необходимо длину дуги разделить на длину радиуса окружности. Рассматриваемому углу соответствует длина дуги, равная половине длины окружности π·r. Разделим длину дуги на радиус и получим радианную меру угла: π·rr=π рад.

Итак, рассматриваемый угол равен π радиан. С другой стороны, это развернутый угол, равный 180°. Следовательно 180°=π рад. 

π радиан =180°

Формулы перевода радианов в градусы и наоборот

Из формулы, полученной выше, можно вывести другие формулы для перевода углов из радианов в градусы и из градуов в радианы.

Выразим один радиан в градусах. Для этого разделим левую и правую части радиуса на пи.

1 рад=180π° — градусная мера угла в 1 радиан равна 180π.

Также можно выразить один градус в радианах.

1°=π180рад

Можно произвести приблизтельные вычисления величин угла в радианах и наоборот. Для этого возьмем значения числа π с точностью до десятитысячных и подставим в полученные формулы. 

1 рад=180π°=1803,1416°=57,2956°

Значит, в одном радиане примерно 57 градусов

1°=π180рад=3,1416180рад=0,0175 рад

Один градус содержит 0,0175 радиана.

x рад=х·180π°

Чтобы перевести угол из радианов в градусы, нужно значение угла в радианах умножить на 180 и разделить на пи.

zaochnik.com

Что такое один градус? Что такое один радиан? Перевод радианов в градусы и обратно.

        В прошлый раз мы с вами ответили на первый вопрос, касаемый работы с углами. А именно – как отсчитываются углы. Рассмотрели положительные и отрицательные углы, а также углы, большие 360 градусов. И на круге углы порисовали.)

        В этом же уроке настал черёд ответить на второй вопрос, связанный с измерением углов. Здесь мы разберёмся с загадочными радианами и особенно – с пресловутым числом «пи», которое будет мозолить нам глаза на протяжении всего дальнейшего изучения тригонометрии. Поймём, что это за число, откуда оно берётся и как с ним работать. И задания порешаем, само собой. Стандартные и не очень…)

        Разберёмся? Ну сколько же можно бояться числа «пи», в конце-то концов!)

        Итак, в чём же измеряются углы в математике? Начнём с привычного и знакомого. С градусов.

Что такое один градус? Градусная мера угла.

        К градусам вы уже попривыкли. Геометрию изучаете, да и в жизни постоянно сталкиваетесь. Например, «повернул на 90 градусов».) Короче, градус – штука простая и понятная.

        Вы и вправду так думаете? Тогда сможете сказать мне, что такое градус? Нет, гуглить и потрошить Википедию не надо. Ну как, слабо с ходу? Вот так-то…

        Начнём издалека. С древнейших времён. А именно – с двух очагов древних цивилизаций Вавилона и Египта.)

        Градус – это 1/360 часть окружности. И всё!

        Смотрим картинку:

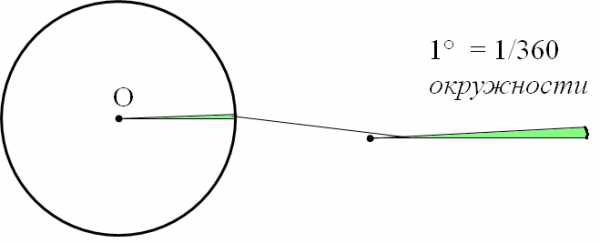
        Придумали градусы в Древнем Вавилоне.) Как? Очень просто! Просто взяли да разбили окружность на 360 равных кусочков. Почему именно на 360? А не на 100 или на 1000? Вроде бы, число 100 поровнее, чем 360… Вопрос хороший.

        Основная версия – астрономическая. Ведь число 360 очень близко к числу дней в году! А для наблюдений за Солнцем, Луной и звёздами это было оч-чень удобно.)

        Кроме того, в астрономии (а также строительстве, землемерии и прочих смежных областях) очень удобно делить окружность на равные части. А теперь давайте прикинем чисто математически, на какие числа делится нацело 100 и на какие – 360? И в каком из вариантов этих делителей нацело больше? А людям такое деление очень удобно, да…)

Что такое число «пи»? Как оно возникло?

        А теперь переместимся из Древнего Вавилона в Древний Египет. Примерно в то же самое время там разгадывали другую загадку. Не менее интересную, чем вопрос, на сколько частей бить окружность. А именно – во сколько раз длина окружности больше её диаметра?

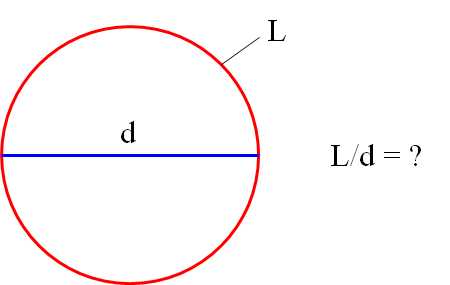
        И так измеряли и сяк… Каждый раз получалось чуть-чуть больше трёх. Но как-то коряво получалось, неровно…

        Но они, египтяне, ни в чём не виноваты. После них математики всех мастей продолжали мучиться аж до 18 века! Пока в 1767 году окончательно не доказали, что, как бы мелко ни нарезать окружность на равные кусочки, из таких кусочков сложить точно длину диаметра нельзя. Принципиально нельзя. Только лишь примерно.

        Нет, конечно же, во сколько раз длина окружности больше её диаметра установили давным-давно. Но, опять же, примерно… В 3,141592653… раза.

        Это число – и есть число «пи» собственной персоной.) Да уж… Корявое так корявое… После запятой – бесконечное число цифр безо всякого порядка, безо всякой логики. В математике такие числа называются

        Конечно, рациональные приближения числа «пи» известны людям ещё со времён Архимеда. Например:

        22/7 = 3,14285714…

        377/120 = 3,14166667…

        355/113 = 3,14159292…

        Сейчас, в век суперкомпьютеров, погоня за десятичными знаками числа «пи» не стихает, и на сегодняшний день человечеству известно уже два квадриллиона (!) знаков этого числа…

        Но нам для практического применения такая сверхточность совершенно не требуется. Чаще всего достаточно запомнить всего лишь две цифры после запятой.

        Запоминаем:

        Вот и всё. Раз уж нам ясно, что длина окружности больше её диаметра в «пи» раз, то можно записать (и запомнить) точную формулу для длины окружности:

        Здесь L – длина окружности, а d – её диаметр.

        В геометрии всяко пригодится.)

        Для общего развития скажу, что число «пи» сидит не только в геометрии или тригонометрии. Оно возникает в самых различных разделах высшей математики. В интегралах, например. Или в теории вероятностей. Или в теории комплексных чисел, а также рядов. Само по себе возникает, хотим мы того или нет… Поступите в ВУЗ – убедитесь лично.)

        Ну а теперь снова вернёмся к старым добрым градусам. Как мы помним, один градус – это 1/360 часть окружности. С исторической и практической точек зрения людям такое деление на 360 равных частей оказалось очень даже удобно, но…

        Как выяснилось гораздо позже Древнего Вавилона, градусы удобны далеко не всем. Например, высшей математике они ой как неудобны! Высшая математика – дама серьёзная. По законам природы устроена. И она справедливо заявляет:

        Против природы не попрёшь… Пришлось прислушаться и уступить. И ввести новую меру угла, не зависящую от наших хотелок. )

        Итак, знакомьтесь – радиан!

Что такое один радиан? Радианная мера угла.

        В основе определения радиана – та же самая окружность. Угол в 1 радиан – это угол, который отсекает от окружности дугу, длина которой (L) равна радиусу окружности (R). И всё!

        Смотрим картинку:

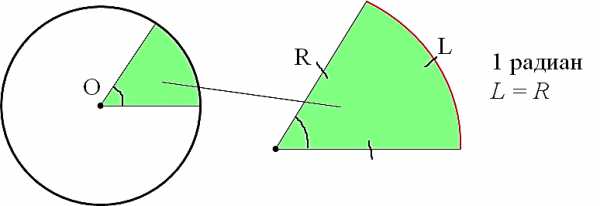
        Причём величина угла в один радиан не зависит от радиуса окружности!

        Запоминаем:

        Угол в один радиан – это угол, вырезающий из окружности дугу, равную радиусу окружности. Величина угла в 1 радиан не зависит от радиуса окружности.

        Кстати говоря, градусная мера угла тоже не зависит от радиуса окружности. Большая окружность, маленькая – углу в один градус без разницы. Но градус – это величина, искусственно придуманная людьми для их личного удобства! Древними вавилонянами, если мы помним.) 1/360 часть окружности. Так уж сложилось чисто исторически. А если бы по каким-то причинам договорились на 100 частей разбить окружность? Или на 200? Кто знает, что тогда называлось бы градусом сегодня… Вот на сколько частей разобьём окружность, такой «градус» и получим. А вот радиан – штука универсальная!) К способу разбиения окружности никак не привязан.

Как переводить радианы в градусы и обратно?

        К этому моменту вам уже должно быть интуитивно понятно, что один радиан существенно больше одного градуса. Всё-таки непонятно? Тогда смотрим снова на картинку:

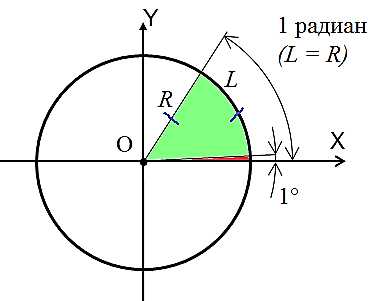
        Будем считать, что малюсенький красный угол имеет величину примерно один градус. Совсем крохотный уголок, почти и нет его… А большой зелёный угол – примерно один радиан! Чувствуете разницу?) Конечно же, один радиан сильно больше одного градуса…

        А вот теперь начинается самое интересное! Вопрос: а во сколько раз один радиан больше одного градуса? Или сколько градусов в одном радиане? Сейчас выясним!)

        Смотрим на очередные картинки:

        На картинке слева изображён полукруг. Обычный развёрнутый угол величиной 180°. А вот на картинке справа – тот же самый полукруг, но нарезанный радианами! Видно, что в 180° помещается примерно три с хвостиком радиана.

        Вопрос на засыпку: как вы думаете, чему равен этот хвостик?)

        Да! Он равен 0,141592653… Привет, число «пи», вот мы про тебя и вспомнили!)

        Стало быть, в 180° укладывается 3,141592653… радиан. Понятное дело, что каждый раз писать такое длинное число неудобно, поэтому пишут приближённо:

        Или точно:

        Вот и всё. Вот и весь секрет тотального присутствия числа «пи» в тригонометрии. Эту простую формулку надо знать железно. Уловили?)

        Так сколько же градусов в одном радиане? Не вопрос! Если в «пи» радианах содержится 180 градусов, то сколько же тогда градусов сидит в одном радиане? Правильно, в «пи» раз меньше! То есть меньше примерно в 3,14 раза.

        Вот и делим обе части нашего соотношения на «пи» и получаем один радиан в градусах:

        Это приближённое равенство также очень полезно запомнить. В одном радиане примерно 60 градусов. Такой грубой оценки бывает вполне достаточно для ответа на очень многие каверзные вопросы, связанные с углами. Бывает и недостаточно, конечно. В своё время мы такие хитрые задачки рассмотрим.)

        Но это не самое главное применение этой формулы!) А самое главное – перевод радианов в градусы и обратно.

        Переводим радианы в градусы!

        Чаще всего углы в тригонометрии заданы в радианах с числом «пи». Это – самая стандартная ситуация. Если угол задан в радианах с числом «пи», то всё очень просто. Мы знаем, что «пи» радиан – это 180 градусов. Вот и подставляем вместо «пи» радиан – число 180. Сокращаем всё что сокращается и получаем угол в градусах.

        Например:

        Или более мудрёный угол:

        Просто, правда?)

        Переводим градусы в радианы!

        Обратный перевод градусов в радианы чуть сложнее, но ненамного. Если угол задан в градусах, то сначала нам надо узнать, сколько составляет один градус в радианах. И умножить это значение на количество градусов.) И чему же равен 1° в радианах?

        Снова смотрим на нашу формулу и соображаем. Если 180° — это «пи» радиан, то 1° в 180 раз меньше. Вот и делим обе части формулы на 180! Получаем, что 1° в радианах равен:

        Вот и все дела. Умножаем дробь π/180 на количество градусов, сокращаем что сокращается и получаем угол в радианах. Например:

        Или аналогично:

        Вот и всё. Заменять «пи» на примерно 3,14 никакой необходимости нет: его всегда буквой пишут. Что правда, то правда: нас же в заданиях обычно точный ответ интересует! А не приближённый.) Кстати, кому интересен приближённый ответ, посчитайте на калькуляторе. Получите примерно 0,628 и 2,356 радиана соответственно.

        Итак, в непринуждённой беседе с лирическими отступлениями мы узнали, что радианы – это очень даже просто, не больно и не страшно.) Да и перевод туда-обратно несложен. И «пи» – не кусается… Так откуда же проблемы?

        Что ж, вскрою тайну. Всё дело в том, что в тригонометрии значок градусов – пишется. Всегда и везде. Например, cos30° — это косинус 30 градусов! А вот значок радианов («рад») – не пишется! Он – подразумевается. В чём причина – неизвестно. Может, обленились математики, может ещё что… Но договорились не писать. Например, sin5 – это синус пяти радианов!

        Это и приводит к казусам. Человек смотрит на пример, видит «пи» и автоматически считает, что это 180°. Везде и всюду. Кстати, это срабатывает. До поры до времени, пока примеры – типовые. Но любое отклонение примера от шаблона – тут же валит наповал! Почему?

        Потому, что само по себе «пи» – это число! А никакие не градусы! Это «пи» радиан = 180°!

        Ещё раз запоминаем:

        Просто «пи» – это число! «Пи» РАДИАН — это 180°!

        Это заклинание надо понимать железно. Причём не просто механически зазубрить, а именно понимать каждое слово и каждый значок! И особенно – слово «радиан». Я не шучу. Ибо, если на вопрос, «Что такое «пи» в тригонометрии?», вы, блистая знаниями, радостно заявляете:

        «Пи – это 180 градусов!!!» ,

        то это говорит о том, что вы не понимаете до конца смысла этой зелёной фразы. И все дальнейшие беседы уже бессмысленны, да…

        Ещё раз: «пи» – это число! Примерно равное 3,14. Точного значения этого числа не знает никто: оно бесконечно длинное, корявое, иррациональное. Но – число! Такое же, как 2 или 7. Можно пройти примерно «пи» километров. Три километра и ещё около 140 метров. Можно купить «пи» килограммов картошки. Если продавец образованный встретится.) Можно выпить «пи» литров кока-колы. Если здоровье не жалко… И так далее…

        Всё равно непонятна зелёная запись? Хорошо, вот вам простые житейские фразы:

        1 километр – это 1000 метров;

        3 часа – это 180 минут;

        2 года – это 730 дней;

        И тому подобное. Точно так же и с градусами/радианами:

        «Пи» радиан – это 180 градусов!

        Уяснили, что «пи» – это просто число? Или я уже достал вас этой заезженной фразой? Ну ладно, убедили. Тогда вот вам парочка нестандартных вопросов:

        1. Что больше?

        или

        2. Что меньше?

        cos5°

        или

        cos5

        Если у вас случился ступор, не беда. Вспоминаем нашу мантру: «Пи» – это число! В первом синусе нам чётко сказано, что угол – в градусах! Следовательно, машинально заменять «пи» на 180° — нельзя. «Пи» градусов – это примерно 3,14°. Вот и пишем:

        Во втором синусе никаких значков нет. Значит, там – радианы. И вот тут замена «пи» на 180° — вполне законна.) Переводим радианы в градусы и получаем:

        А теперь сравниваем эти два синуса. Как? По кругу, разумеется! Рисовать углы мы с вами уже умеем, что такое синус угла на круге – тоже знаем. Вперёд! Рисуем круг, углы примерно 0,79° и 45° и смотрим какие синусы у этих углов. Даже на самом корявом круге будет видно, что sin45° гораздо больше, чем sin0,79°.

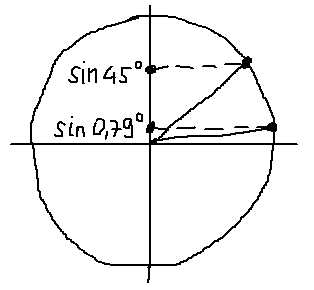
        С косинусами – всё то же самое. Рисуем на круге в правильных четвертях углы примерно 5 градусов и 5 радианов (помним, чему примерно равен один радиан в градусах?). Круг нам всё и подскажет. А именно, что cos5 меньше, чем cos5°.

        Вообще, задачки с углами в радианах без «пи» (типа определить знак выражения sin10∙cos20) относятся к разряду нестандартных. В следующем уроке разберём парочку таких.)

        Ну что, потренируемся с переводом углов?) Решаем несложные задания.

        1. Переведите следующие углы из градусной меры в радианную:

        180°; 0°; 360°; 90°; 270°.

        Ответы (по возрастанию):

        Как вы думаете, что это были за углы? Да! Это углы, которые попадают на координатные оси! Эти опорные значения надо держать в голове надёжно. До автоматизма! Как в градусах, так и в радианах. Зачем? Да всё за тем же! Для правильного распределения любых углов по четвертям.) Это полезное умение – залог успеха в любом задании по тригонометрии. Любом! От примитивных примеров до вполне себе солидных ЕГЭшных задачек части 2 (уравнения с отбором корней, тригонометрические неравенства и прочие хитрые штучки).

        Продолжаем развлекаться.

        2. Переведите углы в радианную меру:

        30°; 45°; 60°.

        Ответы (в беспорядке):

        Получилось? Рад за вас. Почему я выделил именно эти три угла? По той же самой причине. Эти углы – особые личности в тригонометрии. Потому что именно про эти углы вы обязаны знать всё! И где они находятся и весь комплект их тригонометрических функций. Скажем, значение sin20° вы знать не обязаны. А вот sin30° — уж будьте так добры! Это обязательные значения, без которых во всей остальной тригонометрии делать вообще нечего. Но об этом – в отдельном уроке.)

        Продолжим тренировку.

        Переведите следующие углы из радианной меры в градусную:

        Ответы (в беспорядке):

        300°; 225°; 120°; 330°; 240°; 135°; 210°; 315°; 150°.

        А это что за углы? Правильно! Это углы, в пределах одного оборота, кратные предыдущим трём! Но не попадающие на оси координат. Такие углы вы также обязаны уметь просчитывать! И более того, все углы, кратные 30, 45 или 60 градусам, вы обязаны уметь просчитывать! Как в пределах одного оборота, так и за его пределами. Как положительные, так и отрицательные… В соответствующем уроке мы научимся с вами проделывать такие полезные вещи.

        Если и это получилось, то тогда можно считать, что перевод радианов в градусы и обратно – уже не ваша проблема. Но перевод углов из одной размерности в другую – это лишь ещё один шаг вперёд к успешному постижению тригонометрии. Шаг мощный, но недостаточный. Ведь, чаще всего, с углами надо потом ещё и что-то делать.) Рисовать на круге, например. Или синус/косинус считать. Да и тангенс/котангенс тоже…

        Второй серьёзный шаг – это умение правильно определять положение любого угла на тригонометрическом круге. Любого! Как в градусах, так и в радианах. С градусами на круге мы уже плотно поработали в предыдущем уроке. Теперь настал черёд набивать руку в работе с радианами.

        Об этом – в следующей теме.

abudnikov.ru

Как перевести радианы в градусы?

Необходимость в измерении углов появилась у людей с тех пор, как цивилизация достигла минимального технического уровня. Всем известна феноменальная точность соблюдения наклона и ориентации по странам света, обеспеченная строителями египетских пирамид. Современную градусную меру углов, как сейчас считается, изобрели древние аккадцы.

Что такое градусы?

Градус – общепринятая единица измерения углов. В полной окружности 360 градусов. Причина выбора именно этого числа неизвестна. Вероятно, аккадцы разделили окружность на сектора, используя угол равностороннего треугольника, а затем полученные сегменты снова разделили на 60 частей согласно своей системе счисления. Градус тоже делится на 60 минут, а минуты – на 60 секунд. Общепринятыми обозначениями являются:

° – угловые градусы

’ – минуты,

’’ – секунды.

За тысячелетия градусная мера углов прочно вошла во многие сферы человеческой деятельности. Она и сейчас незаменима во всех областях науки и техники – от картографии до расчета орбит искусственных спутников Земли.

Что такое радианы?

Архимеду приписывается открытие постоянства соотношения длины окружности и ее диаметра. Мы называем его числом π. Оно иррационально, то есть не может быть выражено в виде обычной или периодической дроби. Чаще всего используется значение числа π с точностью до двух знаков после запятой – 3,14. Длина окружности L с радиусом R легко вычисляется по формуле: L=2πR.

Окружность радиуса R=1 имеет длину 2π. Это соотношение используется в геометрии как формулировка радианной меры угла.

По определению, радиан – угол с вершиной в центре окружности, опирающийся на дугу с длиной, равной радиусу окружности. Международное обозначение радиана – rad, отечественное – рад. Размерности он не имеет.

Дуга окружности с радиусом R с угловой величиной α радиан, имеет длину α * R.

Зачем понадобилось вводить новую единицу измерения угла?

Развитие науки и техники привело к появлению тригонометрии и математического анализа, необходимых для точных расчетов механических и оптических устройств. Одной из его задач является измерение длины кривой линии. Самый распространенный случай – определение длины дуги окружности. Использование для этой цели градусной меры углов крайне неудобно. Идея сопоставить длину дуги с радиусом окружности возникала у многих математиков, но сам термин «радиан» был введен в научный обиход только во второй половине XIX века. Сейчас все тригонометрические функции в математическом анализе по умолчанию используют радианную меру угла.

Как переводить градусы в радианы

Из формулы длины окружности вытекает, что в нее укладывается 2π радиусов. Отсюда вытекает, что: 1⁰=2π/360= π/180 рад.

И простая формула перевода из радианов в градусы: 1 рад = 180/π.

Пусть мы имеем угол в N градусов. Тогда формула для перевода из градусов в радианы будет такой: α(радиан) = N/(180/π) = N*π/180.

Остались вопросы?

Ответы на них можно найти в интернет-уроке на тему «Длина дуги окружности», где подробно разъяснены понятия длины окружности, радианной меры углов и на конкретных примерах показан перевод градусов в радианы. Знания упомянутого крайне важны для понимания математики, без которой невозможно существование современной цивилизации.

interneturok.ru

Zero To Hero

Совершенно очевидно, что в круге 360 градусов, не так ли?

А вот и нет. Большинство из нас совершенно не понимают, почему в круге 360 градусов. Мы запоминаем это магическое число как «размер окружности», а затем, изучая физику или высшую математику, удивляемся всем этим «радианам».

«Радианы делают математику проще!» — так говорят математики; вот бы они еще научились конкретнее объяснять, в чем заключается простота (чтобы и мы чувствовали себя в дискуссиях на тему рядов Тейлора, как рыба в воде). Сегодня мы откроем, что на самом деле представляют собой радианы, и поймем, почему именно они делают математику проще.

Откуда берутся градусы?

До чисел и языка слов у нас были звезды. Древние цивилизации использовали астрономию для определения времен года, предсказания будущего и задабривания богов (если уж приносить в жертву богам людей, то лучше делать это в правильное время).

И как всё это относится к углам? Попробуйте разгадать: не странно ли то, что в окружности 360 градусов, а в году 365 дней? И с чего это вдруг созвездия в течение года совершают оборот на небосклоне?

Спорим, вы не сможете определить время года по картине ночного неба? Вот созвездие Большой Медведицы, видимое в 2008 году из Нью-Йорка:

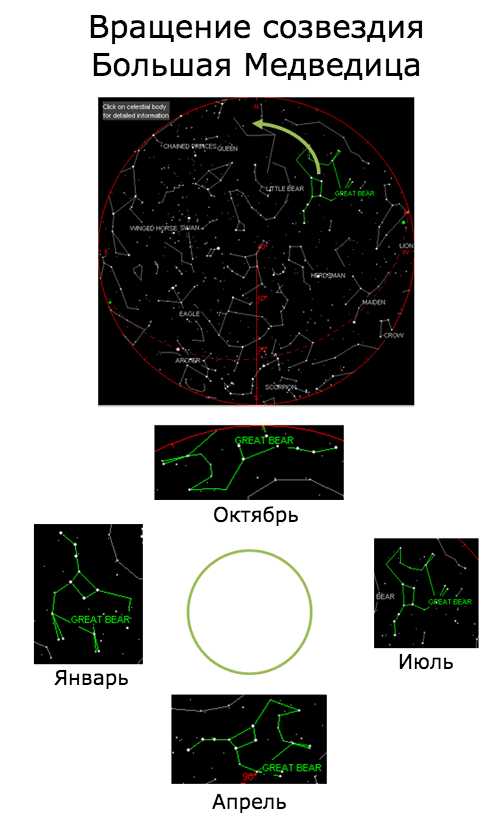
Созвездия каждую ночь немного продвигаются по кругу. Если Вы будете смотреть на небо в одно и то же время (например, в полночь), то заметите, что созвездия совершают полный круг по небу в течение года. Вот теория о возникновении градусов:

• Люди заметили, что за год созвездия совершали полный круг
• Каждый день они отодвигались совсем на немножно (это и есть «градус»)
• Поскольку в году около 360 дней, то и в круге было 360 градусов.

Но, есть одно но… Почему бы не сделать 365 градусов в окружности?

Простим древним эту погрешность: они пользовались солнечными часами, и не знали, что за год должно было набежать ровно 365.242199 градусов или дней, как вам теперь известно.

360 — достаточно точная цифра для тех времен. Она отлично согласуется с Вавилонской 60-ричной системой счисления, а также отлично делится (на 2, 3, 4, 6, 10, 12, 15, 30, 45, 90… ну вы поняли).

Математические расчеты по Солнцу выглядят вполне уместными

Земле везет: ~360 — отличное количество дней в году. Но эта цифра выглядит довольно субъективно: на Марсе у нас было бы ~680 градусов в окружности, так как марсианский год длится дольше (и сам марсианский день также длится дольше, как вы понимаете). В некоторых странах Европы люди пользуются градами, при которых круг приходится делить на 400 частей.

Многие из объяснений сходятся к следующему: «Ну, градус — довольно субъективная мера, но нам нужно было выбрать какое-то число». Не сейчас: далее мы увидим, что же на самом деле скрывают градусы.

Радианы спорят с градусами

Градус — это то, насколько мне, стоя в центре стадиона, приходится повернуть голову, чтобы увидеть человека, бегущего по беговой дорожке.

Представьте, что вы заметили друга, бегущего по огромному кругу:
— Привет, как далеко ты добежал?
— Ну, пробежался я нехило, около 10 километров.
— Ты что, совсем? Как сильно я повернул свою голову, чтобы тебя увидеть?
— Что?
— Я поясню словами покороче для непонятливых. Я в центре круга. Ты бежал вокруг. Насколько… я… повернул… свою… голову?
— Придурок.

Эгоистично, не так ли? Вот как вся эта математика построена! Мы пишем уравнения по типу «Слушай, как сильно я повернул свою голову, чтобы увидеть движущуюся планету/маятник/колесо?» Я уверен, что вы никогда не думали о том, что чувствует, о чем мечтает и на что надеется маятник. Это эгоистичный подход. Не кажется ли вам, что уравнения должны быть простыми не только для зрителя, но и для самого бегуна?

Радианы: скажи эгоизму нет

Многие вещи из физики (да и из жизни!) заставляет нас вылезти из своей привычной системы координат и посмотреть на вещи с другой точки. Вместо того, чтобы вычислять поворот своей головы, задумайтесь, как далеко продвинулся бегун.

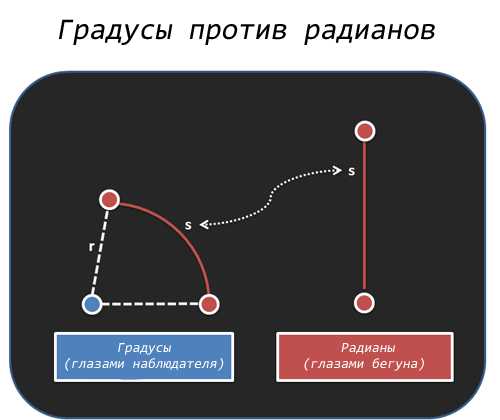
Градусы измеряют уголы по повороту головы. А радианы измеряют углы по пройденной дистанции.

Но само по себе расстояние не особо полезно, так как дистанция в 10 км может состоять из разного количества кругов, всё зависит от длины самого круга. Так что мы делим пройденную дистанцию на радиус круга, чтобы получить приведенный угол:

Вы часто будете встречать эту же формулу в таком виде:

угол в радианах (тета) — это длина дуги (s), поделенная на радиус (r).

Окружность описывает 360 градусов или 2π радиан — пройти весь круг будет 2*π* r / r. То есть, радиан — это примерно 360 /(2 * π) или 57.3 градусов.

Надеюсь, вы не будете думать, как я: «Ну вот, еще одна непонятная единица. 57.3 — такое странное число». Оно странное только потому, что вы всё еще думаете о себе!

Пройти 1 радиан (единицу) — вполне себе нормальная дистанция для путешествия.

Другими словами, наш «чистый, ровный угол в 90°» означает то же, что и непонятные π/2 единицы для пройденного бегуном пути. Подумайте об этом: «Эй, парень, а не пробежишь ли ты для меня еще 90°? Сколько это? А, ну да, для тебя это будет π/2 километра». Для бегуна дистанция в градусах выглядит также странно, как и поворот в радианах для зрителя.

Радианы в математике — это как бы поставить себя на место другого: передвинуть свою точку зрения с поворота головы на движение бегуна.

Что в имени тебе моем?

Радианы — это единица измерения движения по кругу, характеризуемого радиусом. Я думаю, слово «радиан» иллюстрирует как раз связь с радиусом движения.

По сути, радианы — это такие же числа, как 1.5 или 73, без каких либо единиц измерения (в формуле «радианы = пройденный путь / радиус» длина делится на длину, так что любые единицы измерения сокращаются).

Но, говоря практическим языком, мы не математические роботы, так что проще думать о радиане как о «пути», пройденному по единичной окружности.

Использование радиан

Я пока и сам привыкаю думать радианами. Но мы уже довольно близко подобрались к понятию «дистанции бегуна»:

• Мы используем «вращений в минуту», а не «градусов в секунду» при измерении определенных угловых скоростей. Это ближе к точке зрения бегуна («Как много кругов он уже намотал?»)
• Когда спутник движется вокруг Земли, мы понимаем его скорость как «километров в час», а не «градусов в час». Разделите эту скорость на расстояние от земли к спутнику, и вы получите орбитальную скорость в радианах в час.
• Синус, эта замечательная функция, определяется в радианах, как:

Эта формула работает, только если х представлен в радианах! Почему? Синус непосредственно связан с пройденным путем, а не с поворотом головы. Но мы отложим эту беседу до следующего раза.

Пример 1: Колеса автобуса

Давайте попробуем разобрать реальный пример: у вас есть автобус с колесами, радиус которых 2 метра (это автобус в стиле монстр-трак). Я скажу, как быстро вращаются колеса, а вы мне скажете, как быстро едет автобус. Готовы? «Колеса вращаются со скоростью 2000 градусов в секунду». Вы думаете:

• Хорошо, колеса вращаются на 2000 градусов в секунду. Это значит, они делают 2000/360 или 5 и 5/9 оборота в секунду. Длина окружности = 2*π*r, так что автобус движется со скоростью, эм, 2 * 3.14 * 5 и 5/9… где же мой калькулятор…

«Колеса проходят 6 радиан в секунду». Вы подумаете:

• Радианы — это длина единичной окружности, мы просто масштабируем эту величину согласно реальному радиусу, чтобы рассчитать, как далеко мы уедем. 6 * 2 = 12 метров в секунду. Следующий вопрос.

Вау! Никаких сумасшедших формул, никакого π — просто умножаем, чтобы конвертировать угловую скорость в линейную. А всё потому, что радианы говорят на языке движущегося тела.

Обратное действие также простое. Предположим, что мы несёмся 30 метров в секунду по автостраде (108 км/ч) на 24-дюймовых колесах (радиус которых равен 30 см). Как быстро вращаются колеса?

Ну, 30 метров в секунду / 0.3 м радиуса = 100 радианов в секунду.

Это было просто.

Пример 2: sin(x)

Пришло время для примера помощнее. Выберите число градусов (х) и вычислите значение sin(x) в калькуляторе:

Когда вы берете х очень маленьким, вроде 0.01, sin(x) тоже становится маленьким. И отношение sin(x)/x будет около 0.017 — что это означает? И еще страннее, что означает деление или умножение на градусы? Можно ли иметь квадратные или кубические градусы?

Радианы нас спасут. Зная, что они отвечают за пройденную дистанцию (это не просто пропорция!), мы можем интерпретировать уравнение таким образом:

• х — это то, как далеко вы прошли по кругу
• sin(x) — это то, как высоко вы взобрались по нему

• Так что sin(x)/x — это отношение того, как высоко вы находитесь, к тому, как далеко вы прошли: количество энергии, которое ушло в направлении «вверх». Если вы двигались вертикально, то это отношение будет равно 100%. Если вы двигались горизонтально, то равенство будет давать 0%.

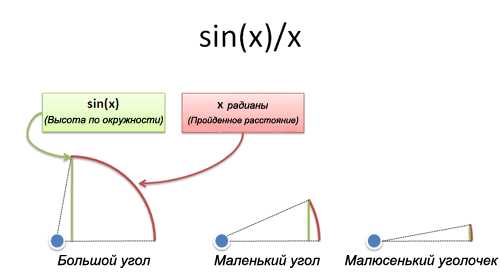
Когда что-то пододвигается на крошечное расстояние, как 0 или 1 градус с прежнего места, оно движется практически вверх. Если вы шагнете еще на меньшее расстояние, например с 0 до 0.00001 градуса, то вы действительно пройдете прямо вверх. Пройденное расстояние (х) очень близко к высоте (sin(x)).

Чем меньше х, тем ближе отношение к 100% — больше движения происходит вверх.

Радианы помогают увидеть, интуитивно, почему sin(x)/x стремится к 1 по мере уменьшения х. Мы просто топчемся на крошечном отрезке пути вверх. Между прочим, это также поясняет, почему sin(x) ~ x для маленьких чисел.

Конечно, вы можете точно доказать это с помощью калькулятора, но мышление радианами помогает вам это понять.

Запомните, эти связи работают только при измерении углов радианами. С градусами вы сравниваете высоты на окружности (sin(x)) с тем, насколько какой-то зритель поверную свою голову (х градусов).

Так в чем же смысл?

Градусы занимают свое место в нашей жизни. Нам ведь важно знать, насколько надо повернуть телескоп, развернуть сноуборд или покрутить рулем? По законам природы мы наблюдаем за тем, как движутся другие. И радианы больше подходят тем, кто движется, чем тем, кто за ними наблюдает. У меня ушло много лет на то, чтобы понять:

• Градусы выбраны произвольно, так как они основываются на солнце (365 дней ~ 360 градусов), но они как бы идут от обратного, потому что описывают процессы с точки зрения наблюдателя.
• Радианы описывают движение с точки зрения самих его участников, и поэтому «всё стает на свои места». Конвертировать угловую скорость в линейную довольно просто, и идеи вроде sin(x)/x приобретают смысл.

Даже углы можно рассматривать с более, чем одной точки зрения. Понимание радиан делают математические и физические формулы более осмысленными.

Приятных вычислений!

Перевод статьи «Intuitive Guide to Angles, Degrees and Radians»

zero2hero.org

Формулы перевода градусов в радианы, длин, площадей и объемов основных геометрических фигур

Во первых, под числом «пи» Администрация Сайта понимает величину близкую к:

3.14159 26535 89793 23846 26433 83279 50288 41971 69399 37510 58209 74944 59230 78164 06286 20899 86280 34825 34211 70679… (100 знаков после запятой)

ФОРМУЛЫ ПЕРЕВОДА

Перевод радиан в градусы

Зная, что углу 2 * пи соответствует угол 360 градусов:

Ad = Ar * 180 / пи
Где Ad — угол в градусах, Ar — угол в радианах.

Перевод градусов в радианы

Зная, что углу 360 градусов соответствует угол 2 * пи:

Ar = Ad * пи / 180
Где Ad — угол в градусах, Ar — угол в радианах.

ФОРМУЛЫ РАСЧЕТА ДЛИНЫ

Длина окружности

L = 2 * пи * R
Где L — длина окружности, R — радиус окружности.

Длина дуги окружности

L = A * R
Где L — длина дуги окружности, R — радиус окружности, A — центральный угол, выраженный в радианах.
Так, для окружности, A = 2*пи (360 градусов), получим L = 2*пи*R.

ФОРМУЛЫ РАСЧЕТА ПЛОЩАДИ

Площадь треугольника.

Формула Герона.

S = (p * (p-a) * (p-b) * (p-c) )^1/2.
Где S — площадь треугольника, a, b, c — длины сторон,
p=(a+b+c)/2 — полупериметр.

Площадь круга

S = пи * R²
Где S — площадь круга, R — радиус круга.

Площадь сектора

S = (Ld * R)/2 = (A * R²)/2
Где S — площадь сектора, R — радиус круга, Ld — длина дуги.

Площадь поверхности шара (сферы)

S = 4 * пи * R²
Где S — площадь поверхности шара, R — радиус шара.

Площадь боковой поверхности цилиндра

S = 2 * пи * R * H
Где S — площадь боковой поверхности цилиндра, R — радиус основания цилиндра, H — высота цилиндра.

Площадь полной поверхности цилиндра

S = 2 * пи * R * H + 2 * пи * R²
Где S — площадь боковой поверхности цилиндра, R — радиус основания цилиндра, H — высота цилиндра.

Площадь боковой поверхности конуса

S = пи * R * L
Где S — площадь боковой поверхности конуса, R — радиус основания конуса, L — длина образующей конуса.

Площадь полной поверхности конуса

S = пи * R * L + пи * R²
Где S — площадь полной поверхности конуса, R — радиус основания конуса, L — длина образующей конуса.

ФОРМУЛЫ РАСЧЕТА ОБЪЕМА

Объем шара

V = 4 / 3 * пи * R³
Где V — объем шара, R — радиус шара.

Объем цилиндра (прямого, круглого)

V = пи * R² *H
Где V — объем цилиндра, R — радиус основания цилиндра, H — высота цилиндра.

Объем конуса (прямого, круглого)

V = пи * R * L = пи * R * H/cos (A/2) = пи * R * R/sin (A/2)
Где V — объем конуса, R — радиус основания конуса, L — длина образующей конуса, A — угол при вершине конуса.

tehtab.ru

как перевести градусы в радианы?

180 градусов — Пи радиан (3,14) или 1 радиан приблизительно 57 градусов Берешь тупо пропорцию 180-3,14 например 60-х тогда 60 градусов это х= 60*3,14/180 радиан

<a rel=»nofollow» href=»http://ru.wikipedia.org/wiki/Радиан» target=»_blank»>http://ru.wikipedia.org/wiki/Радиан</a>

1 градус = pi/180 радиан 1 радиан = 180/pi градусов

Перевод градусов в радианы: Зная, что углу 360 градусов соответствует угол 2 * пи: Ar = Ad * пи / 180 Где Ad — угол в градусах, Ar — угол в радианах. Найдено по ссылке: <a href=»/» rel=»nofollow» title=»5992303:##:http://www.dpva.ru/informations/MathematicsQuiery/RadanLengthSqireVolume/?sid» target=»_blank» >[ссылка заблокирована по решению администрации проекта]</a>= Здесь вообще неплохая подборка различных математических формул.

Один радиан имеет приблизительно 57 градусов!! ! В одном круге 6 радиан и 18градусов!:)

touch.otvet.mail.ru

Радианы и градусы. Фаренейты и Цельсии

На этой странице дано решение примеров Begin29 — Begin32 из задачника Абрамяна. Здесь мы занимаемся преобразованием угла из радианов в градусы и наоборот, а также преобразованием температуры из градусов Цельсия в Фаренгейты и наоборот.

Begin29. Дано значение угла α в градусах (0 ≤ α < 360). Определить значение этого же угла в радианах, учитывая, что 180° = π радианов. В качестве значения π использовать 3.14.

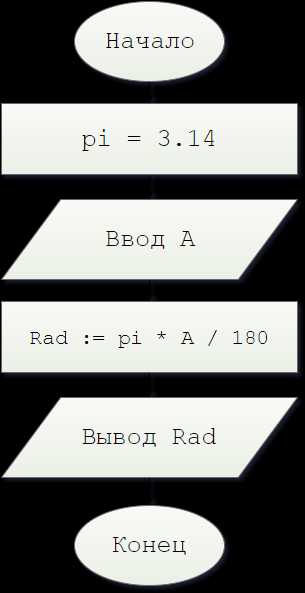
Код Pascal

1  
2  
3  
4  
5  
6  
7  
8  
9  
10  
11  
12  
13  
14  
15  
16  

const
  pi = 3.14;

var
  A, Rad: real;

begin
  writeln('Введите градусную меру угла(0 <= A < 360):');
  write(' A = ');
  readln(A);
  writeln;
  Rad := pi * A / 180; { <-- Вычисляем радианную меру угла }
  writeln('Результат:'); 
  writeln(' Угол ', A, '° имеет ', Rad:0:2, ' радиан.');
  readln
end.

Сравните Begin29 с задачей Proc32.

Begin30. Дано значение угла α в радианах (0 ≤ α < 2·π). Определить значение этого же угла в градусах, учитывая, что 180° = π радианов. В качестве значения π использовать 3.14.

Код Pascal

1  
2  
3  
4  
5  
6  
7  
8  
9  
10  
11  
12  
13  
14  
15  
16  
17  

const
  pi = 3.14;

var
  Alpha, gradus: real;

begin
  writeln('Введите радианную меру угла(0 <= Alpha < 6.28):');
  write(' Alpha = ');
  readln(Alpha);
  writeln;
  gradus := 180 * Alpha / pi; { <-- Вычисляем градусную меру угла }
  writeln('Результат:'); 
  writeln(' Угол ', Alpha, ' радиан составляет ', 
    gradus:0:2, ' градусов.');
  readln
end.

Рекомендую сравнить с задачей Proc33.

TC = (TF − 32)·5/9.

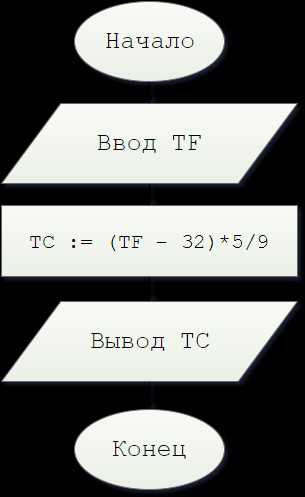
Код Pascal

1  
2  
3  
4  
5  
6  
7  
8  
9  
10  
11  
12  
13  

var
  TC, TF: real;

begin
  writeln('Введите температуру в градусах Фаренгейта:');
  write(' TF = ');
  readln(TF);
  TC := (TF - 32) * 5 / 9; { <-- температура по цельсию }
  writeln;
  writeln('Температура в градусах Цельсия:'); 
  writeln(' TC = ', TC:0:2);
  readln
end.

TF = 9·FC/5 + 32.

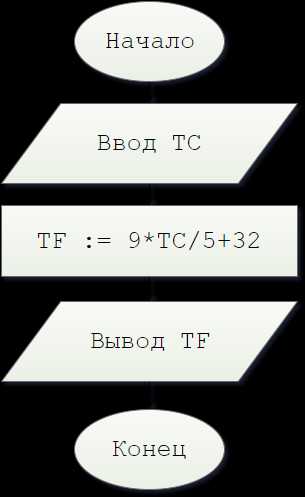
Код Pascal

1  
2  
3  
4  
5  
6  
7  
8  
9  
10  
11  
12  

var
  TC, TF: real;

begin
  writeln('Введите температуру в градусах Цельсия:');
  write(' TC = ');
  readln(TC);
  TF := 9 * TC / 5 + 32; { <== температура по Фаренгейту }
  writeln;
  writeln('Температура по Фаренгейту: TF = ', TF:0:2);
  readln
end.

progmatem.ru