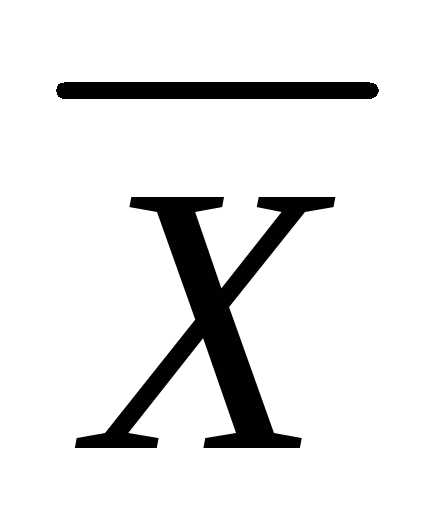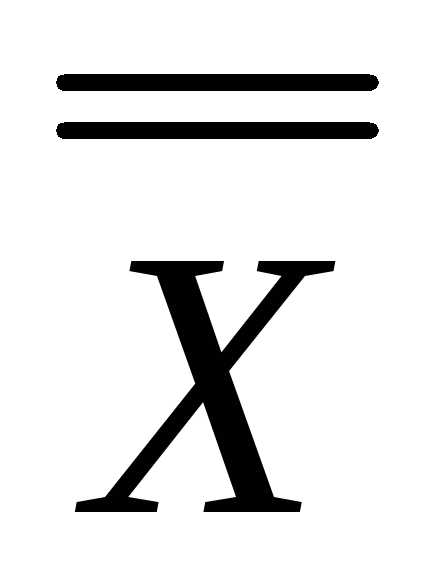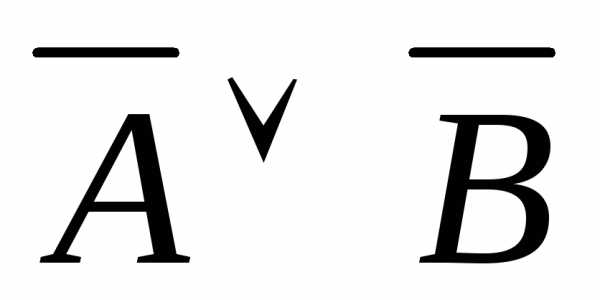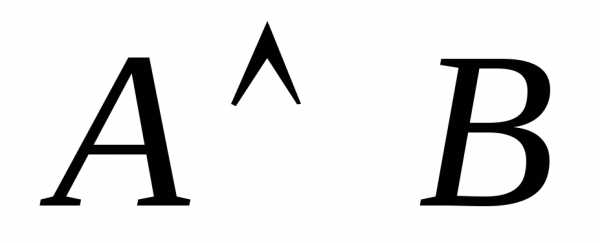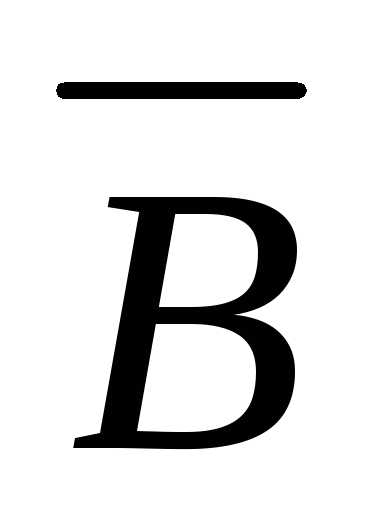§ 2. Равносильные формулы алгебры логики.
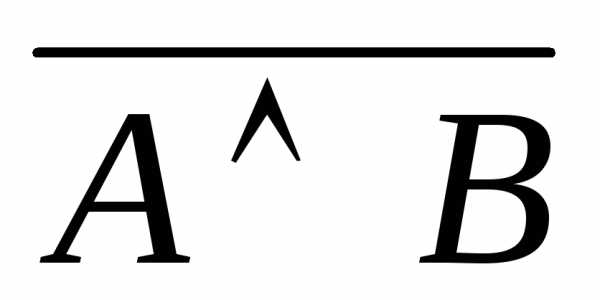
Определение. Две
формулы алгебры логики A и B называется
равносильными, если они принимают
одинаковые логические значения на любом
наборе значений входящих в них высказываний 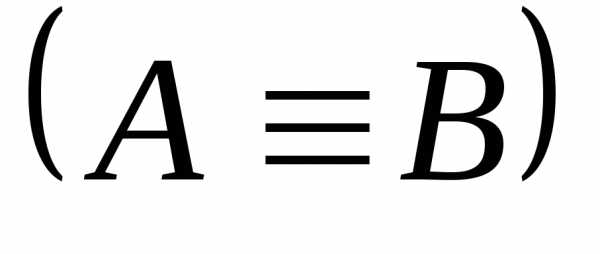 .
.
Важнейшие равносильности можно разбить на три группы:
I. Основные равносильности.
3. .
4. .
5. .
6. .
7. 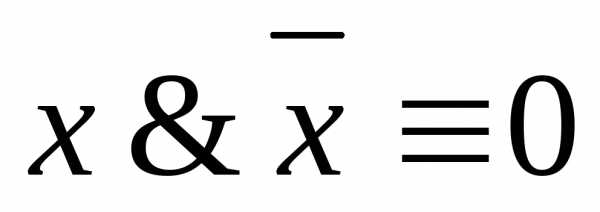 — закон противоречия.
— закон противоречия.
8. 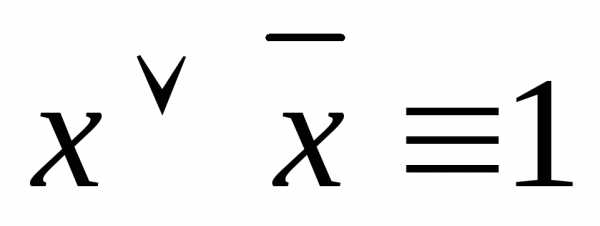 — закон исключительного третьего.
— закон исключительного третьего.
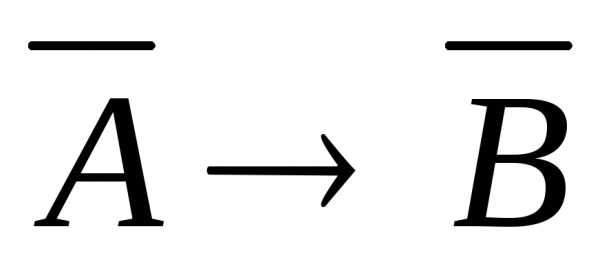
9. 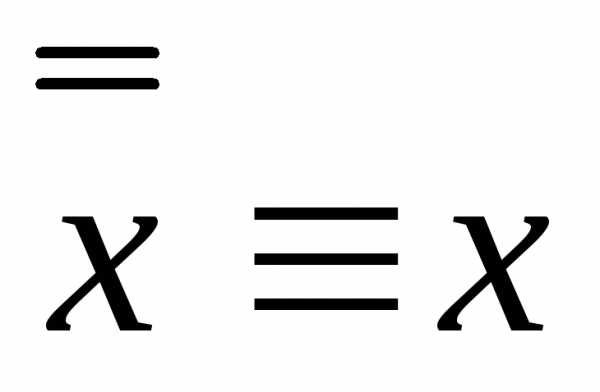 — закон снятия двойного отрицания.
— закон снятия двойного отрицания.

II. Равносильности, выражающие одни логические операции через другие.
1. ;
2. .
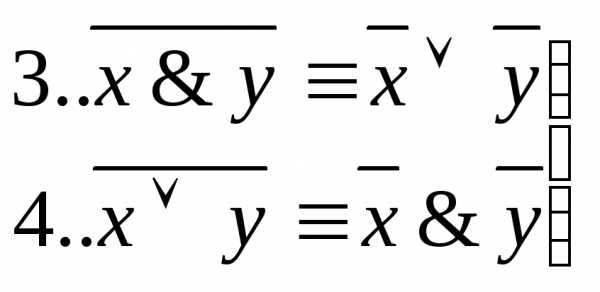
5. .
6. .
III. Равносильности, выражающие основные законы алгебры логики.
1. .
2. .
3. .
4. .
5. .
6. .
Используя равносильности групп I, II, III, можно часть формулы алгебры логики или всю формулу заменить равносильной ей формулой.
Такие преобразования формул применяются для доказательства равносильностей, для приведения формул к заданному виду,для упрощения формул.
Пример 1. Доказать равносильность .
Решение. Для доказательства равносильности подвергнём её левую часть равносильными преобразованиями:
.
Пример 2. Упростить
формулу  .
.
Решение. Подвергнём формулу A равносильным преобразованиям:
Пример 3. Доказать, что формула тождественно истинная.
Решение. Подвергнём формулу A равносильным преобразованиям
1.20. Доказать равносильность:
1) ;
2) ;
3) ;
4) ;
5) ;
6) ;
7) ;
8) ;
9) ;
10) .
1.21. Упростить формулу:
1) ;
2) ;
3) ;
4) ;
5) ;
6) ;
7) ;
8) ;
9) ;
10) .
1.22. Доказать тождественную истинность или тождественную ложность формул:
1) ;
2) ;
3) ;
4) ;
5) ;
6) ;
7) ;
8) ;
9) ;
10) ;
11) ;
12) ;
13) ;
14) ;
15) .
_________
1 Здесь и в дальнейшем означает , подобно тому, как в алгебре не пишется знак умножения (или пишетсяв место).
1.23. Пусть F – тождественно ложная формула. Доказать, что .
1.24. Найдите x, если .
1.15. Последовательность
высказываний 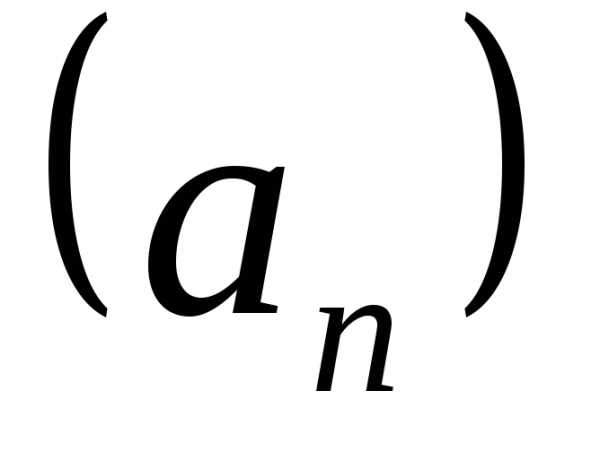 определяется следующим рекуррентным
соотношением:
определяется следующим рекуррентным
соотношением:
, n > 3.
Высказывания
,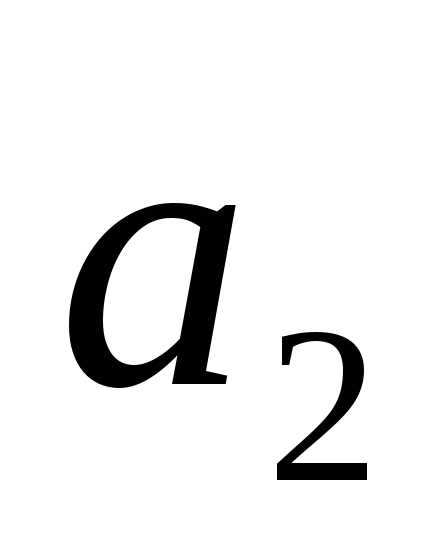 ,
, заданы, причём
заданы, причём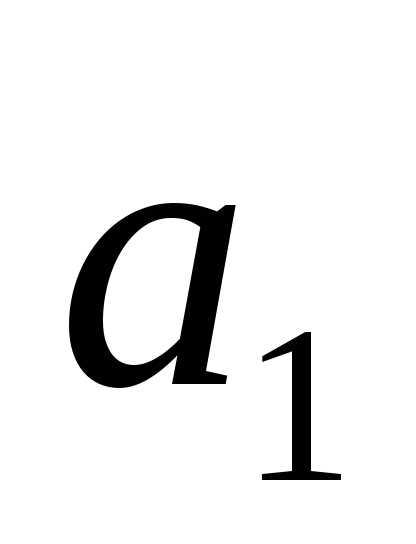 и
и истинны, а
истинны, а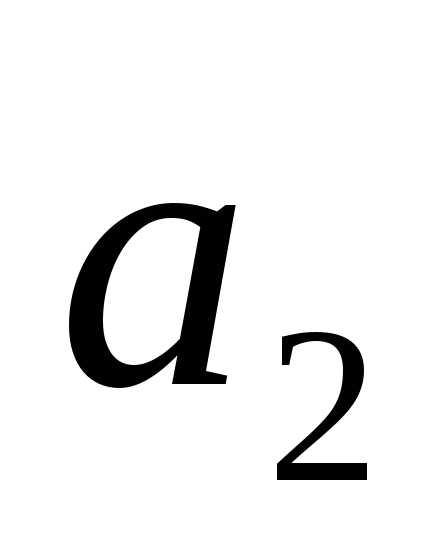 ложно. Истинно или ложно высказывание
ложно. Истинно или ложно высказывание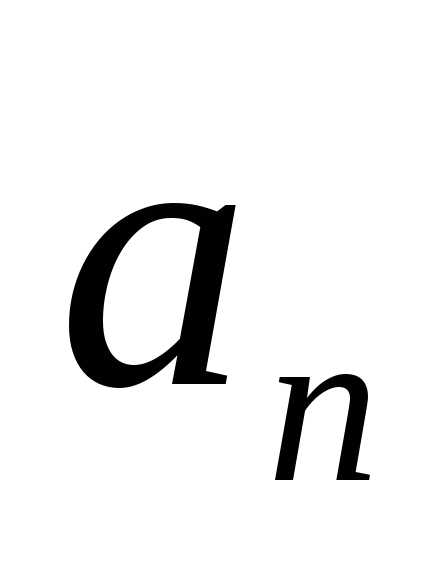 ?
Как выражается
?
Как выражается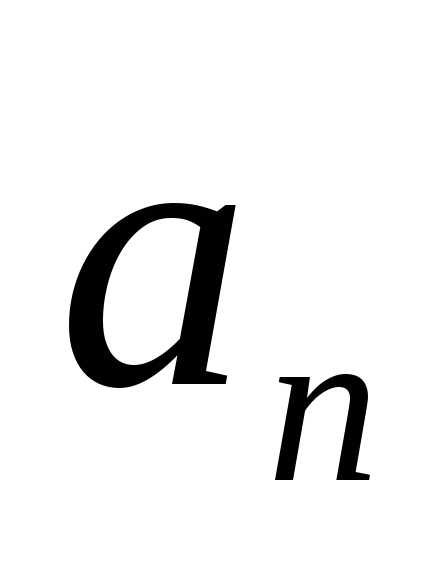 через
через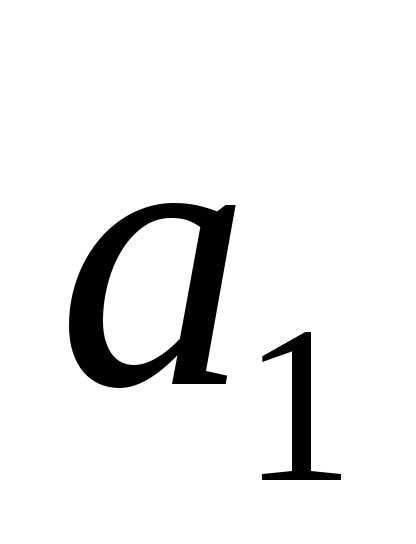 ,
,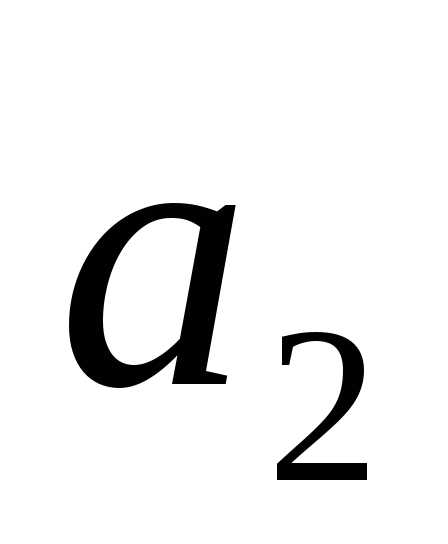 ,
, ?
?
1.26. Выразить все основные операции:
1) через операции дизъюнкции, конъюнкции и отрицания;
2) через конъюнкции и отрицания;
3) через дизъюнкции и отрицания;
4) через импликацию и отрицание.
1.27.
1) Выразить отрицание импликации через основные операции так, чтобы отрицания стояли только над аргументами.
2) Выразить операцию дизъюнкцию через импликацию.
1.28. Исключающей
дизъюнкцией двух высказываний a и b называется новое высказывание,
обозначаемое 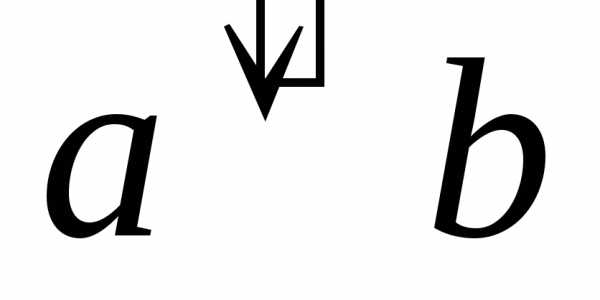 ( читают «либоa,
либо b»),
которое истинно, когда одно и только
одно из данных высказываний истинно, и
ложно а остальных случаях. Составить
таблицу истинности исключающей дизъюнкции
и выразить её через основные операции
над высказываниями.
( читают «либоa,
либо b»),
которое истинно, когда одно и только
одно из данных высказываний истинно, и
ложно а остальных случаях. Составить
таблицу истинности исключающей дизъюнкции
и выразить её через основные операции
над высказываниями.
1.29. Штрихом Шеффера двух высказываний a и b называется
новое высказывание, обозначаемое 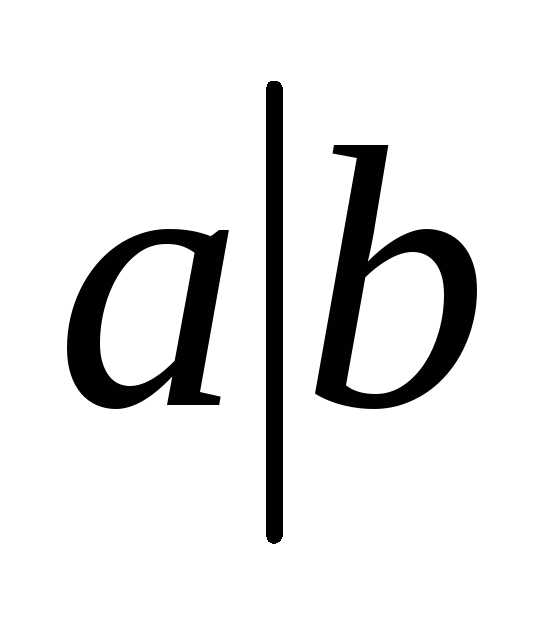 (Читают «a не совместно с b»),
которое ложно только тогда, когда они
оба данные высказывания истинны.
Составить таблицу истинности штриха
Шеффера и выразить его через основные
операции над высказываниями. Доказать,
что все основные операции над высказываниями
можно выразить через штрих Шеффера.
(Читают «a не совместно с b»),
которое ложно только тогда, когда они
оба данные высказывания истинны.
Составить таблицу истинности штриха
Шеффера и выразить его через основные
операции над высказываниями. Доказать,
что все основные операции над высказываниями
можно выразить через штрих Шеффера.
1.30. Штрихом
Лукасевича двух высказываний a и b называется
новое высказывание  ( читают «ниa,
ни b»)
, которое истинно в том и только в том
случае, когда оба данные высказывания
ложны. Составить таблицу истинности
штриха Лукасевича и выразить его через
основные операции над высказываниями.
Доказать, что все основные операции над
высказываниями можно выразить через
штрих Лукасевича.
( читают «ниa,
ни b»)
, которое истинно в том и только в том
случае, когда оба данные высказывания
ложны. Составить таблицу истинности
штриха Лукасевича и выразить его через
основные операции над высказываниями.
Доказать, что все основные операции над
высказываниями можно выразить через
штрих Лукасевича.
1.31. Доказать, что операции отрицания не может быть выражена через основные операции (бинарные) над высказываниями.
1.32. Можно ли для каждой формулы найти равносильную, не содержащую знака отрицания?
1.33. Мальчик решил в воскресенье закончить чтение книги, сходить в музей или кино, а если будет хорошая погода – пойти купаться. В каком случае можно сказать, что решение мальчика не выполнено? В ответе отрицания должны содержаться лишь в простых высказываниях.
studfiles.net
Равносильные формулы алгебры высказываний / Алгебра логики [Ф.Г. Кораблёв] / 3dstroyproekt.ru
Две формулы алгебры высказываний $A$ и $B$ называются равносильными или эквивалентными, если они принимают одинаковые логические значения на любом наборе значений входящих в формулы элементарных высказываний.
Равносильность формул будем обозначать знаком $\equiv$, а запись $A\equiv B$ означает, что формулы $A$ и $B$ равносильны.
Например, равносильны формулы:
$\overline { \overline { X } } \equiv X$,
$X\vee X\equiv X$,
Тождественно истинная формула
Формула $A$ называется тождественно истинной { или тавтологией } , если она принимает значение 1 при всех значениях входящих в нее переменных.
Например, тожественно истинны формулы $X\vee \overline { X } $, $X\rightarrow (Y\rightarrow X)$
Тождественно ложная формула
Формула $A$ называется тождественно ложной { или противоречием } , если она принимает значение 0 при всех значениях входящих в нее высказываний.
Например, тождественно ложна формула $X\wedge \overline { X } $
Выполнимая формула
Формула $A$ называется выполнимой, если она принимает значение 1 при всех значениях входящих в нее высказываний.
Например, выполнима формула $X\vee \overline { X } $
Ясно, что отношение равносильности рефлексивно, симметрично и транзитивно.
Группы равносильностей
Между понятиями равносильности и операцией $\leftrightarrow$ существует следующая связь: если формулы $A$ и $B$ равносильны, то формула $A\leftrightarrow B$ — тавтология, и обратно, если формула $A\leftrightarrow B$ — тавтология, то формулы $A$ и $B$ равносильны.
Важнейшие равносильности алгебры высказываний можно разбить на следующие группы.
Равносильности алгебры Буля
Закон двойного отрицания: $\overline { \overline { X } } \equiv X$
Коммутативность: $X\wedge Y\equiv Y\wedge X$; $X\vee Y\equiv Y\vee X$
Ассоциативность: $X\wedge (Y\wedge Z)\equiv (X\wedge Y)\wedge Z$; $X\vee (Y\vee Z)\equiv (X\vee Y)\vee Z$
Дистрибутивность $\wedge$ относительно $\vee$: $X\wedge (Y\vee Z)\equiv (X\wedge Y)\vee (X\wedge Z)$; $(X\vee Y)\wedge Z\equiv (X\wedge Z)\vee (Y\wedge Z)$
Дистрибутивность $\vee $ относительно $\wedge $: $X\vee (Y\wedge Z)\equiv (X\vee Y)\wedge (X\vee Z)$; $(X\wedge Y)\vee Z\equiv (X\vee Z)\wedge (Y\vee Z)$
Законы де Моргана: $\overline { X\wedge Y } \equiv \overline { X } \vee \overline { Y } $; $\overline { X\vee Y } \equiv \overline { X } \wedge \overline { Y } $
Законы поглощения: $X\wedge (Y\vee X)\equiv X$; $X\vee (Y\wedge X)\equiv X$
Законы идемпотентности: $X\wedge X\equiv X$; $X\vee X\equiv X$
Свойства констант: $X\wedge 1\equiv X$; $X\vee 1\equiv 1$; $X\wedge 0\equiv 0$; $X\vee 0\equiv X$
Закон противоречия: $X\wedge \overline { X } \equiv 0$
Закон исключения третьего: $X\vee \overline { X } \equiv 1$
Равносильности, выражающие одни логические операции через другие
$X\leftrightarrow Y\equiv (X\rightarrow Y)\wedge (Y\rightarrow X)$
$X\leftrightarrow Y\equiv (\overline { X } \vee Y)\wedge (\overline { Y } \vee X)$
$X\leftrightarrow Y\equiv (X\wedge Y)\wedge (\overline { Y } \wedge \overline { X } )$
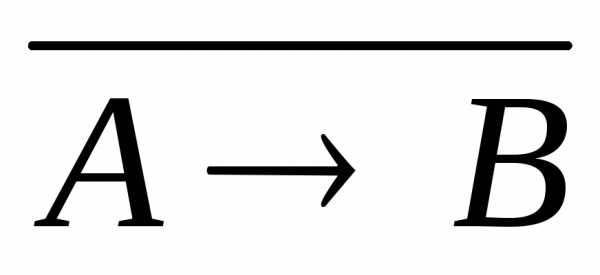
$X\rightarrow Y\equiv \overline { X } \vee Y$
$X\wedge Y\equiv \overline { \overline { X } \vee \overline { Y } } $
$X\vee Y\equiv \overline { \overline { X } \wedge \overline { Y } } $
$X | Y\equiv \overline { X\cdot Y } $
$X \downarrow Y\equiv \overline { X\vee Y } $
$X \rightarrow Y\equiv \overline { X } \vee Y$
$X \bigoplus Y\equiv (X \cdot \bar { Y } )\vee (\bar { X } \cdot Y)$
$X \sim Y\equiv \overline { X \bigoplus Y } \equiv (XY)\vee (\bar { X } \bar { Y } )$
3dstroyproekt.ru
Равносильности, выражающие основные законы алгебры логики
Название | Дизъюнктивная форма | Конъюнктивная форма |
1. Коммутативный закон | ||
2. Ассоциативный закон | ||
3. Дистрибутивный закон | ||
4. Закон поглощения | ||
5. Закон слияния | ||
6. Закон идемпотентности | ||
7. Законы исключения констант | ||
Законы отрицания |
Следует отметить, что между равносильностями, записанными в дизъюнктивной форме и в конъюнктивной форме, существует свойство симметрии: если дизъюнкцию заменить конъюнкцией, а конъюнкцию заменить дизъюнкцией, 0 заменить на 1, а 1 заменить на 0, при этом отрицания сохранить без изменений, то записанные слева и справа равносильности перейдут друг в друга. Следовательно, с помощью указанных замен можно из одних равносильностей получить другие. Это называется законом двойственности.
Следствия алгебры логики. Многие законы можно обобщить на случай большого числа переменных.
Законы де Моргана в обобщенной форме можно записать так:
и
2. Законы дистрибутивности для многих переменных:
ABCD…P = (AB)(AC)(AD) … (AP)
и A(BCD…P) = ABACAD…A P
.
Законы поглощения для нескольких переменных:
А AB ABСD = A;
A(ACD…P) = A;
;
.
Из симметрии трехчлена вида получим полезные эквивалентности:
Если одна из переменных входит в одну из трех конъюнкций с отрицанием, то .
Заметим, что здесь симметрия нарушена по B. И конъюнкция, не содержащая этого “нарушителя симметрии ” поглотилась согласно закону поглощения (4).
Если симметрия нарушена по двум переменным, например, имеем трехчлен вида , то его можно упростить следующим образом:
.
Пример. Упростить выражение .Решение. Упростим выражения в скобках:
Перемножим полученные выражения.
Таким образом, .
Нормальные формы логических выражений. Одна и та же логическая функция может быть записана различным образом. Например, функция F(A,B) может быть записана следующими эквивалентными выражениями:
F(A,B)=илиF(A,B)=илиF(A,B)=.
Эквивалентность этих формул легко проверить по таблицам истинности или выполнив необходимые преобразования. Для исключения неоднозначности записи логические функции представляют в унифицированных формах. Такими формами являются: дизъюнктивная и конъюнктивная
Элементарной дизъюнкцией называется дизъюнкция, состоящая только из переменных или их отрицаний. Например, .
Элементарной конъюнкцией называется конъюнкция, состоящая только из переменных или их отрицаний. Например, .
Дизъюнктивно нормальная форма (ДНФ): дизъюнкция элементарных конъюнкций. Например, .
Конъюнктивно нормальная форма (КНФ): конъюнкция элементарных дизъюнкций. Например, .
Минимальная дизъюнктивно-нормальная форма (МДНФ): ДНФ, имеющая самую короткую запись.
Минимальная конъюнктивно нормальная форма (МКНФ): КНФ, имеющая самую короткую запись.
Использование нормальных форм не устраняет полностью неоднозначности записи логических функций. Например, может быть записана такими выражениями:
или .
Поэтому среди нормальных форм выделяют такие, в которых функции записываются единственным образом. Их называют совершенными. Применяются совершенная дизъюнктивная и совершенная конъюнктивная формы (СДНФ и СКНФ), которые имеют отличительные особенности:
Совершенная дизъюнктивно нормальная форма (СДНФ): ДНФ, удовлетворяющая условиям:
Все элементарные конъюнкции различны;
Нет нулевых конъюнкций;
Ни одна из элементарных конъюнкций не повторяется;
Каждая элементарная конъюнкция содержит все переменные или их отрицания.
Совершенная конъюнктивно нормальная форма (СДНФ): КНФ, удовлетворяющая условиям:
Все элементарные дизъюнкции различны;
Нет нулевых дизъюнкций;
Ни одна из элементарных дизъюнкций не повторяется;
Каждая элементарная дизъюнкция содержит все переменные или их отрицания.
Совершенная дизъюнктивная и совершенная конъюнктивная формы используются при проектировании элементов и узлов компьютера. Поскольку при проектировании отдельных узлов компьютера необходимо решить проблему построения логических и электрических схем, имея лишь описание алгоритма его работы (виде таблицы истинности или логической формулы). Воспользовавшись этими данными можно построить логическую, а затем электрическую или электронную схемы. Рассмотрим построение логической функции по известной таблице истинности.
А | В | С | F |
0 | 0 | 0 | 1 |
0 | 0 | 1 | 0 |
0 | 1 | 0 | 0 |
0 | 1 | 1 | 1 |
1 | 0 | 0 | 0 |
1 | 0 | 1 | 0 |
1 | 1 | 0 | 0 |
1 | 1 | 1 | 1 |
Пусть необходимо получить логическую формулу, которая бы отвечала следующей таблице истинности.
Зададимся вопросом, в какой форме удобнее искать логическую формулу, отвечающую заданной таблице истинности? Для однозначности описания состояния входных переменных наилучшим образом подходит совершенная форма, т.к. только в ней присутствует информация о каждой логической переменной, что соответствует таблице истинности. Иначе говоря, функция принимает единичные значения при наборах входных переменных, соответствующих 0, 3 и 7.
Анализируя приведенную таблицу, заметим, что она содержит три строки, где функция F=1 и пять строк, где функция равна нулю. Для обеспечения состояний логического устройства, где F=1 воспользуемся построением логической формулы в виде СДНФ следующим образом. Для обеспечения единичного значения функции при А=0, В=0 и С=0 СДНФ должна иметь вид , при значенияА=0, В=1 и С=1 (четвертая строка), значение F=1 даст . Аналогично для последней строки –. Следовательно, для получения общей формулы, удовлетворяющей каждой из выделенных строк, необходимо взять дизъюнкцию этих трех конъюнкций и общая формула будет иметь вид.
Правило записи СДНФ функции по таблице истинности.
Для всех наборов переменных, на которых функция принимает единичные значения, записываются конъюнкции этих переменных, инвертируя те переменные, которым соответствуют нулевые значения. Затем конъюнкции соединяют знаком дизъюнкции.
Например, дана таблица истинности функции F:
A | B | F |
0 | 0 | 0 |
0 | 1 | 1 |
1 | 0 | 1 |
1 | 1 | 0 |
СДНФ функции F будет состоять из двух наборов: .
По аналогичным соображениям строится логическая функция, соответствующая заданной таблице истинности. Учитывая свойство двойственности, правило записи СКНФ можно сформулировать следующим образом.
Правило записи СКНФ функции по таблице истинности.
Для всех наборов переменных, на которых функция принимает нулевые значения, записываются конъюнкции этих переменных, инвертируя те переменные, которым соответствуют единичные значения. Затем дизъюнкции соединяют знаком конъюнкции.
СКНФ функции F из предыдущего примера будет: .
Решение текстовых задач. Для успешного решения текстовых задач необходимо знать, как записываются. Составим для себя таблицу соответствия высказываний естественного языка и формул алгебры логики.
При решении текстовых задач желательно обходиться минимальным количеством переменных. Поэтому высказывания альтернативного типа, например «Погода пасмурная» и «Погода ясная», следует обозначать одной переменной, соответственно П и .
Задача. В олимпиаде по информатике участвовали трое друзей: А, В и С. Перед олимпиадой каждый из них высказал свои предположения.
A: Не может быть, чтобы победили В и С вместе. Не может быть также, чтобы победил либо В, либо С. Значит, не могу победить и я.
В: Если победит С, то победит и А, а я победить не смогу.
С: Не может быть, чтобы не победили А и В, я бы победил.
По результатам олимпиады оказалось, что прав был только один из друзей.
Кто победил в олимпиаде? Чье высказывание оказалось правдой?
Форма высказывания естественного языка | Формула |
Не А; неверно, что А; А не имеет места. | |
А или В; А, или В, или оба. | АЪВ |
А и В; как А, так и В; не только А, но и В; А вместе с В; А, несмотря на В; А, в то время как В. | АВ |
Если А, то В; А, значит В; А влечет В; А, только если В; А, только тогда, когда В; А только при условии, что В; из А следует В; А достаточно для В; для А необходимо В; для В достаточно А; В необходимо для А; В тогда, когда А. | А®В |
А эквивалентно В; А тогда и только тогда, когда В; А, если и только если В; А необходимо и достаточно для В. | А«В |
А, но не В; не В, но А | |
А либо В; А, разве что В; либо А, либо В; не А, разве что не В; либо не А, либо не В; А или В, но не оба | |
Либо А, либо В и С; А, разве что В и С | |
Либо А и В, либо С и D |
Решение.
Обозначим переменные: A — «Победил А«, В — «Победил В«, С — «Победил С«.
Запишем высказывания друзей на языке алгебры логики и упростим их.
A: ===
==
В:
С:
Возможны три ситуации, когда прав лишь один из друзей.
Пусть не правы А и В:
=
Пусть не правы А и С:
Пусть не правы В и С:
Ответ: Победил С, правильное предположение сделал А.
Контрольные задания
Задано двоичное число 1101. На какое наименьшее двоичное число его необходимо умножить, чтобы результатом в десятичной системе счисления было число 19? Если решения нет, то в ответе записать 0, в противном случае запишите это число в двоичной системе счисления.
Даны три числа в различных системах счисления: A=16(10), B=21(8), C=12(10). Выполните следующие логические операции: AB+C. Ответ напишите в шестнадцатеричной системе счисления и в десятичной системе.
Постройте таблицу истинности для логической функции
Построить логическую функцию по заданной таблице истинности, которая имеет нулевые значения при следующих наборах переменных A, B, C: (001), (010), (011), (110).
Является ли данная функция тождественно ложной?
У трех приятелей Ленчика, Пончика и Батончика был четвертый друг, который был заядлым грибником, за что его прозвали Сыроежка. Определить, кто из четырех приятелей поехал в лес за грибами, если стало известно:
Если Ленчик поехал, то и Батончик поехал.
Если Батончик поехал, то Пончик поехал или Ленчик не поехал.
Если Сыроежка не поехал, то Ленчик поехал, Пончик не поехал.
Укажите правильный ответ в следующей задаче.
Собирая грибы, три приятеля Ленчик, Пончик и Батончик нашли клад и, чтобы не перессориться, разделили его на три части. Каждый спрятал свою часть под своим деревом. Но, встретив лесника, они сбивчиво начали рассказывать о случившемся.
Ленчик: Я спрятал клад под дубом, а Пончик — под елкой.
Пончик: Батончик спрятал клад под сосной, а Ленчик — под дубом.
Батончик: Пончик спрятал клад под дубом, Я — под сосной.
Наблюдательный лесник понял, что один из них один раз соврал и один раз сказал правду, а двое — дважды сказали правду. Где каждый грибник спрятал свой клад?
Ответы:
Пончик — под елкой, Ленчик — под сосной, Батончик — под дубом.
Пончик — под сосной, Ленчик — под дубом, Батончик — под елкой.
Пончик — под елкой, Ленчик — под дубом, Батончик — под сосной.
Пончик — под сосной, Ленчик — под елкой, Батончик — под дубом.
Пончик — под дубом, Ленчик — под елкой, Батончик — под сосной.
studfiles.net
3. Равносильные формулы алгебры логики
3.1 Классификация формул алгебры высказываний.
Формула Хназываетсятождественно истинной (или тавтологией),если она превращается в истинное высказывание, то есть принимает значение 1, при всех наборах значений входящих в нее переменных. Тавтологии представляют собой схемы построения истинных высказываний, независимо от содержания и истинности составляющих элементарных высказываний.
Формула Хназываетсятождественно ложной,если она принимает значение 0 при всех наборах значений входящих в нее переменных.
Две формулы алгебры логики XиYназываютсяравносильными, если при любых значениях входящих в них высказывательных переменных логические значения высказываний, получающихся из формулXиY, совпадают. Для указания равносильности формул используют обозначение.
Существует тесная связь между понятием равносильности формул и понятием тавтологии.
Признак равносильности формул.Две формулыXиYалгебры высказываний равносильны тогда и только тогда, когда формулаявляется тавтологией, и обратно, если формула– тавтология, то формулыXиYравносильны.
Отношение равносильности между формулами алгебры высказываний:
а) рефлексивно: ;
б) симметрично: если , то ;
в) транзитивно: если и, то.
3.2 Примеры равносильных формул.Равносильности формул алгебры логики часто называютзаконами логики.
Вот наиболее важные из них:
–закон тождества.
–закон противоречия.
–закон исключенного третьего.
–закон двойного отрицания.
.
.
.
.
; – законы идемпотентности.
; – законы поглощения.
; – законы склеивания.
законы коммутативности (переместительности):
–коммутативность конъюнкции;
–коммутативность дизъюнкции.
законы ассоциативности (сочетательности):
–ассоциативность конъюнкции;
–ассоциативность дизъюнкции.
законы дистрибутивности (распределительности):
–дистрибутивность конъюнкции относительно дизъюнкции;
–дистрибутивность дизъюнкции относительно конъюнкции.
; – законы де Моргана.
Доказать эти равносильности можно, например, с помощью таблиц истинности.
Пример.
Докажем равносильность – закон де Моргана. При любых комбинациях значений, от которых зависят формулыXиY, эти формулы принимают некоторые логические значения. Всего будет четыре способа распределения логических значенийXиY. Надо показать, что в каждом из этих случаев значения левой и правой части равносильностисовпадают.
X | Y | ||||||
0 | 0 | 1 | 1 | 0 | 1 | 1 | |
0 | 1 | 1 | 0 | 0 | 1 | 1 | |
1 | 0 | 0 | 1 | 0 | 1 | 1 | |
1 | 1 | 0 | 0 | 1 | 0 | 0 |
Логические значения в последних двух столбцах совпадают, следовательно, закон де Моргана справедлив.
Имеют место равносильности, выражающие одни логические операции через другие.
Импликация выражается через:
–дизъюнкцию и отрицание;
–конъюнкцию и отрицание.
Эквиваленциявыражается через:
–конъюнкцию и импликацию;
–конъюнкцию, дизъюнкцию и отрицание;
–конъюнкцию и отрицание.
Из этих равносильностей следует вывод, что любую формулу алгебры логики можно заменить равносильной ей формулой, которая будет содержать только две логические операции: конъюнкцию и отрицание или дизъюнкцию и отрицание. Дальнейшее исключение логических операций невозможно.
Существует логическая операция, через которую можно выразить любую из пяти логических операций, которыми мы пользуемся: отрицание, конъюнкция, дизъюнкция, импликация, эквиваленция. Эта операция называется «штрих Шеффера», обозначается символом и определяется таблицей истинности
X | Y | |
1 | 1 | 0 |
1 | 0 | 1 |
0 | 1 | 1 |
0 | 0 | 1 |
Согласно таблице, имеем: ;.
studfiles.net
Раздел 2. Логическая равносильность формул
2.1. Отношение равносильности
С помощью таблиц истинности можно установить, при каких наборах значений истинности входящих переменных формула будет принимать истинное или ложное значение (а также высказывание, имеющее соответствующую логическую структуру), какие формулы будут тавтологиями или противоречиями, а также установить, являются ли две данные формулы равносильными.
В
логике говорят, что два предложения
равносильны, если они одновременно
истинны, либо одновременно ложны. Слово
«одновременно» в этой фразе неоднозначно.
Так, для предложений «Завтра будет
вторник» и «Вчера было воскресенье»
это слово имеет буквальный смысл: в
понедельник они оба истинны, а в остальные
дни недели – оба ложны. Для уравнений
«х
= 2»
и «2х
= 4»
«одновременно» означает «при одних и
тех же значениях переменной». Прогнозы
«Завтра будет дождь» и «Неверно, что
завтра не будет дождя» одновременно
подтвердятся (окажутся истинными) либо
не подтвердятся (окажутся ложными). В
сущности, это один и тот же прогноз,
выраженный в двух разных формах, которые
можно представить формулами Х и 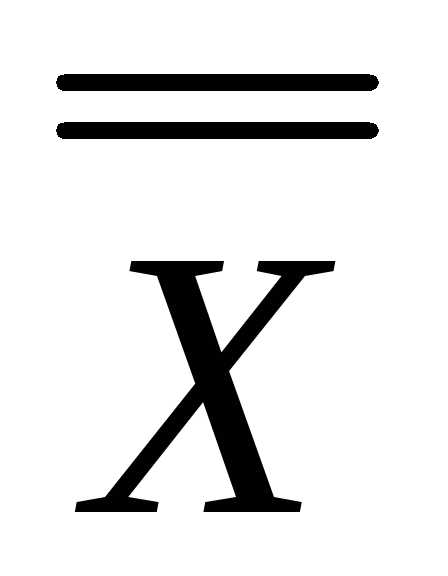 .
Эти формулы одновременно принимают
значение «истина» либо значение «ложь».
Для проверки достаточно составить
таблицу истинности:
.
Эти формулы одновременно принимают
значение «истина» либо значение «ложь».
Для проверки достаточно составить
таблицу истинности:
Х | | |
1 | 0 | 1 |
0 | 1 | 0 |
Видим, что значения истинности в первом и последнем столбцах совпадают. Такие формулы, как и соответствующие им предложения, естественно считать равносильными.
Формулы F1 и F2 называются равносильными, если их
эквиваленция  –
тавтология.
–
тавтология.
Равносильность
двух формул записывается так: 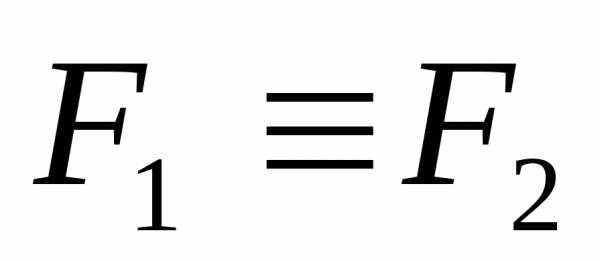 (читается: формулаF1 равносильна формуле F2).
(читается: формулаF1 равносильна формуле F2).
Проверить, равносильны ли формулы, можно двумя способами: 1) составить их эквиваленцию и с помощью таблицы истинности проверить, не является ли она тавтологией; 2) для каждой формулы составить таблицу истинности и сравнить итоговые результаты; если в итоговых столбцах при одинаковых наборах значений переменных значения истинности обеих формул будут равны, то формулы являются равносильными.
Пример
1: Выяснить, являются ли формулы равносильными:
1) 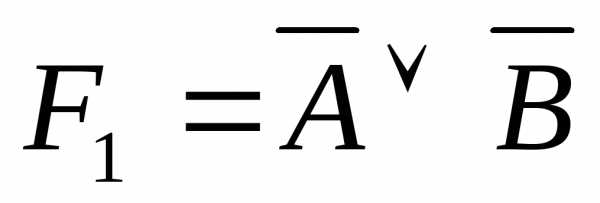 ,;
2),.
,;
2),.
Решение.
1)
Воспользуемся для определения
равносильности первым способом, то есть
выясним, является ли эквиваленция формул  итавтологией.
итавтологией.
Составим
эквиваленцию формул:
.
Полученная формула содержит две различные
переменные (А и В) и 6 операций: 1) ;
2)
;
2)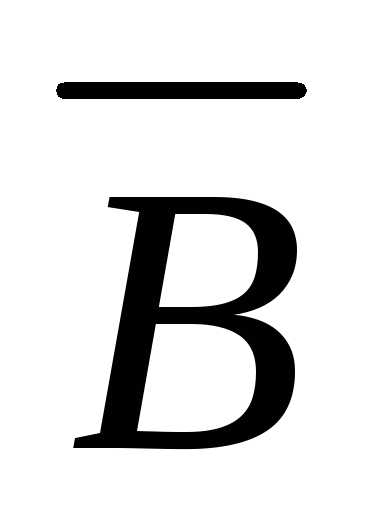 ;
3)
;
3)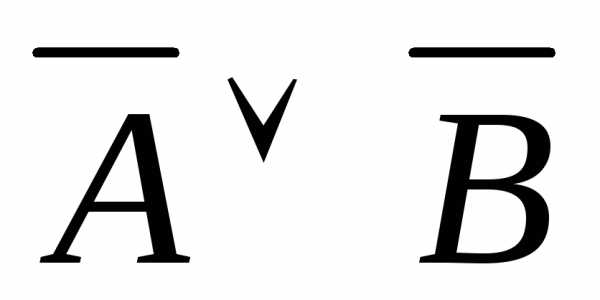 ;
4)
;
4)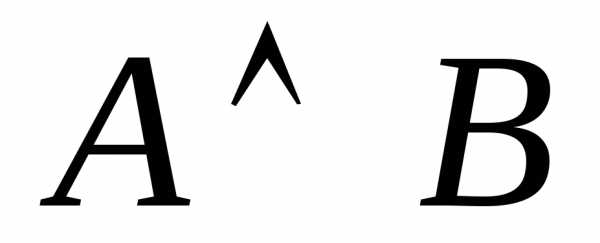 ;
5)
;
5) ;
6)
;
6) .
Значит, в соответствующей таблице
истинности будет 5 строк и 8 столбцов:
.
Значит, в соответствующей таблице
истинности будет 5 строк и 8 столбцов:
А | В | | | | | | |
1 | 1 | 0 | 0 | 0 | 1 | 0 | 1 |
1 | 0 | 0 | 1 | 1 | 0 | 1 | 1 |
0 | 1 | 1 | 0 | 1 | 0 | 1 | 1 |
0 | 0 | 1 | 1 | 1 | 0 | 1 | 1 |
Из
итогового столбца таблицы истинности
видно, что составленная эквиваленция
является тавтологией и, значит, 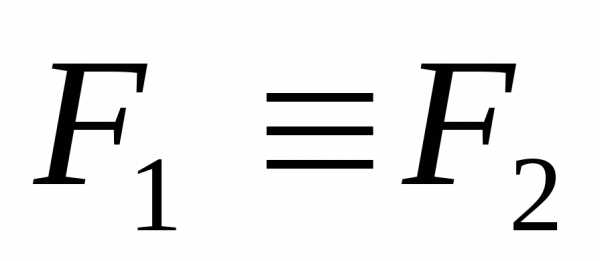 .
.
2) Для того чтобы выяснить являются ли формулы иравносильными, используем второй способ, то есть составим для каждой из формул таблицу истинности и сравним итоговые столбцы. (Замечание. Для того чтобы эффективно использовать второй способ, необходимо, чтобы все составленные таблицы истинности начинались одинаково, то есть наборы значений переменных были одинаковы в соответствующих строках.)
В формуле две различные переменные и 2 операции, значит, в соответствующей таблице истинности 5 строк и 4 столбца:
А | В | | |
1 | 1 | 1 | 0 |
1 | 0 | 0 | 1 |
0 | 1 | 1 | 0 |
0 | 0 | 1 | 0 |
В формуле две различные переменные и 3 операции, значит, в соответствующей таблице истинности 5 строк и 5 столбцов:
А | В | | | |
1 | 1 | 0 | 0 | 1 |
1 | 0 | 0 | 1 | 1 |
0 | 1 | 1 | 0 | 0 |
0 | 0 | 1 | 1 | 1 |
Сравнивая
итоговые столбцы составленных таблиц
истинности (так как таблицы начинаются
одинаково, мы можем не обращать внимание
на наборы значений переменных), видим,
что они не совпадают и, следовательно,
формулы не равносильны (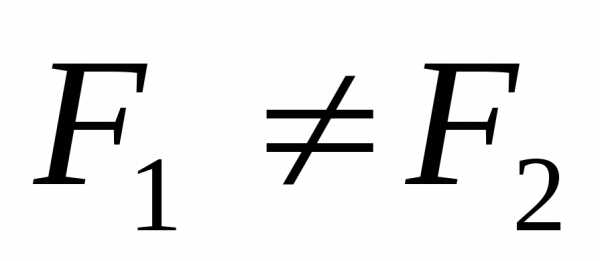 ).
).
Выражение 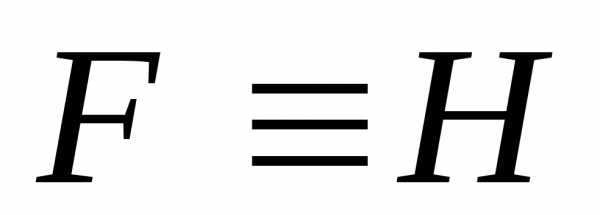 не является формулой (так как символ
«
не является формулой (так как символ
« »
не относится к какой-либо логической
операции). Оно выражаетотношение между формулами (также как равенство
между числами, параллельность между
прямыми и т.п.).
»
не относится к какой-либо логической
операции). Оно выражаетотношение между формулами (также как равенство
между числами, параллельность между
прямыми и т.п.).
Справедлива теорема о свойствах отношения равносильности:
Теорема 2.1. Отношение равносильности между формулами алгебры высказываний:
1)
рефлексивно: 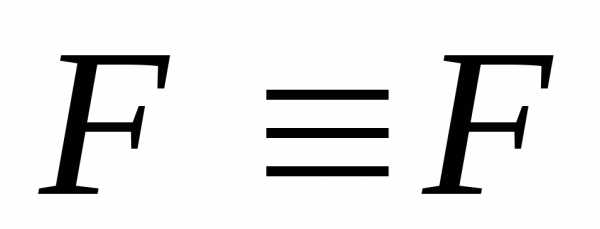 ;
;
2)
симметрично: если 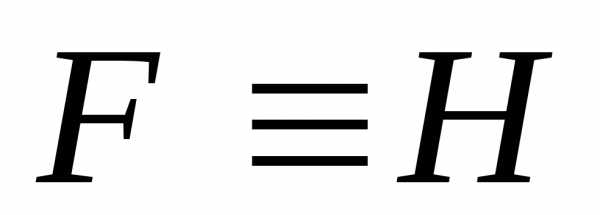 ,
то
,
то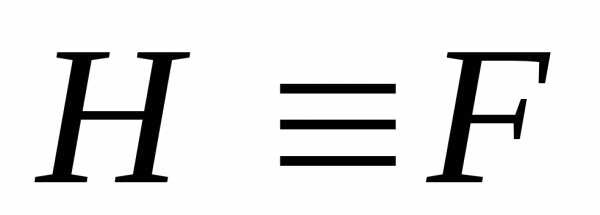 ;
;
3)
транзитивно: если 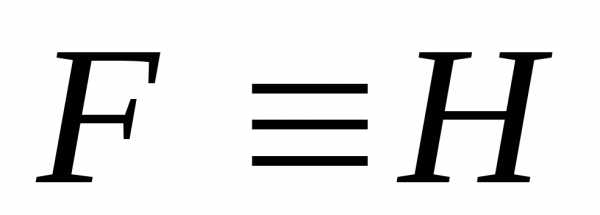 и
и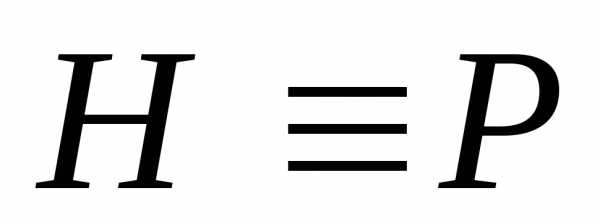 ,
то
,
то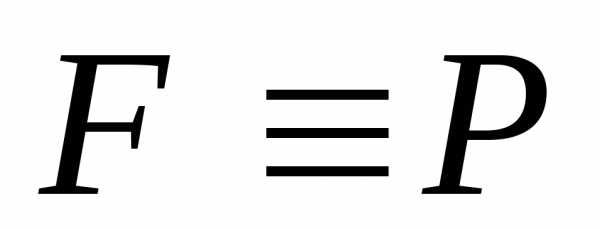 .
.
studfiles.net
1. Основные равносильности
–законы идемпотентности.
–закон снятия двойного отрицания.
–законы поглощения.
Докажем формулу 4.
Пусть А ≡ при x = 1, значение А = 1, при х = 0, значение А = 0. Итак во всех случаях значения формулы А совпадают со значениями х, следовательно, А ≡ х.
2. Равносильности, выражающие одни логические операции через другие
1.
2.
3.
4.
5.
6.
Замечание. Формулы 5 и 6 получаются из 3 и 4, если от обеих частей последних взять отрицания и воспользоваться законом снятия двойного отрицания.
Докажем формулы 1–4.
Докажем формулу 1.
1) при одинаковых логических значениях x и y формулы и – истинны, следовательно, истинной будет и коньюнкция т. е. обе части равносильности имеют одинаковые истинные значения.
2) пусть теперь x и y имеют разные логические значения, тогда будут ложными и одна из или При этом будет ложной и коньюнкция т. е. обе части равносильности имеют одинаковые ложные значения. Что и требовалось доказать.
Докажем формулу 3.
1) пусть x и y одновременно принимают истинные значения, тогда будет истинной и коньюнкция и ложным ее отрицание В то же время будут ложными и , следовательно, будет ложной и дизьюнкция
2) пусть хотя бы одна из переменных x или y принимает значение ложь, тогда тоже ложь, а – истина. В то же время отрицание хотя бы одной из переменных будет истинным, следовательно, будет истиной и дизьюнкция
Следовательно, во всех случаях обе части равносильности 3 принимают одинаковые логические значения.
Аналогично доказываются равносильности 2 и 4.
Из равносильностей группы 2 следует, что всякую формулу алгебры логики можно заменить равносильной ей формулой, содержащей только две логические операции: коньюнкцию и отрицание или дизьюнкцию и отрицание.
3. Равносильности, выражающие основные законы алгебры логики
–коммутативность коньюнкции и дизьюнкции.
–ассоциативность коньюнкции и дизьюнкции.
–дистрибутивность коньюнкции относительно дизьюнкции и наоборот.
Докажем формулу 6.
При х = 1, формулы и будут истинны, тогда и – тоже истинна.
При х = 0, ≡ ≡ ≡ следовательно, ≡
Таким образом, обе части формулы 6 равносильны одной и той же формуле и поэтому принимают одинаковые логические значения. Что и требовалось доказать.
Равносильности 3-ей группы выражают основные законы алгебры логики: коммутативность, ассоциативность и дистрибутивность (относительно логических операций – коньюнкции и дизьюнкции). Эти же законы имеют место в алгебре чисел. Поэтому над формулами алгебры логики можно производить те же преобразования, которые проводятся в алгебре чисел, т. е.
1) раскрытие скобок;
2) заключение в скобках;
3) вынесения за скобки общего множителя.
Кроме этих преобразований над формулами алгебры логики можно производить и преобразования, основанные на использовании равносильностей.
Равносильные преобразования формул используют
1) для доказательства равносильностей,
2) для приведения формул к заданному виду,
3) для упрощения формул.
Под упрощением формулы, не содержащей операций импликации и эквиваленции, понимают равносильное преобразование, приводящее к формуле, которая либо содержит по сравнению с исходной меньшее число операций коньюнкции и дизьюнкции и не содержит отрицаний неэлементарных формул, либо содержит меньшее число вхождений переменных.
Пример.
1. Доказать равносильность
Доказательство:
2. Упростить формулу
3. Доказать тождественную истинность формулы
Запишем цепочку равносильных формул:
Что и требовалось доказать.
studfiles.net
§ 2. Равносильные формулы алгебры логики.
Определение. Две
формулы алгебры логики A и B называется
равносильными, если они принимают
одинаковые логические значения на любом
наборе значений входящих в них высказываний 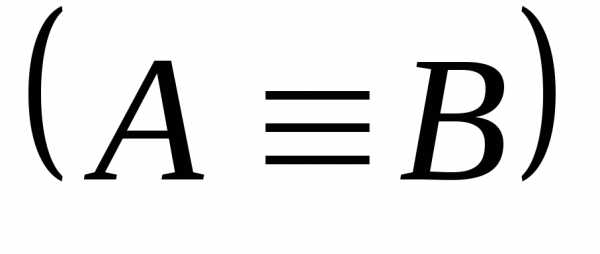 .
.
Важнейшие равносильности можно разбить на три группы:
I. Основные равносильности.
3. .
4. .
5. .
6. .
7. 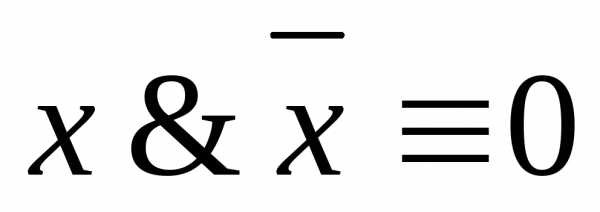 — закон противоречия.
— закон противоречия.
8. 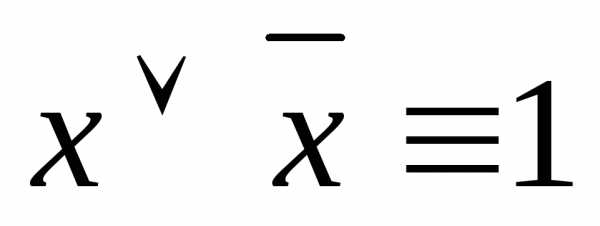 — закон исключительного третьего.
— закон исключительного третьего.
9. 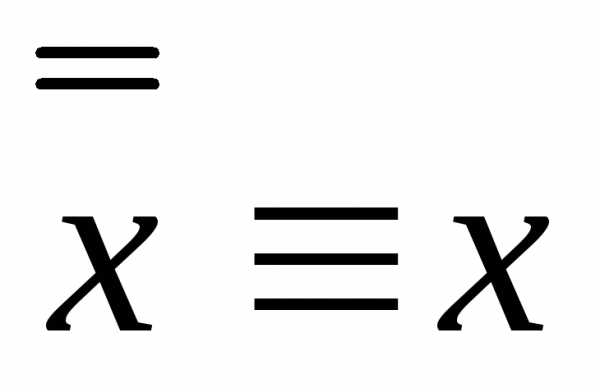 — закон снятия двойного отрицания.
— закон снятия двойного отрицания.

II. Равносильности, выражающие одни логические операции через другие.
1. ;
2. .
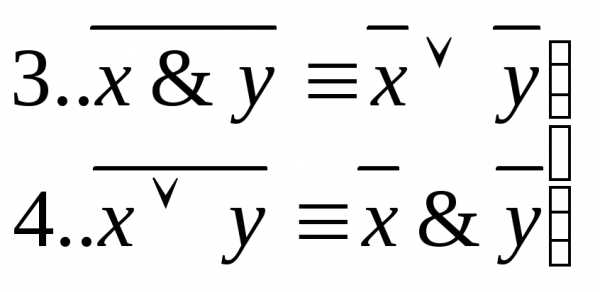 —
законы де Моргана.
—
законы де Моргана.
5. .
6. .
III. Равносильности, выражающие основные законы алгебры логики.
1. .
2. .
3. .
4. .
5. .
6. .
Используя равносильности групп I, II, III, можно часть формулы алгебры логики или всю формулу заменить равносильной ей формулой.
Такие преобразования формул применяются для доказательства равносильностей, для приведения формул к заданному виду, для упрощения формул.
Пример 1. Доказать равносильность .
Решение. Для доказательства равносильности подвергнём её левую часть равносильными преобразованиями:
.
Пример 2. Упростить
формулу  .
.
Решение. Подвергнём формулу A равносильным преобразованиям:
Пример 3. Доказать, что формула тождественно истинная.
Решение. Подвергнём формулу A равносильным преобразованиям
1.20. Доказать равносильность:
1) ;
2) ;
3) ;
4) ;
5) ;
6) ;
7) ;
8) ;
9) ;
10) .
1.21. Упростить формулу:
1) ;
2) ;
3) ;
4) ;
5) ;
6) ;
7) ;
8) ;
9) ;
10) .
1.22. Доказать тождественную истинность или тождественную ложность формул:
1) ;
2) ;
3) ;
4) ;
5) ;
6) ;
7) ;
8) ;
9) ;
10) ;
11) ;
12) ;
13) ;
14) ;
15) .
_________
1 Здесь и в дальнейшем означает , подобно тому, как в алгебре не пишется знак умножения (или пишетсяв место).
1.23. Пусть F – тождественно ложная формула. Доказать, что .
1.24. Найдите x, если .
1.15. Последовательность
высказываний 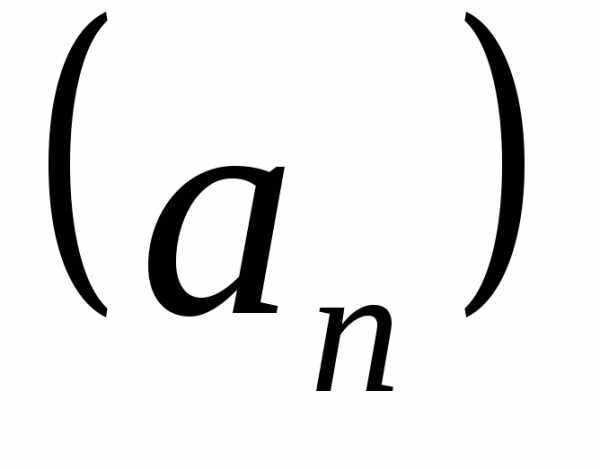 определяется следующим рекуррентным
соотношением:
определяется следующим рекуррентным
соотношением:
, n > 3.
Высказывания 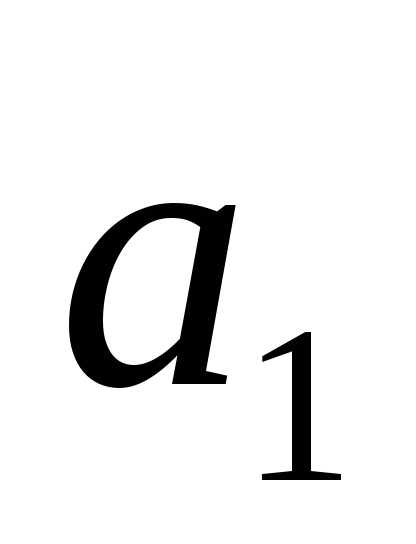 ,
,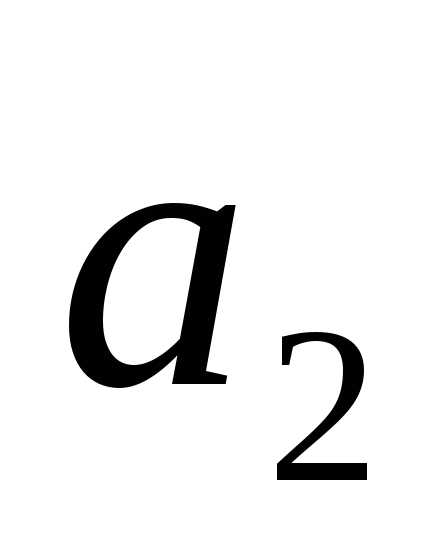 ,
, заданы, причём
заданы, причём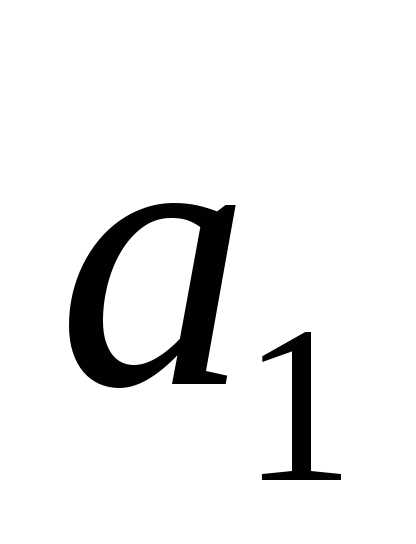 и
и истинны, а
истинны, а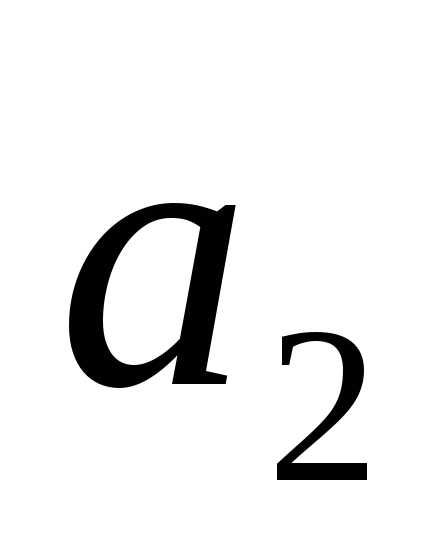 ложно. Истинно или ложно высказывание
ложно. Истинно или ложно высказывание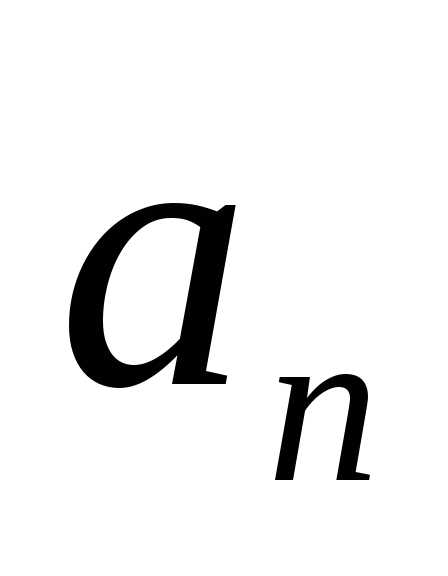 ?
Как выражается
?
Как выражается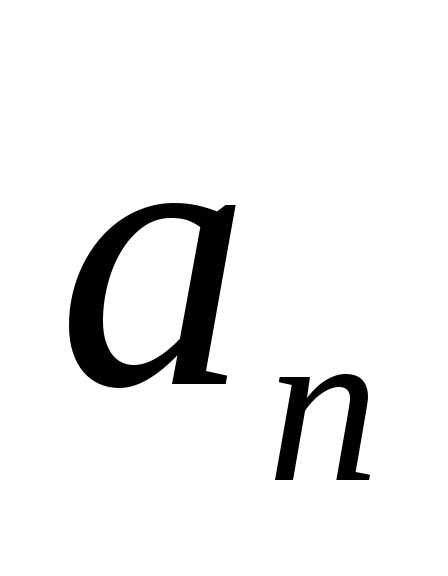 через
через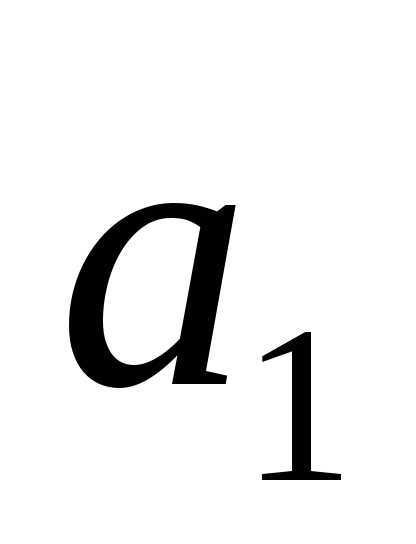 ,
,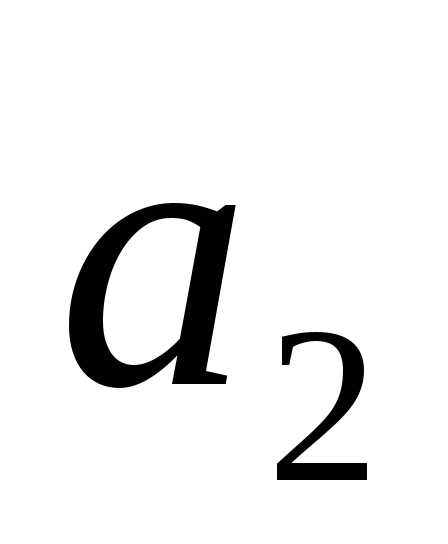 ,
, ?
?
1.26. Выразить все основные операции:
1) через операции дизъюнкции, конъюнкции и отрицания;
2) через конъюнкции и отрицания;
3) через дизъюнкции и отрицания;
4) через импликацию и отрицание.
1.27.
1) Выразить отрицание импликации через основные операции так, чтобы отрицания стояли только над аргументами.
2) Выразить операцию дизъюнкцию через импликацию.
1.28. Исключающей
дизъюнкцией двух высказываний a и b называется новое высказывание,
обозначаемое 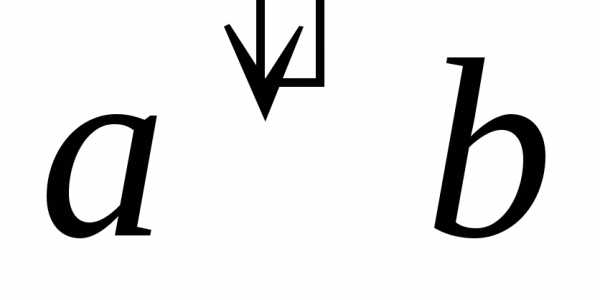 ( читают «либоa,
либо b»),
которое истинно, когда одно и только
одно из данных высказываний истинно, и
ложно а остальных случаях. Составить
таблицу истинности исключающей дизъюнкции
и выразить её через основные операции
над высказываниями.
( читают «либоa,
либо b»),
которое истинно, когда одно и только
одно из данных высказываний истинно, и
ложно а остальных случаях. Составить
таблицу истинности исключающей дизъюнкции
и выразить её через основные операции
над высказываниями.
1.29. Штрихом Шеффера двух высказываний a и b называется
новое высказывание, обозначаемое 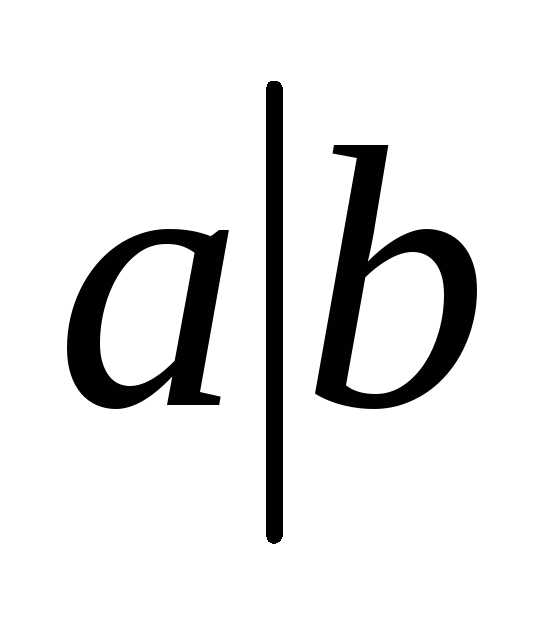 (Читают «a не совместно с b»),
которое ложно только тогда, когда они
оба данные высказывания истинны.
Составить таблицу истинности штриха
Шеффера и выразить его через основные
операции над высказываниями. Доказать,
что все основные операции над высказываниями
можно выразить через штрих Шеффера.
(Читают «a не совместно с b»),
которое ложно только тогда, когда они
оба данные высказывания истинны.
Составить таблицу истинности штриха
Шеффера и выразить его через основные
операции над высказываниями. Доказать,
что все основные операции над высказываниями
можно выразить через штрих Шеффера.
1.30. Штрихом
Лукасевича двух высказываний a и b называется
новое высказывание 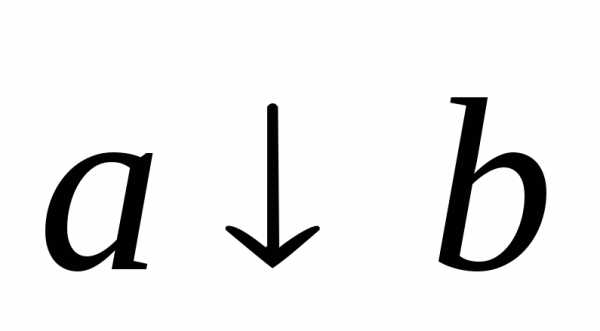 ( читают «ниa,
ни b»)
, которое истинно в том и только в том
случае, когда оба данные высказывания
ложны. Составить таблицу истинности
штриха Лукасевича и выразить его через
основные операции над высказываниями.
Доказать, что все основные операции над
высказываниями можно выразить через
штрих Лукасевича.
( читают «ниa,
ни b»)
, которое истинно в том и только в том
случае, когда оба данные высказывания
ложны. Составить таблицу истинности
штриха Лукасевича и выразить его через
основные операции над высказываниями.
Доказать, что все основные операции над
высказываниями можно выразить через
штрих Лукасевича.
1.31. Доказать, что операции отрицания не может быть выражена через основные операции (бинарные) над высказываниями.
1.32. Можно ли для каждой формулы найти равносильную, не содержащую знака отрицания?
1.33. Мальчик решил в воскресенье закончить чтение книги, сходить в музей или кино, а если будет хорошая погода – пойти купаться. В каком случае можно сказать, что решение мальчика не выполнено? В ответе отрицания должны содержаться лишь в простых высказываниях.
studfiles.net