Как найти ребро куба | Сделай все сам
Зная некоторые параметры куба, дозволено легко обнаружить его ребро. Для этого довольно лишь иметь информацию о его объеме, площади грани либо длине диагонали грани либо куба.

Вам понадобится
Инструкция
1. В основном встречаются четыре типа задач, в которых нужно обнаружить ребро куба. Это определение длины ребра куба по площади грани куба, по объему куба, по диагонали грани куба и по диагонали куба. Разглядим все четыре варианта таких задач. (Остальные задания, как водится, являются вариациями вышеперечисленных либо задачами по тригонометрии, имеющими крайне косвенное отношение к рассматриваемому вопросу)Если вестима площадь грани куба, то обнаружить ребро куба дюже легко. Потому что грань куба представляет собой квадрат со стороной, равной ребру куба, то ее площадь равняется квадрату ребра куба. Следственно длина ребра куба равняется корню квадратному из площади его грани, то есть:а=?S, гдеа – длина ребра куба,S – площадь грани куба.
2. Нахождение грани куба по его объему еще проще. Рассматривая, что объем куба равен кубу (третьей степени) длины ребра куба, получаем что длина ребра куба равняется корню кубическому (третьей степени) из его объема, т.е.:а=?V (кубический корень), гдеа – длина ребра куба,V – объем куба.
3. Немногим труднее нахождение длины ребра куба по знаменитым длинам диагоналей. Обозначим через:а – длину ребра куба;b – длину диагонали грани куба;c – длину диагонали куба.Как видно из рисунка, диагональ грани и ребра куба образуют прямоугольный равносторонний треугольник. Следственно, по теореме Пифагора:a^2+a^2=b^2(^ – значок возведения в степень).Отсель находим:a=?(b^2/2)(дабы обнаружить ребро куба надобно извлечь квадратный корень из половины квадрата диагонали грани).
4. Дабы обнаружить ребро куба по его диагонали, вновь воспользуемся рисунком. Диагональ куба (с), диагональ грани (b) и ребро куба (а) образуют прямоугольный треугольник. Значит, согласно теореме Пифагора:a^2+b^2=c^2.Воспользуемся вышеустановленной зависимостью между a и b и подставим в формулуb^2=a^2+a^2. Получаем:a^2+a^2+a^2=c^2, откуда находим:3*a^2=c^2, следственно:a=?(c^2/3).
Куб – это прямоугольный параллелепипед, все ребра которого равны. Следственно всеобщая формула для объема прямоугольного параллелепипеда и формула для площади его поверхности в случае куба упрощаются. Также объем куба и его площадь поверхности дозволено обнаружить, зная объем шара, вписанного в него, либо шара, описанного вокруг него.

Вам понадобится
- длина стороны куба, радиус вписанного и описанного шара
Инструкция
1. Объем прямоугольного параллелепипеда равен: V = abc – где a, b, c – его измерения. Следственно объем куба равен V = a*a*a = a^3, где a – длина стороны куба .Площадь поверхности куба равна сумме площадей всех его граней. Каждого у куба шесть граней, следственно площадь его поверхности равна S = 6*(a^2).
2. Пускай шар вписан в куб. Видимо, диаметр этого шара будет равен стороне куба . Подставляя длину диаметра в выражения для объема взамен длины ребра куба и применяя, что диаметр равен удвоенному радиусу, получим тогда V = d*d*d = 2r*2r*2r = 8*(r^3), где d – диаметр вписанной окружности, а r – радиус вписанной окружности.Площадь поверхности куба тогда будет равна S = 6*(d^2) = 24*(r^2).
3. Пускай шар описан вокруг куба . Тогда его диаметр будет совпадать с диагональю куба . Диагональ куба проходит через центр куба и соединяет две его противоположные точки.Разглядите для начала одну из граней куба . Ребра этой грани являются катетами прямоугольного треугольника, в котором диагональ грани d будет гипотенузой. Тогда по теореме Пифагора получим: d = sqrt((a^2)+(a^2)) = sqrt(2)*a.
4. После этого разглядите треугольник в котором гипотенузой будет диагональ куба , а диагональ грани d и одно из ребер куба a – его катетами. Подобно, по теореме Пифагора получим: D = sqrt((d^2)+(a^2)) = sqrt(2*(a^2)+(a^2)) = a*sqrt(3).Выходит, по выведенной формуле диагональ куба равна D = a*sqrt(3). Отсель, a = D/sqrt(3) = 2R/sqrt(3). Следственно, V = 8*(R^3)/(3*sqrt(3)), где R – радиус описанного шара.Площадь поверхности куба равна S = 6*((D/sqrt(3))^2) = 6*(D^2)/3 = 2*(D^2) = 8*(R^2).
Кубом называют объемный многоугольник с шестью гранями положительной формы – верный гексаэдр. Число положительных граней определяет форму всякой из них – это квадраты. Это, вероятно, самая комфортная из многогранных фигур с точки зрения определения ее геометрических свойств в привычной нам трехмерной системе координат. Все ее параметры дозволено вычислить, зная каждого лишь длину одного ребра.
Инструкция
1. Если у вас имеется некоторый физический объект в форме куба , то для вычисления его объема измерьте длину всякий грани, а после этого используйте алгорифм, описанный в дальнейшем шаге. Если же такое измерение нереально, то дозволено, скажем, испробовать определить объем вытесненной воды, разместив в нее данный кубический объект. Если удастся узнать число вытесненной воды в литрах, то итог дозволено перевести в кубические дециметры – один литр в системе СИ приравнен к одному кубическому дециметру.
2. Возводите в третью степень знаменитое значение длины ребра куба , то есть длину стороны квадрата, составляющего всякую из его граней. Утилитарные расчеты дозволено произвести на любом калькуляторе либо с подмогой поисковой системы Google. Если в поле поискового запроса ввести, скажем, «3,14 в кубе», то поисковик сразу (без нажатия кнопки) покажет итог.
3. Если знаменита только длина диагонали куба , то этого тоже абсолютно довольно для вычисления его объема. Диагональю положительного октаэдра называют отрезок, соединяющий две его противоположные касательно центра вершины. Длину такой диагонали через теорему Пифагора дозволено выразить как длину ребра куба , поделенную на корень из 3. Из этого вытекает, что для нахождения объема куба нужно его диагональ поделить на корень из 3 и итог построить в куб.
4. Подобно дозволено вычислить объем куба , зная только длину диагонали его грани. Из той же теоремы Пифагора вытекает, что длина ребра куба равна диагонали грани, поделенной на корень из 2-х. Объем в этом случае дозволено вычислить, поделив вестимую длину диагонали ребра на корень из 2-х и построив итог в куб.
5. Не забывайте о размерности полученного итога – если вы вычисляете объем исходя из вестимых размеров в сантиметрах, то итог будет получен в кубических сантиметрах. Один дециметр содержит десять сантиметров, а один кубический дециметр (литр) – 1000 (десять в кубе) кубических сантиметров. Соответственно, для перевода итога в кубические дециметры нужно поделить полученное значение в сантиметрах на 1000.
Видео по теме
jprosto.ru
Если каждое ребро куба увеличить
Продолжаем рассматривать задания с кубами и параллелепипедами. Основные формулы можно посмотреть в начале этой статьи. Представленные ниже задачи связаны с изменением объёма и площади поверхности при увеличении (уменьшении) ребра.
В одной из задач используется понятие равновеликости. Что это означает? Равновеликие тела это тела имеющие равный объём. Например, если сказано, что шар равновелик кубу – это означает, что шар и куб имеют равный объём. Рассмотрим задачи:
Если каждое ребро куба увеличить на 9, то его площадь поверхности увеличится на 594. Найдите ребро куба.
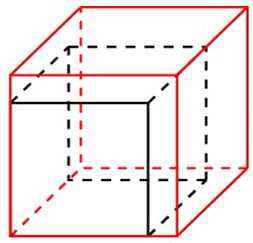
Так как существует зависимость площади поверхности куба от его ребра, то, конечно же, воспользуемся формулой площади поверхности куба:
Сказано, что при увеличении ребра на 9 площадь поверхности увеличивается на 594. Запишем формулу площади поверхности для увеличенного куба:
Ребро куба равно 1.
Ответ: 1
Три ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 4, 16, 27. Найдите ребро равновеликого ему куба.
Равновеликий куб – это куб, объём которого равен объёму параллелепипеда. Известно, что объём куба находится по формуле:
Значит если мы найдём объём параллелепипеда, то сможем найти ребро куба. Объём параллелепипеда равен:
Таким образом:
*Как извлечь корень третьей степени из большого числа можно посмотреть здесь.
Ответ: 12
Во сколько раз увеличится объем куба, если его ребра увеличить в шесть раз?
Объем куба с ребром a равен V1 = a3.
Объем куба с ребром в шесть раз большим равен V2 = (6a)3.
Разделим V2 на V1 и получим искомую величину:
Объём куба увеличится в 216 раз.
Ответ: 216
Если каждое ребро куба увеличить на 3, то его объем увеличится на 819. Найдите ребро куба.
Пусть ребро куба равно a.
Запишем чему равен объём для исходного куба и для увеличенного:
Объем куба с ребром a равен V1 = a3.
Объем куба с ребром a + 3 равен V2 = (a + 3)3.
Сказано, что объём увеличился на 819, значит:

Решим уравнение:
Подходящее значение a = 8. Отрицательное значение для данной задачи не имеет физического смысла. Таким образом, ребро куба равно 8.
Ответ: 8
Во сколько раз увеличится площадь поверхности куба, если его ребро увеличить в 24 раза?
Запишем формулу площади поверхности исходного куба и формулу площади поверхности для куба с увеличенным ребром:
Теперь остаётся только лишь найти отношение площадей:
Таким образом, площадь поверхности увеличится в 576 раз.
Ответ: 576
Объем одного куба в 729 раз больше объема другого куба. Во сколько раз площадь поверхности первого куба больше площади поверхности второго куба?
Отметим, что первый куб это больший куб, второй это меньший куб. Мы без труда решим эту задачу, если определим во сколько раз ребро первого куба больше ребра второго. Пусть ребро малого (второго) куба равно х, а большего у. Тогда
По условию:
Значит
Получили, что ребро первого куба большего ребра второго в 9 раз, то есть
Теперь запишем площадь поверхности для обоих кубов:
Остаётся найти отношение площадей поверхностей кубов:
Площадь поверхности первого куба больше площади поверхности второго куба в 81 раз.
Ответ: 81
27061. Если каждое ребро куба увеличить на 1, то его площадь поверхности увеличится на 54. Найдите ребро куба.
Посмотреть решение
27080. Три ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 4, 6, 9. Найдите ребро равновеликого ему куба.
Посмотреть решение
27081. Во сколько раз увеличится объем куба, если его ребра увеличить в три раза?
Посмотреть решение
27102. Если каждое ребро куба увеличить на 1, то его объем увеличится на 19. Найдите ребро куба.
Посмотреть решение
27168. Объем одного куба в 8 раз больше объема другого куба. Во сколько раз площадь поверхности первого куба больше площади поверхности второго куба?
Посмотреть решение
Есть ещё отличный подход для решения задач, в которых где речь идёт о изменении объёма и площади поверхности для таких тел как: куб, параллелепипед, шар, правильная четырёхугольная пирамида, конус, цилиндр, при увеличении (уменьшении) ребра (радиуса) в некоторое количество раз. Такие задания практически можно решать в одну строчку. Об этом расскажу в будущем, не пропустите!
Всего доброго! Успеха Вам!
С уважением, Александр.
P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.
matematikalegko.ru
напарник ребра куба, 5 букв, сканворд
напарник ребра куба
Альтернативные описания• выступ, проходящий вдоль клинка, в сочетании с которым в сечении клинок приобретает форму ромба или треугольника
• выступ, проходящий вдоль клинка, образующий в сечении ромб или треугольник
• линия раздела
• плоская часть поверхности геометрического тела
• перейти последнюю …
• рассказ Айзека Азимова «… завтра»
• техника резьбы по стеклу
• поверхность куба
• сторона пирамиды
• перейти … дозволенного
• сторона октаэдра
• у куба их шесть
• сторона куба
• сторона призмы
• сторона характера (перен.)
• плоская поверхность куба
• рубеж
• плоская сторона куба
• чем блестит бриллиант?
• межа
• Плоская поверхность геометрического тела
• Сторона многогранника
• Плоская часть поверхности геометрического тела
• То, что отличает, отделяет одно от другого
• граница ж. рубеж, предел, межа, конт, край, кромка, конец и начало, стык, черта раздела. Граница земель, владения. *Честолюбию его нет границ, ни меры. Он выходит из границ приличия. Межи да грани, ссоры да брани. Рубеж (рубить) и грань (гранить) встарь означали межу и межевые знаки, которые нередко нарубались на деревьях. на березе рубежи и грани т. е. знаки, резы. каменя на вяз, а на вязе граница крестьян. этом знач. грановитый, граничный знак: Да со леху долом прямо через поперек бору к грановитой сосне. При изломе плоскости, самый гребень назыв. гранью; но в мелких вещах, напр. у граненых камней, гранью же зовут и самую площадку (фасетку), а затем и самый способ гранения или род огранки камней: мелкая, крупная грань; бриллиантовая, розетовая грань и пр. Грань в арифметич. каждое отделение в три цифры, для удобнейшего произношения написанного числа. песнях, попадается гран м. и грань, гранка: Распадися дуб на четыре грана. т. е. плахи, части. Граничить, быть пограничну, порубежну, смежну, смежаться. Когда-то мы (земля наша) граничивали с ними, а ныне прошла чересполосица. Граниченье ср. состояние граничащего. Граничный, на границе находящийся, к ней относящийся. Граничанин, граничник, пограничник, житель границы земли, области. Гранить, гранивать что, огранять, делать грани; обрабатывать твердое тело, придавая ему плоскости и гребни; гранят особ. ценные, честные камни. Граниться, быть граниму. Алмаз алмазом гранится, вор вором губится. Огранить камень. Выгранить печать. Отгранить почище. Догранить начатое. Изгранить бороздками. Награнить много камней. Подгранить порчу. Перегранить снова. перегранил более сотни топазов. Програнить еще грань. Програнил до вечера. Разгранил на грани. Гранение ср. длит. гранка ж. об. действ. по глаг. Гранкой зовут также сросшиеся в кучку русские орехи, как родятся они на одном общем стебле. Гранка орехов. Кристалл, самогранка; типограф. верстать, набор в столбцах, неверстанный в страницы. Гранчатый, гранный, граненый, с гранями. Трех-, пяти-, многогранный. Грановитка ж. шпанская вишня, растущая гранками, гроздами. Гранистый, грановитый, гранчатый, гранный, граненый, со многими гранями. Гранистый стебелек, не округлый, а угольчатый. Грановитая палата, в Москве, одетая граненым камнем. Гранчатые подвески. Гранковый, ко гранке орехов, либо к кристаллу относящийся. Гранник м. вообще, гранная вещь, многогранное тело; тело, кругом ограниченное плоскостями, образующими на стыках углы, изломы. Гранник, относительно тел то же, что угольник или сторонник, относительно плоскостей. правильном граннике все плоскости равны и одинаковы, и число их ставится перед названием, слитно; просто гранником называют призму. Гранильный, ко гранению, ко гранке относящийся. Гранильня ж. заведение, где гранят камень, стекло и пр. гранильная фабрика. Гранильщик м. гранила м. гранильный мастер. Гранило ср. орудие для огранки камней. Гранильщиков, гранильщику принадлежащий; гранильщичий, относящийся ко гранильщикам, к ремеслу, работе их
• рассказ Айзека Азимова «… завтра»
• чем блестит бриллиант
• плоская поверхность бриллианта
scanwordhelper.ru
Куб — Вікіпедія
Матеріал з Вікіпедії — вільної енциклопедії.
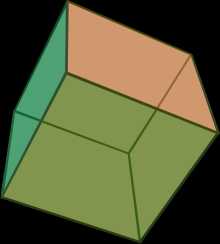 Будова куба у стереопроекції.
Будова куба у стереопроекції. 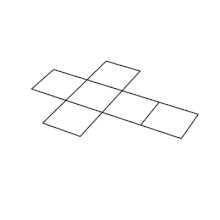 Розгортка куба
Розгортка кубаКуб (від лат. cubus, первісно — «кубічна кістка для гри»)[1] або гекса́едр (від дав.-гр. ἑξα- — «шість» + ἕδρα — «грань, поверхня») — правильний многогранник, кожна грань якого є квадратом. Окремий випадок паралелепіпеда і призми.
У різних дисциплінах використовуються значення терміну, що мають відношення до тих або інших властивостей геометричного прототипу. Зокрема, в алгебрі кубом числа називають значення цього числа, піднесене до 3-го степеня. В аналітиці (OLAP-аналіз) застосовуються так звані аналітичні багатовимірні куби, що дозволяють в наочному вигляді зіставити дані з різних таблиць.
Декартові координати[ред. | ред. код]
Якщо центр куба сумістити з початком координат, а ре
uk.wikipedia.org
