Решение алгебраических дробей онлайн 8 класс – Калькулятор дробей онлайн

Алгебраические дроби. Видеоурок. Алгебра 8 Класс

Этот урок является одним из итоговых по знаниям алгебры 8-ого класса. Мы с вами вспомним основные определения и примеры решения задач на тему «Алгебраические дроби».

Тема: Повторение курса алгебры 8-ого класса

Урок: Алгебраические дроби

Для начала давайте вспомним, что же такое алгебраические дроби. Алгебраической дробью называют выражение вида  , где  – многочлены,  – числитель,  – знаменатель.

Поскольку  – многочлены, то необходимо иметь в виду стандартные действия, возможные с многочленами, а именно: приведение к стандартному виду, разложение на множители, а также сокращение числителя и знаменателя.

Пример №1

Сократите дробь

 – воспользуемся формулами сокращённого умножения для квадрата суммы и разности квадратов.

Комментарии: вначале мы разложили дробь на множители с помощью формул сокращённого умножения, а дальше воспользовались одним из основных свойств дроби:

и числитель, и знаменатель алгебраической дроби можно умножить или разделить на один и тот же многочлен, в том числе число, который не равен 0. Таким образом получается, что мы и числитель, и знаменатель разделили на многочлен , поэтому обязательно необходимо учесть, что этот многочлен не равен 0, т. е. .

Пример №2

Из условия нам пока не ясно, какая связь между этими двумя функциями. Для этого нам необходимо упростить первую из них методом разложения на множители.

однако необходимо не забыть про условие сокращения дроби, т. е. про то, что

После всех сокращений мы получаем, что

 лишь с тем отличием, что .

Построим график двух функций.

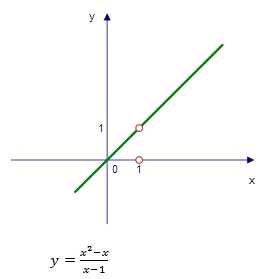
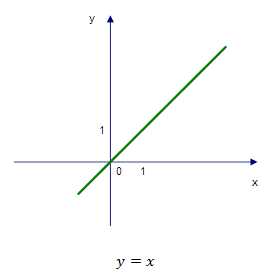
Мы видим яркое различие этих двух графиков: по сути они одинаковы, но на первом графике нам необходимо выколоть точку с координатой (1;0), поскольку эта точна не входит в ОДЗ первой функции.

Итого, мы с вами рассмотрели, что такое дробь,  решили пару примеров о том, как важно следить за областью определения (областью допустимых значений), т. е. за теми значениями, которые может принимать

interneturok.ru

Основные понятия. Видеоурок. Алгебра 8 Класс

На данном уроке рассматривается понятие алгебраической дроби. С дробями человек встречается в самых простых жизненных ситуациях: когда необходимо разделить некий объект на несколько частей, например, разрезать торт поровну на десять человек. Очевидно, что каждому достанется почасти торта. В указанном случае мы сталкиваемся с понятием числовой дроби, однако возможна ситуация, когда объект делится на неизвестное количество частей, например, на x. В таком случае возникает понятие дробного выражения. С целыми выражениями (не содержащими деление на выражения с переменными) и их свойствами вы уже познакомились в 7 классе.  Далее мы рассмотрим понятие рациональной дроби, а также допустимых значений переменных.

Рациональные выражения делятся на целые и дробные выражения.

                         

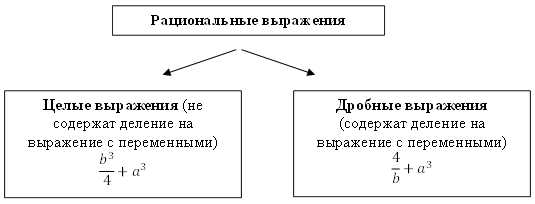
Определение. Рациональная дробь – дробное выражение вида , где  – многочлены.  – числитель,  – знаменатель.

Примеры рациональных выражений:  – дробные выражения;  – целые выражения. В первом выражении, к примеру, в роли числителя выступает , а знаменателя – .

Значение алгебраической дроби, как и любого алгебраического выражения

, зависит от численного значения тех переменных, которые в него входят. В частности, в первом примере значение дроби зависит от значений переменных  и , а во втором только от значения переменной .

Рассмотрим первую типовую задачу: вычисление значения рациональной дроби при различных значениях входящих в нее переменных.

Пример 1. Вычислить значение дроби  при а) , б) ,    в)

Решение. Подставим значения переменных в указанную дробь: а) , б) , в)  – не существует (т. к. на ноль делить нельзя).

Ответ: а) 3; б) 1; в) не существует.

Как видим, возникает две типовые задачи для любой дроби: 1) вычис

interneturok.ru

Умножение, деление и сокращение алгебраических дробей

В этой статье мы рассмотрим основные действия с алгебраическими дробями:

Начнем с сокращения алгебраических дробей.

Казалось бы, алгоритм очевиден.

Чтобы сократить алгебраические дроби, нужно

1. Разложить числитель и знаменатель дроби на множители.

2. Сократить одинаковые множители.

Однако, школьники часто делают ошибку, «сокращая» не множители, а слагаемые. Например, есть любители, которые в дроби «сокращают» на и получают в результате , что, разумеется, неверно.

Рассмотрим примеры:

1. Сократить дробь:

1. Разложим на множители числитель по формуле квадрата суммы, а знаменатель по формуле разности квадратов

2. Разделим числитель и знаменатель на

2.  Сократить дробь: 

 

1. Разложим на множители числитель. Так как числитель содержит четыре слагаемых, применим группировку.

2. Разложим на множители знаменатель. Так же применим группировку.

3. Запишем дробь, которая у нас получилась и сократим одинаковые множители:

Умножение алгебраических дробей.

При умножении алгебраических дробей мы числитель умножаем на числитель, а знаменатель умножаем на знаменатель.

Важно! Не нужно торопиться выполнять умножение в числителе и знаменателе дроби. После того, как мы записали в числителе произведение числителей дробей, а в знаменателе — произведение знаменателей, нужно разложить на множители каждый множитель и сократить дробь.

Рассмотрим примеры:

3. Упростите выражение:

1. Запишем произведение дробей: в числителе произведение числителей, а в знаменателе произведение знаменателей:

2. Разложим каждую скобку на множители:

Теперь нам нужно сократить одинаковые множители. Заметим, что выражения и отличаются только знаком: и в результате деления первого выражения на второе получим -1.

Итак,

 

Деление алгебраических дробей мы выполняем по такому правилу:

То есть чтобы разделить на дробь, нужно умножить на «перевернутую».

Мы видим, что деление дробей сводится к умножению, а умножение, в конечном итоге, сводится к сокращению дробей.

Рассмотрим пример:

4. Упростите выражение:

Разложим на множители числитель и знаменатель второй дроби:

Получим:

Итак,

Сложение и вычитание алгебраических дробей мы рассмотрим в следующей статье.

И.В. Фельдман, репетитор по математике.

 

ege-ok.ru

8 класс. Алгебра. Алгебраические дроби. — Умножение алгебраических дробей.

Комментарии преподавателя

На данном уроке будут рассмотрены правила умножения  алгебраических дробей, а также примеры на применение данных правил. Умножение  алгебраических дробей не отличается от умножения  обыкновенных дробей. Вместе с тем, наличие переменных приводит к несколько более сложным способам упрощения полученных выражений. Несмотря на то, что умножение дробей выполняется проще, чем их сложение и вычитание, к изучению данной темы необходимо подойти крайне ответственно, поскольку в ней существует много «подводных камней», на которые обычно не обращают внимания. В рамках урока мы не только изучим правила умножения  дробей, но и разберём нюансы, которые могут возникнуть при их применении. 

 

Тема: Ал­геб­ра­и­че­ские дроби. Ариф­ме­ти­че­ские опе­ра­ции над ал­геб­ра­и­че­ски­ми дро­бя­ми

Урок: Умно­же­ние  ал­геб­ра­и­че­ских дро­бей

Пра­ви­ла умно­же­ния и деления  ал­геб­ра­и­че­ских дро­бей аб­со­лют­но ана­ло­гич­ны пра­ви­лам умно­же­ния и деления обык­но­вен­ных дро­бей. На­пом­ним их:

То есть, для того, чтобы умно­жить дроби, необ­хо­ди­мо умно­жить их чис­ли­те­ли (это будет чис­ли­тель про­из­ве­де­ния), и умно­жить их зна­ме­на­те­ли (это будет зна­ме­на­тель про­из­ве­де­ния).

 

Несмот­ря на про­сто­ту дан­ных пра­вил, мно­гие при ре­ше­нии при­ме­ров по дан­ной теме до­пус­ка­ют ошиб­ки в ряде част­ных слу­ча­ев. Рас­смот­рим по­дроб­нее эти част­ные слу­чаи:

Во всех этих пра­ви­лах мы поль­зо­ва­лись сле­ду­ю­щим фак­том: .

Решим несколь­ко при­ме­ров на умно­же­ние  обык­но­вен­ных дро­бей, чтобы вспом­нить, как поль­зо­вать­ся ука­зан­ны­ми пра­ви­ла­ми.

При­мер 1

При­ме­ча­ние: при со­кра­ще­нии дро­бей мы поль­зо­ва­лись раз­ло­же­ни­ем числа на про­стые мно­жи­те­ли. На­пом­ним, что про­сты­ми чис­ла­ми на­зы­ва­ют­ся такие на­ту­раль­ные числа, ко­то­рые де­лят­ся толь­ко на  и на с

www.kursoteka.ru

Сложение и вычитание алгебраических дробей с разными знаменателями. Алгебра, 8 класс: уроки, тесты, задания.

1.	Сложение или вычитание дробей (числа) Сложность: лёгкое	2
2.	Разность алгебраических дробей Сложность: среднее	3
3.	Сложение алгебраических дробей (биномы и числа) Сложность: лёгкое	4
4.	Сложение или вычитание дробей (переменные, степени) Сложность: лёгкое	2
5.	Сложение алгебраических дробей (одночлены) Сложность: лёгкое	3
6.	Сложение или вычитание дробей (произведение переменной и бинома) Сложность: лёгкое	2
7.	Сложение или вычитание числа и дроби Сложность: лёгкое	2
8.	Разность переменной и дроби Сложность: среднее	3
9.	Разность алгебраических дробей (биномы и переменные) Сложность: среднее	4
10.	Сумма двух алгебраических дробей (степени) Сложность: среднее	3
11.	Сумма трёх дробей (степени) Сложность: среднее	7
12.	Сумма алгебраических дробей (переменная и бином) Сложность: среднее	4
13.	Сумма алгебраических дробей (общий множитель, буквы и числа) Сложность: среднее	5
14.	Сумма алгебраических дробей (общий множитель, буквы) Сложность: среднее	6
15.	Сложение или вычитание дробей (разность квадратов) Сложность: среднее	6
16.	Разность алгебраических дробей (квадрат разности) Сложность: среднее	4
17.	Разность алгебраических дробей (общий множитель, разность квадратов) Сложность: среднее	7
18.	Значение выражения Сложность: среднее	7
19.	Сложение или вычитание дробей (формулы сокращённого умножения) Сложность: сложное	6
20.	Сумма трёх дробей (разность квадратов, квадрат бинома) Сложность: сложное	7

www.yaklass.ru

8 класс. Алгебра. Алгебраические дроби. — Деление алгебраических дробей.

Комментарии преподавателя

 

На данном уроке будут рассмотрены правила  деления алгебраических дробей, а также примеры на применение данных правил. Деление алгебраических дробей не отличается от  деления обыкновенных дробей. Вместе с тем, наличие переменных приводит к несколько более сложным способам упрощения полученных выражений. Несмотря на то, что  деление дробей выполняется проще, чем их сложение и вычитание, к изучению данной темы необходимо подойти крайне ответственно, поскольку в ней существует много «подводных камней», на которые обычно не обращают внимания. В рамках урока мы не только изучим правила умножения и деления дробей, но и разберём нюансы, которые могут возникнуть при их применении. 

Тема: Ал­геб­ра­и­че­ские дроби. Ариф­ме­ти­че­ские опе­ра­ции над ал­геб­ра­и­че­ски­ми дро­бя­ми

Урок: Де­ле­ние ал­геб­ра­и­че­ских дро­бей

Пра­ви­ла умно­же­ния и де­ле­ния ал­геб­ра­и­че­ских дро­бей аб­со­лют­но ана­ло­гич­ны пра­ви­лам умно­же­ния и де­ле­ния обык­но­вен­ных дро­бей. На­пом­ним их:

То есть, для того, чтобы умно­жить дроби, необ­хо­ди­мо умно­жить их чис­ли­те­ли (это будет чис­ли­тель про­из­ве­де­ния), и умно­жить их зна­ме­на­те­ли (это будет зна­ме­на­тель про­из­ве­де­ния).

Де­ле­ние на дробь – это умно­же­ние на пе­ре­вёр­ну­тую дробь, то есть, для того, чтобы раз­де­лить две дроби, необ­хо­ди­мо первую из них (де­ли­мое) умно­жить на пе­ре­вёр­ну­тую вто­рую (де­ли­тель).

Несмот­ря на про­сто­ту дан­ных пра­вил, мно­гие при ре­ше­нии при­ме­ров по дан­ной теме до­пус­ка­ют ошиб­ки в ряде част­ных слу­ча­ев. Рас­смот­рим по­дроб­нее эти част­ные слу­чаи:

Во всех этих пра­ви­лах мы поль­зо­ва­лись сле­ду­ю­щим фак­том: .

Решим несколь­ко при­ме­ров на  де­ле­ние обык­но­вен­ных дро­бей, чтобы вспом­нить, как поль­зо­вать­ся ука­зан­ны­ми пра­ви­ла­ми.

 

При­ме­ча­ние: при со­кра­ще­нии дро­бей мы поль­зо­ва­лись раз­ло­же­ни­ем числа на про­стые мно­жи­те­ли. На­пом­ним, что про­сты­ми чис­ла­ми на­зы­ва­ют­ся такие на­ту­раль­ные числа, ко­то­рые де­лят­ся толь­ко на 

www.kursoteka.ru