УРАВНЕНИЯ И НЕРАВЕНСТВА С МОДУЛЕМ – Репетитор по математике
Сайт репетитора по математике Фельдман Инны Владимировны. Профессиональные услуги репетитора по математике в Москве. Подготовка к ГИА и ЕГЭ, помощь отстающим. 2016-04-2424 Апр 2016
13 Задание (2016) (C1)Диагностические работыУРАВНЕНИЯ И НЕРАВЕНСТВА С МОДУЛЕМ
Задание 13 из Досрочного экзамена, резерв. 16.04.2016
Задание 13. а) Решите уравнение
б) Укажите корни этого уравнения, принадлежащие отрезку [].
Решение.
показать
а) Введем замену: , получим уравнение:
Разложим левую часть на множители способом группировки:
или
или .
Вернемся к исходной переменной:
или :
Отметим эти значения на линии тангенсов и получим корни:
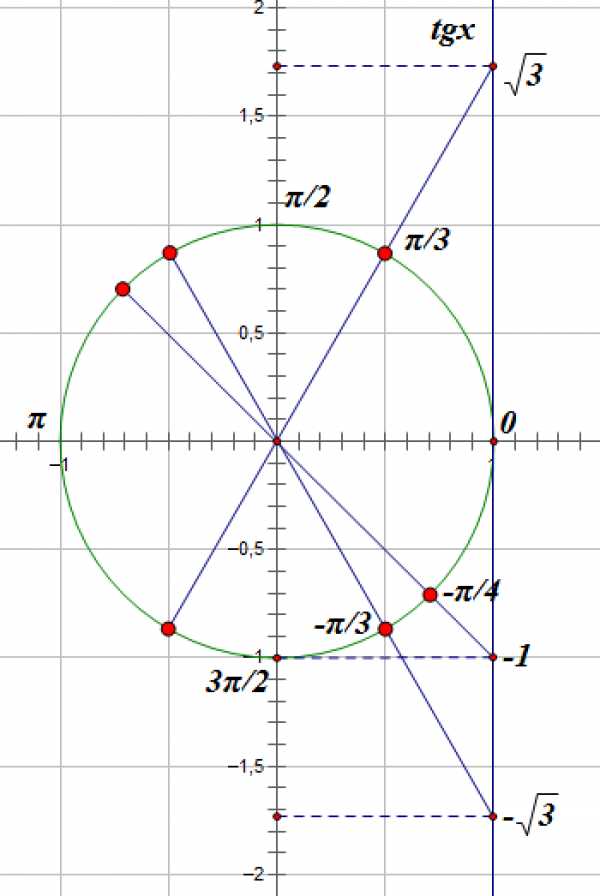
Корни, лежащие во второй и третьей четверти отстоят от корней, лежащих в первой и четвертой четвертях на промежуток, равный , то есть на период функции :
б) Выберем корни, принадлежащие промежутку [].
Этот промежуток выделим дугой:
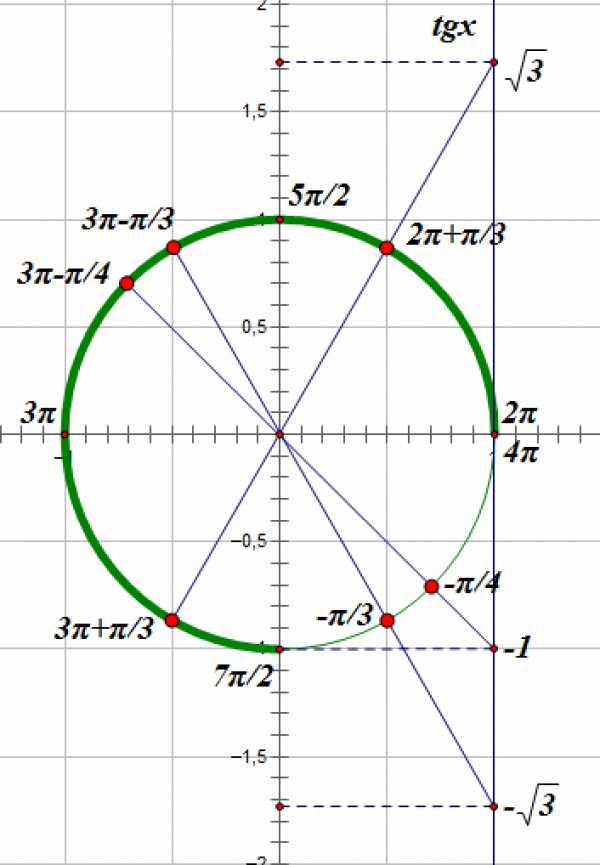
Получим значения , принадлежащие указанному промежутку:
Ответ: а)
б)
И.В. Фельдман, репетитор по математике
Инна | Отзывов (6)
Сайт репетитора по математике Фельдман Инны Владимировны. Профессиональные услуги репетитора по математике в Москве. Подготовка к ГИА и ЕГЭ, помощь отстающим. 2014-11-2020 Ноя 2014
ВИДЕОЛЕКЦИИВИДЕОТЕКАУРАВНЕНИЯ И НЕРАВЕНСТВА С МОДУЛЕМ
Видеотека. Построение графиков функций, содержащих модуль
1. Видеолекция. Построение графиков функций, содержащих модуль Далее
Инна | Отзывов (2)
Сайт репетитора по математике Фельдман Инны Владимировны. Профессиональные услуги репетитора по математике в Москве. Подготовка к ГИА и ЕГЭ, помощь отстающим. 2014-11-2020 Ноя 2014
ВИДЕОТЕКАВИДЕОУРОКИУРАВНЕНИЯ И НЕРАВЕНСТВА С МОДУЛЕМ
Видеотека. Решение уравнений и неравенств с модулем
1. Видеолекция. Решение уравнений и неравенств с модулем. Далее
Инна | Отзывов нет
Сайт репетитора по математике Фельдман Инны Владимировны. Профессиональные услуги репетитора по математике в Москве. Подготовка к ГИА и ЕГЭ, помощь отстающим. 2014-11-20ВИДЕОТЕКАВИДЕОУРОКИУРАВНЕНИЯ И НЕРАВЕНСТВА С МОДУЛЕМ
Видеотека. Решение простейших уравнений с модулем.
Инна | Отзывов нет
Сайт репетитора по математике Фельдман Инны Владимировны. Профессиональные услуги репетитора по математике в Москве. Подготовка к ГИА и ЕГЭ, помощь отстающим. 2014-04-1414 Апр 2014
13 Задание (2016) (C1)ТРИГОНОМЕТРИЯУРАВНЕНИЯ И НЕРАВЕНСТВА С МОДУЛЕМ
Тригонометрическое уравнение с модулем
Решим тригонометрическое уравнение с модулем:
Так как уравнение содержит модуль, нам нужно этот модуль раскрыть по определению модуля.
Рассмотри два случая: Далее
Инна | Отзывов (5)
Сайт репетитора по математике Фельдман Инны Владимировны. Профессиональные услуги репетитора по математике в Москве. Подготовка к ГИА и ЕГЭ, помощь отстающим. 2014-03-3131 Мар 2014
15 Задание (2016) (C3)РАЦИОНАЛЬНЫЕ УРАВНЕНИЯ, НЕРАВЕНСТВА И СИСТЕМЫУРАВНЕНИЯ И НЕРАВЕНСТВА С МОДУЛЕМ
Решение системы неравенств с модулем
Решим систему неравенств с модулем из варианта №50 А. Ларина.
Далее
Инна | Отзывов (2)
Сайт репетитора по математике Фельдман Инны Владимировны. Профессиональные услуги репетитора по математике в Москве. Подготовка к ГИА и ЕГЭ, помощь отстающим. 2012-11-1919 Ноя 2012
ВИДЕОЛЕКЦИИУРАВНЕНИЯ И НЕРАВЕНСТВА С МОДУЛЕМ
Видеолекция 10. Комбинированные методы решения уравнений и неравенств с модулем
Содержание видеолекции:
1. Как правильно раскрывать модуль с учетом ОДЗ.
2. Решение уравнения
3. Как правильно учитывать условие существования корней при раскрытии модуля.
Далее
Инна | Отзывов нет
Сайт репетитора по математике Фельдман Инны Владимировны. Профессиональные услуги репетитора по математике в Москве. Подготовка к ГИА и ЕГЭ, помощь отстающим. 2012-10-1717 Окт 2012
18 Задание (2015) (C6)ВИДЕОЛЕКЦИИЗАДАЧИ С ПАРАМЕТРОМУРАВНЕНИЯ И НЕРАВЕНСТВА С МОДУЛЕМ
Видеолекция 7. «Графический метод решения задач с параметрами»
В видеолекции подробно разобрано 7 примеров задач с параметрами, начиная с очень простых и заканчивая реальными заданиями С5 из ЕГЭ. Далее
Инна | Отзывов нет
Сайт репетитора по математике Фельдман Инны Владимировны. Профессиональные услуги репетитора по математике в Москве. Подготовка к ГИА и ЕГЭ, помощь отстающим. 2012-10-1717 Окт 2012
18 Задание (2015) (C6)ВИДЕОЛЕКЦИИЗАДАЧИ С ПАРАМЕТРОМУРАВНЕНИЯ И НЕРАВЕНСТВА С МОДУЛЕМ
Видеолекция «Графический метод решения задач с параметрами»
В видеолекции «Графический метод решения задач с параметрами» подробно разобрано 7 примеров задач с параметрами, начиная с очень простых и заканчивая реальными задачами из Задания 18 ЕГЭ по математике. Далее
Инна | Отзывов нет
09 Сен 2012
ВИДЕОЛЕКЦИИОНЛАЙН КУРСЫУРАВНЕНИЯ И НЕРАВЕНСТВА С МОДУЛЕМФУНКЦИИ И ГРАФИКИ
Видеолекция «Построение графика функции, содержащей модуль»
Содержание Видеолекции «Построение графика функции, содержащей модуль»:
1. График функции y=|x|.
2. Построение графика функции y=|x+3|+|2x+1|-x с помощью раскрытия модуля.
3. Построение графика функции y=|x+3|+|2x+1|-x по четырем точкам. Далее
Инна | Отзывов (62)
ege-ok.ru
Неравенство с несколькими модулями | Подготовка к ЕГЭ по математике
«Неравенство с двумя модулями. Часть I» смотрим здесь.
Решим неравенство
Правило раскрытия модуля говорит, что раскрытие модуля зависит от того, какой знак имеет подмодульное выражение. Стало быть, нас будут интересовать нули подмодульных выражений, – смена знака подмодульного выражения возможна только в них.
В нашем случае нуль первого модуля – это 4, нули второго подмодульного выражения – это -3 и 2.
Вся числовая ось указанными точками разбивается на 4 промежутка. Нам предстоит поработать с неравенством в каждом из них.
Если у вас возник вопрос, почему, например, в крайнем левом промежутке у нас число -3 не включено, а на следующем включено (аналогично с другими), – ответим на него. На самом деле, – все равно, куда именно вы включите концы промежутков. Лишь бы при склейке все промежутки давали бы нам всю числовую прямую, если мы работаем на R.
Выясним, как распределяются знаки подмодульных выражений на каждом из промежутков.
Начнем с первого подмодульного выражения. Очевидно, что при знак выражения – минус, то есть , а при .
«Переключателями» же знака второго подмодульного выражения из неравенства являются точки -3 и 2. Если , то при остальных имеем: . Если вам не кажутся очевидными знаки этого подмодульного выражения на указанных промежутках, загляните сюда (метод интервалов).
Мы замечаем, что на двух промежутках (первом и третьем слева) знаки подмодульных выражений распределены одинаково.
Итак, первый случай:
Предстоит решить систему (мы объединили первый и третий промежутки в совокупность):
Во второй строке системы приводим подобные слагаемые и раскладываем на множители:
Теперь переходим на ось, пересекаем два множества между собой:
.
Второй случай:
.
Третий случай:
.
Нам осталось объединить решения каждого из случаев между собой:
Ответ:
Для тренировки предлагаю Вам решить следующее неравенство:
Ответ: + показать
egemaximum.ru
Презентация «Неравенства с модулем»
Презентация «Неравенства с модулем» может быть использована в 9-11 классах при изучении нового материала, при повторении, закреплении, подготовке к ЕГЭ. Можно использовать при организации дистанционного обучения. В презентауии имеются задания для самостоятельного решения с ответами и указанием способа решения.
Просмотр содержимого документа
«Презентация «Неравенства с модулем»»
Неравенства с модулем
Способы решения неравенств с модулями:
- 1. По определению модуля
- 2. Возведение обоих частей неравенства в квадрат
- 3. Замена переменной
- 4. Раскрытие модуля на промежутке знакопостоянства
- 5. Равносильность неравенств системам
- 6. Важный частный случай
а -a a a -a |3 x -1|-7x -1 -6x -2x Ответ: «
1.По определению модуля
| f ( x ) | а
| f ( x ) | а
-a
a
a
-a
|3 x -1|
-7x -1
-6x
-2x
Ответ:
| x 2 — x | ( x 2 -1) 2 ( x 2 — x ) 2 — равносильность не нарушена ( x 2 -1+ x 2 — x )( x 2 -1- x 2 + x ) 0 – разность квадратов (2 x 2 — x -1)( x -1) 0 + — + 1 «
2.Возведение обеих частей в квадрат
| x 2 -1| | x 2 — x |
( x 2 -1) 2 ( x 2 — x ) 2 — равносильность не нарушена
( x 2 -1+ x 2 — x )( x 2 -1- x 2 + x ) 0 – разность квадратов
(2 x 2 — x -1)( x -1) 0
+
—
+
1
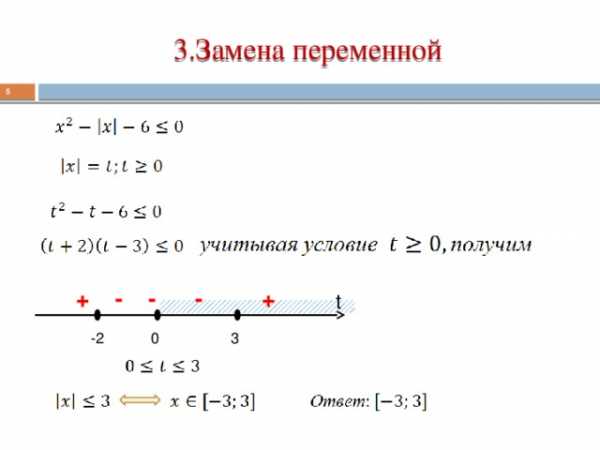
3.Замена переменной
+ — — — +
t
3
-2
0
3 Нули подмодульных выражений: x =1 и x =2 1 2 + x -1 + — + + 2- x — 2 3 0 1 «
4. Раскрытие модуля на промежутках знакопостоянства
| x -1| + |2- x | 3 Нули подмодульных выражений: x =1 и x =2
1
2
+
x -1
+
—
+
+
2- x
—
2
3
0
1
5. Равносильность неравенств системам или их совокупности
См. решение по определению
Неравенство равносильно двум неравенствам:
Равносильно неравенству:
Можно записать в виде системы
Можно записать в виде совокупности
5. Равносильность неравенств системам (примеры)
№ 2
№ 1
0 в ОДЗ возведем в квадрат, обе части для преобразования используем разность квадратов Учитывая ОДЗ, получим: «
6. Один частный случай
умножим на | x +2|0 в ОДЗ
возведем в квадрат, обе части
для преобразования используем разность квадратов
Учитывая ОДЗ, получим:
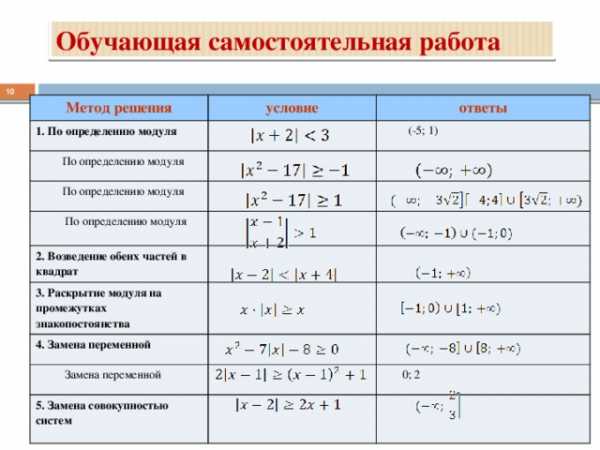
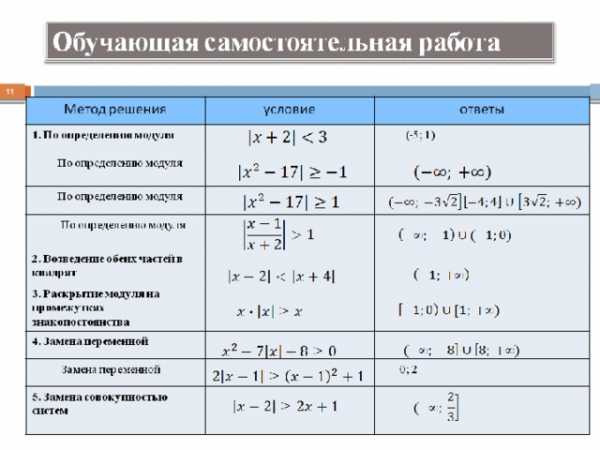
Обучающая самостоятельная работа
Метод решения
условие
1. По определению модуля
По определению модуля
ответы
По определению модуля
(-5; 1)
По определению модуля
2. Возведение обеих частей в квадрат
3. Раскрытие модуля на промежутках знакопостоянства
4. Замена переменной
Замена переменной
5. Замена совокупностью систем
0; 2
multiurok.ru
Система неравенств с модулем. Задание С3
Решим задачу из Задания С3 для подготовки к ЕГЭ по математике:
Решите систему неравенств:
Как обычно, решим каждое неравенство системы по отдельности.
Начнем с первого неравенства исходной системы:
1. Умножим обе части неравенства на — это выражение всегда больше нуля, поэтому знак неравенства не меняется:
2. Возьмем от обеих частей неравенства логарифм по основанию 2 (основание больше 1, поэтому знак неравенства не меняется):
Так как , перепишем неравенствов таком виде:
Первый множитель , следовательно,
Отсюда:
Итак, решение первого неравенства .
Решим второе неравенство исходной системы:
Неравенство вида равносильно системе:
Запишем систему, равносильную нашем неравенству:
Решим каждое неравенство системы:
Перенесем все влево:
Умножим обе части на 2:
Дискриминант квадратного трехчлена, стоящего в левой части неравенства меньше нуля, следовательно неравенство верно при любом
Рассмотрим второе неравенство:
Корни квадратного трехчлена
:
Итак, решение второго неравенства исходной системы:
Совместим решения первого и второго неравенства на одной координатной прямой. Для этого нам надо выяснить расположение точек.
Очевидно, что
Сравним числа и :
Итак, совмещаем решения обоих неравенств системы на одной координатной прямой:
Ответ: [ ]
И.В. Фельдман, репетитор по математике.
ege-ok.ru
«Решение уравнений и неравенств с модулем». Видеолекция 1
ВИДЕОЛЕКЦИИУРАВНЕНИЯ И НЕРАВЕНСТВА С МОДУЛЕМ
Содержание Видеолекции 1:
1. Определение понятия «модуль».
2. Геометрический смысл модуля.
3. Противоположные числа.
4. Уравнение |x|=a.
5. Полезные примеры: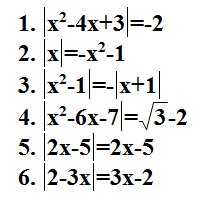
6. Неравенство |x|<a.
7. Полезные примеры:
8. Неравенство |x|>a.
9. Полезные примеры: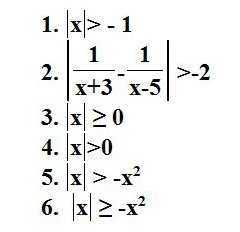
10. Решение уравнения ||=1.
11. Видеорешение уравнения .
12. Видеорешение неравенства .
13. Видеорешение неравенства .
Фрагмент видеолекции:
Получить ссылку на просмотр видеолекции.
И.В. Фельдман, репетитор по математике.
Вернуться на страницу ВИДЕОЛЕКЦИИ
ege-ok.ru