Свойства декартова произведения множеств – . . —

Декартово произведение множеств — ПриМат

Декартовым (или прямым) произведением множеств $A$ и $B$ называется такое результирующее множество пар вида $(x,y)$, построенных таким образом, что первый элемент из множества $A$, а второй элемент пары —  из множества $B$. Общепринятое обозначение:

$ A\times B = \{(x,y)|x \in A, y \in B \}$

Произведения трёх и более множеств можно построить следующим образом:

$ A\times B\times C = \{(x,y,z)|x \in A, y \in B, z \in C \}$

Произведения вида $  A\times A, A\times A\times A, A\times A\times A\times A$ и т.д. принято записывать в виде степени: $A^2, A^3, A^4$ (основание степени — множество-множитель, показатель — количество произведений). Читают такую запись как «декартов квадрат» (куб и т.д.). Существуют и другие варианты чтения для основных множеств. К примеру, $  \mathbb{R}^n$ принято читать как «эр энное».

Рассмотрим несколько свойств декартова произведения:

1. Если $A, B$ — конечные множества, то $A\times B$ — конечное. И наоборот, если одно из множеств-сомножителей бесконечное, то и результат их произведения — бесконечное множество.
2. Количество элементов в декартовом произведении равно произведению чисел элементов множеств-сомножителей (в случае их конечности, разумеется): $|A\times B| = |A| \cdot |B|$.
3. $A^{np} \ne (A^n)^p$ — в первом случае целесообразно рассмотреть результат декартова произведения как матрицу размеров $1\times np$, во втором же — как матрицу размеров $n\times p$.
4. Коммутативный закон не выполняется, т.к. пары элементов результата декартова произведения упорядочены: $A\times B \ne B\times A$.
5. Ассоциативный закон не выполняется: $(A\times B)\times C \ne A\times (B\times C)$.
6. Имеет место дистрибутивность относительно основных операциях на множествах: $(A * B)\times C = (A\times C) * (B\times C), * \in \{\cap, \cup, \backslash \}$

1. Положим $ A = \{1,2\}, B = \{3, 4\}$. Тогда результат декартова произведения можно записать так: $  A\times B = \{(1,3), (1,4), (2,3), (2,4)\}$, а $  B\times A = \{(3,1), (3,2), (4,1), (4,2)\}$
2. Если в предыдущем примере положить $B=A$, очевидно, что $  A\times B = B\times A = \{(1,3), (1,4), (2,3), (2,4)\}$
3. Возьмём $  A = \{x \in \mathbb{R}|0\leq x \leq 5\}, B = \{x \in \mathbb{R}|5\leq x \leq 10\}$. Тогда $  A\times B = \{(x,y) \in \mathbb{R}^2|0\leq x \leq 5 \wedge 5\leq x \leq 10\}$
4. Множества декартова произведения могут и не быть привычными числовыми множествами: $A = \{\circ, \diamond\}, B = \{2,8\}, A\times B = \{(\circ,2),(\circ,8),(\diamond,2),(\diamond,8)\}$

5. Спойлер

   
   Множество точек некой функции $f(x)$ можно отождествить как подмножество множества $\mathbb{R}^2$: $F = \{(x,y)\in \mathbb{R}^2 | f(x) = y\}$

   [свернуть]

6. Спойлер

   
   Множество клеток игрового поля «Морского боя» можно представить в виде декартова произведения множеств $A = \{1,2,3,4,5,6,7,8\}, B =\{A,B,C,D,E,F,G,H\}$

   [свернуть]

С помощью декартова произведения множеств определяется понятие бинарного отношения. Кроме этого, декартово произведение используется очень часто для обозначения множества числовых наборов, особенно в математическом анализе.

Часто говорят, например, что некая функция $f$ действует следующим образом: $f:\mathbb{R}^n\rightarrow\mathbb{R}$ (числовая функция $n$ переменных).

1. Белозёров Г.С. Конспект по алгебре и геометрии.
2. Ануфриенко С.А. — Введение в теорию множеств и комбинаторику. Екатеринбург: Уральский государственный университет им. А.М. Горького, 1998 (стр. 11-13).

Декартово произведение множеств

Лимит времени: 0

Информация

Тест предназначен для проверки знаний по теме «Декартово произведение множеств».

Вы уже проходили тест ранее. Вы не можете запустить его снова.

Тест загружается…

Вы должны войти или зарегистрироваться для того, чтобы начать тест.

Вы должны закончить следующие тесты, чтобы начать этот:

1. С ответом
2. С отметкой о просмотре

1. Задание 1 из 6

   Какая из представленных записей является правильной записью определения декартова произведения множеств?

   Правильно
   

   Неправильно
   

2. Задание 2 из 6

   Выберите два правильно построенных декартова произведения.

   • $A=\{0, 1\}, B=\{a, b\}, A\times B = \{(0,a), (0, b), (1, a),$ $(1, b)\}$
   • $A=\{2,3\}, B=\{\oplus , \ominus \}, C = \{\alpha, \beta \}, A \times B \times C =$ $\{(2, \oplus, \alpha), (2, \oplus, \beta), (2, \ominus, \alpha), (2, \ominus, \beta),(3, \oplus, \alpha),$ $(3, \oplus, \beta), (3, \ominus, \alpha), (3, \ominus, \beta) \}$
   • $A=\{f, g\} B = \{f\}, A\times B = \{(f, f), (f, g), (g, f), (g, g)\}$
   • $A=\{2,3\}, B=\{\oplus , \ominus \}, C = \{\alpha, \beta \}, A \times B \times C =$ $\{(2, \oplus, \alpha), (2, \oplus, \beta), (2, \ominus, \alpha), (3, \ominus, \beta),(3, \oplus, \alpha),$ $(3, \oplus, \beta), (3, \ominus, \alpha) \}$

   Правильно
   

   Неправильно
   

3. Задание 3 из 6

   Выберите правильное утверждение.
   $A,B,C$ — произвольные непустые множества.

   Правильно
   

   Неправильно
   

4. Задание 4 из 6

   Выберите те пары, которые принадлежат произведению $A\times B$, где $A=\{x \in \mathbb{N} | 1 \le x \le 10\}$, а $B=\{x \in \mathbb{R} | x^2 > 9\}$

   • $(3, 3.101), (9, 4), (1, -4)$
   • $(8, -7), (5, 14), (2, -12)$
   • $(4, -7), (5, -2.84), (7, -14)$
   • $(11, -7), (3, 9), (1, -17)$

   Правильно
   

   Неправильно
   

5. Задание 5 из 6

   Запишите хотя бы одну пару, принадлежащую $A\times B$.
   Пример ввода: (2,3)
   $A = \{0, 3\}, B = \{-1, 1\}$

   Правильно
   

   Неправильно
   

6. Задание 6 из 6

   Отсортируйте произведения по количеству элементов в результирующих множествах (от большего к меньшему).

   • $A\times B$, причём $A = \mathbb{N}$, а $B = \{-3, 3, 18\}$

   • $A\times B$, причём $A = \{1, 9, 33\}$, а $B = \{-0.35, -0.45, -0.55\}$

   • $A\times B$, причём $A = \{9, 81\}$, а $B = \{7, 49\}$

   • $A\times B$, причём $A = \{1, 2\}$, а $B = \{ \oplus \}$

   Правильно
   

   Неправильно
   

Поделиться ссылкой:

Похожее

ib.mazurok.com

Декартово произведение множеств, его свойства. Понятие кортежа. Примеры заданий из начального курса математики, связанных с образованием декартова произведения множеств.

Декартово произведение множеств.

В начальных классах ученики решают задачу: используя цифры 1,2,3 образовать всевозможные двузначные числа.

Путем перебора дети получают
11 12 13
21 22 23
31 32 33

Запись каждого числа состоит из двух цифр, причем существенен порядок их следования. Например, из цифр 1, 2 образованы числа 12 и 21.
В том случае, когда важен порядок следования элементов множества, в математике говорят об упорядоченных наборах элементов. В данной задаче – упорядоченные пары (a;b) образованные из элементов a и b. Это (1;2), (1;3), (1;4) и тд. Первый элемент аназывают первой координатой пары, элемент b – второй.
Значит в нашей задаче мы оперировали множеством A={1,2,3} и образовали всевозможные пары.
Рассмотрим другой пример. Пусть А={1,2,3}, B={4,5}. Образуем всевозможные пары (a;b) так, что a A, b  B. Получим некоторое новое множество { (1;5), (1;4), (2;4), (2;5), (3;4), (3;5)}, элементами которого являются упорядоченные пары чисел. Это новое множество называют декартовым произведением множеств A и B.
Декартовым произведением множеств А и В называется множество пар, первая компонента которых принадлежит множеству А, вторая множеству В. Обозначают А  В. Таким образом А В ={(х;у) |х  А, у  В}
Операцию нахождения декартового произведения множеств А и В называют

декартовым умножениемэтих множеств.

Рассмотрим следующий пример. Известно, что А В= {(2;3),(2;5), (2;6), (3;3), (3;5), (3;6)}.Установим, из каких элементов состоят множества А и В. Так как первая компонента пары декартового произведения принадлежит множеству А, вторая множеству В, то данные множества имеют следующий вид А={2,3}, В={3,5,6}.
Перечислим элементы принадлежащие множеству А В, если А={a,b,c,d}, В=А. Декартово произведение А В={(a,a), (a,b), (a,c), (a,d), (b,a), (b,b), (b,c), (b,d), (c,a), (c,b), (c,c), (c,d), (d,a), (d,b), (d,c), (d,d)}

Количество пар в декартовом произведении А В будет равно произведению числа элементов множества А и числа элементов множества В: n(A B)=n(A) n(B).

В математике рассматривают не только упорядоченные пары, но и наборы из трех, четырех и тд. элементов.

Такие упорядоченные наборы называют кортежами.Так, набор (1,5,6) есть кортеж длины 3, т.к в нем три элемента. Используя понятие кортежа, можно определить понятие декартового произведения n множеств.

Декартовым произведением множеств А1, А2….Аn называют множество кортежей длины n, образованных так, что первая компонента принадлежит множеству А1, вторая А2, n-ая множеству А: А1 А2 …. Аn.

Пусть даны множества А1 ={2,3} ; А2={3,4,5}; А3={7,8}. Декартово произведение А1 А2 А3 ={(2,3,7), (2,3,8), (2,4,7), (2,4,8),(2,5,7),(2,5,8),(3,3,7),(3,4,7),(3,3,8),(3,4,8),(3,5,7),(3,5,8)}

Примеры из начального курса математики.
Например: построй четырехугольник ABCD по координатам его вершин. Если возможно, проведи его оси симметрии. А(0;1), В(2;5), С(6;5) и D(8;1).

Для изображения декартового произведения нечисловых множеств используется таблица. Например: «Фабрика верхнего трикотажа изготавливает мужские пуловеры, женские костюмы, кофты, платья следующих расцветок: бордовая, синяя, голубая,зеленая, коричневая, серая. Составьте таблицу, иллюстрирующую каких цветов могут быть данные изделия».

5.Особенности математический понятий. Объем и содержание понятий. Отношение между понятиями. Остенсивные и контекстуальные определения понятий, их отличие от определений через род и видовое отличие.

Термин понятие соединяет в себе целый класс объектов или отношений произвольной природы, обладающий определенным характеристическим свойством или целым набором таких свойств.

Например понятие четырехугольник обозначает класс всевозможных многоугольников, обладающих свойствами: иметь четыре стороны; иметь четыре вершины; иметь; иметь четыре угла. Понятия условимся обозначать строчными буквами латинского алфавита: a b c

Понятия, изучаемые в начальном курсе математики, представляют в виде четырех групп:

Понятия, связанные с числами и операциями над ними: число, сложение, слагаемое, меньше и др.

Выражение, равенство, уравнение

Геометрические понятия: прямая, отрезок, треугольник

Понятия, связанные с величинами и их измерениями.

Особенности математических понятий: 1)математические объекты, о которых необходимо составить понятия, в реальности не существуют, а существуют лишь в мышлении человека и в тех знаках и символах, которые образуют математический язык

2)в математике рассматриваются не только понятия, появившиеся при изучении реальных предметов, но и понятия, возникшие на основе первых ( например, понятие переменной является абстракцией конкретных переменных величин, т.е. абстракцией от абстракции).

Объем и содержание понятия.

Всякий математический объект обладает определенными свойствами. Например, квадрат имеет четыре стороны, четыре прямых угла и др. Различают свойства существенные и несущественные.

Существенное свойство- свойство, без которого объект не может существовать.

Несущественное свойство- свойство, отсутствие которого не влияет на существование объекта.

Совокупность всех существенных свойств объекта называют содержанием понятия.

Когда говорят о математическом объекте, имеют в виду всю совокупность объектов, обозначаемых одним термином.

Совокупность всех объектов, обозначенное одним термином, составляет объем понятия.

Например, содержание понятия «квадрат»- это совокупность всех существенных свойств, которыми обладают квадраты, а в объем этого понятия входят квадраты различных размеров.

Итак, любое понятие характеризуется:

-термином( название)

-объемом( совокупность всех объектов, называемых этим термином)

-содержанием( совокупность всех существенных свойств объектов, входящих в объем понятия).

Между объектом понятия и его содержанием существует связь: чем «больше» объем понятия, тем « меньше» его содержание, и наоборот. Объем понятия « треугольник» « больше», чем объем понятия « прямоугольный треугольник», так как все объекты второго понятия являются и объектами первого понятия. Содержание понятия «треугольник» « меньше», чем содержание понятия «прямоугольный треугольник», так как прямоугольный треугольник обладает всеми свойствами любого треугольника и еще другими свойствами, присущими только ему.

Отношения между понятиями.

Определив объем понятия, можно рассмотреть, какие отношения могут существовать между различными их типами.

Отношение эквивалентности существует тогда и только тогда, когда объемы сравниваемых понятий полностью совпадают. Это означает, что отличительные и существенные признаки, присущие сравниваемым понятиям, принадлежат всем элементам множеств, составляющих их объемы. Так, понятия эквивалентности характеризует отношение между классами равносторонних и равноугольных треугольников, равноугольных ромбов и квадратов, понятий, все они принадлежат к одному классу элементов, т.е. имеют тот же самый объем. Обратите внимание на то, что все перечисленные понятия оказываются эквивалентными только по объему, содержание же их различию. Так, признаки « иметь равные стороны» или « обладать равными углами» отличаются друг от друга по смыслу.

Отношение перекрещивания (частичного совпадения) объемов понятий существует тогда и только тогда, когда часть объема одного понятия входит в объем другого, и в свою очередь часть объема второго понятия входит в объем первого. Таковы отношения между объемами понятий «студенты» и «спортсмены», «студенты» и «филателисты», ибо ясно, что не все студенты являются спортсменами или филателистами. Обычно для наглядного изображения отношений между объемами понятий употребляются диаграммы Эйлера, в которых объем понятий представляются кругом. Поскольку у эквивалентных понятий объемы совпадают, то отношение между ними изображается одним кругом. В случае частичного совпадения объемов отношение изображается пересечением двух кругов. Если обозначить объем одного понятия через A , другого через В, то графически отношения эквивалентности (Рис.1) и перекрещивания (Рис.2) можно представить соответствующими диаграммами.

Отношение субординации (подчинение объемов) понятий существует тогда и только тогда, когда объем одного понятия полностью входит в объем второго. Понятие меньше объема составляет часть, или, точнее, вид понятия с большим объемом, который по отношению к нему называют родом. На диаграмме Эйлера (рис.3) это отношение изображается включением меньшего круга в больший.
Все перечисленные выше отношения имеют место между совместными понятиями, объемы которых либо совпадают, либо перекрещиваются, либо составляют часть другого.

Несравнимые («неположенные») понятия – это понятия, объемы которых либо полностью исключают друг друга, либо находятся в отношении противоречия друг другу . Так объемы понятий «треугольник» и «растение» не содержит ни одного общего элемента, их пересечение – пусто. То же самое можно сказать о понятиях которые употребляются в хорошо известном утверждении, характеризующем несравнимость: «в огороде бузина, а в Киеве дядька». Особый интерес представляют понятия, объемы которых находится в отношении контрарности (противности) друг другу, как, например, «белый» и «черный», «холодный» и «горячий» «длинный» «короткий» и т.д, которые представляют собой свойства, расположенный на границе соответствующих множеств, свойств. Между «белым» и «черным» «холодным» и «горячим» и т.д располагаются промежуточные свойства. В силу этого объемы контрарных понятий занимают крайние положения на круговых диаграммах (рис.4).

Отношение контрадикторности (противоречивость) между объемами понятий существует тогда , когда они, с одной стороны, отрицают друг друга, а с другой стороны исчерпывают объем целого понятия (рис.5).
В языке противоречий выражается отрицательной частицей перед словом, выражающем свойство. Примерами могут служить свойства, выражающие такие понятий, как белый и не белый, холодный не холодный, черный и не черный и т.д. На диаграмме (рис.5) объемы таких понятий составляют две половины круга, хотя гораздо лучше представить объем положительного понятия кругом, а отрицательного – прямоугольником, в который входит этот круг, поскольку противоположное (отрицательное) понятие содержит обычно больше число элементов (рис.6).

Поскольку объемы понятий образуют классы (или множества) предметов, элементы которых обладают признаками, сформулированными в их содержании, то над этими классами (или множествами) можно производит определенные логические операции. Они тождественны операциям, которые изучаются в теории множеств.
Объединением классов (или множеств) называют класс, который содержит в своём составе те элементы, входящие в каждый отдельный класс. Если обозначить отдельные классы через , то объединенные множества можно представить как дизъюнкцию (или логическое сложение) всех перечисленных классов (или множеств):

Например, объединение плоских фигур будет состоять из класса треугольников, классы четырехугольников, окружностей и других фигур, класс деревьев – из классов хвойных, лиственных и др. деревьев.
Пересечение (или умножение) классов называется новый класс, который содержит в своём составе те и только те элементы, которые входят в каждый из отдельных классов. Иначе говоря, он содержит элементы, общие всем отдельным классам. Поэтому сама операция пересечения классов иногда называется взятием их общей части. Обозначив отдельные классы через , их пересечение можно представить в виде , где знак л обозначает операцию пересечения, умножения или конъюнкции классов.

Остенсивные и контекстуальные определения понятий, их отличие от определений через род и видовое отличие.

Контекстуальное (от лат. Contextus-«соединение», «связь») определение характеризуется тем, что она позволяет выяснить суть, значение слова, смысла которого мы не знаем, через контекст, т.е. через относительно законченный отрывок информации, которое сопровождает данное слово, относится к нему и содержит его признаки.

Остенсивное определение устанавливает значение термина, прибегая к демонстрации предмета, обозначаемого этим термином. Такие определения применяются при раскрытии сущности предмета чувственного мира, другими словами, предметов, которые доступны, для непосредственного восприятия.

 

studopedia.net

Основные свойства декартова произведения.

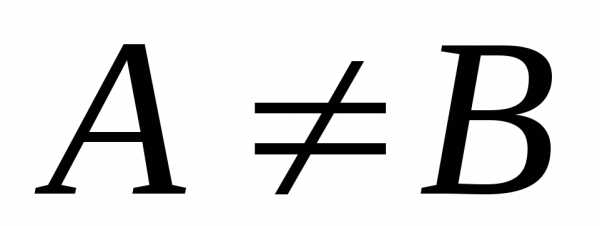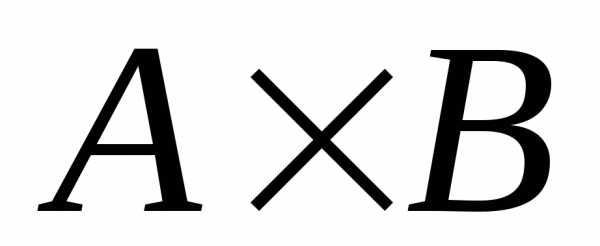
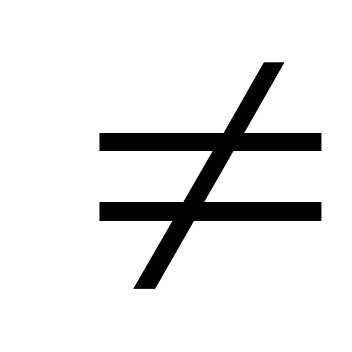
1. Если , то 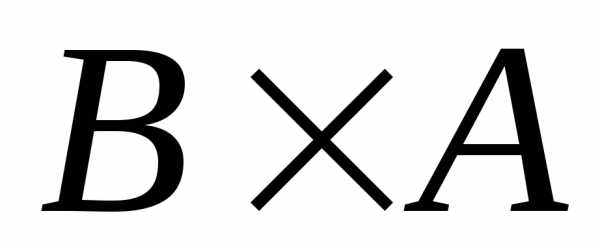. То есть декартово произведение множеств не обладает свойством коммутативности.

Действительно, по определению если то , а . Но так как 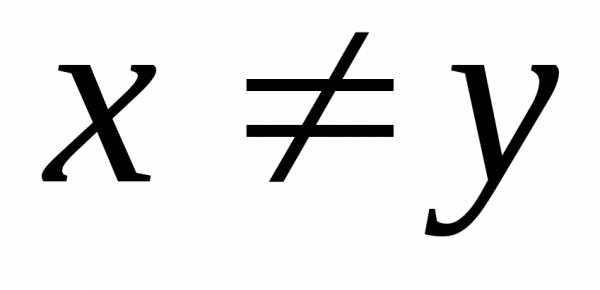, то . Отсюда .

2. Декартово произведение множеств не обладает свойством ассоциативности: для любых множеств .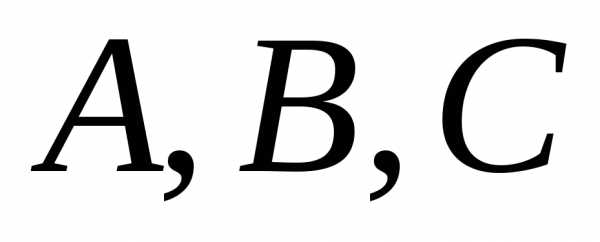

3. Если хотя бы одно из множеств А или В пусто, то и декартово произведение этих множеств есть множество пустое:

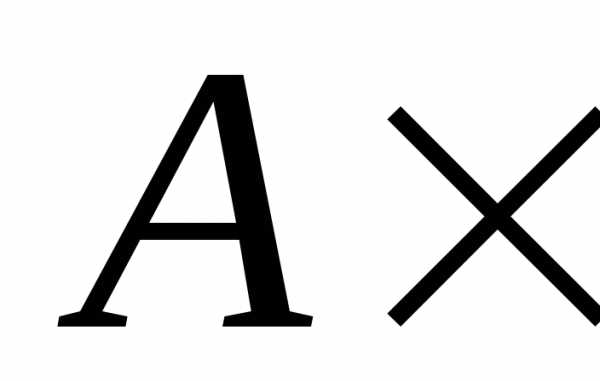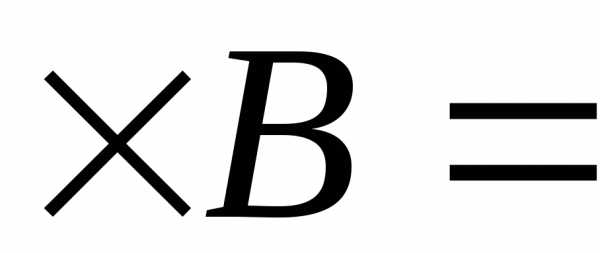Ø= Ø Ø Ø = Ø.

Это свойство следует из понятия декартова произведения и понятия пустого множества.

4. Для любых трех множеств 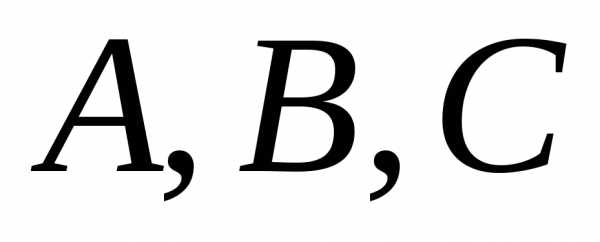справедливы следующие утверждения:

4.1.

4.2.

4.3.

Докажем, например, свойство 4.3.

Обозначим множество , а множество . Покажем, что .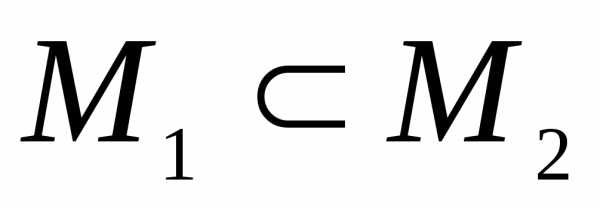

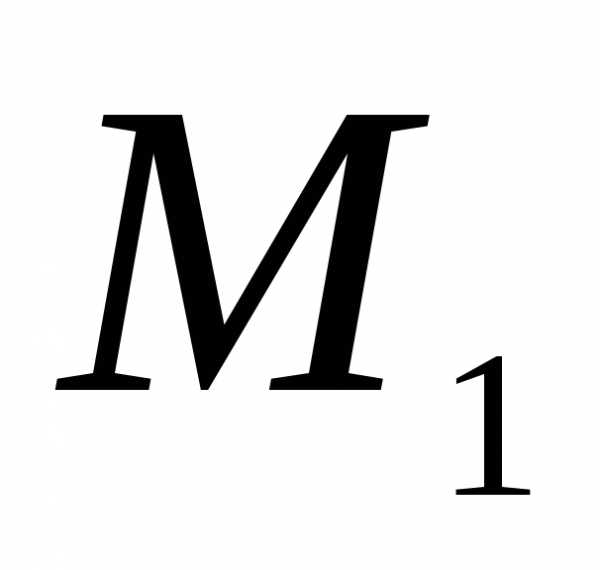Пусть , тогда по определению декартова произведения множеств . По определению разности двух множеств получим: . Так как , то пара . Из того, что следует, что пара . Тогда по определению разности двух множеств пара . В силу доказанного и произвольности выбора элемента во множестве можно сделать вывод о том, что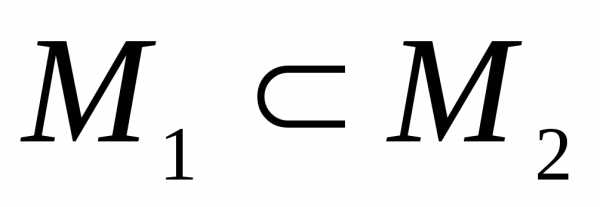

Докажем, что .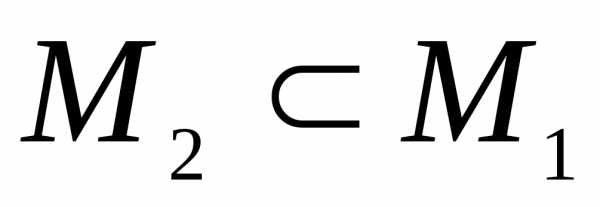

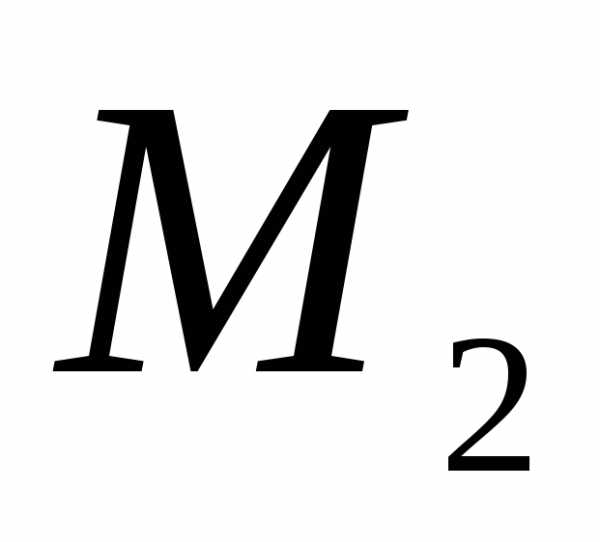Пусть . Тогда по определению разности двух множеств , и . По определению декартова произведения двух множеств . Так как , то . Тогда будем иметь , откуда следует, что . В силу доказанного и произвольности выбора элемента во множестве можно сделать вывод о том, что .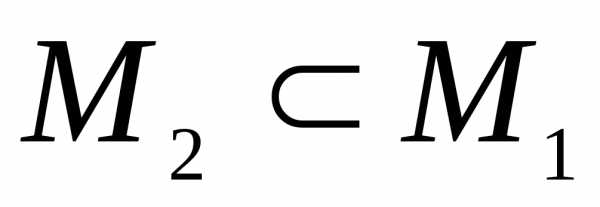

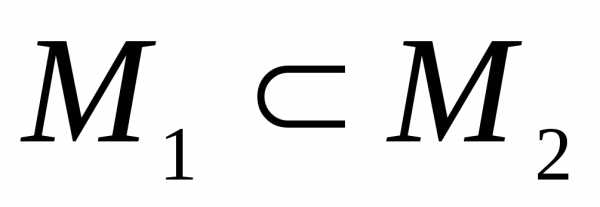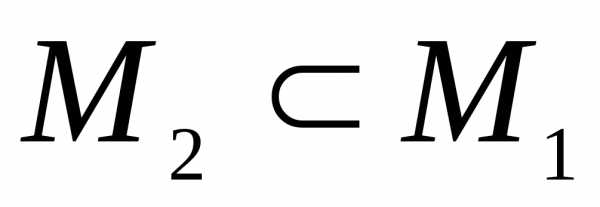Так как и , то 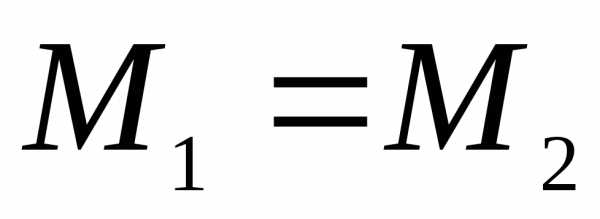, что и требовалось доказать.

Теорема: Число элементов в декартовом произведении двух конечных множеств А и В равно произведению чисел элементов в каждом из них:

.

Раздел II. Элементы комбинаторики

Лекция № 7. АЛГОРИТМЫ И МОДЕЛИ.

Контрольные вопросы:

1. Понятие алгоритма и его свойства.

2. Способы задания алгоритмов.

3. Классификация алгоритмов.

4. Понятия модели и моделирования.

5. Метод математического моделирования. Ос­новные виды математических моделей.

6. Аксиоматический метод и моделирование.

7. Связь с начальным курсом математики.

Литература:

Лекции №№ 8 — 9. ОСНОВЫ КОМБИНАТОРИКИ.

Контрольные вопросы:

1. Понятие о комбинаторной задаче.

2. Правила суммы и произведения.

3. Соединения без повторений и с повторениями.

4. Бином Ньютона и треугольник Паскаля. Число подмножеств конечного множества.

5. Комбинаторные задачи в начальном курсе математики.

Литература: (1) гл. I, § 2 пп. 8-11; (2) гл. I, § 6, с. 142-149; (3) гл. I, § 2 пп.6-8; (4) гл. V, с. 151-155; (5) гл. IV, §§ 4.1 – 4.7.

Комбинаторика – это раздел математики, в котором изучаются вопросы о том, сколько различных комбинаций, удовлетворяющих тем или иным условиям, можно составить из заданных объектов.

Как раздел математики комбинаторика возникла в 16 веке. Ее возникновение и развитие связано с именами ученых Н. Тарталья (1500-1557гг), Б. Паскаля (1623-1662гг), П. Ферма (1601-1665гг). Позднее крупный вклад в развитие комбинаторных методов был сделан Г. Лейбницем (1646-1716гг), я. Бернулли (1654-1705 гг), л. Эйлером (1707-1783гг).

Решение большинства комбинаторных задач основано на применении двух основных правил: правила суммы и правила произведения.

Задача 1: В вазе лежит 8 слив и 6 абрикосов. Сколькими способами можно выбрать из вазы один плод?

Переведем задачу на язык теории множеств. Имеются 2 множества: . Эти множества не имеют общих элементов: 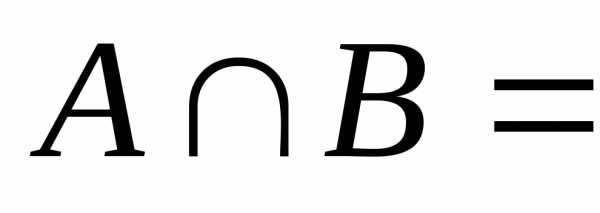Ø. Требуется узнать, сколько существует способов выбора одного элемента, принадлежащего множеству А или множеству В, т.е. объединению этих множеств.

Элемент из множества А можно выбрать 8-ю способами, из множества В – 6-ю способами. А так как эти множества не имеют общих элементов, то выбрать один элемент, принадлежащий А или В можно 8+6 =14 способами.

Таким образом, задача свелась, к нахождению числа элементов в объединении двух непересекающихся множеств: .

Правило суммы: если элемент а можно выбрать n способами, а элемент b – m способами, причем ни один из способов выбора элемента а не совпадает со способом выбора элемента b, то выбор элемета «а либо b» можно осуществить (n+m) cпособами.

Задача 2: В столовой имеется 4 вида первых блюд и 6 видов вторых. Сколькими способами можно выбрать обед, состоящий из одного первого и одного второго блюда?

Решение такого вида задач сводится к подсчету числа упорядоченных пар, когда известно число способов выбрать первую компоненту и вторую компоненту.

Пусть . Множество всех упорядоченных пар элементов, состоящих из элементов множеств А и В, образует декартово произведение этих множеств. Известно, что . Тогда наша задача будет иметь решение: (способа).

Правило произведение: если элемент а можно выбрать n способами, а элемент b – m способами, то пару (а; b) можно выбрать способами.

Правило суммы и произведения легко распространяется на тот случай, когда множеств не два, а «n».

Пусть даны множества Ø . Тогда

Замечание: если множества А и В пересекаются, то

studfiles.net

[Билет 4] Упорядоченные пары. Декартово произведение двух и более множеств, его свойства.

Упорядоченные пары.

Упорядоченной парой называется объект вида (a, b), который состоит из 2 не обязательно разных элементов и в котором определено какой из этих элементов первый, а какой второй. . Декартово произведение двух и более множеств, его свойства.

Декартовым произведением множеств А и В называется множество пар, первая компонента которых принадлежит множеству А, вторая множеству В. Обозначают А x В. Таким образом А x В = {(x;y) | x принадлеж A, y принадлеж B}.

Определение 1.3. Множество всех кортежей длины  на множествах  называют декартовым (прямым) произведением множеств  и обозначают .

Операцию нахождения декартового произведения множеств А и В называют декартовым умножением этих множеств.

Рассмотрим следующий пример. Известно, что А x В={(2, 3), (2, 5), (2, 6), (3, 3), (3, 5), (3, 6)}. Установим, из каких элементов состоят множества А и В. Так как первая компонента пары декартового произведения принадлежит множеству А, а вторая – множеству В, то данные множества имеют следующий вид: А={2, 3}, B={3, 5, 6}.

Перечислим элементы, принадлежащие множеству АxВ, если
А={a, b, c, d}, B=A. Декартово произведение АxВ={(a, a), (a, b), (a, c),
(a, d), (b, a), (b, b), (b, c), (b, d), (c, a), (c, b), (c, c), (c, d), (d, a), (d, b) ,(d, c), (d, d)}.

Свойства

Эти свойства нетрудно доказать методом двух включений. Докажем, например, первое тождество. Если , то  и . Из того, что , следует  или . Если , то , а если , то . Итак,  или , то есть . Следовательно,

fizmatinf.blogspot.com

§ 3. Декартово произведение множеств. Соответствия. Бинарные отношения и их свойства. Отображения.

Рассмотрим следующую реальную ситуацию. Фабрика верхнего трикотажа изготовляет мужские пуловеры, женские костюмы, кофты и платья следующих расцветок: бордо, синяя, голубая, зеленая, коричневая, серая. Обозначим через А множество видов изделий: А={мужской пуловер, женский костюм, кофта, платье}, через В – множество предлагаемых расцветок: В={бордо, синяя, голубая, зеленая, коричневая, серая}. Посмотрим, какие изделия можно получить, учитывая возможные для них расцветки. Для этого составим список всех пар из элементов множества А и элементов множества В таким образом, что сначала будем записывать элемент множества А, затем элемент множества В. получим множество С упорядоченных парэлементов множеств А и В. Возможные изделия можно перечислить с помощью таблицы. Итак, мы имеем дело с особым множеством, составленным из элементов двух данных множеств. Такое произведение называетсядекартовым произведением двух множеств.

А В	мужской пуловер	женский костюм	Кофта	Платье
Бордо	пуловер-бордо	костюм женский – бордо	кофта–бордо	Платье – бордо
Синяя	пуловер — синий
Голубая
Зеленая			кофта – зеленая
Коричневая				Платье – коричневое
Серая		костюм – серый

Опр. 3.1Декартовым (или прямым) произведениеммножества А на множество В называется множество всех упорядоченных пар, в которых первая компонента – элемент множества А, а вторая – элемент множества В. Обозначают АВ.

Таким образом, АВ={(x,y)xA,yB}.

Может случиться , что множества А и В окажутся одинаковыми. Рассмотрим следующий пример. Фабрика «Авторучка» изготовляет отдельно корпус и колпачок авторучек следующих цветов: белый, красный, зеленый, оранжевый.

Обозначим через А – множество цветов корпуса ручки, через В – множество цветов колпачка. Тогда получим: А=В={белый, красный, зеленый, оранжевый}. Можно составить список возможных колоритов для авторучки: цвет корпуса и цвет колпачка.

Объединяя всеми возможными способами цвет из А с цветом из В=А, получим элементы прямого произведения множества А «самого на себя», которое называется прямым илидекартовым квадратоми обозначается: АА=А².

Из этого примера видно, что каждая пара прямого произведения должна быть упорядочена: красная ручка с белым колпачком отличается от белой ручки с красным колпачком.

Для описания прямого произведения множеств бывает удобно использовать «геометрический язык». При этом элементы множества АВ называютсяточками. Например, еслиz=(x,y), тохА называетсяабсциссой, аyВ –ординатой точки z. В связи с этим заметим, что множество точек плоскости по существу являются элементами прямого квадратаRR=R²множестваR действительных чисел.

На рис.11 точками показаны элементы декартова произведения множеств А={1, 2, 3} и В={4, 5, 6, 7}. Отсюда легко видеть способ нахождения общего числа элементов в декартовом произведении двух множеств:

если m(А)=n, m(B)=k, то m(АВ)=nk(5).

Пример 3.1.Применим формулу (5) для подсчета количества двухзначных чисел. Двухзначное число можно принять за упорядоченную пару, где на первом месте может стоять цифра из множества А={1, 2, 3, 4, 5, 6, 7, 8, 9}, а на втором – из множества В={0, 1, 2, 3, 4, 5, 6, 7, 8, 9}, т.е. за элемент прямого произведения этих множеств, тогда получаем:m(А)=9,m(B)=10, тоm(АВ)=910=90. Итак, всего имеется 90 различных двухзначных чисел.

Перейдем к знакомству с другим новым понятием. Рассмотрим два множества: первое (А), состоящее из 11 учащихся, второе (В), состоящее из 9 городов. Чтобы получить прямое произведение этих множеств, надо составить все пары: (ученик – город).

Из множества всех таких пар мы выберем лишь такие, которые «связывают» каждого ученика с тем городом, где он бывал. Очевидно, что «список» таких пар (ученик – известный город) будет являться подмножеством декартова произведения. Такой «список» удобно заменить таблицей, где можно указать все города, в которых побывал каждый ученик:

	Москва	Тула	Одесса	Тамбов	Воронеж	Липецк	Елец	Задонск	Лебедянь
Петя							
Вася							
Коля							
Саша								
Лена							
Таня							
Ирина							
Вера							
Андрей							
Витя								
Катя							

Можно сказать, что данная таблица задает определенное соотношение между элементами множеств А и В.

Опр.3.2 Будем говорить, что между элементами двух множеств А и В установлено соответствие , если в их произведении АВ выделено некоторое подмножество . Если пара (a,b), это означает по определению, что элементы a и b множеств А и В находятся в отношении  (пишется ab).

Еще один пример соответствия: Пусть даны множества А – студентов и В – множество групп. Утверждение “студент aучится в группеb” задает соответствие между множеством студентов и множеством групп. Здесьапробегает множество значений А,b– множество значений В. Такое соотношение называется бинарным соответствием, т.е. соответствием между двумя множествами А и В.

Бинарные соответствия можно задавать таблицами (например, расписание занятий) или ориентированными графами.

	Пн.	Вт.	Ср.
Педагогика
Математика
Физкультура

Рис.12.

Если соответствие  задано между элементами одного и того же множества, то говорят, что между элементами этого множества задано отношение . Итак, задать на множестве А 2-хместное (бинарное) отношение означает выделить в прямом квадрате А² этого множества некоторое подмножество .

Опр.3.3 Бинарным отношением, заданным на множестве А называется всякое подмножество декартова произведения АА.

Местность отношения показывает сколько объектов могут разом находиться в данном отношении. Чаще всего рассматриваются бинарные (двухместные) или тернарные (трехместные) отношения.

Таким образом, бинарные соответствия между XиXназываются бинарными отношениями на множествеX, т.е. соответствиями между элементами одного и того же множества (или равных множеств). Например, отношения: “2>1”, “3=3”, “человек х старше человекаy” и др.

Пример 3.2. Возьмем в качестве элементов множества А случайную группу людей (например, едущих в одном поезде). И выберем бинарное отношение  на этом множестве следующим образом: два человека из А будут находиться в данном отношении, если они родились в одном и том же месяце (под одним знаком зодиака; имеют одинаковые имена и пр.). И еще элемент а₁ из А будет находиться в отношении  с элементом а₂ из того же множества, если, допустим, первый человек выше ростом, чем второй (старше, тяжелее и пр.).

Из этих примеров можно заметить, что если Таня родилась в том же месяце, что и Петя, то же самое можно сказать и о Пете: Петя родился в том же месяце, что и Таня. С учетом введенных обозначений можно записать: если ТаняПетя, то ПетяТаня. Иначе дело обстоит с другим отношением : если Таня ростом выше Пети, то неверно, что и Петя ростом выше Тани.

Таким образом, различные отношения могут иметь и различные свойства. Рассмотрим основные из них.

Опр.3.4 Бинарное отношение (БО) , заданное на множестве А, называется рефлексивным, если любой элемент этого множества находится в данном отношении с самим собой, т.е. аА: аа.

Опр.3.5 БО  называется симметричным, если из того, что пара (a,b) находится в отношении , следует, что и симметричная ей пара (b,a) тоже находится в этом отношении, т.е a,bA: ab ba.

Опр.3.6 БО называется антисимметричным ,если

a,bA: ab  ba  a=b.

Опр.3.7 БО называется транзитивным, если a,b,cA:

ab  bc  ac.

Примерами рефлексивного и транзитивного отношения является отношение равенства, не симметричного – отношения «больше» или «меньше» на множестве действительных чисел.

БИНАРНЫЕ ОТНОШЕНИЯ (ОПРЕДЕЛЕНИЯ)

БО , заданное на Множестве А, является:	Если выполняется Следующее условие:
Рефлексивным Симметричным Антисимметричным Транзитивным	aA aa a,bA ab  ba a,bA ab  ba  a=b a,b,cA ab  bc  ac

Опр.3.8 Бинарное отношение, обладающее свойствами рефлексивности, симметричности и транзитивности, называется отношением эквивалентности (или просто эквивалентностью).

Бинарное отношение  можно задать перечислением всех пар из АА, принадлежащих отношению, указанием характеристического свойства, которым обладают все элементы отношения, а также с помощью так называемогоориентированного графа. Для этого элементы множества А изображают в виде точек и вводят соглашение: еслиxy, то от точкиx проводят стрелку к точкеy. Еслиxх, то начало и конец стрелки совпадают, такую стрелку называют петлей. Выполнив указанные построения, получим фигуру – ориентированный граф. Точки, соединенные стрелками, называются вершинами графа, а сами стрелки – ребрами графа.

Пример 3.3.Пусть на множестве М={2,3,4,5,6} задано отношение —кратности элементов, т.е.xy, еслиxy(x делится наyбез остатка). Построить ориентированный граф данного бинарного отношения.

Решение:Заметим, что по графу (рис. 13) наглядно можно судить о свойствах данного отношения: замкнутые накаждомэлементе круглые стрелочки – признак рефлексивности отношения; единственная стрелка (а не с обеих сторон) у линии, соединяющей один элемент данного множества с другим, говорит о том, что отношение не является симметричным; отсутствие хотя бы у одной пары элементов соединяющих их стрелок указывает на то, что отношение не антисимметрично и т.д.

Рассмотрим еще один частный случай общего понятия “соответствие” – отображение множеств.

Рассмотрим два множества XиY.

Опр 3.9Если каждому элементу xX поставлен в соответствие единственный элементyY, то такое соответствие называется отображением множества Х в множествоY. Т.е., каждому элементу х соответствует только один элементy(рис.14).

Обозначается отображение множеств так: f:XY, здесьf– символ самого отображения.

Пример 3.4Пусть Х – множество студентов в аудитории,Y– множество столов в этой аудитории. Соответствие “студентхсидит за столомy” задает отображение множества Х в множествоY. Это очевидно, так как все студенты сидят за столом, иногда по двое, по трое и т.д., но есть и пустые столы. При таком отображении множества Х в множествоY, элементyYназывается образом элемента xX, а элемент xX называется прообразом элемента yY.

Опр 3.10Если при отображенииfкаждый элемент множестваYявляется образом хотя бы одного элемента из Х, тоfназывают отображением Х наYили сюръективным (рис.15).

Пример 3.5Пусть Х – множество студентов,Y– множество книг. Соответствие “студентуxпринадлежит книгаy” задает сюръективное отображение множества Х на множествоY. Это очевидно, так как каждая книга принадлежит одному или нескольким студентам, а некоторые студенты книг не имеют.

Опр 3.11Если при отображенииfвсе различные элементы множества Х переходят в различные элементы множестваY, то отображениеfназывается инъективным отображением (рис.16).

Пример 3.6Пусть Х – множество студентов,Y– множество стульев. Соответствие “студентхсидит на стулеy” задает инъективное отображение между множествами Х иY. Это очевидно, так как все студенты сидят на стульях, причем каждый на своем, но в аудитории есть и пустые стулья.

Опр 3.12Если при отображенииfкаждому элементуxXпоставлен в соответствие один элементyY, при этом соответствии каждому элементуyYсоответствует единственный элементxX, то такое отображение называется взаимно-однозначным (рис.17).

Пример 3.7Пусть Х – множество студентов,Y– множество зачетных книжек. Соответствие “студентухпринадлежит зачетная книжкаy” задает взаимно-однозначное отображение между множествами Х иY. Это очевидно, так как все студенты имеют зачетные книжки, причем каждый только одну и каждая зачетная книжка принадлежит своему студенту.

Пример 3.8 пусть Х – множество пальто в гардеробе, аY– множество крючков в этом гардеробе. Поставим в соответствие каждому пальто крючок, на котором оно висит. Если каждое пальто висит на крючке (а не лежит на полу), то это соответствие является отображениемXвY. Это отображение инъективно, если ни на одном крючке не висит более 1-го пальто (крючки могут быть пустыми), и сюръективно, если все крючки заняты, но на некоторых крючках висит несколько пальто. Это отображение взаимно-однозначно, если на каждом крючке висит одно и только одно пальто.

Примеры

1. Перечислить и указать на координатной плоскости все элементы декартова произведения множеств А={-2, 1, 3} и В={-1, 0, 2, 5}.

Решение:АВ={(-2,-1), (-2,0), (-2,2), (-2,5), (1,-1), (1,0), (1,2), (1,5), (3,-1), (3,0), (3,2), (3,5)}.

З

Рис. 18

аметим, что точки на координатной плоскости, изображающие элементы декартова произведения ВА, будут симметричны соответствующим точкам из АВ относительно биссектрисы первого и третьего координатных углов.

2. Записать с помощью декартова произведения некоторых множеств фигуры, изображенные на рисунке (рис. 19):

Решение:

1. АВ, где А=(-3, -1], В=[2,6];

2) СD, где С=[3, 7), D=(-, +).

3. Выяснить, какими свойствами обладает бинарное отношение - «отношение больше» на множествеN.

Решение:Для любых натуральных чисел ху, если ху.

1. хх – неверно для всех х, т.е. данное отношение не является рефлексивным;

2. для всякой пары натуральных чисел из ху не следует ух, т.е. БО не является симметричным;

3. для любых х,увыполняется одно из неравенств: ху или ух, т.е. отношениеантисимметрично;

4. если ху, а уz, то справедливо хz, т.е. БОтранзитивно.

Задачи для самостоятельной работы

1. Записать множества А и В, если известно, что АВ={(3;1), (-3;4), (0; 2), (1;3), (0;1), (5;7), (0;0), (5;5)}. Найти АВ, В\А. Изобразить на координатной прямой элементы множества ВА. Сколько элементов содержится в каждом из рассмотренных множеств?

2. На каком множестве задано БО ={(2;3), (3;5), (5;7)}. Что можно сказать о его свойствах?

3. Выберите некоторое множество, задайте на нем БО, постройте для этого отношения ориентированный граф, по графу определите свойства БО.

4. Определить свойства следующих бинарных отношений: 1) - «родство по крови»; 2)- «быть знакомым»; 3) отношение «=» — равенства на множествеR (а также,,).

5. Записать с помощью декартова произведения множества точек координатной плоскости, указанные на рис. 20.

1. Постройте граф отношения, обладающего указанными ниже свойствами:

а) рефлексивность и транзитивность;

б) антисимметричность;

в) рефлексивность, симметричность и транзитивность.

2. Какие отношения эквивалентности можно задать на множестве N(R)? Какими еще свойствами они обладают?

8. Изобразить на координатной плоскости прямое произведение NR.

studfiles.net

§1.2. Декартово произведение множеств, бинарные отношения

Этот параграф будет полезен и при изучении компьютерной математики.

1.2.1. Декартово произведение множеств

Определение 1.2.1.Пусть даны два множества ,и. Образуем множество упорядоченных пар элементов, у которых первый элемент принадлежит, а второй -. Полученное множество называетсядекартовым произведением множеств и_, оно обозначается .

Перечислим некоторые простейшие свойства декартова произведения.

Если , то ;

Отметим, что тогда и только тогда, когда.

1.2.2. Бинарные отношения

Определение 1.2.2.Любое подмножество множестваназываетсябинарным отношением.

Аналогичным образом можно рассматривать декартовы произведения трёх и более множеств. Их подмножества будут называться тернарными и т.п. отношениями.

Изучим понятие бинарного отношения более подробно, так как оно является важным не только для математического анализа, но и для компьютерной математики.

Задавать бинарные соотношения конечных множеств можно, например, с помощью таблиц. Например, пусть . Зададим отношениесвойством: парапринадлежит отношениютогда и только тогда, когда числоделит число. Отношение, таким образом, состоит из пар:

Изобразим это отношение следующим образом. Проведём три прямые, соответствующие трём элементам множества . Проведём шесть перпендикулярных им прямых, соответствующих элементам множества. Отметим жирной точкой те точки пересечения этих прямых, которые соответствуют отношению.(рис.1)

Рис.1 Рис.2 Рис.3

Другой способ задания бинарного отношения – использование стрелок. Элементы иизображаются в виде точек плоскости. Стрелками соединены те и только те элементы, для которых.(рис.2)

Это же бинарное отношение можно задать матрицей, состоящей из 0 и 1. Её строки соответствуют элементам множества , столбцы – элементам множества. Элемент этой матрицы равен 1 тогда и только тогда, когда он стоит на пересечении строки и столбца, соответствующих паре , для которой.

Определение 1. 2.3.Элемент называетсяпроекцией элементана множество. Для произвольного подмножестваегопроекцией на называется множество, состоящее из проекций навсех элементов множества.

Определение 1. 2.4. Сечением множества называется множествоэлементов, для которых. Множество сечений отношенияназываетсяфактормножеством по отношениюи обозначается.

Так как отношения представляют собой множества, к ним можно применить операции, определённые в предыдущем параграфе. Но кроме этих операций есть ещё важные операции композиции и симметризации.

Пусть даны множестваи отношения

Определение 1.2.5.Композиция отношений — это отношениемежду элементами множествитакое, что для всехсечение множествапосовпадает с сечением множествапо подмножеству, т.е..

Если даны две пары отношений, и , причёми, то операция композиции обладает следующим свойством:.

Определение 1. 2.6.Отношение, симметричное к некоторому отношению и обозначаемое, представляет собой подмножество множестваобразованное теми парами, для которых. Еслии, то.

Предположим, что задано некоторое основное множество . Отношениеназываетсяотношением эквивалентности, если оно обладает такими свойствами:

1. Рефлексивностью: всякий элемент эквивалентен самому себе. Иными словами, для любогопара.

2. Симметричностью: для любых двух элементов из того, чтоэквивалентенследует, чтоэквивалентен. Другими словами, если, то. Это означает, что отношениесовпадает со своим обратным,.

3. Транзитивностью: если эквивалентен, аэквивалентен, тоэквивалентен. Иначе говоря, еслии, то.

Очень часто отношение эквивалентности элементов обозначается так:.

Важным понятием является понятие класса эквивалентности. Класс эквивалентности элемента состоит из всех элементов , эквивалентных элементу. Для неэквивалентных элементов их классы эквивалентности не пересекаются. Множество классов эквивалентности называетсяфактормножеством множества по отношениюи обозначается. Если взять ровно по одному элементу из каждого класса эквивалентности, получим систему представителей.

В качестве примера рассмотрим множество целых чисел. Зафиксируем произвольное целое число и назовём два целых числасравнимыми по модулю (что обозначается) , если разностьделится на. Легко видеть, определённое таким образом отношение обладает всеми свойствами отношения эквивалентности. Классы эквивалентности называютсяклассами вычетов по модулю , в качестве системы представителей можно взять всевозможные остатки от деления на, т.е. числа. Это множество обозначается. На нём можно определить операции сложения и умножения естественным образом. Имеется в виду, что следует просуммировать вычеты, как обычные целые числа, разделить сумму нас остатком и этот остаток назвать суммой вычетов. Аналогично определим произведение вычетов.

studfiles.net

11. Число элементов в декартовом произведении конечных множеств

Нам известно, как находят декартово произведение конечных множеств. Например, если А = {х, у, z}, а В = {m,p}, то А х В = {(х,m), (х, р), (у,m), (у, р ), (z,m), (z, р)}. Чтобы ответить на вопрос: «Сколько элементов в полученном множестве?», достаточно пересчитать их. А как определить число элементов в декартовом произведении множеств, не образуя его и не обращаясь к пересчету элементов?

Можно доказать, что если в множестве А содержится а элементов, а в множестве В – bэлементов, то в декартовом произведении множеств А и В содержится а• bэлементов, т.е.

n(А х В) = n(А) • n(В) = а • b. (3)

Правило распространяется на случай tмножеств, т.е.

n(А₁х А₂ х …х Аt) =n(А₁)•n(А₂) •…•n(Аt).

Например, если в множестве А содержится 3 элемента, в множестве В – 4 элемента, в множестве С – 5 элементов, то в их декартовом произведении будет содержаться 3•4•5 = 60 упорядоченных наборов из трех элементов.

Полученные формулы можно использовать при решении задач.

Задача 1. У Маши 3 различных юбки и 4 различных кофты. Сколько различных комплектов, состоящих из юбки и кофты, она может составить?

Решение. Пусть А – множество юбок у Маши, В – множество кофт. Тогда, по условию задачи, n(А) = 3,n(В) = 4. Требуется найти число возможных пар, образованных из элементов множества А и В, т.е.n(А х В). Но согласно правилуn(А х В) =n(А)•n(В) = 3 • 4 = 12. Таким образом, из 3 юбок и 4 кофт Маша может составить 12 различных комплектов.

Задача 2. Сколько двузначных чисел можно записать, используя цифры 5, 4 и 7?

Решение. Запись любого двузначного числа состоит из двух цифр и представляет собой упорядоченную пару. В данном случае эти пары образуются из элементов множества А = {5, 4, 7}. В задаче требуется узнать число таких пар, т.е число элементов в декартовом произведении А х А. Согласно правилу n(А х А) =n(А)•n(А) = 3 • 3 = 9. Значит, двузначных чисел, записанных с помощью цифр 5, 4 и 7, будет 9.

Часто при решении задач, аналогичных рассмотренным выше, требуется не только ответить на вопрос о том, сколько существует возможных вариантов ее решения, но и осуществить перебор этих вариантов. Например, в задаче 2 можно предложить записать все двузначные числа, используя цифры 4, 5 и 7.

Существует единый подход к осуществлению такого перебора – строится схема, называемая деревом возможных вариантов. Она будет иметь вид:

12. Основные понятия:

Множество, элемент множества, характеристическое свойство элементов множества, подмножество, равные множества, пересечение множеств, объединение множеств, вычитание множеств, дополнение подмножества, декартово произведение множеств.

Лекция 5. Математические понятия

План:

1. Объем и содержание понятия. Отношения между понятиями

2. Определение понятий. Определяемые и неопределяемые понятия.

3. Способы определения понятий.

4. Основные выводы

§ 2. Математические понятия

Понятия, которые изучаются в начальном курсе математики, обычно представляют в виде четырех групп. В первую включаются понятия, связанные с числами и операциями над ними: число, сложение, слагаемое, больше и др. Во вторую входят алгебраические понятия: выражение, равенство, уравнения и др. Третью группу составляют геометрические понятия: прямая, отрезок, треугольник и т.д. Четвертую группу образуют понятия, связанные с величинами и их измерением.

Чтобы изучать все разнообразие понятий, надо иметь представление о понятии как логической категории и особенностях математических понятий.

В логике понятия рассматривают какформу мысли, отражающую объекты (предметы и явления) в их существенных и общих свойствах. Языковой формой понятия являетсяслово (термин) или группа слов.

Составить понятие об объекте – это значит уметь отличить его от других сходных с ним объектов. Математические понятия обладают рядом особенностей. Главная заключается в том, что математические объекты, о которых необходимо составить понятие, в реальности не существуют. Математические объекты созданы умом человека. Это идеальные объекты, отражающие реальные предметы или явления. Например, в геометрии изучают форму и размеры предметов, не принимая во внимание другие свойства: цвет, массу, твердость и т.д. От всего этого абстрагируются. Поэтому в геометрии вместо слова «предмет» говорят «геометрическая фигура».

Результатом абстрагирования являются и такие математические понятия, как «число» и «величина».

Вообще математические объекты существуют лишь в мышлении человека и в тех знаках и символах, которые образуют математический язык.

К сказанному можно добавить, что, изучая пространственные формы и количественные отношения материального мира, математика не только пользуется различными приемами абстрагирования, но и само абстрагирование выступает как многоступенчатый процесс. В математике рассматривают не только понятия, появившиеся при изучении реальных предметов, но и понятия, возникшие на основе первых. Например, общее понятие функции как соответствия является обобщением понятий конкретных функции, т.е. абстракцией от абстракций.

1. Объем и содержание понятия. Отношения между понятиями

Всякий математический объект обладает определенными свойствами. Например, квадрат имеет четыре стороны, четыре прямых угла, равные диагонали. Можно указать и другие его свойства.

Среди свойств объекта различают существенные и несущественные. Свойство считаютсущественным для объекта, если оно присуще этому объекту и без него он не может существовать. Например, для квадрата существенными являются все свойства, названные выше. Несущественно для квадрата АВСDсвойство «сторона АВ горизонтальна».

Когда говорят о математическом понятии, то обычно имеют в виду множество объектов, обозначаемых одним термином (словом или группой слов). Так, говоря о квадрате, имеют в виду все геометрические фигуры, являющиеся квадратами. Считают, что множество всех квадратов составляет объем понятия «квадрат».

Вообще, объем понятия – это множество всех объектов, обозначаемых одним термином.

Любое понятие имеет не только объем, но и содержание.

Содержание понятия – это множество всех существенных свойств объекта, отраженных в этом понятии.

Рассмотрим, например, понятие «прямоугольник».

Объем понятия – это множество различных прямоугольников, а в его содержание входят такие свойства прямоугольников, как «иметь четыре прямых угла», «иметь равные противоположные стороны», «иметь равные диагонали» и т.д.

Между объемом понятия и его содержанием существует взаимосвязь: если увеличивается объем понятия, то уменьшается его содержание, и наоборот. Так, например, объем понятия «квадрат» является частью объема понятия «прямоугольник», а в содержании понятия «квадрат» содержится больше свойств, чем в содержании понятия «прямоугольник» («все стороны равны», «диагонали взаимно перпендикулярны» и др.).

Любое понятие нельзя усвоить, не осознав его взаимосвязи с другими понятиями. Поэтому важно знать, в каких отношениях могут находиться понятия, и уметь устанавливать эти связи.

Отношения между понятиями тесно связаны с отношениями между их объемами, т.е. множествами.

Условимся понятия обозначать строчными буквами латинского алфавита: а, b,c,d, …,z.

Пусть заданы два понятия а и b. Объемы их обозначим соответственно А и В.

Если А ⊂ В (А≠В), то говорят, что понятие а – видовое по отношению к понятиюb, а понятиеb– родовое по отношению к понятию а.

Например, если а – «прямоугольник», b– «четырехугольник», то их объемы А и В находятся в отношении включения (А⊂ В и А≠В), поэтому всякий прямоугольник является четырехугольником. Поэтому можно утверждать, что понятие «прямоугольник» — видовое по отношению к понятию «четырехугольник», а понятие «четырехугольник» — родовое по отношению к понятию «прямоугольник».

Если А = В, то говорят, что понятия А и В тождественны.

Например, тождественны понятия «равносторонний треугольник» и «равнобедренный треугольник», так как их объемы совпадают.

Рассмотрим подробнее отношение рода и вида между понятиями.

1. Во-первых, понятия рода и вида относительны: одно и то же понятие может быть родовым по отношению к одному понятию и видовым по отношению к другому. Например, понятие «прямоугольник» — родовое по отношению к понятию «квадрат» и видовое по отношению к понятию «четырехугольник».

2. Во-вторых, для данного понятия часто можно указать несколько родовых понятий. Так, для понятия «прямоугольник» родовыми являются понятия «четырехугольник», «параллелограмм», «многоугольник». Среди указанных можно указать ближайшее. Для понятия «прямоугольник» ближайшим является понятие «параллелограмм».

3. В-третьих, видовое понятие обладает всеми свойствами родового понятия. Например, квадрат, являясь видовым понятием по отношению к понятию «прямоугольник», обладает всеми свойствами, присущими прямоугольнику.

Так как объем понятия – множество, удобно, устанавливая отношения между объемами понятий, изображать их при помощи кругов Эйлера.

Установим, например, отношения между следующими парами понятий а и b, если:

1. а – «прямоугольник», b– «ромб»;

2. а – «многоугольник», b– «параллелограмм»;

3. а – «прямая», b– «отрезок».

Отношения между множествами отображены на рисунке соответственно

А В А А В

1) 2) 3)

2. Определение понятий. Определяемые и неопределяемые понятия.

Появление в математике новых понятий, а значит, и новых терминов, обозначающих эти понятия, предполагает их определение.

Определением обычно называют предложение, разъясняющее суть нового термина (или обозначения). Как правило, делают это на основе ранее введенных понятий. Например, прямоугольник можно определить так: «Прямоугольником называется четырехугольник, у которого все углы прямые». В этом определении есть две части – определяемое понятие (прямоугольник) и определяющее понятие (четырехугольник, у которого все углы прямые). Если обозначить через а первое понятие, а черезb– второе, то данное определение можно представить в таком виде:

а есть (по определению) b.

Слова «есть (по определению)» обычно заменяют символом ⇔, и тогда определение выглядит так:

а ⇔ b.

опр.

Читают: «а равносильно bпо определению». Можно прочитать эту запись еще и так: «а тогда и только тогда, когдаb.

Определения, имеющие такую структуру, называются явными. Рассмотрим их подробнее.

Обратимся ко второй части определения «прямоугольник».

В нем можно выделить:

1) понятие «четырехугольник», которое является родовым по отношению к понятию «прямоугольник».

2) свойство «иметь все углы прямые», которое позволяет выделить из всевозможных четырехугольников один вид – прямоугольники; поэтому его называют видовым отличием.

Вообще видовое отличие – это свойства (одно или несколько), которые позволяют выделить определяемые объекты из объема родового понятия.

Итоги нашего анализа можно представить в виде схемы:

Знак «+» используется как замена частица «и».

Нам известно, что любое понятие имеет объем. Если понятие а определено через род и видовое отличие, то о его объеме – множестве А – можно сказать, что в нем содержатся такие объекты, которые принадлежат множеству С (объему родового понятия с) и обладают свойством Р:

А = {х/ х ∈С и Р(х)}.

Так как определение понятия через род и видовое отличие является по существу условным соглашением о введении нового термина для замены какой-либо совокупности известных терминов, то об определении нельзя сказать, верное оно или неверное; его не доказывают и не опровергают. Но, формулируя определения, придерживаются ряда правил. Назовем их.

1. Определение должно быть соразмерным. Это означает, что объемы определяемого и определяющего понятий должны совпадать.

2. В определении (или их системе) не должно быть порочного круга. Это означает, что нельзя определять понятие через само себя.

3. Определение должно быть ясным. Требуется, например, чтобы значения терминов, входящих в определяющее понятие, были известны к моменту введения определения нового понятия.

4. Одно и то же понятие определить через род и видовое отличие, соблюдая сформулированные выше правила, можно по-разному. Так, квадрат можно определить как:

а) прямоугольник, у которого соседние стороны равны;

б) прямоугольник, у которого диагонали взаимно перпендикулярны;

в) ромб, у которого есть прямой угол;

г) параллелограмм, у которого все стороны равны, а углы прямые.

Различные определения одного и того же понятия возможны потому, что из большого числа свойств, входящих в содержание понятия, в определение включаются только некоторые. И тогда из возможных определений выбирают одно, исходят из того, какое из них проще и целесообразнее для дальнейшего построения теории.

Назовем ту последовательность действий, которую мы должны соблюдать, если хотим воспроизвести определение знакомого понятия или построить определение нового:

1. Назвать определяемое понятие (термин).

2. Указать ближайшее родовое понятие (по отношению к определяемому) понятие.

3. Перечислить свойства, выделяющие определяемые объекты из объема родового, т.е сформулировать видовое отличие.

4. Проверить, выполнены ли правила определения понятия (соразмерно ли оно, нет ли порочного круга и т.д.).

studfiles.net