Решение транспортной задачи в MS Excel (фиктивный поставщик или потребитель)
- Курсы
- Новости
- Статьи
- Excel
- PowerPoint
- Windows
- Word
- Заметки
- Excel
- PowerPoint
- Windows
- Word
- Другие заметки
- Видео
- Excel
- PowerPoint
- Windows
- Word
- Другие видео
- Блог
- Shop
- Доступ к курсам
- Услуги
Поиск
- Главная
- Центр обучения
- Справочник
- Поддержка
- Контакт
- Курсы
msoffice-prowork.com
Решение транспортных задач в среде Excel
Продолжение темы, начатой в «КВ» №21/2005
Одной из самых распространенных проблем во всех областях экономики является транспортировка груза или товара с минимальными материальными и временными затратами. Так как огромное количество возможных вариантов перевозок затрудняет получение самого экономичного плана эмпирическим или экспертным путем, то появилась необходимость разработки специальной теории, позволяющей быстро решать подобные задачи с помощью алгоритмизации. Применение математических методов в планировании перевозок дает большой экономический эффект. В этом нам и предстоит сейчас убедиться при помощи нашего знакомого Васи, который как раз устроился работать курьером.
Постановка задачи
Компания, где Василий нашел вакантное место курьера, имеет два склада, на которых хранится товар, и три магазинчика — конторы, где этот товар реализуется. Задача Васи заключается в строгом выполнении плана, который он получает каждый день. В качестве транспортного средства он использует старый, но выносливый советский велосипед, который не позволяет перевозить всю партию за раз. Поэтому нашему ненасытному другу приходится мотаться туда-сюда. На что он опять копит? Что же он там перевозит? Не ждите от меня ответов на эти вопросы, если б знал — давно бы уже сказал бы.
И тут Василий, изнывая от мучительных болей в ногах и предвидя жесткий выговор со стороны начальства за невыполнение работы в намеченный срок, задумался: можно ли составить с учетом выдаваемого ему плана такой маршрут движения, чтобы на выполнение всего задания уходило минимум времени и сил. Конечно, можно! Этим мы сейчас и займемся.
Составление математической модели
Сначала необходимо проделать подготовительную работу, а именно — определить тарифы на каждом участке будущего оптимального плана перевозок. Поскольку Вася заинтересован в том, чтобы делать свою работу максимально быстро, то в качестве тарифов в данной задаче выступает время, потраченное на перевозку единицы товара из n-го склада в m-ую контору. При помощи карты Минска (CityInfo) с учетом времени на перекур и на подкачку шин, Вася оценил среднее время перевозки товара из каждого склада в каждую контору. В результате была составлена таблица 1.
| Таблица 1. Время на перевозку | ||||
| Склад\Контора | Контора №1 | Контора №2 | Контора №3 | Есть на складах |
| Склад №1 | 5 | 20 | 8 | 20 |
| Склад №2 | 10 | 15 | 12 | 30 |
| Потребность | 15 | 12 | 20 | 47/50 |
Данная транспортная задача относится к типу задач с неправильным балансом (47<>50), но нас это не должно смущать. Я вас уверяю, мы ничего не будем решать вручную. Хотелось бы отметить, что в реальной жизни транспортные задачи с правильным балансом встречаются не очень часто. Далее задачу необходимо, как говорится, формализировать, т.е. записать в виде уравнений (формул). Пусть X — количество единиц товара, перевозимых из каждого склада в каждую контору. Тогда X11 — количество единиц товара, перевозимых из первого склада в первую контору, X12 — количество единиц товара, перевозимых из первого склада во вторую контору, и т.д. (такие предложения пишутся простым копированием, если вы не знали.;) Поскольку задача с неправильным балансом, то необходимо ввести также фиктивную контору. Все переменные представлены в таблице 2.
| Таблица 2. Количество перевозимых товаров | |||||
| Склад\Контора | Контора №1 | Контора №2 | Контора №3 | Фиктивная | Есть на складах |
| Склад №1 | X11 | X12 | X13 | X14 | 20 |
| Склад №2 | X21 | X22 | X23 | X24 | 30 |
| Потребность | 15 | 12 | 20 | 3 | 50/50 |
Теперь все готово для составления системы уравнений и целевой функции, определяющей время выполнения плана перевозок и направленной на минимум. По смыслу ясно, что количество единиц товара, привезенных с каждого склада в контору, в сумме должно равняться потребности этой конторы. Т.е.
X11+ X21=15
X12+ X22=12
X13+ X23=20
X14+ X24=3
Аналогично получаем следующие условия:
X11+X12+X13+X14=20
X21+X22+X23+X24=30
Целевая функция, как я уже говорил, определяет время выполнения намеченного плана транспортировки товара. Поэтому:
E=5* X11 + 20* X12 + 8* X13 + 10* X21 + 15* X22 + 12* X23 ->min
Тарифы на доставку товара в виртуальную контору принимаются равными нулю, поэтому слагаемое «0*X14+0*X24» в записи формулы для целевой функции можно опустить. Теперь приступим непосредственно к решению поставленной задачи. Согласитесь, проделанные до сих пор операции не вызывают больших трудностей.
Выбор метода решения
А найти решение нам поможет мощный табличный процессор Microsoft Excel, широко используемый не только как удобное средство для хранения разнообразных данных и многофункциональный инструмент, позволяющий выполнять над ними многочисленные математические операции, но и как орудие для решения несложных оптимизационных задач. Последним, в частности, и занимается программная надстройка «Поиск решения». Если она у вас не установлена, то проделайте следующие действия: «Сервис» > «Надстройки», потом поставьте галочку около пункта «Поиск решения». Для поиска ответа остается только занести шесть ограничений и целевую функцию в Excel. Я не буду докучать читателю ((с) Джонатан Свифт, «Путешествия Гулливера»;) подробным описанием того, как следует вводить данные в ячейки таблицы или как нужно составлять ограничения в «Поиск решения». Этот титанический труд был проделан в первой статье по оптимизации в среде Excel, опубликованной в 21-м номере. Отмечу, что хоть задача про изготовление баннеров и задача про перевозки принадлежат к различным типам задач, для нахождения ответа на которые разработано множество «своих» методов, все-таки обе задачи являются задачами линейного программирования. Поэтому их можно решать и общим для всех задач линейного программирования способом — симплекс-методом. Конечно, для решения транспортных задач вручную намного предпочтительнее использовать специально разработанные для этих целей алгоритмы. Но в конкретном случае мы переложим наше бремя на плечи машины. Ей-то какая разница, выполнять 10 или 100 итераций. Если мы собираемся использовать тот же самый подход, что и при решении задачи об изготовлении баннеров, то алгоритм поиска оптимального ответа в данном примере почти не будет отличаться от алгоритма, описанного в предыдущей статье. Различия будут заключаться лишь в подготовительных работах, которые мы, сами того не зная, уже проделали выше.
Итак, в ячейки строки с целевой функцией запишем коэффициенты перед переменными, входящими в целевую функцию. Так же поступим и cо всеми ограничениями в виде равенств (в столбце «L» записывается правая часть уравнений). В столбце с решением «J» в каждую ячейку введем формулу вида «=СУММПРОИЗВ(Bn:Gn;B2:G2)», где n изменяется от 3 до 9. Теперь открываем рабочее окно «Поиск решения» и записываем все ограничения, показанные на рисунке.
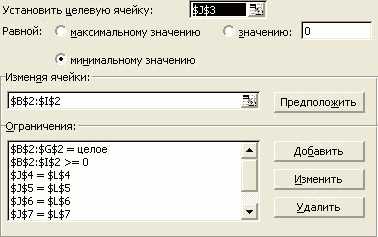
Нажимаем на кнопку «Выполнить» и вместе с Васей радуемся полученным результатам.
Анализ полученных результатов
Оптимальный план перевозок груза выглядит следующим образом: с первого склада нужно переправить 15 ед. груза в первую контору и 5 ед. груза в третью контору, а со второго — 12 ед. груза во вторую и 15 ед. груза в третью конторы. На все это Вася будет тратить 475 минут (7 часов и 55 минут). Это оптимальный вариант. Сравним его с любым другим возможным. Допустим, что Вася решил делать все наобум и выбирал маршрут случайным образом. Пусть план следующий: (X11, X12, X13, X21, X22, X23)=(0, 0, 20, 15, 12, 0). Тогда целевая функция будет равна 490 минут (за смену Вася не управится). С одной стороны, это не много, с другой, если бы в качестве тарифов выступало не время, а деньги, то экономия была бы существенной. Да и если вспомнить фразеологизм «Время — деньги», то всякие сомнения по поводу рациональности использования оптимизации в управлении и финансах отпадают. Ведь выгода заключается не в том, что Васе приходится быстрее крутить педали, а в том, что при помощи математической модели находится наилучший вариант протекания реального процесса.
В качестве следствия можно отметить, что если предстоит решать задачу с правильным балансом, то из всех рассуждений необходимо просто исключить переменные X14 и X24.
Конечно, существует много программ, которые специализируются именно на исследовании транспортных задач. Но с Excel’ем как-то проще ((с) Реклама про «Биосистему»). Иногда время и деньги, потраченные на поиски нужной программы в интернете, сравнимы с выгодой, полученной в ходе оптимизации. На одной web-странице программу, работающую с транспортными задачами, предлагалось приобрести за $100. Другое приложение оказалось бесплатным, но не умело решать задачи в общем случае (с неправильным балансом). Вот такие пироги (или проги ;).
В современном обществе методы оптимизации применяются повсеместно, принося существенную экономическую выгоду и предупреждая финансовые крахи. Они позволяют принимать разнообразные управленческие решения в условиях риска и неопределенности. Правда, уже при помощи более мощных программных комплексов, работающих на основе генетических алгоритмов, нечеткой логики и нейронных сетей.
Виталий КРАСИЛЬНИКОВ
www.kv.by
Решение транспортных задач в Excel
гарантирует выполнение каждой работы лишь одним исполнителем, ограничение
Стоимость выполнения всего комплекса работ равна
Таким образом, задачу о назначениях можно записать следующим образом:
Задача о назначениях является частным случаем классической транспортной задачи, в которой надо положить n = m, Si = 1, i = 1,…,n, Dj = 1, j = 1,…,n. При этом условие xij Î{0, 1}, i,j = 1,…,n, означает выполнение требования целочисленности переменных xij . Это связано с тем, что мощности всех источников и стоков равны единице, откуда следует, что в допустимом целочисленном решении значениями переменных могут быть только 0 и 1.
Как частный случай классической транспортной задачи, задачу о назначениях можно рассматривать как задачу линейного программирования. Поэтому в данном случае используют терминологию и теоретические результаты линейного программирования.
В задаче о назначениях переменное xij , может принимать значение 0 или 1. При этом в любом допустимом решении лишь n переменных могут принимать значения 1. Таким образом, любое допустимое базисное решение задачи о назначениях будет вырожденным.
На практике встречаются задачи о назначениях, в постановках которых параметр cij для i,j= 1,…,n понимается как эффективность выполнения i-й работы j-м исполнителем. В этих случаях нужно так распределить работы между исполнителями, чтобы суммарная эффективность их выполнения был бы максимальной, т.е.
mirznanii.com
Решение транспортной задачи в Excel
(bj =0) запрещаем такие же клетки вj-ом столбце.
В случае одновременного исчерпания запасов потребностей (ai =bj= 0) запрещаем перевозки или в строке (тогда считаем, что у потребителя осталась потребность в количестве равном нулю, которую необходимо удовлетворить), или в столбце (в этом случае считаем, что у поставщика остается запас равный нулю, который необходимо вывезти). Это делается для того, чтобы при одновременном запрещении перевозок в строке и столбце количество заполненных клеток таблицы не стало меньшим, чем m+n-1.
Получим новую текущую таблицу, в которую не входят заполненные и запрещенные клетки. Если таблица не пуста, переходим к шагу 1. (При исчерпании таблицы — конец).
Способ минимальной стоимости.
1.Клетки с минимальной ценой (3,1), (3,2) и (3,3). Выбираем, например, (3,2). (Далее все шаги, как в предыдущем способе).
2 . x32 = min{50,60} = 50
3. a‘3 =50-50=0, b‘2 = 100-50=50
4.Запрещаем строку 3.
1.Клетка с min ценой ~ (2,3)
2.x23 = min{70,80} = 70
3.a2 =70-70=0, b’3 = 80-70=10
4.Запрещаем строку 2.
1. Клетка с min ценой ~ (1,1)
2. x 11 =min{120,60} = 60
3. a 1′ =120-60 = 60, b1′ = 0
4.В первом столбце запрещать уже нечего. Текущая таблица содержит две клетки (1,2) и (1,3).
1.Выбираем клетку (1,2)
2 . x12 =min{110,100} = 100
3.a1 =110-100 = 10, b‘1 = 0
4.Текущая таблица содержит одну клетку (1,3).
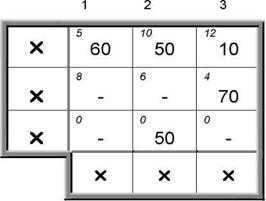
1. Выбираем последнюю клетку(1,3)
2. x13 =min{10,10} = 10
3.a1‘ = b3 = 0
4.Таблица исчерпана. Конец.
Переходим к описанию следующего шага метода потенциалов.
ШАГ 2. Проверка текущего плана на оптимальность.
Признаком того, что текущий план перевозок является оптимальным, служит условие
(1)ui +vj -cij ≤0
которое выполняется для всех клеток таблицы. Неизвестные здесь величины ui и vj(называемые потенциалами) определяются из условий
(2)ui + vj = cij
Условие (1) означает невозможность появления «спекулятивной» цены. Само же название «потенциалы» заимствовано из физического закона о том, что работа по перемещению заряда в электростатическом поле равна разности потенциалов в данных точках поля (У нас: «…цена перевозки единицы продукции по коммуникации равна разности цен в конце и в начале пути»)
Так как заполненных клеток в таблице (m+n-1) штук, а неизвестных и (m+n) штук, то для их определения имеется система из (m+n-1) уравнений относительно (m+n) неизвестных. Чтобы найти решение (хотя бы какое-нибудь) такой системы, достаточно положить одно из неизвестных (произвольное) равным некоторому произвольно выбранному числу. Тогда остальные определяются единственным образом. Можно решать эту систему непосредственно (продолжаем работать с нашим «старым» примером и найдем потенциалы для начального плана, построенного способом МС).
Заполненные клетки Уравнения
(1,1) u1 + v1 =5
(1,2) u1 + v2 =10
(1,3) u1 + v3 =12
(2,3) u2 +v3 =4
(3,2) u3 +v2 =0
Положим, например, неизвестное u1 равным 0 (через него можно из первых трех уравнений найти v1 , v2 и v3 ). Последовательно из них находим u2 , u3.
Этот метод можно сформулировать в виде единого правила:
Неизвестный потенциал находится вычитанием известного из цены перевозки в заполненной клетке
Применим это правило для определения u и vв нашем примере и получим:
u1 =0, u2 =-8, u3 =-6
v1 =5, v2 =10, v3 =12
Переходим к проверке условий оптимальности (1). Достаточно проверять их для незаполненных клеток, так как для клеток заполненных эти условия выполняются как равенства. Для проверки берется незаполненная клетка, складываются соответствующие ей потенциалы (первый элемент строки и последний элемент столбца) и из них вычитается цена перевозки в данной клетке. Если полученное число отрицательное (или ноль), то оптимальность в данной клетке не нарушается (в случае выполнения условия (1) для всех незаполненных клеток, имеем оптимальный план перевозок). Если же в таблице встретилась хотя бы одна клетка, для которой это число положительно, тогда решение не является оптимальным и может быть улучшено.
Проверим на оптимальность имеющееся решение
(2,1)u2 +v1 -c21 =-8+5-8=-11<0
(2,2) u 2 +v2 -c22 =-8+10-6=-4<0
(3,1)u3 +v1 -c31 =-10+ 5-0=-5<0
(3,3)u3 +v3 -c33 =-10+12-0=2>0
Следовательно, условие оптимальности нарушено в клетке (3,3).
Имеющийся план перевозок можно улучшить.
Дадим описание заключительного шага алгоритма метода потенциалов.
ШАГ 3 Улучшение плана перевозок .
Улучшение плана происходит путем назначения перевозки θ>0 в ту клетку (i , j) таблицы, в которой нарушилось условие оптимальности. Но назначение ненулевой перевозки нарушает условия баланса вывоза продукции от поставщика i (вывозит весь запас и еще плюсθ>0 ) и условия баланса привоза продукции к потребителю j(получает все что можно и еще плюс θ > 0). Условия баланса восстанавливают путем уменьшения вывоза от i-поставщика к какому-то другому потребителю j(уменьшают на θ перевозку в какой-то заполненной клетке (i , j) строки i). При этом нарушается баланс привоза продукции к потребителю j (получает на θ меньше, чем ему требуется). Восстанавливают баланс в столбце j, тогда он нарушается в некоторой строке i и т.д. до тех пор, пока цикл перемещения перевозок не замкнется на клетке, в которой нарушалось условие оптимальности. Продемонстрируем эти рассуждения на нашем примере.
1. Оптимальность нарушена в клетке (3,3). Назначим в нее перевозку θ>0 (+θ означает, увеличение на θ).
2.Нарушается баланс вывоза от поставщика 3 (вывозит 50+ θ, а это больше его запаса!). Уменьшаем на θ перевозку в заполненной клетке строки 3 (вне заполненной уменьшать нельзя, так как это приведет к отрицательной перевозке).
Рассмотрим те клетки цикла в которых уменьшаем на θ перевозку и берём минимум из вычетаемых, у нас это min{10- θ ,50- θ }=10.
И данное число надо подставить в цикл
§3. Транспортные задачи по различным критериям
Транспортная задача по критерию времени
Иногда возникает ситуация, когда в условиях (ТЗ) необходимо минимизировать не стоимость перевозок, а время их выполнения (Срочные грузы, перевозки скоропортящихся продуктов, работа «скорой помощи» и т.д.)
Имеется m поставщиков
однородного груза и n потребителей груза. Для каждой пары (,) известно время , за которое груз перевозится от к . Требуется составить такой план перевозок, при котором все запасы поставщиков будут вывезены, а все запросы потребителей будут полностью удовлетворенны и наибольшее время доставки всех грузов будет минимизирован.Задача о назначениях (Венгерский метод)
Имеется n видов работ и n рабочих. Каждый рабочий может выполнить любую из nработ за некоторое время (цена рабочего). Требуется распределить все работы между всеми рабочими так, чтобы время выполнения работ было минимальным, а каждую работу выполнял только один рабочий.
§4. Решение транспортной задачи в Excel
В качестве примера я рассмотрел транспортную задачу для 2 складов и 5 магазинов.
· В ячейки C4:C5 записал объемы продукции, имеющиеся на 2 складах.
· В ячейки E5:I5 — заявки на продукцию, поступившие от магазинов.
· В ячейки B8:F9 — матрицу транспортных расходов, задающую расходы на перевозку из I-го склада в J-й магазин единицы продукции.
· В ячейки B13:F14 — план перевозок — матрицу, задающую количество товара, перевезенного из I-го склада в J-й магазин. Начальное распределение плана задано по принципу «каждой сестре по серьге», равномерно распределив всю имеющуюся на складе продукцию по магазинам. Эти ячейки являются регулируемыми и Решатель должен найти более подходящее решение, изменив значения в этих ячейках.
· В ячейку D15 — записал целевую функцию:
{ =СУММ((B8:F8*B13:F13)+(B9:F9*B14:F14))}
· В ячейки D17:h27 записал ограничения, задающие требование о точном выполнении заявки каждого магазина. Как обычно, я записал соответствующую формулу в первую из этих ячеек:
{=СУММ(B13:B14) — E5 }
Затем скопировал ее. При копировании формула автоматически меняется, задавая нужное ограничение. Правда, нужно следить при этом за правильной ориентацией данных. Например, в данном случае формулу нужно копировать в строку, а не в столбец.
mirznanii.com
Транспортные задачи в Excel
Государственное образовательное учреждение
средняя общеобразовательная школа № 218
Фрунзенского административного района Санкт-Петербурга
Реферат
Транспортные задачи в Excel
Выполнили: ученики 10 А класса
Фёдоров Артём
Верещагин Михаил
Научные руководители:
учитель математики Сеферян К.О.,
учитель информатики Махаева Е.П.
Санкт-Петербург, 2011 год
Содержание
Введение……………………………………………………………3
Глава 1.
Классическая транспортная задача……………………………………4
1.1. Решение классической сбалансированной транспортной задачи в Excel……………………………………………………………………5
1.2. Решение классической несбалансированной транспортной задачи в Excel………………………..…………………………………..…….10
Глава 2.
Транспортная задача с промежуточными пунктами………………….13
2.1. Решение транспортной задачи с промежуточными пунктами в Excel………………………………………………………………….14
Заключение……………………………………………………….19
Список литературы………………………………………………20
Введение
В настоящее время в условиях жесткой конкуренции автомобильным компаниям приходится бороться за каждый рубль прибыли, поэтому вопрос об уменьшении издержек производства становится первостепенным. И, конечно же, рациональное размещение производственных объектов играет здесь ключевую роль [2].
Так, например, перед ООО «MG Auto» стоит реальная задача: стоит ли изменить действующую на сегодняшний день схему транспортировки автомобилей с заводов до распределительных центрах в Денвере и Майами или же действующая схема наиболее эффективна? Таким образом, в этой работе делается попытка показать пути снижения общих затрат предприятия путем снижения транспортных издержек.
На практике при планировании различных экономических процессов, в частности при решении вопросов рационализации поставок важнейших видов промышленной и сельскохозяйственной продукции, а также оптимального планирования грузопотоков и работы различных видов транспорта широко применяется транспортная задача линейного программирования. Поэтому в данном проекте будет рассмотрена сама транспортная задача, ее постановка и способы решения, а также особенности постановки задачи развития и размещения объектов автомобильной промышленности. Конечной целью является экономическая оценка эффективности транспортировки автомобилей до конечного пункта.
Глава 1
Классическая транспортная задача
Транспортная задача является частным видом линейной оптимизационной задачи. Наиболее часто транспортная задача представляется следующим образом: имеются n пунктов производства и m пунктов распределения продукции. Стоимость перевозки единицы продукции с i-гo пункта производства в j-й центр распределения cji приведена в таблице, где под строкой понимается пункт производства, а под столбцом — пункт распределения. Кроме того, в этой таблице в i-той строке указан объем производства в i-м пункте производства, а в j-м столбце указан спрос в j-м центре распределения[6]. Необходимо составить план перевозок по доставке требуемой продукции в пункты распределения, минимизирующий суммарные транспортные расходы.
Для математического описания транспортной задачи введем переменные xij , обозначающие объемы поставок товара от i -го источника к j -му стоку. В этом случае x i1 + x i2 +…+ xin — общий объем поставок товара от i -го источника, т.е. мощность этого источника; x 1 j + x 2 j +…+ xmj — общий объем поставок товара к j-му стоку, т.е. мощность этого стока; c 11 x 11 + c 12 x 12 +…+ cmn xmn — суммарная стоимость перевозок товара от источников к стокам[7]. С учетом этого рассматриваемая задача может быть представлена в следующем виде:
Задача состоит в определении неизвестных величин xij , минимизирующих суммарные транспортные расходы и удовлетворяющих ограничениям, накладываемым на объемы грузов в пунктах отправления (предложение) и пунктах назначения (спрос).
1.1. Решение классической сбалансированной транспортной задачи в Excel
Рассмотрим решение классической транспортной задачи.
Автомобильная компания MG Auto имеет три завода в Лос-Анджелесе, Детройте и Новом Орлеане и два распределительных центра в Денвере и Майами. Объемы производства заводов компании в следующем квартале составят соответственно 1000, 1500 и 1200 автомобилей. Ежеквартальная потребность распределительных центров составляет 2300 и 1400 автомобилей. Расстояние (в милях) между заводами и распределительными центрами приведены в Таблице 1.
Таблица 1
Транспортная компания оценивает свои услуги в 8 центов за перевозку одного автомобиля на одну милю. В результате получаем, представленную в Таблице 2, стоимость перевозок (с округлением до доллара) по каждому маршруту.
Таблица 2
Решение :
В данной задаче общий объем произведенных автомобилей (S =1000+1500+1200=3700) равен суммарному спросу распределительных центров (D =2300+1400=3700).
Задачу можно решить с помощью транспортной таблицы. Исходные данные для решения классической транспортной задачи целесообразно представить в виде двух таблиц, в первой из которых представлены значения стоимости перевозок единицы товара cij от i -го поставщика к j -му потребителю (см. Рисунок 1).
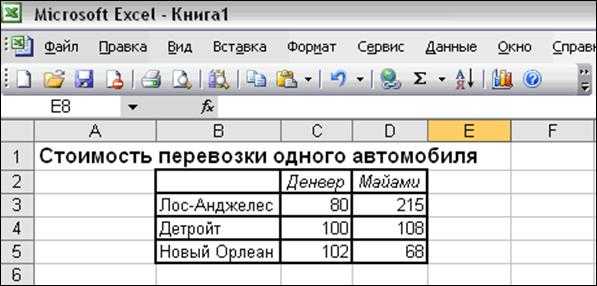
Рисунок 1
Во второй таблице представлены: значения Si предложения каждого i -го поставщика; значения Dj спроса каждого j -го потребителя; переменные xij , первоначально принимающие нулевые значения; вспомогательная строка и вспомогательный столбец «Сумма» (см. Рисунок 2).
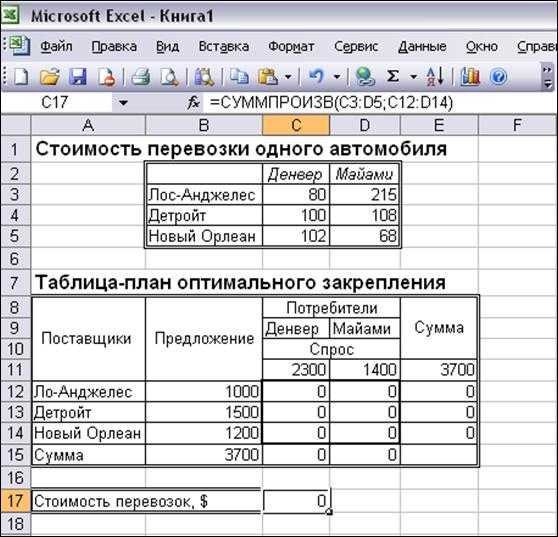
Рисунок 2
Целевая ячейка C 17 должна содержать формулу, выражающую целевую функцию: = СУММПРОИЗВ( C 3: D 5; C 12: D 14) . (Рисунок 3)
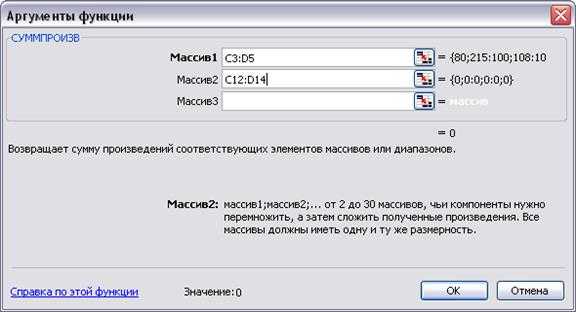
Рисунок 3
Используя меню Сервис Þ Поиск решения открываем диалоговое окно Поиск решения (см. Рисунок 4), в котором устанавливаем целевую ячейку равной минимальному значению, определяем диапазон изменяемых ячеек и ограничения и запускаем процедуру вычисления, щелкнув по кнопке Выполнить [3].
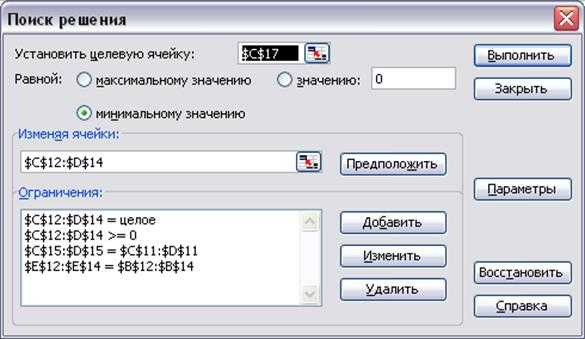
Рисунок 4
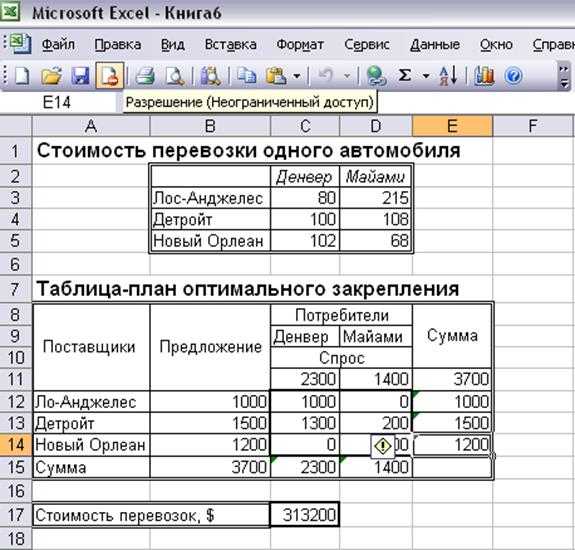
Рисунок 5
Оптимальное решение задачи (Рисунок 5). Оно предполагает перевозку 1000 автомобилей из Лос-Анджелеса в Детройт, 1300 автомобилей – из Детройта в Денвер, 200 автомобилей – из Детройта в Майами и 1200 – из Нового Орлеана в Майами. Минимальная стоимость перевозок составляет 313200 долларов.
1.2. Решение классической несбалансированной транспортной задачи в Excel
Несбалансированная классическая транспортная задача – это когда суммарный объем предложений (грузов, имеющихся в пунктах отправления) не равен общему объему спроса на товары (грузы), запрашиваемые пунктами назначения. В этом случае, при решении классической транспортной задачи вводят фиктивные пункты назначения или отправления [4]. В Excel несбалансированная транспортная задача решается путем изменения ограничений по спросу (если спрос превышает предложение) или по предложению (если предложение превышает спрос), т.е. система ограничений будет иметь вид:
илиРассмотрим решение несбалансированной транспортной задачи в Excel
В рамках модели компании MG Auto предположим, что завод в Детройте уменьшил выпуск продукции до 1300 автомобилей (вместо 1500, как было ранее). В этом случае общее количество произведенных автомобилей (=3500) меньше общего количества заказанных (=3700) автомобилей. Таким образом, очевидно, что часть заказов распределительных центров Денвера и Майами не будет выполнена.
mirznanii.com
