|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
onlinetestpad.com
7 класс. Алгебра. Системы двух уравнений с двумя переменными. — Способы решения систем уравнений с двумя неизвестными.
Комментарии преподавателя
Метод подстановки.
Существует несколько методов решения систем. Один из них метод подстановки. Рассмотрим пример.
Пример 1:
Суть метода подстановки заключается в том, что в одном из уравнений нужно выразить одну переменную через вторую и подставить полученное выражение во второе уравнение.
В данном случае удобно выразить х во втором уравнении:
Подставим полученное выражение в первое уравнение:
Преобразуем первое уравнение:
,
,
,
Подставим полученное значение во второе уравнение:
, ,
Получаем следующее решение системы:
Пример 2:
В данном случае некоторая сложность заключается в том, что исходную систему нужно преобразовать, чтобы была возможность удобно и без ошибок применить метод подстановки. Для этого умножим оба уравнения на шесть:
Выразим у из первого уравнения:
Подставим полученное выражение во второе уравнение и выполним преобразования:
, ,
,
Подставим полученное значение в первое уравнение:
Получаем единственное решение системы, пара чисел:
Вывод:
на данном уроке мы ознакомились с понятием системы двух линейных уравнений с двумя неизвестными и одним из методов ее решения – способом подстановки. Мы решили примеры для понимания и закрепления данной техники.
Источник конспекта: http://interneturok.ru/ru/school/algebra/7-klass/glava-3-sistema-dvuh-lineynyh-uravneniy-s-dvumya-peremennymi/osnovnye-ponyatiya-metod-podstanovki?konspekt&chapter_id=10
Метод сложения.
Рассмотрим еще один способ решения систем двух линейных уравнений с двумя неизвестными – способ алгебраического сложения. Мы решим несколько различных примеров для закрепления техники.
Метод алгебраического сложения, как и метод подстановки, заключается в том, что изначально из двух уравнений с двумя переменными нужно
www.kursoteka.ru
Памятка по теме «Решение уравнений» для 7 класса
Памятка для учащихся 7 класса
по теме: «Решение уравнений»
Алгоритм решения:
1. Умножьте обе части уравнения на общий знаменатель дробей (НОК).
2. Запишите дополнительные множители к каждой дроби, которые получаются после сокращения. Не забудьте умножить на общий знаменатель и целую часть уравнения!
3. Умножьте числители на дополнительный множитель.
4. Раскройте скобки, если необходимо.
5. Перенесите неизвестные члены уравнения в левую часть, а известные — в правую.
6. Приведите подобные слагаемые в левой части уравнения и найдите значение правой части.
Получилось линейное уравнение вида ax=b, где x=b:a.
Примеры решения уравнений с дробной частью.
1)
Или:Решение:
— пропорция
Решение:
1 / 3/
|•6
x — 7 = 3(x+1)
x – 7 = 3x + 3
x — 3x = 3+7
-2x = 10
x = 10: (–2)
x = –5
Основное свойство пропорции: произведение крайних членов пропорции
равно произведению ее средних членов.
(x – 7)·2 = 6·(x+1)
2 x – 14 = 6x + 6
2 x –6 x = 6 + 14
-4x = 20
x = 20: (-4)
x = –5
Решение:
8/ 7/ 56/
= 5 |·56
8(5y + 8) – 7(3y — 1) = 56·5
40y + 64 – 21y +7 = 280
19y = 280 – 64 – 7
19y = 209
y = 209 : 19
y = 11
Решение:
3/ 5/ 15/
— 7
|·15
3(х — 5) = 5(2х + 1) — 15·7
3х – 15 = 10х +5 – 105
3х – 10х = -100 + 15
-7х = -85
х = -85: (-7)
х =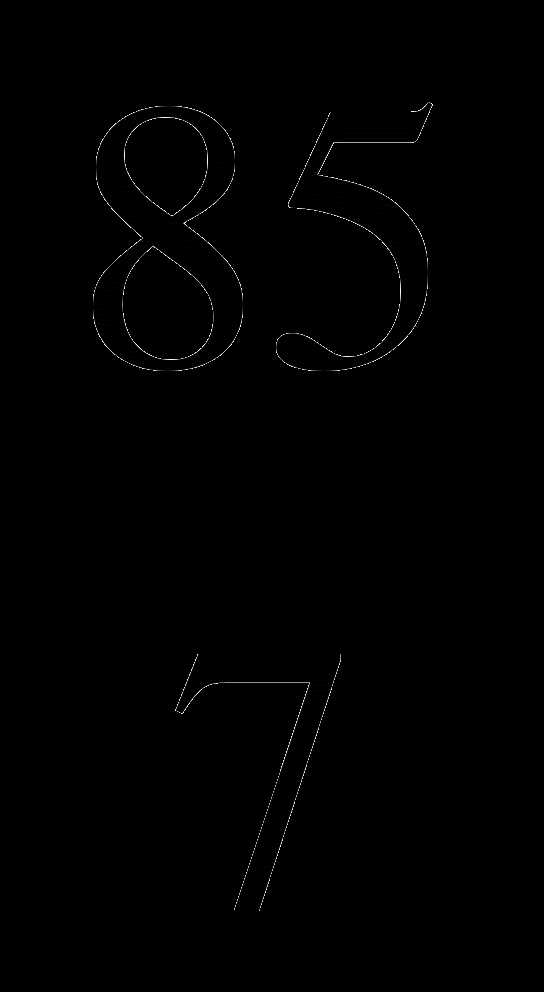 
= 12
Решение:
3/ 2/ 42/
–
+ 
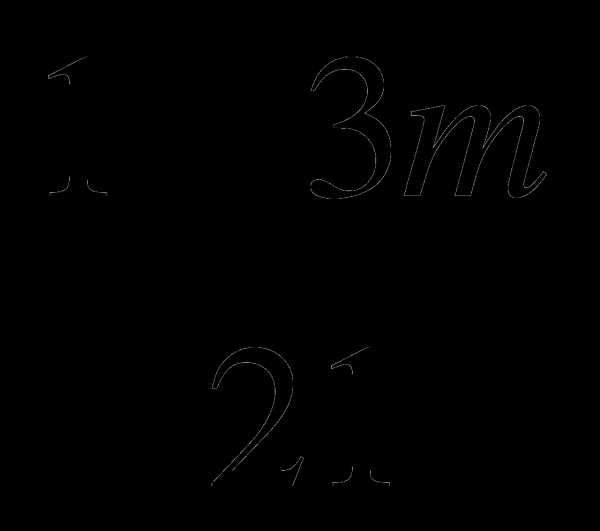= 0 |·42
–3(1 – 5m) + 2(1 +3m) = 0
–3 + 15m + 2 + 6m = 0
21m = 0 + 3 – 2
21m = 1
m = 1 : 21
m = 
Решение:
6/ 2/ 3/ 6/
2x —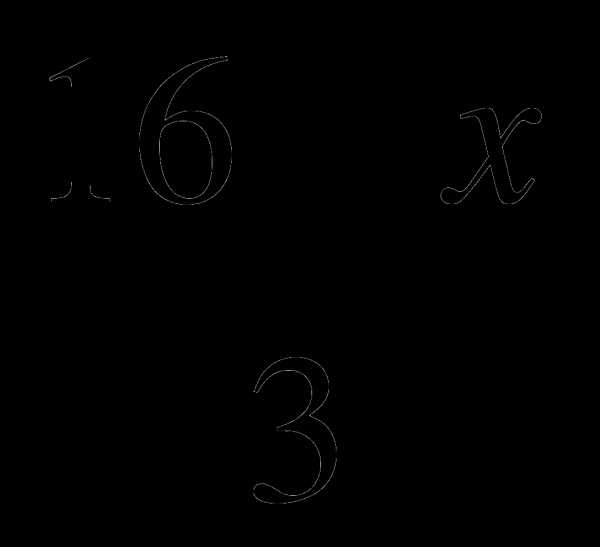 
= 
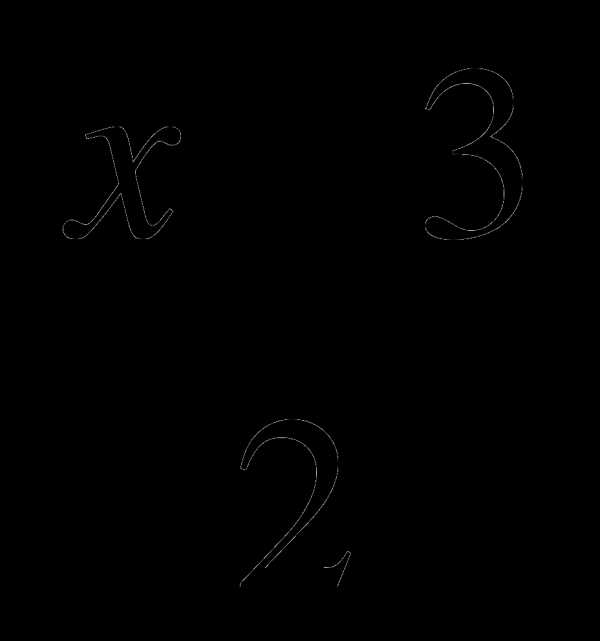+ 6 |·6
6·2x – 2(16 – x) = 3(x +3) +6·6
12x – 32 + 2x = 3x + 9 + 36
14x – 3x = 45 + 32
11x = 77
x= 77 : 11
x = 7
Ответ: 1) —5; 2) 11; 3) 12; 4) ; 5) 7.
infourok.ru
Решение уравнений по алгебре в 7 классе
ИТОГОВОЕ ПОВТОРЕНИЕ ПО АЛГЕБРЕ В 7 КЛАССЕ
Тема: Решение уравнений
Подобранные уравнения могут быть использованы как при изучении темы, так и при повторении или при подведении итогов. Уравнения отличаются своей тематикой и сложностью. Таким образом их применение возможно при дифференцированном подходе к каждому ученику. Есть уравнения, которые можно использовать в классах с углубленным изучением математики.
№
А
В
С
Д
Е
F
5х – 2 = 8
7 (2х -3) – х = 3х — 11
— (3 — х) : 12 = 3
|х – 4 |= 2
3а – 2(b – x) + 2 = b
-5,6(x — 3) + 2,1x = -3,5x + 10
2(x — 4) = 15
-4x + 34 = -2(x — 5)
(x — 4) : 5 = (2x — 3) : 3
|2x — 1| = 3
3a + bx = 12 – 3a
7(x – 4) + 3 = 3(2x — 7) + x — 8
3 – 4x = -5
2,5(x — 4) + 2 = 0,5x
(-6x + 1) : 4 = 2x : 3
|x + 4| = 9
4b – ax + 12 = 0
-12x + 4(x — 3) = -8x — 12
12 – 3x = 7
-5x + 12(x — 1) = 2
(8 — x) : 4 = (x — 3) : 3
|2x — 3| = 5
4(a – 2x) + b = 6
10(x — 3) + 1 = 5(2x + 3)
35(x + 1) = -14
-12(2 — x) = -6x + 2
(x + 3) : 4 = (2x — 1) : 3
|3x + 1| = 4
a(b – 3x) + 2 = 23
12(x + 2) – 2,1 = 2(6x + 12) — 3x
14 – (x – 2) = 23
-(x – 3) + 2(3 — x) = 5
-2(x + 1) : 3 = (3x — 1) : 2
|2x — 5| = 3
b – ax + 12 = ax
2,1x + 0,3(7 – x ) = 2,1
32x + (2 – 3x) = 5
-4x + 21 + (3 — x) = 12
x : 4 = 2x : 3
|x — 3| = 12
3b – a(x — 3) = 2
-2(x + 21) – 3(x — 14) = -5x
34(x — 2) = 2
-2(x — 3) + (4 — x) = 12
(13 — x) : 12 = 3(x — 2) : 5
|2x — 13| = 1
a(3x — b) = 12
-2(x + 21) – 3(x — 4) = -5(x +6)
3x – 12 + x = 4
23x – 2(3x — 4) = 12
(3x — 1) : 2 = 2(x + 2) : 3
|3x — 13| = 2
3xa – 2b = 3a — 4
2,1(x – 0,3) + 0,7x = 2,8x
11(x — 3) = 33
23(x + 2) – (2x — 1) = 1
-x : 4 = (3 – 2x) : 5
|5x + 1| = 4
-b(x — 3) = a
2,4(x – 0,01) = 24x : 10
3x + 12 + x = -4
-(3 — x) + 2(x — 3) = 3
(x – 3,4) : 3 = (2x — 3) :2
|x + 12| = 1
(x — a) :b = 12
-11(x — 2) + (2x — 3) = -9x + 19
2(x — 3) + 4 = 1
2(3x — 2) – (3 — x) = 5
(3 — x) : 3 = (2x — 1) : 2
|2x — 7| = 3
xb + a(x — 2) = 0
-11(x — 2) + (2x — 3) = -9(x + 2)
-3x + 2 = 17
-2(x — 3) + 3(2 — x) =1
2(x — 1) :3 = 3(2x + 1) : 2
|3x — 1| = 3
b + 2(ax — 4) = 2
-1,7(x +2) – 0,3x = 2(2 — x)
12 – (x — 2) = 3
-(2x — 1) – 2(5 – 3x) = 0
-(x — 2) : 5 = 2x : 3
|5x — 1| = 2
ax – 4bx + 12 = 9
-11(x — 2) + 2(3 – 2x) + 15x = 0
3x + 12 = 3
5(x — 2) + 2(3 — x) = 12
(4x — 3) : 3 = 2x : 5
|x + 1| = 1
bx – 2ax + 5 = 2bx
2(x — 23) + 3(15 — x) = -(x + 1)
43(x — 2) = 12
12(x — 2) + (-4 + x) = 0
-(0,6 + x) : 25 = x : 3
|x – 2| = 3
a(x — b) = 12
2(x — 23) + 3(15 — x) = -x + 1
4x – 21 = 4
-(2 — x) + 3(2x — 3) = 2
3 : x = 2 : (3 — x)
|21x + 2| = 23
a : (3x — b) = 21
2,1(2 — x) + 1,4(1,5x – 3) = 0
3 : (2x — 1) = 3
2(3 — x) – 21(x — 1) = 0
(2 – 3x) : 2 = (3 – 2x) : 3
|x + 3| = 12
b – 2ax + 4 = 0
2,1(2 – x) + 1,4(1,5x — 3) = 2
2 : (3 – 2x) = 1
-2(x — 12) – 3(x + 1) = 1
-(-3x -1) : 2 = x : 2
|3x — 2| = 4
(2ax — 3) : b = 1
21(2x — 1) = 14(3x — 4)
3(5x + 2) = 12
-7(2 — x) + 2(x — 3) = 0
(x — 2) : 5 = x : 3
|x — 6| = 3
bx – 4a = 8
21(x — 3) + 20 = 7(3x — 2)
21x – 3 = 12
7(2x — 1) + (4 — x) = 2x
(21x + 1) : 3 = 2x
|21x — 1| = 20
b : (ax – 5) + 1 = 0
7(2x — 3) + 1 = 2(7x — 10)
21(x — 3) = 12
2(7x + 1) – (x — 4) = 0
21 : x = 7 : (x — 3)
|21x + 1| = 20
2(bx – 4a) + 8x = 0
2(8x — 1) – 8(2x — 3) = 13
21(3 – x) = 12
3x – 2(2 — x) = 7(x — 2)
12 : (1 — x) = 4 : (3x — 1)
|x + 11| = 1
2b – 2(a + 3x) = 2b
8(2x — 1) – 2(8x – 3) = 2
21 : (x — 3) = 7
-2(x — 2) + 3(2x – 1) = 0
(3 + x) : 2 = (3x — 1) : 3
|7x — 1| = 6
3(ax — 1) = 2b
8(2x — 1) – 2(8x — 3) = -2
7(3x + 1) = -14
-12(2x — 1) – (x – 1) = x
(-12x + 1) : 2 = 3x
|7x + 3| = 4
2(x – 3a) = 4b
11(2x — 3) = 5(4x — 6) + 2x
3x + 12 – 2x = 11
-2(x — 2) – (3x + 1) = 3
3x : 2 = (3 + x) : 4
|x — 23| = 22
3(a + x) = 2b
9(2x — 1) + 2 = 2(9x — 3) — 1
5x – 2 = 13
-3(4 — x) + (2 – x) = 3x
(3x + 2) : 4 = (x + 3) : 3
|2x — 5| = 5
3bx + 2a = 4a
9(2x — 1) + 2 = 2(9x — 3)
5(x — 2) = 15
-(2x — 1) + 2(2 — x) = x
(x + 2) : 3 = x : 2
|2x + 5| = 5
ax – 4b = 2
3(x + 2) = 2(1,5x + 4)
www.metod-kopilka.ru
Алгебра. Урок 4. Уравнения, системы уравнений
Содержание страницы:
Линейное уравнение – уравнение вида ax=b, где x — переменная, a и b некоторые числа, причем a≠0.
Примеры:
Линейными уравнениями называют не только уравнения вида ax=b, но и любые уравнения, которые при помощи преобразований и упрощений сводятся к этому виду.
Как же решать уравнения, которые приведены к виду ax=b? Достаточно поделить левую и правую часть уравнения на величину a. В результате получим ответ: x=ba.
Как распознать, является ли произвольное уравнение линейным или нет? Надо обратить внимание на переменную, которая присутствует в нем. Если старшая степень, в которой стоит переменная, равна единице, то такое уравнение линейное.
Для того, чтобы решить линейное уравнение, необходимо раскрыть скобки (если они есть), перенести «иксы» в левую часть, числа – в правую, привести подобные слагаемые. Получится уравнение вида ax=b. Решение данного уравнения: x=ba.
Примеры:
- 2x+1=2(x−3)+8
Это линейное уравнение, так как переменная стоит в первое степени.
Попробуем преобразовать его к виду ax=b:
Для начала раскроем скобки:
2x+1=4x−6+8
В левую часть переносятся все слагаемые с x, в правую – числа:
2x−4x=2−1
−2x=1
Теперь поделим левую и правую часть на число (-2):
−2x−2=1−2=−12=−0,5
Ответ: x=−0,5
- x2−1=0
Это уравнение не является линейным, так как старшая степень, в которой стоит переменная x равна двум.
- x(x+3)−8=x−1
Это уравнение выглядит линейным на первый взгляд, но после раскрытия скобок старшая степень становится равна двум:
x2+3x−8=x−1
Это уравнение не является линейным.
Особые случаи (в 4 задании ОГЭ они не встречались, но знать их полезно)
Примеры:
- 2x−4=2(x−2)
Это линейное уравнение. Раскроем скобки, перенесем иксы влево, числа вправо:
2x−4=2x−4
2x−2x=−4+4
0=0
И как же здесь искать x, если его нет? После выполнения преобразований мы получили верное равенство (тождество), которое не зависит от значения переменной x . Какое бы значение x мы ни подставляли бы в исходное уравнение, в результате всегда получается верное равенство (тождество). Значит x может быть любым числом.
Ответ: x∈(−∞; +∞)
- 2x−4=2(x−8)
Это линейное уравнение. Раскроем скобки, перенесем иксы влево, числа вправо:
2x−4=2x−16
2x−2x=−16+4
0=−12
В результате преобразований x сократился, но в итоге получилось неверное равенство, так как . Какое бы значение x мы ни подставляли бы в исходное уравнение, в результате всегда будет неверное равенство. А это означает, что нет таких значений x, при которых равенство становилось бы верным.
Ответ: x∈∅
Квадратное уравнение — уравнение вида ax2+bx+c=0, где x — переменная, a,b и c — некоторые числа, причем a≠0.
Алгоритм решения квадратного уравнения:
- Раскрыть скобки, перенести все слагаемые в левую часть, чтобы уравнение приобрело вид: ax2+bx+c=0
- Выписать, чему равны в числах коэффициенты: a=…b=…c=…
- Вычислить дискриминант по формуле: D=b2−4ac
- Если D>0, будет два различных корня, которые находятся по формуле: x1,2=−b±D2a
- Если D=0, будет один корень, который находится по формуле: x=−b2a
- Если D<0, решений нет: x∈∅
Примеры:
- −x2+6x+7=0
a=−1,b=6,c=7
D=b2−4ac=62−4⋅(−1)⋅7=36+28=64
D>0 — будет два различных корня:
x1,2=−b±D2a=−6±642⋅(−1)=−6±8−2=[−6+8−2=2−2=−1−6−8−2=−14−2=7
Ответ: x1=−1,x2=7
- −x2+4x−4=0
a=−1,b=4,c=−4
D=b2−4ac=42−4⋅(−1)⋅(−4)=16−16=0
D=0 — будет один корень:
x=−b2a=−42⋅(−1)=−4−2=2
Ответ: x=2
- 2×2−7x+10=0
a=2,b=−7,c=10
D=b2−4ac=(−7)2−4⋅2⋅10=49−80=−31
D<0 — решений нет.
Ответ: x∈∅
Квадратный трехчлен можно разложить на множители следующим образом:
ax2+bx+c=a⋅(x−x1)⋅(x−x2)где a — число, коэффициент перед старшим коэффициентом,
x — переменная (то есть буква),
x1 и x2 — числа, корни уравнения ax2+bx+c=0, которые найдены через дискриминант.
Если уравнение имеет только один корень , то разложение выглядит так:
ax2+bx+c=a⋅(x−x0)2
Примеры:
- −x2+6x+7=0⇒x1=−1, x2=7
−x2+6x+7=(−1)⋅(x−(−1))(x−7)=−(x+1)(x−7)=(x+1)(7−x)
- −x2+4x−4=0;⇒x0=2
−x2+4x−4=(−1)⋅(x−2)2=−(x−2)2
Если квадратный трехчлен является неполным, ( (b=0 или c=0) то его можно разложить на множители следующими способами:
- b=0⇒ применить формулу сокращенного умножения для разности квадратов.
Пусть f(x) и g(x) — некоторые функции, зависящие от переменной x.
Дробно рациональное уравнение – это уравнение вида f(x)g(x)=0.
Для того, чтобы решать дробно рациональные уравнения, надо вспомнить, что такое ОДЗ и когда оно возникает.
ОДЗ – область допустимых значений переменной.
В выражении вида f(x)g(x)=0
ОДЗ: g(x)≠0 (знаменатель дроби не может быть равен нулю).
Алгоритм решения дробно рационального уравнения:
- Привести выражение к виду f(x)g(x)=0.
- Выписать ОДЗ: g(x)≠0.
- Приравнять числитель дроби к нулю f(x)=0 и найти корни.
- Указать в ответе корни из числителя, исключив те корни, которые попали в ОДЗ.
Пример:
Решить рациональное уравнение x2−42−x=1.
Решение:
Будем действовать в соответствии с алгоритмом.
- Привести выражение к виду f(x)g(x)=0.
Переносим единичку в левую часть, записываем к ней дополнительный множитель, чтобы привести оба слагаемых к одному общему знаменателю:
x2−42−x−1\2−x=0
x2−42−x−2−x2−x=0
x2−4−(2−x)2−x=0
x2−4−2+x2−x=0
x2+x−62−x=0
Первый шаг алгоритма выполнен успешно.
- Выписать ОДЗ:
g(x)≠0
2−x≠0
−x≠−2
x≠2
Обводим в рамочку ОДЗ, не забываем про него: x≠2
- Приравнять числитель дроби к нулю f(x)=0 и найти корни:
x2+x−6=0 — Квадратное уравнение. Решаем через дискриминант.
a=1,b=1,c=−6
D=b2−4ac=12−4⋅1⋅(−6)=1+24=25
D>0 — будет два различных корня.
x1,2=−b±D2a=−1±252⋅1=−1±52=[−1+52=42=2−1−52=−62=−3
[x1=2×2=−3
- Указать в ответе корни из числителя, исключив те корни, которые попали в ОДЗ.
Корни, полученные на предыдущем шаге:
[x1=2×2=−3
ОДЗ: x≠2
Значит, в ответ идет только один корень, x=−3.
Ответ: x=−3.
Системой уравнений называют два уравнения с двумя неизвестными (как правило, неизвестные обозначаются x и y), которые объединены в общую систему фигурной скобкой.
Пример системы уравнений
{x+2y=83x−y=−4
Решить систему уравнений — найти пару чисел x и y, которые при подстановке в систему образуют верное равенство в обоих уравнениях системы.
Существует два метода решений систем линейных уравнений:
- Метод подстановки.
- Метод сложения.
Алгоритм решения системы уравнений методом подстановки:
- Выразить из любого уравнения одну переменную через другую.
- Подставить в другое уравнение вместо выраженной переменной полученное значение.
- Решить уравнение с одной неизвестной.
- Найти оставшуюся неизвестную.
Пример:
Решить систему уравнений методом подстановки
{x+2y=83x−y=−4
Решение:
- Выразить из любого уравнения одну переменную через другую.
{x=8−2y3x−y=−4
- Подставить в другое уравнение вместо выраженной переменной полученное значение.
{x=8−2y3x−y=−4
{x=8−2y3(8−2y)−y=−4
- Решить уравнение с одной неизвестной.
3(8−2y)−y=−4
24−6y−y=−4
−7y=−4−24
−7y=−28
y=−28−7=287=4
y=4
- Найти оставшуюся неизвестную.
y=4
x=8−2y=8−2⋅4=8−8=0
Ответ можно записать одним из трех способов:
Ответ:
- x=0,y=4
- {x=0y=4
- (0; 4)
Решение системы уравнений методом сложения.
Метод сложения основывается на следующем свойстве:
если
{a=bc=d
то
(a+c)=(b+d)
Идея метода сложения состоит в том, чтобы избавиться от одной из переменных, сложив уравнения.
Пример:
Решить систему уравнений методом сложения
{x+2y=83x−y=−4
Давайте избавимся в данном примере от переменной x. Суть метода состоит в том, чтобы в первом и во втором уравнении перед переменной x стояли противоположные коэффициенты. Во втором уравнении перед x стоит коэффициент 3. Для того, чтобы метод сложения сработал, надо чтобы перед переменной x оказался коэффициент (−3). Для этого домножим левую и правую часть первого уравнения на (−3).
{x+2y=8 | ⋅(−3)3x−y=−4
{(−3)⋅(x+2y)=(−3)⋅83x−y=−4
{−3x−6y=−243x−y=−4
Теперь, когда перед переменной в обоих уравнениях стоят противоположные коэффициенты, при сложении левых частей уравнений переменная x исчезнет.
{−3x−6y=−243x−y=−4⊕
(−3x−6y)+(3x−y)=(−24)+(−4)
−3x−6y+3x−y=−24−4
−7y=−28
y=−28−7=287=4
Осталось найти переменную x. Для этого подставим y=4 в любое из двух уравнений системы. Например, в первое.
x+2y=8
x+2⋅4=8
x+8=8
x=8−8=0
Ответ можно записать одним из трех способов:
Ответ:
- x=0,y=4
- {x=0y=4
- (0; 4)
Скачать домашнее задание к уроку 4.
epmat.ru
Тренажер по математике на тему «Решение уравнений, сводящихся к линейным» (7 класс)
Государственное бюджетное общеобразовательное учреждение школа №60
Выборгского района Санкт-Петербурга
Учитель: Воронова Лариса Валентиновна
Методическая разработка тренажера по математике
для 6 — 7 класса по теме:
«Решение уравнений, сводящихся к линейным»
Аннотация.
Тренажер предназначен для учащихся 6–7 классов с целью отработки и совершенствования навыков решения уравнений первой степени, содержащих дробную часть.
Тренажер содержит:
— пошаговую инструкцию преобразования заданного уравнения к более простому виду, что в итоге приводит к линейному уравнению вида ax=b;
— задания в двух уровнях: уровень А (базовый) и уровень В (повышенный).
— ответы к заданиям;
— примеры решения уравнений.
Тренажер может быть использован для самостоятельной работы учащихся в классе и дома, на дополнительных индивидуальных занятиях, а также при подготовке к итоговой аттестации.
Материал тренажера можно использовать для составления раздаточного материала.
Тренажер по теме:
«Решение уравнений, сводящихся к линейным»
(уровень А)
Алгоритм решения.
Найти общий знаменатель всех дробей, входящих в уравнение (наименьшее общее кратное всех знаменателей).
Умножить каждый член в левой и правой частях уравнения на общий знаменатель.
Сократить получившиеся дроби.
Упростить левую и правую части уравнения (раскрыть скобки).
Перенести неизвестные члены уравнения в левую часть, а известные – в правую, изменив при этом их знак на противоположный.
Привести подобные слагаемые в левой части и найти значение правой части.
Получится линейное уравнение вида ax = b.
Найти значение x, разделив обе части уравнения на коэффициент при неизвестном a.
Решить уравнения
У р о в е н ь А
№п/п
Вариант 1
Вариант 2
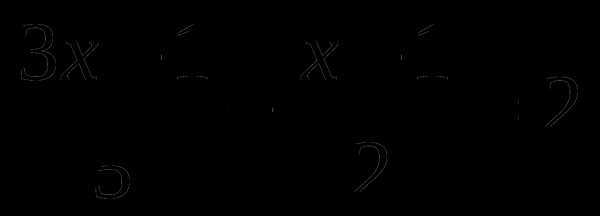
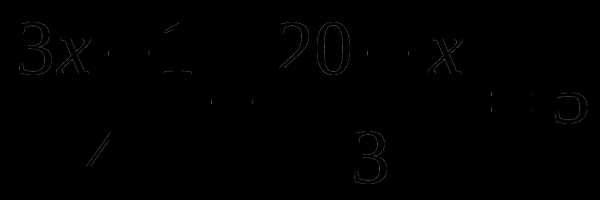
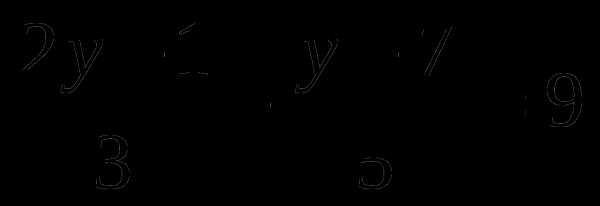
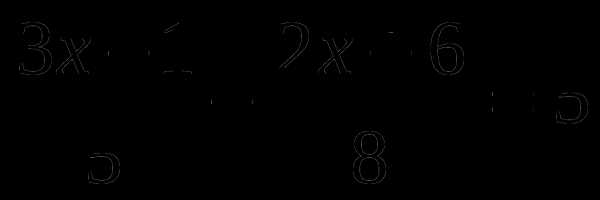
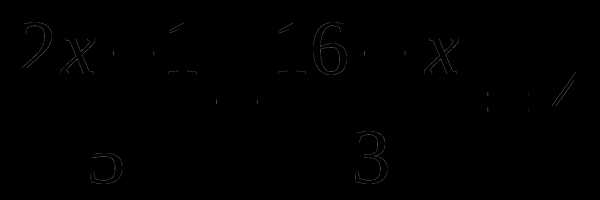
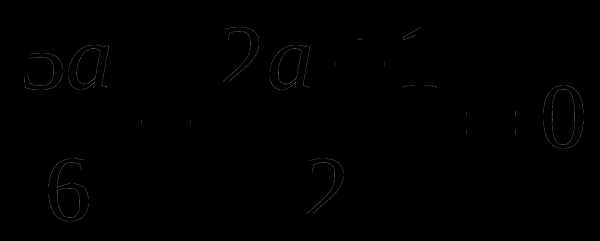
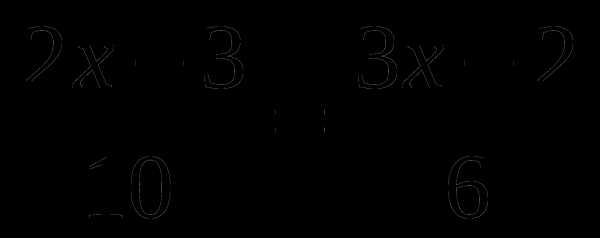
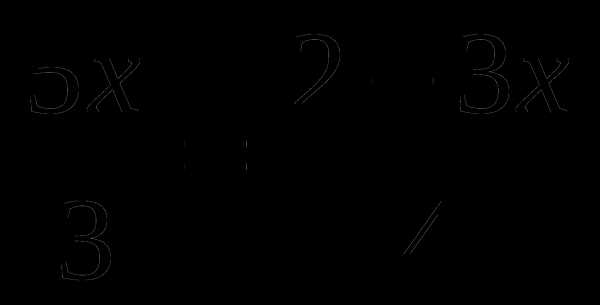
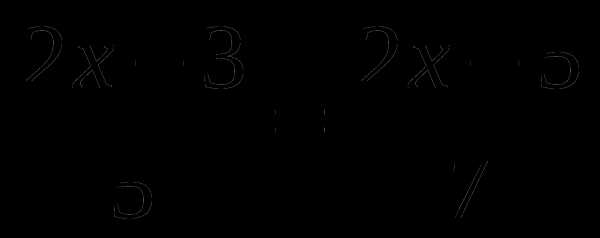
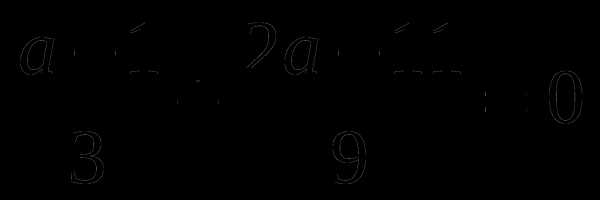
Тренажер по теме:
Решение уравнений, сводящихся к линейным
(уровень В)
Алгоритм решения.
1. Найти общий знаменатель всех дробей, входящих в уравнение (наименьшее общее кратное всех знаменателей).
2. Умножить каждый член в левой и правой частях уравнения на общий знаменатель.
3. Сократить получившиеся дроби.
4. Упростить левую и правую части уравнения (раскрыть скобки).
5. Перенести неизвестные члены уравнения в левую часть, а известные – в правую, изменив при этом их знак на противоположный.
6. Привести подобные слагаемые в левой части и найти значение правой части.
Получится линейное уравнение вида ax = b.
7. Найти значение x, разделив обе части уравнения на коэффициент при неизвестном a.
Решить уравнения
У р о в е н ь В
№п/п
Вариант 1
Вариант 2
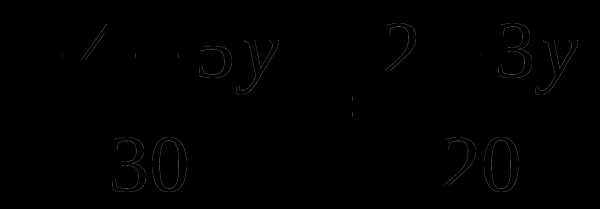
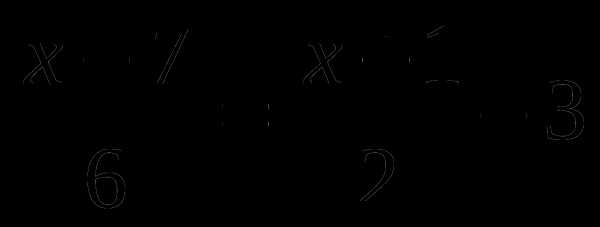
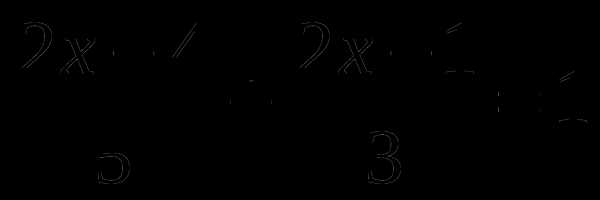
9 — 
2x —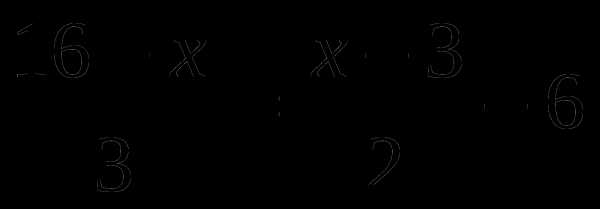
6 —
Ответы к тренажеру
«Решение уравнений, сводящихся к линейным»
Уровень А
Уровень В
Вариант 1
Вариант 2
1
17
13
2
11
-4
3
-3
11
4
17
17
5
13
2
6
-7
-7
7
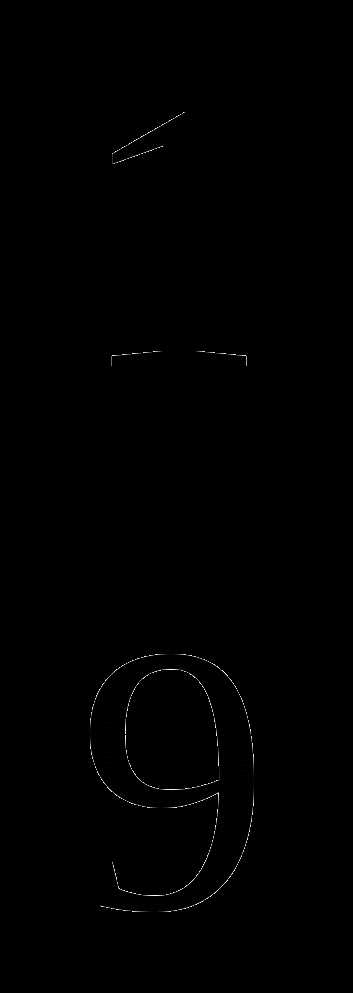
2
8
1
9
2,5
10
-1
Вариант 1
Вариант 2
1
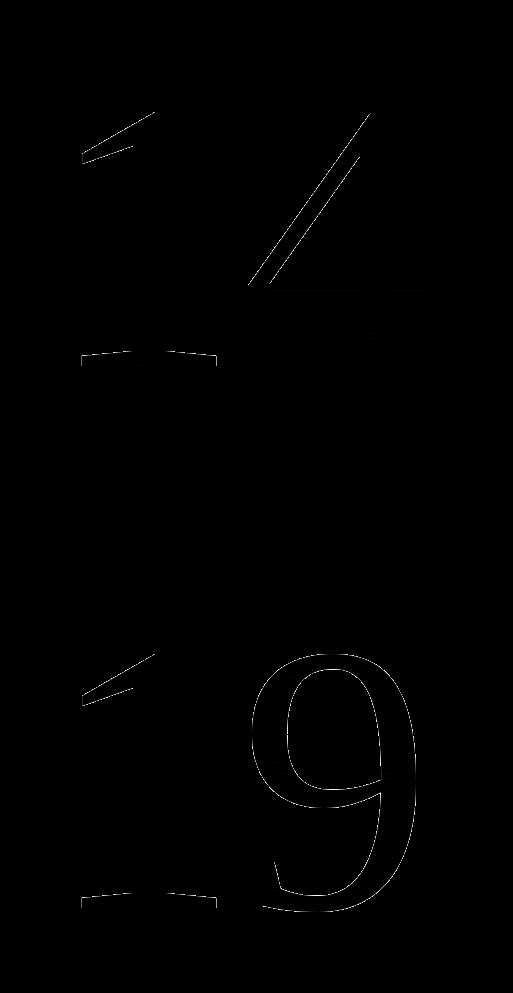
2
3
-2,5
4
45
170
5
4
—
6
12
2
7
2
2
8
49
7
9
11
-8
10
5
7
Примеры решения уравнений
I способ II способ
1) 
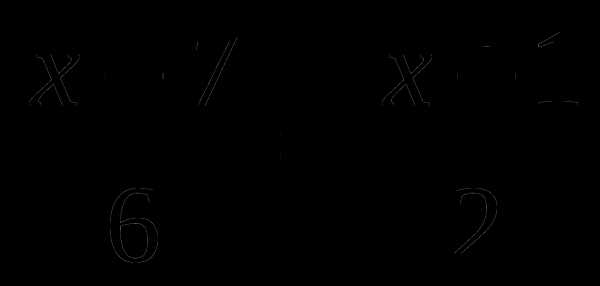или
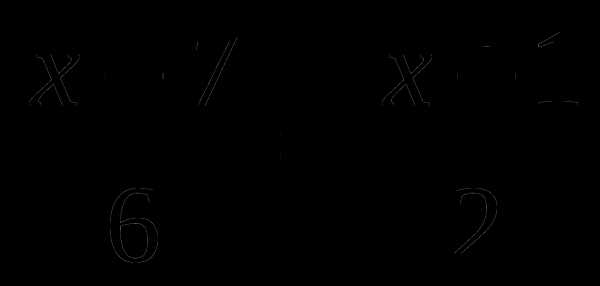— пропорция
1 / 3/
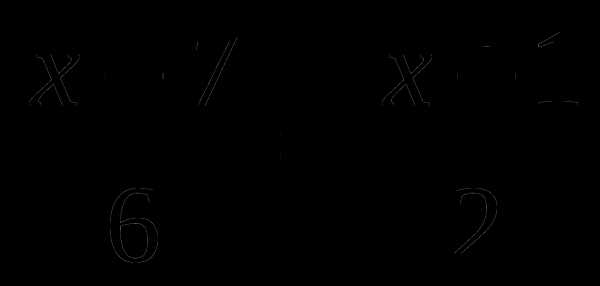|•6
x — 7 = 3(x+1)
x – 7 = 3x + 3
x — 3x = 3+7
-2x = 10
x = 10: (–2)
x = –5
Основное свойство пропорции: произведение крайних членов пропорции
равно произведению ее средних членов.
(x – 7)·2 = 6·(x+1)
2 x – 14 = 6x + 6
2 x –6 x = 6 + 14
-4x = 20
x = 20: (-4)
x = –5
2)
3) 
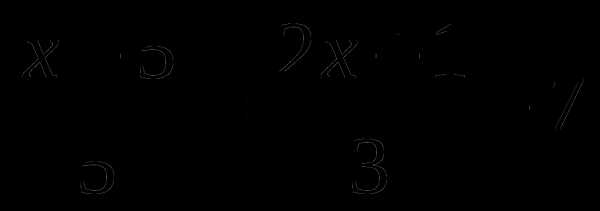
8/ 7/ 56/
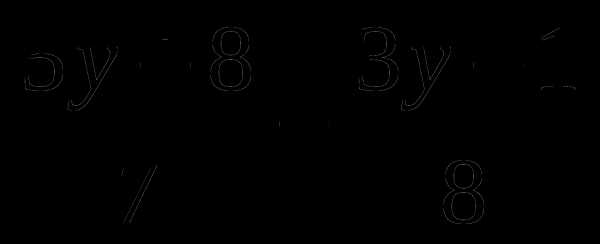= 5 |·56
8(5y + 8) – 7(3y — 1) = 56·5
40y + 64 – 21y +7 = 280
19y = 280 – 64 – 7
19y = 209
y = 209 : 19
y = 11
3/ 5/ 15/
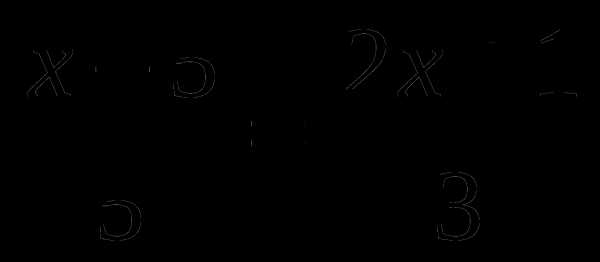— 7|·15
3(х — 5) = 5(2х + 1) — 15·7
3х – 15 = 10х +5 – 105
3х – 10х = -100 + 15
-7х = -85
х = -85: (-7)
х = 
= 12
4)
5)
3/ 2/ 42/
–
+ 
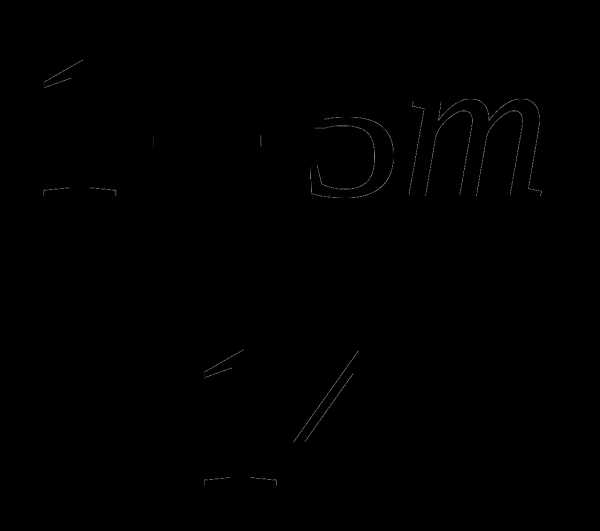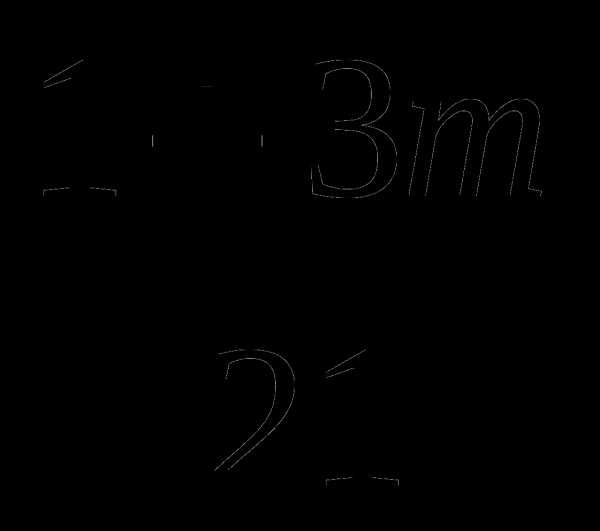= 0 |·42
–3(1 – 5m) + 2(1 +3m) = 0
–3 + 15m + 2 + 6m = 0
21m = 0 + 3 – 2
21m = 1
m = 1 : 21
m =
6/ 2/ 3/ 6/
2x — 
= 
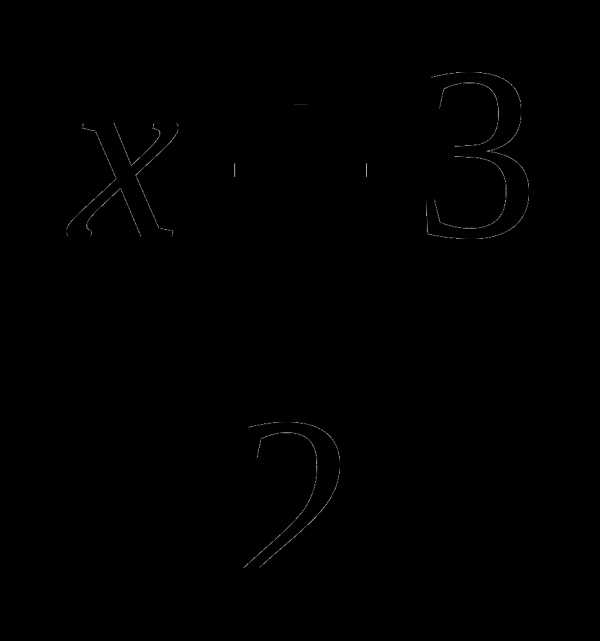+ 6 |·6
6·2x – 2(16 – x) = 3(x +3) +6·6
12x – 32 + 2x = 3x + 9 + 36
14x – 3x = 45 + 32
11x = 77
x= 77 : 11
x = 7
Ответ: 1) —5; 2) 11; 3) 12; 4) ; 5) 7.
infourok.ru
Тест по алгебре (7 класс) по теме: Тренажер по решению линейных уравнений.
Тренажер по теме «Решение линейных уравнений»
Чтобы найти неизвестный множитель, нужно произведение разделить на известный множитель |
Образец: 2х=10 х=10:2 х=5 |
Решите уравнение по образцу:
- 5х=10
- 10х=90
- 13у=78
- 25m=375
- 2х=-12
- -3к=15
- -12у=-36
- 31в=-93
- -4х=1,2
- 6у=-0,36
- -12к=-1,44
- -0,2х=-1,2
- 1.7у=-0,34
- -7,4m=-1,48
- 3х=1
- 7r =-4
- 13у=-10
- -10v=-7
- х=4
- у=6
- к=-.
- х=-1
- а=-1
Корни уравнения не изменяются, если какое-нибудь слагаемое перенести из одной части уравнения в другую, изменив при этом знак на противоположный. |
Образец: х+5=10 х=10-5 х=5 | Образец: х-4=10 х=10+4 х=6 |
Решите уравнения:
- Х+6=10.
- У+14=19,
- а+41=60,
- 2х+3=13,
- 3у+14=77,
- 5х+13=73,
- Х-4,5=10,
- 5-у=4,
- 10-х=6,
- х -7,8=1,2,
- 2х-3=16,
- 100-5х=17,
- 0,2х+3=-1,5,
- -1,2у-4,7=-3,5,
- 4х+х=-15,
- 3у-5у=7,
- -4х-3у=-49,
- Х+4=3х,
- -3у+7=2у.
- 5а-1,5=2а.
- -0,2х+7=-1,6х,
- t+5=t-7,
- 2у=7у,
- -3к+8=-3к+9,
- 6,9-9n=-5n-33,1,
Образец: 3х+6=4х-1 3х-4х=-1-6 -х=-7 х=7 |
Решить уравнения:
- 2х+8=6х-2,
- 10у+3=2у-1,
- -4+3к=8к+5.
- 9+4а=8а-9,
- 3в+9=8в+2,
- 6-2с=3с-10,
- 5-2у=8у+9,
- -4х+3=4х-5,
- 4а+4=-6а-5.
- 3у+3=-2-7у.
- -10х+3=-1-8х,
- 9-4х=-4-9х,
- -8а+9=3-4а,
- с+3=с+5,
- t-t+2=t-3,
- x+x+5=x,
- 0,2f+2,3=0,7f-3,2,
- -0,4x-14=0,3x,
- -40·(-7x+5)=-1600,
- (-20t-50)·2=100,
- 2,1·(4-6e)=-42,
- -3·(2-15k)=-6,
- -20·(x-13)=-220,
- (30-7r)·8=352,
- (2,8-0,1h)·3,7=7,4,
- (3x-1,2)·7=10,5,
- x-=.
Образец: 2·(х-7)=3, 2х-14=3, 2х=3+14, 2х=17, х=17:2, х=8,5. |
Решить уравнение.
- 5·(у-9)=-2.
- 3=4·(к+2),
- 5·(с+5)=-7,
- 7·(а-1)=3а.
- 7·(-3+2х)=-6х-1,
- 2·(7+9к)=-6к+2,
- 6·(5-3с)=-8с-7,
- 4·(2-3х)=-7х+10,
- -4·(-к+7)=к+17,
- -5·(0,8t-1,2)=-t+7,2,
- -5·(3а+1)-11=-16,
- -3,2n+4,8=-2·(1,2n+2,4),
- -5·(0,8f-1,4)=-f+7,
- 5·(r-7)=3·(r-4)-27,
- 8-7·(c-2)=2·(2c-3)+3c,
- 4·(x-3)-16=5·(x-5),
- 5·(y-3)+27=4y+3·(2y-5),
- -4·(3-5z)=18z-7,
- 1,2-2·(1,3y+1)=5,6y-27,04,
- 8·(2f-6)=2·(4f+3),
- -3·(2,1m-1)+4,8=-6,7m+9,4,
- 6·(2c-3)+2·(4-3c)=5,
- h+- =2-h+2h,
- 1-1x+3x=1x-2x+2,5,
- 2·(z+1)+3=4-·(z-1).
Образец: =, 9х=5·4 9х=20 х=, х=2, |
Решить уравнения.
- =,
- = ,
- =,
- = ,
- = ,
- = ,
- = ,
- =4,
- =7,
- = ,
- = ,
- = ,
- = ,
- = ,
Решите уравнения:
nsportal.ru