Синтез логических выражений – Синтез логических выражений Поверина — Saratov FIO Wiki

Синтез логических выражений Поверина — Saratov FIO Wiki

Тема урока «Синтез логических выражений» (урок информатики в 10 классе информационно-технологического профиля)

Учитель Поверина Ирина Александровна

МОУ «СОШ п. Знаменский Ивантеевского района Саратовской области»

Организационный момент

(Слайды 2-5)

Приветственное слово учителя.

Сделать в жизни важный шаг — это, братцы, не пустяк!

Всё надо тщательно продумать, посмотреть и так, и сяк.

Посоветоваться с мамой, у отца совет спросить,

Вспомнить: «Я — десятиклассник!», свою логику включить.

Сразу ты, дружок, поймёшь, что есть ИСТИНА, что — ЛОЖЬ.

У компьютера внутри тоже логика. Смотри!

Определение задач урока.

Учитель:Мы с вами изучили достаточно большой блок материала из раздела «Логика». Как вы думаете, какие задачи мы можем обозначить для первой части урока?

Учащиеся:

1. Применение на практике полученных знаний
2. Развитие логического мышления
3. Формирование информационной культуры

Правила заполнения Карты индивидуальных достижений.

Учитель: На столах для вас приготовлены карточки-задания. Результаты выполнения необходимо занести в Карту индивидуальных достижений. В конце урока вы сами оцените свою работу по имеющимся критериям.

Актуализация опорных знаний.

Основные логические операции

(Слайд 6)

Учитель: Давайте вместе вспомним формулы и запишем таблицы истинности основных логических операций.

Учащиеся: пятеро учащихся выходят к доске и заполняют таблицу, остальные — делают записи в тетрадях.

Основные логические элементы

(Слайд 7)

Учитель: Установить соответствие между названиями логических элементов и изображениями.

Ученик: на доске соединяет линиями соответствующие элементы.

Построение таблицы истинности сложного выражения

(Слайд 8)

Учитель: Составим таблицу истинности для сложного выражения F=A&B \/ B&C \/ A&C

Учащиеся: заполняют таблицу на доске и делают записи в тетрадях.

Учитель:Таблицу истинности можно построить и с помощью электронных таблиц Microsoft Office Excel. (Слайды 9, 10, 11)

Проблемная ситуация

(Слайд 12)

А если наоборот задачу поставить:

Как по таблице истинности функцию составить?

Тема урока: «Синтез логических выражений».

Цель: Сегодня мы будем учиться составлять логические функции по таблицам истинности и строить логическую схему в Конструкторе

Объяснение нового материала.

(Слайды 13, 14, 15, 16)

(При демонстрации слайдов можно использовать функцию доски «затемнение экрана» для постепенного погружения учащихся в материал)

Учитель: Синтезировать (составить) логическое выражение по таблице истинности можно двумя способами:

а) Алгоритм №1

Шаг 1. Отметить строки в таблице, где F = 1.

Шаг 2. Для каждой из них записать логическое выражение, которое истинно только для этой строки.

Шаг 3. Сложить эти выражения и упростить результат.

б) Алгоритм №2

Шаг 1. Отметить строки в таблице, где F = 0.

Шаг 2. Для каждой из них записать логическое выражение, которое истинно только для этой строки.

Шаг 3. Сложить эти выражения и упростить результат.

Шаг 4. Сделать инверсию полученного выражения.

(Алгоритм желательно повторить учащимся самостоятельно с помощью учителя)

Построение логического выражения по таблице истинности

(Слайд 17)

Учитель: Предлагаю выполнить задание, применив законы алгебры логики.

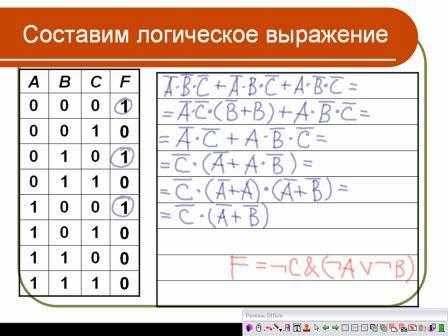
Учащиеся: Выполняют работу в тетради и на доске.

Знакомство с «Конструктором логических схем»

(Слайд 18)

Учитель знакомит учащихся с новым программным продуктом.

Предлагаю услуги инструктора по освоению нового конструктора. Он доступен, прост, понятен всем и помогает в построении логических схем.

Здесь есть элементы простые и сложные, и провода – соединения всевозможные. По логической функции схему построим. Для этого режим «Редактор» откроем. Нужные блоки на сетку поместим и проводами все соединим.

В режим «Контроль» без промедления входим, и тестирование схемы проводим: На входы полный набор значений подаем и выходные сигналы узнаем. Таблицу истинности в тетради сохраним и, если есть, вопросы зададим.

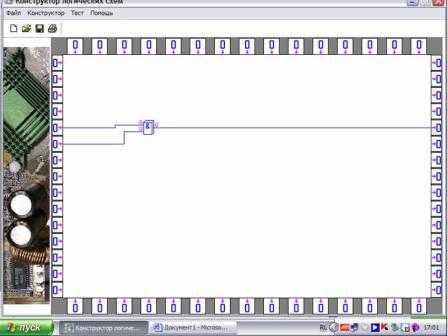
Учитель, используя интерактивную доску, демонстрирует работу в Конструкторе на примере простого логического выражения F=A&B (повторяет алгоритм работы в программе, показывает все режимы работы Конструктора — редактор и контроль) и отвечает на вопросы учащихся.

Конструктор логических схем для Windows Версия 1.11

Физкультурная минутка

(Слайд 19)

Выполнение упражнений под веселую музыку.

Формирование умений и навыков.

Составление таблицы истинности в редакторе электронных таблиц

Задание №1(на карточке)

Синтез логического выражения

Самостоятельная работа (на карточке)

Работа с Конструктором

Построить логическую схему по полученному выражению и провести ее тестирование (ввести полный набор значений входных сигналов и записать выходные сигналы)

Тестирование

Итог урока.

• Рефлексия (Слайд 21)

Учитель: Чем я вас сегодня удивила? Что нового узнали? Что не поняли?

• Запись домашнего задания (Слайд 22)
• Выставление отметок.

Учитель:Посмотрите, пожалуйста, на свои Карты индивидуальных достижений. Отметку «отлично» получает тот, у кого совпадают записи логических выражений и таблицы истинности в двух первых заданиях. Дополнительные бонусные баллы получают ученики, прошедшие тестирование.

Учитель: Всем большое спасибо. До свидания

wiki.soiro.ru

Опорный конспект на тему «Синтез логических выражений»

Синтез логических выражений.

Логический элемент – это устройство, реализующих одну из логических операций. Логические элементы, используемые в вычислительной технике и системах автоматики, основаны на использовании самых различных физических явлений и свойств. Наиболее часто применяются электронные устройства в виде интегральных микросхем. Промышленность выпускает серии интегральных схем, выполняющих самые разнообразные логические операции.

Любую логическую функцию можно выполнить с помощью логических операций И, ИЛИ, НЕ. Эти операции называются элементарными, а устройства для их реализации называются элементарными логическими элементами.

Условные обозначения элементарных логических элементов:

Элемент НЕ Элемент И Элемент ИЛИ

Все логические элементы изображаются в виде прямоугольников с линиями, по которым подводятся входные и отводятся выходные сигналы. Обычно слева располагаются линии входных сигналов, а справа – выходных. В прямоугольнике ставится знак логических операций: & – И, 1 – ИЛИ. Если выход обозначен окружностью, то элемент производит логическое отрицание результата операции, указанной внутри прямоугольника. Логическое отрицание называют инверсией, а выход, обозначенным окружностью называют инверсным выходом.

Работу элементов НЕ, ИЛИ, И поясняют таблицы, приведенные ниже, в которых показано соответствие выходного сигнала любой возможной комбинацией входных сигналов.

Такие таблицы называются таблицами истинности.

Входные и выходные сигналы могут принимать одно из двух значений: логическая 1 и логический 0. При конкретной реализации эти сигналы эти сигналы представляются различными физическими величинами (например, электрическим напряжением или потенциалом).

Существуют серии микросхем, построенных на основе составной логической схемы И-НЕ и ИЛИ-НЕ.

Условные обозначения элементарных логических элементов

И-НЕ и ИЛИ-НЕ:

Применение таких элементов позволяет использовать единую технологию для всей серии микросхем, увеличить объем выпуска и снизить стоимость каждого элемента.

infourok.ru

7. Синтез логических выражений. Синтез логических выражений.

Используя таблицу истинности любой логической формулы, можно определить ее в СДНФ или СКНФ. Для построения СДНФ в таблице истинности необходимо выбрать строки, в которых функция принимает значение 1 и сформировать конституанту 0. Переменная будет находиться в этой конституанте без знака отрицания, если она принимает значение 1 в этой строке и с отрицанием в противном случае. Соединить полученные конституанты знаком дизъюнкции.

Для получения СКНФ ищутся строки, в которых функция принимает значение 0. Строятся конституанты 1. Переменная берется со знаком отрицания, если она равна 1 и наоборот. Конституанты соединяются знаком конъюнкции.

Пример: Дана таблица истинности. Построить СДНФ и СКНФ.

x	y	z	f
0	0	0	0
0	0	1	1
0	1	0	0
0	1	1	0
1	0	0	1
1	0	1	0
1	1	0	1
1	1	1	0

СДНФ:

СКНФ:

8. Минимизация булевых функций. Импликанты. Минимальная нф. Приведенная нф.

Метод Петрика. Алгоритм Квайна. Диаграммы Вейча.

Минимизация булевых функции

Под минимизацией булевых функций понимается нахождение наиболее простого представления этой функции в виде суперпозиции функций, составляющих какую-нибудь фиксированную функционально полую систему Sбулевых функций. Наиболее простым обычно считается представление, содержащее наименьшее возможное число суперпозиций. При решении задачи минимизации важную роль играет понятие импликанты.

Булева функция называется импликантой функции, если на любом значении переменных, на котором значениеgравно 1, значениеfтакже равно 1.

Простой импликантой функции fназывается элементарное произведение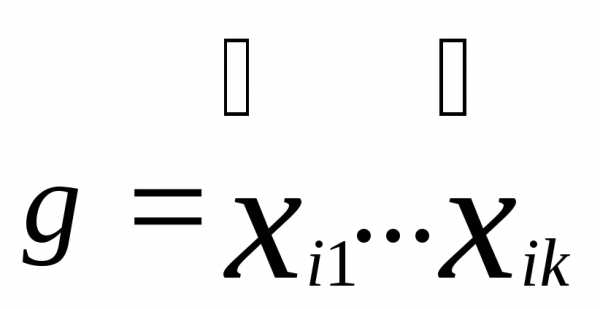, являющееся импликантойfи такое, что никакая его собственная часть (то есть произведение, получаемое изgотбрасыванием одного или нескольких компонент) уже не является импликантой функцииf.

Дизъюнкция любого множества импликант одной и той же функции является импликантой этой функции.

Дизъюнкция всех простых импликант булевой функции совпадает с этой функцией и называется сокращенной дизъюнктивной нормальной формой.

Сокращенная нормальная форма является более экономной, чем СДНФ. Однако часто допускает дальнейшее упрощение за счет того, что некоторые из простых импликант могут поглощаться дизъюнкцией других простых импликант. Например, в сокращенной ДНФ простая импликантаyzпоглощается дизъюнкцией остальных элементов формы:.

Однако справедливо следующее утверждение для сокращенной дизъюнктивной формы. Если сокращенная ДНФ не содержит никакой переменной, входящей в нее одновременно с отрицанием и без него, то эта форма является минимальной дизъюнктивной формой.

Приведение к минимальной нормальной форме от сокращенной ДНФ можно осуществит с помощью импликантной таблицы. Импликантная таблица представляет собой прямоугольную таблицу, строки которой обозначаются различными простыми импликантами, а столбцы конституантами единицы, на которых функция обращается в единицу.

На пересечении p-й строкиk-го столбца импликантной таблицы ставится * тогда и только тогда, когда импликанта составляет некоторую часть конституантыk. Для примера:

Система Sпростых импликант булевых функцийfназывается приведенной, если эта система полна и никакая ее часть не является полной системой импликант функцииf. Дизъюнкция всех простых импликант, составляющихS, называется приведенной или тупиковой дизъюнктивной нормальной формой. Всякая минимальная ДНФ является тупиковой ДНФ.

Выделение приведенной системы простых импликант может быть проведено на основе импликантной таблицы. Для этой цели надо выбрать минимальные системы строк таблицы так, чтобы для каждого столбца среди выбранных строк нашлась хотя бы одна строка содержащая звездочку. Этот метод является методом перебора и практически применим для простых импликантных таблиц. В случае сложных таблиц можно применять алгебраический метод Петрика.

Суть этого метода заключается в том, что по импликантной таблице строится некоторое выражение, называемое конъюнктивным представлением этой таблицы. Для этого производится обозначение всех простых импликант различными буквами (например, A,B,C, …). После этого для каждого столбцаимпликантной таблицы строится дизъюнкция

всех букв, обозначающих строки, на пересечении которых со столбцом стоит *. Беря произведение полученныхq_для всех столбцов, конъюнктивное представление таблицы. Обозначим для нашего примера :. Тогда получим следующее представление таблицы:

Если в конъюнктивном представлении раскрыть все скобки в соответствии с законом дистрибутивности, получим дизъюнктивное представление.

Простые импликанты, символы которых в любой фиксированный терм дизъюнктивного представления составляют полную систему простых импликант функции.

Выполняя в дизъюнктивном представлении импликантной таблицы все элементарные поглощения и устраняя повторения в соответствии с тождествами АА=А и АА = А, приходим к приведенному дизъюнктивному представлению импликантной таблицы.

Термам этого представления соответствуют все приведенные системы простых импликант функции.

В примере получим:

.

То есть получим 2 приведенные системы простых импликант (A,B,C) и (A,B,D). Им соответствуют две тупиковые ДНФ исходной функции:

studfiles.net

Синтез логических схем по логическим выражениям

Логические схемы строятся на основе логических элементов, набор которых определяется заданным логическим базисом.

Для базиса Буля в качестве логических элементов используются элементы, реализующие базовые логические функции И, ИЛИ, НЕ, которые имеют приведенные на рис. 1.2.1 обозначения.

При синтезе схемы по логическому выражению, составляющие логические операции представляются в виде соответствующих логических элементов, связи между которыми определяются последовательностью выполнения логических операций в заданном выражении.

Рис. 1.2‑1

Пример

Синтезировать логическую схему в базисе И, ИЛИ, НЕ, реализующую логическое выражение

y1=	______________ ( x1x2 +x1x3 +x2 x3 )(x1 +x2 +x3 ) +x1 x2 x3.

Решение

Входными сигналами синтезируемой схемы являются x₁, x₂, x₃, а выходным — y₁.

Реализацию заданного выражения в виде логической схемы можно начать или с последней операции, или с первой.

Последней операцией в заданном выражении является операция логического сложения двух операндов

________________ ( x1x2 +x1x3 +x2 x3 )(x1 +x2 +x3 ) и х1 x2 x3,

поэтому для её реализации требуется элемент ИЛИ(1) с двумя входами, на выходе которого будет сформирован сигнал, соответствующий y₁, если на его входы будут поданы эти два слагаемые (например, первое слагаемое на второй вход, а второе слагаемое на первый вход).

На первый вход ИЛИ(1) подается логическое произведение х₁ x₂ x₃,

для реализации которого необходимо использовать логический элемент И с тремя входами, на которые подаются входные переменные х₁, x_2, x₃. Аналогичным образом рассматривается последовательность формирования выражения

__________________ ( x1x2 +x1x3 +x2 x3 )(x1 +x2 +x3 ),

которое соответствует сигналу, подаваемому на второй вход элемента ИЛИ(1). В результате синтезируется схема для заданного выражения, приведенная на рис.1.2.2 .

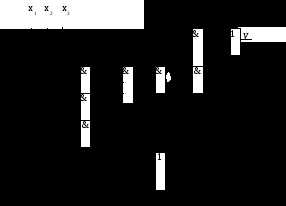
Рис. 1.2‑2

4. Минимизация логических выражений

Учитывая то, что одну и ту же логическую функцию можно представить различными выражениями, перед реализацией функции в виде логической схемой весьма важным является выбор из всех возможных выражений, соответствующих данной функции, самого простого. Решить эту проблему можно за счет использования процедуры минимизации логического выражения. Из множества методов минимизации наиболее часто используются:

1. минимизация методом Квайна;

1. минимизация методом с использованием диаграмм Вейча (или карт Карно).

studfiles.net

Логические основы компьютеров — Информатика

Логические основы компьютеров

• Логические выражения и операции
• Диаграммы
• Преобразование логических выражений
• Синтез логических выражений
• Логические элементы компьютера
• Логические задачи

Логические основы компьютеров

Тема 1. Логические выражения и операции

Булева алгебра

Двоичное кодирование – все виды информации кодируются с помощью 0 и 1.

Задача – разработать оптимальные правила обработки таких данных.

Джордж Буль разработал основы алгебры, в которой используются только 0 и 1 (алгебра логики, булева алгебра).

Почему «логика»? Результат выполнения операции можно представить как истинность (1) или ложность (0) некоторого высказывания.

Логические высказывания

Логическое высказывание – это повествовательное предложение, относительно которого можно однозначно сказать, истинно оно или ложно.

Высказывание или нет ?

• Сейчас идет дождь. Жирафы летят на север. История – интересный предмет. У квадрата – 10 сторон и все разные. Красиво! В городе N живут 2 миллиона человек. Который час?
• Сейчас идет дождь.
• Жирафы летят на север.
• История – интересный предмет.
• У квадрата – 10 сторон и все разные.
• Красиво!
• В городе N живут 2 миллиона человек.
• Который час?

Обозначение высказываний

A – Сейчас идет дождь.

B – Форточка открыта.

простые высказывания (элементарные)

!

Любое высказывание может быть ложно (0) или истинно (1).

Составные высказывания строятся из простых с помощью логических связок (операций) » и «, » или «, » не «, » если … то «, » тогда и только тогда » и др.

A и B

A или не B

если A, то B

не A и B

A тогда и только

тогда, когда B

Сейчас идет дождь и открыта форточка.

Сейчас идет дождь или форточка закрыта.

Если сейчас идет дождь, то форточка открыта.

Сейчас нет дождя и форточка открыта.

Дождь идет тогда и только тогда, когда открыта форточка.

5

5

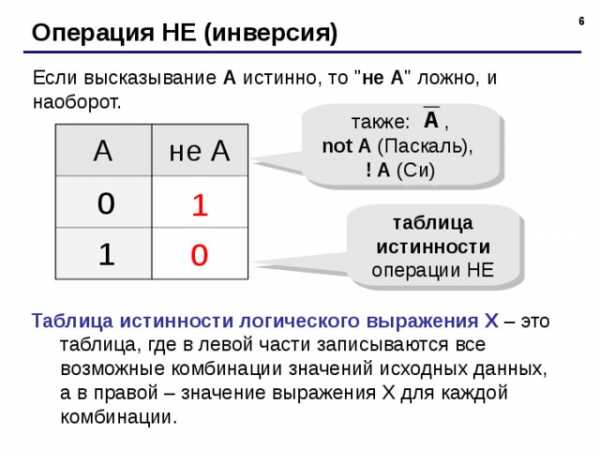
Операция НЕ (инверсия)

Если высказывание A истинно, то » не А » ложно, и наоборот.

также: , not A (Паскаль), ! A (Си)

А

не А

0

1

таблица истинности операции НЕ

1

0

Таблица истинности логического выражения Х – это таблица, где в левой части записываются все возможные комбинации значений исходных данных, а в правой – значение выражения Х для каждой комбинации.

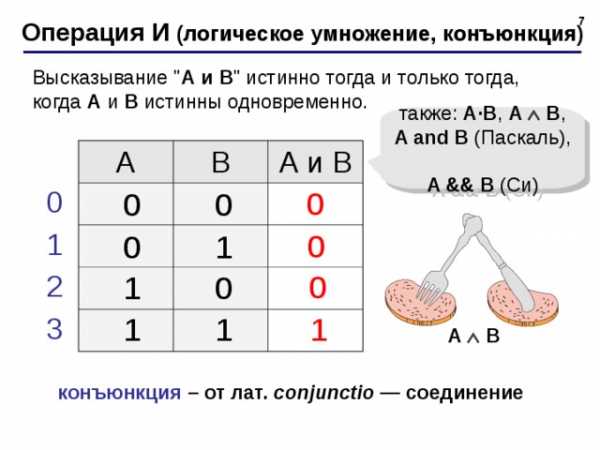
Операция И (логическое умножение, конъюнкция)

Высказывание » A и B » истинно тогда и только тогда, когда А и B истинны одновременно.

также: A·B , A  B , A and B (Паскаль), A && B (Си)

A

B

А и B

0

1

2

3

0

0

0

0

0

1

0

1

0

1

1

1

A  B

конъюнкция – от лат. conjunctio — соединение

Операция ИЛИ (логическое сложение, дизъюнкция)

Высказывание » A или B » истинно тогда, когда истинно А или B , или оба вместе.

также: A+B , A  B , A or B (Паскаль), A || B (Си)

A

B

А или B

0

0

0

1

0

1

1

1

0

1

1

1

дизъюнкция – от лат. disjunctio — разъединение

8

8

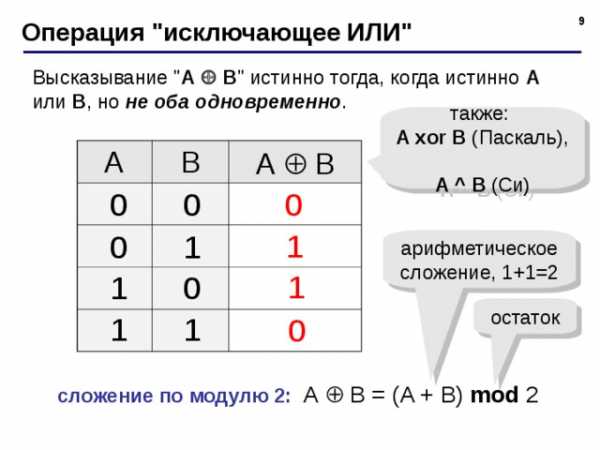
Операция «исключающее ИЛИ»

Высказывание » A  B » истинно тогда, когда истинно А или B , но не оба одновременно .

также: A xor B (Паскаль), A ^ B (Си)

A

B

А  B

0

0

0

1

0

1

арифметическое сложение, 1+1=2

1

1

0

остаток

1

1

0

сложение по модулю 2: А  B = (A + B) mod 2

9

9

Свойства операции «исключающее ИЛИ»

0

A  A =

( A  B)  B =

A

A  0 =

A  1 =

?

A

A

0

B

0

0

1

1

1

0

А  B

1

0

0

0

0

1

0

1

1

1

1

1

0

0

0

0

0

10

10

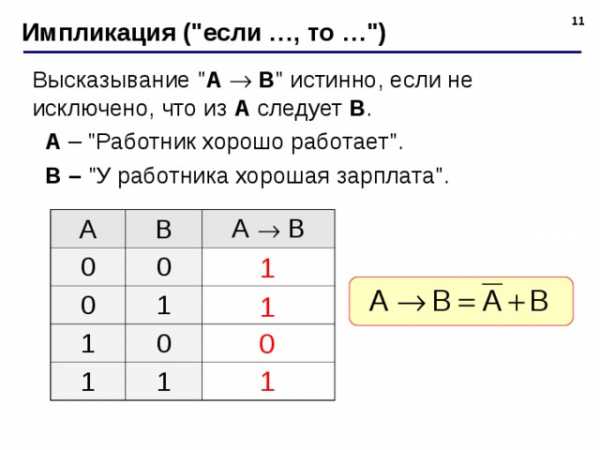
Импликация («если …, то …»)

Высказывание » A  B » истинно, если не исключено, что из А следует B .

A – «Работник хорошо работает».

B – «У работника хорошая зарплата».

A

0

B

А  B

0

0

1

1

1

0

1

1

1

0

1

11

11

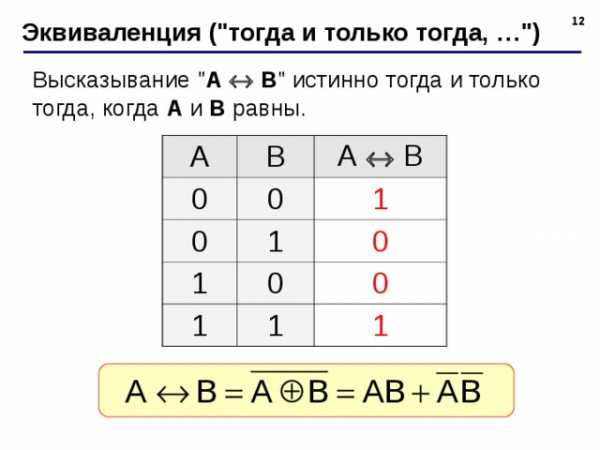
Эквиваленция («тогда и только тогда, …»)

Высказывание » A  B » истинно тогда и только тогда, когда А и B равны.

A

B

0

0

А  B

0

1

1

1

0

0

1

1

0

1

12

12

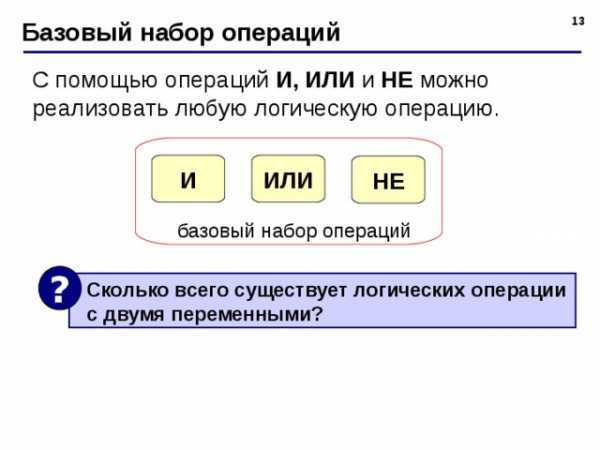
Базовый набор операций

С помощью операций И, ИЛИ и НЕ можно реализовать любую логическую операцию.

ИЛИ

И

НЕ

базовый набор операций

?

Сколько всего существует логических операции с двумя переменными?

13

13

Логические формулы

Система имеет три датчика и может работать, если два из них исправны.

A – «Датчик № 1 неисправен».

B – «Датчик № 2 неисправен».

C – «Датчик № 3 неисправен».

Аварийный сигнал :

X – «Неисправны два датчика».

X – «Неисправны датчики № 1 и № 2″ или

«Неисправны датчики № 1 и № 3″ или

«Неисправны датчики № 2 и № 3″.

логическая формула

14

14

Составление таблиц истинности

A

B

0

0

A · B

0

1

1

0

1

1

X

0

1

1

0

0

1

2

3

0

1

0

1

0

0

1

1

1

0

0

1

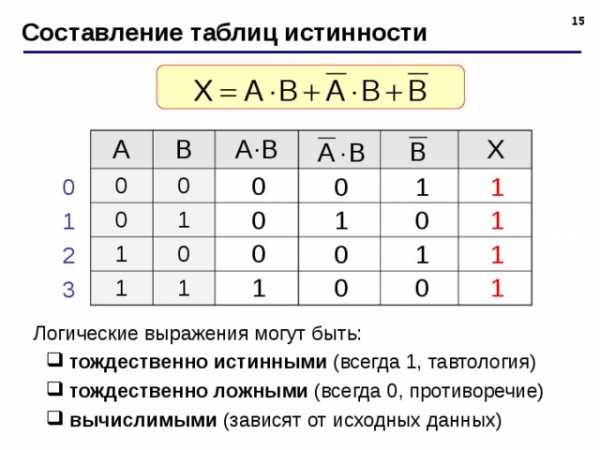
Логические выражения могут быть:

• тождественно истинными (всегда 1, тавтология) тождественно ложными (всегда 0, противоречие) вычислимыми (зависят от исходных данных)
• тождественно истинными (всегда 1, тавтология)
• тождественно ложными (всегда 0, противоречие)
• вычислимыми (зависят от исходных данных)

15

15

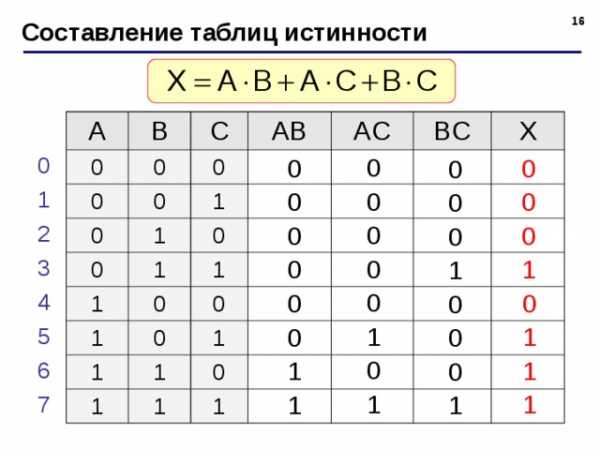
Составление таблиц истинности

A

B

0

C

0

0

AB

0

0

0

AC

0

1

1

1

BC

0

1

1

X

0

1

0

0

1

1

1

1

1

0

1

0

0

1

2

3

4

5

6

7

0

0

0

0

0

0

0

0

0

0

0

0

1

0

1

0

0

0

0

1

1

0

0

0

1

1

0

1

1

1

1

16

16

Логические основы компьютеров

Тема 2. Диаграммы

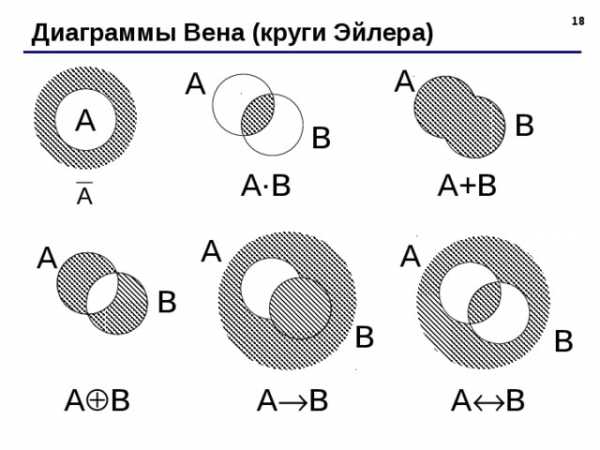
Диаграммы Вена (круги Эйлера)

A

A

A

B

B

A · B

A+B

A

A

A

B

B

B

A  B

A  B

A  B

18

18

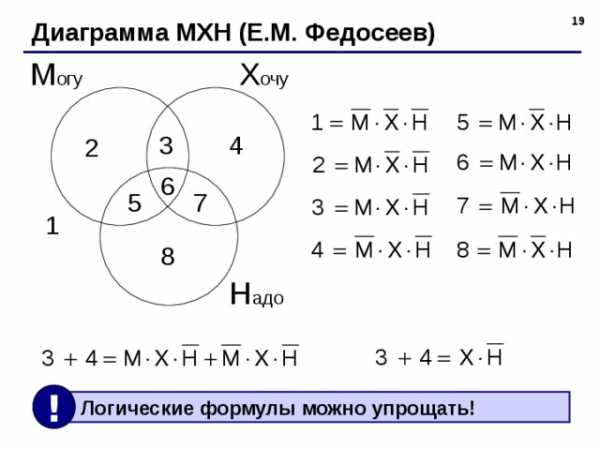
Диаграмма МХН (Е.М. Федосеев)

Х очу

М огу

4

3

2

6

7

5

1

8

Н адо

!

Логические формулы можно упрощать!

19

19

Логические основы компьютеров

Тема 3. Преобразование логических выражений

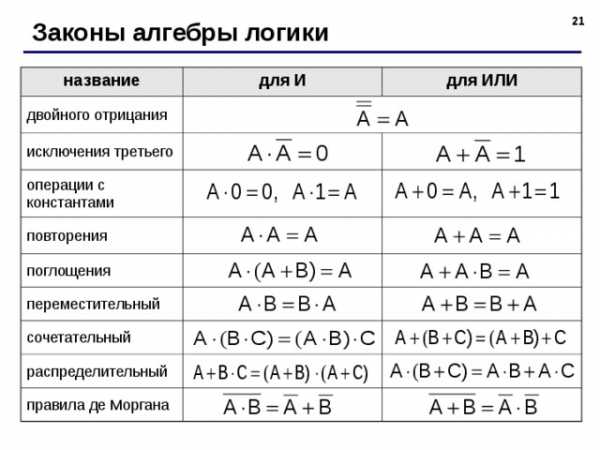
Законы алгебры логики

название

для И

двойного отрицания

для ИЛИ

исключения третьего

операции с константами

повторения

поглощения

переместительный

сочетательный

распределительный

правила де Моргана

Упрощение логических выражений

Шаг 1. Заменить операции  на их выражения через И , ИЛИ и НЕ :

Шаг 2. Раскрыть инверсию сложных выражений по формулам де Моргана:

Шаг 3. Используя законы логики, упрощать выражение, стараясь применять закон исключения третьего.

Упрощение логических выражений

раскрыли 

формула де Моргана

распределительный

исключения третьего

повторения

поглощения

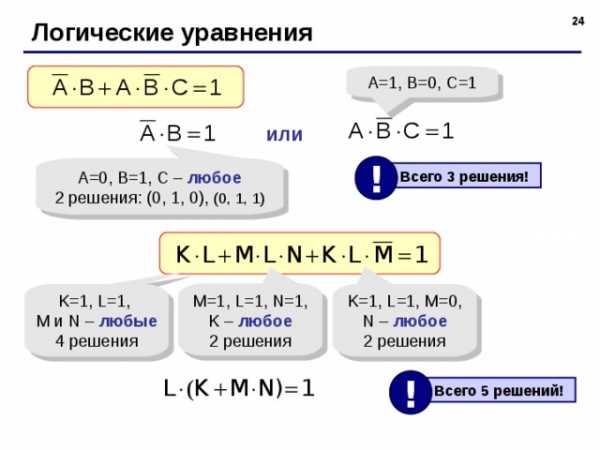
Логические уравнения

A=1, B=0, C=1

или

!

A=0, B=1, C – любое

2 решения: (0, 1, 0), (0, 1, 1)

Всего 3 решения!

M=1, L=1, N=1,

K – любое

2 решения

K=1, L=1,

M и N – любые

4 решения

K=1, L=1, M=0,

N – любое

2 решения

!

Всего 5 решений!

24

24

Логические основы компьютеров

Тема 4. Синтез логических выражений

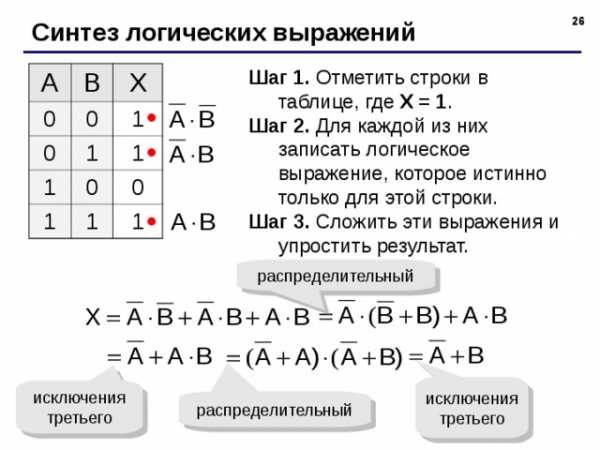
Синтез логических выражений

Шаг 1. Отметить строки в таблице, где X = 1 .

Шаг 2. Для каждой из них записать логическое выражение, которое истинно только для этой строки.

Шаг 3. Сложить эти выражения и упростить результат.

A

B

0

0

0

X

1

1

1

1

0

1

0

1

1

распределительный

исключения третьего

исключения третьего

распределительный

Синтез логических выражений (2 способ)

Шаг 1. Отметить строки в таблице, где X = 0 .

Шаг 2. Для каждой из них записать логическое выражение, которое истинно только для этой строки.

Шаг 3. Сложить эти выражения и упростить результат, который равен .

Шаг 4. Сделать инверсию.

A

B

0

X

0

0

1

1

1

1

0

1

0

1

1

?

Когда удобнее применять 2-ой способ?

27

27

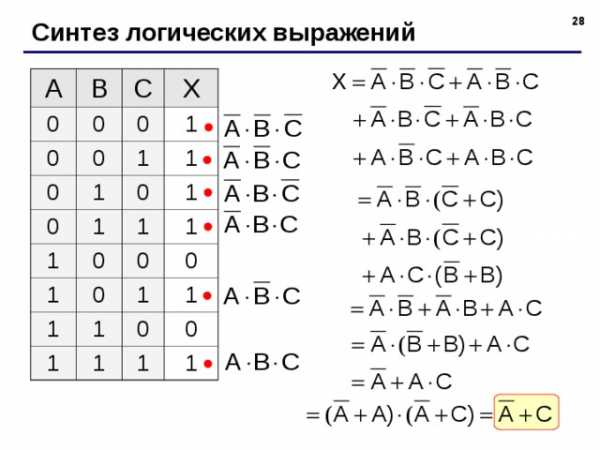
Синтез логических выражений

A

B

0

C

0

0

0

X

0

0

0

1

1

1

1

0

1

1

1

1

0

1

1

0

1

0

0

1

1

1

0

1

1

0

1

1

Синтез логических выражений (2 способ)

A

B

0

C

0

0

0

X

0

0

0

1

1

1

1

0

1

1

0

1

1

1

1

0

1

0

0

1

1

1

1

1

0

0

1

1

Логические основы компьютеров

Тема 5. Логические элементы компьютера

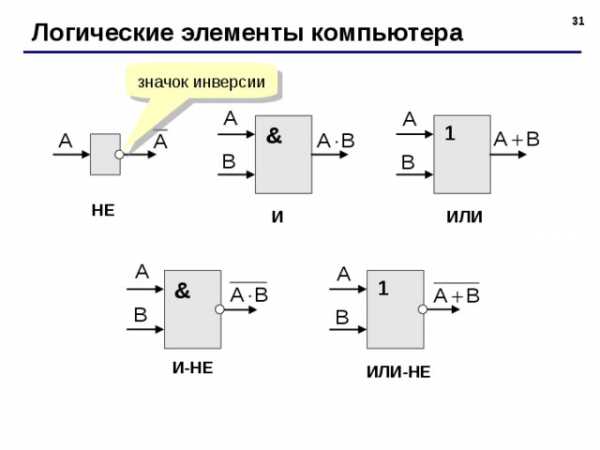
Логические элементы компьютера

значок инверсии

&

1

НЕ

И

ИЛИ

&

1

И-НЕ

ИЛИ-НЕ

31

31

Логические элементы компьютера

Любое логическое выражение можно реализовать на элементах И-НЕ или ИЛИ-НЕ.

И :

НЕ:

&

&

&

&

ИЛИ:

&

&

32

32

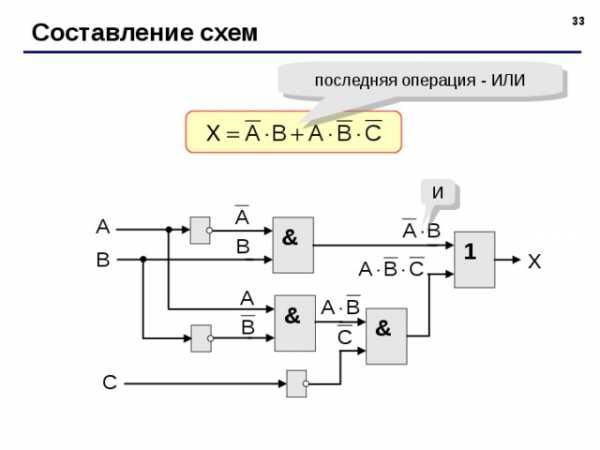
Составление схем

последняя операция — ИЛИ

И

&

1

&

&

33

33

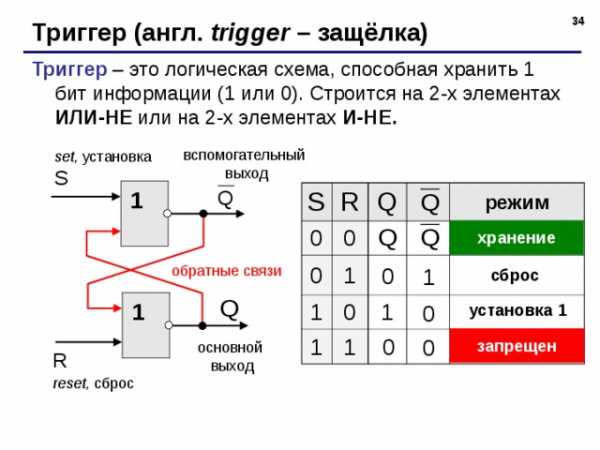
Триггер (англ. trigger – защёлка)

Триггер – это логическая схема, способная хранить 1 бит информации (1 или 0). Строится на 2-х элементах ИЛИ-НЕ или на 2-х элементах И-НЕ.

вспомогательный

выход

set, установка

1

S

R

0

Q

0

0

1

1

0

1

режим

1

хранение

обратные связи

0

сброс

1

установка 1

1

1

0

запрещен

0

0

основной

выход

reset, сброс

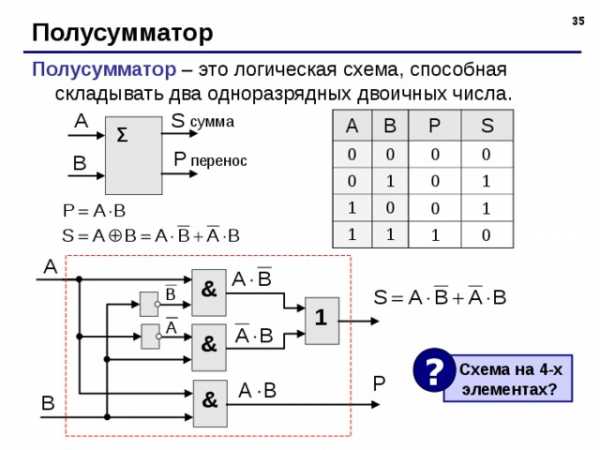
Полусумматор

Полусумматор – это логическая схема, способная складывать два одноразрядных двоичных числа.

сумма

A

B

0

0

P

0

1

1

S

0

1

1

Σ

0 0

перенос

0 1

0 1

1 0

&

1

&

?

Схема на 4-х элементах?

&

35

35

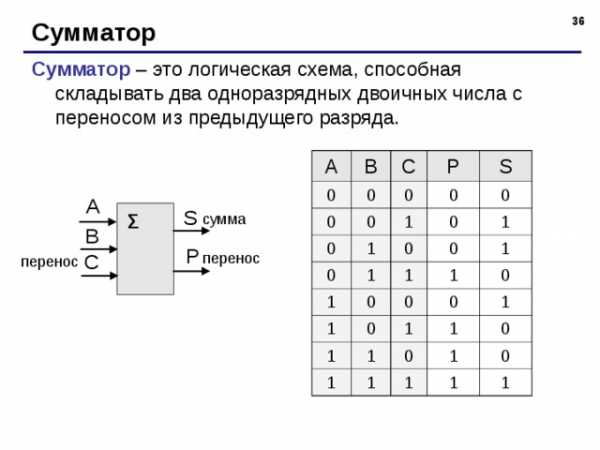
Сумматор

Сумматор – это логическая схема, способная складывать два одноразрядных двоичных числа с переносом из предыдущего разряда.

A

B

0

0

C

0

P

0

0

0

1

0

0

1

S

0

1

1

0

0

0

1

1

0

1

1

0

1

1

0

0

1

1

0

1

1

1

0

1

0

1

1

1

0

1

Σ

сумма

перенос

перенос

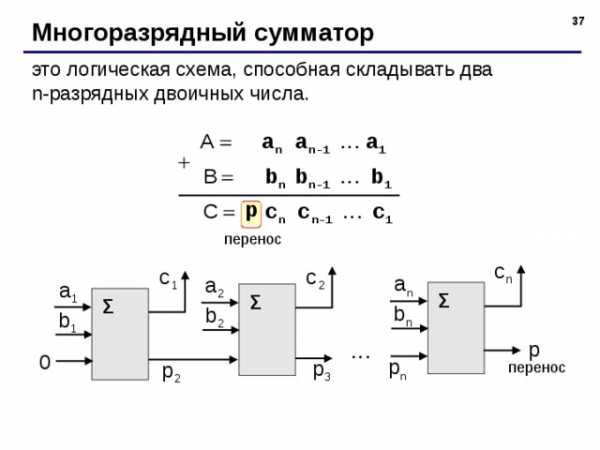
Многоразрядный сумматор

это логическая схема, способная складывать два n-разрядных двоичных числа.

перенос

Σ

Σ

Σ

перенос

37

37

Логические основы компьютеров

Тема 6. Логические задачи

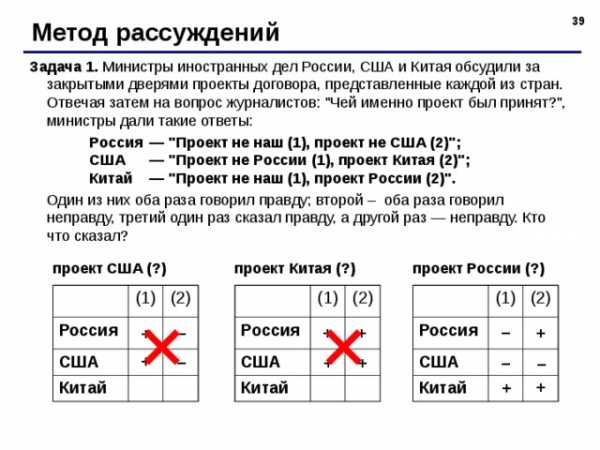
Метод рассуждений

Задача 1. Министры иностранных дел России, США и Китая обсудили за закрытыми дверями проекты договора, представленные каждой из стран. Отвечая затем на вопрос журналистов: «Чей именно проект был принят?», министры дали такие ответы:

Россия — «Проект не наш (1), проект не США (2)»;

США — «Проект не России (1), проект Китая (2)»;

Китай — «Проект не наш (1), проект России (2)».

Один из них оба раза говорил правду; второй – оба раза говорил неправду, третий один раз сказал правду, а другой раз — неправду. Кто что сказал?

проект России (?)

проект Китая (?)

проект США (?)

Россия

Россия

Россия

(1)

(1)

(1)

(2)

(2)

(2)

США

США

США

Китай

Китай

Китай

–

–

+

+

+

+

+

–

–

–

+

+

+

+

Табличный метод

Задача 2. Дочерей Василия Лоханкина зовут Даша, Анфиса и Лариса. У них разные профессии и они живут в разных городах: одна в Ростове, вторая – в Париже и третья – в Москве. Известно, что

• Даша живет не в Париже, а Лариса – не в Ростове, парижанка – не актриса, в Ростове живет певица, Лариса – не балерина.
• Даша живет не в Париже, а Лариса – не в Ростове,
• парижанка – не актриса,
• в Ростове живет певица,
• Лариса – не балерина.

• Много вариантов.
• Есть точные данные.

Париж

Ростов

Москва

Певица

Даша

Балерина

Анфиса

Актриса

Лариса

0

1

0

1

0

0

0

1

0

1

0

0

0

0

1

0

0

1

!

В каждой строке и в каждом столбце может быть только одна единица!

40

40

Задача Эйнштейна

Условие: Есть 5 домов разного цвета, стоящие в ряд. В каждом доме живет по одному человеку отличной от другого национальности. Каждый жилец пьет только один определенный напиток, курит определенную марку сигарет и держит животное. Никто из пяти человек не пьет одинаковые напитки, не курит одинаковые сигареты и не держит одинаковых животных.

Известно, что:

• Англичанин живет в красном доме. Швед держит собаку. Датчанин пьет чай. Зеленой дом стоит слева от белого. Жилец зеленого дома пьет кофе. Человек, который курит Pallmall , держит птицу. Жилец среднего дома пьет молоко. Жилец из желтого дома курит Dunhill . Норвежец живет в первом доме. Курильщик Marlboro живет около того, кто держит кошку. Человек, который содержит лошадь, живет около того, кто курит Dunhill . Курильщик Winfield пьет пиво. Норвежец живет около голубого дома. Немец курит Rothmans . Курильщик Marlboro живет по соседству с человеком, который пьет воду.
• Англичанин живет в красном доме.
• Швед держит собаку.
• Датчанин пьет чай.
• Зеленой дом стоит слева от белого.
• Жилец зеленого дома пьет кофе.
• Человек, который курит Pallmall , держит птицу.
• Жилец среднего дома пьет молоко.
• Жилец из желтого дома курит Dunhill .
• Норвежец живет в первом доме.
• Курильщик Marlboro живет около того, кто держит кошку.
• Человек, который содержит лошадь, живет около того, кто курит Dunhill .
• Курильщик Winfield пьет пиво.
• Норвежец живет около голубого дома.
• Немец курит Rothmans .
• Курильщик Marlboro живет по соседству с человеком, который пьет воду.

Вопрос: У кого живет рыба?

40

40

Использование алгебры логики

Задача 3. Следующие два высказывания истинны:

1. Неверно, что если корабль A вышел в море, то корабль C – нет.

2. В море вышел корабль B или корабль C , но не оба вместе.

• 1. Неверно, что если корабль A вышел в море, то корабль C – нет. 2. В море вышел корабль B или корабль C , но не оба вместе.

Определить, какие корабли вышли в море.

Решение:

… если корабль A вышел в море, то корабль C – нет.

1. Неверно, что если корабль A вышел в море, то корабль C – нет.

2. В море вышел корабль B или корабль C , но не оба вместе.

42

42

Использование алгебры логики

Задача 4. Когда сломался компьютер, его хозяин сказал «Память не могла выйти из строя». Его сын предположил, что сгорел процессор, а винчестер исправен. Мастер по ремонту сказал, что с процессором все в порядке, а память неисправна. В результате оказалось, что двое из них сказали все верно, а третий – все неверно. Что же сломалось?

Решение:

A – неисправен процессор, B – память, C – винчестер

сын:

мастер:

хозяин:

Если ошибся хозяин:

Если ошибся сын:

Если ошибся мастер:

!

Несколько решений!

В общем случае:

43

multiurok.ru

Презентация на тему: Упрощение логических выражений

Шаг 1. Заменить операцию на её выражение через

И, ИЛИи НЕ:

A B A B A B

Шаг 2. Раскрыть инверсию сложных выражений по формулам де Моргана:

A B A B, A B A B

Шаг 3. Используя законы логики, упрощать выражение, стараясь применять закон исключения третьего.

Синтез логических выражений

Шаг 1. Отметить строки в таблице, гдеX = 1.

Шаг 2. Для каждой из них записать логическое выражение, которое истинно только для этой строки.

Шаг 3. Сложить эти выражения и упростить результат.

распределительный

X

A B

A

B

A B

A) (

B)

B

A

A B (

A

A

A

исключения

распределительный

исключения

третьего

третьего

Синтез логических выражений (2 способ)

A	B	X
0	0	1
0	1	1
1	0	0	A B
1	1	1

Шаг 1. Отметить строки в таблице, гдеX = 0.

Шаг 2. Для каждой из них записать логическое выражение, которое истинно только для этой строки.

Шаг 3. Сложить эти выражения и упростить результат, который равенX .

Шаг 4. Сделать инверсию.

X A B X A B A B

? Когда удобнее применять2-ойспособ?

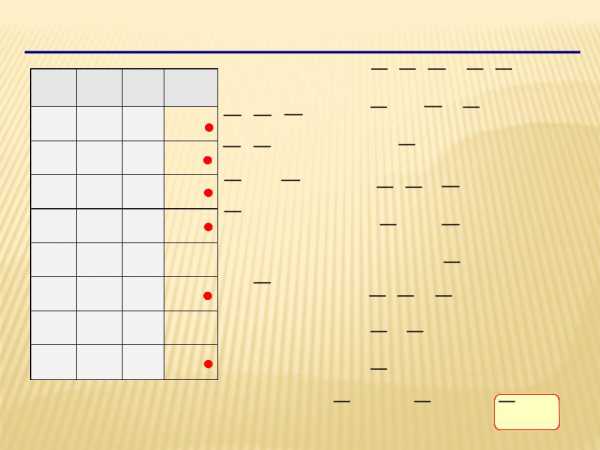
Синтез логических выражений

A	B	C	X
0	0	0	1	A B C
0	0	1	1	A B C
0	1	0	1	A B C
0	1	1	1	A B C
1	0	0	0
1	0	1	1	A B C
1	1	0	0
1	1	1	1	A B C

XA B C A B C

A B C A B C

A B C A B C

A B (C C)

A B (C C)

A C (B B)

A B A B A C

A (B B) A C

A A C

(A A) (A C) A C

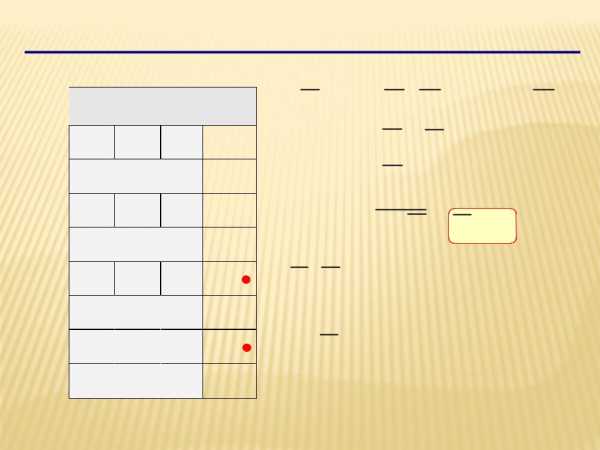
Синтез логических выражений (2 способ)

	X	X A B C A B C
	1	A C (B B)
	1	A C
	1	X A C A C
	1
	0	A B C
	1
	0	A B C
	1

Логические элементы компьютера

значок инверсии

A		A B	A	1	A B
		B	B
	НЕ	И		ИЛИ

	A	& A B	A	1	A B
	B		B
		И-НЕ		ИЛИ-НЕ

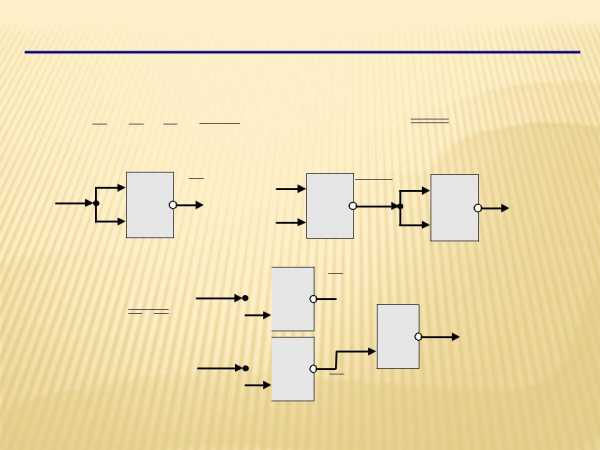
Логические элементы компьютера

Любое логическое выражение можно реализовать на элементах И-НЕ илиИЛИ-НЕ.

НЕ: A A A A A			И: A B A B
A	& A	A	& A B&	A B
		B

A

&A B

B

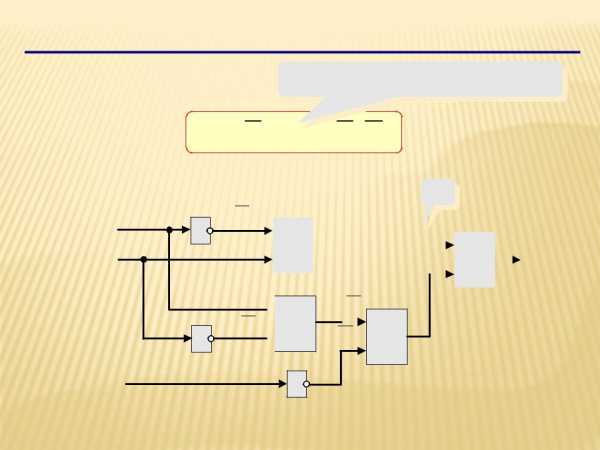
Составление схем

последняя операция — ИЛИ

X A B A B C

И

&

A

1

X

A B C

&ACB &

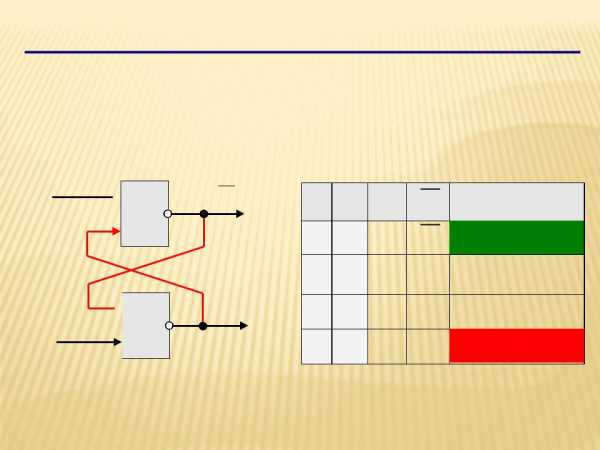
Триггер (англ. trigger – защёлка)

Триггер – это логическая схема, способная хранить 1

бит информации (1 или 0). Строится на 2-хэлементахИЛИ-НЕ или на2-хэлементахИ-НЕ.

set, установка

S

1

1

R

reset, сброс

вспомогательный

выход

Q	S R Q			Q
	0	0	Q	Q
обратные связи	0	1	0	1
Q	1	0	1	0
основной	1	1	0	0
выход

режим

хранение

сброс

установка 1

запрещен

Полусумматор

Полусумматор – это логическая схема, способная складывать два одноразрядных двоичных числа.

A	Σ	S сумма			A	B	P	S
		P перенос			0	0	0	0
B
					0	1	0	1
P A B					1	0	0	1
S A B A B A B					1	1	1	0
A
			& A B
		B			1	S A B A B
		A	& A B
								Схема на 4-х
B			&	A B		P	? элементах?

studfiles.net

31. Синтез логических схем по логическим выражениям в булевом базисе.

Логические схемы строятся на основе логических элементов, набор которых определяется заданным логическим базисом. Для базиса Буля в качестве логических элементов используются элементы, реализующие базовые логические функции И, ИЛИ, НЕ, которые имеют приведенные на рис. 2.2-1 обозначения. При синтезе схемы по логическому выражению, составляющие логические операции представляются в виде соответствующих логических элементов, связи между которыми определяются последовательностью выполнения логических операций в заданном выражении. Пример: Синтезировать логическую схему в базисе И, ИЛИ, НЕ, реализующую логическое выражение:

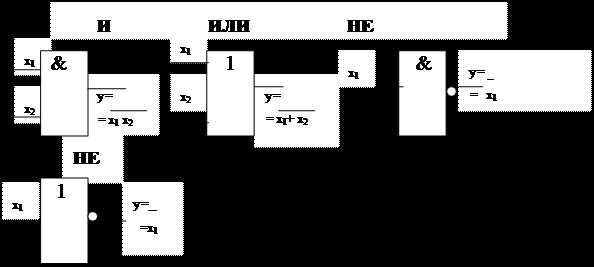
Рис. 2.2‑1

Решение

Входными сигналами синтезируемой схемы являются x1, x2, x3, а выходным — y1.

Реализацию заданного выражения в виде логической схемы можно начать или с последней операции, или с первой.

Последней операцией в заданном выражении является операция логического сложения двух операндов

y= ( x1x2 +x1x3 +x2 x3 )(x1 +x2 +x3 ) и х1 x2 x3,

поэтому для её реализации требуется элемент ИЛИ(1) с двумя входами, на выходе которого будет сформирован сигнал, соответствующий y1, если на его входы будут поданы эти два слагаемые (например, первое слагаемое на второй вход, а второе слагаемое на первый вход).

На первый вход ИЛИ(1) подается логическое произведение х1 x2 x3, для реализации которого необходимо использовать логический элемент И с тремя входами, на которые подаются входные переменные х1, x2, x3. Аналогичным образом рассматривается последовательность формирования выражения

y= ( x1x2 +x1x3 +x2 x3 )(x1 +x2 +x3 ),

которое соответствует сигналу, подаваемому на второй вход элемента ИЛИ(1). В результате синтезируется схема для заданного выражения, приведенная на рис.2.2-2 .

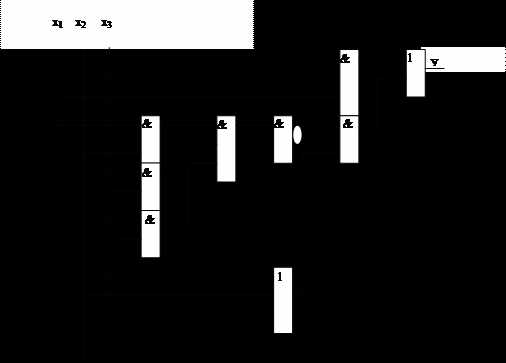
32. Минимизация логических выражений методом Квайна.

В качестве исходной формы представления логического выражения используется СДНФ. Если подлежащее минимизации выражение имеет другую форму, то приведение к СДНФ осуществляется за счет открытия скобок, избавления от отрицаний логических выражений, более сложных чем отрицание переменной (используется правило де Моргана).

Метод Квайна выполняется в два этапа.

Первый этап имеет своей целью получение тупиковой формы, представляющей собой дизъюнкцию, в качестве слагаемых которой используются конъюнкции (каждая из них не склеивается ни с одной другой конъюнкцией, входящей в это выражение). Такие конъюнкции называются простыми импликантами.

Данный этап выполняется за счет реализации отдельных шагов. На каждом шаге на основании выражения, полученного на предыдущем шаге, выполняются все возможные операции склеивания для пар имеющихся конъюнкций. Каждый шаг понижает ранг исходных конъюнкций на единицу. Шаги повторяются до получения тупиковой формы.

Второй этап имеет своей целью устранение из тупиковой формы всех избыточных простых импликант, что дает в результате минимальное логическое выражение.

Над конъюнкциями проставлены их номера; в скобках под каждой конъюнкцией (i–j) указывают, что данная конъюнкция является результатом склеивания i-й и j-й конъюнкций исходного выражения.

К результатам склеивания логически добавлен ни с чем не склеенный пятый член исходного выражения; несколько одинаковых конъюнкций представляются одной конъюнкцией.

Последнее выражение получено из предыдущего посредством удаления повторяющихся членов.

2—й этап:

На основании исходного выражения и полученной тупиковой формы составляется и заполняется импликантная таблица (табл.2.7).

Таблица 2.7

Импликантная таблица

	_ _ х1х2х3х4	_ _ х1х2х3х4	_ _ х1х2х3х4	_ _ х1х2х3х4	_ _ _ х1х2х3х4	_ х1х2х3х4	_ ­_ х1х2х3х4	_ х1х2х3х4	_ х1х2х3х4	_ _ _ х1х2х3х4
	1	2	3	4	5	6	7	8	9	10
_ х2х3	*						*		*	*
_ х2х3		*	*		*	*
_ х2х4		*		*	*			*
_ х3х4				*			*	*		*
_ _ х1х2х3			*		*

Колонки приведенной таблицы помечены конституентами единицы, имеющимися в исходном логическом выражении.

Строки таблицы помечены простыми импликантами полученной тупиковой формы.

Звездочками в каждой строке отмечены те конституенты единицы, которые покрываются соответствующей простой импликантой (практически отмечаются те конституенты единицы, которые включают простую импликанту как свою составную часть)

studfiles.net