Системы уравнений
Если перед нами ставится задача найти все общие решения двух уравнений с двумя переменными, то говорят, что нужно решить систему уравнений. Решением системы уравнений называется каждая пара значений переменных, обращающая каждое уравнение системы в верное равенство. Иными словами, решить систему – это значит найти все решения этой системы или доказать, что их нет.
Запись системы уравнений сопровождается фигурной скобкой {.
Две системы уравнений называются равносильными, если эти системы имеют одни и те же решения. Системы уравнений считаются равносильными также и в случае, когда каждое уравнение системы не имеет решения.
Теорема 1. Пусть дана система двух уравнений с двумя переменными. Если одно уравнение системы оставить без изменения, а другое уравнение системы заменить уравнением, ему равносильным, то полученная система будет равносильна заданной.
{х – 3у = 10, {х = 3у + 10
{3х – 2у = 2 {3х – 2у = 2
Следствие. Если каждое уравнение системы заменить равносильным уравнением, то получится система, равносильная данной. Так, равносильными являются системы:
{х – 3у = 10, {х = 3у + 10
{3х – 2у = 2 {х = 2/3у + 2/3.
Теорема 2. Пусть дана система двух уравнений с двумя переменными. Если одно уравнение оставить без изменения, а другое уравнение заменить суммой или разностью обоих уравнений системы, то полученная системы будет равносильна данной.
Так, равносильны системы:
{х – 3у = 10, {(х – 3у) + (3х – 2у) = 10 + 2
{3х – 2у = 2 {3х – 2у = 2.
Существует несколько методов решения систем уравнений с двумя переменными.
Метод подстановки реализуется так:
1. В одном из уравнений мы выражаем одну переменную через другую (например, х через у).
2. Полученное выражение подставляем во второе уравнение вместо х. В результате получается уравнение с одной переменной.
3. Находим корни этого уравнения.
4. Воспользовавшись нашим выражением из пункта 1, находим вторую переменную.
Решим систему уравнений:
{х – 3у = 10,
{х2 – 24у = 100.
Решение.
1. В уравнении 1 выразим х через у и получим: х – 3у = 10 → х = 3у + 10
2. В уравнение 2 подставим полученное выражение: х2 – 24у = 100 – (3у + 10)2 – 24 у = 100.
3. Решим преобразованное уравнение 2 и получим корни 0 и -4.
4. Исходя из полученных значений у, найдем значения х.
Если у = 0, х = 10.
Если у = -4, х = -2.
Т.о., система уравнений имеет два решения: (-2; -4) и (10; 0).
Ответ. (-2; -4) и (10; 0).
Метод сложения основан на рассмотренных нами теориях. Изучим данный метод, работая с примером:
Решим систему:
{2х + 3у = 7,
Решение.
1. Умножим обе части второго уравнения на 3, получим систему:
{2х + 3у = 7,
{9х – 3у = 48.
Эта система, в соответствии с теоремами, равносильна первоначальной.
2. Сложим оба уравнения новой системы и получим:
{2х + 3у = 7,
{(2х + 3у) + (9х – 3у) = 7 + 48.
3. Преобразуем полученную систему:
{2х + 3у = 7,
{11х = 55.
4. Из уравнения 2 получаем х = 5. Подставим получившееся значение в уравнение 1 и получим у = -1 .
Ответ. х = 5, у = -1.
Метод введения новых переменных работает так: либо мы вводим новую переменную только для одного уравнения, либо вводим две новых переменных сразу для обоих уравнений.
Решим систему
{х/у = у/х = 13/6
{х = у = 5.
Решение.
1. Предположим, что х/у = a, тогда у/х = 1/а → уравнение 1 примет вид: а + 1/а = 13/6.
Решим полученное уравнение относительно переменной а: 6а2
+ 6 = 13а6а2 – 13а + 6 = 0. Корнями уравнения являются а1 = 2/3 и а2 = 3/2.
2. Отсюда получим, что либо х/у = 2/3, т.е. у = 3х/2, либо х/у = 3/2, т.е. у = 2х/3.
3. Т.к. с учетом полученных результатов, уравнение 1 распалось на два уравнения, нам предстоит решить совокупность двух систем:
{у = 2х/3, {у = 2х/3.
{х + у = 5 {х + у = 5.
Из системы 1 находим х = 2, у = 3, из системы 2 находим х = 3, у = 2.
Ответ: (2; 3) и (3; 2).
© blog.tutoronline.ru, при полном или частичном копировании материала ссылка на первоисточник обязательна.
blog.tutoronline.ru
Понятие системы уравнений. |
|||||
|
|||||
Свойства систем уравнений: |
|||||
Линейные системы уравнений с двумя неизвестными: |
|||||
|
Линейные системы уравнений с двумя переменными — это система вида: |
|||||
|
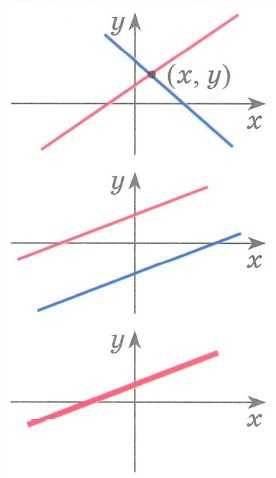
Прямые — графики уравнений системы пересекаются в одной точке. Система имеет единственное решение: |
 |
||||
| Прямые — графики уравнений системы — параллельны. Система не имеет решений. | |||||
|
Прямые — графики уравнений системы совпадают. Система имеет бесконечно много решений: |
|||||
Основные методы решения систем уравнений: |
|||||
| Графический метод: | |||||
| 1. Построить в одной системе координат графики обоих уравнений: | |||||
| 2. Найти координаты точек пересечения графиков. | |||||
| Метод подст | |||||
Система уравнений — это… Что такое Система уравнений?
Система уравнений — это условие, состоящее в одновременном выполнении нескольких уравнений относительно нескольких (или одной) переменных.
Формальная запись общего вида может выглядеть так:
Решением системы уравнений называется упорядоченный набор чисел (значений переменных), при подстановке которых вместо переменных каждое из уравнений обращается в верное равенство.
Классификация
- Алгебраические уравнения:
- Дифференциальные уравнения:
Решение системы уравнений
Существует множество методов решения системы уравнений. Подход зависит от типа системы. Так, решение систем линейных уравнений полностью исследовано: у них найдены аналитические методы (метод Крамера) и предложено несколько численных как точных (простейший — метод Гаусса), так и приближённых (метод итераций).
Общего аналитического решения системы нелинейных уравнений не найдено. Существуют лишь численные методы.
Некоторое программное обеспечение, основанное на интервальном анализе, в частности бесплатный interalg, способно находить все решения системы уравнений в заданном регионе lbi <= xi <= ubi
Для решения систем дифференциальных уравнений разработана целая отрасль численных методов.
Разные факты
- Любая система уравнений над действительными числами может быть представлена одним равносильным уравнением, если взять все уравнения в форме , возвести их в квадрат и сложить.
- Обыкновенное дифференциальное уравнение любого порядка можно записать как систему диф. уравнений первого порядка.
См. также
dic.academic.ru
