Свойства средней линии в трапеции – Свойства средней линии трапеции, с примерами

Свойства средней линии трапеции — энциклопедический справочник и словарь для студента от А до Я

ОПРЕДЕЛЕНИЕ

Средняя линия трапеции — это сегмент, соединяющий середины боковых сторон трапеции.

Свойства средней линии

Средняя линия трапеции параллельна основаниям:

Центральная линия трапеции составляет половину базы

Примеры решения проблем

ПРИМЕР 1

Задача

Основание трапеции — 1: 2. Средняя линия — 9 см. Найдите основы трапеции.

Решение.

Пусть меньшая база трапеции будет BC = x, тогда AD = 2x. Запишем соотношение для центральной линии трапеции:

Решая уравнение, получим x = 6. Таким образом,

Ответ

BC = 6 см, AD = 12 см

ПРИМЕР 2

Задача

Основание трапеции составляет 3 см и 4 см. Найдите сегмент, соединяющий середины диагоналей трапеции.

Решение

В трапеции ABCD мы рисуем среднюю линию MN. Найдите свою длину

Сегмент KL, соединяющий середины диагоналей трапеции, лежит на центральной линии. Сегменты MK и LN являются срединными линиями треугольников ABC и BCD, что означает

Теперь найдите сегмент

Ответ

KL = 0,5 см

sciterm.ru

Запоминаем и применяем свойства трапеции

В этой статье мы постараемся насколько возможно полно отразить свойства трапеции. В частности, речь пойдет про общие признаки и свойства трапеции, а также про свойства вписанной трапеции и про окружность, вписанную в трапецию. Затронем мы и свойства равнобедренной и прямоугольной трапеции.

Пример решения задачи с использованием рассмотренных свойств поможет вам разложить по местам в голове и лучше запомнить материал.

Трапеция и все-все-все

Для начала коротко вспомним, что такое трапеция и какие еще понятия с ней связаны.

Итак, трапеция – фигура-четырехугольник, две из сторон которой параллельны друг другу (это основания). И две не параллельны – это боковые стороны.

В трапеции может быть опущена высота – перпендикуляр к основаниям. Проведены средняя линия и диагонали. А также из любого угла трапеции возможно провести биссектрису.

Про различные свойства, связанные со всеми эти элементами и их комбинациями, мы сейчас и поговорим.

Свойства диагоналей трапеции

Чтобы было понятнее, пока читаете, набросайте себе на листке трапецию АКМЕ и проведите в ней диагонали.

1. Если вы найдете середины каждой из диагоналей (обозначим эти точки Х и Т) и соедините их, получится отрезок. Одно из свойств диагоналей трапеции заключается в том, что отрезок ХТ лежит на средней линии. А его длину можно получив, разделив разность оснований на два: ХТ = (a – b)/2.
2. Перед нами все та же трапеция АКМЕ. Диагонали пересекаются в точке О. Давайте рассмотрим треугольники АОЕ и МОК, образованные отрезками диагоналей вместе с основаниями трапеции. Эти треугольники – подобные. Коэффициент подобия k треугольников выражается через отношение оснований трапеции: k = АЕ/КМ.
   Отношение площадей треугольников АОЕ и МОК описывается коэффициентом k².
3. Все та же трапеция, те же диагонали, пересекающиеся в точке О. Только в этот раз мы будем рассматривать треугольники, которые отрезки диагоналей образовали совместно с боковыми сторонами трапеции. Площади треугольников АКО и ЕМО являются равновеликими – их площади одинаковые.
4. Еще одно свойство трапеции включает в себя построение диагоналей. Так, если продолжить боковые стороны АК и МЕ в направлении  меньшего основания, то рано или поздно они пересекутся к некоторой точке. Дальше, через середины оснований трапеции проведем прямую. Она пересекает основания в точках Х и Т.
   Если мы теперь продлим прямую ХТ, то она соединит вместе точку пересечения диагоналей трапеции О, точку, в которой пересекаются продолжения боковых сторон и середины оснований Х и Т.
5. Через точку пересечения диагоналей проведем отрезок, который соединит основания трапеции (Т лежит на меньшем основании КМ, Х – на большем АЕ). Точка пересечения диагоналей делит этот отрезок в следующем соотношении:
   ТО/ОХ = КМ/АЕ.
6. А теперь через точку пересечения диагоналей проведем параллельный основаниям трапеции (a и b) отрезок. Точка пересечения разделит его на две равных части. Найти длину отрезка можно по формуле 2ab/(a + b).

Свойства средней линии трапеции

Среднюю линию проведите в трапеции параллельно ее основаниям.

1. Длину средней линии трапеции можно вычислить, если сложить длины оснований и разделить их пополам: m = (a + b)/2.
2. Если провести через оба основания трапецию любой отрезок (высоту, к примеру), средняя линия разделит его на две равных части.

Свойство биссектрисы трапеции

Выберите любой угол трапеции и проведите биссектрису. Возьмем, например, угол КАЕ нашей трапеции АКМЕ. Выполнив построение самостоятельно, вы легко убедитесь – биссектрисой отсекается от основания (или его продолжения на прямой за пределами самой фигуры) отрезок такой же длины, что и боковая сторона.

Свойства углов трапеции

1. Какую бы из двух пар прилежащих к боковой стороне углов вы не выбрали, сумма углов в паре всегда составляет 180⁰: α + β = 180⁰  и γ + δ = 180⁰.
2. Соединим середины оснований трапеции отрезком ТХ. Теперь посмотрим на углы при основаниях трапеции. Если сумма углов при любом из них составляет 90⁰ , длину отрезка ТХ легко вычислить исходя из разности длин оснований, разделенной пополам: ТХ = (АЕ – КМ)/2.
3. Если через стороны  угла трапеции провести параллельные прямые, те разделят стороны угла на пропорциональные отрезки.

Свойства равнобедренной (равнобокой) трапеции

1. В равнобедренной трапеции равны углы при любом из оснований.
2. Теперь снова постройте трапецию, чтобы проще было представить, о чем речь. Посмотрите внимательно на основание АЕ – вершина противоположного основания М проецируется в некую точку на прямой, которая содержит АЕ. Расстояние от вершины А до точки проекции вершины М и средняя линия равнобедренной трапеции – равны.
3. Пару слов о свойстве диагоналей равнобедренной трапеции – их длины равны. А также одинаковы углы наклона этих диагоналей к основанию трапеции.
4. Только около равнобедренной трапеции можно описать окружность, поскольку сумма противолежащих углов четырехугольника 180⁰ – обязательное условие для этого.
5. Из предыдущего пункта следует свойство равнобедренной трапеции – если возле трапеции можно описать окружность, она является равнобедренной.
6. Из особенностей равнобедренной трапеции вытекает свойство высоты трапеции: если ее диагонали пересекаются под прямым углом, то длина высоты равна половине суммы оснований: h = (a + b)/2.
7. Снова проведите отрезок ТХ через середины оснований трапеции – в равнобедренной трапеции он является перпендикуляром к основаниям. И одновременно ТХ – ось симметрии равнобедренной трапеции.
8. На этот раз опустите на большее основание (обозначим его a) высоту из противолежащей вершины трапеции. Получится два отрезка. Длину одного можно найти, если длины оснований сложить и разделить пополам: (a + b)/2. Второй получим, когда из большего основания вычтем меньшее и полученную разность разделим  на два: (a – b)/2.

Свойства трапеции, вписанной в окружность

Раз уже речь зашла о вписанной в окружность трапеции, остановимся на этом вопросе подробней. В частности на том, где находится центр окружности по отношению к трапеции. Тут тоже рекомендуется не полениться взять карандаш в руки и начертить то, о чем пойдет речь ниже. Так и поймете быстрее, и запомните лучше.

1. Расположение центра окружности определяется углом наклона диагонали трапеции к ее боковой стороне. Например, диагональ может выходить из вершины трапеции под прямым углом к боковой стороне. В таком случае большее основание пересекает центр описанной окружности точно посередине (R = ½АЕ).
2. Диагональ и боковая сторона могут встречаться и под острым углом – тогда центр окружности оказывается внутри трапеции.
3. Центр описанной окружности может оказаться вне пределов трапеции, за большим ее основанием, если между диагональю трапеции и боковой стороной – тупой угол.
4. Угол, образованный диагональю и большим основанием трапеции АКМЕ (вписанный угол) составляет половину того центрального угла, который ему соответствует:МАЕ = ½МОЕ.
5. Коротко про два способа найти радиус описанной окружности. Способ первый: посмотрите внимательно на свой чертеж – что вы видите? Вы без труда заметите, что диагональ разбивает трапецию на два треугольника. Радиус можно найти через отношение стороны треугольника к синусу противолежащего угла, умноженному на два. Например, R = АЕ/2*sinАМЕ. Аналогичным образом формулу можно расписать для любой из сторон обоих треугольников.
6. Способ второй: находим радиус описанной окружности через площадь треугольника, образованного диагональю, боковой стороной и основанием трапеции: R = АМ*МЕ*АЕ/4*S_АМЕ.

Свойства трапеции, описанной около окружности

Вписать окружность в трапецию можно, если соблюдается одно условие. Подробней о нем ниже. И вместе эта комбинация фигур имеет ряд интересных свойств.

1. Если в трапецию вписана окружность, длину ее средней линии можно без труда найти, сложив длины боковых сторон и разделив полученную сумму пополам: m = (c + d)/2.
2. У трапеции АКМЕ, описанной около окружности, сумма длин оснований равна сумме длин боковых сторон: АК + МЕ = КМ + АЕ.
3. Из этого свойства оснований трапеции вытекает обратное утверждение: окружность можно вписать в ту трапецию, сумма оснований которой равна сумме боковых сторон.
4. Точка касания окружности с радиусом r, вписанной в трапецию, разбивает боковую сторону на два отрезка, назовем их a и b. Радиус окружности можно вычислить по формуле:
   r = √ab.
5. И еще одно свойство. Чтобы не запутаться, этот пример тоже начертите сами. У нас есть старая-добрая трапеция АКМЕ, описанная около окружности. В ней проведены диагонали, пересекающиеся в точке О. Образованные отрезками диагоналей и боковыми сторонами треугольники АОК и ЕОМ – прямоугольные.
   Высоты этих треугольников, опущенные на гипотенузы (т.е. боковые стороны трапеции), совпадают с радиусами вписанной окружности. А высота трапеции – совпадает с диаметром вписанной окружности.

Свойства прямоугольной трапеции

Прямоугольной называют трапецию, один из углов которой является прямым. И ее свойства проистекают из этого обстоятельства.

1. У прямоугольной трапеции одна из боковых сторон перпендикулярна основаниям.
2. Высота и боковая сторона трапеции, прилежащая к прямому углу, равны. Это позволяет вычислять площадь прямоугольной трапеции (общая формула S = (a + b) * h/2) не только через высоту, но и через боковую сторону, прилежащую к прямому углу.
3. Для прямоугольной трапеции актуальны уже описанные выше общие свойства диагоналей трапеции.

Доказательства некоторых свойств трапеции

Равенство углов при основании равнобедренной трапеции:

• Вы уже наверное и сами догадались, что тут нам снова потребуется трапеция АКМЕ – начертите равнобедренную трапецию. Проведите из вершины М прямую МТ, параллельную боковой стороне АК (МТ || АК).

Полученный четырехугольник АКМТ – параллелограмм (АК || МТ, КМ || АТ). Поскольку МЕ = КА = МТ, ∆ МТЕ – равнобедренный и МЕТ = МТЕ.

АК || МТ, следовательно МТЕ = КАЕ, МЕТ = МТЕ = КАЕ.

Откуда АКМ = 180⁰ — МЕТ = 180⁰ — КАЕ = КМЕ.

Что и требовалось доказать.

Теперь на основании свойства равнобедренной трапеции (равенства диагоналей) докажем, что трапеция АКМЕ является равнобедренной:

• Для начала проведем прямую МХ – МХ || КЕ. Получим параллелограмм КМХЕ (основание – МХ || КЕ и КМ || ЕХ).

∆АМХ – равнобедренный, поскольку АМ = КЕ = МХ, а МАХ = МЕА.

МХ || КЕ, КЕА = МХЕ, поэтому МАЕ = МХЕ.

У нас получилось, что треугольники АКЕ и ЕМА равны между собой, т.к АМ = КЕ и АЕ – общая сторона двух треугольников. А также МАЕ = МХЕ. Можем сделать вывод, что АК = МЕ, а отсюда следует и что трапеция АКМЕ – равнобедренная.

Задача для повторения

Основания трапеции АКМЕ равны 9 см и 21 см, боковая сторона КА, равная 8 см, образует угол 150⁰ с меньшим основанием. Требуется найти площадь трапеции.

Решение: Из вершины К опустим высоту к большему основанию трапеции. И начнем рассматривать углы трапеции.

Углы АЕМ и КАН являются односторонними. А это значит, в сумме они дают 180⁰. Поэтому КАН = 30⁰ (на основании свойства углов трапеции).

Рассмотрим теперь прямоугольный ∆АНК (полагаю, этот момент очевиден читателям без дополнительных доказательств). Из него найдем высоту трапеции КН – в треугольнике она является катетом, который лежит напротив угла в 30⁰. Поэтому КН = ½АВ = 4 см.

Площадь трапеции находим по формуле: S_АКМЕ = (КМ + АЕ) * КН/2 = (9 + 21) * 4/2 = 60 см².

Послесловие

Если вы внимательно и вдумчиво изучили эту статью, не поленились с карандашом в руках начертить трапеции для всех приведенных свойств и разобрать их на практике, материал должен был неплохо вами усвоиться.

Конечно, информации тут много, разнообразной и местами даже запутанной: не так уж сложно перепутать свойства описанной трапеции со свойствами вписанной. Но вы сами убедились, что разница огромна.

Теперь у вас есть подробный конспект всех общих свойств трапеции. А также специфических свойств и признаков трапеций равнобедренной и прямоугольной. Им очень удобно пользоваться, чтобы готовиться к контрольным и экзаменам. Попробуйте сами и поделитесь ссылкой с друзьями!

© blog.tutoronline.ru, при полном или частичном копировании материала ссылка на первоисточник обязательна.

blog.tutoronline.ru

Трапеция, Средняя линия трапеции, треугольник

Четырёхугольник, у которого только две стороны параллельны называются трапецией.

Параллельные стороны трапеции называются её основаниями, а те стороны, которые не параллельны, называются боковыми сторонами. Если боковые стороны равны, то такая трапеция является равнобедренной. Расстояние между основаниями называется высотой трапеции.

Средняя Линия Трапеции

Средняя линия — это отрезок, соединяющий середины боковых сторон трапеции. Средняя линия трапеции параллельна её основаниям.

Теорема:

Если прямая, пересекающая середину одной боковой стороны, параллельна основаниям трапеции, то она делит пополам вторую боковую сторону трапеции.

Теорема:

Длина средней линии равна среднему арифметическому длин её оснований

MN || AB || DC
AM = MD; BN = NC

MN средняя линия, AB и CD — основания, AD и BC — боковые стороны

MN = (AB + DC)/2

Теорема:

Длина средней линии трапеции равна среднему арифметическому длин её оснований.

Основная задача: Доказать, что средняя линия трапеции делит пополам отрезок, концы которого лежат в середине оснований трапеции.

Средняя Линия Треугольника

Отрезок, соединяющий середины двух сторон треугольника, называется средней линией треугольника. Она параллельна третьей стороне и её длина равна половине длины третьей стороны.
Теорема: Если прямая, пересекающая середину одной стороны треугольника, параллельна другой стороне данного треугольника, то она делит третью сторону пополам.

AM = MC and BN = NC =>

MN || AB

MN = AB/2

Применение свойств средней линии треугольника и трапеции

Деление отрезка на определённое количество равных частей.
Задача: Разделить отрезок AB на 5 равных частей.
Решение:
Пусть p это случайный луч, у которого начало это точка А, и который не лежит на прямой AB. Мы последовательно откладываем 5 равных сегментов на p AA₁ = A₁A₂ = A₂A₃ = A₃A₄ = A₄A₅
Мы соединяем A₅ с B и проводим такие прямые через A₄, A₃, A₂ и A₁, которые параллельны A₅B. Они пересекают AB соответственно в точках B₄, B₃, B₂ и B₁. Эти точки делят отрезок AB на 5 равных частей. Действительно, из трапеции BB₃A₃A₅ мы видим, что BB₄ = B₄B₃. Таким же образом, из трапеции B₄B₂A₂A₄ получаем B₄B₃ = B₃B₂

В то время как из трапеции B₃B₁A₁A₃, B₃B₂ = B₂B₁.
Тогда из B₂AA₂ следует, что B₂B₁ = B₁A. В заключении получаем :
AB₁ = B₁B₂ = B₂B₃ = B₃B₄ = B₄B
Ясно, что для разделения отрезка AB на другое количество равных частей, нам нужно проецировать то же самое количество равных сегментов на луч p. И далее продолжать вышеописанным способом.

www.math10.com

Подготовка школьников к ЕГЭ и ОГЭ в учебном центре «Резольвента» Справочник по математике — Планиметрия

Средние линии треугольника

      Определение. Средней линией треугольника называют отрезок, соединяющий середины двух сторон треугольника (рис. 1).

Рис.1

      На рисунке 1 средней линией является отрезок DE.

      Утверждение 1. Средняя линия треугольника параллельна не пересекающейся с ней стороне треугольника и равна половине этой стороны.

      Доказательство. Рассмотрим произвольный треугольник   ABC   и обозначим буквой   D   середину стороны   AB   (рис. 2). Проведем через точку   D   до пересечения с прямой   BC   прямую, параллельную прямой   AC .   Обозначим буквой   E   точку пересечения прямых   DE   и   BC .

Рис.2

      Поскольку   AD = DB ,   а прямые   AC   и   DE   параллельны, то выполнены все условия теоремы Фалеса, и можно заключить, что выполнено равенство:   CE = EB .   Отсюда вытекает, что точка   E   является серединой стороны   CB ,   а отрезок   DE   является средней линией треугольника.

      Первую часть утверждения 1 мы доказали.

      Для того, чтобы доказать вторую часть утверждения 1, заметим, что в любом треугольнике можно провести три средних линии – отрезки   DE , EF   и   FD   (рис.3).

Рис.3

      Поскольку

DE | | FC ,       DF | | EC ,

то четырёхугольник DECF – параллелограммчетырёхугольник DECF – параллелограмм, следовательно,   DE = FC .

      Поскольку

DE | | AF ,       AD | | FE ,

то четырёхугольник   DEFA   – параллелограммчетырёхугольник   DEFA   – параллелограмм, следовательно,   DE = AF .

      Но поскольку   AF = FC ,   то отсюда вытекает равенство

что и требуется доказать.

      Доказательство утверждения 1 закончено.

      Следствие.

Рис.4

Средняя линия трапеции

      Напомним, что трапециейтрапецией называют четырёхугольник, у которого две стороны параллельны, а две другие – не параллельны.

      Параллельные стороны трапеции называют основаниями, а непараллельные стороны – боковыми сторонами трапеции.

      Отрезки, соединяющие противоположные вершины трапеции, называют диагоналями трапеции.

      Определение. Средней линией трапеции называют отрезок, соединяющий середины боковых сторон трапеции (рис. 5).

Рис.5

      На рисунке 5 средней линией трапеции является отрезок   EF .

      Утверждение 2. Средняя линия трапеции параллельна основаниям трапеции и равна половине суммы этих оснований.

Рис.6

      Доказательство. Проведем через вершину   B   и середину боковой стороны   F   трапеции прямую линию (рис. 6). Обозначим точку пересечения прямых   BF   и   AD   буквой   G .   Рассмотрим треугольники   BCF   и   FDG .   У этих треугольников стороны   CF   и   FD   равны, поскольку точка   F   – середина стороны   CD .   Углы   BCF   и   FDG   равны, поскольку они являются внутренними накрест лежащими углами, образованными при пересечении параллельных прямых   BC   и   AD   с секущей   CD .   Углы   BFC   и   DFG   равны, поскольку они являются вертикальными. Тем самым выполнены все условия признака равенства треугольников «По стороне и прилежащим к ней углам», и можно заключить, что треугольники   BCF   и   FDG   равны. Из равенства треугольников   BCF   и   FDG   следует равенство отрезков   BF   и   FG ,   откуда вытекает, что отрезок   EF   является средней линией треугольника   ABG .   Поэтому

что и требовалось доказать.

      Задача 1. Доказать, что средняя линия трапеции делит пополам любой отрезок с концами на основаниях трапеции.

Рис.7

      Решение. Пусть   ABCD   – трапеция,   EF   –  её средняя линия,   LM   – указанный отрезок (рис.7). Поскольку   AE = EB ,   то, в силу теоремы Фалеса, выполнено равенство:   LN = NM ,   что и требовалось доказать.

      Задача 2. Доказать, что отрезок, который диагонали трапеции высекают на средней линии трапеции, равен половине разности оснований трапеции.

Рис.8

      Решение. Пусть   ABCD   – трапеция,   EF   – её средняя линия,   KL   – указанный отрезок (рис.8). В соответствии с задачей 1 можем заключить, что точка   K   – середина отрезка   AC ,   а точка   L   – середина отрезка   BD .   Поэтому отрезок   EK   – средняя линия треугольника   BAC ,   а отрезок   EL   – средняя линия треугольника   ABD .   В силу утверждения 1 выполнены равенства:

      Следовательно,

что и требовалось доказать.

      Утверждение 3. Прямая, проходящая через середины оснований трапеции, проходит через точку пересечения боковых сторон трапеции.

Рис.9

      Доказательство. Пусть   K   и   L   – середины оснований   BC   и   AD   трапеции   ABCD   соответственно (рис.9). Обозначим буквой   M   точку пересечения боковых сторон   AB   и   CD .   Проведем через точки   M   и   K   прямую и обозначим точку пересечения этой прямой с основанием   AD   символом   N .   Докажем, что точки   N   и   L   совпадают. Для этого заметим, что треугольник   BMK   подобен треугольнику   AMN .   Следовательно, выполнено равенство:

      Заметим также, что треугольник   KMC   подобен треугольнику   NMD .   Поэтому

      Из этих соотношений получаем:

откуда вытекает, что точки   N   и   L   совпадают. Доказательство завершено.

      Почти те же рассуждения позволяют доказать следующий факт, который мы предоставляем читателю в качестве упражнения.

      Утверждение 4. Прямая, проходящая через точку пересечения диагоналей и середину одного из оснований трапеции, проходит через середину другого основания трапеции.

      Следствие. Точка пересечения диагоналей, середины оснований и точка пересечения боковых сторон трапеции лежат на одной прямой.

Средние линии четырехугольника. Теорема Вариньона

      Определение. Средней линией четырехугольника называют отрезок, соединяющий середины непересекающихся сторон четырёхугольника.

      Поскольку у каждого четырехугольника имеются две пары непересекающихся сторон, то у каждого четырехугольника имеются две средних линии (рис.10).

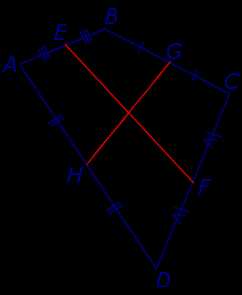
Рис.10

      На рисунке 10 средние линии – это отрезки   EF   и   GH .

      Замечание 1. Приведенное определение средней линии относится не только к плоским четырехугольникам, но и к «пространственным четырехугольникам» (рис.11). «Пространственным четырехугольником» мы называем замкнутую ломаную линию из 4 звеньев без самопересечений, не лежащую в одной плоскости.

Рис.11

      На рисунке 11 изображен «пространственный четырёхугольник»   ABCD ,   средними линиями которого являются отрезки   EF   и   GH .

      Замечание 2. Несмотря на то, что трапеция является четырехугольником, принято средней линией трапеции называть только отрезок, соединяющий середины её боковых сторон.

      Замечание 3. В данном разделе справочника не рассматриваются невыпуклые четырёхугольники и четырёхугольники с самопересечениями.

      Теорема Вариньона. Середины сторон произвольного плоского или «пространственного» четырёхугольника являются вершинами параллелограммапараллелограмма.

      Доказательство. Рассмотрим плоский четырёхугольник   ABCD ,   изображенный на рисунке 12. Точки   E, G, F, H   – середины сторон, отрезок   AC   – диагональ четырёхугольника.

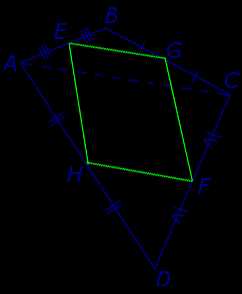
Рис.12

      Поскольку отрезок   EG   – средняя линия треугольника   ABC ,   то отрезок   EG   параллелен диагонали   AC   и равен её половине. Поскольку отрезок   FH   – средняя линия треугольника   CDA ,   то отрезок   FH   параллелен диагонали   AC   и равен её половине. Таким образом, в четырёхугольнике   EGFH   противоположные стороны   EG   и   FH   равны и параллельны. В силу признака параллелограммапризнака параллелограммапризнака параллелограмма отсюда вытекает, что четырёхугольник   EGFH   – параллелограмм, что и требовалось доказать.

      Замечание 4 . В случае «пространственного четырёхугольника»   ABCD   доказательство остаётся тем же (рис. 13).

Рис.13

      Поскольку диагонали параллелограмма в точке пересечения делятся пополамдиагонали параллелограмма в точке пересечения делятся пополамдиагонали параллелограмма в точке пересечения делятся пополам, то справедливо следующее утверждение, непосредственно вытекающее из теоремы Вариньона.

      Утверждение 5. Средние линии произвольного четырёхугольника пересекаются и в точке пересечения делятся пополам (рис. 14).

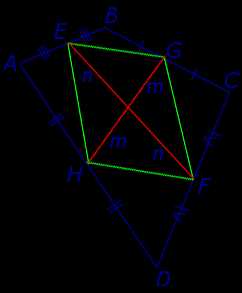
Рис.14

      Утверждение 6. Рассмотрим произвольный плоский или «пространственный» четырёхугольник   ABCD ,   у которого отрезок   EF   является одной из средних линий (рис. 15). Тогда будет выполнено векторное равенство:

Рис.15

      Доказательство. Рассмотрим в пространстве или на плоскости произвольную декартову систему координат с началом в некоторой точке   O   (рис. 16).

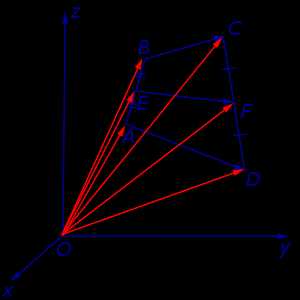
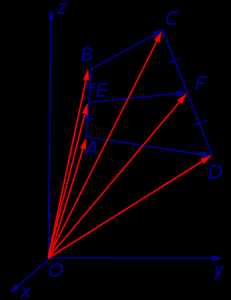
Рис.16

      В соответствии со свойствами векторов справедливы следующие равенства:

что и требовалось доказать.

      Следствие. Средняя линия четырёхугольника меньше или равна половине суммы не пересекающих её сторон четырёхугольника, причём равенство достигается лишь в том случае, когда указанные стороны четырёхугольника параллельны.

      Другими словами, средняя линия четырёхугольника равна половине суммы не пересекающих её сторон четырёхугольника лишь в том случае, когда этот четырехугольник является трапециейтрапецией, а не пересекающие среднюю линию стороны четырёхугольника – основания трапеции.

Средние линии тетраэдра

      Тетраэдром называют произвольную треугольную пирамиду (рис.17).

Рис.17

      У каждого тетраэдра имеется   4   вершины,   4   грани и   6   рёбер, причем все рёбра делятся на   3   пары непересекающихся рёбер. На рисунке 17 каждая пара непересекающихся рёбер выделена отдельным цветом. Каждые два непересекающихся ребра тетраэдра лежат на скрещивающихся прямых скрещивающихся прямых.

      Определение. Средней линией (бимедианой) тетраэдра называют отрезок, соединяющий середины двух непересекающихся рёбер тетраэдра.

Рис.18

      У каждого тетраэдра имеется 3 средних линии. Изображённый на рисунке 18 отрезок   EF   является одной из средних линий тетраэдра.

      Утверждение 7. Все средние линии тетраэдра пересекаются в одной точке и делятся этой точкой пополам.

      Доказательство. Выберем какую-нибудь среднюю линию тетраэдра, например,   EF   и докажем, что любая другая средняя линия тетраэдра проходит через середину отрезка   EF .   Для этого рассмотрим, например, среднюю линию   GH ,   соединяющую середины рёбер   AC   и   BD ,   и соединим отрезками точки   E, H, F, G   (рис.19).

Рис.19

      Заметим, что отрезок   EH   является средней линией треугольника   ADB ,   поэтому

      Отрезок GF является средней линией треугольника   ACB ,   поэтому

      Отсюда вытекает, что отрезки   EH   и   GF   равны и параллельны, следовательно, четырёхугольник   EHFG   – параллелограммследовательно, четырёхугольник   EHFG   – параллелограммследовательно, четырёхугольник   EHFG   – параллелограмм. Поскольку средние линии тетраэдра   EF   и   GH   являются диагоналями этого параллелограмма, то в точке пересечения они делятся пополамв точке пересечения они делятся пополамв точке пересечения они делятся пополам, что и требовалось доказать.

      Определение. Точку пересечения средних линий тетраэдра называют центроидом тетраэдра.

      Утверждение 8. Рассмотрим в пространстве декартову систему координат с началом в точке   O   и произвольный тетраэдр   ABCD .   Если обозначить буквой   M   центроид этого тетраэдра (рис. 20), то будет выполнено векторное равенство:

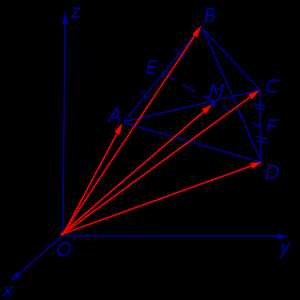
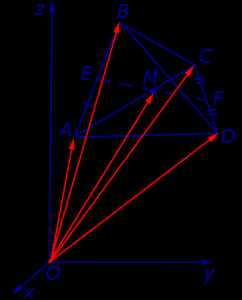
Рис.20

      Доказательство. По свойствам векторов

что и требовалось доказать.

      На нашем сайте можно также ознакомиться с разработанными преподавателями учебного центра «Резольвента» учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.

Приглашаем школьников (можно вместе с родителями) на бесплатное тестирование по математике, позволяющее выяснить, какие разделы математики и навыки в решении задач являются для ученика «проблемными». Запись по телефону (495) 509-28-10

      Для школьников, желающих хорошо подготовиться и сдать ЕГЭ или ОГЭ по математике или русскому языку на высокий балл, учебный центр «Резольвента» проводит

      У нас также для школьников организованы

МОСКВА, СВАО, Учебный центр «РЕЗОЛЬВЕНТА»

www.resolventa.ru

math-public:srednyaya_liniya_trapecii [Президентский ФМЛ №239]

Определение

Отрезок, соединяющий середины боковых сторон трапеции, называется средней линией трапеции.

Свойства средней линии трапеции

Средняя линия трапеции параллельна основаниям трапеции и равна их полусумме.

Доказательство

Рассмотрим трапецию $ABCD$, в которой проведена средняя линия $MN$.

Докажем, что $MN\parallel AD$ и $MN=\frac{AD+BC}{2}$.

Проведем через точку $M$ прямую $FE$ параллельно $CD$ ($F\in CB, E\in AD$).

Тогда $FCDE$ – параллелограмм ($FC\parallel ED, FE\parallel CD$).

Следовательно, $FE=CD$, $FC=ED$.

Кроме того $\triangle FBM=\triangle AME$, по второму признаку равенства ($\angle 1=\angle 2$, как накрест лежащие, $\angle 3=\angle 4$, как вертикальные, $AM=MB$, так как $M$ – середина).

Следовательно, $FM=ME$.

Тогда $FMNC$ и $MNDE$ — параллелограммы ($FM=ME=ND=NC$ и $FE\parallel CD$).

Следовательно, $MN\parallel BC$.

Кроме того, из равенства треугольников $\triangle FBM=\triangle AME$ следует,что $FB=AE$.

Пусть $FB=AE=x$ и $BC=x$.

Тогда $FC=ED=x+y$.

Следовательно, $MN=x+y$.

Кроме того, $BC+AD=BC+AE+ED=y+x+(x+y)=2x+2y$.

Таким образом, $MN=x+y=\dfrac{BC+AD}{2}$.

Признаки средней линии трапеции

1. Пусть отрезок $MN$ соединяет точки на боковых сторонах трапеции. Если $M$ – середина боковой стороны, и $MN$ параллелен основаниям трапеции, то $MN$ – это средняя линия трапеции.

2. Пусть отрезок $MN$ соединяет точки на боковых сторонах трапеции. Если $MN$ параллелен основанием трапеции и равен их полусумме, то $MN$ – средняя линия трапеции.

Доказательство

Первый пункт теоремы является прямым следствием теоремы Фалеса.

Докажем второй пункт теоремы.

Рассмотрим трапецию $ABCD$, в которой на боковых сторонах $AB$ и $CD$ выбраны точки $M$ и $N$ соответственно, и при этом $MN=\dfrac{AD+BC}{2}$.

Докажем, что тогда $MN$ – средняя линия трапеции $ABCD$.

Предположим противное, то есть $MN$ – не средняя линия данной трапеции.

Если ровно одна из точек $M$ или $N$ является серединой, то по первому пункту теоремы $MN$ – это средняя линия, так как $MN$ параллельна основаниям трапеции.

Пусть точки $M$ и $N$ – не середины боковых сторон.

Тогда пусть $M’N’$ – средняя линия трапеции.

Следовательно, $M’N’=\frac{BC+AD}{2}=MN$ и $MN\parallel BC\parallel MN$.

Но тогда $MNN’M’$ – параллелограмм, и, следовательно, $MM’\parallel NN’$, что противоречит тому, что $ABCD$ – это трапеция.

Следовательно, $MN$ – средняя линия.

Теорема (об отрезке, соединяющем середины диагоналей трапеции)

Отрезок, соединяющий середины диагоналей трапеции, равен полуразности ее оснований.

Доказательство

Рассмотрим трапецию $ABCD$, в которой точки $E$ и $F$ – это середины диагоналей $AC$ и $BD$ соответственно.

Докажем, что $EF=\frac{AD-BC}{2}$.

По теореме Фалеса средняя линия трапеции $MN$ делит диагонали $AC$ и $BD$ пополам, то есть точки $E$ и $F$ лежат на средней линии.

Тогда $ME$ и $FN$ – это средние линии треугольников $\tri ABC$ и $\tri DBC$.

Следовательно, если обозначить $BC=2x$, то $ME=FN=x$.

Тогда $EF=\frac{2x+AD}{2}-x-x=\frac{AD-2x}{2}=\frac{AD-BC}{2}$.

math-public/srednyaya_liniya_trapecii.txt · Последние изменения: 2016/04/14 00:01 — labreslav

wiki.sch239.net

Свойства трапеции, с примерами

Параллельные стороны называются основаниями трапеции. Две другие стороны называются ее боковыми сторонами. Отрезок, соединяющий середины боковых сторон, называется средней линией трапеции.

Трапеция, у которой боковые стороны равны, называется равнобокой (равнобедренной) трапецией. Трапеция, у которой при одной боковой стороне прямые углы называется прямоугольной.

Свойства трапеции

1. Средняя линия трапеции параллельна основаниям и равна их полусумме.
2. Отрезок, соединяющий середины диагоналей, равен половине разности оснований и лежит на средней линии.
3. Точка пересечения диагоналей трапеции, точка пересечения продолжений её боковых сторон и середины оснований лежат на одной прямой.
4. Треугольники, образованные при пересечении диагоналей и лежащие на основаниях трапеции, подобные:

      

5. Треугольники, образованные при пересечении диагоналей и лежащие на боковых сторонах трапеции, равновеликие:

      

6. Если трапеция равнобокая, то ее диагонали равны и углы при основании равны.
7. Если трапеция равнобокая, то около нее можно описать окружность.
8. Если сумма оснований трапеции равна сумме боковых сторон, то в нее можно вписать окружность.
9. Площадь трапеции вычисляется по формуле

      

   где – основания трапеции, – высота трапеции.

10. Если в трапецию вписана окружность радиуса и она делит боковую сторону точкой касания на два отрезка длины и , то .

Примеры решения задач

Понравился сайт? Расскажи друзьям!

ru.solverbook.com

Средняя линия трапеции

Четырёхугольник, у которого две противоположные стороны параллельны, а другие две — не параллельны, называется трапецией.

На чертеже 252 у четырёхугольника АВDС АВ || СD, AC ||BD. АВDС — трапеция.

Параллельные стороны трапеции называются её основаниями; АВ и СD — основания трапеции. Остальные две стороны называются боковыми сторонами трапеции; АС и ВD — боковые стороны трапеции.

Если боковые стороны равны, то трапеция называется равнобедренной.

Трапеция АВОМ равнобедренная, так как АМ=ВО (рис. 253).

Трапеция, у которой одна из боковых сторон перпендикулярна к основанию, называется прямоугольной (рис. 254).

Средней линией трапеции называется отрезок, соединяющий середины боковых сторон трапеции.

Теорема. Средняя линия трапеции параллельна каждому из ее оснований и равна их полусумме.

Дано: ОС — средняя линия трапеции АВDК, т. е. ОК = ОА и ВС = СD (рис. 255).

Надо доказать:

1) ОС || КD и ОС || АВ;

2) OC = \(\frac{KD + AB}{2}\)

Доказательство. Через точки А и С проведём прямую, пересекающую продолжение основания КD в некоторой точке Е.

В треугольниках АBС и DСЕ:

ВС = СD — по условию;

∠1 = ∠2, как вертикальные,

∠4 = ∠3, как внутренние накрест лежащие при параллельных АВ и KЕ и секущей ВD. Следовательно, \(\Delta\)АBС = \(\Delta\)DСЕ.

Отсюда АС = СЕ, т.е. ОС является средней линией треугольника КАЕ. Следовательно:

1) ОС || КЕ и, значит, ОС || КD и ОС || AВ;

2) OC = \(\frac{KE}{2} = \frac{KD + DE}{2}\), но DЕ = АВ (из равенства треугольников АBС и DСЕ), поэтому отрезок DЕ можно заменить равным ему отрезком АВ. Тогда получим:

OC = \(\frac{KD + AB}{2}\)

Теорема доказана.

Свойства трапеции, которые часто используются при решении задач:

1. Диагонали трапеции разбивают её начетыре треугольника с общей вершиной. Площади треугольников, прилежащие к боковым сторонам, равны.



2. В любой трапеции середины оснований, точка пересечения диагоналей и точка пересечения прямых, на которой лежат боковые стороны, лежат на одной прямой (точки М, N, О и К).



3. В равнобокой трапеции углы при основании равны.



4. В равнобокой трапеции прямая, проходящая через середины оснований, перпендикулярна основаниям и является осью симметрии этой трапеции



5. В равнобокой трапеции диагонали равны.



6. В равнобокой трапеции высота, опущенная на большее основание из конца меньшего основания, делит его на два отрезка, один из которых равен полуразности оснований, а другой — их полусумме.



7. Во всякой трапеции серединам боковых сторон и середины диагоналей лежат на одной прямой.


8. Во всякой трапеции отрезок, соединяющий середины диагоналей, параллелен основаниям и равен полуразности оснований.



9. Во всякой трапеции сумма квадратов диагоналей равна сумме квадратов боковых сторон и удвоенного произведения оснований.


10. Трапецию можно вписать в окружность тогда и только тогда, когда она равнобокая.


11. Трапецию можно описать около окружности тогда и только тогда, когда сумма оснований равна сумме боковых сторон.

razdupli.ru