Уравнения с заменой как решать – Метод замены переменной. Подробная теория с примерами.

Содержание

Решение иррациональных уравнений с помощью замены переменной

В этой статье я расскажу о том, как решать довольно сложные иррациональные уравнения с помощью замены переменной.

Я не устаю повторять, что замена переменной и разложение на множители — два универсальных приема, которые надо всегда держать в голове. Однако, не всегда замена переменной очевидна, и о некоторых видах замены догадаться сложно, их нужно знать.

В этой статье я хочу поделиться с вами несколькими красивыми способами решения иррациональных уравнений.

1. Решим уравнение:

Мы видим, что в уравнении присутствует корень третьей степени и квадратный корень. Чтобы избавиться от иррациональности, нам пришлось бы, в конечном итоге, возводить уравнение в шестую степень. Можете при желании попробовать самостоятельно этот способ, но мы пойдем другим путем.

Давайте введем замену:

пусть и ,

Выразим подкоренные выражения:

, ,

Теперь перед нами стоит задачи найти линейную комбинацию покоренных выражений, в результате которой получилось бы просто число. В данном случае все просто: если мы сложим подкоренные выражения, то получим число 1:

Тогда вместо нашего уравнения мы получим систему:

Выразим в первом уравнении через , так как возводить выражение в квадрат проще, чем в третью степень:

Подставим во второе уравнение:

Отсюда:

, ,

Найдем соответствующие значения :

, , . Условию удовлетворяют все значения.

Теперь самое время вернуться к исходной переменной. Вспомним, что,

Отсюда , , ,

, ,

Ответ: {2; 10; 1}

2. Теперь я предлагаю вам рассмотреть решение более сложного иррационального уравнения, уровня С3.

Решим уравнение:

Введем замену

Получим уравнение:

Перенесем все слагаемые влево:

Теперь мы видим, что имеем дело с однородным уравнением, и, так как не является корнем уравнения (при этом значении х переменная t обращается в ноль), разделим обе части уравнения на

Получим:

Решим квадратное уравнение относительно

Получим: или

Вернемся к исходной переменной.

Теперь нам надо решить два уравнения:

(1)

(2)

Решим уравнение (1):

Вспомним, как решаются простейшие иррациональные уравнения и перейдем к равносильной системе:

Решим первое уравнение системы. Получим:

Условию удовлетворяет только корень

Решим уравнение (2):

Возведем обе части уравнения в квадрат и перейдем к равносильной системе:

Решим первое уравнение системы. Получим:

Условию удовлетворяет только корень

Ответ: ,

3. И, наконец, я предлагаю вам посмотреть ВИДЕОУРОК с подробным решением уравнения уровня С3:

И.В. Фельдман, репетитор по математике.

ege-ok.ru

Решение тригонометрических уравнений методом замены переменной

Разделы: Математика

Тип урока
: изучение нового материала.
Цели урока
:

Познакомить учащихся с методом решения тригонометрических уравнений методом замены переменной.
Формировать умения анализировать, устанавливать связь между элементами содержания ранее изученного материала, навыки поисковой деятельности, способность к самоанализу, рефлексии.
Содействовать развитию познавательного интереса и личностной активности учащихся; создать условия для творческой самореализации личности.

Оборудование урока:

экран,
мультимедиа проектор,
компьютер,
авторская презентация к уроку,
набор карточек для конструирования уравнений на магнитной доске,
комплекты дидактической игры “Лото”,
бланки с заданием теста.

Компьютерное программное обеспечение
: программа Power Point

На уроке сочетаются фронтальный, парный и индивидуальный виды работы учащихся. У каждого ученика на рабочем месте находиться листы индивидуальной работы, на которых он подписывает свою фамилию, строит график самоанализа своей деятельности на занятии. Для самоанализа своей деятельности на занятии ученики строят график. На вертикальной оси отмечают самооценку от 1 до 5, а по горизонтальной отмечают этапы урока

Ход урока

Организационный момент. (1 мин.)

Учитель: Методы решения тригонометрических уравнений разрабатывались математиками уже многие годы. Ими выделены различные классы тригонометрических уравнений, для которых известны алгоритмы решения. Сегодня на уроке мы рассмотрим один из методов решения тригонометрических уравнений – “ Метод замены переменной”. Этот метод решения уравнений вам хорошо известен, вы не раз применяли его при решении алгебраических уравнений. Покажем, как он применяется при решении тригонометрических уравнений

I этап. (6 мин.) Учащиеся отвечают на вопросы учителя: Какие уравнения называются тригонометрическими? Что значить решить тригонометрическое уравнение? Какие тригонометрические уравнения относятся к простейшим? При каком условии уравнения имеют решения? Какие уравнения называются квадратными? Какие виды квадратных уравнений они знают? Какова связь числа корней квадратного уравнения с его дискриминантом? Ответы иллюстрируются слайдами презентации на экране

Ученики в парах выполняют задания теста по теме: “Простейшие тригонометрические уравнения”. По окончании работы над тестом учитель показывает правильные ответы на экране. Пары обмениваются бланками с тестовыми заданиями и проводят взаимопроверку. Во время проверки ученики корректируют свои знания по этой теме. Ученики отмечают свою оценку на графике и сдают бланк учителю. Критерии оценок: “5”-5 верных ответов, “4”-4 верных ответа, “3”-3 верных ответа, “2”-1-2 верных ответа.

Tест. Вариант№1.

Задание. Найдите ошибку.

Правильные ответы отметь кругом.

Ответ: 3,4,5,7,8

Tест. Вариант№2.

Задание. Найдите ошибку.

Правильные ответы отметь кругом

Ответ: 2,4,5, 8,9

II этап. Объяснение нового материала (10 мин).

Учитель:- Проанализируйте два уравнения и ,где заданные числа и определите какое из этих уравнений сложнее и почему?

Учащиеся: – Второе уравнение сложнее, так как в него входят две тригонометрические функции ,.

Начинаем искать метод решения первого уравнения. Так как в этом уравнении коэффициенты известные числа и у двух элементов один и тот же аргумент обращаемся к аналогичной ситуации в алгебраических уравнениях. Вспоминаем с учащимися, что для решения, уравнения вида , где заданные числа, делаем замену , при этом отвечаем на вопросы подтверждающие возможность замены: Можно ли решить “новое” уравнение? Будет ли работать данный метод при решении тригонометрического уравнения. Отвечая на эти вопросы, приходим к выводу, что уравнение можно решать заменой .

Шаги алгоритма Возможные ошибки Пути исправления ошибок
1 Замена переменной. Неправильно записано новое уравнение. Проверить запись нового уравнения
2 Решение квадратного уравнения. Ошибки при вычислении корней квадратного уравнения. Проверить правильность решения квадратного уравнения различными способами.
3 Решение простейших тригонометрических уравнений Формальное применение формул для решения простейших уравнений. Неправильно решены уравнения при частных случаях Вспомнить ограниченность синуса и косинуса, выучить формулы для решения простейших уравнений, частных случаев.

Пример 1. Решить уравнение .

В итоге ученики совместно с учителем выделяют шаги реализации рассматриваемого метода и формулируют алгоритм решения данного уравнения, заполняют таблицу. Шаги алгоритма, возможные ошибки и пути их исправления иллюстрируются слайдами презентации на экране.

Учитель: – Какие уравнения могут иметь аналогичный метод решения?

Учащиеся: – Это уравнения вида: , , где заданные числа.

Учитель:- Вернемся ко второму уравнению . Чем оно отличается от уже решенного уравнения? Можно ли свести это уравнение к уравнению с одной функцией?

Учащиеся: – Его можно свести к уравнению с одной функцией, применяя формулу . Уравнение в этом случае примет вид: или .

В итоге ученики совместно с учителем разбирают, как можно решить уравнения вида и гдезаданные числа.

III этап (18 мин). “Конструктор” Задание 1. Составьте уравнения рассматриваемых видов из предложенных выражений, если корнями это уравнения являются числа:

а) ;

б) ;

в) ,

На магнитной доске трое учеников собирают полученные уравнения, а остальные учащиеся сверяют свои записи с полученными уравнениями, результаты отмечают на графике. Критерии оценок: “5”-3 верных ответа, “4”-2верных ответа, “3”-1 верный ответ , “2”-нет верных ответов

“Крестики- нолики” Задание 2. Предварительное домашнее задание: решите уравнения, для каждого уравнения из таблицы укажите его вид и способы какими его можно решить.

“Крестики- нолики”: вычеркните прямой линией три уравнения, которые не имеют решения Таблица №1

Ответы: линия 1,5,9.

Критерии оценки: ”5” верный и полный ответ , “4”– ответ с одной ошибкой, “3”– ответ с двумя ошибками , “2”– неверный ответ.

Задание 3. Решите задачи с параметром.

Задача 1. Определить, при каких значениях параметра уравнение имеет решения.

Задача 2. Определить, при каких значениях параметра уравнение имеет решения. Решите уравнение.

Учащийся по желанию выходят к доске для оформления решения задач.

VI этап. (7 мин) Класс приступает к решению задач в группах. Учащиеся выполняют задания в зависимости от восприятия материала

“Лото”. У каждого ученика на рабочем месте находится лото, которое состоит из поля 3 1 и 6 двусторонних карточек. На клетках поля записаны уравнения, на лицевых сторонах карточек – ответы к уравнениям, на обратных сторонах – буквы, которые вместе позволят ответить на вопрос. Какой математик однажды заметил что: “Математическую теорию можно считать совершенной только тогда, когда ты сделал ее настолько ясной, что берешься изложить ее содержание первому встречному”?

Ответ: Гильберт.

Ответы иллюстрируются слайдами презентации на экране. Необходимо проверить решение задач, поэтому от каждой группы выступает учащийся, демонстрируя решение задач на доске.

Итог урока (2 мин) Подводя итог урока, учитель и учащиеся выясняют на каком этапе учащиеся испытывают наибольшие затруднения, какие задания для них были наиболее интересными, на что они должны обратить внимание при решении домашнего задания.

VI этап. Домашнее задание (1мин.)

Алгебра и начала анализа. Ч.1.Учебник для 10 класс А. Г. Мордкович, П.В.Семенов (профильный уровень). §34 п.1.стр179-180.

1-й уровень – задания репродуктивного характера – Решить уравнения №23.4(б), №23. 5(г), №23.7(б). Ч.2.Задачник для 10 кл. А.Г.Мордкович и д.р (профильный уровень) Алгебра и начала анализа. Решить задачу. Определить, при каких значениях параметра уравнение имеет решения.

2-й уровень – задания поискового плана: подобрать тригонометрические уравнения аналогичные уравнениям 1,5,9 из таблицы №1; Подобрать и решить задачу по физике при решении которой встречаются уравнения, рассмотренные на уроке.

3-й уровень – творческое; составить задания к дидактической игре “Лото” по теме: “ Решение тригонометрических уравнений методом замены переменной”.
17.03.2008
xn--i1abbnckbmcl9fb.xn--p1ai
Схема решению уравнений, замена переменных
Решению уравнений с помощью уравнений-следствий
Преобразования, гарантирующие сохранение правильной равенства

Проверка корней подстановкой в исходное уравнение

Решению уравнений с помощью равносильных преобразований
Учесть ОДЗ правильную равенство при прямых и обратных преобразованиях

Сохранять на ОДЗ правильную равенство при прямых и обратных преобразованиях

Решению уравнений. Замена переменных
Если в уравнение переменная входит в одном и том же виде, то удобно соответствующее выражение с переменной обозначить одной буквой (новой переменной).
Пример 1.
Розвяжіть уравнения:
Розвязання.
1. При уравнение корней не имеет, поскольку
2. При имеем , тогда
Ответ:
Пример 2.
Розвяжіть уравнения:
Розвязання. Поскольку под знаком корня парного степеня могут стоять только невідємні выражения, то область допустимых значений (ОДЗ) заданного уравнения задается системой розвязком которой является
Произведение равно нулю тогда и только тогда, когда один из множителей равен нулю, а все остальные множители существуют: при при при
Значение не входит в ОДЗ заданного уравнения, следовательно, они не являются корнями заданного уравнения.
Значение входит в ОДЗ, значит, является корнем заданного уравнения.
Ответ:
cubens.com
ЗАМЕНА ПЕРЕМЕННЫХ В ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЯХ ПЕРВОГО ПОРЯДКА

Сведения из теории

Сделаем в уравнении замену переменных: введем новую неизвестную функцию , связанную с искомой функцией соотношением , где – дифференцируемая функция. Подставляя выражения и через в (3.1), получим для нахождения уравнение вида , которое при удачном выборе замены может оказаться «проще» первоначального. Например, уравнение

заменой переменной сводится к уравнению с разделяющимися переменными

.

Примеры решения задач

3.2.1.Решить уравнение .

◄ Введем новую неизвестную функцию . Выразим и через z: . Подставим эти выражения в исходное уравнение и решим полученное уравнение с разделяющимися переменными.

.

.

– общее решение уравнения.►

3.2.2.Найти решение дифференциального уравнения , удовлетворяющее начальному условию .

◄ Так как , то естественно сделать замену . Для функции получим дифференциальное уравнение с разделяющимися переменными и начальное условие . Разделяем переменные: , , интегрируем: , выражаем z, а затем и y через x

, , ,

, ,

– искомое решение.►

3.3. Задачи для самостоятельного решения

Решить уравнения.

Однородные уравнения

Сведения из теории

Дифференциальное уравнение, которое можно записать в виде

называется однородным. Оно сводится заменой переменной

к уравнению с разделяющимися переменными для функции .

.

Важным примером однородного уравнения является уравнение, правая часть которого – отношение однородных многочленов относительно и одного порядка

.

Оно приводится к виду , если числитель и знаменатель разделить на .

Примеры решения задач

4.2.1.Решить уравнение .

◄ Правая часть уравнения – отношение однородных многочленов 2-го порядка. Разделив числитель и знаменатель на , получим

– однородное уравнение. Делаем замену . Тогда , . Для функции получаем уравнение с разделяющимися переменными: — общий интеграл. ►

4.2.2.Найти решение дифференциального уравнения , удовлетворяющее условию .

◄ Приведем уравнение к нормальному виду . Так как х и у входят в правую часть только в виде отношения , то это – однородное уравнение. Делаем замену , . Для функции получаем уравнение и начальное условие . Разделяем переменные: , ; ; , и потому – искомое решение.►

4.3. Задачи для самостоятельного решения

Решить уравнения.

Линейные уравнения ПЕРВОГО порядка

Сведения из теории

Дифференциальное уравнение первого порядка, разрешенное относительно производной, называется линейным, если его правая часть – линейная функция от

.

При получаем линейное однородное уравнение

.

Оно является уравнением с разделяющимися переменными, и его общее решение

,

где – одна из первообразных функции . Общее решение линейного неоднородного уравнения можно найти одним из следующих методов.

1) Метод вариации произвольной постоянной (метод Лагранжа).

Сначала находится общее решение соответствующего линейного однородного уравнения . Решение неоднородного уравнения ищем в виде

,

получающемся из заменой постоянной на функцию . Подставляя в уравнение , получаем для новой неизвестной функции уравнение . Интегрируя, находим

Подставляя в , получаем общее решение уравнения .

Метод Бернулли.

Ищем решение уравнения в виде . Тогда . Подставляя в уравнение , получим . Перепишем это уравнение в виде

.

Подберем так, чтобы скобка в уравнении обратилась в нуль. Для этого нужно найти какое-нибудь частное решение уравнения с разделяющимися переменными . Подставляя в , получим уравнение с разделяющимися переменными для функции

.

Интегрируя, находим его общее решение . Перемножая найденные значения и , получим общее решение неоднородного уравнения .

Примеры решения задач

5.2.1.Решить уравнение

.

◄ Уравнение записано в нормальной форме. Его правая часть является линейной функцией аргумента у. Следовательно, уравнение – линейное. Решаем его методом вариации произвольной постоянной. Сначала находим общее решение однородного уравнения . . .

Решение неоднородного уравнения ищем в виде , где – новая неизвестная функция. Подставляя в уравнение , получим

.

Итак, общее решение , где справа буквой С обозначена, как и везде, произвольная постоянная. После преобразований запишем его в виде

. ►

5.2.2.Решить задачу Коши .

◄ – линейное уравнение. Решаем методом Бернулли: . Подставляя и в исходное уравнение, получаем . Сгруппируем члены, содержащие в качестве множителя

.

Приравняем скобку к нулю и решаем полученное уравнение.

.

Поскольку нам нужно только частное решение уравнения , то примем , тогда . Подставляя в уравнение , получим

.

Перемножая u и v, находим общее решение . Подставляя в общее решение начальные значения и , получим . Искомое решение .►

5.3. Задачи для самостоятельного решения

Решить уравнения.

5.3.9.Известно, что сила тока в цепи, имеющей сопротивление , самоиндукцию удовлетворяет уравнению , где – электродвижущая сила. Найти силу тока , если , в случаях

а) , б) .

УравнениЯ Бернулли

Сведения из теории

Уравнение Бернулли – это уравнение первого порядка, имеющее в нормальной форме вид

, .

Методы решения те же, что и для линейного неоднородного уравнения, являющегося частным случаем уравнения Бернулли при .

Примеры решения задач

6.2.1.Решить уравнение Бернулли .

◄ Решаем методом Бернулли , . Подберем v, так чтобы . Тогда . Возьмем . Подставляя в уравнение, получаем для функции u уравнение с разделяющимися переменными

– общее решение.►

6.3. Задачи для самостоятельного решения

Решить уравнения.

infopedia.su
«Решение показательных уравнений с помощью замены переменных». 11-й класс
Разделы: Математика
Цель урока: изучить способ решения показательных уравнений с помощью замены переменных.

Задачи:

1) образовательная:

– повторить известные способы решения показательных уравнений;

– показать алгоритм решения с помощью замены переменных;

2) воспитательная:

– создавать условия для формирования навыков организации своей деятельности – самостоятельного поиска решения, самоконтроля;

– приучать к аккуратности выполнения записей в тетради и на доске;

– воспитывать умение работать в парах, взаимопомощь;

– воспитывать умение анализировать результаты своей деятельности;

3) развивающая:

– формировать умение сравнивать, выявлять закономерности, обобщать;

– формировать грамотную математическую речь;

– формировать умение применять знания в конкретной ситуации.

Преподавание ведется по учебнику А.Н.Колмогорова.

Ход урока

1. Оргмомент.

Приветствие.

Сегодня мы продолжим знакомство с методами решения показательных уравнений.

Запишите тему урока: “Решение показательных уравнений”, но оставьте строчку, тему мы чуть позже уточним.

2. Актуализация знаний.

Устная работа с классом.

Решите уравнения.

3. Постановка проблемы.

Уравнения 1 – 7 решали, приводя их к виду или . Последнее уравнение решить таким способом не удается.

Обратите внимание: . Предложите способ решения. Нужно ввести новую переменную у = и решить полученное квадратное уравнение.

Какова будет наша цель сегодня? Научиться решать показательные уравнения с помощью замены переменных.

Уточним тему урока: “Решение показательных уравнений с помощью замены переменных”.

4. Изучение нового материала.

Пусть у = , причем у > 0.

Уравнение примет вид .

Решим это уравнение: = –1; = 5.

не удовлетворяет условию у > 0.

= 5; х = 1.

Ответ: 1.

Решим уравнение .

Перепишем его в виде .

Далее решает ученик у доски с комментированием.

Пусть , причем у > 0.

3у – 8 = ; 3– 8у = 3; 3– 8у – 3 = 0;

Решим это уравнение: = –; = 3.

не удовлетворяет условию у > 0.

= 3; х = 1.

Ответ: 1.

Решим уравнение .

Почему не удается решить? Нельзя привести степени к одному основанию.

Перепишем уравнение в виде

Разделим обе части уравнения на : .

Далее решает у доски ученик с комментированием.

Пусть у =, причем у > 0.

Уравнение примет вид .

.

Решим это уравнение: = 1; =.

= 1; х = 0. = ; х = 1.

Ответ: 0; 1.

Можно было делить на ? Что изменилось бы в решении? Ввели бы обозначение у =.

5. Первичное закрепление изученного материала.

Ученики работают в парах, более сильные ребята помогают соседям.

Два ученика работают за крыльями доски.

6. Самостоятельная работа.

Чтобы проверить, как усвоен новый материал, выполните самостоятельную работу.

1) ;

2) ;

3) .

По окончании работы ученики самостоятельно проверяют решение по образцу (раздаточный материал), фиксируя места, где допущены ошибки.

7. Итог урока.
Обсуждение результатов самостоятельной работы.

Кто выполнил правильно все задания?

Кто допустил ошибки в первом (втором, третьем) задании? Какие?

Повторим, какие приемы использовали при решении показательных уравнений.

Оцените свою работу на уроке.

Вам предстоит еще раз применить полученные знания при выполнении домашнего задания: № 464(в,г), 470(в,г), 166(г) (стр. 299).

28.05.2013
Поделиться страницей:
xn--i1abbnckbmcl9fb.xn--p1ai
4. Уравнения, решаемые с помощью замены переменной
Пример 8. Решить уравнение
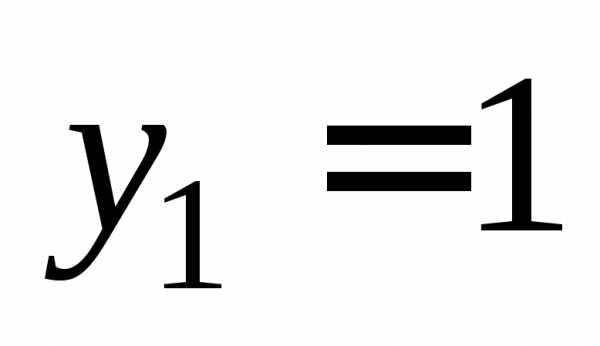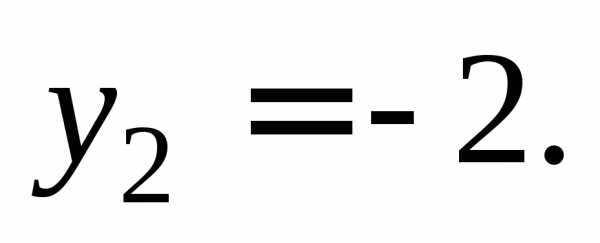Решение. Данное уравнение является квадратным относительно Заменяемполучим уравнениеЕго корнииТаким образом, решение исходного уравнения свелось к решению совокупности простейших уравнений:

Уравнение корней не имеет, т. е.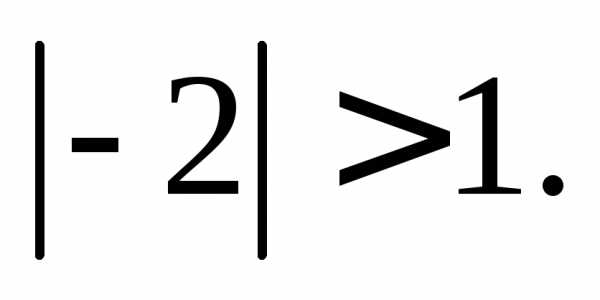
Решением второго является:

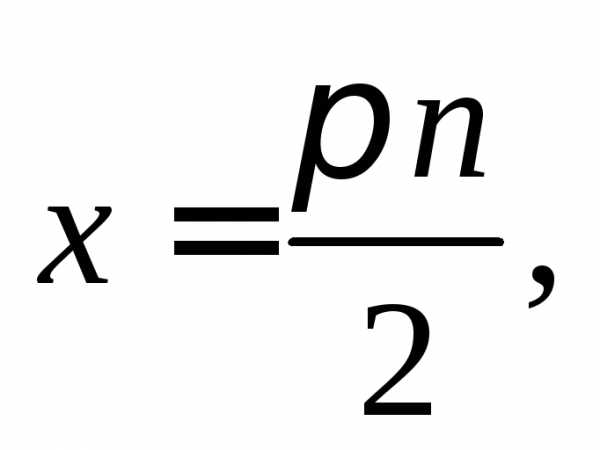
Получаем ответ: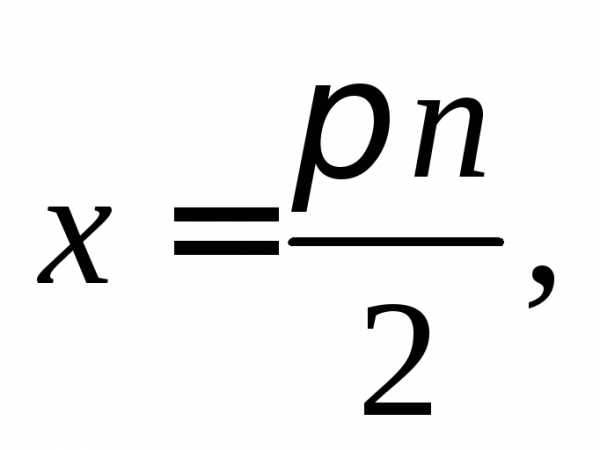
Пример 9. Решить уравнение
Решение. Используем тождество и формулуУравнение сводится к виду
Мы получили квадратное уравнение относительно 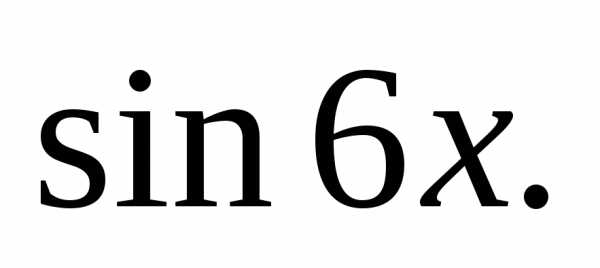Заменяемполучим уравнениеоткуда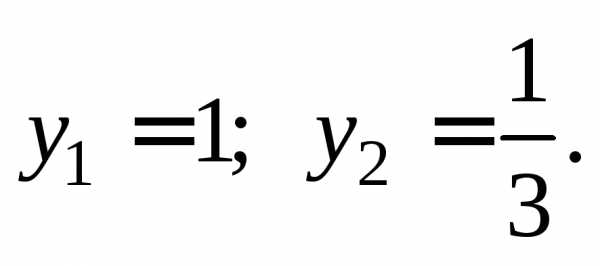
Приходим к совокупности простейших уравнений:
Получаем ответ:
Пример 10. Найти сумму корней уравнения
если
Решение. поскольку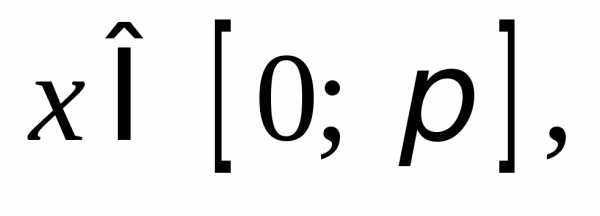
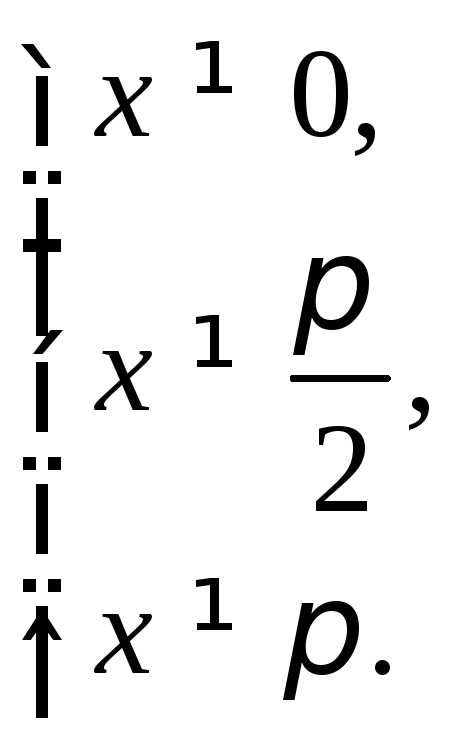
Упростим исходное уравнение:

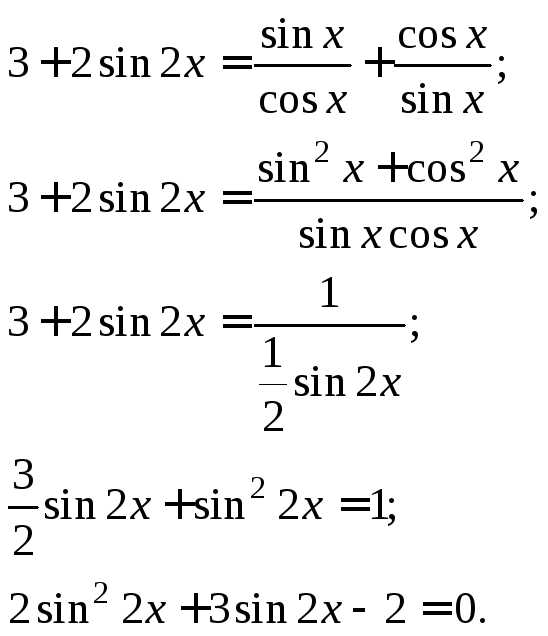
Получили квадратное уравнение относительно Сделав заменугдеимеем уравнениеоткудаили
Вернувшись к прежней неизвестной, получим совокупность уравнений:

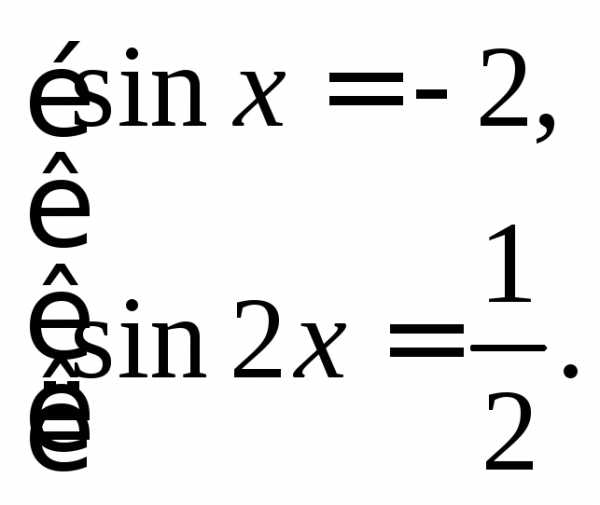
Первое уравнение не имеет решения. Решаем второе:
Придаем n значение n = 0, получаем:

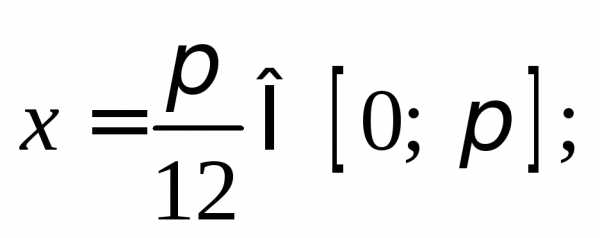
при n = 1 имеем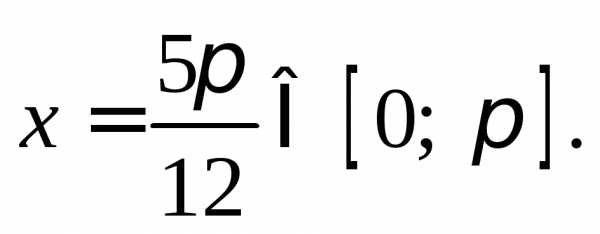
Нетрудно убедиться, что при всех других значениях n корни не попадут на отрезок 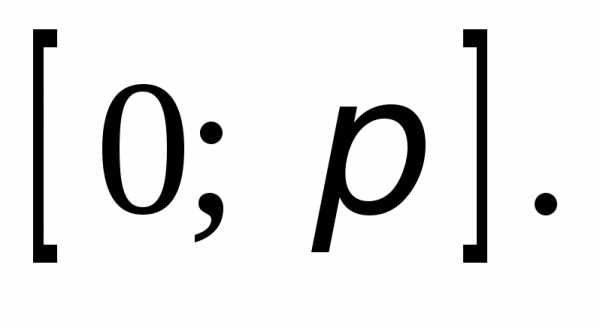Значит сумма корней, принадлежащих отрезку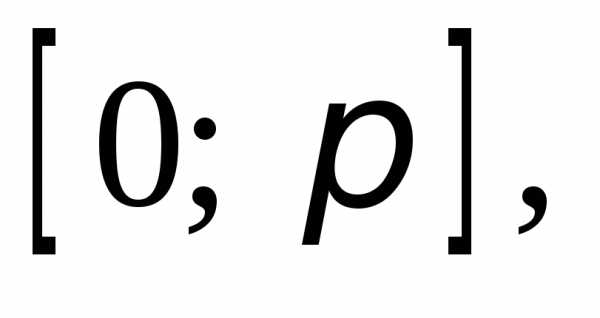равна

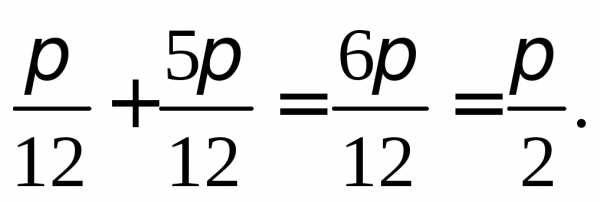
Получаем ответ:
5. Однородные уравнения
Однородным тригонометрическим уравнением n-й степени относительно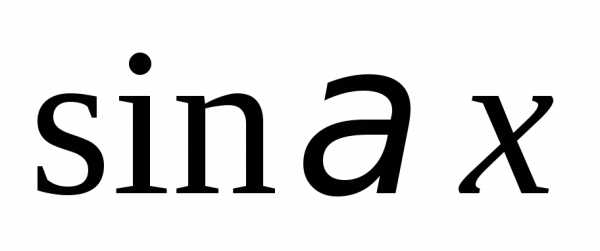и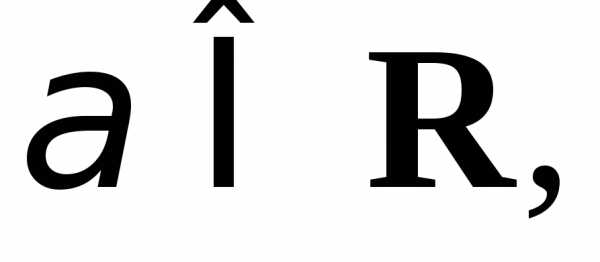называется уравнение вида
(7.27)
где – действительные числа,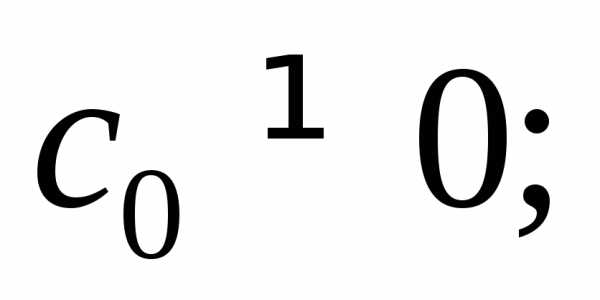
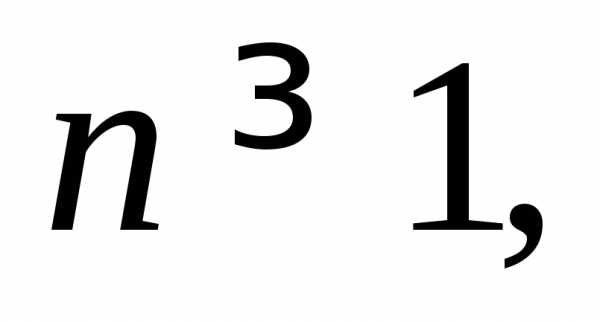
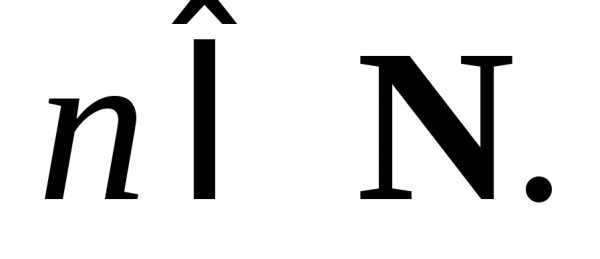
В уравнении (7.27) так как приисходное уравнение примет вид:откудачто невозможно, посколькуине могут одновременно равняться нулю.
Разделив исходное уравнение на 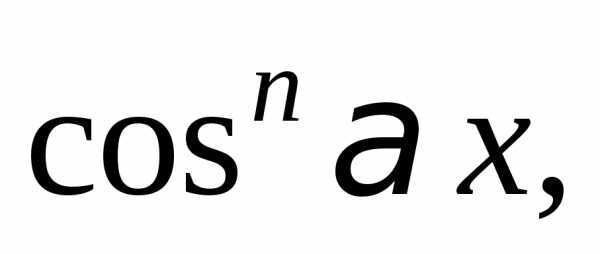получим:
С помощью замены имеем алгебраическое уравнение
которое решаем и возвращаемся к старой переменной.
Пример 11. Решить уравнение
Решение. Разделив уравнение на получимоткуда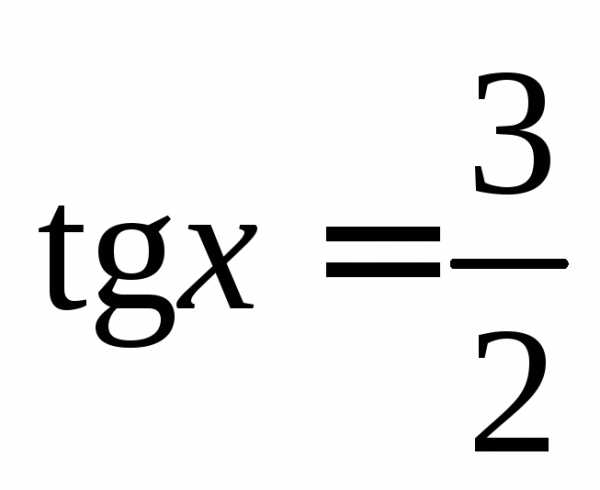и
Получаем ответ:
Пример 12. Решить уравнение
Решение. Используя формулу приведем данное уравнение к однородному:
Разделим почленно на
откуда
Введем замену 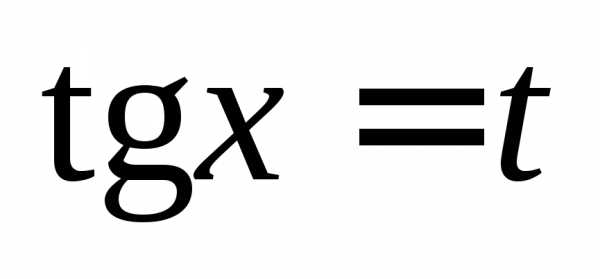и получим уравнениекорнями которого будут
После чего перейдем к решению совокупности простейших уравнений:
Получаем ответ:
6. Неоднородные уравнения 2-й степени
Неоднородным тригонометрическим уравнением 2-й степени называется уравнение вида
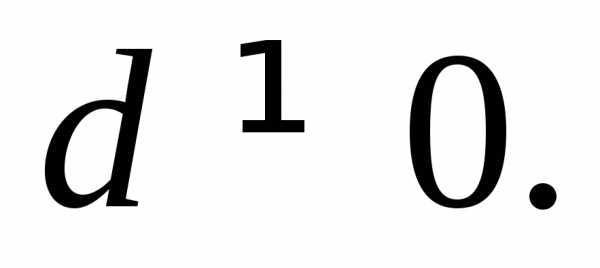(7.28)
Используя основное тригонометрическое тождество, приводим уравнение к однородному
которое решаем далее как уравнение (7.27).
Пример 13. Решить уравнение
Решение. Используя формулы:
и
преобразуем данное уравнение к однородному:
Разделим на
Введем замену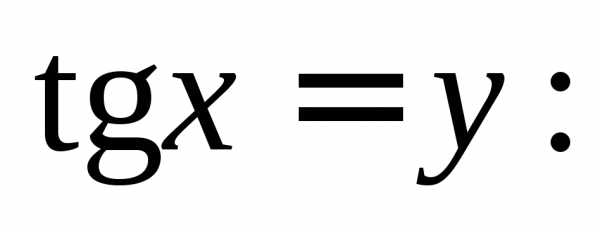
откуда
Решим совокупность уравнений:
Получаем ответ:
7. Неоднородные уравнения 1-й степени
Неоднородным уравнением 1-й степениназывается уравнение вида
(7.29)
1-й способ решения. Используем формулы двойного аргумента:
Тогда уравнение (7.29) сводится к однородному уравнению 2-й степени, которое решаем как уравнение (7.28).
2-й способ решения.Используем метод введения вспомогательного аргумента.
Разделив обе части уравнения (7.29) на 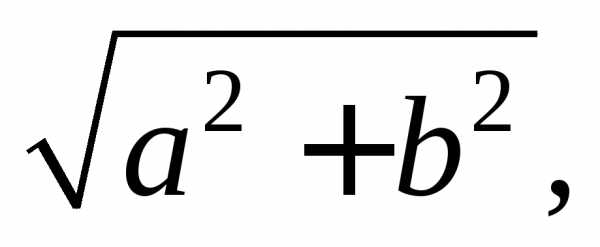получим:
Так как то существует угол, такой, что
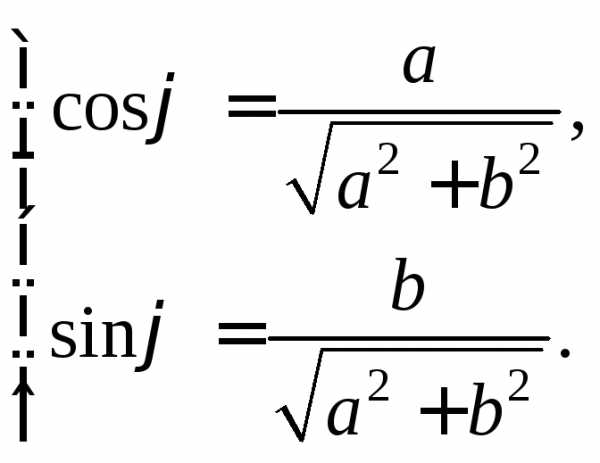(7.30)
Тогда исходное уравнение (7.29) примет вид:
или, используя формулу (7.8) для синуса суммы, получим:
Если то последнее уравнение имеет решение:
Угол находят из формулы (7.30), например,

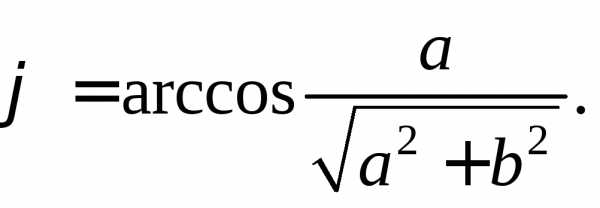
Приходим к ответу:
Пример 14. Решить уравнение
Решение. Разделив левую и правую часть уравнения на 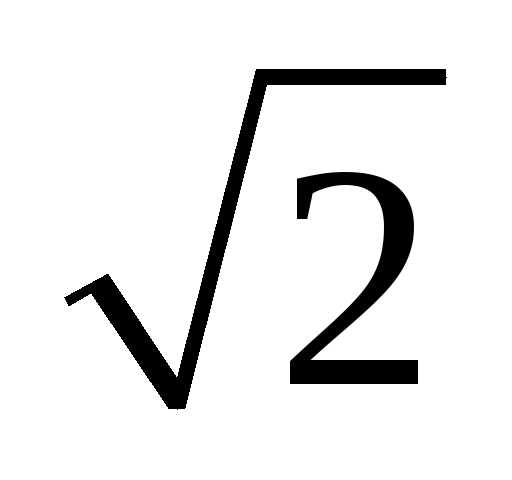(так как), получим:
Тогда
и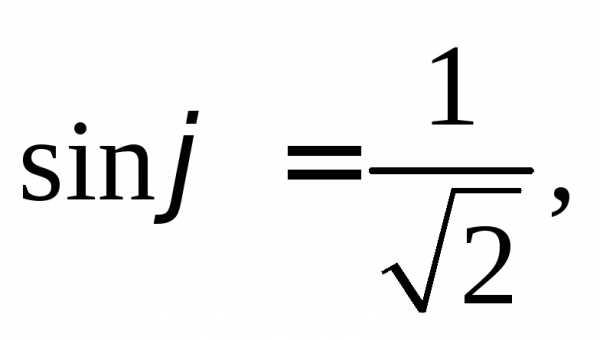
откуда

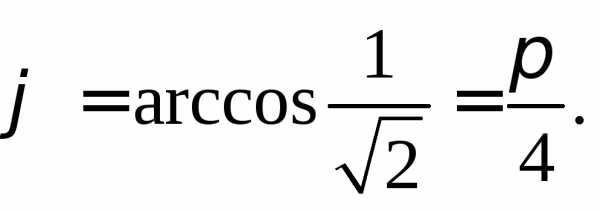
Таким образом, получаем уравнение:

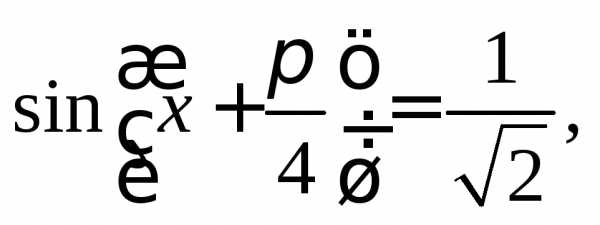
откуда приходим к ответу:
studfiles.net
Урок-семинар по теме «Решение алгебраических уравнений высших степеней методом замены переменной». 11-й класс
Разделы: Математика
Умение решать алгебраические уравнения первой и второй степени входит в “прожиточный” минимум любого выпускника средней общеобразовательной школы. А как быть с уравнениями выше второй степени? Такие уравнения называются уравнениями высших степеней, изучение их в общем виде выходит за рамки программы средней школы. На самом деле для уравнений третьей и четвертой степени есть формулы корней (формулы Кордано и Феррари), выведенные итальянскими математиками в 1545 году, но в силу своей громоздкости эти формулы используют очень редко в школьной программе. После того, как были выведены формулы корней для уравнений третьей и четвёртой степени, на протяжении почти 300 лет, учёные-математики пытались вывести формулы для нахождения корней уравнений пятой степени и выше, но труды их оказались безуспешными. В 1826 году норвежский математик Абель доказал, что нельзя вывести формулы для решения уравнений пятой степени и выше. Но всё же есть хорошие уравнения, которые решаются различными методами и способами.

В последнее время уравнения выше второй степени являются частью выпускных экзаменов за курс средней школы, они встречаются на вступительных экзаменах в ВУЗы, а также являются неотъемлемой частью ЕГЭ. Основными методами решения таких уравнений являются следующие:
Разложение многочлена на множители,

Метод замены переменной.

Функционально-графический метод.

Метод перехода от равенства, связывающего функции, к равенству, связывающему аргументы.

Одним из распространённых методов решения уравнений выше второй степени является метод замены переменной. Суть этого метода заключается в том, что путём замены некоторого выражения, входящего в уравнение, понижается его степень. Основными способами реализации этого метода являются:
Использование основного свойства дроби.

Выделение квадрата двучлена.

Переход к системе уравнений.

Раскрытие скобок парами.

Раскрытие скобок парами и деление обеих частей уравнения на х 0.

Двойная замена.

Понижение степени уравнения.

Один из уроков по теме “Решение уравнений выше второй степени я прилагаю ниже.

Цели:

Формирование знаний о методах и способах решения алгебраических уравнений высших степеней;

Развитие познавательных и исследовательских умений;

Воспитание культуры общения, воспитание умения работать в группах.

Оформление доски: число, тема, запись уравнений в общем виде.

Урок начинается с вступительного слова, в котором напоминаю задачу семинара, порядок его проведения. Напоминаю учащимся основные методы решения алгебраических уравнений (метод замены переменных, функционально-графический, метод разложения многочлена на множители). Ставлю цель реализовать метод замены переменных четырьмя способами.

I группа – раскрытие скобок парами.

II группа – раскрытие скобок парами и деление обеих частей уравнения на х² 0.

III группа – применение основного свойства дроби.

IV группа – выделение квадрата двучлена.

На доске написаны уравнения в общем виде:
(х + а)(х + b)(x + c)(x + d) = m;

(х + а)(х + b)(x + c)(x + d) = Eх²;

;

;

;

.

У каждой группы в карточке два уравнения, одно из них с параметром.

Представитель каждой группы находит на доске свое уравнение, записанное в общем виде, и раскрывает суть его решения (сначала решаются обычные уравнения).

I группа показывает решение уравнения

х(х + 1)(x + 2)(x + 3) = 24

Решение. Воспользуемся симметрией левой части (0 + 3 = 3, 1 + 2 = 3). Перемножим первый и четвертый множители, второй и третий. Получим: (х² + 3х)(x² + 3x + 2) = 24

Вводим замену: x² + 3x = t, тогда t(t + 2) = 24, t² + 2t – 24 = 0, t₁ = -6? t₂ = 4. Возвращаемся к “старой” переменной, получим: x² + 3x = -6, x² + 3x + 6 = 0, D < 0, уравнение не имеет действительных корней.

Уравнение x² + 3x = 4 имеет корни х_{1 =}-4, х_2 =1.

Ответ: х_{1 =}-4, х_{2 =}1.

Комментарий. Задаю вопрос: можно ли это уравнение решить другим способом?

Ответ: Можно, для этого нужно использовать симметрию относительно .

Идет выступление второй группы.

Ученица этой группы решает уравнение, а остальные записывают в тетради.

(х – 4)(х² + 15 + 50)(х – 2) = 18х²

Решение. Разложим на множители х² + 15 + 50.

х² + 15 + 50 = 0, х₁ = -5, х₂ = -10, тогда х² + 15х + 50 = (х + 5)(х + 10). Уравнение примет вид: (х – 4)(х + 5)(х + 10)(х – 2) = 18х²

Так как (-4)•5 = -20, 10•(-2) = -20, то перемножая первую скобку со второй, третью с четвертой, будем иметь: (х² + х – 20)( х² + 8х – 20) = 18х²

Поскольку х = 0 не корень, разделим обе части уравнения на х² ? 0. Получим:

Вводим замену: , тогда (t+1)(t+8)=18, т.е. t²+9t-10=0, t₁= -10, t₂= 1.

Вернемся к исходной переменной:

Решим первое уравнение х² + 10х – 20 = 0, D = 180,

Решим второе уравнение х² — х – 20 = 0, D =81, х₃ = — 4, х₄ = 5.

Ответ: , , х₃ = — 4, х₄ = 5.

Ученица III группы показывает решение уравнения

, используя основное свойство дроби.

Решение. х = 0 не является корнем уравнения, поэтому числитель и знаменатель каждой дроби делим на х 0. , вводим замену: , тогда

Решим это уравнение

Вернемся к “старой” преременной:

Решаем первое уравнение уравнение х² – 14х + 15 = 0

; .

Второе уравнение не имеет действительных корней.

Ответ: ;

Комментарий: Можно ли решить уравнение по другому?

Ответ: Можно, если ввести замену х² + 15х = t.

Ученик четвертой группы для решения уравнения

выбирает способ выделения квадрата двучлена. Приведу решение этого уравнения.

Решение. В левой части выделим полный квадрат разности:

Сгруппируем первый, второй и четвертый члены:

Вводим замену: t² + 18t – 40 = 0; t₁ = -20, t₂ = 2.

Вернемся к “старой” переменной, получим:

Ответ: , .

Задаю вопрос: А есть ли ещё способ решения этого уравнения? Ответ: Да. Уравнение легко решается переходом к системе уравнений

заменив .

Вторая часть урока отводится на решение алгебраических уравнений высших степеней с параметрами. Учащиеся показывают, как эти же способы реализуются при решении уравнений с параметрами.

I группа докладывает.

“Найдите все действительные значения параметра а, при которых уравнение х(х+1)(х+а)(х+1+а) = а² имеет четыре действительных корня.

Решение. Используя специфику решения уравнения

(х + а)(х + b)(x + c)(x + d) = m

будем иметь х(х+1+а)(х+1)(х+а) = а², (х²+х+ах)(х²++х+ах+а) = а²

вводим замену х²+х+ах = t, тогда t(t+a) = a²; t² +at – a² = 0.

Решим уравнение относительно t.

D = a² + 4a² = 5a²; ; .

Подставляя вместо t найденные значения, получим совокупность двух уравнений:

Рассмотрим первое уравнение:

;

D₁ = (a+1)² — 4.

Рассмотрим второе уравнение:

;

D₂ = (a+1)² — 4.

Чтобы исходное уравнение имело четыре действительных корня, необходимо чтобы т.е.

Решим первое неравенство:

, D = 16,

,

т.е. а >, a <.

Решим второе неравенство:

, D = 16,

,

т.е. а >, a <.

В итоге получим

a>, <a<, a<

При |a| >, |a| < уравнение имеет 4 действительных корня, но ещё проверяется, при каком а, корни уравнения совпадают, при а = 0.

Ответ: |a| >, |a| <

Ученица II группы комментирует: Необходимо решить уравнение

(х + 2а)(х +3а)(x + 8а)(x +12а) = 4а²х²,

где а – параметр.

Решение. Используя специфику решения уравнения, будем иметь:

(х² +14ах +24а²)(x² + 11аx +24а²) = 4а²х²,

исследуем уравнение: если а = 0, то х = 0; если а 0, то х 0.

Разделим обе части уравнение на а²х² 0, тогда

Введем замену и получим уравнение: (t+14)(t+11)=4, решая это уравнение, получим t₁ = -15, t₂ = 10. Таким образом, получим два уравнения:

и .

Решим первое уравнение: х² + 15ах + 24а² = 0, D = 129а², тогда

.

Решим второе уравнение х² + 10ах + 24а = 0, D = 4а², тогда

.

Ответ: если, а = 0, то х = 0; если, а 0, то , х₃ = -6а; х₄ = -4а.

Ученица третьей группы показывает решение уравнения

Решение. Уравнение – дробно-рациональное, при а = 0 уравнение не имеет действительных корней. Рассмотрим а ? 0, х ? 0, найдем дискриминант квадратного трехчлена х² –ах + а², D = -3a², значит х² –ах + а² > 0 при х R.

Перейдем теперь к уравнению-следствию, получим:

х⁴ + ах³ +а²х² = а²х² – а³х + а⁴;

(х⁴ – а⁴) + (ах³ + а³х) = 0;

(х² – а²)(х² +а²) + ах(х² + а²) = 0;

(х² + а²)(х² +ах – а²) = 0; х² + а² ? 0,

тогда х² +ах – а² = 0, D = 5a²,

Ответ: если а = 0, то уравнение не имеет действительных корней; если а 0, то .

Заканчивается урок – семинар выступлением ученика 4 группы. У него задание:

В зависимости от значений параметра а решить уравнение

.

Решение.

если а=0, то х=0; если а=1, то х=0; если 0<a<1, то уравнение не имеет действительных корней. Далее, используя специфику решения этого уравнения будет иметь:

;

; .

Вводим замену, , тогда будем иметь уравнение

t²— t = a² – a; t²— t – (a² – a) = 0; D = 1+4(a² – a) = 4a² – 4a + 1 = (2a – 1)².

Находим корни: t₁ = a; t₂ = 1 – a.

Возвращаясь к “старой” переменной, будем иметь:

Рассмотрим уравнение

Исследуем уравнение

при а = 0, х = 0; при а = 2, уравнение не имеет действительных корней;

при , а > 2, а < 0 – уравнение имеет 2 действительных корня,

при 0 < a < 2 уравнение не имеет действительных корней.

Проверим, при каких значениях а

а = а-2, 0 = -2 (нет смысла), нет таких значений а, при которых

Рассмотрим уравнение

Исследуем уравнение

при а = 1 х = 0, при а = -1 — уравнение не имеет действительных корней

при , а > 1, a < -1 уравнение имеет два действительных корня,

при -1< a < 1 – нет действительных корней.

Проверим, при каких значениях а , а-1=а+1, 0 = 2 (нет смысла), нет таких значений а, при которых .

Проверим, сколько корней имеет уравнение при а = -2,

х² = 3, два действительных корня.

Проверим, сколько корней имеет уравнение при а = -1

х² = 1/3 – два действительных корня, далее собираем ответ

Ответ: при а < -1, a > 2 уравнение имеет 4 действительных корня

,

при -1 a < 0 – два действительных корня,

при а = 0, а = 1 – уравнение имеет корень х = 0; при 0 < a < 1 – нет действительных корней

при 1 < a 2 – уравнение имеет два действительных корня

Подводя итог урока, я отмечаю, что учащиеся проделали большую работу, показав 4 способа реализации метода замены переменной, увязав эти способы с уравнениями, содержащими параметр. Работа учащихся оценивается и задается домашнее задание.
х³ — 4х² + 5х — 2 = 0

28.01.2008
xn--i1abbnckbmcl9fb.xn--p1ai
No related posts.