Вероятность произведения событий
Рассмотрим следующую задачу.
Пример5.Из колоды карт (36 листов) наудачу извлекаются две карты. Найти вероятности следующих событий:
а) вероятность появления двух тузов;
б) вероятность появления туза на втором месте при условии, что на первом месте был туз.
Решение. Ведем обозначения: событиеА– туз на первом месте, событиеВ– туз на втором, тогдаАВ– два туза.
Имеем:.
Два туза из имеющихся в колоде четырех
можно вытащить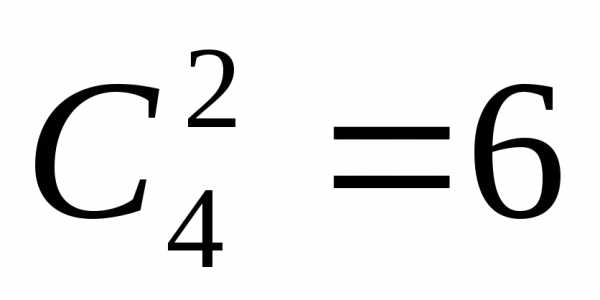 способами;
две карты из 36 можно вытащитьспособами. Тогда.
Обозначимр(В/А) илирА(В)–условная вероятность события В при
условии, что событие А уже произошло. Если событиеА
способами;
две карты из 36 можно вытащитьспособами. Тогда.
Обозначимр(В/А) илирА(В)–условная вероятность события В при
условии, что событие А уже произошло. Если событиеА
В общем случае, вероятность произведения двух событий равна вероятности произведения одного из них на условную вероятность второго при условии, что первое уже произошло:
р(АВ) = р(А) · р(В/А). | (7) |
Если события АиВ независимы (т.е. появление любого из них не зависит от того, произошло другое событие или не произошло), тор(А/В) = р(А), р(В/А) = р(В) (не путать с несовместимыми событиями!). Для независимых событий вероятность произведения равна произведению вероятностей:р(АВ) = р(А) · р(В).
Для вероятности произведения nсобытий справедлива формула:
р(А1 · А2 ·…·Аn) = р(А1) · р(А2 /А1) · р(А3 /А1А2) ·…·р(Аn /А1А2…Аn-1), | (8) |
т.е. вероятность произведения nсобытий равна произведению вероятности одного из них на условные вероятности остальных, причем вероятность каждого последующего события вычисляется в предположении, что все предыдущие события произошли.
Для независимых в совокупности событий А1,…,Аn,т.е. событий попарно независимых, формула вероятности произведения существенно упрощается, а именно, вероятность произведения событий равна произведению вероятностей:
р(А1 · А2 ·…·Аn) = p(A1) · p(A2) · p(A3) ·… · p(An). | (9) |
Пример 6. На карточках написаны буквы Ю, Р, Т, А. Карточки наудачу раскладываются на столе одна за другой. Найти вероятность появление слова ЮРТА.
Решение.Введем обозначения: событиеА1 — буква Ю на первом месте;А2 – Р на втором месте;А3– Т на третьем месте;А 4 – на четвертом месте; слово ЮРТА появится, если событияА1, А2, А3, А4произойдут вместе. Вероятность этого события есть
Р(А1 ·А2 ·
А3 · А4) = р(А1)
· р(А2 / А1) ·
р(А3 / А1А2)
· р(А4 / А1А2А3)
= 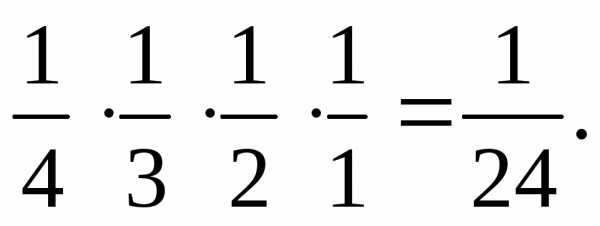
Эту задачу можно решить непосредственно пользуясь классическим определением вероятности: здесь число равновозможных исходов равно числу перестановок из четырех букв, т.е. n = P4 = 4!
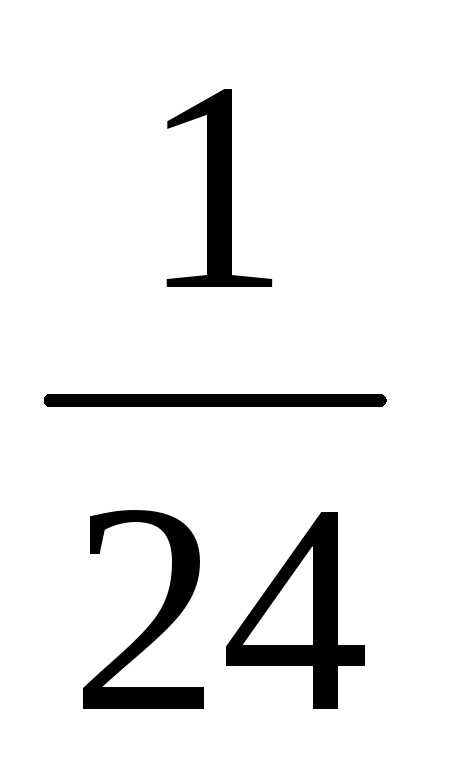 .
.Вероятность суммы двух событий
В случае классического определения вероятности дается способ ее вычисления. В общем случае дать способ вычисления вероятности конечно же нельзя. Тогда постулируют свойства вероятностей случайных событий.
Предположим, что имеется некоторое множество случайных событий S:
а) U  S, V
S, V  S;
S;
б) если А,В  S,
то иА +В
S,
то иА +В  S,
S,
 S,А ·В S,
S,А ·В S, т.е.
мы всегда можем говорить о достоверном
и невозможном событиях, о противоположных
событиях, о сумме и произведении случайных
событий.
т.е.
мы всегда можем говорить о достоверном
и невозможном событиях, о противоположных
событиях, о сумме и произведении случайных
событий.
Для любого случайного события Аопределено некоторое числор = р(А), которое мы называем его вероятностью, причем0
 р(А)
р(А) 1.
1.р(U) = 1: вероятность достоверного события равна 1.
Если события А1, А2,…,
Аnпопарно несовместимы, то вероятность их суммы равна сумме вероятностей этих событий, т.е. еслиАi Аj= Vприi j,
тор(А1 + А2 +…+ An)
= p(A1)
+ p(A2)
+…+ p(An).
j,
тор(А1 + А2 +…+ An)
= p(A1)
+ p(A2)
+…+ p(An).
Все эти аксиомы совпадают с соответствующими свойствами классической вероятности, и в случае классического определения вероятности они могут быть доказаны. Из сформулированных аксиом можно легко получить формулы:
Р(А) + Р( )
= 1, р(V) = 0.
)
= 1, р(V) = 0.
Также нетрудно доказать, что вероятность суммы двух событий равна сумме вероятностей этих событий без вероятности их совместного появления:
p(А + В) = р(А) + р(В) – р(АВ). | (10) |
Заметим, что эта формула не противоречит аксиоме 4, т.к., если события АиВнесовместимы, тор(АВ) = 0.
Пример 7.Два стрелка выстрелили в цель по одному разу. Вероятность попадания в цель первым стрелком равна 0.9; вторым – 0.8. Найти вероятность поражения цели.
Решение.Пусть событиеА – в цель попал первый стрелок,В – второй. Тогда событиеВ + Аозначает, что цель поражена:
Р(А + В) = р(А) + р(В) – р(АВ) = 0.8 + 0.9 – 0.80.9 = 0.98.
Эту задачу можно решить и другим способом:
Вероятность произведения событий
Рассмотрим следующую задачу.
Пример5.Из колоды карт (36 листов) наудачу извлекаются две карты. Найти вероятности следующих событий:
а) вероятность появления двух тузов;
б) вероятность появления туза на втором месте при условии, что на первом месте был туз.
Решение. Ведем обозначения: событиеА– туз на первом месте, событиеВ– туз на втором, тогдаАВ– два туза.
Имеем:.
Два туза из имеющихся в колоде четырех
можно вытащить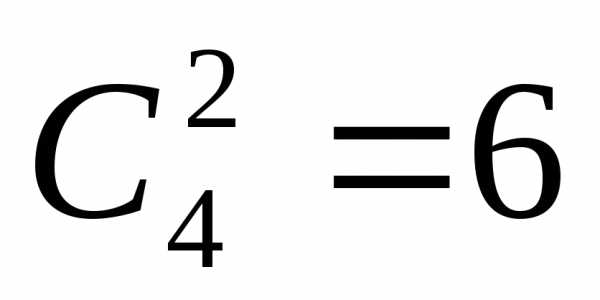 способами;
две карты из 36 можно вытащитьспособами. Тогда.
Обозначимр(В/А) илирА(В)–условная вероятность события В при
условии, что событие А уже произошло.
способами;
две карты из 36 можно вытащитьспособами. Тогда.
Обозначимр(В/А) илирА(В)–условная вероятность события В при
условии, что событие А уже произошло.
В общем случае, вероятность произведения двух событий равна вероятности произведения одного из них на условную вероятность второго при условии, что первое уже произошло:
р(АВ) = р(А) · р(В/А). | (7) |
Если события АиВ независимы (т.е. появление любого из них не зависит от того, произошло другое событие или не произошло), тор(А/В) = р(А), р(В/А) = р(В) (не путать с несовместимыми событиями!). Для независимых событий вероятность произведения равна произведению вероятностей:р(АВ) = р(А) · р(В).
Для вероятности произведения
р(А1 · А2 ·…·Аn) = р(А1) · р(А2 /А1) · р(А3 /А1А2) ·…·р(Аn /А1А2…Аn-1), | (8) |
т.е. вероятность произведения nсобытий равна произведению вероятности одного из них на условные вероятности остальных, причем вероятность каждого последующего события вычисляется в предположении, что все предыдущие события произошли.
Для независимых в совокупности событий А1,…,Аn,т.е. событий попарно независимых, формула вероятности произведения существенно упрощается, а именно, вероятность произведения событий равна произведению вероятностей:
р(А1 · А2 ·…·Аn) = p(A1) · p(A2) · p(A3) ·… · p(An). | (9) |
Пример 6. На карточках написаны буквы Ю, Р, Т, А. Карточки наудачу раскладываются на столе одна за другой. Найти вероятность появление слова ЮРТА.
Решение.Введем обозначения: событиеА1 — буква Ю на первом месте;А2 – Р на втором месте;А3– Т на третьем месте;А4 – на четвертом месте; слово ЮРТА появится, если событияА1, А2, А3, А4произойдут вместе. Вероятность этого события есть
Р(А1 ·А2 ·
А3 · А4) = р(А1)
· р(А2 / А1) ·
р(А3 / А1А2)
· р(А4 / А1А2А3)
= 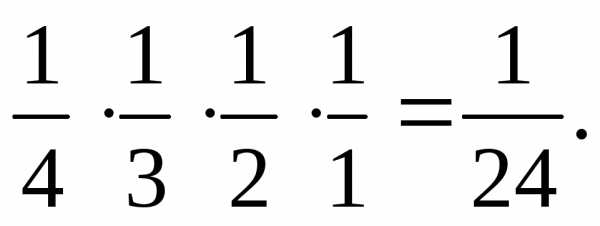
Эту задачу можно решить непосредственно
пользуясь классическим определением
вероятности: здесь число равновозможных
исходов равно числу перестановок из
четырех букв, т.е. n = P4 = 4! = 1 ·2 ·3 ·4 = 24. появлению слова ЮРТА благоприятствует одна перестановка.
Следовательно, искомая вероятность
равнар = 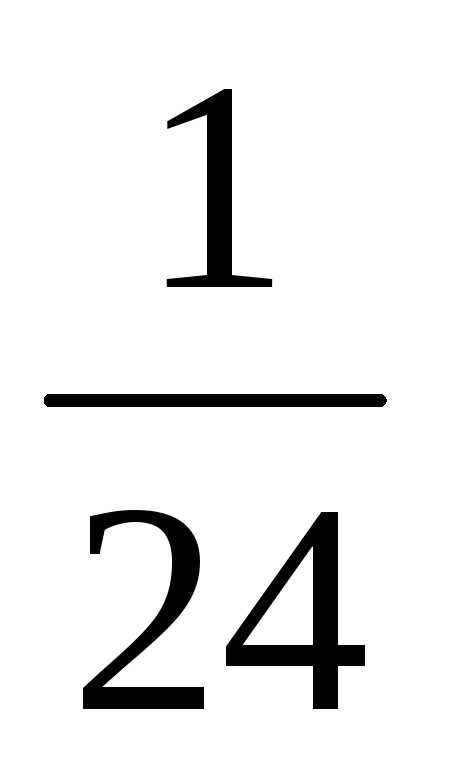 .
.
Вероятность суммы двух событий
В случае классического определения вероятности дается способ ее вычисления. В общем случае дать способ вычисления вероятности конечно же нельзя. Тогда постулируют свойства вероятностей случайных событий.
Предположим, что имеется некоторое множество случайных событий S:
а) U  S, V
S, V  S;
S;
б) если А,В  S,
то иА +В
S,
то иА +В  S,
S,
 S,А ·В
S,А ·В  S,
S, т.е.
мы всегда можем говорить о достоверном
и невозможном событиях, о противоположных
событиях, о сумме и произведении случайных
событий.
т.е.
мы всегда можем говорить о достоверном
и невозможном событиях, о противоположных
событиях, о сумме и произведении случайных
событий.
Для любого случайного события Аопределено некоторое числор = р(А), которое мы называем его вероятностью, причем0
 р(А)
р(А) 1.
1.р(U) = 1: вероятность достоверного события равна 1.
Если события А1, А2,…, Аnпопарно несовместимы, то вероятность их суммы равна сумме вероятностей этих событий, т.е. еслиАi Аj= Vприi
 j,
тор(А1 + А2 +…+ An)
= p(A1)
+ p(A2)
+…+ p(An).
j,
тор(А1 + А2 +…+ An)
= p(A1)
+ p(A2)
+…+ p(An).
Все эти аксиомы совпадают с соответствующими свойствами классической вероятности, и в случае классического определения вероятности они могут быть доказаны. Из сформулированных аксиом можно легко получить формулы:
Р(А) + Р( )
= 1, р(V) = 0.
)
= 1, р(V) = 0.
Также нетрудно доказать, что вероятность суммы двух событий равна сумме вероятностей этих событий без вероятности их совместного появления:
p(А + В) = р(А) + р(В) – р(АВ). | (10) |
Заметим, что эта формула не противоречит аксиоме 4, т.к., если события АиВнесовместимы, тор(АВ) = 0.
Пример 7.Два стрелка выстрелили в цель по одному разу. Вероятность попадания в цель первым стрелком равна 0.9; вторым – 0.8. Найти вероятность поражения цели.
Решение.Пусть событиеА – в цель попал первый стрелок,В – второй. Тогда событиеВ + Аозначает, что цель поражена:
Р(А + В) = р(А) + р(В) – р(АВ) = 0.8 + 0.9 – 0.80.9 = 0.98.
Эту задачу можно решить и другим способом:
studfiles.net
Вероятность произведения событий.
Обратная связь
ПОЗНАВАТЕЛЬНОЕ
Сила воли ведет к действию, а позитивные действия формируют позитивное отношение
Как определить диапазон голоса — ваш вокал
Как цель узнает о ваших желаниях прежде, чем вы начнете действовать. Как компании прогнозируют привычки и манипулируют ими
Целительная привычка
Как самому избавиться от обидчивости
Противоречивые взгляды на качества, присущие мужчинам
Тренинг уверенности в себе
Вкуснейший «Салат из свеклы с чесноком»
Натюрморт и его изобразительные возможности
Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д.
Как научиться брать на себя ответственность
Зачем нужны границы в отношениях с детьми?
Световозвращающие элементы на детской одежде
Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия
Как слышать голос Бога
Классификация ожирения по ИМТ (ВОЗ)
Глава 3. Завет мужчины с женщиной
Оси и плоскости тела человека — Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
Отёска стен и прирубка косяков — Когда на доме не достаёт окон и дверей, красивое высокое крыльцо ещё только в воображении, приходится подниматься с улицы в дом по трапу.
Дифференциальные уравнения второго порядка (модель рынка с прогнозируемыми ценами) — В простых моделях рынка спрос и предложение обычно полагают зависящими только от текущей цены на товар.
Теорема. (Умножения вероятностей) Вероятность произведения двух событий (совместного появления этих событий) равна произведению вероятности одного из них на условную вероятность другого, вычисленную при условии, что первое событие уже наступило.
Также можно записать:
Доказательство этой теоремы непосредственно вытекает из определения условной вероятности.
Если события независимые, то , и теорема умножения вероятностей принимает вид:
В случае произведения нескольких зависимых событий вероятность равна произведению одного из них на условные вероятности всех остальных при условии, что вероятность каждого последующего вычисляется в предположении, что все остальные события уже совершились.
Из теоремы произведения вероятностей можно сделать вывод о вероятности появления хотя бы одного события.
Если в результате испытания может появиться п событий, независимых в совокупности, то вероятность появления хотя бы одного из них равна
Здесь событие А обозначает наступление хотя бы одного из событий Ai, а qi – вероятность противоположных событий .
Пример 1. Из полной колоды карт (52 шт.) одновременно вынимают четыре карты. Найти вероятность того, что среди этих четырех карт будет хотя бы одна бубновая или одна червонная карта.
Решение.
Обозначим появление хотя бы одной бубновой карты – событие А, появление хотя бы одной червонной карты – событие В. Таким образом нам надо определить вероятность события С = А + В.
Кроме того, события А и В – совместны, т.е. появление одного из них не исключает появления другого.
Всего в колоде 13 червонных и 13 бубновых карт.
Найдем вероятность события, противоположного событию С (среди извлеченных карт не будет ни бубновых ни червовых):
при вытаскивании первой карты вероятность того, что не появится ни червонной ни бубновой карты равна , при вытаскивании второй карты — , третьей — , четвертой — .
Тогда вероятность того, что среди вынутых карт не будет ни бубновых, ни червонных равна .
Искомая вероятность
Пример 2. Чему равна вероятность того, что при бросании трех игральных костей 6 очков появится хотя бы на одной из костей?
Решение.
Вероятность выпадения 6 очков при одном броске кости равна . Вероятность того, что не выпадет 6 очков — . Вероятность того, что при броске трех костей не выпадет ни разу 6 очков равна .
Тогда вероятность того, что хотя бы один раз выпадет 6 очков равна .
Пример 3. В барабане револьвера находятся 4 патрона из шести в произвольном порядке. Барабан раскручивают, после чего нажимают на спусковой крючок два раза. Найти вероятности: а) хотя бы одного выстрела, б) двух выстрелов, в) двух осечек.
Решение.
Вероятность выстрела при первом нажатии на курок (событие А) равна , вероятность осечки — Вероятность выстрела при втором нажатии на курок зависит от результата первого нажатия.
Так если в первом случае произошел выстрел, то в барабане осталось только 3 патрона, причем они распределены по 5 гнездам, т.к. при втором нажатии на курок напротив ствола не может оказаться гнездо, в котором был патрон при первом нажатии на курок.
Условная вероятность выстрела при второй попытке — если в первый раз был выстрел, — если в первый раз произошла осечка.
Условная вероятность осечки во второй раз — , если в первый раз произошел выстрел, — если в первый раз была осечка.
Рассмотрим вероятности того, что во втором случае произойдет выстрел (событие В) или произойдет осечка (событие ) при условии, что в первом случае произошел выстрел (событие А) или осечка (событие ).
— два выстрела подряд
— первая осечка, второй выстрел
— первый выстрел, вторая осечка
— две осечки подряд
Эти четыре случая образуют полную группу событий (сумма их вероятностей равна единице)
Анализируя полученные результаты, видим, что вероятность хотя бы одного выстрела равна сумме
Пример 4. Два стрелка стреляют по мишени. Вероятность попадания в мишень при одном выстреле для первого стрелка равна 0,7, а для второго – 0,8. Найти вероятность того, что при одном залпе в мишень попадает только один из стрелков.
Решение.
Обозначим попадание в цель первым стрелком – событие А, вторым – событие В, промах первого стрелка – событие , промах второго – событие .
Вероятность того, что первый стрелок попадет в мишень, а второй – нет равна
Вероятность того, что второй стрелок попадет в цель, а первый – нет равна
Тогда вероятность попадания в цель только одним стрелком равна
Тот же результат можно получить другим способом – находим вероятности того, что оба стрелка попали в цель и оба промахнулись. Эти вероятности соответственно равны:
Тогда вероятность того, что в цель попадет только один стрелок равна:
Пример 5. Вероятность того, что взятая наугад деталь из некоторой партии деталей, будет бракованной равна 0,2. Найти вероятность того, что из трех взятых деталей 2 окажется не бракованными.
Решение.
Обозначим бракованную деталь – событие А, не бракованную – событие .
Если среди трех деталей оказывается только одна бракованная, то это возможно в одном из трех случаев: бракованная деталь будет первой, второй или третьей.
Пример 6. Вероятности того, что нужная деталь находится в первом, втором, третьем или четвертом ящике, соответственно равны 0,6, 0,7, 0,8, 0,9. Найти вероятности того, что эта деталь находится: а) не более, чем в трех ящиках; б) не менее, чем в двух ящиках.
Решение.
а) Вероятность того, что данная деталь находится во всех четырех ящиках, равна
Вероятность того, что нужная деталь находиться не более, чем в трех ящиках равна вероятности того, что она не находится во всех четырех ящиках.
.
б) Вероятность того, что нужная деталь находится не менее, чем в двух ящиках, складывается из вероятностей того, что деталь находиться только в двух ящиках, только в трех ящиках, только в четырех ящиках. Конечно, эти вероятности можно посчитать, а потом сложить, однако, проще поступить иначе. Та же вероятность равна вероятности того, что деталь не находится только в одном ящике и имеется вообще.
megapredmet.ru
6). Произведение событий. Условная вероятность. Теорема умножения вероятностей.
Произведением двух событий А и В называют событие АВ, состоящее в совместном появлении этих событий. Например, если А — деталь годная, В — деталь окрашенная, то АВ — деталь годна и окрашена.
Произведением нескольких событий называют событие, состоящее в совместном появлении всех этих событий. Например, если А, В, С — появление «герба» соответственно в первом, втором и третьем бросаниях монеты, то АВС — выпадение «герба» во всех трех испытаниях.
Условной вероятностью (два обозначения) называют вероятность события В, вычисленную в предположении, что событие А уже наступило.
Вероятность совместного появления двух зависимых событий равна произведению вероятности одного из них на условную вероятность второго, вычисленную при условии, что первое событие произошло, т.е.
.
В частности, отсюда получаем .
Теорема умножения. Вероятность совмещения событий А и В равна произведению вероятности одного из них на условную вероятность другого, вычисленную в предположении, что первое событие осуществилось, т. е.
7). Независимые события. Теорема умножения для независимых событий. Вероятность появления хотя бы одного события.
Два события называются независимыми, если вероятность появления одного из них не зависит от появления другого события
Теорема.Вероятность совместного появления двух событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную в предположении, что первое событие уже наступило:
Р (АВ) = Р (А) РA(В). (*)
Для независимых событий теорема умножения
Р(АВ) = Р(А) ·РA(В)
имеет вид
Р(АВ) = Р(А) ·Р (В), (5)
т. е. вероятность совместного появления двух независимыхсобытий равна произведению вероятностей этих событий.
Вероятность появления хотя бы одного из событий А1 , А2 , …, Аn , независимых в совокупности, равна разности между единицей и произведением вероятностей противоположных событий
Р (A) = 1 — q1q2 … qn.(*)
Если события А1 , А2 , …, Аn имеют одинаковую вероятность, равную р, то вероятность появления хотя бы одного из этих событий
P (A) = l — qn. (**)
8). Теорема сложения вероятностей совместных событий. Формула полной вероятности.
Вероятность появления хотя бы одного из двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления:
P(A+B)=P(A)+P(B)-P(AB)
Теорема может быть обобщена на любое конечное число совместных событий. Для трех совместных событий:
P(A+B+C)=P(A)+P(B)+P(C)-P(AB)-P(AC)-P(BC)+P(ABC)
Формула полной вероятности.
Теорема 1. Если события Н1, Н2,…,Нn образуют полную группу, то вероятность любого события А можно вычислить по формуле полной вероятности:
, или .
Так как события образуют полную группу, то можно записать .
Событие
А может произойти только с одним из
событий Hi, i {1,2,…,n},
то А=АН1+АН2+…+АНn. По теореме сложения
вероятностей
{1,2,…,n},
то А=АН1+АН2+…+АНn. По теореме сложения
вероятностей
Замечание: при применении формулы полной вероятности события Н1,Н2,…,Нn , образующие полную группу, называются гипотезами.
studfiles.net
8.Вероятность произведения событий
Р/м 2 события:А и В.Пусть Р(А) и Р(В) извсетны.Как найти вероятность совмещения этих событий,т.е вероятность того,что появится и событие А и событие В
Т-ма.Вероятность совместного появления двух событий равна произведению
вероятности одного из них на условную вероятность другого,вычисленную в предположении,что первое событие уже наступило:
Р(АВ)=Р(А)Р(В)
Док-во.
По определению условной вероятности Р(В)=Р(АВ)/Р(А)
отсюда Р(АВ)=Р(А)Р(В)(*)
Применив формулу Р(В)=Р(АВ)/Р(А) к событию ВА,получим Р(ВА)=Р(В)Р(А)
поскольку событие ВА не отличается от события АВ
Р(АВ)=Р(В)Р(А)(**)
Справедливость равенства выходит Р(А)Р(В)=Р(В)Р(А)
9.Сумма вероятностей совместных событий
Два события совместны,если появление одного из них не исключает появление другого в одном и том же испытании.Пример:А-повяление 4 очков при бросании игральной кости,В-появление четного числа очков.События А и В-совместные.
Т-ма.Вероятность появления хотя бы 1го из 2 совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления:
Р(А+В)=Р(А)+Р(В)-Р(АВ)
10.Формулы полной вероятности и Бейеса.
Если событие А может произойти только при выполнении одного из несовместных событий B1, B2,…, Bn, которые образуют полную группу несовместных событий, то вероятность события А вычисляется по формуле:
P(A)=P(B1)P(A/B1)+P(B2)(A/B2)+…+P(Bn)P(A/Bn).
Эта формула называется формулой полной вероятности.
Вновь рассмотрим полную группу несовместных событий B1, B2,…, Bn, вероятности появления которых P(B1), P( B2),…, P(Bn). Событие А может произойти только вместе с каким-либо из событий B1, B2,…, Bn, которые будем называть гипотезами. Тогда по формуле полной вероятности: (A)=P(B1)P(A/B1)+P(B2)(A/B2)+…+P(Bn)P(A/Bn).
Если событие А произошло, то это может изменить вероятности гипотез P(B1), P( B2),…, P(Bn).
По теореме умножения вероятностей P(AB1)=P(B1)P(A/B1)=P(A)P(B/A), откуда P(B1/A)=(P(B1)P(A/B1)) / P(A).
Аналогично, для остальных гипотез: P(Bi/A)=(P(Bi)P(A/Bi)) / P(A), i=1,…,n.
Полученная формула называется формулой Байеса (формулой Бейеса). Вероятности гипотез P(Bi/A) называются апостериорными вероятностями, тогда как P(Bi) — априорными вероятностями.
11.Повторение испытаний,формула Бернулли.
Вероятность одного сложного события,состоящего в том,что в n испытаниях событие А наступит k раз и не наступит k-n раз,по теореме умножения вероятностей независимых событий равна p в степени k*q в степени n-k.Событий может быть столько,сколько возможно составить сочетаний из n элементов по k элементам.С k/n.Т.к эти сложные события несовместны,то по т. сложения вероятностей нес. событий искомая вероятность=сумме вероятностей всех возможных сложных событий.Т.к вероятности всех сложных событий одинаковы,то искомая вероятность=вероятности одного сложного событий,умноженной на число:
Pn(k)=C n/k * p^k * q^n-k
Pn(k)= n!/k!(n-k)!*p^k*q^n-k
12. Предельные формулы Пуассона и Муавра-Лапласа.
Формула Бернуллиудобна для вычислений лишь при сравнительно небольшом числе испытаний. При больших значенияхпользоваться этой формулой неудобно. Чаще всего в этих случаях используют формулу Пуассона. Эта формула определяется теоремой Пуассона.
Теорема.Если вероятностьнаступления событияв каждом испытании постоянна и мала, а число независимых испытанийдостаточно велико, то вероятность наступления событияровнораз приближенно равна
формулу Пуассона:
Эта формула дает удовлетворительное приближение для p?0,1 и np?10. При больших np рекомендуется применять формулы Лапласа (Муавра-Лапласа). Cобытия, для которых применима формула Пуассона, называют редкими, так как вероятность их осуществления очень мала (обычно порядка 0,001-0,0001).
Локальная теорема Лапласа.
Если n – велико, а р – отлично от 0 и 1, то
где- функция Гаусса (функция табулирована, таблицу можно скачать на страницеформул по теории вероятностей).
Интегральная теорема Лапласа.
Если n – велико, а р – отлично от 0 и 1, то
P(n; k1, k2)где- функция Лапласа (функция табулирована, таблицу можно скачать на страницеформул по теории вероятностей).
Функции Гаусса и Лапласа обладают свойствами, которые необходимо знать при использовании таблиц значений этих функций:
а)
б) при больших верно.
Теоремы Лапласа дают удовлетворительное приближение при . Причем чем ближе значенияк 0,5, тем точнее данные формулы. При маленьких или больших значениях вероятности (близких к 0 или 1) формула дает большую погрешность (по сравнению с исходной формулой Бернулли).
studfiles.net
УСЛОВНАЯ ВЕРОЯТНОСТЬ. ВЕРОЯТНОСТЬ ПРОИЗВЕДЕНИЯ СОБЫТИЙ
⇐ ПредыдущаяСтр 2 из 8Следующая ⇒
Определение2.2.Вероятность события А, вычисленная при условии, что произошло событие В, называется условной вероятностью события А при наличии события В и обозначается Р(А|В).
Пример 2.10. Опыт: подбрасывание двух монет. События:
А = {выпадение «орла» на обеих монетах};
В = {выпадение «орла» на одной из монет}.
Найти вероятность Р(А). Общее число возможных исходов опыта n=4 (оо, ор, рр, ро), благоприятствующий исход один (оо), следовательно, Р(А)=1/4. (Здесьобозначено за «о» – «орел», за «р» – «решка»).
Найти теперь условную вероятность Р(А|В). Поскольку известно, что произошло событие В, число возможных исходов испытания п–1(оо, ор, ро), благоприятствующий исход по–прежнему один, следовательно, Р(А|В)=1/3.
Теорема. Вероятность произведения двух событий А и В, равна произведению вероятности одного из этих событий на условную вероятность другого при наличии первого:
Р(АВ) = Р(А)Р(В|А)или Р(АВ) = Р(В)Р(А|В). (2.1)
Эта теорема обобщается на любое конечное число событий следующим образом:
(2.2)
Определение2.3. Два события называются независимыми, если появление любого из них не изменяет вероятности другого, т.е. события А и В независимы, если Р(А|В)=Р(А).
Из формул (2.1) следует, что если выполняется равенство Р(А|В)=Р(А),.то выполняется и равенство Р(В\А)=Р(В).
Определение2.4.Несколько событий, А1, А2, …, Ап, называются независимыми в совокупности (или просто независимыми), если появление любых из них не изменяет вероятностей остальных. Для независимых событий формула (2.2) принимает вид:
Р(А1 А2…Ап) = Р(А1)×Р(А2×…×Р(Ап).
Пример 2.11. Из урны, содержащей 3 белых и 7 черных шаров, наудачу извлекают два шара. Найти вероятность того, что оба шара белые.
Решение. Считаем, что шары извлекаются поочередно. Пусть
А = {первый шар – белый}, В = {второй шар – белый}, тогда АВ – {оба шара – белые}.
По теореме умножения вероятностей Р(АВ)=Р(А)Р(В|А). Согласно классическому определению вероятности Р(А)=3/10, Р(В|А)=2/9.Следовательно, Р(АВ)= (3/10)×(2/9).
Пример 2.12. Два стрелка стреляют по одной мишени. Вероятность поражения мишени первым стрелком равна 0.6, вторым – 0.8. Найти вероятность того, что в мишени будет две пробоины.
Решение. Введем в рассмотрение события, вероятности которых известны:
А = {поражение мишени первым стрелком},
В = {поражение мишени вторым стрелком}.
Интересующее нас событие выразим через эти события. Для того, чтобы имело место событие С={две пробоины в мишени}, надо, чтобы произошли вместе события А и В, т.е. С=АВ.
Естественно считать события А и В независимыми, поэтому
Р(С)=Р(А)×Р(В)=0.6×0.8.
ВЕРОЯТНОСТЬ СУММЫ СОБЫТИЙ
Теорема 2.1. Вероятность суммы двух несовместных событий равна сумме вероятностей этих событий:
Теорема 2.2. Для любого события А вероятность противоположного события А выражается равенством
Р(`А) = 1 – Р(А)
Теорема 2.3. Вероятность суммы двух совместных событий равна сумме вероятностей этих событий минус вероятность их совместного появления:
Р(А + В) = Р(А)+ Р(В) – Р(АВ).
Теорема сложения обобщается на любое конечное число событий следующим образом:
(2.3)
Если события А1, А2, …, Аппопарно несовместные, то формула (2.3) принимает вид:
Замечание. При решении задач с использованием формулы (2.3) приходится производить громоздкие вычисления, поэтому часто выгоднее перейти к противоположным событиям, т.е. вместо вероятности суммы событий А1+А2+…+Апнаходить вероятность произведения противоположного события . Очевидно, что эти два события противоположны, поэтому
(2.4)
Пример 2.13. В условиях примера 2 предыдущего пункта найти вероятность появления хотя бы одной пробоины.
Решение. Данное событие есть сумма событий А и В, причем эти события совместные, поэтому вероятность интересующего нас события равна Р(А + В) = Р(А) + Р(В) – Р(АВ). Ранее было найдено, что Р(АВ)=0.48, следовательно, Р(А + В) = 0.6 + 0.8 – 0.48 = 0.92.
Пример 2.14. Устройство содержит четыре независимо работающих элемента и сохраняет работоспособность, если работает хотя бы один из элементов. Вероятности безотказной работы элементов в течение определенного срока соответственно равны 0.9, 0.8, 0.7 и 0.6. Найти вероятность безотказной работы устройства.
Решение. Пусть события А1 А2, А3и А4означают безотказную работу соответственно первого, второго, третьего и четвертого элементов. Событие А={безотказная работа устройства} есть сумма событий: А=А1+А2+А3+А4.События А1 А2, А3и А4совместные, поэтому вероятность Р(А)надо вычислять по формуле (2.3). Чтобы упростить вычисления, воспользуемся формулой (2.4):
.
Так как события А1 А2, А3и А4независимые, то противоположные события также независимы, поэтому
= (1 – 0.9)(1 – 0.8)(1 – 0.7)(1 – 0.6) = 0.0024; и
Р(А) = 1 – 0.0024 = 0.9976.
Пример 2.15. Производится три независимых выстрела по мишени. Вероятности попадания в мишень при первом, втором и третьем выстрелах соответственно равны 0.2, 0.5, 0.4. Найти вероятность того, что будет ровно два попадания в мишень.
Решение. Событие А={ровно два попадания в мишень} выражается через события А1={попадание при первом выстреле}, А2={попадание при втором выстреле), А3={попадание при третьем выстреле} следующим образом:
Отсюда, учитывая несовместность суммируемых произведений событий и независимость событий А1, А2, А3,находим
Пример 2.16. В двух урнах находятся шары, отличающиеся только цветом: в первой урне 5 белых шаров, 11 черных и 8 красных, во второй 10 белых, 8 черных и 6 красных. Из обеих урн наудачу извлекают по одному шару. Найти вероятность того, что оба шара одного цвета.
Решение. Введем в рассмотрение следующие события:
В1={извлечение белого шара из первой урны},
В2={извлечение белого шара из второй урны},
С1={извлечение черного шара из первой урны},
С2={извлечение черного шара из второй урны},
D1={извлечение красного шара из первой урны},
D2={извлечение красного шара из второй урны}.
Выразим событие А= {извлечение шаров одного цвета} через эти события:
А= В1 В2+ С1 С2+ D1 D2
Следовательно,
Р(А) = Р(В1)Р(В2) + Р(С1)Р(С2) + Р(D1)P(D2).
Вероятности событий В, С, D найдем из классического определения: Р(В1)=5/24, Р(В2)=10/24, Р(С1)=11/24, Р(С2)=8/24, Р(D1)=8/24, P(D2)=6/24.
Таким образом, получаем
ФОРМУЛА ПОЛНОЙ ВЕРОЯТНОСТИ
Пусть А – некоторое событие, которое может появиться совместно с одним из ряда попарно несовместных событий Н1, Н2,…,Нn образующих полную группу ( ). Будем называть события Н гипотезами.
Теорема 2.4. Вероятность события А, которое может произойти вместе с одной из гипотез Н1, Н2,…,Нn, равна сумме парных произведений вероятностей этих гипотез на соответствующие им условные вероятности события А:
Эта формула называется формулой полной вероятности.
Пример 2.17.Первый станок производит 25%, второй – 35%, третий – 40% всех изделий. Брак в их продукции составляет соответственно 5%, 4% и 2%. Найти вероятность того, что взятое наугад изделие окажется бракованным.
Решение. Введем гипотезы:
Н1={взятое изделие изготовлено на первом станке},
Н2={взятое изделие изготовлено на втором станке},
Н3={взятое изделие изготовлено на третьем станке}.
События Н1, Н2и Н3 несовместные, образуют полную группу, и событие А ={взятое изделие – брак} происходит вместе с одним из них, следовательно, они действительно могут быть взяты в качестве гипотез для события А. Согласно формуле полной вероятности
По условию задачи
Р(Н1)= 0.25, Р(Н2)=0.35, Р(Н3)=0.40, =0.05,
=0.04, =0.02,
следовательно, Р(А)= 0.25 • 0.05 + 0.35 • 0.04 + 0.40 • 0.02 = 0.0345.
Замечание. Вероятности характеризуют возможность осуществления некоторых условий , а возможность появления А при этих условиях.
ФОРМУЛА БАЙЕСА
Пусть событие А может произойти совместно с одной из гипотез Н1, Н2,…, Нn . Если до проведения опыта были известны вероятности гипотез , а в результате опыта произошло событие А, то условные вероятности гипотез вычисляются по формуле Байеса:
Пример 2.18. Первый станок производит 20%, а второй 80% всех деталей. Брак в их производстве составляет соответственно 4% и 2%. Взятая наугад деталь оказалась бракованной. Найти вероятность того, что эта деталь изготовлена на первом станке.
Решение. Введем две гипотезы для события А={взятая деталь оказалась бракованной}:
Н1={взятая деталь изготовлена на первом станке},
Н2={взятая деталь изготовлена на втором станке}.
Из условия задачи известно: Р(Н1)= 0.2, Р(Н2)=0.8, =0.04, =0.02.. По формуле Байеса находим
Замечание. Формула Байеса указывает путь использования новых экспериментальных данных для коррекции априорных (доопытных) вероятностных представлений об исследуемом объекте.
2.10. ПОСЛЕДОВАТЕЛЬНОСТИ ИСПЫТАНИЙ.
ФОРМУЛА БЕРНУЛЛИ
Пусть производится ряд испытаний, в каждом из которых с определенной вероятностью р может произойти событие А. Если вероятность события А в каждом испытании не зависит от исходов предыдущих испытаний, то такие испытания называют независимыми относительно события А. Если при этом вероятность события А в каждом испытании одна и та же, то последовательность испытаний называют схемой Бернулли. Вероятность того, что в п испытаниях по схеме Бернулли событие А произойдет т раз в любой последовательности, вычисляется по формуле Бернулли:
где
Значение m = m0 появлений события А в п испытаниях, при котором вероятность принимает наибольшее значение, называется наивероятнейшим числом успехов и определяется из неравенств:
np – q £ m0£np + p.
Разность граничных значений в этом двойном неравенстве равна 1. Если np + p не является целым числом, то наивероятнейшее число одно и равно m0 . Если np + p – целое число, то имеется два наивероятнейших числа m0 : np – q и np + p.
Пример 2.19. Вероятность попадания в цель при одном выстреле равна 0.6. Найти вероятность двух попаданий при трех выстрелах.
Решение. Имеем дело с тремя независимыми испытаниями, в каждом из которых с вероятностью p=0.6 может произойти событие А={попадание в цель}. Вероятность двух попаданий (в любой последовательности) при трех выстрелах находим по формуле Бернулли:
Пример 2.20. Испытывается 15 одинаковых изделий. Вероятность того, что изделие выдержит испытание, равна 0.9. Найти наивероятнейшее число изделий, выдержавших испытание.
Решение. По условию имеем: Подставим эти данные в неравенства для m0:
15×0.9–0.1 £ m0<15×0.9+ 0.9 => 13.4 < m0 < 14.4.
Отсюда следует, что m0=14.
Рекомендуемые страницы:
lektsia.com
14 . Вероятность произведения событий
Самая большая ценность формулы (13.1) состоит в том, что из нее можно получить формулу для вероятности произведения событий: Р(А·В) = Р(В)ּР(А/В). Эта формула говорит о том, что вероятность произведения двух событий равна вероятности второго события умножить на условную вероятность первого события. Поскольку при составлении произведения событий не важно, какое из них поставить при умножении первым, а какое вторым (события А·В и В·А равны – оба они означают одно и то же событие, которое состоит в том, что оба события А и В произошли одновременно), тогда формулу можно записать и в таком виде (поменяв местами А и В): Р(А·В) = =Р(А)ּР(В/А). Сформулируем полученные формулы в виде теоремы.
Теорема (формула умножения вероятностей). Вероятность совместного появления двух событий равна произведению одного из них на условную вероятность другого:
Р(АВ) = Р(А) Р(В/А) или Р(АВ) = Р(В) Р(А/В). (14.1)
Сделаем важное пояснение. Если мы захотим по формулам (14.1) (например, по второй из них) вычислить вероятность произведения событий Р(А·В), то необходимо прежде вычислить условную вероятность Р(А/В), для которой есть определяющая ее формула (13.1). Но для вычисления по этой формуле нам снова необходимо знать вероятность Р(А·В). Получается замкнутый круг! На самом деле при решении конкретных задач, использующих формулу (14.1), условную вероятность Р(А/В) для нее вычисляют не по формуле (13.1), а используя такого же рода “разумные соображения”, по которым мы вычисляли условные вероятности в примере с кубиком в начале предыдущего параграфа еще до написания формулы (13.1), строго определяющей условную вероятность.
Замечание. Формула (14.1) может быть обобщена на случай трех
Р(А·В·С) = Р(А) Р(В/А) Р(С/А·В) (14.2)
и большего числа сомножителей:
Р(А1·А2·А3· ּּּ ·Аn) =
= Р(А1)Р(А2/А1)Р(А3/А1·А2) ּּּ Р(Аn/А1·А2· ּּּ ·Аn–1). (14.3)
Действительно, по формуле (14.1) имеем
Р(А·В·С) = Р( (А·В)С ) = Р(А·В) Р(С/А·В) = Р(А) Р(В/А) Р(С/А·В),
что дает (14.2). Формула (14.3) может быть получена по индукции (если Вам этого сильно захочется). Рассмотрим примеры.
Пример 1. Из обычной колоды (36 карт – только такие и будут рассматриваться здесь и далее) вынимаются по очереди 2 карты без возвращения. Какова вероятность, что первая из них бубновая, а вторая червовая?
Пусть событие А1– первой вынута бубновая карта, а А2– второй вынута червовая карта. Интересующее нас событие А состоит в том, что после вытягивания двух карт произошли оба этих события, а это означает, что А = А1·А2. По формуле (14.1) получаем Р(А) = =Р(А1·А2) = Р(А1) Р(А2/А1). Перед первым вытягиванием карты в колоде имеется 36 карт, из них 9 бубновых, а потому для события А1 вероятность Р(А1) = 9/36 = 1/4 (в этом рассуждении есть одна тонкая неточность, но на результате она не сказывается, а ее объяснение может только внести сумятицу в неопытную голову и принести больше вреда, чем пользы). Найдем Р(А2/А1) – вероятность того, что вторая карта червовая при условии, что первый раз вынули бубновую карту. Поскольку перед вторым вытягиванием в колоде осталось 35 карт, а червовых в ней как и ранее осталось 9 (т. к. первый раз вынута бубновая), то Р(А2/А1) = 9/35. Поэтому Р(А) = 1/4 ּ 9/35 = 9/140 = 0,0643. Попробуйте теперь самостоятельно найти вероятность того, что при таком вытягивании обе карты окажутся бубновыми. А если после первого раза карта возвращается в колоду (выбор с возвращением)?
Пример 2. Студент знает 20 из 25 вопросов зачета. Какова вероятность, что он сдаст зачет, если условием этого являются правильные ответы на 3 предложенных вопроса?
Введем события: А1 – отвечено на первый вопрос, А2 – отвечено на второй вопрос, А3 – отвечено на третий вопрос, А – зачет сдан (т. е. отвечено на все три вопроса). По определению произведения событий А = А1·А2·А3, поэтому по формуле (14.2) имеем Р(А) = =Р(А1·А2·А3) = Р(А1) Р(А2/А1) Р(А3/А1·А2). Поскольку первым вопросом может быть задан любой из 25, а студент знает 20 из них, то вероятность того, что он ответит на первый вопрос Р(А1) = 20/25 = 4/5. Какова вероятность Р(А2/А1), т.е. вероятность того, что он ответит на второй вопрос при условии, что он ответил на первый? Поскольку во второй раз ему вряд ли зададут тот же вопрос, на который он только что ответил (экзаменаторы не такие дураки), то из оставшихся 24 вопросов он знает только 19, а потому Р(А2/А1) = 19/24. Найдем вероятность Р(А3/ А1·А2), т. е. вероятность того, что студент правильно ответит на третий вопрос, при условии, что он правильно ответил на первые два. Понятно, что теперь ему могут задать любой из оставшихся 23 вопросов, а среди них осталось всего 18 из тех, на которые он сможет ответить. Поэтому вероятность того, что именно такой ему и зададут Р(А3/А1·А2) = 18/23. Итак, Р(А) = 4/5ּ19/24ּ18/23 = = 57/115 ≈ 0,496. Как видим, шансов сдать зачет, как говорится, 50 на 50.
Попробуем решить эту задачу (и получить, естественно, тот же ответ) прежними комбинаторными методами, используя не раз помогавшую нам аналогию с выбором шаров из корзины. Переформулируем эту задачу следующим образом. Имеется корзина с 25 шарами (т. к. всего есть 25 вопросов), из которых 20 шаров белых (это те 20 вопросов, которые студент знает). Из корзины случайно вынимается 3 шара (т. е. студенту задается 3 вопроса). Какова вероятность, что все вытянутые шары белые (т. е. все вопросы попались из тех, которые студент знает)? В такой постановке задача о шарах была нами решена в общем виде в § 9 и получена там формула (9.1) (взгляните на нее снова!). В нашей задаче количество белых шаров n = 20, количество черных m = 5, вынимается k = 3 шара, Какова вероятность, что среди них i = 3 белых. По формуле (9.1) получим
Р(Аi)
= 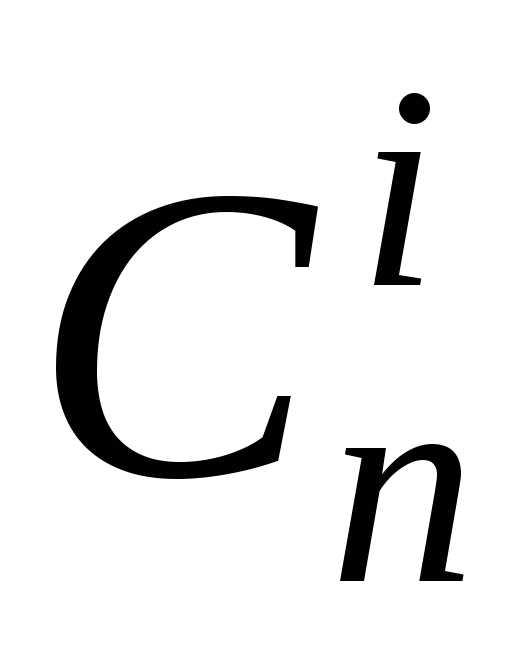
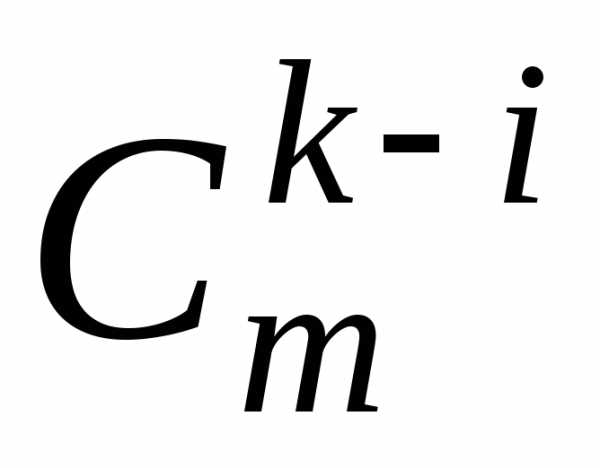 /
/ 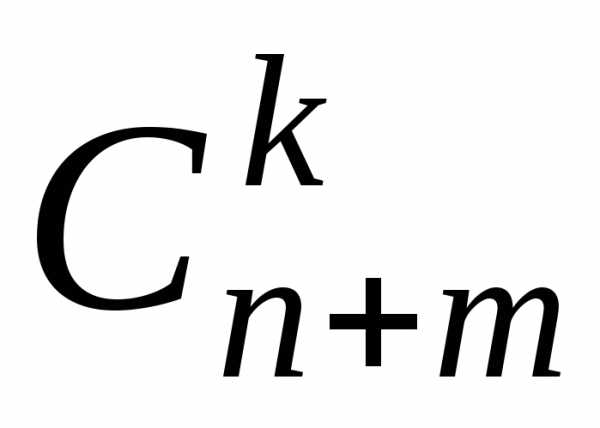 =
= 
 /
/  =
57/115 ≈ 0,496 .
=
57/115 ≈ 0,496 .
Получен тот же ответ.
Как мы видели в § 13, вероятность некоторого события А при условии, что произошло событие В (т. е. условная вероятность Р(А/В)), может отличаться от изначальной (безусловной) вероятности этого события Р(А). В этом случае шансы события А зависят от того, произошло событие В или нет, а потому мы можем говорить о зависимости события А от события В. Однако бывает так, что условная и безусловная вероятности совпадают.
studfiles.net

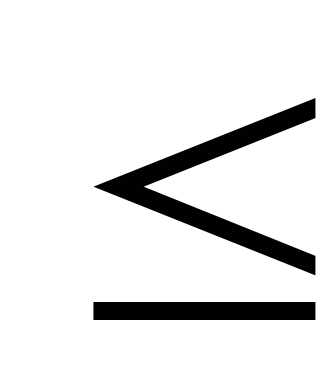 р(А)
р(А)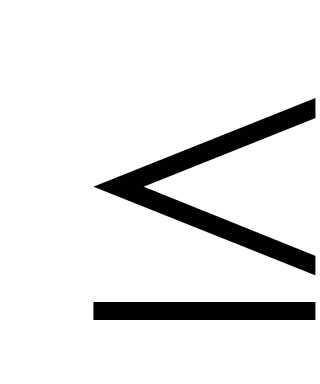 1.
1.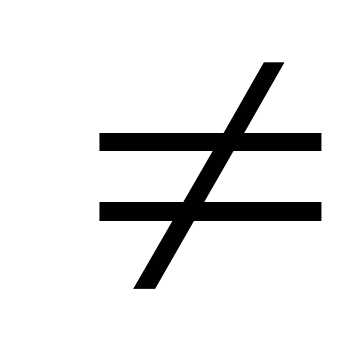 j,
тор(А1 + А2 +…+ An)
= p(A1)
+ p(A2)
+…+ p(An).
j,
тор(А1 + А2 +…+ An)
= p(A1)
+ p(A2)
+…+ p(An).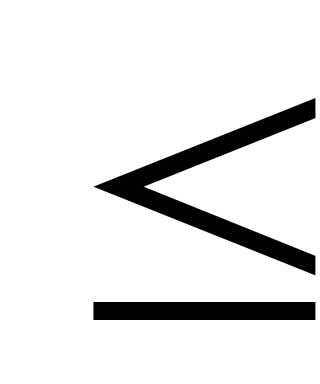 р(А)
р(А)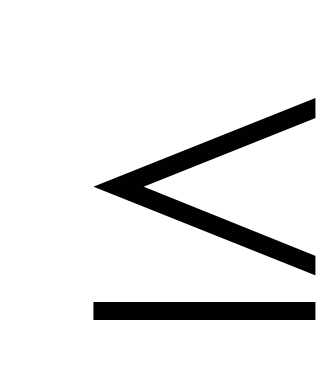 1.
1. j,
тор(А1 + А2 +…+ An)
= p(A1)
+ p(A2)
+…+ p(An).
j,
тор(А1 + А2 +…+ An)
= p(A1)
+ p(A2)
+…+ p(An).