Теорема вероятности суммы совместных событий. —
Теорема. Вероятность суммы двух совместных событий равна сумме вероятностей этих событий без вероятности их произведения, т.е.
р(А+В) = р(А) + р(В) – р(А∙В) . (1.11)
Доказательство. Действительно, представим событие А + В , состоящее в наступлении хотя бы одного из двух событий А и В, в виде суммы трёх несовместных событий:
А+В = А∙+∙В+А∙В.
Тогда по теореме сложения: р(А+В) = р(А∙) + р(∙В) + р(А∙В).
Учитывая, что А = А∙+А∙В, р(А) = р(А∙) + р(А∙В), получим р(А∙) = р(А) – – р(А∙В). Аналогично, В = ∙ В + А∙В, р(∙В) = р(В) – р(А∙В). Подставляя выражения для р(А∙) и р(∙В) в выражение для р(
p(А + В) = p(А) – p(А∙В) + p(В) – p(А∙В) + p(А∙В) = p(А) + p(В) – p(А∙В). Чт.и.д.
Расчленение суммы двух зависимых событий поясняется на рисунке ниже.
А+В = А∙ + ∙ В + А∙В.
Замечание. Для суммы трёх и более совместных событий формула вероятности суммы р(А1 + А2 + … + Аn) является очень громоздкой, поэтому при расчёте вероятности такой совокупности переходят к противоположному событию :
= = ∙ ∙ … ∙
Тогда
р(А1 + А2 + … + Аn) = 1– р() или р(А1 + А2 + … + Аn) = 1– р(А1 ∙ А2 ∙ А3 … Аn ),
т.е. вероятность суммы нескольких совместных событий А1, А2, … , Аn равна разности между единицей и вероятностью произведения противоположных событий , , … , . Если события А1, А2, … , Аn – независимые, то
р(А1 + А2 + … + Аn) = 1 – р( ) ∙ р()∙ … ∙ р(). ( 1.12 )
В частном случае, когда вероятности независимых событий одинаковы, то вместо формулы (1.12) имеет место формула
р(А1 +А2 +… +Аn) = 1 – ( 1 – р )n . (1.13)
einsteins.ru
Формула вероятности суммы совместных событий (теорема сложения вероятностей)
Пусть мы имеем два совместных события АиВ. Преобразуем их сумму в сумму несовместных событий (см. диаграмму Венна).
Подставляя второе выражение в первое, получим
. (2.10)
Пример. По мишени один раз стреляют два стрелка. Вероятность попадания первого стрелка в мишеньр1 = 0,7, второго –р2 = 0,8. Какова вероятность того, что кто-нибудь из них попадет в мишень?
А = А1 + А2, где А попадание в мишень;
А1 – попал первый стрелок;
А2– попал второй стрелок.
Р(А) = Р(А1 + А2) = Р(А1) + Р(А2 ) – Р(А1А2)=
= Р(А1) + Р(А2) – Р(А1 )Р(А2)=
= 0.7 + 0,8 – 0,7· 0,8 = 0,94.
Получим вероятность суммы трех совместных событий.
Получена формула
Р(А + В + С) = Р(А) + Р(В) + Р(С) – Р(АВ) – Р(АС) – Р(ВС) + Р(АВС) (2.11)
Обобщая полученный результат на сумму nсовместных событий, получим формулу
(2.12)
Формула полной вероятности
Пусть требуется
определить вероятность события А,
которое может произойти в сочетании с
одним из событийН1, Н2,…,
Н n,
образующих полную группу несовместных
событий (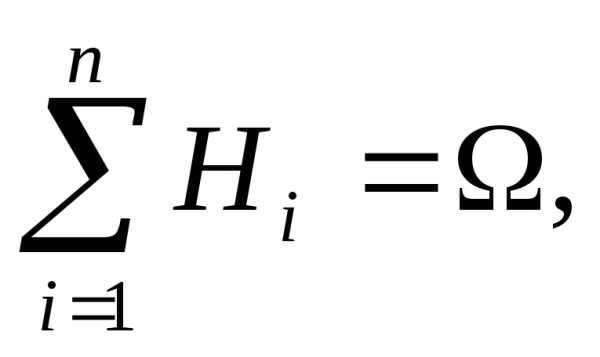
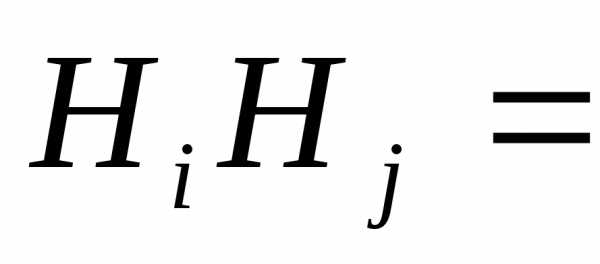 Ø,
Ø,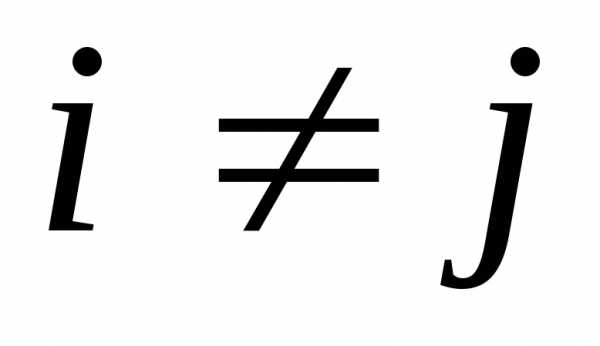
Н1 Н2 Н3
АН1 АН2 АН3
АНn-2 АНn-1 АНn
Hn-2 Hn-1 Hn
В соответствии со свойством 3) вероятности и теоремой умножения вероятностей
(2.13)
Пример. Изn экзаменационных билетов студент знаетm («хорошие билеты»). Что лучше: брать на экзамене билет первым или вторым?
Решение. Введем событие А – студент взял «хороший» билет.
Студент берет
билет первым. В этом случае 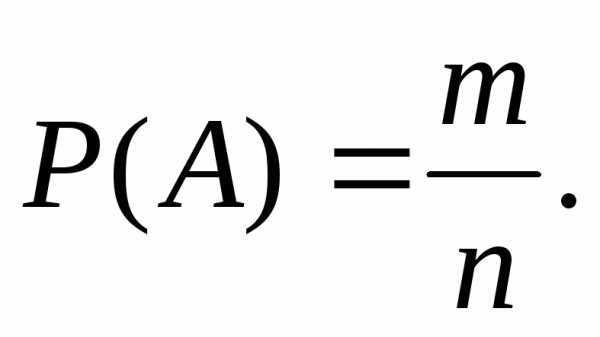
Студент берет билет вторым. Введем две гипотезы:
Н1 – первый студент взял «хороший»
билет,Н2 = .
.
Вывод: безразлично, брать билет первым или вторым.
Формула Байеса (теорема гипотез)
В соответствии с теоремой умножения вероятностей
Р(АНi) = Р(Hi)·Р(А/Hi) = Р(A)·Р(Hi/А).
В это равенство подставим значение Р(А),вычисленное по формуле полной вероятности (2.13) и найдемР(Hi/А).
Р(Нi/A) = (2.14)
Это следствие
из теоремы умножения и формулы полной
вероятности называется
В формуле полной вероятности определяется вероятность события до его появления, т.е. до того, как произведен опыт, в котором оно могло появиться. Вероятности гипотез Р(Нi), входящие в формулу полной вероятности, называютаприорными, т.е. «до опытными».
Пусть опыт произведен и его результат известен, т.е. мы знаем, произошло или не произошло событие А.Получившийся результат мог произойти при осуществлении какой-то одной гипотезыНi.Дополнительная информация об исходе опыта перераспределяет вероятности гипотез. Эти перераспределенные вероятности гипотезР(Нi/A)называютапостериорными, т.е. «после опытными».
ПримерВ одной из корзин 1 камешек и 4 кусочка хлеба, во второй – 4 камешка и 1 кусочек хлеба. Мышка наугад выбирает корзину, бежит к ней и вытаскивает кусочек хлеба — событие А (предполагается, что он затем вновь возвращается в корзину). Какова вероятность события А? Каковы вероятности того, что второй раз мышка побежит к первой корзине, ко второй корзине? Какова вероятность того, что она второй раз вытащит кусочек хлеба?
Рассмотрим гипотезы
Н1– мышка бежит к первой корзине,
Н2– мышка бежит ко второй корзине.
Р(Н1)=1/2 =Р(Н2)(априорные вероятности)
.
Р(Н1/A)
Р(Н2/A) (апостериорные вероятности).
При втором подходе
Мышка обучилась, второй раз она выберет первую корзину с большей вероятностью и добьется большего успеха.
Заметим, что это – один из основных принципов обучения кибернетических систем.
4. Теорема сложения вероятностей совместных
событий.
Теорема: Вероятность суммы двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления:
Р(А+В) = Р(А) + Р(В) — Р(АВ)
Для трех совместных событий имеем:
Р(А+В+С)=Р(А)+Р(В)+Р(С)-Р(АВ)-Р(АС)-Р(ВС)+Р(АВС).
Задача. Два стрелка стреляют по мишени. Вероятность попадания для первого стрелка равна 0,8; для второго — 0,9. Найти вероятность поражения цели, т.е. вероятность того, что хотя бы один из стрелков попадет в цель.
Решение: Событие А — попадание первого стрелка в мишень; событие В — попадание второго стрелка в мишень. События А и В совместны и независимы. По условию Р(А)=0,8; Р(В)=0,9. Находим вероятность события А+В: Р(А+В)=Р(А)+Р(В)-Р(АВ)= 0,8+0,9 — 0,80,9= 0,98
Иногда при решении задач для сложных событий со многими исходами используют «дерево вероятностей».
5. Формула полной вероятности. Формула Бейеса (Байеса).
Пусть некоторое событие А может произойти при условии, что появляется одно из несовместных событий (гипотез) В1,В2,…,Вn, образующих полную группу событий, а значит сумма их вероятностей равна единице.
Вероятность события А, которое может произойти лишь при появлении одного из несовместных событий В1,В2,…,Вn, образующих полную группу событий, равна сумме произведений вероятностей каждого из этих событий на соответствующую условную вероятность события А:
Это
равенство называют формулой
полной вероятности,
где —
условная вероятность
наступления события А при
наступлении гипотезы В
Пусть событие А, о котором шла речь в формуле полной вероятности, уже произошло. То, что событие А произошло, изменит вероятности гипотез В1,В2,…,Вn и условная вероятность гипотез РA (Вi) в предложении, что событие А произошло, определится по формуле Бейеса:
Замечание: иногда эту формулу называют формула Байеса.
Значение формулы Байеса состоит в том, что при наступлении события А, т.е. по мере получения новой информации, мы можем проверять и корректировать выдвинутые до испытания гипотезы. Такой подход, называемый байесовским, дает возможность корректировать управленческие решения в экономике, оценки неизвестных параметров распределения изучаемых признаков в статистическом анализе и т.д.
Задача. На сборку поступают детали из трех цехов в отношении 1:3:6. Количество бракованных деталей в продукции цехов соответственно равно 5 %, 2 %, 8 %. Определить вероятность того, что :
а) наудачу взятая деталь окажется бракованной;
б) оказавшаяся бракованной деталь изготовлена во втором цехе.
Решение: Обозначим через А — событие, что взятая наудачу деталь окажется бракованной. Так как на сборку поступают детали из трех цехов, то эта деталь может быть изготовлена либо 1 цехом (гипотеза В1), либо 2 (гипотеза В2), либо 3 (гипотеза В3). Следовательно, вероятность события А может быть найдена по формуле полной вероятности :
Вероятности гипотез В1,В2,…,Вn, определим по классической формуле Р=m/n, если в качестве n принять сумму всех частей, а в качестве m — соответствующее количество частей для данного цеха.
n=1+3+6=10 , m1=1 ; m2= 3 ; m3=6 ;
Находим условные вероятности:
.
а) Вычисляем вероятность события А.
Р (А)=0,1 0,05 + 0,3 0,02 + 0,6 0,08 = 0,059
б) Используя формулу Бейеса, получим:
Если по формуле Бейеса подсчитать условные вероятности всех гипотез, то они в сумме должны равняться единице.
studfiles.net
Формула вероятности суммы совместных событий (теорема сложения вероятностей)
В соответствии со свойством 3) классической вероятности вероятность суммы несовместных событий равна сумме вероятностей этих событий. А если события совместны?
Пусть мы имеем два совместных события АиВ. Преобразуем их сумму в сумму несовместных событий (см. диаграмму Венна).
Подставляя второе выражение в первое, получим
. (2.10)
Пример. По мишени один раз стреляют два стрелка. Вероятность попадания первого стрелка в мишеньр1 = 0,7, второго –р2 = 0,8. Какова вероятность того, что кто-нибудь из них попадет в мишень?
А = А1 + А2, где А попадание в мишень;
А1 – попал первый стрелок;
А2– попал второй стрелок.
Р(А) = Р(А1 + А2) = Р(А1) + Р(А2) – Р(А1А2)=
= Р(А1) + Р(А2) – Р(А1 )Р(А2)=
= 0.7 + 0,8 – 0,7· 0,8 = 0,94.
Получим вероятность суммы трех совместных событий.
Получена формула
Р(А + В + С) = Р(А) + Р(В) + Р(С) – Р(АВ) – Р(АС) – Р(ВС) + Р(АВС) (2.11)
Обобщая полученный результат на сумму nсовместных событий, получим формулу
(2.12)
Формула полной вероятности
Пусть требуется
определить вероятность события А,
которое может произойти в сочетании с
одним из событийН1, Н2,…,
Н n,
образующих полную группу несовместных
событий (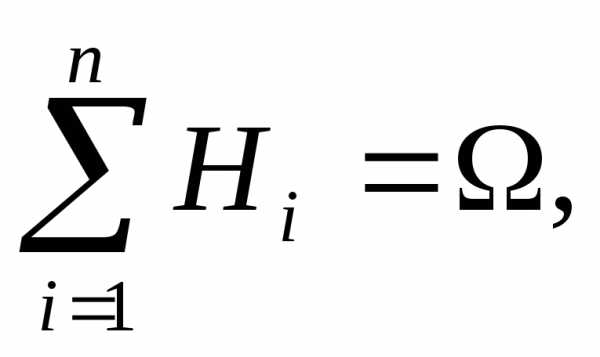
 Ø,
Ø,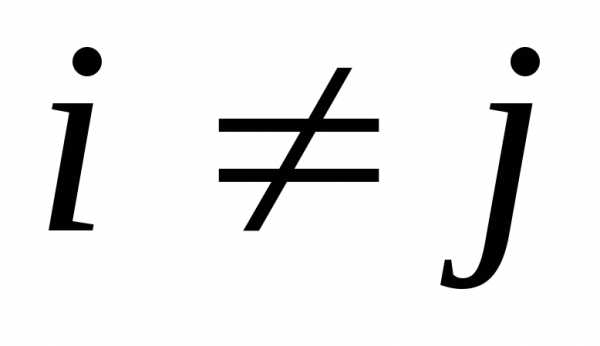 ).
Эти события будем называть гипотезами.
).
Эти события будем называть гипотезами.
Н1 Н2 Н3
АН1 АН2 АН3
АНn-2 АНn-1 АНn
Hn-2 Hn-1 Hn
В соответствии со свойством 3) вероятности и теоремой умножения вероятностей
(2.13)
Пример. Изn экзаменационных билетов студент знаетm («хорошие билеты»). Что лучше: брать на экзамене билет первым или вторым?
Решение. Введем событие А – студент взял «хороший» билет.
Студент берет
билет первым. В этом случае 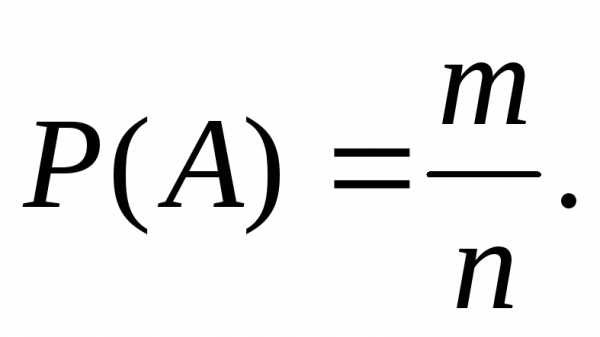
Студент берет билет вторым. Введем две гипотезы:
Н1 – первый студент взял «хороший»
билет,Н2 =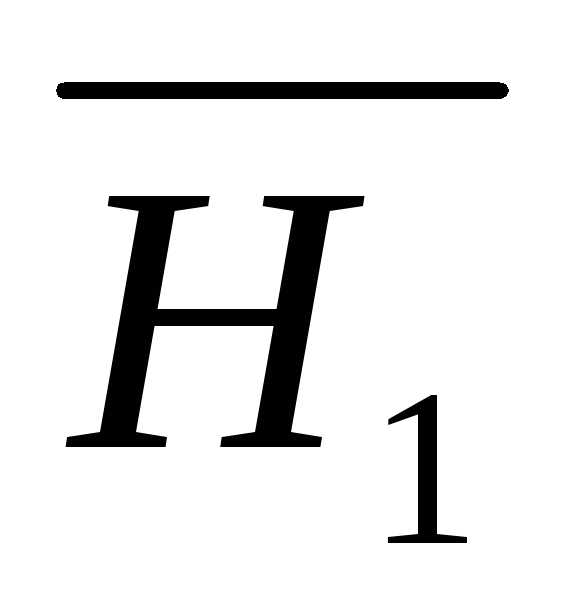 .
.
Вывод: безразлично, брать билет первым или вторым.
Формула Байеса (теорема гипотез)
В соответствии с теоремой умножения вероятностей
Р(АНi) = Р(Hi)·Р(А/Hi) = Р(A)·Р(Hi/А).
В это равенство подставим значение Р(А),вычисленное по формуле полной вероятности (2.13) и найдемР(Hi/А).
Р(Нi/A) = (2.14)
Это следствие из теоремы умножения и формулы полной вероятности называется формулой Байесаили теоремой гипотез.
В формуле полной вероятности определяется вероятность события до его появления, т.е. до того, как произведен опыт, в котором оно могло появиться. Вероятности гипотез Р(Нi), входящие в формулу полной вероятности, называютаприорными, т.е. «до опытными».
Пусть опыт произведен и его результат известен, т.е. мы знаем, произошло или не произошло событие А.Получившийся результат мог произойти при осуществлении какой-то одной гипотезыНi.Дополнительная информация об исходе опыта перераспределяет вероятности гипотез. Эти перераспределенные вероятности гипотезР(Нi/A)называютапостериорными, т.е. «после опытными».
ПримерВ одной из корзин 1 камешек и 4 кусочка хлеба, во второй – 4 камешка и 1 кусочек хлеба. Мышка наугад выбирает корзину, бежит к ней и вытаскивает кусочек хлеба — событие А (предполагается, что он затем вновь возвращается в корзину). Какова вероятность события А? Каковы вероятности того, что второй раз мышка побежит к первой корзине, ко второй корзине? Какова вероятность того, что она второй раз вытащит кусочек хлеба?
Рассмотрим гипотезы
Н1– мышка бежит к первой корзине,
Н2– мышка бежит ко второй корзине.
Р(Н1)=1/2 =Р(Н2)(априорные вероятности)
.
Р(Н1/A)
Р(Н2/A) (апостериорные вероятности).
При втором подходе
Мышка обучилась, второй раз она выберет первую корзину с большей вероятностью и добьется большего успеха.
Заметим, что это – один из основных принципов обучения кибернетических систем.
studfiles.net
3.2. Вероятность суммы событий
Пусть А и В – два несовместных события. Тогда в соответствии с третьей аксиомой для вероятности имеем
P(A+B) = P(A) + P(B). (3.6)
Это равенство известно как теорема сложения вероятностей несовместных событий. Для классической схемы это свойство не нужно постулировать, т.к. легко выводится из классического определения вероятности (доказать самостоятельно).
Пример 3.5. Из колоды в 36 карт наугад вынимают 3 карты. Найти вероятность того, что среди них окажется хотя бы один туз.
Решение. Введем следующие события: B={появление хотя одного туза}, A1={появление одного туза}, A2={появление двух тузов}, A3={появление трех тузов}. Очевидно, что B=A1+A2+A3. Поскольку события A1, A2 и A3.несовместны, то
P(B) = P(A1)+P(A2)+P(A3) =
Эту задачу можно решить иначе. Событие , противоположное событию В, состоит в том, что среди вынутых из колоды трех карт нет ни одного туза. ПосколькуP(B)+P()=1, то
P(B) = 1 – P() =
Пусть А и В – два произвольных события, т.е. они, в общем случае, совместны. Запишем события А+В и В в виде
A+B = A+Bи B = B+BA.
(объясните эти равенства, используя диаграммы Вьенна). Поскольку событие, стоящие в правых частях этих равенств, несовместны, то
P(A+B) = P(A) + P(B), P(B) = P(B)+P(BA).
Исключая P(B),получим
P(A+B) = P(A)+P(B)–P(AB). (3.7)
Это равенство известно как теорема сложения вероятностей совместных событий.
Полученная формула сложения вероятностей хорошо иллюстрируется при помощи диаграмм Вьенна. Здесь следует помнить, что вероятность события пропорциональна площади фигуры, которая соответствует данному событию. Событию А+В на рисунке соответствует вся заштрихованная фигура, площадь которой можно представить в виде суммы трех слагаемых SA+B=S1+S2+SAB, где S1 соответствует событию А–АВ, а S2 – событию В–АВ. Тогда, событию А будет соответствовать фигура с площадью SА= S1+SАВ, а событию В – SВ= S2+SАВ. В результате получим, что SА+В= SА+SВ–SАВ. Полученное равенство соответствует теореме сложения вероятностей.Теорему сложения вероятностей можно обобщить на случай произвольного числа слагаемых. В частности,
P(A+B+C) = P(A)+P(B)+P(C)–(AB)–P(AC)–P(BC)+P(ABC). (3.8)
Докажите данную формулу самостоятельно.
Пример 3.6. Два стрелка делают по одному выстрелу по мишени. Вероятность попадания для первого стрелка равна 0,8, для второго – 0,7. Какова вероятность поражения цели?
Решение. Пусть A1={первый стрелок попал по цели}, A2={второй стрелок попал по цели}. Мишень будет поражена (событие В), если произойдет событие А1+А2. Поскольку события А1 и А2 совместны, но независимы, то
P(А1+А2) = P(А1)+P(А2)–P(А1)P(А2) = 0,7+0,8–0,70,8 = 0,94.
Отметим, что событие В можно записать также в виде A1+A2+A1A2. Тогда получим
P(B) = P(A1)P()+P()P(A2)+P(A1)P(A2) = = 0,80,3+0,20,7+0,70,8 = 0,94.
Однако такой путь слишком длинный.
Пример 3.7. Дана электрическая цепь:
Вероятность выхода из строя элемента А равна 0,1, элемента В – 0,2, элемента С – 0,3. Найти вероятность разрыва цепи.
Решение. В данном случае разрыв цепи произойдет только тогда, когда выйдет из строя элемент А, или сразу два элемента В и С. При помощи алгебры событий разрыв цепи можно описать следующим образом: . Поскольку эти события совместные и независимые, то получим
= .
studfiles.net
Формула вероятности суммы совместных событий (теорема сложения вероятностей)
В соответствии со свойством 3) классической вероятности вероятность суммы несовместных событий равна сумме вероятностей этих событий. А если события совместны?
Пусть мы имеем два совместных события АиВ. Преобразуем их сумму в сумму несовместных событий (см. диаграмму Венна).
Подставляя второе выражение в первое, получим
. (2.10)
Пример. По мишени один раз стреляют два стрелка. Вероятность попадания первого стрелка в мишеньр1 = 0,7, второго –р2 = 0,8. Какова вероятность того, что кто-нибудь из них попадет в мишень?
А = А1 + А2, где А попадание в мишень;
А1 – попал первый стрелок;
А2– попал второй стрелок.
Р(А) = Р(А1 + А2) = Р(А1) + Р(А2) – Р(А1А2)=
= Р(А1) + Р(А2) – Р(А1 )Р(А2)=
= 0.7 + 0,8 – 0,7· 0,8 = 0,94.
Получим вероятность суммы трех совместных событий.
Получена формула
Р(А + В + С) = Р(А) + Р(В) + Р(С) – Р(АВ) – Р(АС) – Р(ВС) + Р(АВС) (2.11)
Обобщая полученный результат на сумму nсовместных событий, получим формулу
(2.12)
Формула полной вероятности
Пусть требуется
определить вероятность события А,
которое может произойти в сочетании с
одним из событийН1, Н2,…,
Н n,
образующих полную группу несовместных
событий (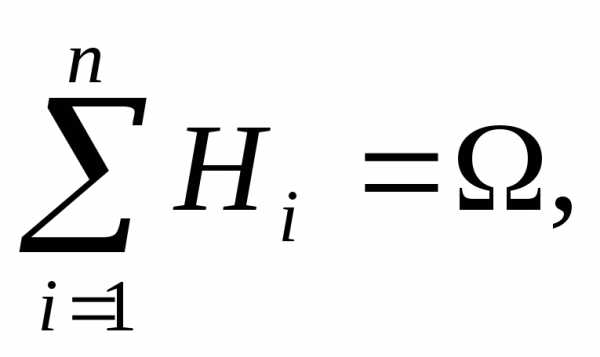
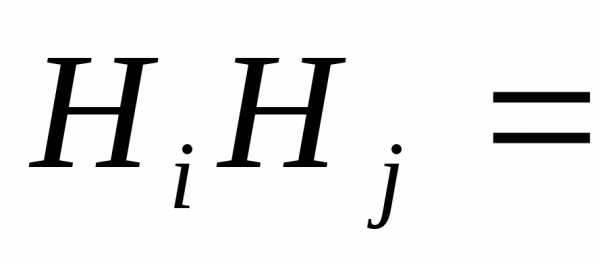 Ø,).
Эти события будем называть гипотезами.
Ø,).
Эти события будем называть гипотезами.
Н1 Н2 Н3
АН1 АН2 АН3
АНn-2 АНn-1 АНn
Hn-2 Hn-1 Hn
В соответствии со свойством 3) вероятности и теоремой умножения вероятностей
(2.13)
Пример. Изn экзаменационных билетов студент знаетm («хорошие билеты»). Что лучше: брать на экзамене билет первым или вторым?
Решение. Введем событие А – студент взял «хороший» билет.
Студент берет
билет первым. В этом случае 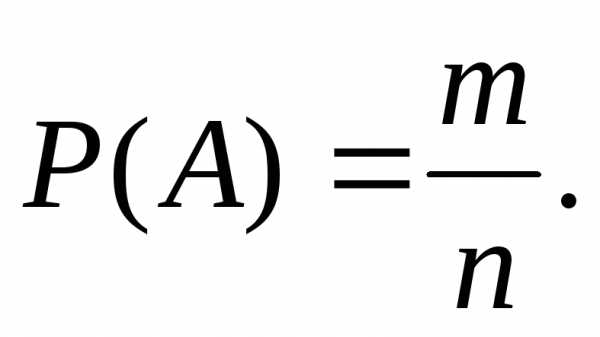
Студент берет билет вторым. Введем две гипотезы:
Н1 – первый студент взял «хороший»
билет,Н2 =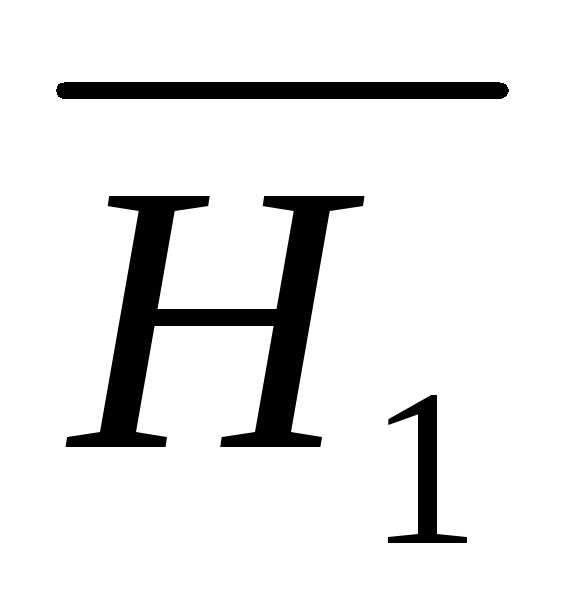 .
.
Вывод: безразлично, брать билет первым или вторым.
Формула Байеса (теорема гипотез)
В соответствии с теоремой умножения вероятностей
Р(АНi) = Р(Hi)·Р(А/Hi) = Р(A)·Р(Hi/А).
В это равенство подставим значение Р(А),вычисленное по формуле полной вероятности (2.13) и найдемР(Hi/А).
Р(Нi/A) = (2.14)
Это следствие из теоремы умножения и формулы полной вероятности называется формулой Байесаили теоремой гипотез.
В формуле полной вероятности определяется вероятность события до его появления, т.е. до того, как произведен опыт, в котором оно могло появиться. Вероятности гипотез Р(Нi), входящие в формулу полной вероятности, называютаприорными, т.е. «до опытными».
Пусть опыт произведен и его результат известен, т.е. мы знаем, произошло или не произошло событие А.Получившийся результат мог произойти при осуществлении какой-то одной гипотезыНi.Дополнительная информация об исходе опыта перераспределяет вероятности гипотез. Эти перераспределенные вероятности гипотезР(Нi/A)называютапостериорными, т.е. «после опытными».
ПримерВ одной из корзин 1 камешек и 4 кусочка хлеба, во второй – 4 камешка и 1 кусочек хлеба. Мышка наугад выбирает корзину, бежит к ней и вытаскивает кусочек хлеба — событие А (предполагается, что он затем вновь возвращается в корзину). Какова вероятность события А? Каковы вероятности того, что второй раз мышка побежит к первой корзине, ко второй корзине? Какова вероятность того, что она второй раз вытащит кусочек хлеба?
Рассмотрим гипотезы
Н1– мышка бежит к первой корзине,
Н2– мышка бежит ко второй корзине.
Р(Н1)=1/2 =Р(Н2)(априорные вероятности)
.
Р(Н1/A)
Р(Н2/A) (апостериорные вероятности).
При втором подходе
Мышка обучилась, второй раз она выберет первую корзину с большей вероятностью и добьется большего успеха.
Заметим, что это – один из основных принципов обучения кибернетических систем.
studfiles.net
Вероятность суммы совместных событий
Теорема 4.Вероятность суммы двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного наступления.
.
Примеры.
1. Вероятность поражения цели первым орудием равна 0,7, вторым – 0,8. Найти вероятность поражения цели при залпе из двух орудий.
Решение. Пусть событие А: {попадание из 1 орудия}, В: {попадание из 2 орудия}, С: {цель поражена}.
А и В – совместные события, так как они могут попасть два орудия сразу. По теореме 4, получим:
.
Ответ: 0,94
2.На 100 лотерейных билетов приходится 5 выигрышных. Какова вероятность выигрыша хотя бы по одному из двух приобретенных билетов?
Решение. Событие А: {выигрыш по первому билету}, В: {выигрыш по второму билету}, С: {выигрыш хотя бы по одному из двух билетов}. . События А и В – совместные и зависимые, поэтому:
Ответ: 0,098.
Вероятность появления хотя бы одного события
Теорема 5.Пусть события А1,А2,…,Аnпопарно независимы и известно, что . Тогда вероятность хотя бы одного из этих событий находится по формуле:
.
Примеры.
1.Для разрушения моста достаточно попадания одной бомбы. Найти вероятность того, что мост будет разрушен, если на него будут сброшены 4 бомбы с вероятностями попадания соответственно равными 0,3; 0,4; 0,6; 0,7.
Решение. Пусть события А: {мост будет разрушен}, : {попадет i-ая бомба} (i = 1,2,3,4). Тогда, по условию, , , , . По теореме 5 получаем:
Ответ: 0,9496.
2.Малое предприятие в текущем месяце изготовило 8 изделий первого сорта, 2 – второго сорта, 4 – третьего сорта. На ярмарку случайным образом отбирают 4 изделия. Найти вероятность того, что хотя бы одно изделие первого сорта попадёт на ярмарку.
Решение.Событие А: {хотя бы одно изделие первого сорта попадёт на ярмарку} является противоположным событию : {ни одного изделия первого сорта не попадёт на ярмарку}. Событие произойдёт, если произойдёт одно из следующих событий:
– В: {на ярмарку попадёт 4 изделия третьего сорта};
– С: {3 изделия третьего сорта и 1 изделие второго сорта};
– D: {2 изделия третьего сорта и 2 изделия второго сорта}.
Эти события несовместны, значит, по формуле сложения, получим:
,
,
.
.
.
Ответ: .
Задачи для самостоятельного решения
1.Магазин получил продукцию в ящиках с четырех заводов: четыре ящика с первого, пять – со второго, семь – с третьего и четыре – с четвертого завода. Случайным образом выбран ящик для продажи. Какова вероятность того, что это будет ящик с первого или с третьего завода? ( ).
2.Вероятность того, что стрелок при одном выстреле выбьет 10 очков, равна 0,1; вероятность выбить 9 очков – 0,3; вероятность выбить 8 или меньше очков – 0,6. Найти вероятность того, что при одном выстреле стрелок выбьет не меньше 9 очков. (0,4).
3.В партии из 10 деталей 8 – стандартных. Найти вероятность того, что среди наудачу извлеченных 2-х деталей есть хотя бы одна стандартная. ( ).
4.В ящике 10 деталей, среди которых 2 – нестандартные. Найти вероятность того, что в наудачу отобранных 6-ти деталях окажется не более одной нестандартной детали. ( ).
5.По статистическим данным ремонтной мастерской, в среднем на 20 остановок токарного станка приходится: 10 – для смены резца; 3 – из-за неисправности привода; 2 – из-за несвоевременной подачи заготовок. Остальные происходят по другим причинам. Найти вероятность остановки станка по другим причинам. (0,25).
6.Станок-автомат производит изделия трех сортов, при этом изделий первого и второго сорта 80 и 15 % соответственно. Чему равна вероятность того, что наудачу взятое изделие будет или высшего, или первого сорта? .
7.В группе 25 студентов. Из них отлично учатся 5 человек, хорошо – 12, удовлетворительно – 6 и слабо – 2. Преподаватель, не знакомый с группой, вызывает по списку одного из студентов. Определите вероятность того, что вызванный студент или отличник, или хорошист. .
8.Из ящика, содержащего 17 красных и 5 синих шаров, наудачу выбирают 4 шара. Найдите вероятность того, что среди выбранных шаров: а) не более одного синего; б) не менее трех красных; в) не менее половины красных. (а) 0,803; б) 0,79; в) 0,79).
9.Мастер обслуживает 5 станков. 20% времени он проводит у первого станка, 10 – у второго, 15 – у третьего, 25 – у четвертого, 30 % – у пятого. Найти вероятность того, что в наудачу выбранный момент времени он находится: 1) у первого или второго станка; 2) у второго или четвертого станка; 3) у первого, второго или четвертого; 4) у четвертого или пятого станка. (1) 0,3; 2) 0,35; 3) 0,55; 4) 0,55).
10.В магазин трикотажных изделий поступили носки, 60 % которых доставила первая фабрика, 25 % – вторая, а остальные – третья. Какова вероятность того, что купленные наугад носки изготовлены на первой или третьей фабрике? (0,75).
11.На тепловой станции работает 15 сменных инженеров, из которых 3 женщины. В смену занято 3 человека. Найти вероятность того, что в случайно выбранную смену работает не менее двух мужчин. (0,08).
12.В фирме 550 работников, 380 из них имеют высшее образование, а 412 — среднее специальное, 357 сотрудников имеют и высшее образование, и среднее специальное. Чему равна вероятность того, что случайно выбранный работник имеет или среднее, или среднее специальное или высшее образование, или то и другое? (0,791).
13.Какова вероятность того, что последняя цифра наугад набранного номера телефона окажется равной 5 или кратной 3? (0,4).
14.В урне 10 белых, 8 черных и 12 красных шаров. Наугад извлекают 2 шара. Какова вероятность того, что вынутые шары одного цвета, если известно, что не вынут красный шар? (0,1839).
15.В студенческой группе 28 человек. Среди них 20 студентов старше 19-ти лет и 8 студентов – старше 22-х лет. Разыгрывается билет на концерт. Чему равна вероятность того, что он достанется студенту старше 19-ти или старше 22-х лет? (0,7143).
16.Пусть вероятность того, что в магазине будет продана пара мужской обуви 44-го размера, равна 0,12; 45-го – 0,04; 46-го и более – 0,01. Найти вероятность того, что очередной будет продана пара мужской обуви не менее 44-го размера. (0,17).
17.Стрелок ведет огонь по цели, движущейся на него. Вероятность попадания при первом выстреле равна 0,4 и увеличивается на 0,1 при каждом последующем выстреле. Какова вероятность получить два попадания при трех независимых выстрелах? (0,38).
18.Среди 25-ти экзаменационных билетов – 5 «хороших». Два студента по очереди берут по одному билету. Найти вероятность того, что: а) первый студент взял «хороший» билет; б) второй студент взял «хороший» билет; в) оба студента взяли «хорошие» билеты. (а) б) в) ).
19.Вероятность того, что в течение дня произойдет поломка автомобиля, равна 0,03. Какова вероятность того, что в течение четырех дней подряд не произойдет ни одной поломки? (0,885).
20.В классе 12 мальчиков и 18 девочек. Нужно выбрать делегацию из двух человек. Какова вероятность того, что выбраны: а) два мальчика; б) две девочки; в) девочка и мальчик? (а) б) в) ).
21.Прибор состоит из двух элементов, работающих независимо. Вероятность выхода из строя первого элемента при включении прибора – 0,05; второго – 0,08. Найдите вероятность того, что при включении прибора: а) выйдет из строя только первый элемент; б) оба элемента выйдут из строя; в) откажет только второй элемент; г) оба элемента будут работать. (а) 0,046; б) 0,004; в) 0,076; г) 0,874).
22.В первой группе студентов два отличника, шесть – хорошистов, четыре – учатся удовлетворительно и три – плохо. Во второй соответственно – 5; 2; 5; 3. Из каждой группы наудачу выбирают по одному студенту. Найти вероятность того, что оба студента учатся плохо. (0,04).
23.Студент разыскивает нужную формулу в трех справочниках. Вероятности того, что формула содержится в первом, втором, третьем справочнике соответственно равны 0,6; 0,7; 0,8. Найти вероятности того, что формула содержится: а) только в одном справочнике; б) только в двух справочниках; в) во всех трех справочниках. (а) 0,188; б) 0,452; в) 0,336).
24.Брошено три игральные кости. Найти вероятность следующих событий: а) на каждой из выпавших граней появится число 5; б) на всех выпавших гранях появится одинаковое число очков. (а) 0,008; б) 0,048).
25.Всхожесть семян, предназначенных для посева, равна 98 %. Вероятность попадания семян в благоприятные для прорастания условия равна 0,96. Какой процент семян даст всходы? (94 %)
26.Из 12 билетов, пронумерованных числами от 1 до 12, наудачу один за другим выбирают два билета (без возвращения). Найти вероятность того, что: а) номер первого билета четный, а второго – нечетный; б) оба номера четные; в) оба номера нечетные; г) один из номеров четный, а другой – нечетный; д) хотя бы один номер четный; е) второй номер четный. (а) 0,27; б) 0,227; в) 0,227; г) 0,545; д) 0,772; е) 0,4997).
27.В урне 8 черных, 6 красных и 4 белых шара. Последовательно вынимаются три шара (без возвращения). Найти вероятность того, что первый шар окажется черным, второй – красным, третий – белым. (0,039).
28.На пяти одинаковых карточках написаны буквы: М, Л, Т, О, О. Какова вероятность того, что: а) извлекая все карточки по одной наудачу, получим в порядке их выхода слово «МОЛОТ»; б) извлекая три карточки по одной наугад, получим в порядке слово «ТОМ»? (а) 0,0166; б) 0,03).
29.Студент знает 20 из 25 вопросов. Найти вероятность того, что студент знает предложенные ему три вопроса. (0,4956).
30.Два станка работают независимо друг от друга. Вероятность бесперебойной работы первого станка в течение времени t равна 0,9; второго – 0,8. Определить вероятность бесперебойной работы хотя бы одного из двух станков в течение времени t. (0,98).
31.В автопробеге участвуют 3 автомобиля: первый может сойти с маршрута с вероятностью 0,15, второй с вероятностью 0,05, третий – 0,1. Определить вероятность того, что к финишу прибудут: а) только один автомобиль; б) два автомобиля; в) по крайней мере 2 автомобиля. ( а) 0,02525; б) 0,24725; в) 0,974).
32.В первой группе студентов 15 юношей и 10 девушек, во второй группе – 12 юношей и 13 девушек. Из каждой группы выбирают по одному студенту. Найти вероятность того, что среди выбранных студентов есть хотя бы одна девушка. (0,712).
33.В магазине имеются 10 женских и 6 мужских шуб. Для анализа качества случайным образом отобрали три шубы. Определить вероятность того, что среди отобранных шуб окажутся: а) только женские шубы; б) только мужские или только женские шубы. (а) б) ).
34.Вероятность того, что выпускник экономического факультета защитит диплом на «отлично» равна 0,6. Вероятность того, что он защитит диплом на «отлично» и получит приглашение на работу, равна 0,4. Определите вероятность того, что он получит приглашение на работу. (0,6667).
Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте:
zdamsam.ru
