Формулы объема, площади поверхности, объем конуса, объем цилиндра, объем шара
 Тела вращения, изучаемые в школе, — это цилиндр, конус и шар.
Тела вращения, изучаемые в школе, — это цилиндр, конус и шар.
Если в задаче на ЕГЭ по математике вам надо посчитать объем конуса или площадь сферы — считайте, что повезло.
Применяйте формулы объема и площади поверхности цилиндра, конуса и шара. Все они есть в нашей таблице. Учите наизусть. Отсюда начинается знание стереометрии.

Ты нашел то, что искал? Поделись с друзьями!
Смотрите также: Формулы объема и площади поверхности многогранников.
Кроме формул, в решении задач по стереометрии нужны также элементарная логика и пространственное воображение. Есть и свои небольшие секреты.
Например, такой важный факт:
Если все линейные размеры объемного тела увеличить в 2 раза, то площадь его поверхности увеличится в 4 раза, а объем — в 8 раз.
(ведь , ).
Вот такая задача. Как и остальные на нашем сайте, она взята из банка заданий ФИПИ.
1. Объем конуса равен . Через середину высоты параллельно основанию конуса проведено сечение, которое является основанием меньшего конуса с той же вершиной. Найдите объем меньшего конуса.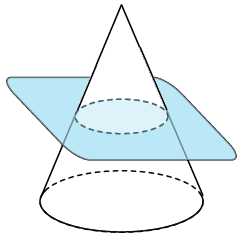
Очевидно, что объем меньшего конуса в раз меньше объема большого и равен двум.
Для решения некоторых задач полезны начальные знания стереометрии. Например — что такое правильная пирамида или прямая призма. Полезно помнить, что у цилиндра, конуса и шара есть еще общее название — тела вращения. Что сферой называется поверхность шара. А, например, фраза «образующая конуса наклонена к плоскости основания под углом 30 градусов предполагает, что вы знаете, что такое угол между прямой и плоскостью. Вам также может пригодиться теорема Пифагора и простые формулы площадей фигур.
Иногда неплохо нарисовать вид сверху. Или, как в этой задаче, — снизу.
2. Во сколько раз объем конуса, описанного около правильной четырехугольной пирамиды, больше объема конуса, вписанного в эту пирамиду?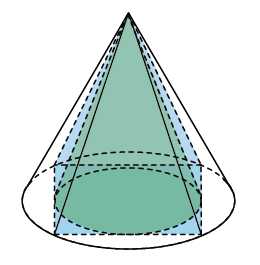
Всё просто — рисуем вид снизу. Видим, что радиус большего круга в раз больше, чем радиус меньшего. Высоты у обоих конусов одинаковы. Следовательно, объем большего конуса будет в раза больше.
Говорят, что хороший чертеж — это уже половина решения. Читайте о том, как строить чертежи в задачах по стереометрии.
Еще один важный момент. Помним, что в задачах части В вариантов ЕГЭ по математике ответ записывается в виде целого числа или конечной десятичной дроби. Поэтому никаких или у вас в ответе в части В быть не должно. Подставлять приближенное значение числа тоже не нужно! Оно обязательно должно сократиться!. Именно для этого в некоторых задачах задание формулируется, например, так: «Найдите площадь боковой поверхности цилиндра, деленную на ».
А где же еще применяются формулы объема и площади поверхности тел вращения? Конечно же, в задаче С2 (16). Мы тоже расскажем о ней.
Звоните нам: 8 (800) 775-06-82 (бесплатный звонок по России) +7 (495) 984-09-27 (бесплатный звонок по Москве)
Или нажмите на кнопку «Узнать больше», чтобы заполнить контактную форму. Мы обязательно Вам перезвоним.
ege-study.ru
Конус как геометрическая фигура
Конус (с греческого «konos») – сосновая шишка. Конус знаком людям с глубокой древности. В 1906 году была обнаружена книга «О методе», написанная Архимедом (287-212 гг. до н. э.), в этой книге дается решение задачи об объеме общей части пересекающихся цилиндров. Архимед говорит, что это открытие принадлежит древнегреческому философу Демокриту (470-380 гг. до н.э.), который с помощью данного принципа получил формулы для вычисления объема пирамиды и конуса.
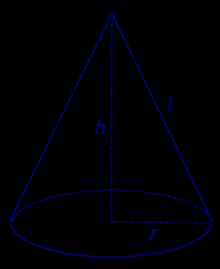
Конус (круговой конус) – тело, которое состоит из круга – основание конуса, точки, не принадлежащей плоскости этого круга, – вершины конуса и всех отрезков, соединяющих вершину конуса и точки окружности основания. Отрезки, которые соединяют вершину конуса с точками окружности основания, называются образующими конуса. Поверхность конуса состоит из основания и боковой поверхности.
Конус называется прямым, если прямая, которая соединяет вершину конуса с центром основания, перпендикулярна плоскости основания. Прямой круговой конус можно рассматривать как тело, полученное при вращении прямоугольного треугольника вокруг его катета как оси.
Высотой конуса называется перпендикуляр, опущенный из его вершины на плоскость основания. У прямого конуса основание высоты совпадает с центром основания. Осью прямого конуса называется прямая, содержащая его высоту.
Сечение конуса плоскостью, проходящей через образующую конуса и перпендикулярная осевому сечению, проведённому через эту образующую, называется касательной плоскостью конуса.
Плоскость, перпендикулярная оси конуса, пересекает конус по кругу, а боковую поверхность – по окружности с центром на оси конуса.
Плоскость, перпендикулярная оси конуса отсекает от него меньший конус. Оставшаяся часть называется усечённым конусом.
Объём конуса равен трети произведения высоты на площадь основания. Таким образом, все конусы, опирающиеся на данное основание и имеющие вершину, находящуюся на данной плоскости, параллельной основанию, имеют равный объём, поскольку их высоты равны.
Площадь боковой поверхности конуса можно найти по формуле:
Sбок = πRl,
где R – радиус основания, l – длина образующей.
Площадь полной поверхности конуса находится по формуле:
Sкон = πRl + πR2,
где R – радиус основания, l – длина образующей.
Объём кругового конуса равен
V = 1/3 πR2H,
где R – радиус основания, Н – высота конуса
Площадь боковой поверхности усеченного конуса можно найти по формуле:
Sбок = π(R + r)l,
где R – радиус нижнего основания, r – радиус верхнего основания, l – длина образующей.
Площадь полной поверхности усеченного конуса можно найти по формуле:
Sкон = πR2 + πr2 + π(R + r)l,
где R – радиус нижнего основания, r – радиус верхнего основания, l – длина образующей.
Объём усечённого конуса можно найти следующим образом:
V = 1/3 πH(R2 + Rr + r2),
где R – радиус нижнего основания, r – радиус верхнего основания, Н – высота конуса.
blog.tutoronline.ru
Подготовка школьников к ЕГЭ в учебном центре «Резольвента» (Справочник по математике — Стереометрия
Конусы
Рассмотрим произвольную плоскость α, точку S, не лежащую на плоскости α, и перпендикуляр SO, опущенный из точки S на плоскость α (точка O – основание перпендикуляра). Рассмотрим также произвольный круг с центром в точке O, лежащий на плоскости α.
Определение 1. Конусом называют фигуру, состоящую из всех отрезков, соединяющих точку S с точками указанного круга с центром в точке O, лежащего на плоскости α (рис. 1).
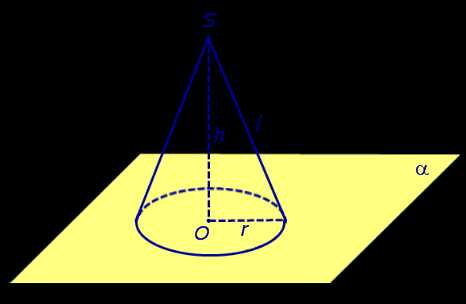
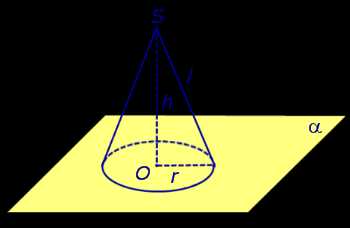
Рис.1
Определение 2.
Точку S называют вершиной конуса. | |
Отрезок SO называют осью конуса. | |
Расстояние от точки S до плоскостиРасстояние от точки S до плоскости α (длину отрезка SO) называют высотой конуса. | |
Круг с центром в точке O, лежащий на плоскости α, называют основанием конуса, радиус этого круга называют радиусом основания конуса, а саму плоскость α называют плоскостью основания конуса. | |
Отрезки, соединяющие точку S с точками окружности называют образующими конуса. | |
Совокупность всех образующих конуса составляет боковую поверхность конуса (коническую поверхность). | |
Полная поверхность конуса состоит из основания конуса и его боковой поверхности. |
Замечание 1. Отрезок SO часто называют высотой конуса.
Замечание 2. Все образующие конуса имеют одинаковую длину. У конуса с высотой h и радиусом основания r длина образующих равна
Усеченные конусы
Рассмотрим конус с вершиной S, осью SO, радиусом основания r и высотой h. Плоскость β, параллельная параллельная плоскости основания конуса и расположенная на расстоянии h1 от вершины расстоянии h1 от вершины S, пересекает конус по кругу радиуса r1 с центром в точке O1 (рис. 2).
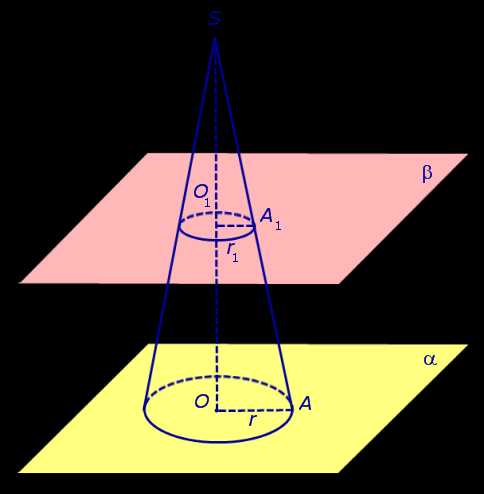
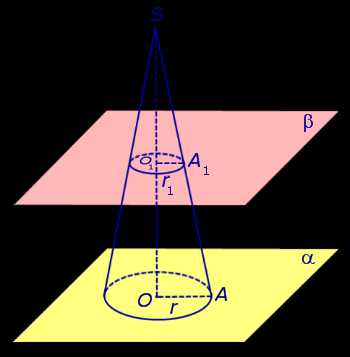
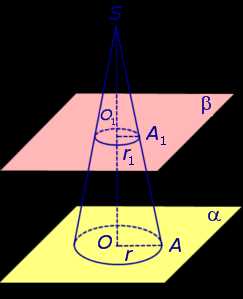
Рис.2
Из подобия прямоугольных треугольников SOA и SO1A1 можно выразить радиус r1 через известные величины r, h и h1:
Таким образом, плоскость β делит конус на две части: конус с осью SO1 и радиусом основания r1, а также вторую часть, называемую усеченным конусом (рис. 3).
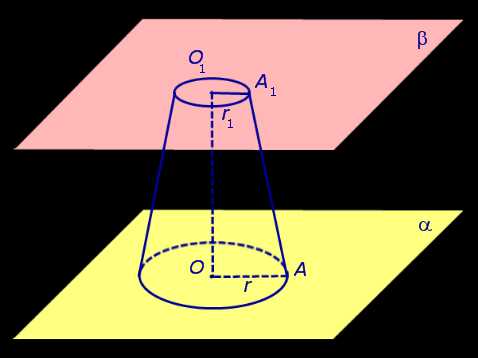
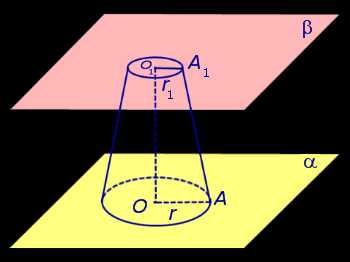
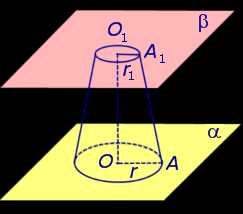
Рис.3
Усеченный конус ограничен двумя основаниями: кругом с центром в точке O радиуса r на плоскости α и кругом с центром в точке O1 радиуса r1 на плоскости β, а также боковой поверхностью усеченного конуса, которая представляет собой часть боковой поверхности исходного конуса, заключенную между плоскостями α и β. Полная поверхность усеченного конуса состоит из двух оснований усеченного конуса и его боковой поверхности. Часть каждой образующей исходного конуса, которая заключена между плоскостями α и β, называют образующей усеченного конуса. Например, на рисунке 3 одной из образующих усеченного конуса является отрезок AA1.
Высотой усеченного конуса называют расстояние между плоскостями расстояние между плоскостями оснований усеченного конуса. У усеченного конуса, изображенного на рисунке 2, высота равна h – h1.
Объем, площади боковой и полной поверхностей конуса и усеченного конуса
Введем следующие обозначения
Тогда справедливы следующие формулы для вычисления объема, площади боковой и полной поверхности конуса, а также формулы для вычисления объема, площади боковой и полной поверхности усеченного конуса.
| Фигура | Рисунок | Формулы для объема, площади боковой и полной поверхности |
| Конус | Sосн = πr2, Sбок= πrl, Sполн = πr2 + πrl, где | |
| Усеченный конус | Sбок= π (r + r1)l , где l – длина образующей усеченного конуса. |
| Конус |
 Формулы для объема, площади боковой и полной поверхности: Sосн = πr2, Sбок= πrl, Sполн = πr2 + πrl, где |
| Усеченный конус |
Формулы для объема, площади боковой и полной поверхности: , Sбок= π (r + r1)l , где l – длина образующей усеченного конуса. |
Замечание 3. Формула для вычисления объема конуса
может быть получена из формулы объема правильной n – угольной пирамиды
при помощи предельного перехода, когда число сторон правильной пирамиды n неограниченно возрастает. Однако доказательство этого факта выходит за рамки школьной программы.
Замечание 4. Формула для вычисления объема усеченного конуса
может быть получена из формулы объема правильной усеченной n – угольной пирамиды
при помощи предельного перехода, когда число сторон правильной усеченной пирамиды n неограниченно возрастает. Однако доказательство этого факта выходит за рамки школьной программы.
На нашем сайте можно также ознакомиться с разработанными преподавателями учебного центра «Резольвента» учебными материалами для подготовки к ЕГЭ по математике.
Приглашаем школьников (можно вместе с родителями) на бесплатное тестирование по математике, позволяющее выяснить, какие разделы математики и навыки в решении задач являются для ученика «проблемными». Запись по телефону (495) 509-28-10 |
Для школьников, желающих хорошо подготовиться и сдать ЕГЭ по математике или русскому языку на высокий балл, учебный центр «Резольвента» проводит
У нас также для школьников организованы
МОСКВА, СВАО, Учебный центр «РЕЗОЛЬВЕНТА»
www.resolventa.ru
все формулы конуса
Вы искали все формулы конуса? На нашем сайте вы можете получить ответ на любой математический вопрос. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и как найти образующую конуса, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение. Например, «все формулы конуса».
Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который может решить задачи, такие, как все формулы конуса,как найти образующую конуса,как найти образующую конуса формула,конус все формулы,конус формула,конус формулы,конус формулы все,образующая конуса формула,радиус конуса,радиус основания конуса формула,уравнение конуса,формула конуса,формула образующая конуса,формула образующей конуса,формула радиус основания конуса,формулы для конуса,формулы конуса,формулы конуса все. На этой странице вы найдёте калькулятор, который поможет решить любой вопрос, в том числе и все формулы конуса. Просто введите задачу в окошко и нажмите «решить» здесь или введите в окно ввода ниже свой запрос (например, как найти образующую конуса формула).
Где можно решить любую задачу по математике, а так же все формулы конуса Онлайн?
Решить задачу все формулы конуса вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на этой странице.
www.pocketteacher.ru
Конус. Формули, ознаки та властивості
Елементи конуса
Означення. Вершина конуса — це точка (K), з якої виходять промені.
Означення. Основа конуса — це площина, що утворена внаслідок перетину плоскої поверхні та всіх променів, що виходять з вершини конуса. У конуса можуть бути такі основи, як круг, еліпс, гіпербола та парабола.
Означення. Твірною конуса (L) називається будь-який відрізок, які сполучає вершину конуса з межею основи конуса. Твірна є відрізком променя, що виходить з вершини конуса.
Формула. Довжина твірної (L) прямого кругового конуса через радіус R та висоту H (через теорему Піфагора):L2 = R2 + H2
Означення. Напрямна конуса — це крива, яка описує контур основи конуса.
Означення. Бічна поверхня конуса — це сукупність усіх твірних конуса. Тобто, поверхня, яка утворюється рухом твірної по напрямній конуса.
Означення. Поверхня конуса складається з бічної поверхні та основи конуса.
Означення.Висота конуса (H) — це відрізок, який виходить з вершини конуса та перпендикулярний до його основи.
Означення. Вісь конуса (a) — це пряма, яка проходить через вершину конуса та центр основи конуса.
Означення.| C = | D | та C = | D — d |
| H | d |
Конусність характеризує гостроту конуса, тобто, кут нахилу твірної до основи конуса. Чим більша конусність, тим гостріший кут нахилу. Кут конуса α буде:
де R — радіус основи, а H — висота конуса.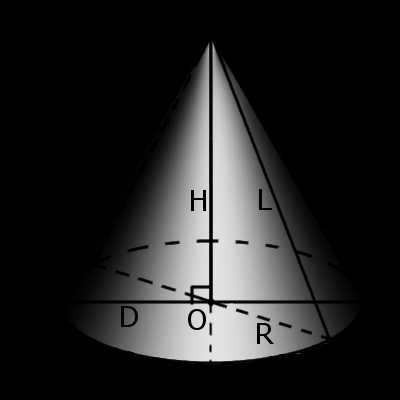 Означення. Осьовий переріз конуса — це переріз конуса площиною, яка проходить через вісь конуса. Такий переріз утворює рівнобедрений трикутник, у якого сторони утворені твірними, а основа трикутника — це діаметр основи конуса.
Означення. Осьовий переріз конуса — це переріз конуса площиною, яка проходить через вісь конуса. Такий переріз утворює рівнобедрений трикутник, у якого сторони утворені твірними, а основа трикутника — це діаметр основи конуса. 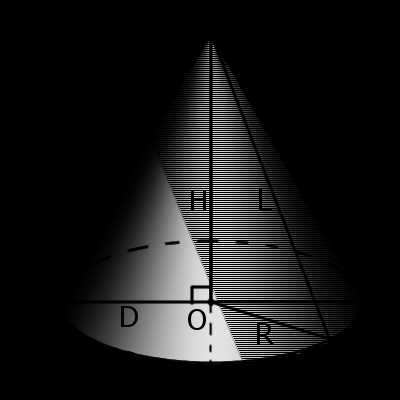 Означення. Дотична площина до конуса — це площина, яка проходить через твірну конуса і перепендикулярна до осьового перерізу конуса.
Означення. Дотична площина до конуса — це площина, яка проходить через твірну конуса і перепендикулярна до осьового перерізу конуса.Означення. Конус, що спирається на круг, еліпс, гіперболу чи параболу називається відповідно круговим, еліптичним, гіперболічним чи параболічним конусом (останні два мають нескінченний об’єм).
Основні властивості кругового конуса
1. Всі твірні прямого кругового конуса рівні між собою.
2. При обертанні прямокутного трикутника навколо свого катета на 360° утворюється прямий коловий конус.
3. При обертанні рівнобедреного трикутника навколо своєї вісі на 180° утворюється прямий коловий конус.
4. В місці перетину конуса площиною, яка паралельна основі конуса, утворюється коло. (див. Зрізаний конус)
5. Якщо при перетині площина не паралельна основі конуса і не перетинається з основою, то в місці перетину утвориться еліпс (мал. 3).
6. Якщо площина перерізу проходить через основу, то в місці перетину утвориться парабола (мал. 4).
7. Якщо площина перерізу проходить через вершину, то в місці перетину утвориться рівнобедрений трикутник (див. Осьовий переріз).
8. Центр ваги будь-якого конуса знаходиться на одній четвертій висоти від центра основи.
Будь-які нецензурні коментарі будуть видалені, а їх автори занесені в чорний список!
ua.onlinemschool.com
Объём конуса. Калькулятор объёма конуса онлайн
Объем конуса равен одной трети произведения площади основания на высоту
Конус — тело, полученное объединением всех лучей, исходящих из одной точки (вершины конуса) и проходящих через плоскую поверхность.
Круглый конус может быть получен вращением прямоугольного треугольника вокруг одного из его катетов, поэтому круглый конус называют также конусом вращения.
Связанные определения для конуса
Образующая конуса. Отрезок, соединяющий вершину и границу основания, называется образующей конуса.
Образующая поверхность конуса. Объединение образующих конуса называется образующей (или боковой) поверхностью конуса.
Коническая поверхность. Образующая поверхность конуса является конической поверхностью.
Высота конуса (H). Отрезок, опущенный перпендикулярно из вершины на плоскость основания (а также длина такого отрезка), называется высотой конуса.
Угол раствора конуса. Угол раствора конуса — угол между двумя противоположными образующими (угол при вершине конуса, внутри конуса).
Прямой конус. Если основание конуса имеет центр симметрии (например, является кругом или эллипсом) и ортогональная проекция вершины конуса на плоскость основания совпадает с этим центром, то конус называется прямым. При этом прямая, соединяющая вершину и центр основания, называется осью конуса.
Косой (наклонный) конус. Косой (наклонный) конус — конус, у которого ортогональная проекция вершины на основание не совпадает с его центром симметрии.
Круговой конус. Круговой конус — конус, основание которого является кругом.
Прямой круговой конус. Прямой круговой конус (часто его называют просто конусом) можно получить вращением прямоугольного треугольника вокруг прямой, содержащей катет (эта прямая представляет собой ось конуса).
Эллиптическим конус. Конус, опирающийся на эллипс, параболу или гиперболу, называют соответственно эллиптическим, параболическим и гиперболическим конусом (последние два имеют бесконечный объём).
Усечённый конус. Часть конуса, лежащая между основанием и плоскостью, параллельной основанию и находящейся между вершиной и основанием, называется усечённым конусом, или коническим слоем.
Объем прямого углового конуса
Конус — это геометрическое тело, которое образовано вращением прямоугольного треугольника около одного из его катетов.
Первый способ вычисления объема конуса
Объем конуса равен одной трети произведения площади основания на высоту
\[ \LARGE V = \frac{H}{3} S \]
где:
V — объем конуса
S — площадь основания конуса
H — высота конуса
Второй способ вычисления объема конуса
Объем конуса равен одной трети произведения числа пи (3.1415) на квадрат радиуса основания на высоту.
\[ \LARGE V = \frac{H}{3} \pi r^2 \]
где:
V — объем конуса
H — высота конуса
π — число пи (3.1415)
r — радиус конуса
Калькулятор объема конуса
Входные данные
Радиус r:
Высота h:
Количество знаков после запятой в результате вычислений
1234567
Результат
Объем усеченного конуса
Усеченный конус получится, если в конусе провести сечение, параллельное основанию. Тело ограниченное этим сечением, основанием и боковой поверхностью конуса называется усеченным конусом.
Первый способ вычисления объема усеченного конуса
Объем усеченного конуса вычисляется по формуле:
\[ \LARGE V = \frac{1}{3} \left( H\cdot S_2 + h \cdot s_1 \right) \]
где:
V — объем конуса
h — расстояния от плоскости верхнего основания до вершины
H — расстояния от плоскости нижнего основания до вершины
S1 — площадь верхнего (ближнего к вершине) основания
S2 — площадь нижнего основания
Второй способ вычисления объема усеченного конуса
Объем усеченного конуса вычисляется по формуле:
\[ \LARGE V = \frac{1}{3} \pi h \left( R^2 + R \cdot r + r^2 \right) \]
где:
V — объем конуса
h — высота конуса
R — радиус нижнего основания
r — радиус верхнего основания
Калькулятор объема усечённого конуса
Входные данные
Радиус нижнего основания усечённого конуса R:
Радиус верхнего основания усечённого конуса r:
Высота усечённого конуса h:
Количество знаков после запятой в результате вычислений
1234567
Результат
В вашем браузере отключен Javascript.Чтобы произвести расчеты, необходимо разрешить элементы ActiveX!
Не можешь написать работу сам?
Доверь её нашим специалистам
от 100 р.стоимость заказа
2 часамин. срок
Узнать стоимость
Поделитесь с другими:
Если материал понравился Вам и оказался для Вас полезным, поделитесь им со своими друзьями!
calcsbox.com
Все о Конусе
Муниципальное обще образовательное учреждение
Средняя общеобразовательная школа №54 с углубленным изучение предметов социально-гуманитарного цикла центрального района города Новосибирска
Экзаменационная работа по геометрии на тему:
I Конус
Конус – тело, полученное вращением прямоугольного треугольника вокруг прямой, содержащей катет.
S- вершина конуса, круг с центром О – основание конуса
Отрезок SA=L образующая.
Отрезок OA=R – радиус основания.
Отрезок BC=2R – диаметр основания.
Треугольник SBC-осевое сечение
Угол BSC – угол при вершине осевого сечения
Угол SBO – угол наклона образующей к плоскости основания
II Сечение конуса
1. Секущая плоскость проходит через ось конуса (осевое сечение – равнобедренный треугольник рис. 1) 2. Секущая плоскость проходит перпендикулярно к оси конуса— круг с центром О1 (рис. 2)
3.Сечение проходящее через верщину конуса – равнобедренныйтреугольник (рис. 3)
4.Параболическое и гиперболическое сечения. (рис. 4 )
В конус всегда можно вписать шар. Его центр на оси конуса
и совпадает с центром окружности, вписанно в треугольник,являющийся осевым сечением конуса.
Rш= Rк * tg a/2 = H*Rк/Rк+L
Около конуса всегда можно описать шар. Его центр лежит на
оси конуса и совпадает с центром окружности, описаной околотреугольника, являющегося осевым сечением конуса.
Rш = Rк / sinb ; R²ш= (H-Rш) ² + Rк²
Rш =L/2H ; (2Rш — Hк)Hк = Rк²
III Площадь поверхности конуса
1.
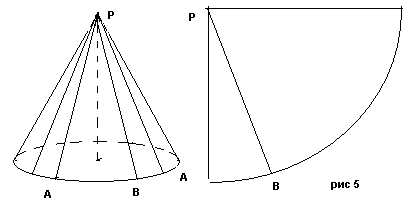 За плщадь боковой поверхности конуса принимается площадь её разертки. Выразим S бок через его опразующую L и радиус основания r. Площадь кругового сектора πL²/360*α . Выразим α через L и r . Длинна дуги ABA равна 2πr (длинна окружности основания конуса) 2πr = πL/180* α, откуда следует α=360r/L следовательно Sбок = πL²360r/360L=πrL
За плщадь боковой поверхности конуса принимается площадь её разертки. Выразим S бок через его опразующую L и радиус основания r. Площадь кругового сектора πL²/360*α . Выразим α через L и r . Длинна дуги ABA равна 2πr (длинна окружности основания конуса) 2πr = πL/180* α, откуда следует α=360r/L следовательно Sбок = πL²360r/360L=πrLSбок = πrL
2. Площадь полной поверхности конуса есть сумма площадей боковой поверхности и основания
Sпол=πrL(L+r)
IV Объем конуса
Объем конуса равен одной трети произведения площади основания на высоту.
Рассмотрим конус с обьемом V, радиусом R, высотой h и вершиной О. Введем ось Ох, чтобы она совпадала с осью конуса -ОН . Произвольное сечение конуса плоскостью, перпендикулярной к оси Ох, является круг с центром в точке Н1 пересечения этой плоскости с осью Ох. Обозначим Радиус этого круга через , ф площадь S(x) через,где х-абсцисса точки Н1. Из подобия треугольников ОН1А1 и ОНА следует,что ОН1/ОН=R1/R,или x/h=R1/R =>R1=XR/h. Так как S(x)= πR², то S(x)= πR²/h²* ²
Применяя основную формулу вычисления обьемов тел при а=0 и b=h получаемV Усеченный конус.
Усеченный конус – часть конуса, заключенная между основанием и паралельным основанию сечением конуса.
Круги с центрами О1 и О2 – верхнее и нижнее основания усеченного конуса, R r – радиусы оснований, АВ= L образующая ,α угол наклона образующе и плоскости нижнего основания.
Отрезок О1О2-высота. Трапеция АВСD – осевое сечение.
Н=L*sinαH²+(R-r) ²=L²
Около усеченного конуса всегда можно описать шар. Его центр лежит на прямой О1О2
CF=FD OF┴Cd=>
О – центр описанного шара R — радиус описанного шара, равный радиусу окружносит описанной около ΔACDВ усеченный конус можно вписать шар тогда и только тогда, когда образующая равна сумме радиусов оснований L=R+r => существует вписанный шар.
VI Площадь поверхности усеченного конуса
1. Пусть Р – вершина конуса, из которого получен усеченный конус, АА1-одна из образующих
Усеченного конуса О и О1 – центры оснований. Используя формулу Sбок для конуса получаем
S бок = πr*PA-πr1*PA1=πr(PA1+AA1)- πr1PA1, отсюда, учитывая, что AA1=L, находим
Sбок =πrL +π (r — r1)PA1
Выразим РА1 через L1, r и r1. Прямоугольные треугольники РО1А1 и РОА подобны, так как имеют общий острый угол Р и поэтому PA1/PA=r/r1 или PA1/PA1+L=r/R1. Получаем PA1=Lr1/R-r1. S=πrL + (π(r-r1)Lr1)/r-r1=πrL+πr1L=πL(r+r1)
Sбок =πL(r+r1)
2. Площадь полной поверхности усеченного конуса равна сумме площадей боковой поверхности усеченного конуса и оснований
Sполн = S1+S2+Sбок=πL(r+r1)+ πR²+πr²VII Обьем усеченного конуса
Обьем усеченного конуса V, высота которого равна h, а площади оснований S и S1 вычисляется по формуле
V=1/3h(S+S1+√S*S1)
комментарии
скачать за 50 рубпосле оплаты нажмите на кнопку «Вернуться на сайт» — документ будет скачан автоматически
Скачанный документ будет содержать только материал уже воспроизведенный на сайте.
mirznanii.com
